Abstract
The isothermal second-order elastic stiffness tensor and isotropic moduli of -1,3,5,7- tetranitro-1,3,5,7-tetrazoctane (-HMX) were calculated, using the P/n space group convention, from molecular dynamics for hydrostatic pressures ranging from to 30 GPa and temperatures ranging from 300 to 1100 K using a validated all-atom flexible-molecule force field. The elastic stiffness tensor components were calculated as derivatives of the Cauchy stress tensor components with respect to linear strain components. These derivatives were evaluated numerically by imposing small, prescribed finite strains on the equilibrated -HMX crystal at a given pressure and temperature and using the equilibrium stress tensors of the strained cells to obtain the derivatives of stress with respect to strain. For a fixed temperature, the elastic coefficients increase substantially with increasing pressure, whereas, for a fixed pressure, the elastic coefficients decrease as temperature increases, in accordance with physical expectations. Comparisons to previous experimental and computational results are provided where possible.
1. Introduction
The high explosive 1,3,5,7-tetranitro-1,3,5,7-tetrazoctane, also known as octahydro-1,3,5, 7-tetranitro-1,3,5,7-tetrazocine (HMX), is an important energetic material which is used in a number of high performance military explosive and propellant formulations [1]. Several polymorphs of HMX are known [2,3,4,5], among which -HMX is the thermodynamically stable form at standard ambient conditions. The elastic properties of -HMX are important for understanding processes such as shock propagation and the resulting hot-spot formation that ultimately lead to ignition and detonation initiation [6].
Accurate experimental determination of elastic coefficients in molecular high explosives is challenging due to the low crystal symmetries characteristic of many energetic substances. This is particularly evident in the case of -HMX for which there exist substantial differences among measured values of the elastic tensor obtained using different experimental techniques [7,8,9]. This disparity in the experimental data has been ascribed to sample purity and processing variations and is further complicated with questions about how to interpret or process the results [6,10].
In part because of these complexities, there are virtually no experimental data for elastic properties of -HMX under the high temperatures and pressures relevant to high-explosive initiation and detonation. In the absence of practical experimental alternatives, molecular dynamics (MD) provides a viable path to obtaining some of the needed information. In the present study, we use MD to obtain elastic coefficients of -HMX for wide intervals of temperature and hydrostatic pressure. The results obtained herein can be used both as a general reference and as input data for mesoscale continuum models of shock propagation and detonation initiation in -HMX [11,12].
2. Computational Details
2.1. Theoretical Background and System Preparation
The elastic stiffness tensor (written here in Voigt notation) was calculated using the direct method, which is based on the following equation
Here, denotes one of six linear strain components and is one of six Cauchy stress components. For monoclinic crystals such as -HMX, the stiffness tensor contains 13 independent non-zero elastic coefficients. We chose linear strain rather than the often-used Lagrange strain because it is work-conjugate to the Cauchy stress (see [13], Section 2.2.4) and it is the Cauchy stress that is typically provided as output from MD simulations. For the small strains used in this work we can expect any differences arising due to the use of linear rather than Lagrange strains to be negligible. The partial derivatives in Equation (1) were calculated numerically using finite differences. To achieve this, we adopted the following four-step procedure.
First, a crystal cell of -HMX (P/n space group setting) was equilibrated for 1 ns at the temperature and pressure of interest using the isobaric-isothermal (NPT) ensemble. Next, 100 ps of isochoric-isothermal (NVT) simulation was performed using the time-averaged crystal cell parameters from the NPT trajectory. In the third step, small linear strains were imposed on the NVT-equilibrated crystal cell and NVT simulations were performed on the strained cells. Finally, the elastic coefficients were obtained by numerical differentiation of the stresses with respect to strains.
We used a 3D-periodic crystal cell consisting of unit-cell replications along the a, b, and c crystallographic axes, respectively. This crystal cell contains 240 HMX molecules (6720 atoms). Similar cell sizes for both -HMX and other molecular-crystal high explosives are thought to be large enough to produce size-converged elastic properties of bulk crystals [6,14]. Temperatures , 500, 700, 900, and 1100 K and pressures , 5, 10, 20, and 30 GPa were considered. These pressures were chosen to match the interval considered in Ref. [15]. At atmospheric pressure ( GPa), -HMX is known to undergo a phase transition to the polymorph (orthorhombic) at approximately 420 K and the polymorph (hexagonal) when heated above approximately 450 K [16,17]; -HMX melts at about 550 K. However, with the force field that we use in this work the crystal remains stable (in the sense that melting does not occur) at 700 K and 1 atm for simulations lasting several nanoseconds. The crystal does melt at 1 atm somewhere between 700 and 900 K. Therefore, for the pressure atm, we only considered temperatures up to 700 K. However, we observed that -HMX remains crystalline all the way to 1100 K at 5 GPa and higher pressures. This is consistent with the MD-based melt curve of -HMX reported recently by Kroonblawd and Austin [18]. They predicted that at 5 GPa -HMX melts at 1320 K and the melting temperatures get higher for pressures above 5 GPa. Thus, overall, we studied 23 temperature and pressure combinations. We emphasize that the results below for the higher temperatures should be interpreted with caution because HMX may decompose on relevant time scales at those temperatures, at least at 1 atm [16].
When choosing the strain size, one has to consider the following arguments. On the one hand, one wants the strain to be sufficiently small to yield a reliable finite-difference approximation for the numerical evaluation of derivatives. On the other hand, if the strain is too small, the resulting change in stress is also small and, because there is a significant thermal noise in stress calculations, long simulation times are required to obtain converged results. Considering these factors, strains were chosen to be when , 2 or 3 and when , 5 or 6. The six strains required to obtain the full set of elastic coefficients were applied by distorting the simulation box in the following way. If the edge vectors of an unperturbed triclinic cell are given by vectors a, b, and c, then the geometry of the simulation box can, with no loss of generality, be described by the upper triangular matrix
by aligning a with the positive x axis and requiring b to lie in the plane [19]. Then, the upper triangular matrix h for the the strained cell is given by
where I is the 3 × 3 identity matrix and is one of the following six upper triangular matrices
Each of the strained simulation cells was equilibrated in the NVT ensemble for 100 ps after which the average stress tensor over a 4 ns NVT production trajectory was accumulated. For the pressure of 1 atm and temperatures of 300, 500, and 700 K the changes in stress tensor were small because the crystal is less rigid at the low pressure. Therefore, for those three cases, the trajectory was run for 12 ns to achieve better convergence of the elastic coefficients. Once the stress tensor components were obtained, the numerical derivatives in Equation (1) were evaluated as follows
where denotes the time-averaged strain tensor component for the equilibrated crystal cell with strain applied. Because of the elastic tensor symmetry, we expect when . This was indeed the case, with differences between and typically less than 0.2 GPa. For these off-diagonal elements of the elastic tensor, we report the average of and . As part of our analysis we also obtained the eight elastic coefficients that are expected to be zero in a monoclinic crystal. These coefficients were, indeed, very small, never exceeding 0.08 GPa in magnitude. Three examples of the full matrices obtained in this work are given in the Supplementary Materials. In addition to the elastic coefficients, the Voigt, Reuss, and Voigt–Reuss–Hill average bulk and shear moduli were calculated using standard expressions [8,20].
2.2. Force Field and MD Simulation Details
All MD simulations were performed using the LAMMPS package [19]. The nonreactive, fully flexible molecular potential for nitramines proposed by Smith and Bharadwaj [21] and further developed by Bedrov et al. [22] was employed in all of the MD simulations. This force field is well-validated and has been used in numerous previous studies of HMX [14,15,22,23,24,25,26]. In the current study, we modified the original nitramine force field used in [22] by adjusting the N-O and C-H harmonic bond stretching force constants to better reproduce the corresponding experimental vibrational mode frequencies (see [25] for more details). We further modified the original force field by adding a repulsive-core term to the non-bonded pair interaction potential. The reason for this latter modification is to eliminate the unphysical very-short-range attractive well in the Buckingham pair potential used in the original force field. The parameters of the repulsive core are chosen in such a way that the system dynamics is practically unaffected under the conditions we study in this paper. More details can be found in the supporting information for the work by Zhao et al. [27]. A cut-off distance of 11 Å was used for repulsion, dispersion, and short-range Coulomb interactions. Long-range electrostatic interactions were calculated using the PPPM method with the relative error in the forces set to . A time step of 0.2 fs was used. Sample input decks including all force-field parameters and the crystal cell description are included in the Supplementary Materials.
2.3. Error Analysis
The output of the MD simulations is the stress tensor as a function of time for a given thermodynamic state. Generally, the observations in this sequence are correlated for time differences that are shorter than some intrinsic correlation time. Therefore, we cannot use the sample standard deviation for error analysis. Instead, we need to apply a more sophisticated analysis applicable to correlated data. We follow the approach of Flyvbjerg and Petersen [28], which requires calculation of , the time correlation function for each dataset (stress component in our case), for data obtained after n time steps ( data points). The correlation function is given by
where angular brackets denote the time average. Then, the error s is calculated using the following equation:
Here, is a cut-off time chosen to be much larger than the correlation time of but much smaller than n. We observed typical relaxation times for of about 5000 time steps (1 ps) so we used = 50,000 (10 ps). The errors for the elastic coefficient values reported in the next section are reported as .
3. Results and Discussion
3.1. Isotherms and Isobars
Although the main topic of the present study is calculation of the elastic coefficients, we also obtain predictions of -HMX unit-cell volume as functions of pressure and temperature. Figure 1 shows unit-cell volume V as a function of pressure P at 300 K obtained in this work, along with MD results due to Sewell et al. [14] and experimental data of Yoo and Cynn [29], Gump and Peiris [30], and Olinger et al. [31]. The inset in Figure 1 shows the lower pressure part of the same data. The red curve in Figure 1 shows the third-order Birch–Murnaghan isotherm [32] fitted to our isotherm data. Fitting compression data to isotherms is subtle [10]. Here, we applied simple, unweighted fits of the Birch–Murnaghan fitting form to the experimental and simulated data. Our results are close to those of Sewell et al. This is not surprising as they used practically the same force field but with all covalent bonds fixed at constant values. The experimental results of Yoo and Cynn [29] are in overall qualitative agreement with our data but show slightly higher compressibility of the material. In addition, our simulations do not predict the subtle phase transition reported in [29] at approximately 27 GPa. Although we have limited results below 10 GPa, the changes in volume that we predict in this region are also similar to the volume changes observed experimentally in [30,31]. We provide in the Supplementary Materials the full set of lattice parameters and unit-cell volumes for all pressures and temperatures studied. The bulk moduli extracted from the experimental isotherm data are compared to our MD results in the next subsection.
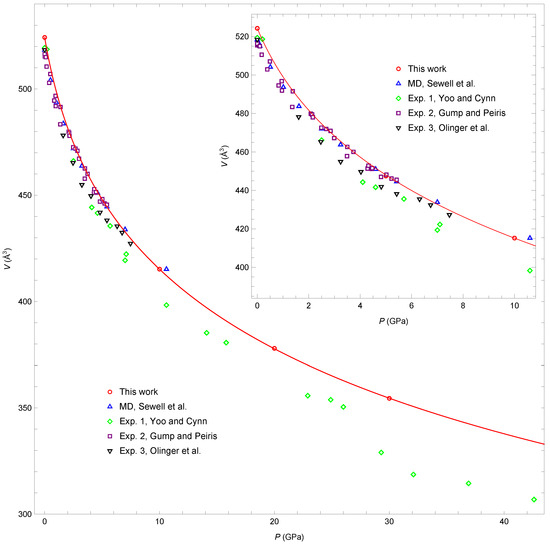
Figure 1.
Comparison of the 300 K isotherm from the present simulations to previous MD [14] and experimental results [29,30,31] at standard ambient temperature. V is the unit-cell volume. The red curve is the third-order Birch–Murnaghan isotherm [32] fitted to our data. The two fitting parameters of the Birch–Murnaghan equation are GPa and . The inset shows the lower pressure part of the same data.
Figure 2 shows the five isotherms calculated in the present study. The higher temperature isotherms lie above the lower temperature ones. This behavior is physically reasonable: unit-cell volume increases as the temperature increases due to thermal expansion. The relative volume increase with increasing temperature becomes less pronounced for higher pressures. Otherwise, the isotherms are all quite similar.
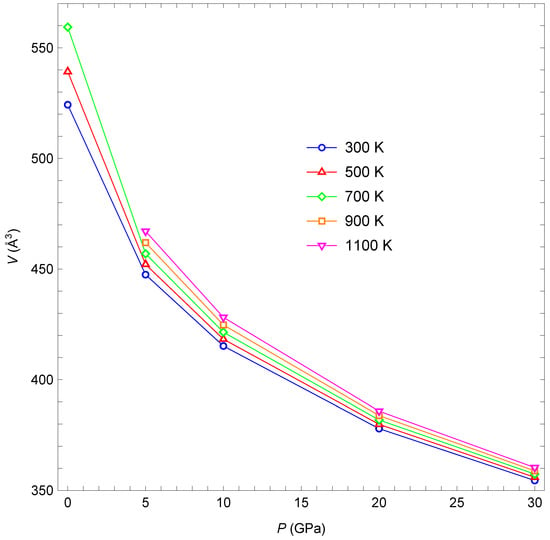
Figure 2.
Isotherms for 300, 500, 700, 900, and 1100 K. V is the unit-cell volume. Lines are added to guide the eye.
Figure 3a shows isobars for the five pressures considered. As expected, the unit-cell volume increases as the temperature increases. The volume increase becomes less pronounced for higher pressure isobars. While the increase in unit-cell volume with increasing temperature is not surprising, the changes in the unit-cell geometry exhibit some interesting features. Figure 3b–d show the lengths of the unit-cell vectors , , and , respectively. Surprisingly, at 5 and 10 GPa, the length of vector decreases as the temperature increases. Somewhat similarly, at 20 and 30 GPa, vector shows almost no change in length as the temperature changes. Similar counterintuitive behavior of some unit-cell lattice vectors was observed experimentally but not emphasized by Gump and Peiris [30]. Figure 3e shows how angle (the angle between vectors and ) changes with temperature and pressure. For a given temperature, decreases with increasing pressure (the crystal becomes “more orthorhombic”). For a given pressure, the angle increases slightly as the temperature increases.
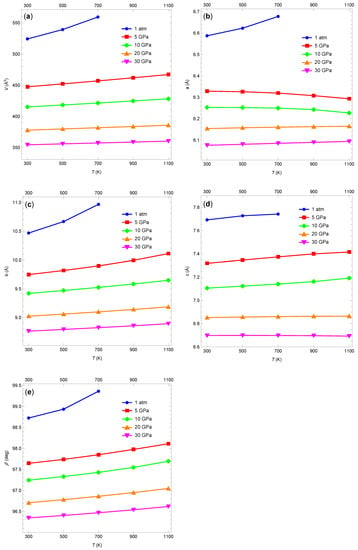
Figure 3.
(a) Unit-cell volume as a function of temperature for five different pressures. (b) The length of unit-cell vector as a function of temperature for five different pressures. (c) The same as (b) but for vector . (d) The same as (b) but for vector . (e) The same as (b) but for monoclinic lattice angle . Lines are added to guide the eye.
3.2. Elastic Coefficients
The calculated elastic coefficients and corresponding bulk and shear moduli on the 300, 500, 700, 900, and 1100 K isotherms are listed, respectively, in Table 1, Table 2, Table 3, Table 4 and Table 5. There are two clear trends in the results. For a given temperature, magnitudes of the elastic coefficients increase substantially with increasing pressure. For a given pressure, magnitudes of the elastic coefficients decrease with increasing temperature. Both trends are physically plausible: As the crystal is compressed at a given temperature, it is expected to become more stiff and so the elastic coefficients become larger. On the other hand, as the crystal temperature increases at constant pressure, the crystal expands and in doing so becomes less stiff.

Table 1.
Pressure-dependent elastic coefficients and isotropic moduli of -HMX at 300 K in units of GPa.

Table 2.
Pressure-dependent elastic coefficients and isotropic moduli of -HMX at 500 K in units of GPa.

Table 3.
Pressure-dependent elastic coefficients and isotropic moduli of -HMX at 700 K in units of GPa.

Table 4.
Pressure-dependent elastic coefficients and isotropic moduli of -HMX at 900 K in units of GPa.

Table 5.
Pressure-dependent elastic coefficients and isotropic moduli of -HMX at 1100 K in units of GPa.
As an example, Figure 4 shows the pressure dependence of the elastic coefficients and isotropic moduli at 300 K (using data from Table 1). As the pressure changes from 1 atm to 30 GPa, the magnitudes of the elastic coefficients increase by a minimum of about four-fold for to about 60-fold for . The Voigt–Reuss–Hill bulk and shear moduli increase by about 12- and 6-fold, respectively. Similar behavior is observed at the higher temperatures (not shown).
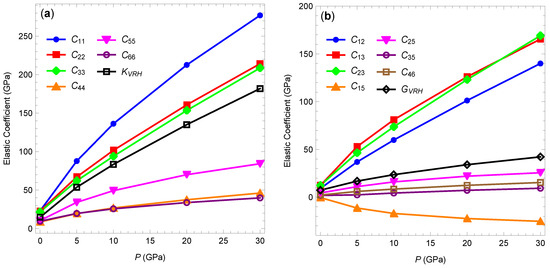
Figure 4.
Components of the elastic stiffness tensor at 300 K as functions of hydrostatic pressure. (a) Diagonal components and the Voigt–Reuss–Hill bulk modulus. (b) Off-diagonal components and the Voigt–Reuss–Hill shear modulus. Lines are added to guide the eye.
The typical temperature dependence of the elastic coefficients is shown in Figure 5, where the results for pressure 5 GPa are presented. This is the lowest pressure among the ones we studied for which -HMX remains crystalline for all temperatures on the time scale considered. The elastic coefficients decrease with increasing temperature approximately linearly. The rate at which the magnitude of the elastic coefficients decreases with temperature ranges from about 2.5 GPa per 100 K for to about 0.07 GPa per 100 K for . The Voigt–Reuss–Hill bulk and shear moduli decrease with temperature at a rate of about 1 GPa per 100 K and 0.5 GPa per 100 K, respectively. Qualitatively similar temperature dependence of the elastic coefficients was observed at higher pressures but the rates at which the coefficients decrease become smaller.
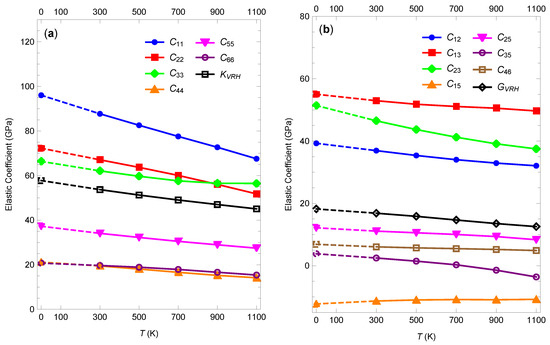
Figure 5.
Components of the elastic stiffness tensor at 5 GPa as functions of temperature. (a) Diagonal components and the Voigt–Reuss–Hill bulk modulus. (b) Off-diagonal components and the Voigt–Reuss–Hill shear modulus. Data for 0 K are taken from Mathew and Sewell [15], who used practically the same force field as here and a similar methodology. Lines are added to guide the eye.
In Figure 6, we compare our results at 1 atm and 300 K to the published theoretical and experimental data for the -HMX elastic coefficients variously at ambient conditions [7,8,9,14] or zero temperature and pressure [15,33,34]. Our results are, in general, consistent with the MD simulations of Sewell et al. [14] for which practically the same force field was used but with all the covalent bonds frozen. As a result of the bond constraints, most of the elastic coefficients in [14] are slightly larger in magnitude compared to our values. Similarly, there is an overall consistency with the MD/energy-minimization results of Mathew and Sewell [15], obtained with practically the same force field used here but at zero temperature. As can be expected, their values are higher than ours because the crystal stiffens with decreasing temperature, as discussed above. The DFT results in [33,34] give higher values of elastic coefficients and elastic moduli compared to ours. This is consistent with the fact that those results correspond to zero temperature and pressure. Note that, although DFT calculations have been used to calculate lattice parameters and unit-cell volumes on the cold curve (see, e.g., [33]), to our knowledge, they have not been used to predict elastic coefficients at elevated pressures. Moreover, incorporating temperature dependence into such calculations using, for example, the quasi-harmonic approximation would be unreliable due to the need to account for (anisotropic) thermal expansion across hundreds of kelvins; and explicit simulations analogous to, and on the scale of, those studied here are practically infeasible. There is a significant disparity among the various experimental results, which has been attributed to variations in measurement techniques and sample purity. Reanalysis [6,14] of the experimental data has shown that this can also result from lack of redundancy in the acoustic velocity measurements and sensitivity of the numerical solution to initial conditions of the multivariate minimization used to extract the elastic coefficients. For example, it is known that only five of the thirteen nonzero elastic coefficients reported in [7] were accurately determined [14]. Our results agree reasonably well with the experimental data of Sun et al. [9], with more pronounced differences compared to the other experimental data.
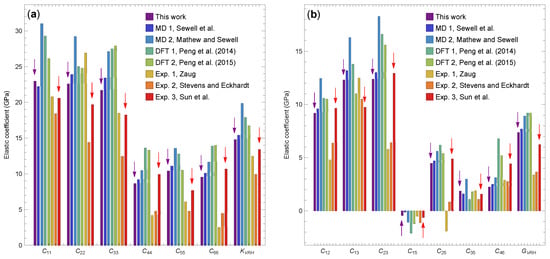
Figure 6.
Components of the elastic stiffness tensor at 1 atm and 300 K from the present study, previous theoretical results [14,15,33,34], and experimental values [7,8,9]. (a) Diagonal components and the Voigt–Reuss–Hill bulk modulus. (b) Off-diagonal components and the Voigt–Reuss–Hill shear modulus. The purple and red arrows emphasize the results from this work and the experimental results due to Sun et al. [9], respectively.
To the best of our knowledge, there are no experimental results for the elastic coefficients of -HMX at higher pressures even for 300 K. However, the room-temperature bulk modulus as a function of pressure can be obtained from fits of experimental isothermal compression data to an equation-of-state fitting form (here, the third-order Birch–Murnaghan equation of state), which yields pressure P as a function of volume V. The volume-dependent bulk modulus can be calculated as . The pressure-dependent bulk modulus can then be obtained by expressing the volume in as a function of pressure using the equation of state. This approach is less precise than obtaining K directly from the elastic tensor at a given T and P due both to the assumed form of the equation of state and the typically small numbers of data points on the isotherm available for fitting. Table 6 lists the room-temperature bulk moduli calculated at five pressures using this approach, for three sets of experimental data [29,30,31] and our calculated 300 K isotherm in Figure 1. The table also includes the pressure-dependent Voigt–Reuss–Hill bulk moduli reported in Table 1. Note that the results for [30,31] at 10, 20, and 30 GPa represent extrapolations of the fitting form to pressures higher than those for which the corresponding isotherms were measured.

Table 6.
Room-temperature bulk moduli of -HMX for five different pressures. Units are GPa.
In the table, one can see that the MD-based results (top two rows) are self-consistent in that the bulk moduli computed directly from the elastic tensor and via the equation-of-state fit are in good agreement for all pressures considered. Our values obtained by the direct approach are slightly larger than those obtained using the data from Yoo and Cynn [29] for all pressures except 30 GPa, for which they are about the same. Our estimates based on the data from [30,31] are less reliable because, as noted above, the pressure states considered in those references were below 8 GPa. Nevertheless, there is good agreement between our results and those obtained based on the work of Gump and Peiris [30] with the exception of P = 1 atm. Our values are lower than those obtained from the data in [31] for all pressures except atm, for which our value is larger.
4. Conclusions
We calculated second-order elastic coefficients of -HMX (P/n space group setting) as derivatives of the Cauchy stress with respect to the linear strain using MD with a well-validated fully flexible force field. A set of pressures between 1 atm ( GPa) and 30 GPa and temperatures between 300 and 1100 K was considered. The resulting elastic coefficients and bulk and shear elastic moduli are reported in tabular form. The following dominant trends are observed. For a given temperature, magnitudes of the elastic coefficients increase substantially with increasing pressure. For a given pressure, magnitudes of the elastic coefficients decrease with increasing temperature. The strong dependence of the elastic coefficients on pressure should be taken into account in mesoscale continuum modeling and simulations.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4352/10/12/1123/s1, Table S1: Equilibrium unit-cell volumes and lattice parameters for -HMX as functions of temperature and pressure. Table S2: Full 6 × 6 matrix of elastic coefficients of -HMX in units of GPa at 300 K and 1 atm ( GPa). The first column on the left and the top row are indices i and j. The matrix is very close to being symmetric. Sixteen coefficients are close to zero as expected for the monoclinic crystal. Table S3: Full 6 × 6 matrix of elastic coefficients of -HMX in units of GPa at 700 K and 1 atm ( GPa). The first column on the left and the top row are indices i and j. The matrix is very close to being symmetric. Sixteen coefficients are close to zero as expected for the monoclinic crystal. Table S4: Full 6 × 6 matrix of elastic coefficients of -HMX in units of GPa at 1100 K and 30 GPa. The first column on the left and the top row are indices i and j. The matrix is very close to being symmetric. Sixteen coefficients are close to zero as expected for the monoclinic crystal.
Author Contributions
Conceptualization, T.S. and A.P.; methodology, A.P. and T.S.; software, A.P.; validation, A.P. and T.S.; formal analysis, A.P.; investigation, A.P.; resources, T.S.; writing—original draft preparation, A.P.; writing—review and editing, A.P. and T.S.; visualization, A.P.; project administration, T.S.; and funding acquisition, T.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Air Force Office of Scientific Research grant number FA9550-19-1-0318.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HMX | 1,3,5,7-tetranitro-1,3,5,7-tetrazoctane |
| MD | Molecular Dynamics |
| NPT | isobaric-isothermal |
| NVT | isochoric-isothermal |
| DFT | density functional theory |
References
- Gibbs, T.; Popolato, A. LASL Explosive Property Data; University of California: Berkeley, CA, USA, 1980. [Google Scholar]
- Choi, C.S.; Boutin, H.P. A study of the crystal structure of β-cyclotetramethylene tetranitramine by neutron diffraction. Acta Crystallogr. B Struct. Cryst. Cryst. Chem. 1970, 26, 1235–1240. [Google Scholar] [CrossRef]
- Kohno, Y.; Maekawa, K.; Azuma, N.; Tsuchioka, T.; Hashizume, T.; Imamura, A. Ab initio calculations for a relationship between impact sensitivity and molecular structure in HMX polymorphs. Kogyo Kayako 1992, 53, 227–237. [Google Scholar]
- Cady, H.H.; Larson, A.C.; Cromer, D.T. The crystal structure of α-HMX and a refinement of the structure of β-HMX. Acta Crystallogr. 1963, 16, 617–623. [Google Scholar] [CrossRef]
- Cobbledick, R.E.; Small, R.W.H. The crystal structure of the δ-form of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (δ-HMX). Acta Crystallogr. B Struct. Cryst. Cryst. Chem. 1974, 30, 1918–1922. [Google Scholar] [CrossRef]
- Hooks, D.E.; Ramos, K.J.; Bolme, C.A.; Cawkwell, M.J. Elasticity of crystalline molecular explosives. Propellants Explos. Pyrotech. 2015, 40, 333–350. [Google Scholar] [CrossRef]
- Zaug, J.M. Elastic constants of β-HMX and Tantalum, equations of state of supercritical fluids and fluid mixtures and thermal transport determinations. In Proceedings of the Eleventh Detonation Symposium, Snowmass, CO, USA, 31 August–4 September 1998; p. 498. [Google Scholar]
- Stevens, L.L.; Eckhardt, C.J. The elastic constants and related properties of β-HMX determined by Brillouin scattering. J. Chem. Phys. 2005, 122, 174701. [Google Scholar] [CrossRef]
- Sun, B.; Winey, J.M.; Gupta, Y.M.; Hooks, D.E. Determination of second-order elastic constants of cyclotetramethylene tetranitramine (β-HMX) using impulsive stimulated thermal scattering. J. Appl. Phys. 2009, 106, 053505. [Google Scholar] [CrossRef]
- Menikoff, R.; Sewell, T.D. Fitting forms for isothermal data. High Press. Res. 2001, 21, 121–138. [Google Scholar] [CrossRef]
- Zaug, J.M.; Austin, R.A.; Armstrong, M.R.; Crowhurst, J.C.; Goldman, N.; Ferranti, L.; Saw, C.K.; Swan, R.A.; Gross, R.; Fried, L.E. Ultrafast dynamic response of single-crystal β-HMX (octahydro-1,3,5, 7-tetranitro-1,3,5,7-tetrazocine). J. Appl. Phys. 2018, 123, 205902. [Google Scholar] [CrossRef]
- Drouet, D.; Picart, D.; Bailly, P.; Bruneton, E. Plastic dissipation and hot-spot formation in HMX-based PBXs subjected to low velocity impact. Propellants Explos. Pyrotech. 2020, 45, 1–11. [Google Scholar] [CrossRef]
- Bower, A.F. Applied Mechanics of Solids; Taylor & Francis: Boca Raton, FL, USA, 2010; Available online: http://solidmechanics.org (accessed on 8 December 2020).
- Sewell, T.D.; Menikoff, R.; Bedrov, D.; Smith, G.D. A molecular dynamics simulation study of elastic properties of HMX. J. Chem. Phys. 2003, 119, 7417–7426. [Google Scholar] [CrossRef]
- Mathew, N.; Sewell, T. Pressure-dependent elastic coefficients of β-HMX from molecular simulations. Propellants Explos. Pyrotech. 2018, 43, 223–227. [Google Scholar] [CrossRef]
- Hall, P.G. Thermal decomposition and phase transitions in solid nitramines. Trans. Faraday Soc. 1971, 67, 556–562. [Google Scholar] [CrossRef]
- Myint, P.C.; Nichols, A.L. Thermodynamics of HMX polymorphs and HMX/RDX mixtures. Ind. Eng. Chem. Res. 2017, 56, 387–403. [Google Scholar] [CrossRef]
- Kroonblawd, M.P.; Austin, R.A. Sensitivity of pore collapse heating to the melting temperature and shear viscosity of HMX. Mech. Mater. 2021, 152, 103644. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. Available online: http://lammps.sandia.gov/ (accessed on 8 December 2020). [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Smith, G.D.; Bharadwaj, R.K. Quantum chemistry based force field for simulations of HMX. J. Phys. Chem. B 1999, 103, 3570–3575. [Google Scholar] [CrossRef]
- Bedrov, D.; Ayyagari, C.; Smith, G.D.; Sewell, T.D.; Menikoff, R.; Zaug, J.M. Molecular dynamics simulations of HMX crystal polymorphs using a flexible molecule force field. J. Comput. Aid. Mater. Des. 2001, 8, 77–85. [Google Scholar] [CrossRef]
- Bedrov, D.; Smith, G.D.; Sewell, T.D. Thermal conductivity of liquid octahydro-1,3,5,7-tetranitro-1,3, 5,7-tetrazocine (HMX) from molecular dynamics simulations. Chem. Phys. Lett. 2000, 324, 64–68. [Google Scholar] [CrossRef]
- Bedrov, D.; Smith, G.D.; Sewell, T.D. Temperature-dependent shear viscosity coefficient of octahydro-1,3, 5,7-tetranitro-1,3,5,7-tetrazocine (HMX): A molecular dynamics simulation study. J. Chem. Phys. 2000, 112, 7203–7208. [Google Scholar] [CrossRef]
- Kroonblawd, M.P.; Mathew, N.; Jiang, S.; Sewell, T.D. A generalized crystal-cutting method for modeling arbitrarily oriented crystals in 3D periodic simulation cells with applications to crystal-crystal interfaces. Comput. Phys. Commun. 2016, 207, 232–242. [Google Scholar] [CrossRef]
- Chitsazi, R.; Kroonblawd, M.P.; Pereverzev, A.; Sewell, T. A molecular dynamics simulation study of thermal conductivity anisotropy in β-octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (β-HMX). Modell. Simul. Mater. Sci. Eng. 2020, 28, 025008. [Google Scholar] [CrossRef]
- Zhao, P.; Lee, S.; Sewell, T.; Udaykumar, H.S. Tandem molecular dynamics and continuum studies of shock-induced pore collapse in TATB. Propellants Explos. Pyrotech. 2020, 45, 196–222. [Google Scholar] [CrossRef]
- Flyvbjerg, H.; Petersen, H.G. Error estimates on averages of correlated data. J. Chem. Phys. 1989, 91, 461–466. [Google Scholar] [CrossRef]
- Yoo, C.S.; Cynn, H. Equation of state, phase transition, decomposition of β-HMX (octahydro-1,3, 5,7-tetranitro-1,3,5,7-tetrazocine) at high pressures. J. Chem. Phys. 1999, 111, 10229–10235. [Google Scholar] [CrossRef]
- Gump, J.C.; Peiris, S.M. Isothermal equations of state of beta octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine at high temperatures. J. Appl. Phys. 2005, 97, 53513. [Google Scholar] [CrossRef]
- Olinger, B.; Roof, B.; Cady, H. The linear and volume compression of β-HMX and RDX to 9 GPa (90 kilobar). In Proceedings of the Symposium (International) on High Dynamic Pressures; Commissariat a l’Energie Atomique: Paris, France, 1978; pp. 3–8. [Google Scholar]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, G.; Liu, G.R.; De, S. Structures, mechanical properties, equations of state, and electronic properties of β-HMX under hydrostatic pressures: A DFT-D2 study. Phys. Chem. Chem. Phys. 2014, 16, 19972–19983. [Google Scholar] [CrossRef]
- Peng, Q.; Wang, G.; Liu, G.R.; Grimme, S.; De, S. Predicting elastic properties of β-HMX from first-principles calculations. J. Phys. Chem. B 2015, 119, 5896–5903. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).