Parity-Time Symmetry and Exceptional Points for Flexural-Gravity Waves in Buoyant Thin-Plates
Abstract
1. Introduction
2. Materials and Methods
2.1. Derivation of Flexural-Gravity Governing Equation
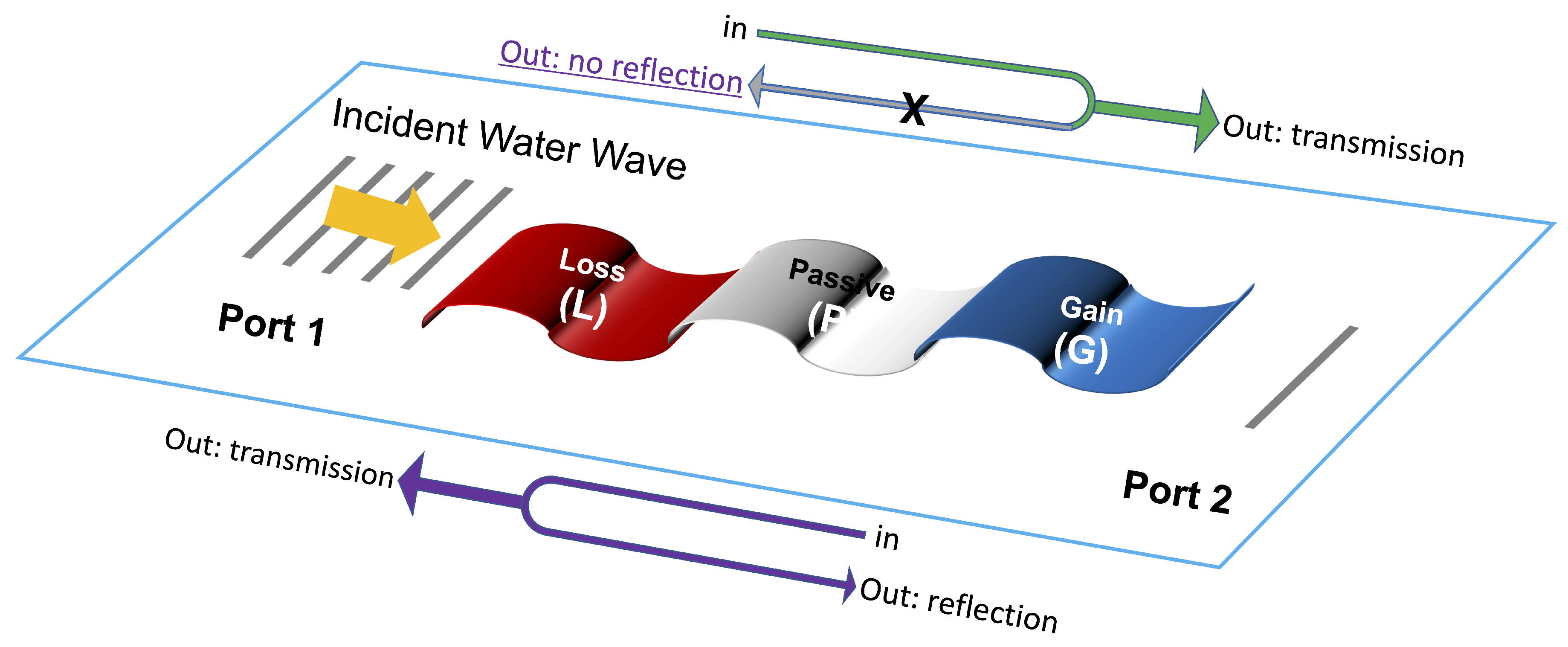
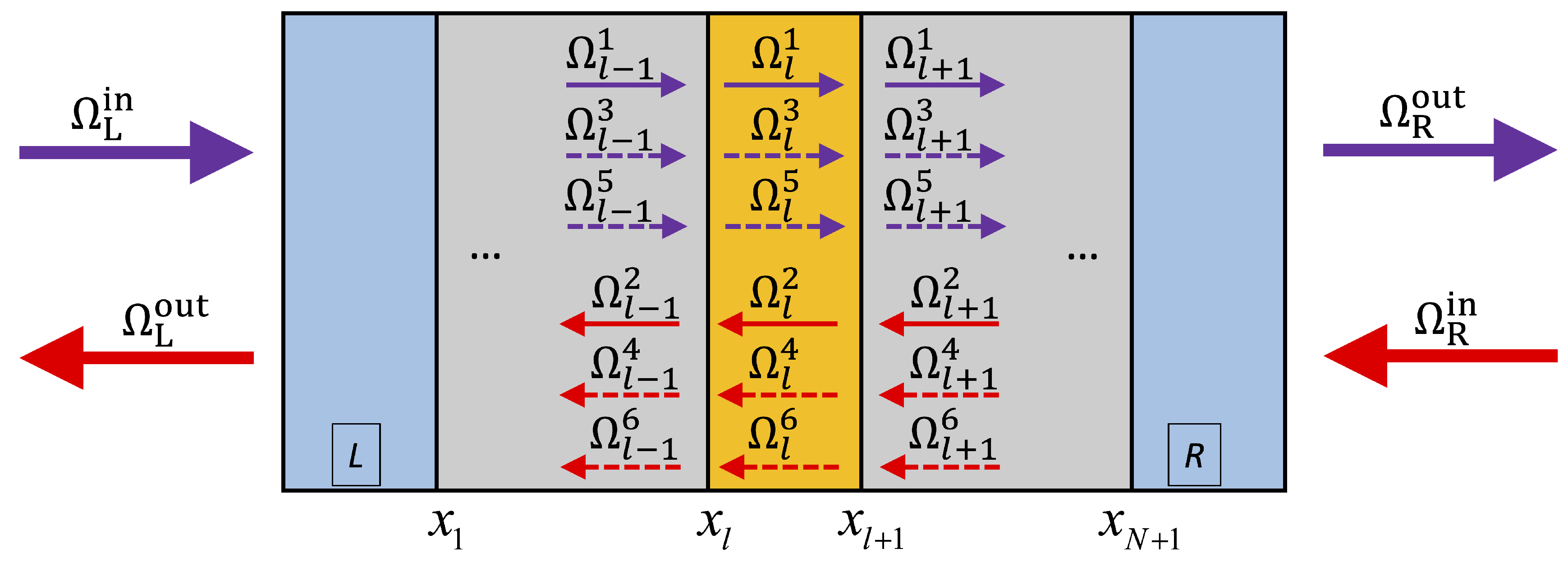
2.2. Transfer and Scattering Matrix Formalism for Flexural-Gravity Waves
2.2.1. Transfer Matrix Formalism
2.2.2. Scattering Matrix Formalism
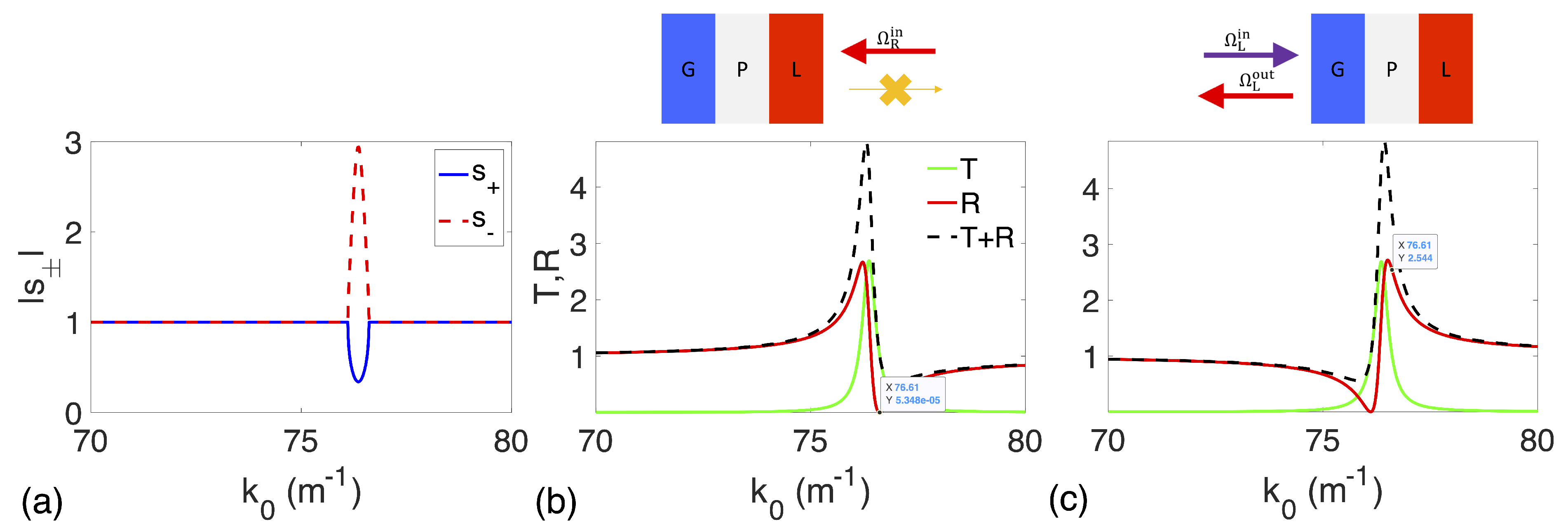
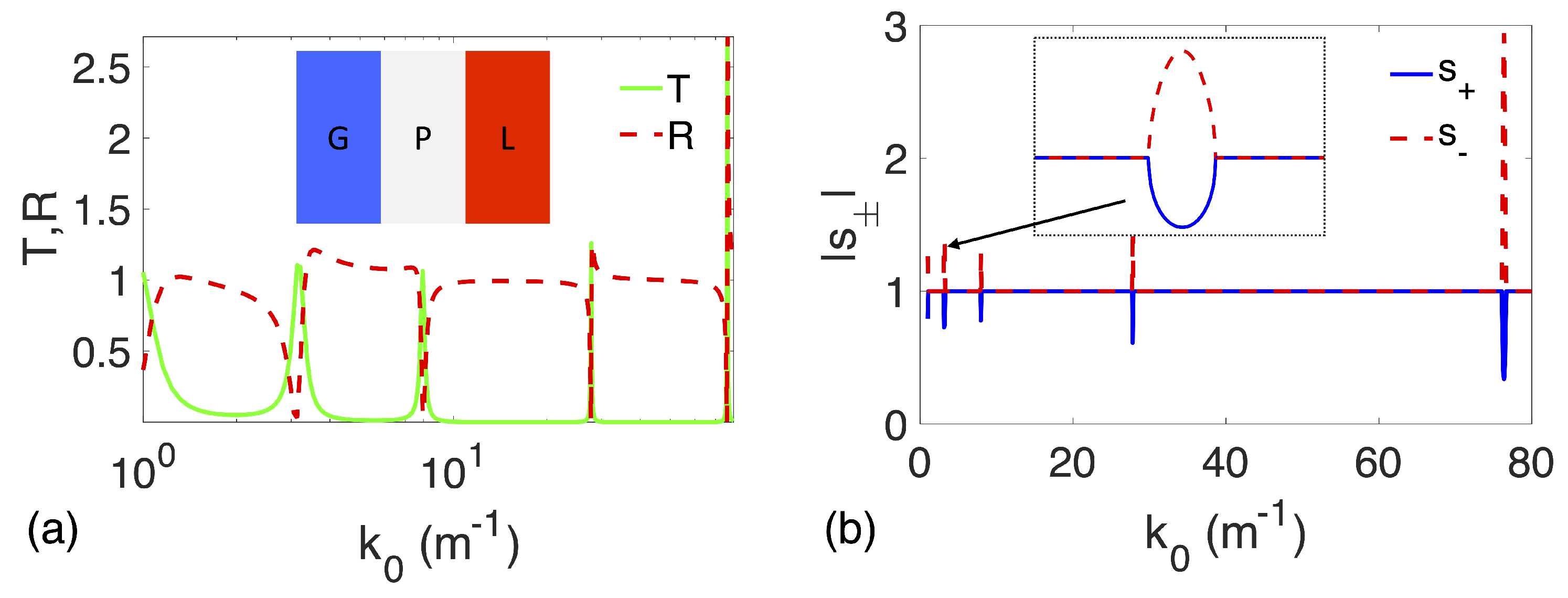
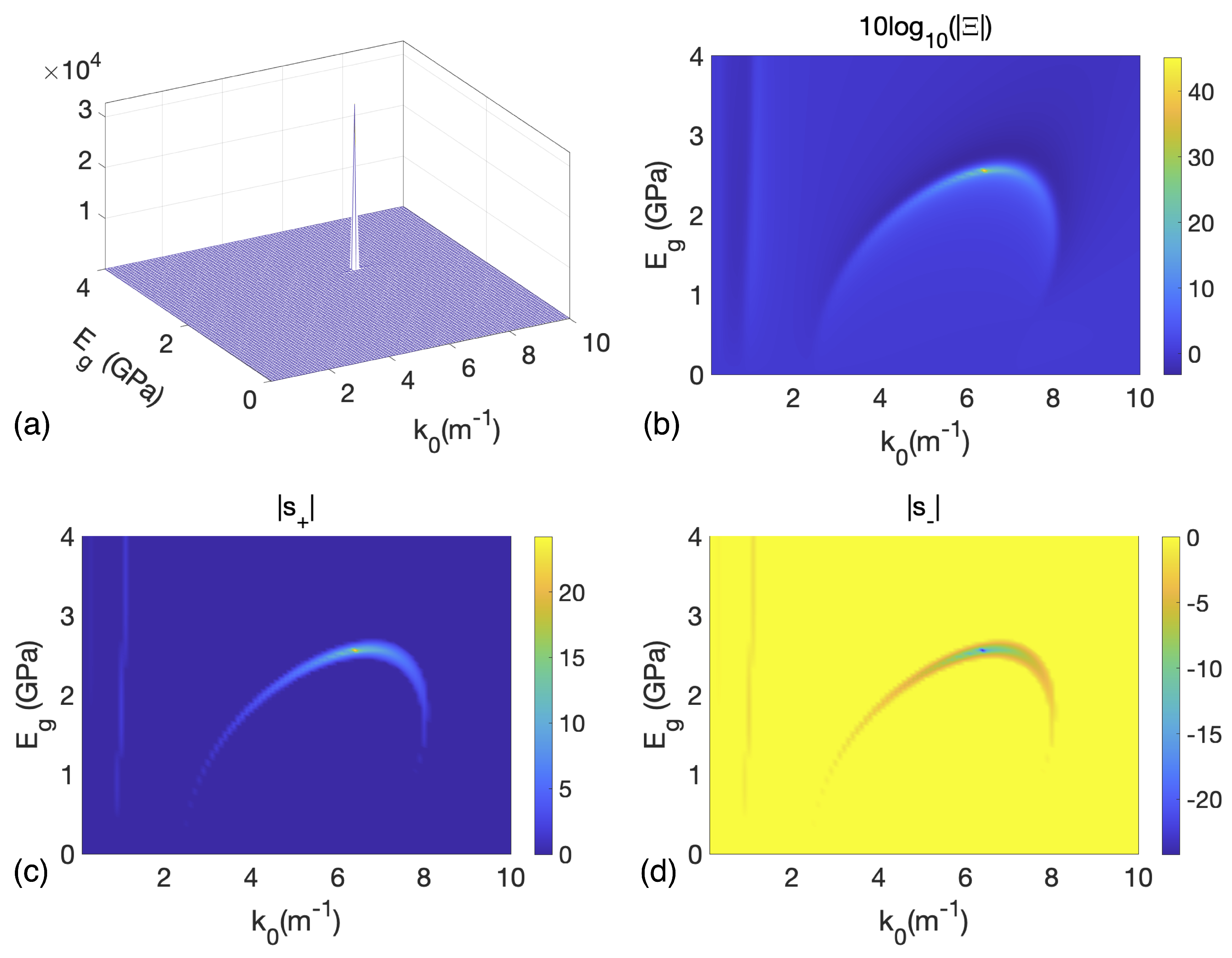
3. Results
4. Discussion: CPAL Effect
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kadic, M.; Bückmann, T.; Schittny, R.; Wegener, M. Metamaterials beyond electromagnetism. Rep. Prog. Phys. 2013, 76, 126501. [Google Scholar] [CrossRef]
- Papanicolaou, G. Wave Propagation in Complex Media; Springer Science & Business Media: Berlin, Germany, 2012; Volume 96. [Google Scholar]
- Pendry, J.B.; Holden, A.; Stewart, W.; Youngs, I. Extremely low frequency plasmons in metallic mesostructures. Phys. Rev. Lett. 1996, 76, 4773. [Google Scholar] [CrossRef]
- Kadic, M.; Bückmann, T.; Schittny, R.; Wegener, M. Experiments on cloaking in optics, thermodynamics and mechanics. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2015, 373, 20140357. [Google Scholar] [CrossRef][Green Version]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Zolla, F.; Guenneau, S.; Nicolet, A.; Pendry, J. Electromagnetic analysis of cylindrical invisibility cloaks and the mirage effect. Opt. Lett. 2007, 32, 1069–1071. [Google Scholar] [CrossRef]
- Cai, W.; Chettiar, U.K.; Kildishev, A.V.; Shalaev, V.M. Optical cloaking with metamaterials. Nat. Photonics 2007, 1, 224. [Google Scholar] [CrossRef]
- Ergin, T.; Stenger, N.; Brenner, P.; Pendry, J.B.; Wegener, M. Three-dimensional invisibility cloak at optical wavelengths. Science 2010, 328, 337–339. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.Y.; Guenneau, S.; Enoch, S. Transformation Wave Physics: Electromagnetics, Elastodynamics, and Thermodynamics; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966. [Google Scholar] [CrossRef]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef]
- Alù, A.; Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 2005, 72, 016623. [Google Scholar] [CrossRef]
- Chen, P.Y.; Soric, J.; Alu, A. Invisibility and cloaking based on scattering cancellation. Adv. Mater. 2012, 24, OP281–OP304. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.Y.; Guenneau, S.; Enoch, S.; Alu, A. Frequency-selective surface acoustic invisibility for three-dimensional immersed objects. Phys. Rev. B 2012, 86, 174303. [Google Scholar] [CrossRef]
- Kasap, S.O. Principles of Electronic Materials and Devices; McGraw-Hill: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Yablonovitch, E. Photonic crystals: Semiconductors of light. Sci. Am. 2001, 285, 46–55. [Google Scholar] [CrossRef]
- Khelif, A.; Aoubiza, B.; Mohammadi, S.; Adibi, A.; Laude, V. Complete band gaps in two-dimensional phononic crystal slabs. Phys. Rev. E 2006, 74, 046610. [Google Scholar] [CrossRef]
- Movchan, A.; Movchan, N.; McPhedran, R. Bloch–Floquet bending waves in perforated thin plates. Proc. R. Soc. Math. Phys. Eng. Sci. 2007, 463, 2505–2518. [Google Scholar] [CrossRef]
- Wu, Y.; Lai, Y.; Zhang, Z.Q. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef]
- Kadic, M.; Bückmann, T.; Stenger, N.; Thiel, M.; Wegener, M. On the practicability of pentamode mechanical metamaterials. Appl. Phys. Lett. 2012, 100, 191901. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Brûlé, S.; Enoch, S.; Guenneau, S. Emergence of seismic metamaterials: Current state and future perspectives. Phys. Lett. A 2020, 384, 126034. [Google Scholar] [CrossRef]
- Ungar, E.E.; Sturz, D.H.; Amick, C.H. Vibration control design of high technology facilities. Sound Vib. 1990, 24, 20–27. [Google Scholar]
- Norris, A.; Vemula, C. Scattering of flexural waves on thin plates. J. Sound Vib. 1995, 181, 115–125. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Farhat, M.; Chen, P.Y.; Bağcı, H.; Enoch, S.; Guenneau, S.; Alu, A. Platonic scattering cancellation for bending waves in a thin plate. Sci. Rep. 2014, 4, 4644. [Google Scholar] [CrossRef] [PubMed]
- Farhat, M.; Guenneau, S.; Enoch, S. Ultrabroadband elastic cloaking in thin plates. Phys. Rev. Lett. 2009, 103, 024301. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, Y.; Liang, Z.; Chen, T.; Li, J. Elastic waves in curved space: Mimicking a wormhole. Phys. Rev. Lett. 2018, 121, 234301. [Google Scholar] [CrossRef]
- Dubois, M.; Farhat, M.; Bossy, E.; Enoch, S.; Guenneau, S.; Sebbah, P. Flat lens for pulse focusing of elastic waves in thin plates. Appl. Phys. Lett. 2013, 103, 071915. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.Y.; Guenneau, S.; Salama, K.N.; Bağcı, H. Localized surface plate modes via flexural Mie resonances. Phys. Rev. B 2017, 95, 174201. [Google Scholar] [CrossRef]
- Haslinger, S.; Movchan, N.; Movchan, A.; Jones, I.; Craster, R. Controlling flexural waves in semi-infinite platonic crystals with resonator-type scatterers. Q. J. Mech. Appl. Math. 2017, 70, 216–247. [Google Scholar] [CrossRef]
- McPhedran, R.; Movchan, A.; Movchan, N.; Brun, M.; Smith, M. ‘Parabolic’ trapped modes and steered Dirac cones in platonic crystals. Proc. R. Soc. Math. Phys. Eng. Sci. 2015, 471, 20140746. [Google Scholar] [CrossRef]
- Hou, Z.; Assouar, B. Tunable elastic parity-time symmetric structure based on the shunted piezoelectric materials. J. Appl. Phys. 2018, 123, 085101. [Google Scholar] [CrossRef]
- Vasseur, J.; Hladky-Hennion, A.C.; Djafari-Rouhani, B.; Duval, F.; Dubus, B.; Pennec, Y.; Deymier, P.A. Waveguiding in two-dimensional piezoelectric phononic crystal plates. J. Appl. Phys. 2007, 101, 114904. [Google Scholar] [CrossRef]
- Hladky-Hennion, A.C.; Decarpigny, J.N. Finite element modeling of active periodic structures: Application to 1–3 piezocomposites. J. Acoust. Soc. Am. 1993, 94, 621–635. [Google Scholar] [CrossRef]
- Rüter, C.E.; Makris, K.G.; El-Ganainy, R.; Christodoulides, D.N.; Segev, M.; Kip, D. Observation of parity–time symmetry in optics. Nat. Phys. 2010, 6, 192. [Google Scholar] [CrossRef]
- Christensen, J.; Willatzen, M.; Velasco, V.; Lu, M.H. Parity-time synthetic phononic media. Phys. Rev. Lett. 2016, 116, 207601. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Dubois, M.; Chen, Y.; Cheng, L.; Ramezani, H.; Wang, Y.; Zhang, X. Accessing the exceptional points of parity-time symmetric acoustics. Nat. Commun. 2016, 7, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; El-Ganainy, R.; Ge, L. Non-Hermitian photonics based on parity–time symmetry. Nat. Photonics 2017, 11, 752. [Google Scholar] [CrossRef]
- Li, H.X.; Rosendo-López, M.; Zhu, Y.F.; Fan, X.D.; Torrent, D.; Liang, B.; Cheng, J.C.; Christensen, J. Ultrathin acoustic parity-time symmetric metasurface cloak. Research 2019, 2019, 8345683. [Google Scholar] [CrossRef]
- Wu, Q.; Chen, Y.; Huang, G. Asymmetric scattering of flexural waves in a parity-time symmetric metamaterial beam. J. Acoust. Soc. Am. 2019, 146, 850–862. [Google Scholar] [CrossRef]
- Fleury, R.; Sounas, D.; Alu, A. An invisible acoustic sensor based on parity-time symmetry. Nat. Commun. 2015, 6, 5905. [Google Scholar] [CrossRef]
- Zilman, G.; Miloh, T. Hydroelastic buoyant circular plate in shallow water: A closed form solution. Appl. Ocean. Res. 2000, 22, 191–198. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.Y.; Bagci, H.; Salama, K.N.; Alù, A.; Guenneau, S. Scattering theory and cancellation of gravity-flexural waves of floating plates. Phys. Rev. B 2020, 101, 014307. [Google Scholar] [CrossRef]
- Farhat, M.; Chen, P.; Guenneau, S.; Wu, Y. CPA-Lasing in Thin-Elastic Plates via Exceptional Points. arXiv 2020, arXiv:2007.01674. [Google Scholar]
- Hou, Z.; Ni, H.; Assouar, B. P T-Symmetry for Elastic Negative Refraction. Phys. Rev. Appl. 2018, 10, 044071. [Google Scholar] [CrossRef]
- Amin, M.; Elayouch, A.; Farhat, M.; Addouche, M.; Khelif, A.; Bağcı, H. Acoustically induced transparency using Fano resonant periodic arrays. J. Appl. Phys. 2015, 118, 164901. [Google Scholar] [CrossRef]
- Farhat, M.; Yang, M.; Ye, Z.; Chen, P.Y. PT-Symmetric Absorber-Laser Enables Electromagnetic Sensors with Unprecedented Sensitivity. ACS Photonics 2020, 7, 2080–2088. [Google Scholar] [CrossRef]
- Lin, Z.; Ramezani, H.; Eichelkraut, T.; Kottos, T.; Cao, H.; Christodoulides, D.N. Unidirectional invisibility induced by P T-symmetric periodic structures. Phys. Rev. Lett. 2011, 106, 213901. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.; Chong, Y.; Stone, A.D. Conservation relations and anisotropic transmission resonances in one-dimensional PT-symmetric photonic heterostructures. Phys. Rev. A 2012, 85, 023802. [Google Scholar] [CrossRef]
- Chong, Y.; Ge, L.; Stone, A.D. P t-symmetry breaking and laser-absorber modes in optical scattering systems. Phys. Rev. Lett. 2011, 106, 093902. [Google Scholar] [CrossRef]
- Feng, L.; Wong, Z.J.; Ma, R.M.; Wang, Y.; Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, B.; Özdemir, Ş.K.; Pichler, K.; Krimer, D.O.; Zhao, G.; Nori, F.; Liu, Y.X.; Rotter, S.; Yang, L. A phonon laser operating at an exceptional point. Nat. Photonics 2018, 12, 479. [Google Scholar] [CrossRef]
- Sakhdari, M.; Estakhri, N.M.; Bagci, H.; Chen, P.Y. Low-Threshold Lasing and Coherent Perfect Absorption in Generalized P T-Symmetric Optical Structures. Phys. Rev. Appl. 2018, 10, 024030. [Google Scholar] [CrossRef]
- Dupont, G.; Remy, F.; Kimmoun, O.; Molin, B.; Guenneau, S.; Enoch, S. Type of dike using C-shaped vertical cylinders. Phys. Rev. B 2017, 96, 180302. [Google Scholar] [CrossRef]
- Bennetts, L.G.; Peter, M.A.; Craster, R.V. Graded resonator arrays for spatial frequency separation and amplification of water waves. J. Fluid Mech. 2018, 854, R4. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farhat, M.; Guenneau, S.; Chen, P.-Y.; Wu, Y. Parity-Time Symmetry and Exceptional Points for Flexural-Gravity Waves in Buoyant Thin-Plates. Crystals 2020, 10, 1039. https://doi.org/10.3390/cryst10111039
Farhat M, Guenneau S, Chen P-Y, Wu Y. Parity-Time Symmetry and Exceptional Points for Flexural-Gravity Waves in Buoyant Thin-Plates. Crystals. 2020; 10(11):1039. https://doi.org/10.3390/cryst10111039
Chicago/Turabian StyleFarhat, Mohamed, Sebastien Guenneau, Pai-Yen Chen, and Ying Wu. 2020. "Parity-Time Symmetry and Exceptional Points for Flexural-Gravity Waves in Buoyant Thin-Plates" Crystals 10, no. 11: 1039. https://doi.org/10.3390/cryst10111039
APA StyleFarhat, M., Guenneau, S., Chen, P.-Y., & Wu, Y. (2020). Parity-Time Symmetry and Exceptional Points for Flexural-Gravity Waves in Buoyant Thin-Plates. Crystals, 10(11), 1039. https://doi.org/10.3390/cryst10111039





