New Insights into the Structure of Glycols and Derivatives: A Comparative X-Ray Diffraction, Raman and Molecular Dynamics Study of Ethane-1,2-Diol, 2-Methoxyethan-1-ol and 1,2-Dimethoxy Ethane
Abstract
1. Introduction
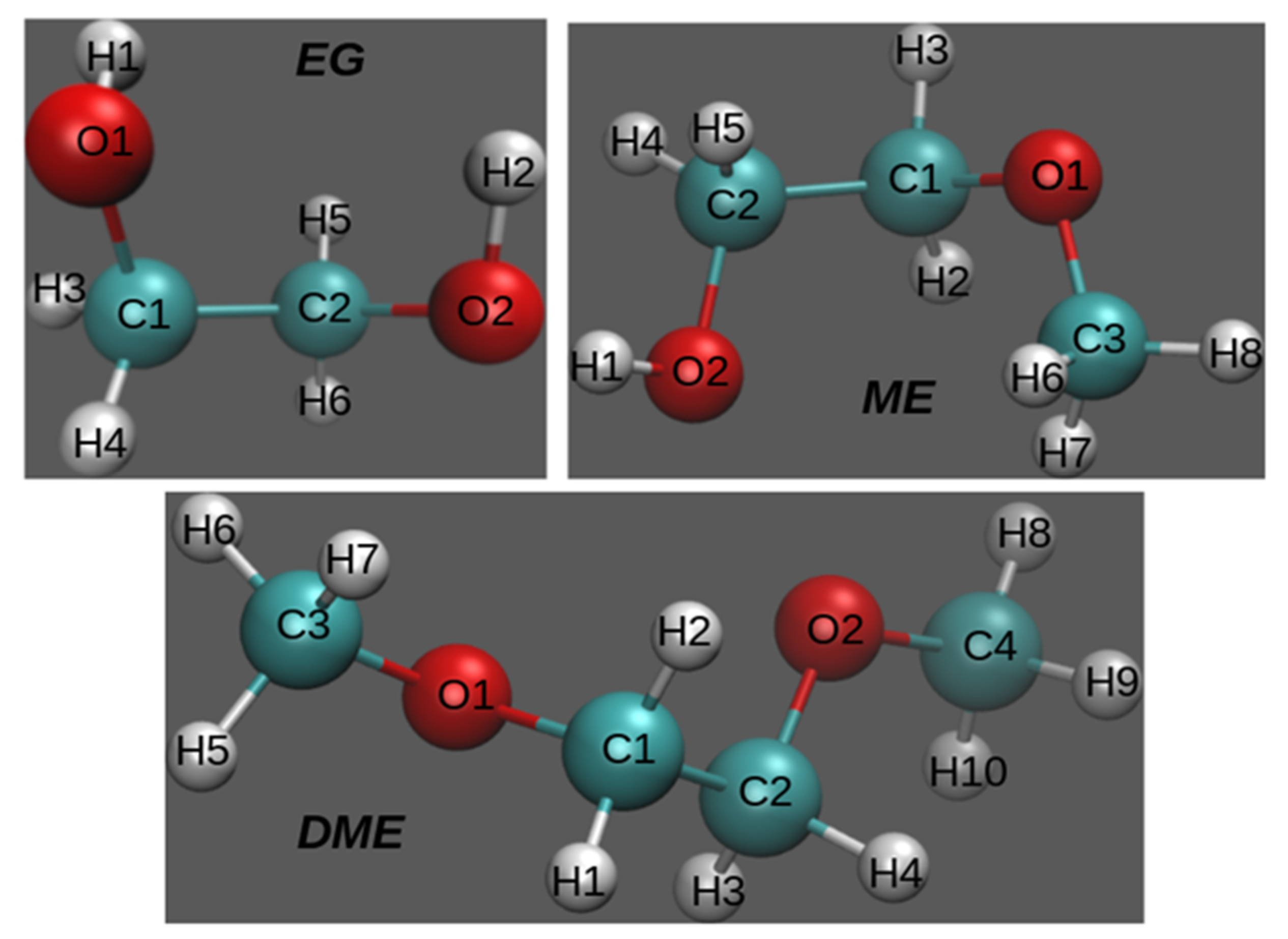
2. Materials and Methods
3. Results and Discussion
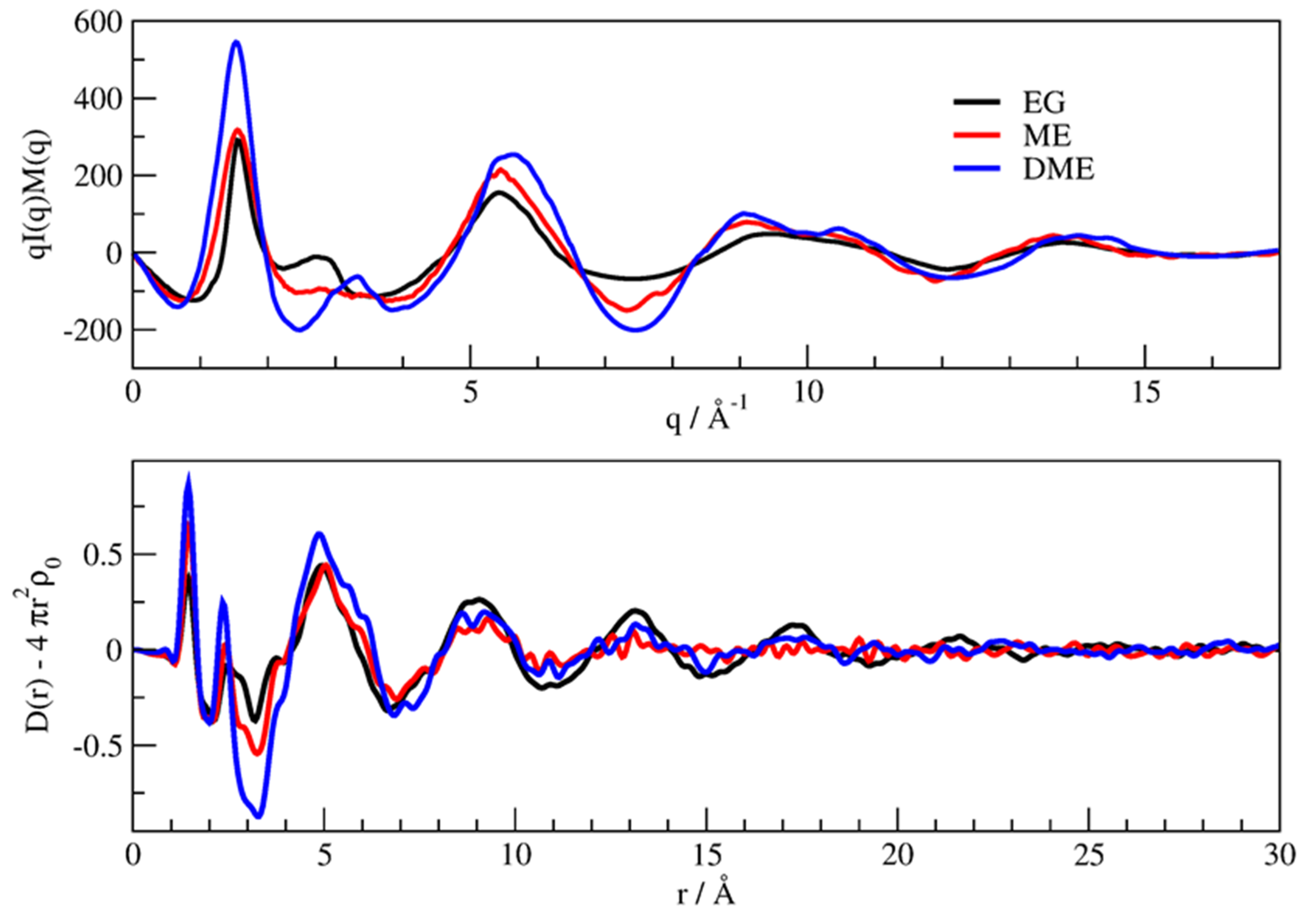
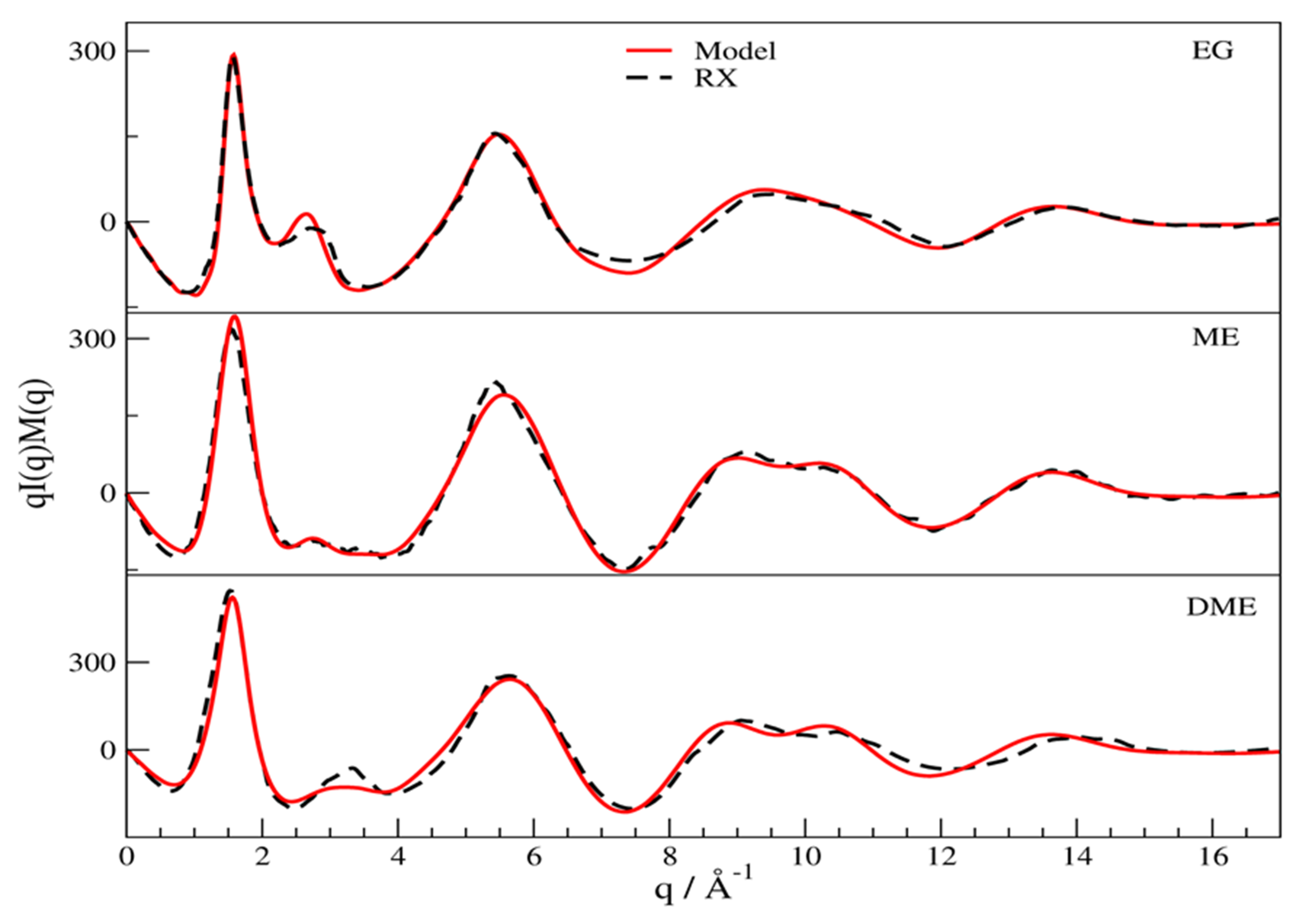
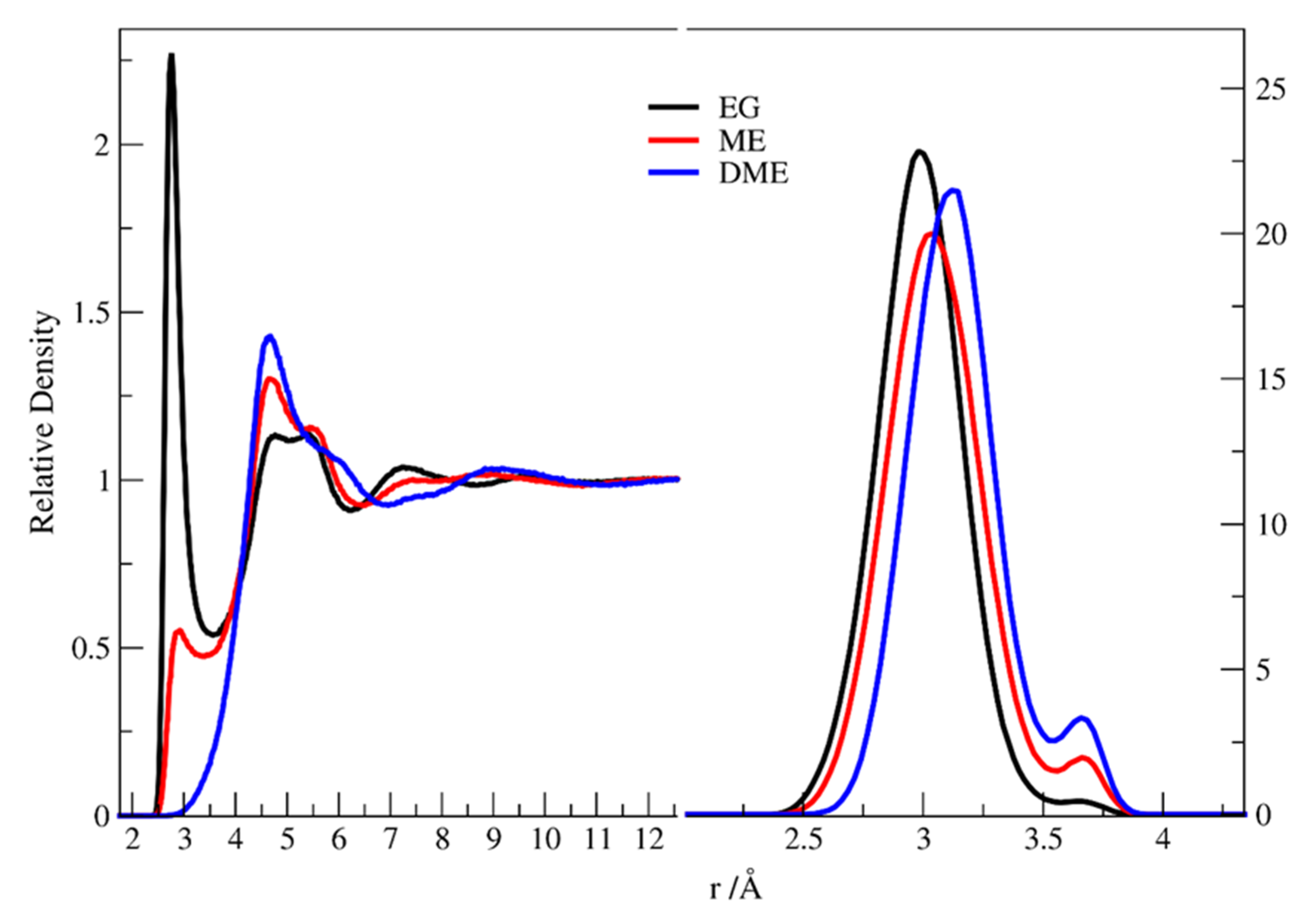
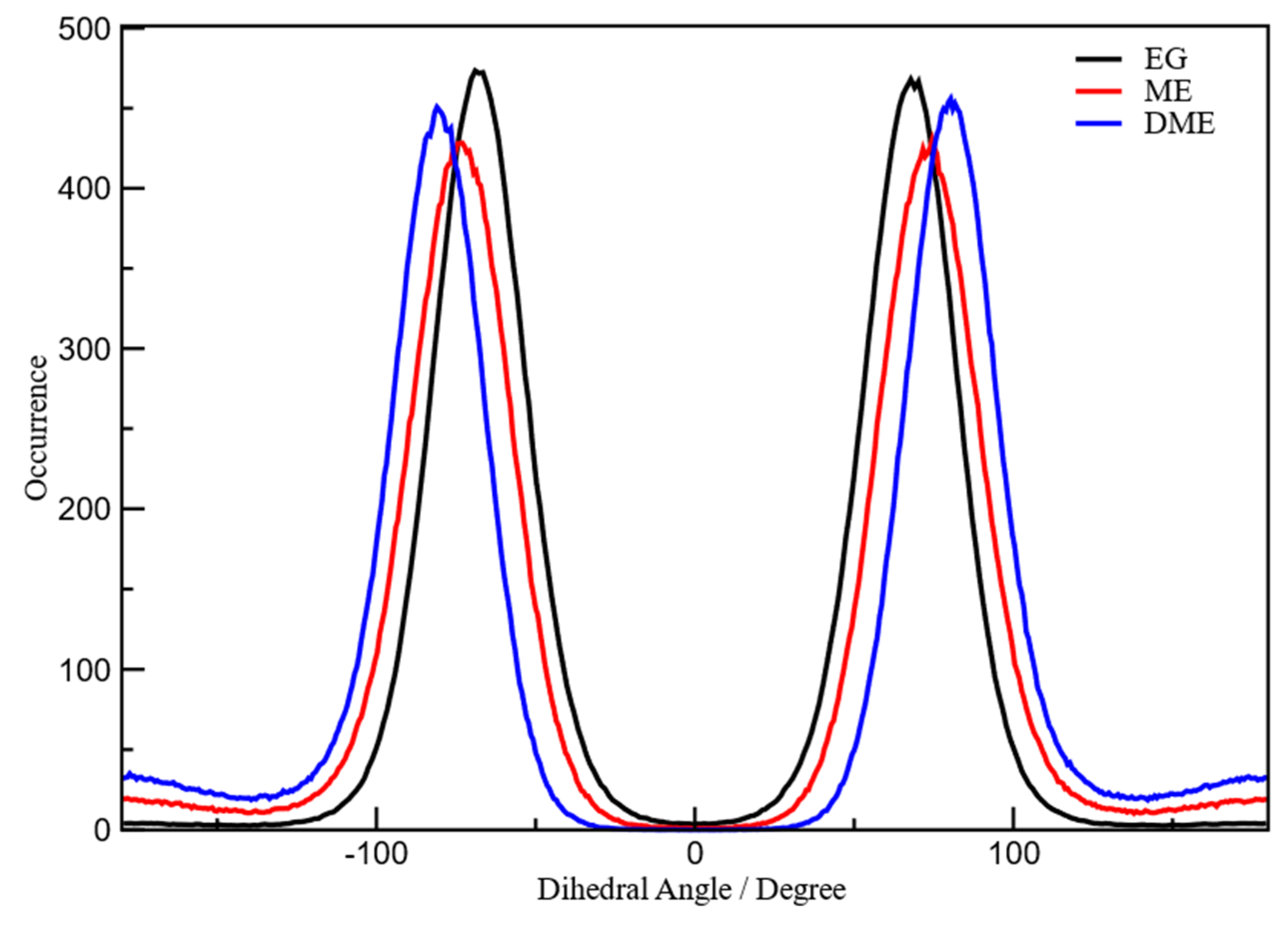
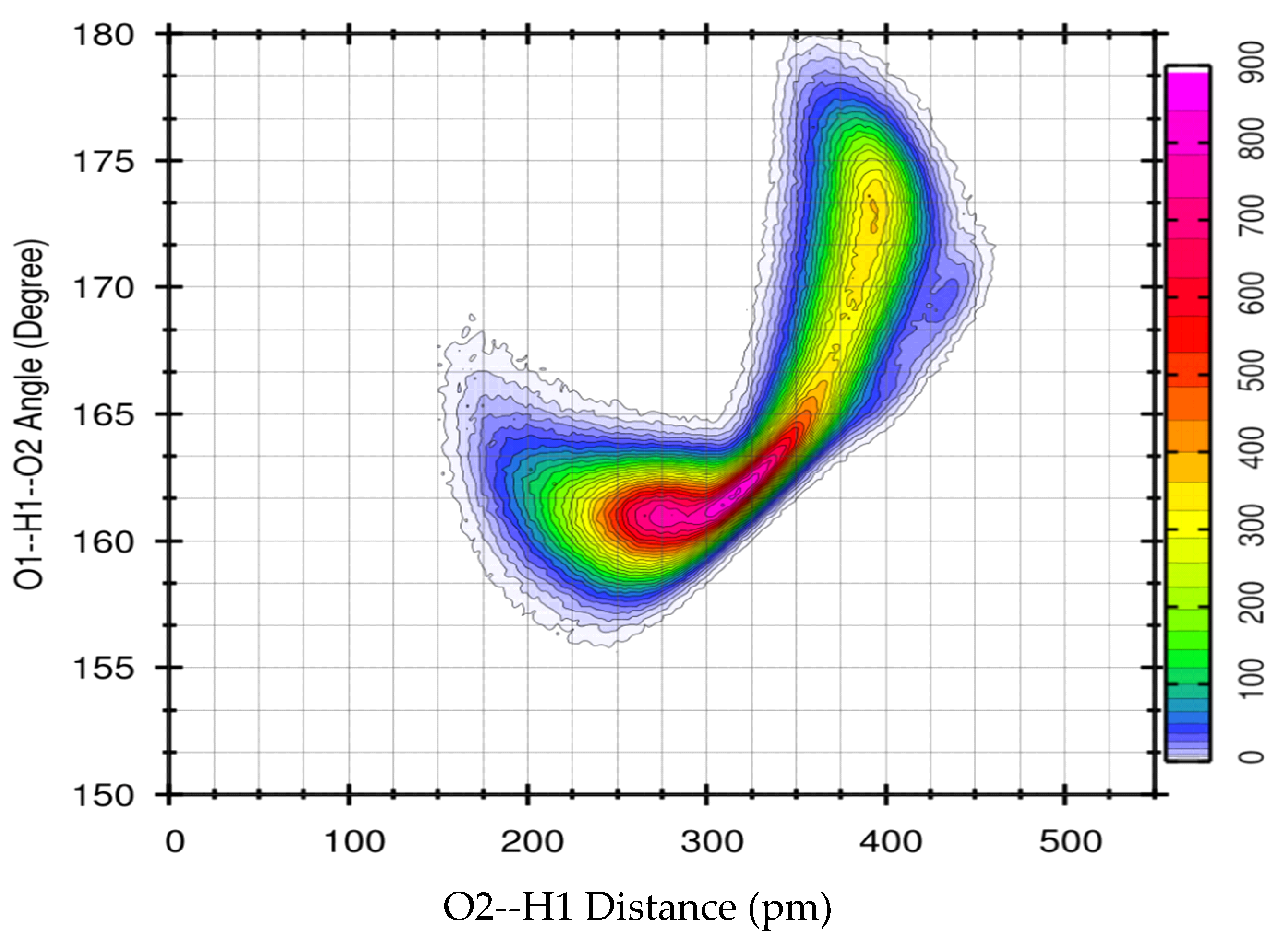
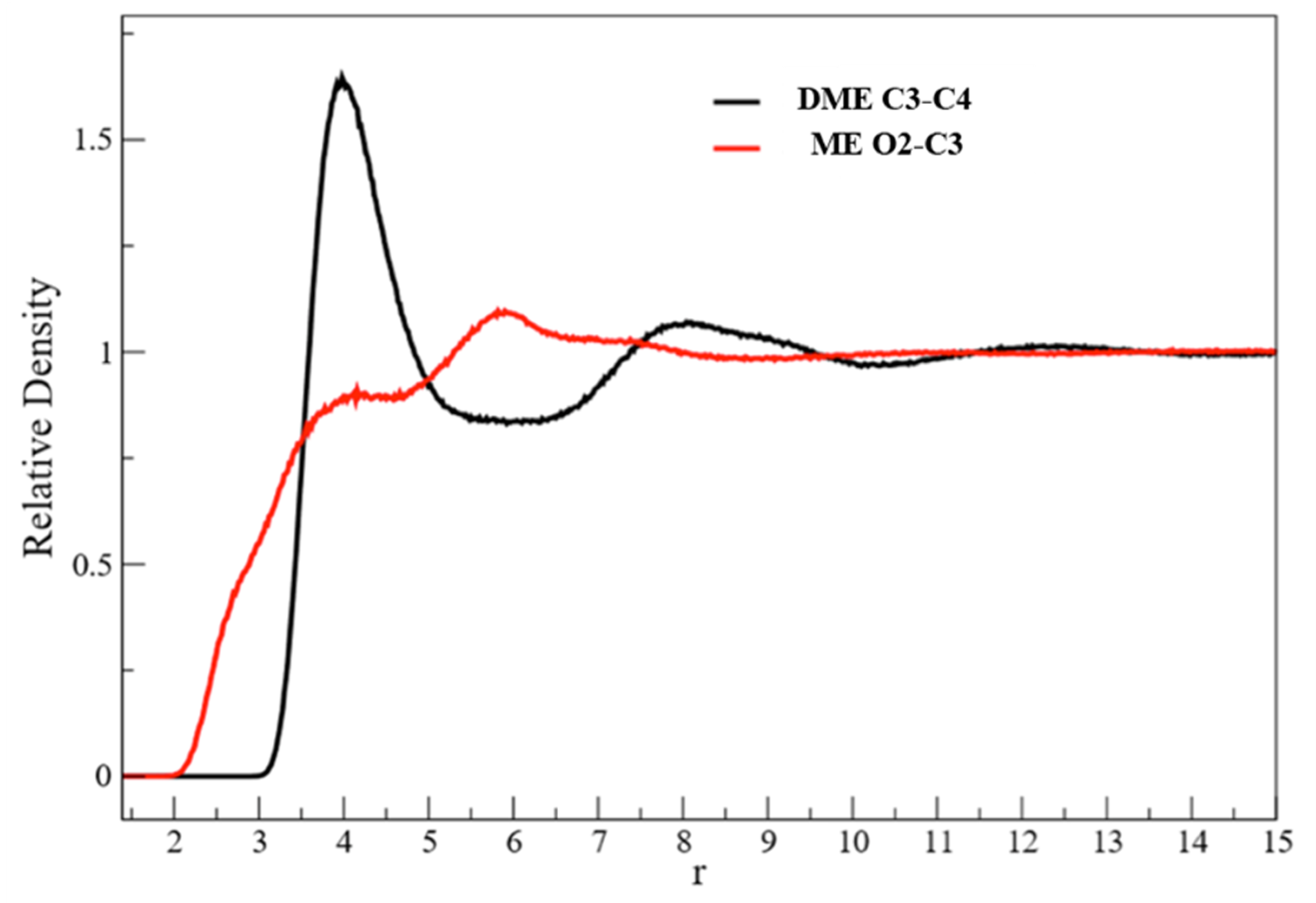
3.1. X-Ray Structural Study
- In the 2–3.5 Å−1 range, that correspond to an effective distance range (estimated as d ≈ 2 π/q) between 1.8 and 3.2 Å, and is the part of reciprocal space data most sensitive to short intermolecular correlations, like hydrogen bonding, a clear decrease of the peak intensity is observed going from EG to ME, while in DME the peak partly recovers the intensity, but is shifted at larger q.
- The faint peak round 10 Å−1 in EG is progressively split into two peaks by OH substitution.
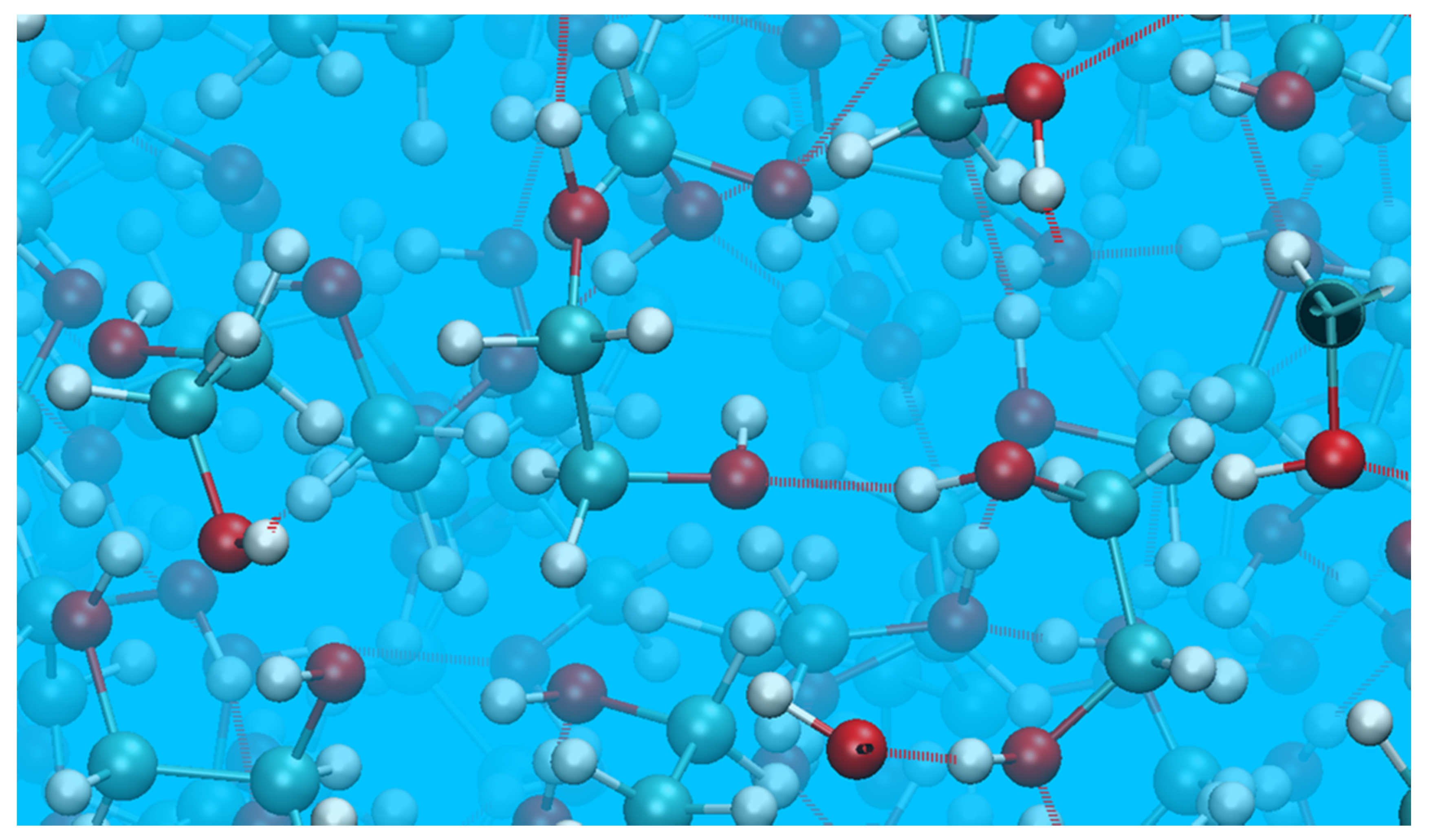
- A cyclic dimer (with both EG molecules in the gauche conformation) containing two intermolecular bonds connecting the monomers, added to four additional hydrogen bonds with other molecules;
- A molecule in the anti configuration, capable of participation in as many as four hydrogen bonds with neighboring molecules.
3.2. Raman Study
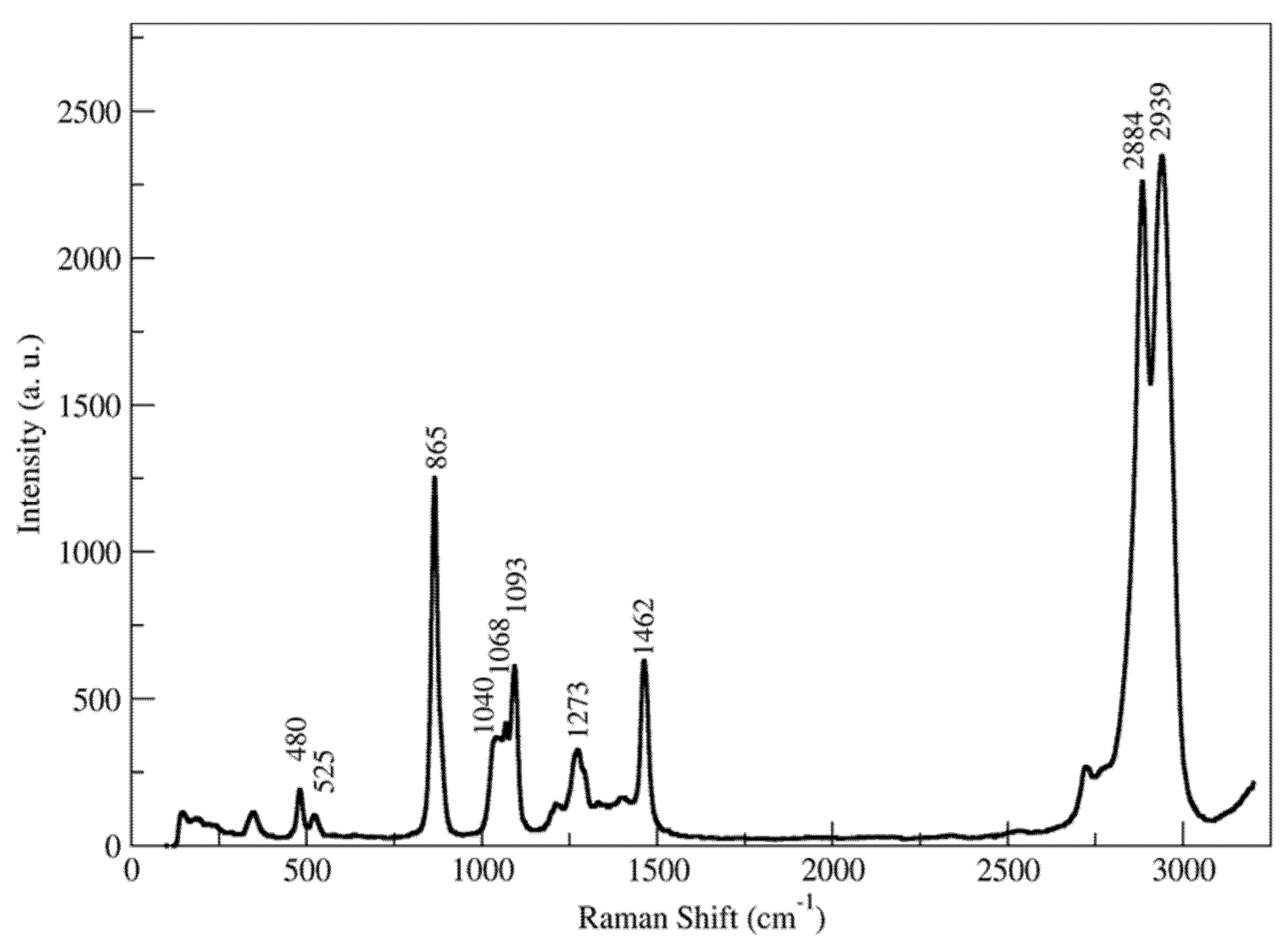
3.2.1. EG
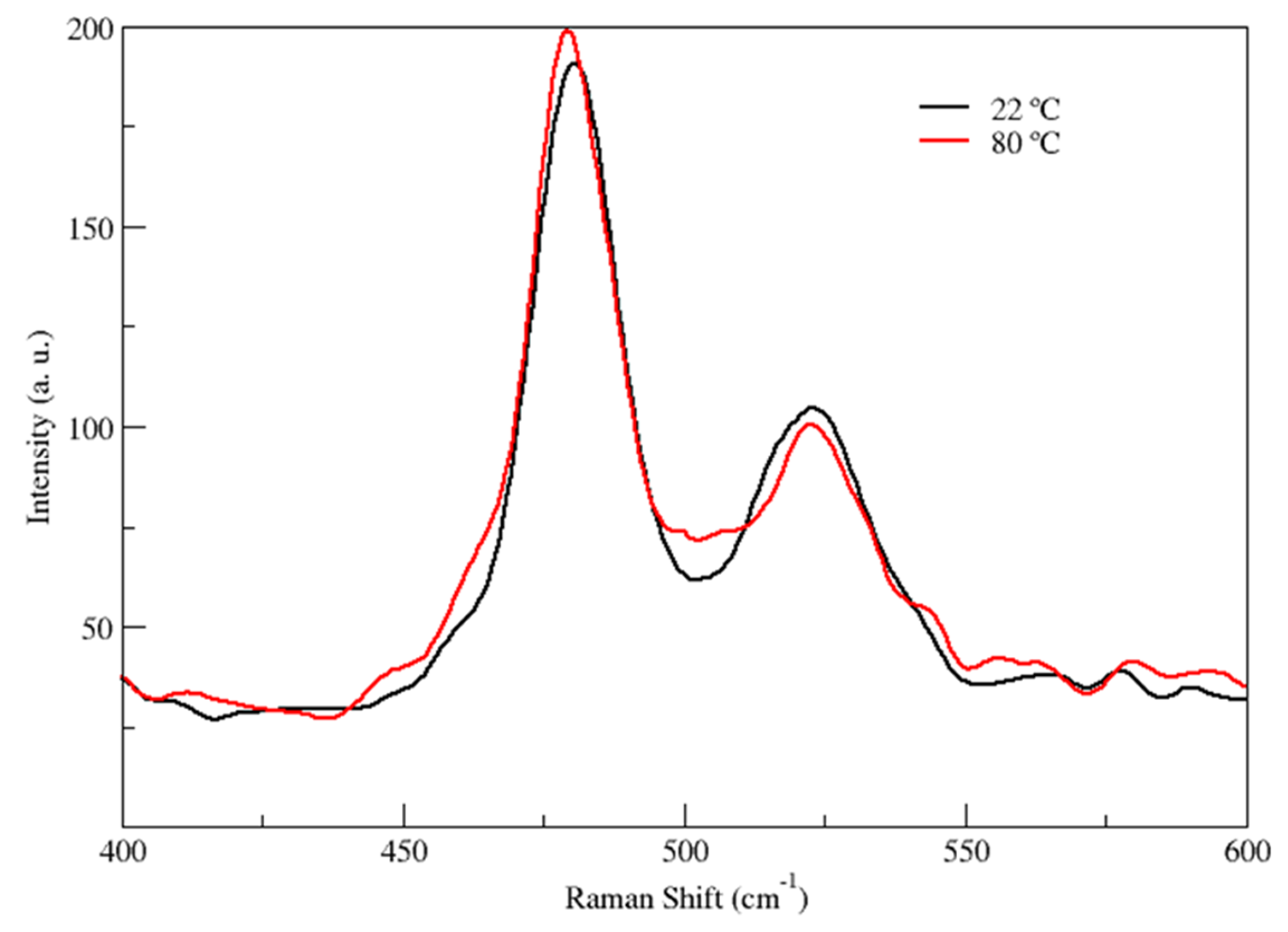
- 400–600 cm−1: This first region is relevant in order to figure out the presence of rotational isomerism of ethylene glycol in the liquid state. In fact, as well known, in this region two main peaks are present, the 525 cm−1 Raman vibration and the 480 cm−1 band, which are assigned to the antisymmetric mode of the gauche conformer and to the symmetric (Ag) C–C–O bending mode of the anti conformer respectively [45,47].
- 800–1100 cm−1: The Raman spectrum of liquid ethylene glycol exhibits a very intense polarized line at about 865 cm−1 due to the C–C stretch mode. The region between 1000 and 1100 displays three overlapping bands at 1040, 1068 and 1093 cm−1. the first and third Raman bands are assigned to the stretching modes of the gauche isomer, and the second band to the anti C–O stretch (Ag) mode [45].
- 1400–1500 cm−1: The vibration located at 1462 cm−1 is unambiguously assigned to the CH2 scissoring vibration [53].
- 1500–3000 cm−1: Dominated by the very intense Raman bands at 2884 and 2939 cm−1 corresponding to the stretching mode of CH2 groups.
3.2.2. ME
- The region below the 800 cm−1 which includes different bending and torsional modes;
- The 800–1500 cm−1 region, which includes the CH3, CH2 and COH bending vibrations and the CC and CO stretching modes.
- The 2700–3200 cm−1 region, the O–H and C–H stretching vibrations.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Diaz, A.; Katsarava, R.; Puiggali, J. Synthesis, Properties and Applications of Biodegradable Polymers Derived from Diols and Dicarboxylic Acids: From Polyesters to Poly(ester amide)s. Int. J. Mol. Sci. 2014, 15, 7064–7123. [Google Scholar] [CrossRef] [PubMed]
- Turecek, P.; Bossard, M.; Schoetens, F.; Ivens, I. PEGylation of Biopharmaceuticals: A Review of Chemistry and Nonclinical Safety Information of Approved Drugs. J. Pharm. Sci 2016, 105, 460–475. [Google Scholar] [CrossRef] [PubMed]
- Fettaka, H.; Lefebvre, M. Ethylene Glycol Dinitrate (EGDN): From Commercial Precursors, Physicochemical and Detonation Characterization. Cent. Eur. J. Energ. Mat. 2015, 12, 287–305. [Google Scholar]
- Zagrebin, P.; Buchner, R.; Nazmutdinov, R.; Tsirlina, G. Dynamic Solvent Effects in Electrochemical Kinetics: Indications for a Switch of the Relevant Solvent Mode. J. Phys. Chem. B 2010, 114, 311–320. [Google Scholar] [CrossRef] [PubMed]
- Ismailova, O.; Berezin, A.S.; Probst, M.; Nazmutdinov, R.R. Interfacial Bond-Breaking Electron Transfer in Mixed Water–Ethylene Glycol Solutions: Reorganization Energy and Interplay between Different Solvent Modes. J. Phys. Chem. B 2013, 117, 8793–8801. [Google Scholar] [CrossRef]
- Ibrahim, R.; Hayyan, M.; AlSaadi, M.; Ibrahim, S.; Hayyan, A.; Hashim, M. Physical properties of ethylene glycol-based deep eutectic solvents. J. Mol. Liq. 2019, 276, 794–800. [Google Scholar] [CrossRef]
- Saiz, L.; Padro, J.; Guardia, E. Structure of liquid ethylene glycol: A molecular dynamics simulation study with different force fields. J. Chem. Phys. 2001, 114, 3187–3199. [Google Scholar] [CrossRef]
- Zhang, N.; Li, M.; Zhang, F. Structure and dynamics properties of liquid ethylene glycol from molecular dynamics simulations. Chem. Phys. Lett. 2019, 718, 12–21. [Google Scholar] [CrossRef]
- Kaur, S.; Shobhna; Kashyap, H. Insights Gained from Refined Force-Field for Pure and Aqueous Ethylene Glycol through Molecular Dynamics Simulations. J. Phys. Chem. B 2019, 123, 6543–6553. [Google Scholar] [CrossRef] [PubMed]
- Kazerouni, M.; Hedberg, L.; Hedberg, K. Conformational analysis.21. Ethane-1,2-diol. An electron-diffraction investigation, augmented by rotational constants and ab initio calculations, of the molecular structure, conformational composition, SQM vibrational force field, and anti-gauche energy difference with implications for internal hydrogen bonding. J. Am. Chem. Soc. 1997, 119, 8324–8331. [Google Scholar]
- Christen, D.; Coudert, L.H.; Larsson, J.A.; Cremer, D. The Rotational-Torsional Spectrum of the g′Gg Conformer of Ethylene Glycol: Elucidation of an Unusual Tunneling Path. J. Mol. Spectrosc. 2001, 205, 185–196. [Google Scholar] [CrossRef]
- Park, C.G.; Tasumi, M. Reinvestigation of Infrared-Induced Conformational Isomerizations of 1,2-Ethanediol in Low-Temperature Ar Matrices and Reverse Reaction in the Dark. J. Phys. Chem. 1991, 95, 2757–2762. [Google Scholar] [CrossRef]
- Frei, H.; Ha, T.-K.; Meyer, R.; Gūnthard, H.H. Ethylene glycol: Infrared spectra, AB initio calculations, vibrational analysis and conformations of 5 matrix isolated isotopic modifications. Chem. Phys. 1977, 25, 271–298. [Google Scholar] [CrossRef]
- Bakó, I.; Grósz, T.; Pálinkás, G.; Bellissent-Funel, M.C. Ethylene glycol dimers in the liquid phase: A study by x-ray and neutron diffraction. J. Chem. Phys. 2003, 118, 3215–3221. [Google Scholar] [CrossRef]
- Fortes, A.D.; Suard, E. Crystal structures of ethylene glycol and ethylene glycol monohydrate. J. Chem. Phys. 2011, 135, 234501. [Google Scholar] [CrossRef]
- Chen, Y.; Ozaki, Y.; Czarnecki, M.A. Molecular structure and hydrogen bonding in pure liquid ethylene glycol and ethylene glycol–water mixtures studied using NIR spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 18694–18701. [Google Scholar] [CrossRef]
- Rodnikova, M.N.; Chumaevskii, N.A.; Troitskii, V.M.; Kayumova, D.B. Structure of liquid ethylene glycol. Russ. J. Phys. Chem. 2006, 80, 826–830. [Google Scholar] [CrossRef]
- Sengwa, R.; Madhvi, A. A comparative study of non-polar solvents effect on dielectric relaxation and dipole moment of binary mixtures of mono alkyl ethers of ethylene glycol and of diethylene glycol with ethyl alcohol. J. Mol. Liq. 2006, 123, 92–104. [Google Scholar] [CrossRef]
- Miller, R.R.; Ayres, J.A.; Calhoun, L.L.; Young, J.T.; McKenna, M.J. Comparative Short-Term Inhalation Toxicity of Ethylene Glycol Monomethyl Ether and Propylene Glycol Monomethyl Ether in Rats and Mice. Toxicol. Appl. Pharmacol. 1981, 61, 368–377. [Google Scholar] [CrossRef]
- Caminiti, R.; Albertini, V.R. The kinetics of phase transitions observed by energy-dispersive X-ray diffraction. Int. Rev. Phys. Chem. 1999, 18, 263–299. [Google Scholar] [CrossRef]
- Gontrani, L.; Ballirano, P.; Leonelli, F.; Caminiti, R. X-Ray Diffraction Studies of Ionic Liquids: From Spectra to Structure and Back. In The Structure of Ionic Liquids; Caminiti, R., Gontrani, L., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 1–37. [Google Scholar]
- Caminiti, R.; Carbone, M.; Mancini, G.; Sadun, C. Study of cetyltrialkylammonium bromide and tribromide salts in the solid phase. J. Mater. Chem. 1997, 7, 1331–1337. [Google Scholar] [CrossRef]
- Carbone, M.; Caminiti, R.; Sadun, C. Structural study by energy dispersive X-ray diffraction of amorphous mixed hydroxycarbonates containing Co, Cu, Zn, Al. J. Mater. Chem. 1996, 6, 1709–1716. [Google Scholar] [CrossRef]
- Caminiti, R.; Carbone, M.; Panero, S.; Sadun, C. Conductivity and structure of poly(ethylene glycol) complexes using energy dispersive X-ray diffraction. J. Phys. Chem. B 1999, 103, 10348–10355. [Google Scholar] [CrossRef]
- Carbone, M.; Ballirano, P.; Caminiti, R. Kinetics of gypsum dehydration at reduced pressure: An energy dispersive X-ray diffraction study. Eur. J. Miner. 2008, 20, 621–627. [Google Scholar] [CrossRef]
- Keen, D.A. A comparison of various commonly used correlation functions for describing total scattering. J. Appl. Crystallogr. 2001, 34, 172–177. [Google Scholar] [CrossRef]
- Gontrani, L.; Ramondo, F.; Caminiti, R. Energy dispersive X-ray diffraction and molecular dynamics meet: The structure of liquid pyrrole. Chem. Phys. Lett. 2006, 417, 200–205. [Google Scholar] [CrossRef]
- Gontrani, L.; Ramondo, F.; Caracciolo, G.; Caminiti, R. A study of cyclohexane, piperidine and morpholine with X-ray diffraction and molecular simulations. J. Mol. Liq. 2008, 139, 23–28. [Google Scholar] [CrossRef]
- Gontrani, L.; Caminiti, R. The structure of liquid N-methyl pyrrolidone probed by X-ray scattering and molecular simulations. J. Chem. Phys. 2012, 136, 074505. [Google Scholar] [CrossRef]
- Campetella, M.; Gontrani, L.; Bodo, E.; Ceccacci, F.; Marincola, F.; Caminiti, R. Conformational isomerisms and nano-aggregation in substituted alkylammonium nitrates ionic liquids: An X-ray and computational study of 2-methoxyethylammonium nitrate. J. Chem. Phys. 2013, 138, 184506. [Google Scholar] [CrossRef]
- Valentini, F.; Roscioli, D.; Carbone, M.; Conte, V.; Floris, B.; Palleschi, G.; Flammini, R.; Bauer, E.M.; Nasillo, G.; Caponetti, E. Oxidized graphene in ionic liquids for assembling chemically modified electrodes: A structural and electrochemical characterization study. Anal. Chem. 2012, 84, 5823–5831. [Google Scholar] [CrossRef] [PubMed]
- Bonomo, M.; Gontrani, L.; Capocefalo, A.; Sarra, A.; Nucara, A.; Carbone, M.; Postorino, P.; Dini, D. A combined electrochemical, infrared and EDXD tool to disclose Deep Eutectic Solvents formation when one precursor is liquid: Glyceline as case study. J. Mol. Liq. 2020, 319, 114292. [Google Scholar] [CrossRef]
- Usula, M.; Mocci, F.; Marincola, F.C.; Porcedda, S.; Gontrani, L.; Caminiti, R. The structural organization of N-methyl-2-pyrrolidone + water mixtures: A densitometry, X-ray diffraction, and molecular dynamics study. J. Chem. Phys. 2014, 140, 124503. [Google Scholar] [CrossRef]
- Salma, U.; Usula, M.; Caminiti, R.; Gontrani, L.; Plechkova, N.V.; Seddon, K.R. X-ray and molecular dynamics studies of butylammonium butanoate–water binary mixtures. Phys. Chem. Chem. Phys. 2017, 19, 1975–1981. [Google Scholar] [CrossRef] [PubMed]
- Caminiti, R.; Carbone, M.; Sadun, C. Palladium (II) and platinum (II) aqueous solutions. Evidence for the solvation of the [PdCl4]2− and [PtCl4]2− ions. J. Mol. Liq. 1998, 75, 149–158. [Google Scholar] [CrossRef]
- Gontrani, L.; Caminiti, R.; Bencivenni, L.; Sadun, C. Molecular aggregation phenomena in solution: An energy dispersive X-ray diffraction study of concentrated imidazole water solutions. Chem. Phys. Lett. 1999, 301, 131–137. [Google Scholar] [CrossRef]
- Fakharuddin, A.; Seybold, M.; Agresti, A.; Pescetelli, S.; Matteocci, F.; Haider, M.; Birkhold, S.; Hu, H.; Giridharagopal, R.; Sultan, M.; et al. Perovskite-Polymer Blends Influencing Microstructures, Nonradiative Recombination Pathways, and Photovoltaic Performance of Perovskite Solar Cells. ACS Appl. Mater. Interfaces 2018, 10, 42542–42551. [Google Scholar] [CrossRef]
- Yadav, S.K.; Ravishankar, S.; Pescetelli, S.; Agresti, A.; Fabregat-Santiago, F.; Di Carlo, A. Stability of dye-sensitized solar cells under extended thermal stress. Phys. Chem. Chem. Phys. 2017, 19, 22546–22554. [Google Scholar] [CrossRef] [PubMed]
- Agresti, A.; Cina, L.; Pescetelli, S.; Taheri, B.; Di Carlo, A. Stability of dye-sensitized solar cell under reverse bias condition: Resonance Raman spectroscopy combined with spectrally resolved analysis by transmittance and efficiency mapping. Vib. Spectrosc. 2016, 84, 106–117. [Google Scholar] [CrossRef]
- Case, D.A.; Belfon, K.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Giambasu, G.; et al. AMBER 2020; University of California: San Francisco, CA, USA, 2020. [Google Scholar]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J. Packmol: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Brehm, M.; Thomas, M.; Gehrke, S.; Kirchner, B. TRAVIS—A Free Analyzer for Trajectories from Molecular Simulation. J. Chem. Phys. 2020, 152, 164105. [Google Scholar] [CrossRef]
- Matsuura, H.; Miyazawa, T. Infrared spectra and molecular vibrations of ethylene glycol and deuterated derivatives. Bull. Chem. Soc. Jpn. 1967, 40, 85–94. [Google Scholar] [CrossRef]
- Matsuura, H.; Hiraishi, M.; Miyazawa, T. Raman spectra and energy difference between rotational isomers of ethylene glycol. Spectrochim. Acta Part A 1972, 28, 2299. [Google Scholar] [CrossRef]
- Takeuchi, H.; Tasumi, M. Infrared-induced conformational isomerization of ethylene glycol in a low-temperature argon matrix. Chem. Phys. 1983, 77, 21–34. [Google Scholar] [CrossRef]
- Schwartz, M. Raman study of the conformational equilibrium of ethylene glycol in dimethyl sulfoxide. Spectrochim. Acta Part A 1977, 33, 1025–1032. [Google Scholar] [CrossRef]
- Richardson, J.W.; Pluth, J.J.; Smith, J.V.; Dytrych, W.J.; Bibby, D.M. Conformation of ethylene glycol and phase change in silica sodalite. J. Phys. Chem. 1988, 92, 243–247. [Google Scholar] [CrossRef]
- Pachler, K.G.R.; Wessels, P.L. Rotational isomerism: X. A nuclear magnetic resonance study of 2-fluoro-ethanol and ethylene glycol. J. Mol. Struct. 1970, 6, 471–478. [Google Scholar] [CrossRef]
- Soper, A.K.; Fernandez-Alonso, F.; Price, D.L. Chapter 3—The Structure of Water and Aqueous Systems. In Experimental Methods in the Physical Sciences; Academic Press: Cambridge, MA, USA, 2017; Volume 49, pp. 135–211. [Google Scholar]
- Head-Gordon, T.; Johnson, M.E. Tetrahedral structure or chains for liquid water. Proc. Natl. Acad. Sci. USA 2006, 103, 7973. [Google Scholar] [CrossRef]
- Migliorati, V.; D’Angelo, P. Unraveling the perturbation induced by Zn2+ and Hg2+ ions on the hydrogen bond patterns of liquid methanol. Chem. Phys. Lett. 2015, 633, 70–75. [Google Scholar] [CrossRef]
- Krischnan, K.; Krisrtnan, R.S. Raman and Infrared Spectra of Ethylene Glycol. Proc. Indian Acad. Sci. 1966, A64, 111–123. [Google Scholar] [CrossRef]
- Palumbo, O.; Paolone, A.; Campetella, M.; Ramondo, F.; Cappelluti, F.; Gontrani, L. New insights into chloromethyl-oxirane and chloromethyl-thiirane in liquid and solid phase from low-temperature infrared spectroscopy and ab initio modeling. Spectrochim. Acta, Part 2020, 247, 119061. [Google Scholar] [CrossRef]
- Amorim da Costa, A.M.; Duarte, A.S.R.; Amado, A.M. Molecular aggregation in neat 2-methoxyethanol and in 2-methoxyethanol/acrylamide solutions—A study by Raman spectroscopy and ab initio calculations. Vib. Spectrosc. 2006, 42, 302–308. [Google Scholar] [CrossRef]
- Gil, F.P.S.C.; Amorim da Costa, A.M.; Teixeira-Dias, J.J.C. Oxygen-by-Sulfur Substitution in CH3OCH2CH2OH: An Ab Initio Comparative Study of Conformational Effects and Intramolecular Interactions. J. Phys. Chem. 1995, 99, 16586–16589. [Google Scholar] [CrossRef][Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gontrani, L.; Tagliatesta, P.; Agresti, A.; Pescetelli, S.; Carbone, M. New Insights into the Structure of Glycols and Derivatives: A Comparative X-Ray Diffraction, Raman and Molecular Dynamics Study of Ethane-1,2-Diol, 2-Methoxyethan-1-ol and 1,2-Dimethoxy Ethane. Crystals 2020, 10, 1011. https://doi.org/10.3390/cryst10111011
Gontrani L, Tagliatesta P, Agresti A, Pescetelli S, Carbone M. New Insights into the Structure of Glycols and Derivatives: A Comparative X-Ray Diffraction, Raman and Molecular Dynamics Study of Ethane-1,2-Diol, 2-Methoxyethan-1-ol and 1,2-Dimethoxy Ethane. Crystals. 2020; 10(11):1011. https://doi.org/10.3390/cryst10111011
Chicago/Turabian StyleGontrani, Lorenzo, Pietro Tagliatesta, Antonio Agresti, Sara Pescetelli, and Marilena Carbone. 2020. "New Insights into the Structure of Glycols and Derivatives: A Comparative X-Ray Diffraction, Raman and Molecular Dynamics Study of Ethane-1,2-Diol, 2-Methoxyethan-1-ol and 1,2-Dimethoxy Ethane" Crystals 10, no. 11: 1011. https://doi.org/10.3390/cryst10111011
APA StyleGontrani, L., Tagliatesta, P., Agresti, A., Pescetelli, S., & Carbone, M. (2020). New Insights into the Structure of Glycols and Derivatives: A Comparative X-Ray Diffraction, Raman and Molecular Dynamics Study of Ethane-1,2-Diol, 2-Methoxyethan-1-ol and 1,2-Dimethoxy Ethane. Crystals, 10(11), 1011. https://doi.org/10.3390/cryst10111011









