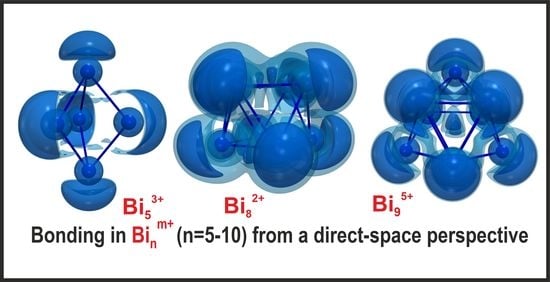
Bismuth Polycations Revisited: Alternative Synthesis and Electronic Structure of Bi6Br7, and Bonding in Main-Group Polyatomic Ions from a Direct Space Perspective
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis and Primary Characterization
2.2. X-ray Crystallography
2.3. Computational Details
3. Results and Discussion
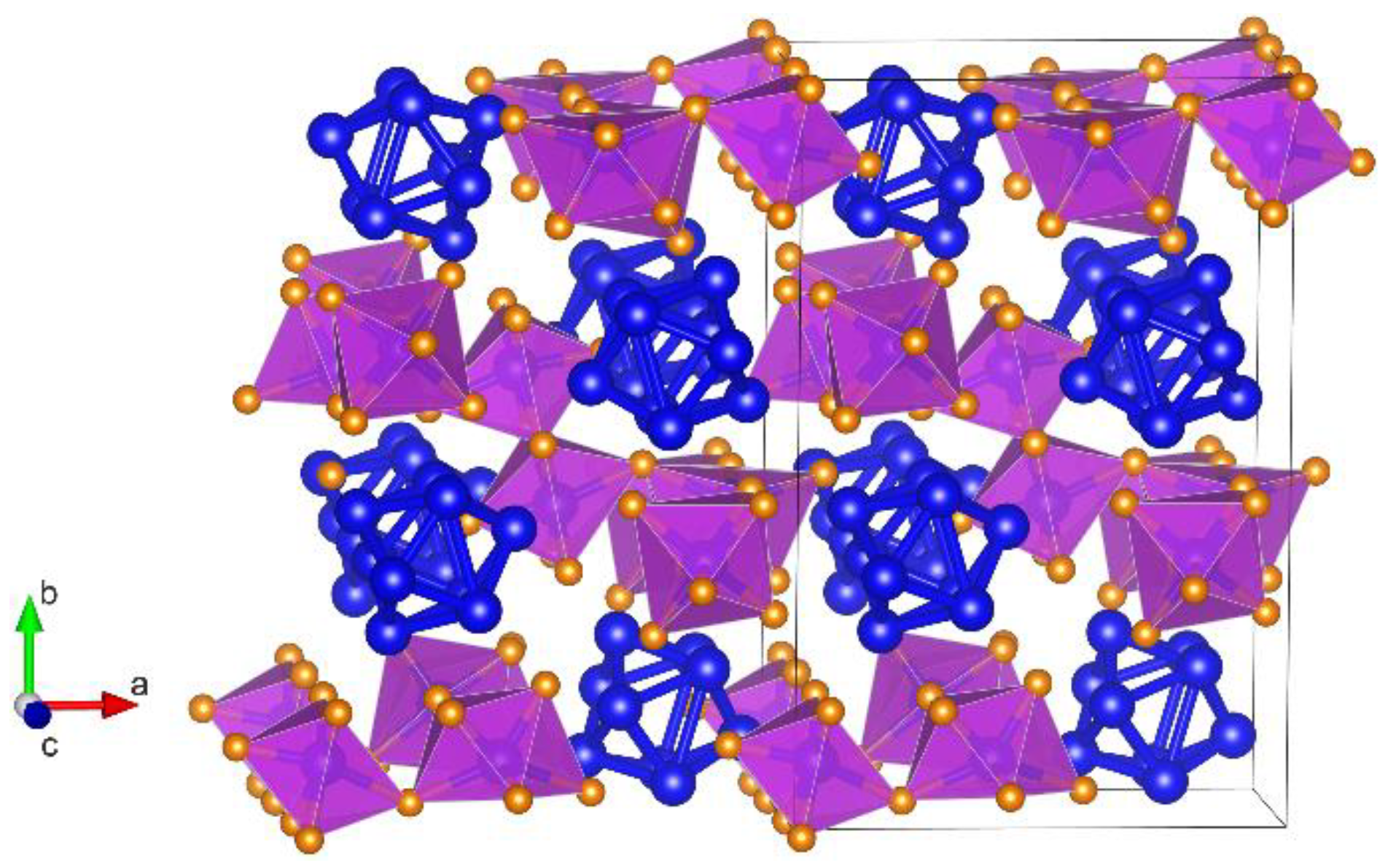
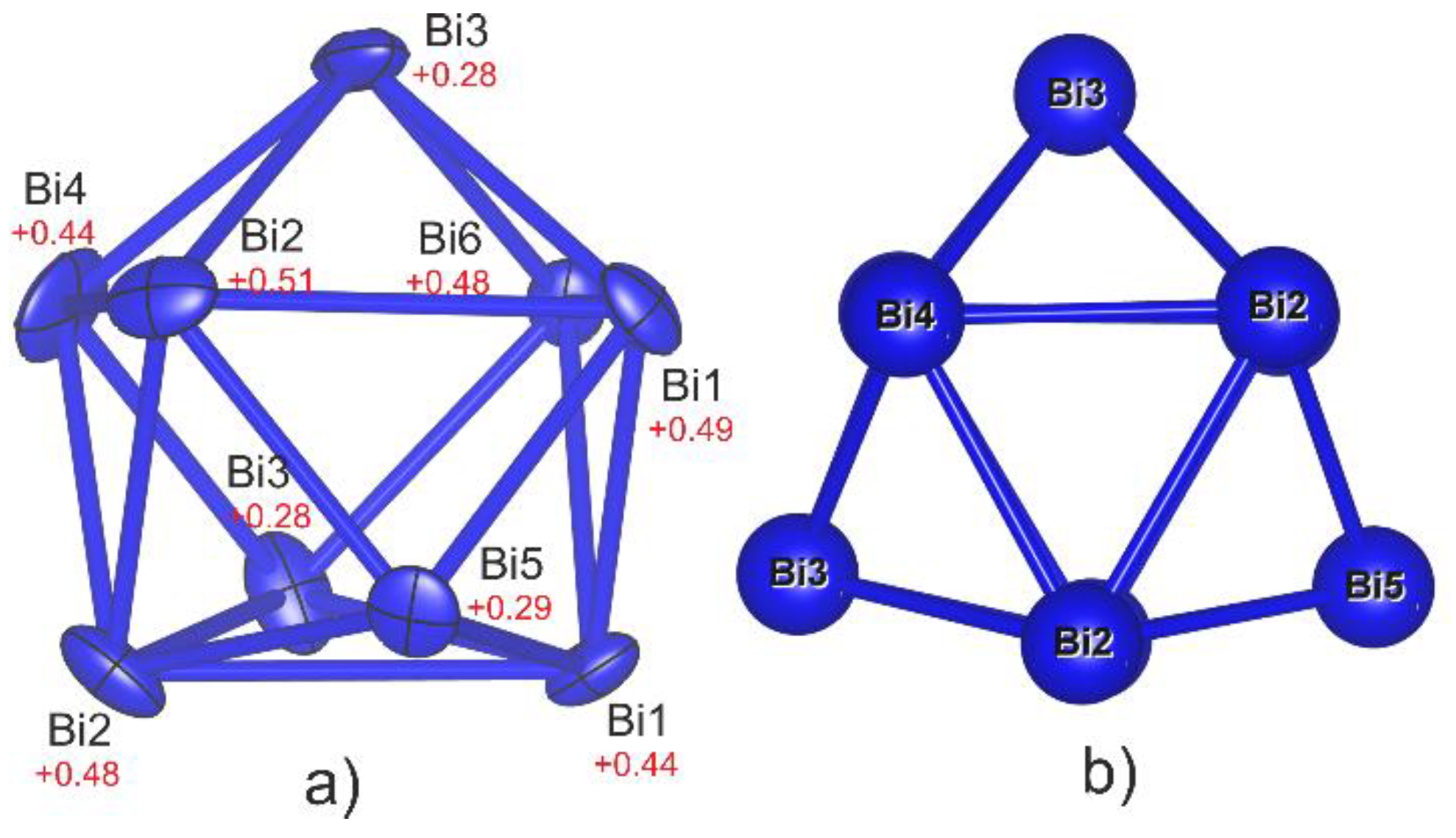
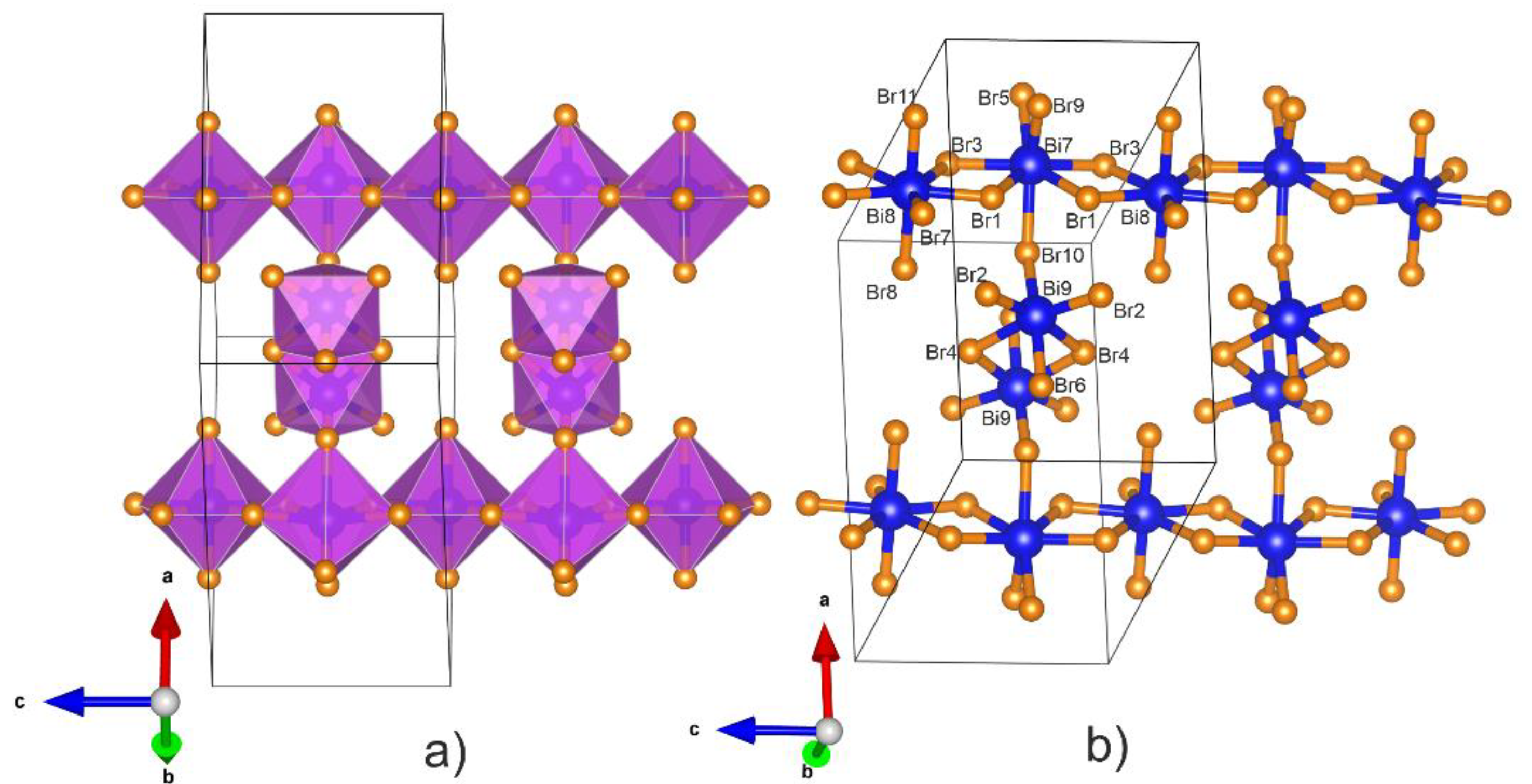
3.1. Crystal Structure of Bi6Br7 and the Geometry of Bi95+
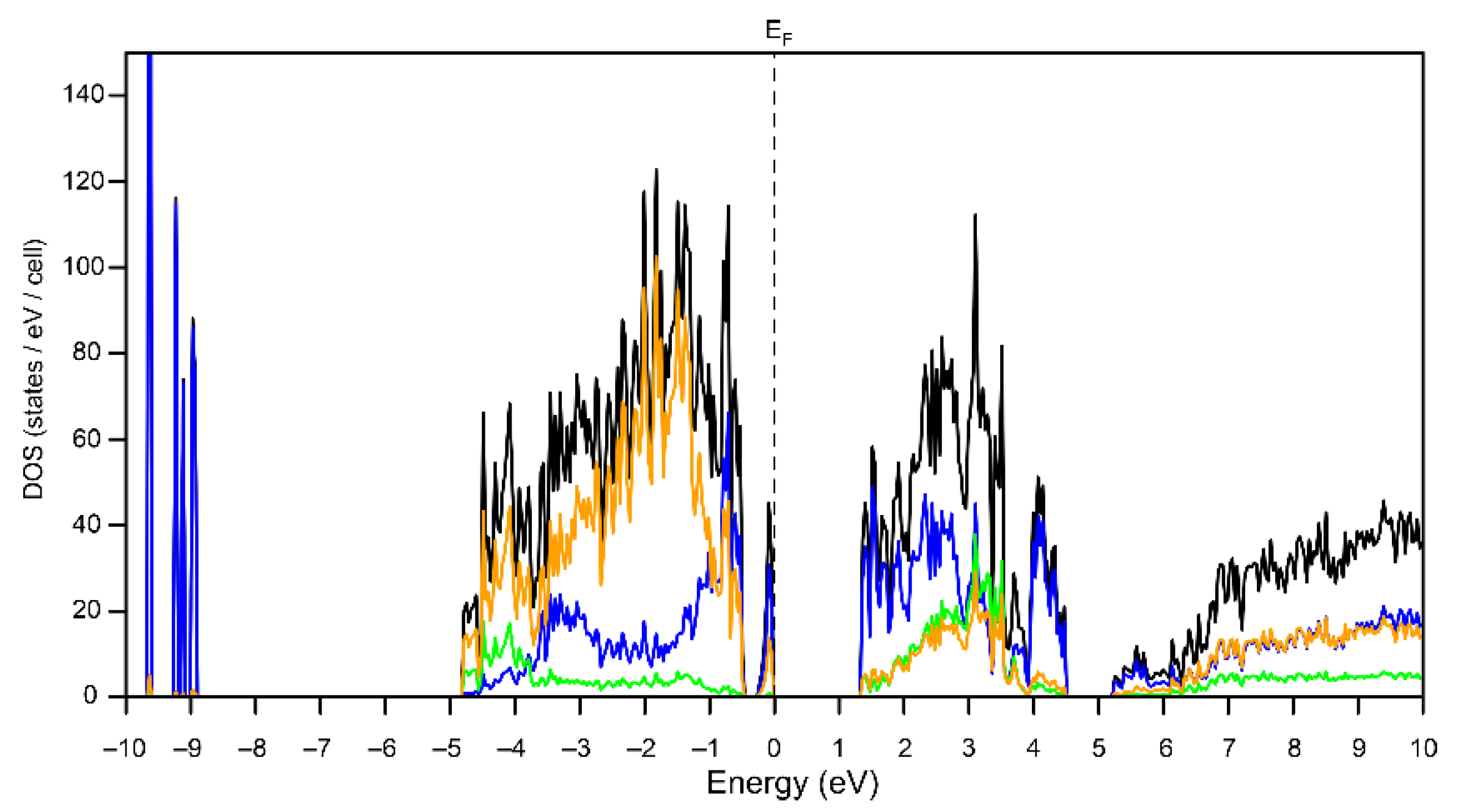
3.2. Electronic Structure of Bi6Br7
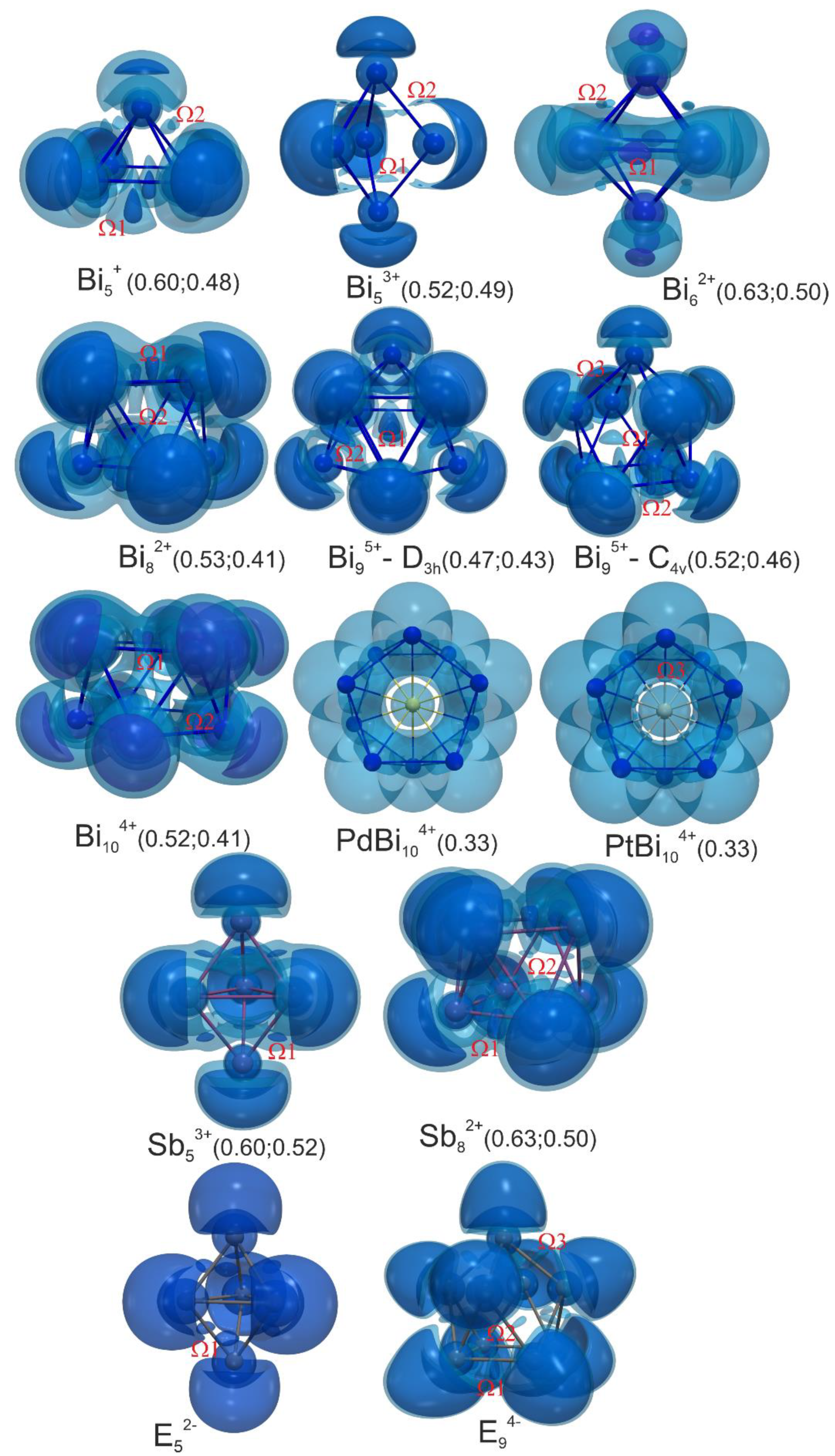
3.3. Bonding in Bismuth Polycations and Isoelectronic Main-Group Metal Clusters: 3D-Aromaticity vs. Localized Bonding
3.3.1. Five-vertex Polyhedra
3.3.2. Six-vertex Polyhedra
3.3.3. Eight-vertex Polyhedra
3.3.4. Nine-vertex Polyhedra
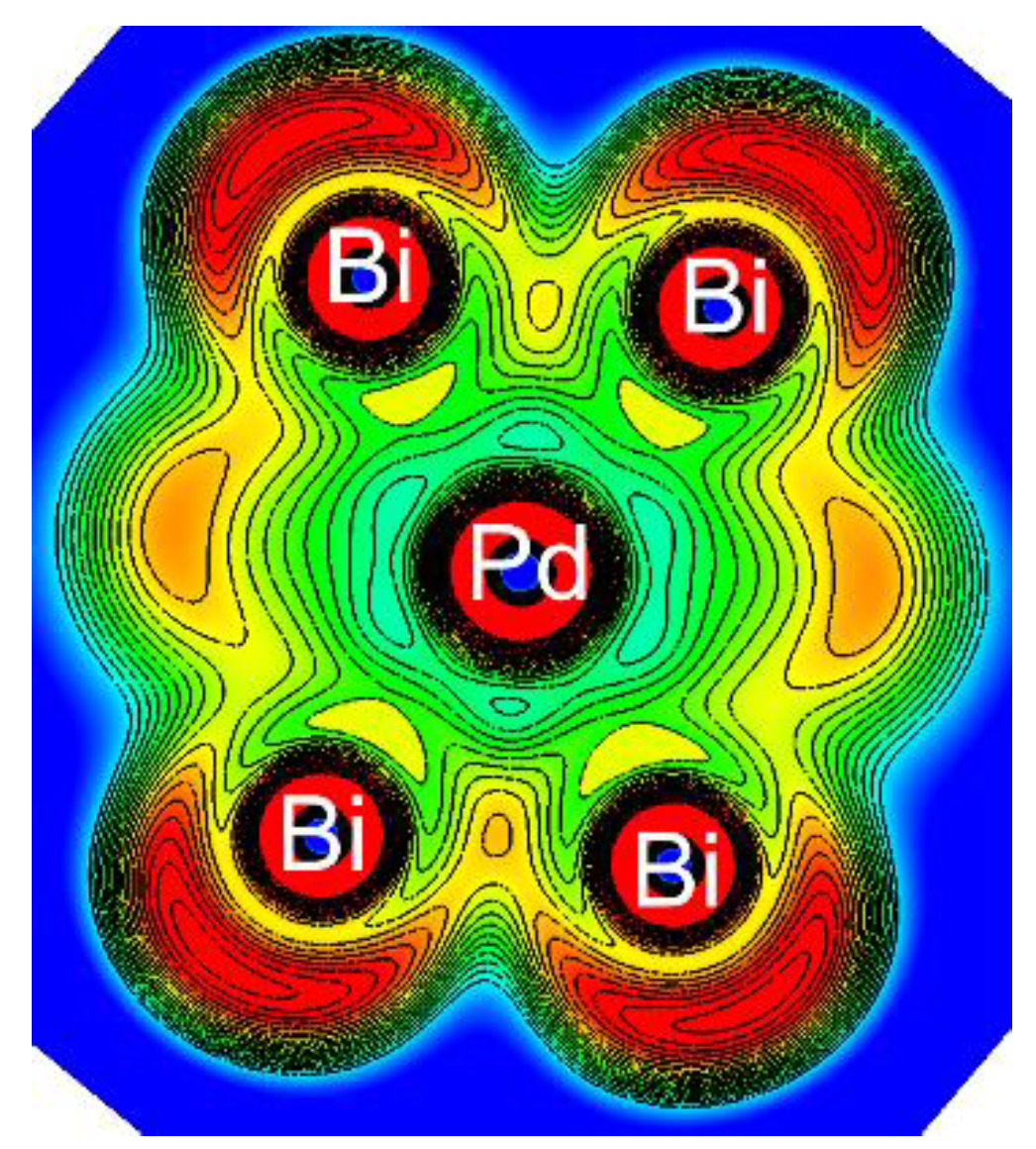
3.3.5. Ten-vertex Polyhedra
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Corbett, J.D. Homopolyatomic ions of the post-transition elements—Synthesis, structure and bonding. In Progress in Inorganic Chemistry; Lippard, S.J., Ed.; Wiley & Sons: New York, NY, USA, 1976; Volume 21, pp. 129–159. [Google Scholar]
- Hershaft, A.; Corbett, J.D. The Crystal Structure of Bismuth Subchloride. Identification of the Ion Bi95+. Inorg. Chem. 1963, 2, 979–985. [Google Scholar] [CrossRef]
- Friedman, R.M.; Corbett, J.D. Synthesis and structural characterization of bismuth(1+) nonabismuth(5+) hexachlorohafnate(IV), Bi+Bi95+(HfCl62−)3. Inorg. Chem. 1973, 12, 1134–1139. [Google Scholar] [CrossRef]
- Von Benda, H.; Simon, A.; Bauhofer, W. Zur Kenntnis von BiBr und BiBr1,167. Z. Anorg. Allg. Chem. 1978, 438, 53–67. [Google Scholar] [CrossRef]
- Kuznetsov, A.N.; Shevelkov, A.V.; Troyanov, S.I.; Popovkin, B.A. New phases containing the Bi-9(5+) cluster polycation: Crystal structure of Bi10Zr3Br18. Russ. J. Inorg. Chem. 1996, 41, 920–923. [Google Scholar]
- Kuznetsov, A.N.; Shevelkov, A.V.; Popovkin, B.A. New Cluster Phases Containing Bi(9)(5+) Polycation: Disordered Structures. Russ. J. Coord. Chem. 1998, 24, 861–866. [Google Scholar]
- Kuznetsov, A.N.; Naumenko, P.I.; Popovkin, B.A.; Kloo, L. New representative of Bi95+-containing phases: Synthesis and crystal structure of the Nb(IV)-containing Bi10Nb3Cl18 compound. Russ. Chem. Bull. 2003, 112, 2100–2104. [Google Scholar] [CrossRef]
- Ruck, M.; Dubenskyy, V. Bi37InBr48: Eine polares Subhalogenid mit Bi95+-Polykationen, komplexen Bromobismutat(III)-Anionen [Bi3Br13]4− und [Bi7Br30]9− sowie Pentabromoindat(III)-Anionen [InBr5]2−. Z. Anorg. Allg. Chem. 2003, 629, 375–380. [Google Scholar] [CrossRef]
- Hampel, S.; Schmidt, P.; Ruck, M. Synthese, thermochemische Eigenschaften und Kristallstruktur von Bi7Cl10. Z. Anorg. Allg. Chem. 2005, 631, 272–283. [Google Scholar] [CrossRef]
- Wahl, B.; Ruck, M. Ag3Bi14Br21: Ein Subbromid mit Bi24+-Hanteln und Bi95+-Polyedern—Synthese, Kristallstruktur und Chemische Bindung. Z. Anorg. Allg. Chem. 2008, 634, 2873–2879. [Google Scholar] [CrossRef]
- Wahl, B.; Ruck, M. Finally Fulfilling Wade’s Rules: The C4v Symmetric Polycation Bi95+ in the Polar Structure of Bi18Sn7Br24 = (Bi95+)2[Sn7Br2410−]. Z. Anorg. Allg. Chem. 2010, 636, 337–342. [Google Scholar] [CrossRef] [Green Version]
- Gerisch, A.; Ruck, M. (Bi9)4[Bi3Pb9Br47]: Probing the limits of the concept “crystal”. Z. Kristallogr. 2011, 226, 613–618. [Google Scholar] [CrossRef]
- Pabst, F.; Chang, J.-H.; Finzel, K.; Kohout, M.; Schmidt, P.; Ruck, M. The Subbromide Bi5Br4—On the Existence of a Hidden Phase. Z. Anorg. Allg. Chem. 2020, 646, 149–155. [Google Scholar] [CrossRef] [Green Version]
- Corbett, J.D. Homopolyatomic ions of the heavy post-transition elements. Preparation, properties, and bonding of Bi5(AlCl4)3 and Bi4(AlCl4). Inorg. Chem. 1968, 7, 198–208. [Google Scholar] [CrossRef]
- Krebs, B.; Mummert, M.; Brendel, C. Characterization of the Bi53+ cluster cation: Preparation of single crystals, crystal and molecular structure of Bi5(AlCl4)3. J. Less Common Met. 1986, 116, 159–168. [Google Scholar] [CrossRef]
- Ulvenlund, S.; Ståhl, K.; Bengtsson-Kloo, L. Structural and Quantum Chemical Study of Bi53+ and Isoelectronic Main-Group Metal Clusters. The Crystal Structure of Pentabismuth(3+) Tetrachlorogallate(III) Refined from X-ray Powder Diffraction Data and Synthetic Attempts on Its Antimony Analogue. Inorg. Chem. 1996, 35, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.N.; Popovkin, B.A.; Ståhl, K.; Lindsjö, M.; Kloo, L. Synthesis of Main-Group Polycations in Molten and Pseudo-Molten GaBr3 Media. Eur. J. Inorg. Chem. 2005, 2005, 4907–4913. [Google Scholar] [CrossRef]
- Lindsjö, M.; Fischer, A.; Kloo, L. Improvements of and Insights into the Isolation of Bismuth Polycations from Benzene Solution—Single-Crystal Structure Determinations of Bi8[GaCl4]2 and Bi5[GaCl4]3. Eur. J. Inorg. Chem. 2005, 2005, 670–675. [Google Scholar] [CrossRef]
- Ruck, M.; Steden, F. Bi53+-Polykationen in geordneten und plastischen Kristallen von Bi5[AlI4]3 und Bi5[AlBr4]3. Z. Anorg. Allg. Chem. 2007, 633, 1556–1562. [Google Scholar] [CrossRef]
- Friedman, R.M.; Corbett, J.D. On the synthesis and crystal structure of dodecabismuth tetradecachloride, Bi12Cl14. Inorg. Chim. Acta 1973, 7, 525–527. [Google Scholar] [CrossRef]
- Krebs, B.; Hucke, M.; Brendel, C.J. Structure of the Octabismuth(2+) Cluster in Crystalline Bi8(AlCl4)2. Angew. Chem. Int. Ed. Engl. 1982, 21, 445–446. [Google Scholar] [CrossRef]
- Kuznetsov, A.N.; Popovkin, B.A. Bi8(InBr4)2: A New Pseudo-hexagonal Bismuth Subbromide Containing Bi82+ Clusters. Z. Anorg. Allg. Chem. 2002, 628, 2179. [Google Scholar] [CrossRef]
- Beck, J.; Hilbert, T. Crystal Structure and Magnetic Properties of Bi(Bi9)[NbCl6]3, a New Member of the Structure Family Bi(Bi9)[MX6]3, and the Crystal Structure of Bi8[Ta2O2Br7]2. Eur. J. Inorg. Chem. 2004, 2014, 2019–2026. [Google Scholar] [CrossRef]
- Knies, M.; Kaiser, M.; Anh, M.L.; Efimova, A.; Doert, T.; Ruck, M. Low-Temperature Ordering in the Cluster Compound (Bi8)Tl[AlCl4]3. Inorganics 2019, 7, 45. [Google Scholar] [CrossRef] [Green Version]
- Ruck, M. Bi34Ir3Br37: Ein pseudosymmetrisches Subbromid aus Bi5+- und Bi62+-Polykationen sowie [IrBi6Br12]−—Und [IrBi6Br13]2−-Clusteranionen. Z. Anorg. Allg. Chem. 1998, 624, 521–528. [Google Scholar] [CrossRef]
- Ruck, M.; Hampel, S. Stabilization of homonuclear Bi5+ and Bi62+ polycations by cluster anions in the crystal structures of Bi12−xIrCl13−x, Bi12−xRhCl13−x and Bi12−xRhBr13−x. Polyhedron. 2002, 21, 651–656. [Google Scholar] [CrossRef]
- Hampel, S.; Ruck, M. Synthesen, Eigenschaften und Kristallstrukturen der Cluster-Salze Bi6[PtBi6Cl12] und Bi2/3[PtBi6Cl12]. Z. Anorg. Allg. Chem. 2006, 632, 1150–1156. [Google Scholar] [CrossRef]
- Ruck, M.; Dubenskyy, V.; Söhnel, T. Structure and Bonding of Pd@[Bi10]4+ in the Subbromide Bi14PdBr16. Angew. Chem. Int. Ed. 2003, 42, 2978–2982. [Google Scholar] [CrossRef] [PubMed]
- Ruck, M.; Dubenskyy, V.; Söhnel, T. Das Subchlorid Bi16PdCl22: Pd@Bi104+-Polykationen in einem Raumnetzwerk aus Chlorobismutat(III)-Anionen. Z. Anorg. Allg. Chem. 2004, 630, 2458–2462. [Google Scholar] [CrossRef]
- Wahl, B.; Erbe, M.; Gerisch, A.; Kloo, L.; Ruck, M. Nobel-Metal Centered Polycations [Au@Bi10]5+ or [Pd@Bi10]4+ Embedded in Halogenido-Bismuthate(III)-Stannate(II) Frameworks. Z. Anorg. Allg. Chem. 2009, 635, 743–752. [Google Scholar] [CrossRef]
- Groh, M.F.; Wolff, A.; Wahl, B.; Rasche, B.; Gebauer, P.; Ruck, M. Pentagonal Bismuth Antiprisms with Endohedral Palladium or Platinum Atoms by Low-Temperature Syntheses. Z. Anorg. Allg. Chem. 2017, 643, 69–80. [Google Scholar] [CrossRef]
- Ahmed, E.; Ruck, M. Homo- and heteroatomic polycations of groups 15 and 16. Recent advances in synthesis and isolation using room temperature ionic liquids. Coord. Chem. Rev. 2011, 255, 2892–2903. [Google Scholar] [CrossRef]
- Groh, M.F.; Wolff, A.; Grasser, M.A.; Ruck, M. Controlled Synthesis of Polyions of Heavy Main-Group Elements in Ionic Liquids. Int. J. Mol. Sci. 2016, 17, 1452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindsjö, M.; Fischer, A.; Kloo, L. Sb8(GaCl4)2: Isolation of a Homopolyatomic Antimony Cation. Angew. Chemie Int. Ed. Engl. 2004, 43, 2540–2543. [Google Scholar] [CrossRef] [PubMed]
- Goicoechea, J.M. Homoatomic Polyanions of the Early p-Block Elements. Struct. Bond. 2016, 174, 63–97. [Google Scholar] [CrossRef]
- Beck, J.; Brendel, C.J.; Bengtsson-Kloo, L.; Krebs, B.; Mummert, M.; Stankowski, A.; Ulvenlund, S. The Crystal Structure of Bi8(AlCl4)2 and the Crystal Structure, Conductivity, and Theoretical Band Structure of Bi6Cl7 and Related Subvalent Bismuth Halides. Chem. Ber. 1996, 129, 1219–1226. [Google Scholar] [CrossRef]
- Groh, M.F.; Müller, U.; Ahmed, E.; Rothenberger, A.; Ruck, M. Substitution of Conventional High-temperature Syntheses of Inorganic Compounds by Near-room-temperature Syntheses in Ionic Liquids. Z. Naturforsch. 2013, 68, 1108–1122. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Kohout, M.; Savin, A. Atomic shell structure and electron numbers. Int. J. Quantum Chem. 1996, 60, 875–882. [Google Scholar] [CrossRef] [Green Version]
- Savin, A.; Jepsen, O.; Flad, J.; Andersen, O.K.; Preuss, H.; von Schnering, H.G. Electron Localization in Solid-State Structures of the Elements: The Diamond Structure. Angew. Chem. Int. Ed. Engl. 1992, 31, 187–188. [Google Scholar] [CrossRef]
- Kuznetsov, A.N.; Kloo, L.; Lindsjö, M.; Rosdahl, J.; Stoll, H. Ab Initio Calculations on Bismuth Cluster Polycations. Chem. Eur. J. 2001, 7, 2821–2828. [Google Scholar] [CrossRef]
- Filatova, T.G.; Gurin, P.V.; Kloo, L.; Kulbachinskii, V.A.; Kuznetsov, A.N.; Kytin, V.G.; Lindsjo, M.; Popovkin, B.A. Electronic structure, galvanomagnetic and magnetic properties of the bismuth subhalides Bi4I4 and Bi4Br4. J. Solid State Chem. 2007, 180, 1103–1109. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELX-2018/2. Program Package for Crystal Structure Solution and Refinement; Georg-August-Universität Göttingen: Göttingen, Germany, 2018. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Vienna Ab-Initio Simulation Package (VASP); v.5.4.4; Vienna University: Vienna, Austria, 2001. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integration. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 8, e1327. [Google Scholar] [CrossRef]
- Rappoport, D.; Furche, F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef]
- Metz, B.; Stoll, H.; Dolg, M. Small-core multiconfiguration-Dirac–Hartree–Fock-adjusted pseudopotentials for post-d main group elements: Application to PbH and PbO. J. Chem. Phys. 2000, 113, 2563–2569. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, X.; Truhlar, D.G. Minimally augmented Karlsruhe basis sets. Theor. Chem. Acc. 2011, 128, 295–305. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyser. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- wxDragon, ver.2.2.3. Available online: http://www.wxdragon.de/ (accessed on 15 October 2020).
- De la Flor, G.; Orobengoa, D.; Tasci, E.; Perez-Mato, J.M.; Aroyo, M.I. Comparison of structures applying the tools available at the Bilbao Crystallographic Server. J. Appl. Cryst. 2016, 49, 653–664. [Google Scholar] [CrossRef]
- Lepetit, C.; Fau, P.; Fajerwerg, K.; Kahn, M.L.; Silvi, B. Topological analysis of the metal-metal bond: A tutorial review. Coord. Chem. Rev. 2017, 345, 150–181. [Google Scholar] [CrossRef] [Green Version]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi. J. Chem. Phys. 1985, 82, 284–298. [Google Scholar] [CrossRef]
- Kuechle, W.; Dolg, M.; Stoll, H.; Preuss, H. Ab initio pseudopotentials for HG through RN. 1. Parameter sets and atomic calculations. Mol. Phys. 1991, 74, 1245–1263. [Google Scholar] [CrossRef]
- Kohout, M.; Wagner, F.R.; Grin, Y. Electron localization function for transition-metal compounds. Theor. Chim. Acc. 2002, 108, 150–156. [Google Scholar] [CrossRef]
- Rosdahl, J.; Fässler, T.F.; Kloo, L. On the Structure of Nonastannide Clusters in Liquid and Solid State. Eur. J. Inorg. Chem. 2005, 2005, 2888–2894. [Google Scholar] [CrossRef]
- Zakharova, E.Y.; Andreeva, N.A.; Kazakov, S.M.; Kuznetsov, A.N. Ternary arsenides based on platinum-indium and palladium-indium fragments of the Cu3Au-type: Crystal structures and chemical bonding. J. Alloy. Compd. 2015, 621, 307–313. [Google Scholar] [CrossRef]
- Zakharova, E.Y.; Kazakov, S.M.; Götze, A.; Kohlmann, H.; Kuznetsov, A.N. Ternary palladium-indium-phosphorus and platinum-indium-phosphorus compounds based on the Cu3Au-type: Structure, bonding, and properties. J. Solid State Chem. 2018, 265, 266–273. [Google Scholar] [CrossRef]
- Zakharova, E.Y.; Kazakov, S.M.; Isaeva, A.A.; Abakumov, A.M.; Van Tendeloo, G.; Kuznetsov, A.N. Pd5InSe and Pd8In2Se—New metal-rich homological selenides with 2D palladium-indium fragments: Synthesis, structure and bonding. J. Alloys Compd. 2014, 589, 48–55. [Google Scholar] [CrossRef]
- Plokhikh, I.V.; Khan, N.; Tsirlin, A.A.; Kuznetsov, A.N.; Charkin, D.O.; Shevelkov, A.V.; Pfitzner, A. Synthesis, crystal and electronic structures of Pt-rich phosphides EuPt3P and EuPt6P2. Dalton Trans. 2019, 48, 15272–15282. [Google Scholar] [CrossRef] [PubMed]

| Atoms | Distance, Å | Atoms | Distance, Å | Atoms | Distance, Å |
|---|---|---|---|---|---|
| Bi(1)-Bi(1) | 3.1847(17) | Bi(3)-Bi(4) | 3.1008(12) | Bi(8)-Br(8) | 2.938(3) |
| Bi(1)-Bi(3) | 3.1229(10) | Bi(7)-Br(1) | 3.024(2) | Bi(8)-Br(11) | 2.739(3) |
| Bi(1)-Bi(5) | 3.1244(11) | Bi(7)-Br(3) | 2.913(2) | Bi(9)-Br(2) | 2.736(2) |
| Bi(1)-Bi(6) | 3.2245(12) | Bi(7)-Br(5) | 3.037(3) | Bi(9)-Br(4) | 3.017(2) |
| Bi(2)-Bi(2) | 3.3017(17) | Bi(7)-Br(9) | 2.775(3) | Bi(9)-Br(6) | 2.781(3) |
| Bi(2)-Bi(3) | 3.1443(11) | Bi(7)-Br(10) | 3.112(3) | Bi(9)-Br(10) | 3.013(3) |
| Bi(2)-Bi(4) | 3.1646(13) | Bi(8)-Br(1) | 2.872(2) | ||
| Bi(2)-Bi(5) | 3.0855(12) | Bi(8)-Br(3) | 3.148(2) | ||
| Bi(3)-Bi(6) | 3.0821(11) | Bi(8)-Br(7) | 2.787(3) |
| Polyion | Symmetry | Basin Population, e | ||
|---|---|---|---|---|
| Ω1 | Ω2 | Ω3 | ||
| Bi5+ | C4v | 1.81 | 0.84 | - |
| Bi53+ | D3h | 0.72 | 0.70 | - |
| Bi62+ | D4h | 1.45 | 0.95 | - |
| Bi82+ | D4d | 1.61 | 0.21 | - |
| Bi95+ | D3h | 1.36 | 1.17 | - |
| Bi95+ | C4v | 1.36 | 1.57 | 1.02 |
| Bi95+ (Bi6Br7) | CS | 1.19 | 0.89/0.83 | |
| Bi104+ | D5d | 1.83 | 1.03 | - |
| PdBi104+ | D5d | 0.85 | 0.58 | 0.21 |
| PtBi104+ | D5d | 0.83 | 0.58 | 0.33 |
| Sb53+ | D3h | 1.7 | - | - |
| Sb82+ | D4d | 1.52 | 0.51 | - |
| Ge52− | D3h | 1.33 | - | - |
| Ge94− | C4v | 1.06 | 0.99 | 0.96 |
| Sn52− | D3h | 1.35 | - | - |
| Sn94− | C4v | 0.95 | 0.94 | 0.92 |
| Pb52− | D3h | 0.89 | - | - |
| Pb94− | C4v | 0.89 | 0.88 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stroganova, E.A.; Troyanov, S.I.; Morozov, I.V.; Kuznetsov, A.N. Bismuth Polycations Revisited: Alternative Synthesis and Electronic Structure of Bi6Br7, and Bonding in Main-Group Polyatomic Ions from a Direct Space Perspective. Crystals 2020, 10, 940. https://doi.org/10.3390/cryst10100940
Stroganova EA, Troyanov SI, Morozov IV, Kuznetsov AN. Bismuth Polycations Revisited: Alternative Synthesis and Electronic Structure of Bi6Br7, and Bonding in Main-Group Polyatomic Ions from a Direct Space Perspective. Crystals. 2020; 10(10):940. https://doi.org/10.3390/cryst10100940
Chicago/Turabian StyleStroganova, Ekaterina A., Sergey I. Troyanov, Igor V. Morozov, and Alexey N. Kuznetsov. 2020. "Bismuth Polycations Revisited: Alternative Synthesis and Electronic Structure of Bi6Br7, and Bonding in Main-Group Polyatomic Ions from a Direct Space Perspective" Crystals 10, no. 10: 940. https://doi.org/10.3390/cryst10100940
APA StyleStroganova, E. A., Troyanov, S. I., Morozov, I. V., & Kuznetsov, A. N. (2020). Bismuth Polycations Revisited: Alternative Synthesis and Electronic Structure of Bi6Br7, and Bonding in Main-Group Polyatomic Ions from a Direct Space Perspective. Crystals, 10(10), 940. https://doi.org/10.3390/cryst10100940