1. Introduction
The Kondo insulator is a class of matter in which the Kondo effect is significant and the electrons are treated as quasiparticles termed heavy fermions [
1]. The most striking feature of the Kondo insulator is that the energy gap opens at a low temperature and it becomes an insulator, in contrast to the fact that most of the materials experiencing the Kondo effect strongly are metal (so-called heavy fermion system). The Kondo effect is a typical quantum many-body correlation effect and induces non-trivial intriguing phenomena, such as exotic superconductors [
2] and non-fermi liquid behaviors [
3]. Two theoretical models for explaining formation of the energy gap in Kondo insulators have been proposed; namely, the
c-
f hybridization gap model [
4,
5] and the localized electron-hole bound model [
6]. Although the localized model can explain the properties of the Kondo insulators with diluted
f electron systems, such as La
Yb
B
, the
c-
f hybridization gap model also reproduces the behavior of magnetic properties of the Kondo insulators well [
6]. Because there have been no experimental findings that clarify which model is closer to the real mechanism of the gap opening of the Kondo insulator, further experimental studies are needed. One of the fundamental properties to be studied is the temperature dependence of the energy gap. This is because the Kondo effect becomes significant only at low temperatures and the temperature variation should give crucial information regarding the mechanism of the gap formation. In addition to the interest in the mechanism of the energy gap’s formation, YbB
has been collecting much attention because quantum oscillations have recently been observed in the insulating phase [
7] and the origin is highly controversial; it could be due to the topological surface metallic state or bulk exotic quasi particles. Hence, understanding of the electronic states in YbB
has become one of the most intriguing issues to be urgently resolved.
We investigated the temperature dependence of the energy gap in a prototypical Kondo insulator YbB
. The energy gap opens around 100 K [
8] and the evolution of the Kondo effect manifests itself in the temperature dependence of magnetic susceptibility (
). The broad maximum in the
curve around 80 K suggests that the Kondo temperature (
) is around 240 K [
9]. YbB
undergoes the magnetic-field-induced insulator-metal (IM) transition at around 50 T and the emergent metal phase has been proven to be in a heavy fermion (HF) state [
10]. The closing of the energy gap occurs along with the metamagnetic transition, and the high-field HF state is expected to be suppressed in higher magnetic fields of around 100 T [
11]. The temperature dependence of the energy gap has never been well understood in the Kondo insulator, although it is important to uncover its nature. In this study, the temperature dependence of the energy gap was investigated by measuring the metamagnetic transition at different temperatures. The transition magnetic field is a good measure of the energy gap through the Zeeman effect [
11]. It was found that the energy gap slightly decreases with increasing temperature. It is more striking that the transition gets broadened when temperature becomes higher than around 30 K, suggesting that the characteristic temperature
K exists in addition to the Kondo temperature
K in YbB
.
2. Experimental Procedures
Magnetic fields are generated by the vertical-type single-turn coil magnetic field generator installed in The Institute for Solid State Physics, The University of Tokyo [
12]. Ultrahigh pulsed magnetic fields of up to 200 T can be generated and used for several kinds of experiments of condensed-matter physics. The duration of the pulsed magnetic fields is around 6
s. The magnetization is measured using a pickup coil that consists of two small solenoids wound by copper wire of 60
m diameter. The two coils are used for compensation of the induction voltage of the pulsed magnetic fields [
13]. They are arranged in parallel to each other and electrically connected in series so that the polarity of the induction voltage is opposite. The sample is inserted into one of the two solenoids so that the induction of the magnetization is only applied to one of the small solenoids. Note that the response time of the magnetization measurement system used in the present work is around 10 ns; that is short enough to follow the magnetization as a function of the
s-duration magnetic field in many spin systems, such as SrCu
(BO
)
[
14]. If a material has a strong spin-lattice coupling such as solid oxygen [
15] the magnetization response delays due to the intrinsic response time of the material. For such a case, we evaluated the dynamics using different sweep speed of the pulsed magnetic fields. A single crystalline sample of YbB
was grown by the traveling solvent floating zone method using a four-xenon-lamp image furnace [
9]. Four xenon lamps are surrounded by ellipsoidal glass-mirrors coated with aluminum and cooled by blowers. The proportion of Yb to that of B in the solvent in a melting zone was set to be relatively a little less than that required for stoichiometric composition of YbB
. The temperature inhomogeneities with radial and circumferential directions were kept less than 50 °C at 2200 °C, which is important to grow a single crystal of YbB
[
9]. The crystals used were characterized with X-ray diffraction experiments and magnetic susceptibility, and it was confirmed that the quality of the crystal was as same as that reported in the previous work [
9,
16]. The sample was powdered and mixed with epoxy resin to suppress the heating by eddy current due to the pulsed high magnetic field.
3. Results
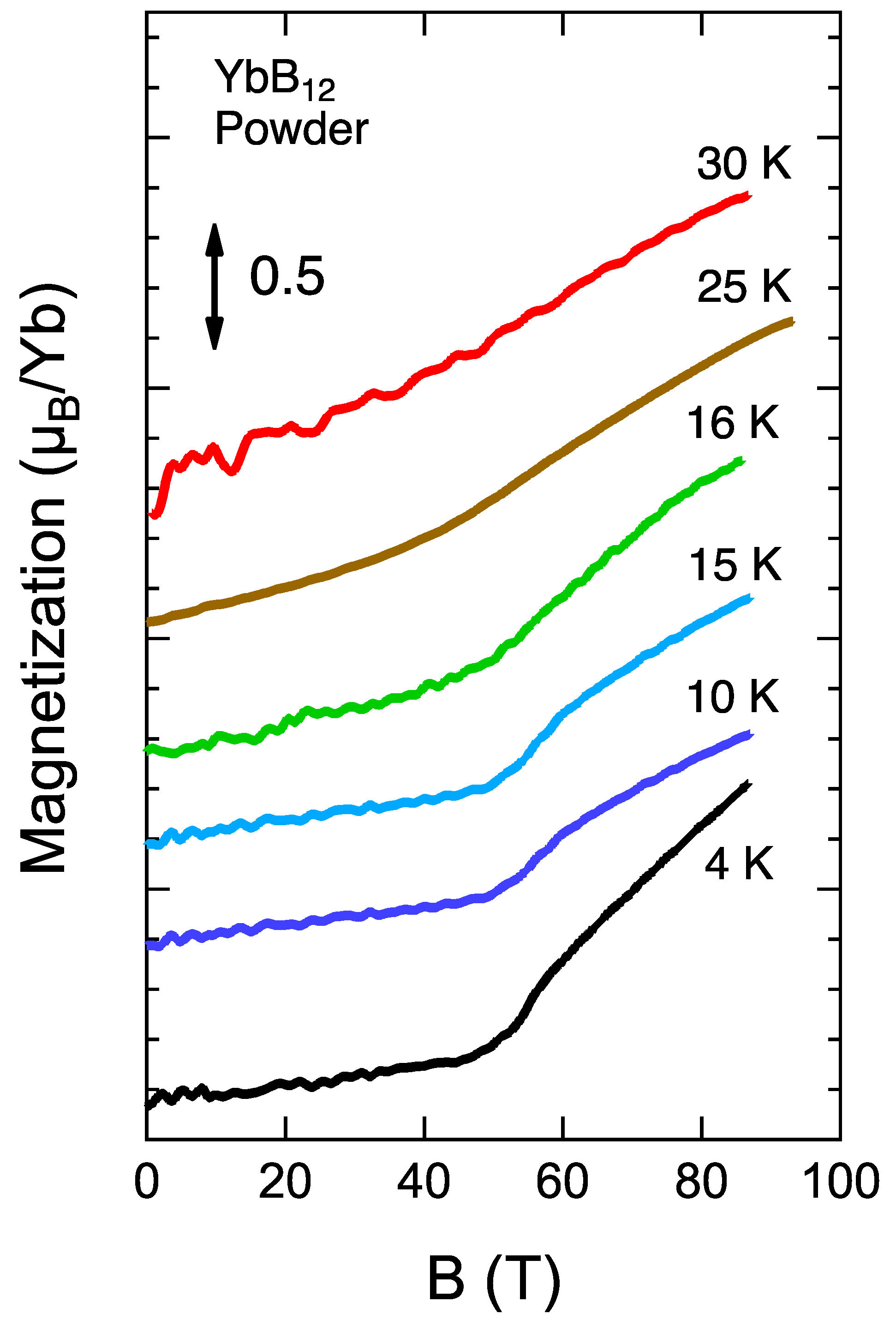
The magnetization processes at different temperatures are shown in
Figure 1. Only the field-ascending magnetization processes are shown because the magnetocaloric effect [
10] becomes significant and the temperature can be changed in the field descending process. The magnetic field was generated up to 105 T. Because the induction voltage from the magnetization change becomes close to zero at near the top of pulsed field, the accuracy of the measurement becomes degraded. Here, only the measured magnetization curves with high reliability are plotted. Because the magnetization process of YbB
in the
s duration pulsed magnetic fields was reported to be in good agreement with that measured in a ms-duration pulsed magnetic field [
11], the magnetization measured here was expected to have intrinsic values without any time delay. The magnetization is almost linear to the magnetic field at low fields and changes the slope at around 50 T. This behavior is consistent with previous reports [
11,
16,
17] and understood as the metamagnetism due to the IM transition. The transition was found to become broad with increasing temperature and obscured at 30 K.
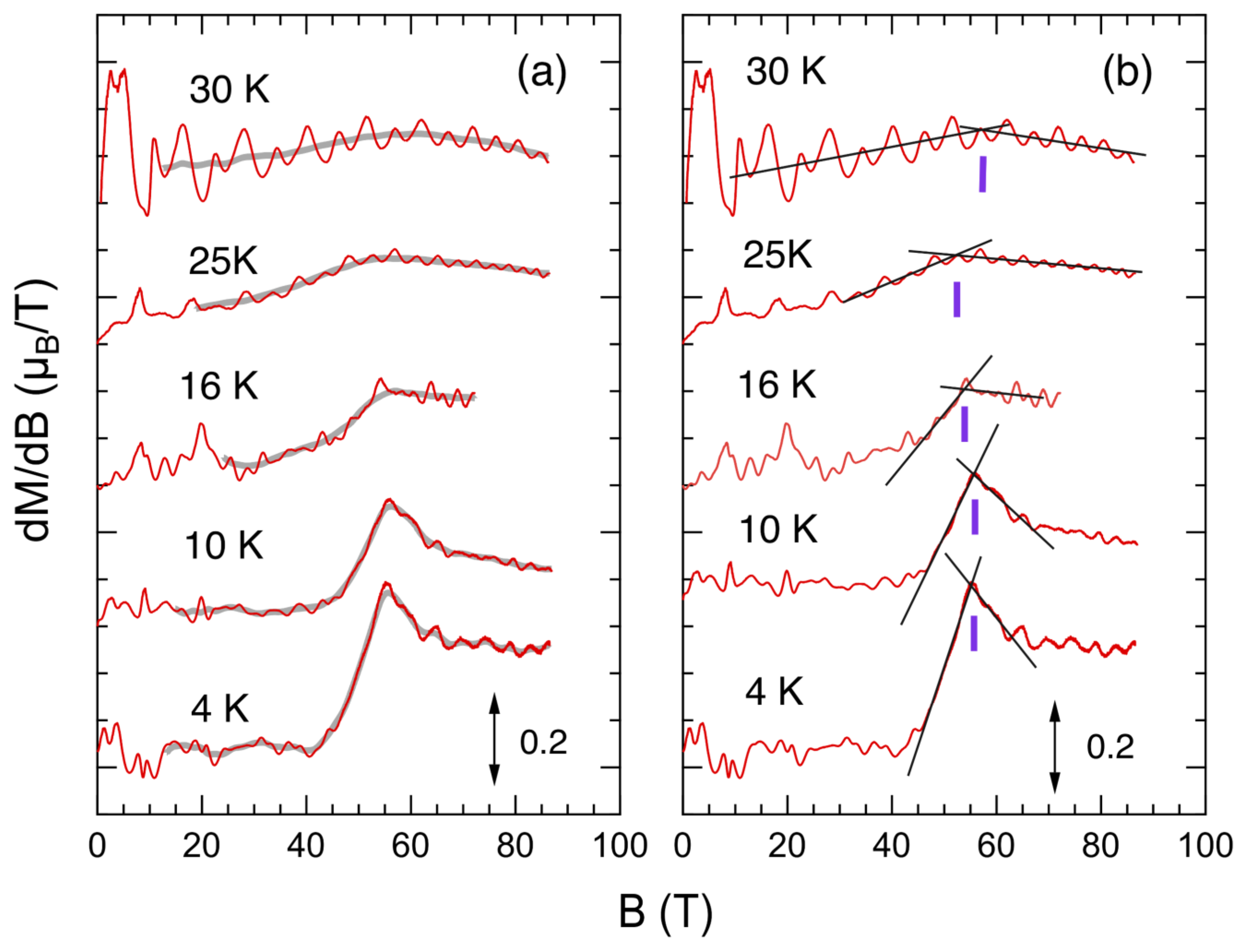
The transition magnetic fields were evaluated with the curves of the derivatives of the magnetization (
M) with respect to the magnetic fields (
B) (
). The temperature variation of the
curve is shown in
Figure 2a. At 4 and 10 K, the
curves exhibit clear peaks, indicating the abrupt change in the magnetization. The peak structure becomes broad and changes its shape to a sort of kink structure with increasing temperature.
The transition magnetic fields (
) can be evaluated by the peak or kink structure. Two tangential lines were computed using data in the vicinity of the peak or the kink, and the
was determined by the crossing point of the two lines, as shown in
Figure 2b.
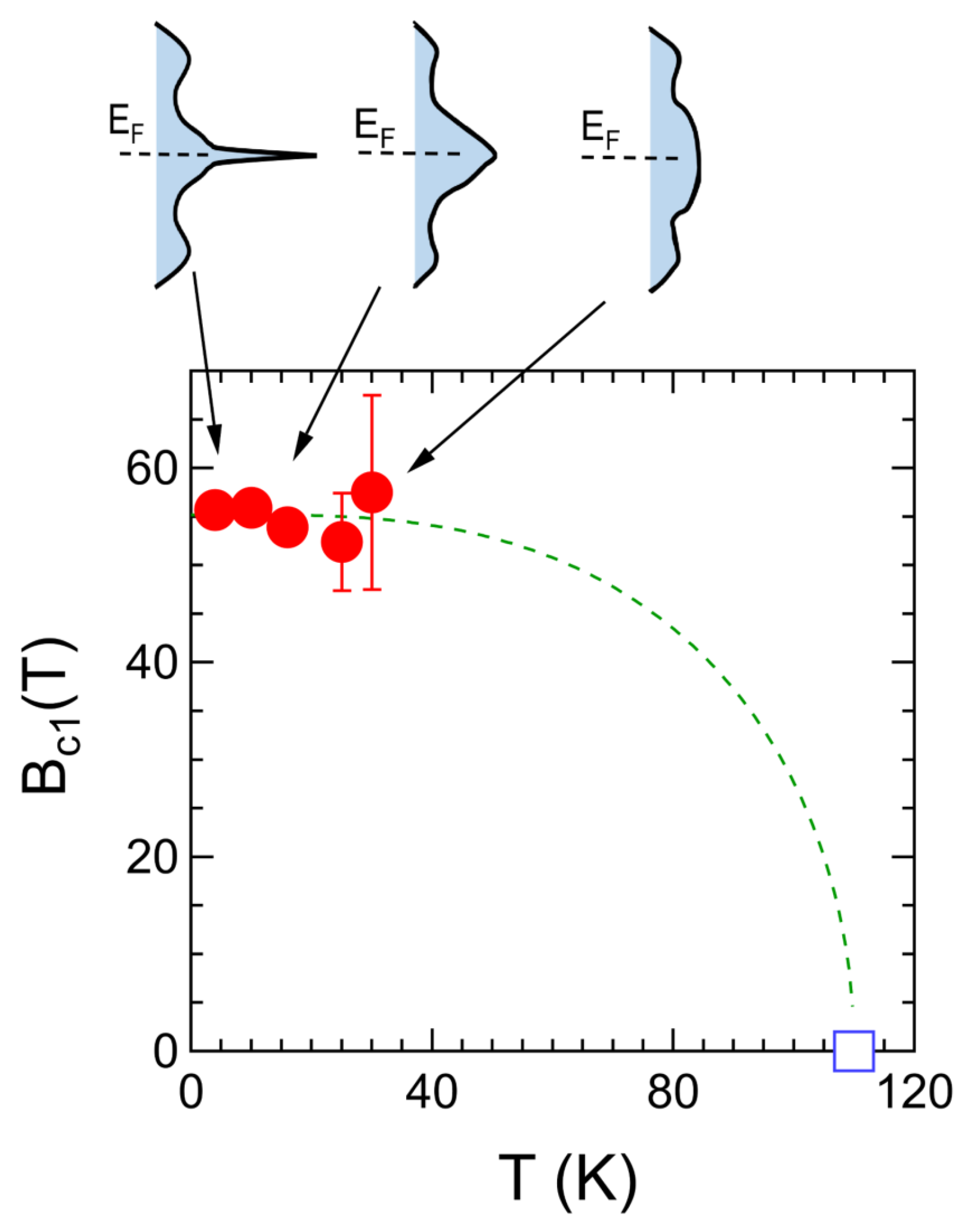
The obtained
is plotted as a function of temperature in
Figure 3. The temperature of starting the energy gap opening is reported to be around 100 K [
8] and it is also plotted in the figure. Since error bars of
at higher temperatures are large, it is difficult to discuss whether
monotonously decreases with increasing temperature or has a slight increase at around 30 K.
4. Discussion
The temperature dependence of the energy gap has not been well understood in strongly correlated electron systems. In YbB
, it was reported that the magnitude of the energy pap (
) is 15 meV at a low temperature [
8,
18], but the temperature variation of the energy gap has been unclear. Since it has been clarified that the magnetic-field-induced IM transition occurs by closing the energy gap due to the Zeeman shift of the energy levels [
11], the transition magnetic field
scales to the magnitude of the
as follows.
where
is given by calculation of the Zeeman shift of the crystal field energy levels of 4
f electrons of Yb
[
11] and not a constant value. It should be noted that the Zeeman energy is given by the local magnetic moment of Yb
and independent of temperature. Hence, the temperature variation of
is straightforwardly measured by
at different temperatures.
As shown in
Figure 3, the temperature dependence of
is not significant at temperatures up to 30 K, suggesting that the
is also weakly temperature dependent. A weak temperature variation of
at relatively low temperature region has been reported in other strongly correlated compounds, NdNiO
[
19] and VO
[
20]. The temperature variation of
in NdNiO
is analyzed by the BCS gap function [
19]. The BCS gap function can be approximately given by
(
T)
tanh(
), where
(
) [
21]. Although the origin of the formation of the energy gap is different between NdNiO
and YbB
, it is likely that the observed temperature dependence of the
is in agreement with the relation
(
T)
tanh(
).
Another feature found in the temperature dependence of the magnetization process is that the phase transition becomes significantly broad and unclear at 30 K, which is several times lower than the corresponding temperature of the
(174 K). If we simply evaluate the electron occupation ratio of the higher energy level at 30 K with
= 174 K; it is exp(–174/30)
. Hence, the effect of the thermal excitation is expected to be small; the significant temperature dependence of the sharpness of the
peak in
Figure 2a cannot be accounted for by the thermal excitation.
Here, it is worth noting that the temperature of the sample can be changed due to eddy current heating (joule heating) and magnetocaloric effect. The temperature rise (
) due to eddy current heating is proportional to the cross section of the sample at which
B penetrates. Hence, it is an effective way to suppress the heating to make the sample small. The diameter of each grain of powdered sample was expected to be several tens of
m, and to help reduce the eddy current heating. Moreover, because the smaller size sample has a large surface-to-volume ratio, a heat exchange between the sample and its environment was expected to be effective for the powdered sample and help to maintain the sample at constant temperature. As we have confirmed in previous work [
11] the magnetization process at 4 K is in good agreement with that obtained with a slower (ms) pulsed magnet, suggesting the temperature change during the magnetization process is not significant. The temperature change due to the magnetocaloric effect is several Kelvin when initial temperature is 4 K [
10].
There can be another smaller-energy-scale characteristic temperature
K than
(240 K). Such a characteristic temperature lower than the Kondo temperature has been reported in a heavy fermion compound YbRh
Si
[
22], and the spatial coherence of the Kondo effect is important in this case. On the other hand, a detailed study of element substitution effect of YbB
in Yb
R
B
(R = Y, Lu, Sc) has also revealed that there can be another Kondo temperature of around 25 K in YbB
[
23]. This temperature corresponds to the Kondo temperature in the hypothetical metallic YbB
and can be said to be a sort of hidden energy scale in the insulating phase of YbB
whose
is 240 K. If we consider the IM transition as a transition from a local Kondo state to a Kondo metal state, it can be said that the local character is suppressed at
, although the energy gap is still expected to be open. The Kondo lattice coherence temperature can be closely related to
. The density of states (DOS) at the Fermi energy at the IM transition magnetic field is suggested to grow and makes the Kondo resonance peak [
5]. The
can be understood as the magnetic susceptibility and is expected to be proportional to the DOS in the band magnetism. The diminishing of the
peak structure can suggest a suppression of the Kondo peak. Hence, one may expect that the Kondo coherence is disturbed at around
. In
Figure 3, we schematically show the temperature dependence of the DOS considering the theoretically calculated DOS [
5] at the IM transition magnetic fields. However, there has been no report on other experimental evidences of the Kondo lattice coherence temperature of YbB
. Detailed temperature dependence of the electrical resistivity or spectroscopic experiments in high magnetic fields could help to solve this issue.