Topological Equivalence of the Phase Diagrams of Molybdenum and Tungsten
Abstract
1. Introduction
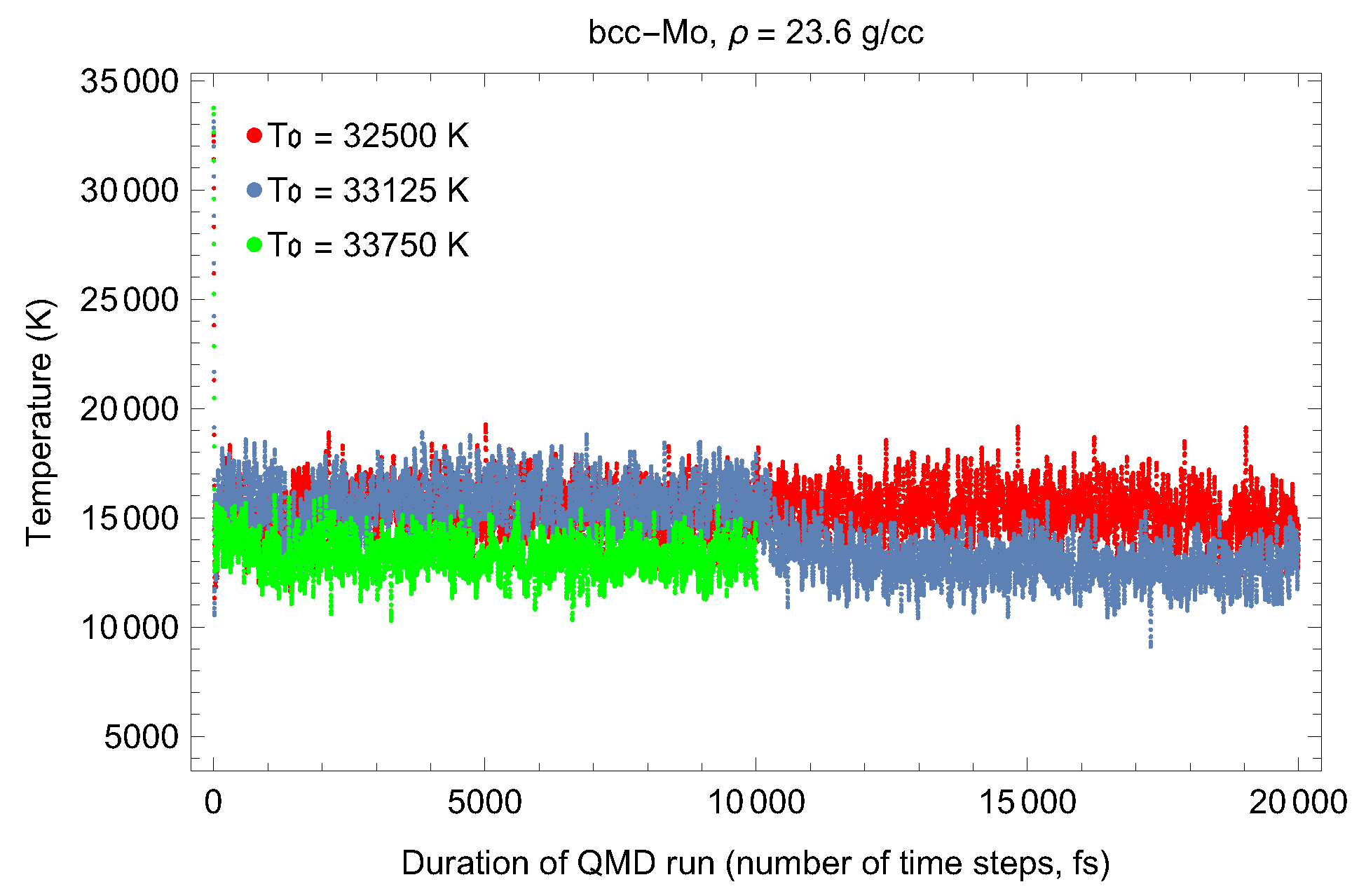
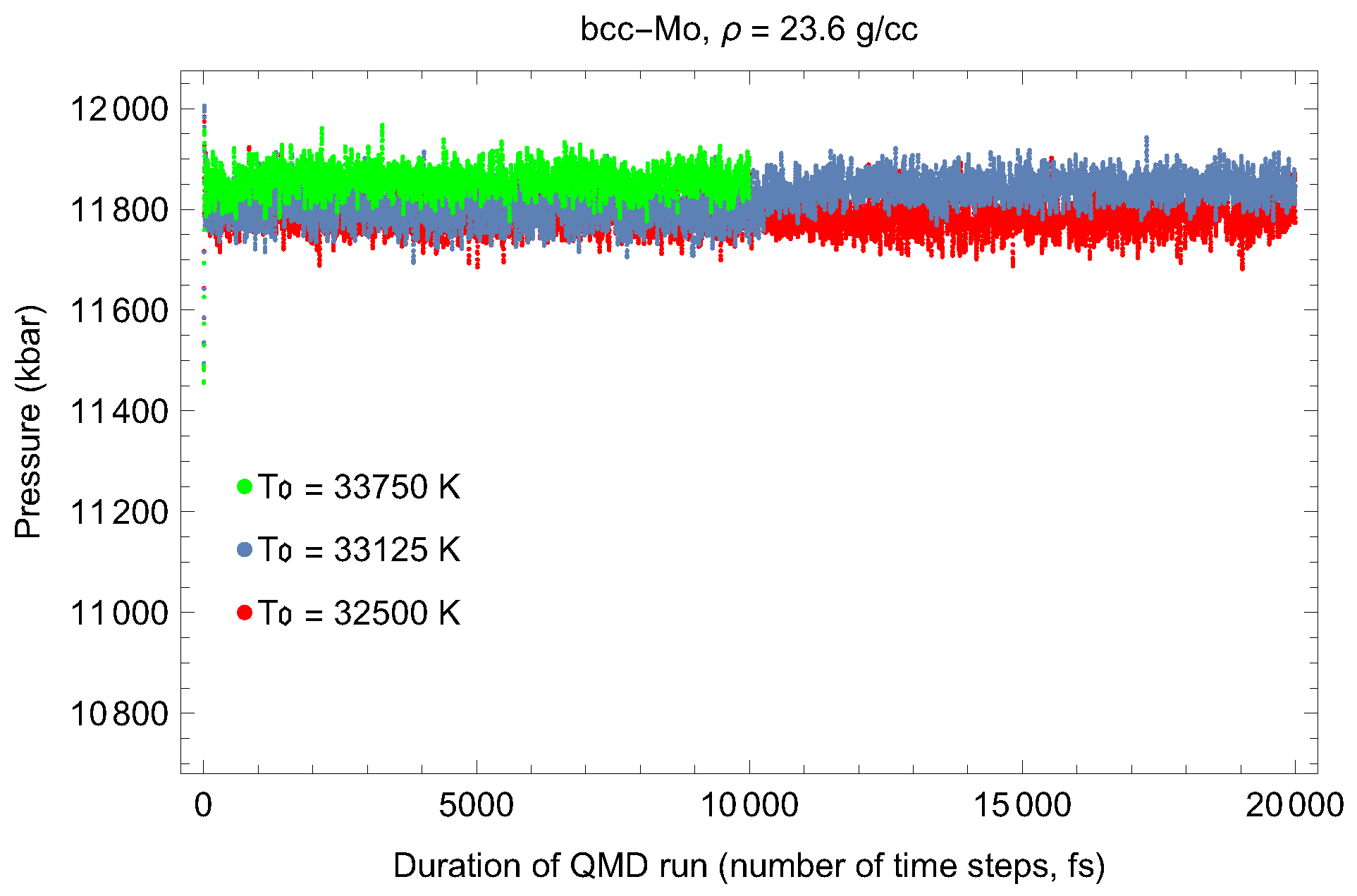
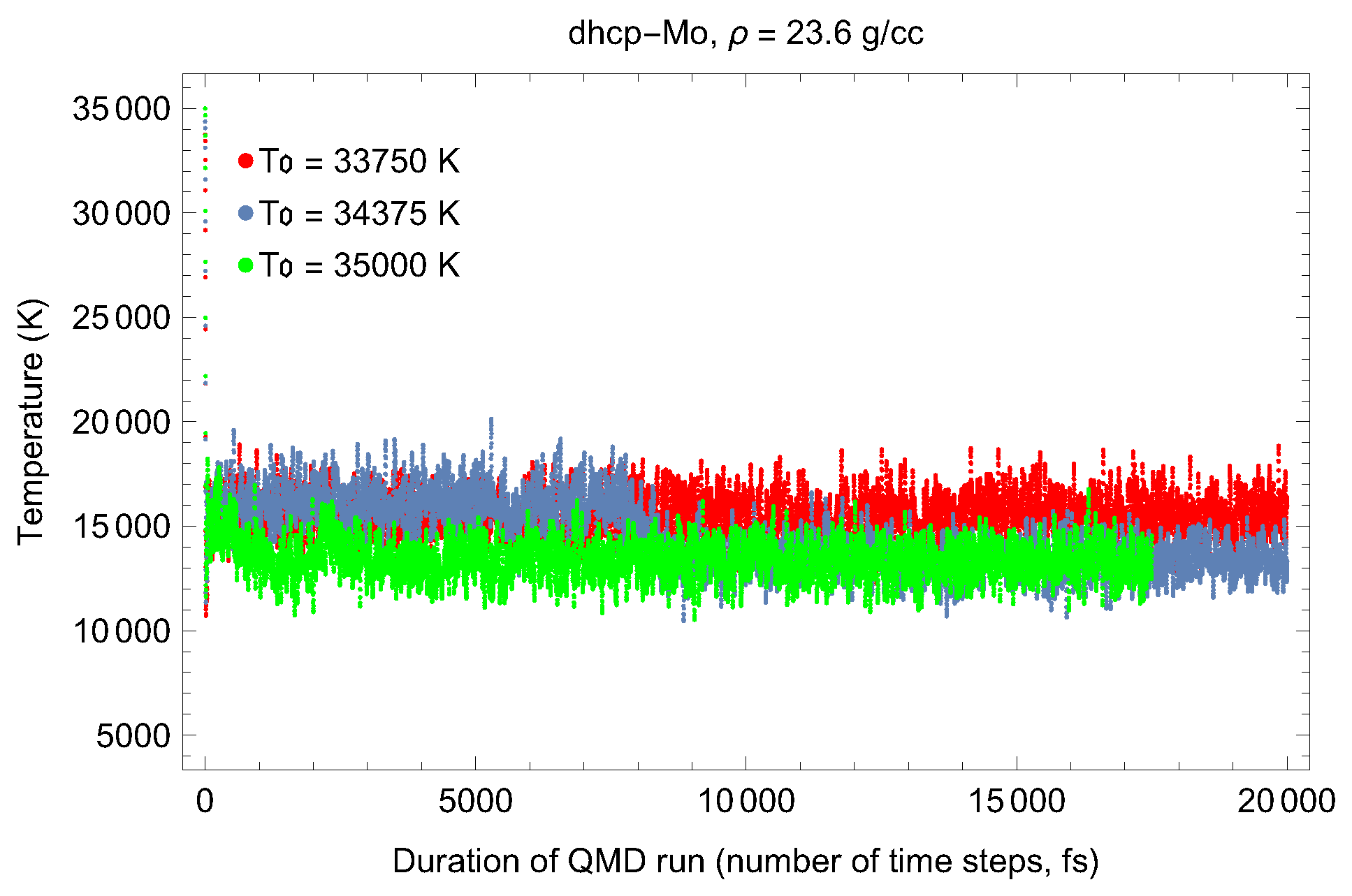
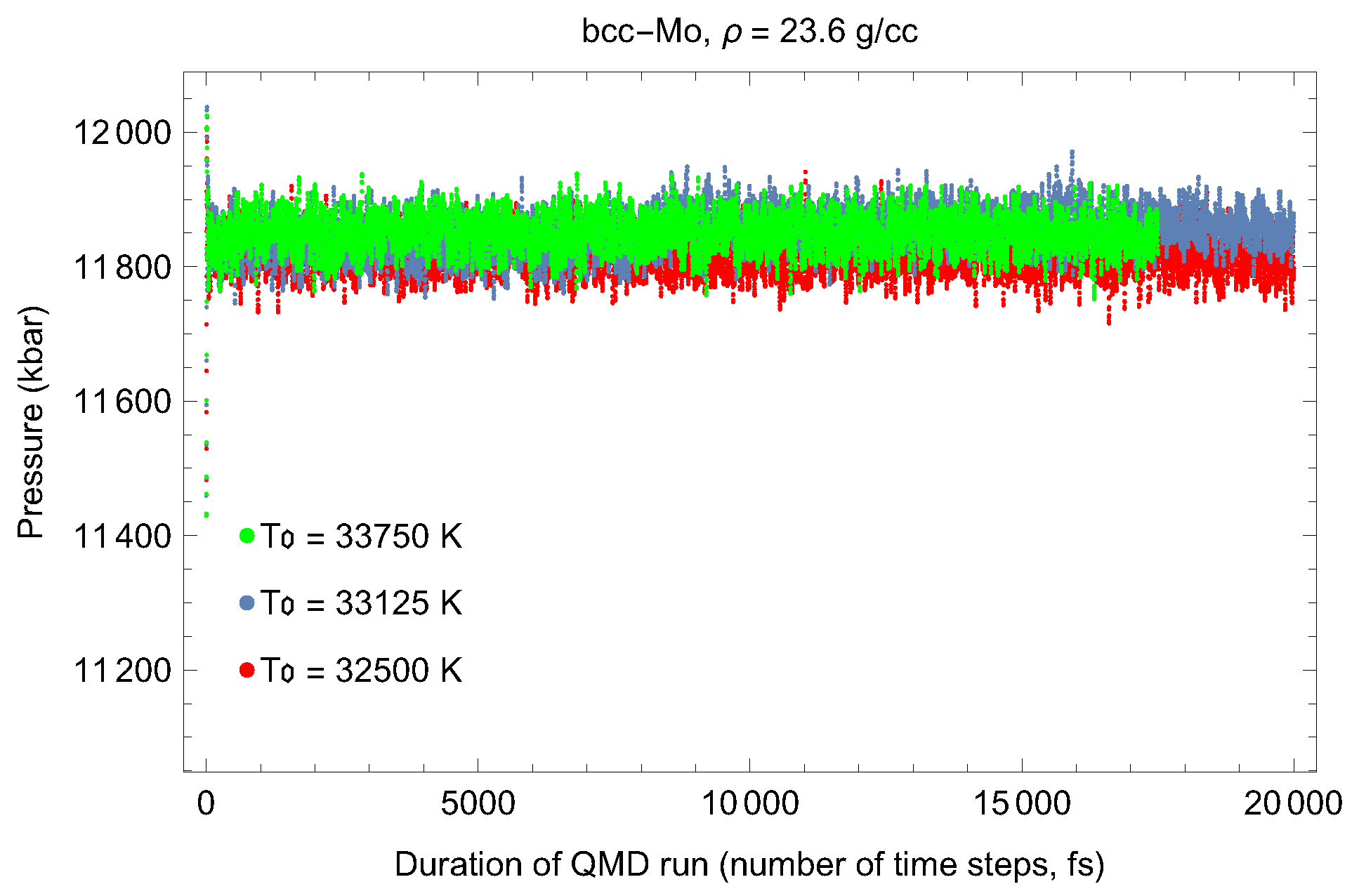
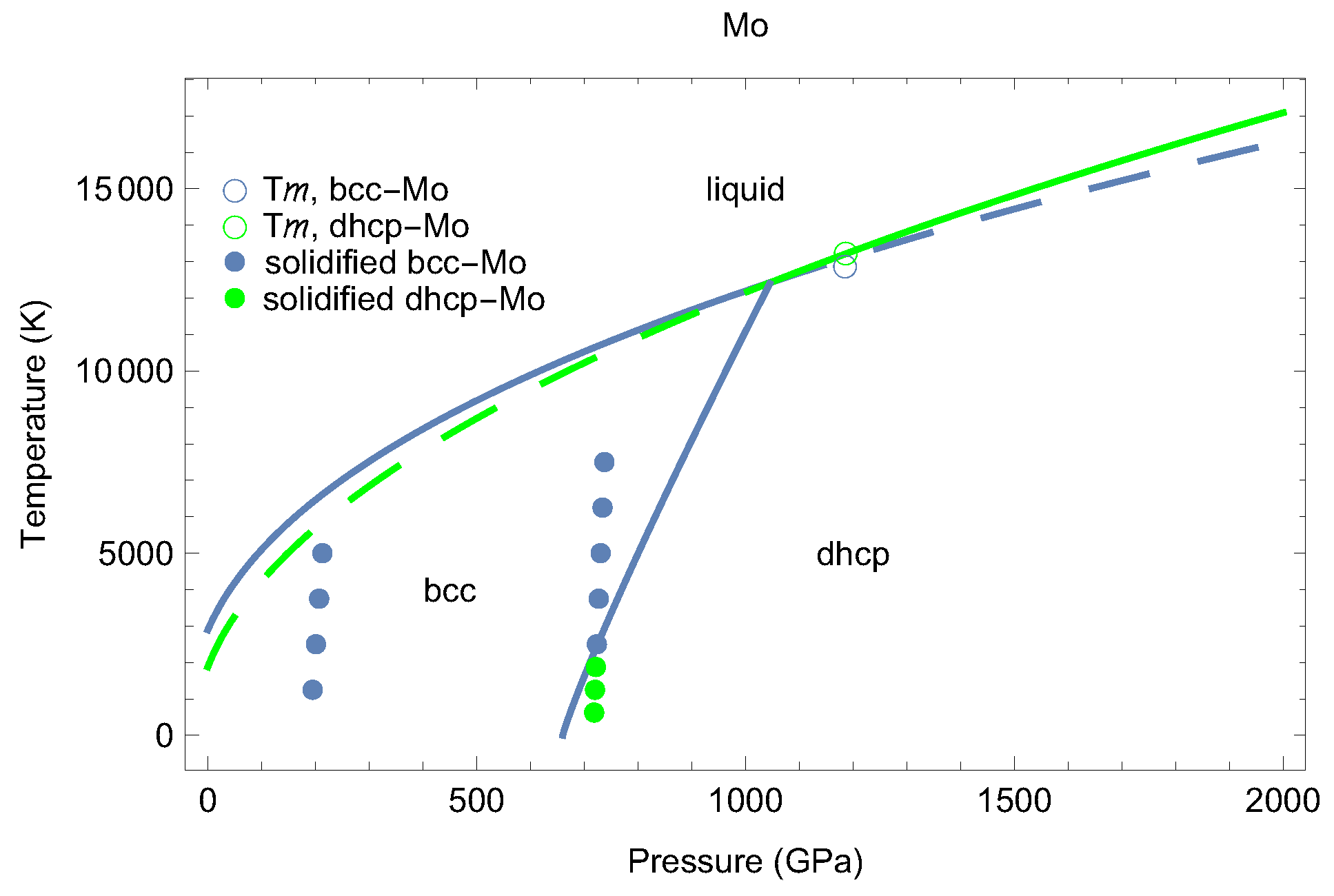
2. The Phase Diagram of Mo
- (i)
- (ii)
- the melting curve of dhcp-Mo in the Simon–Glatzel form ( in K, P in GPa):
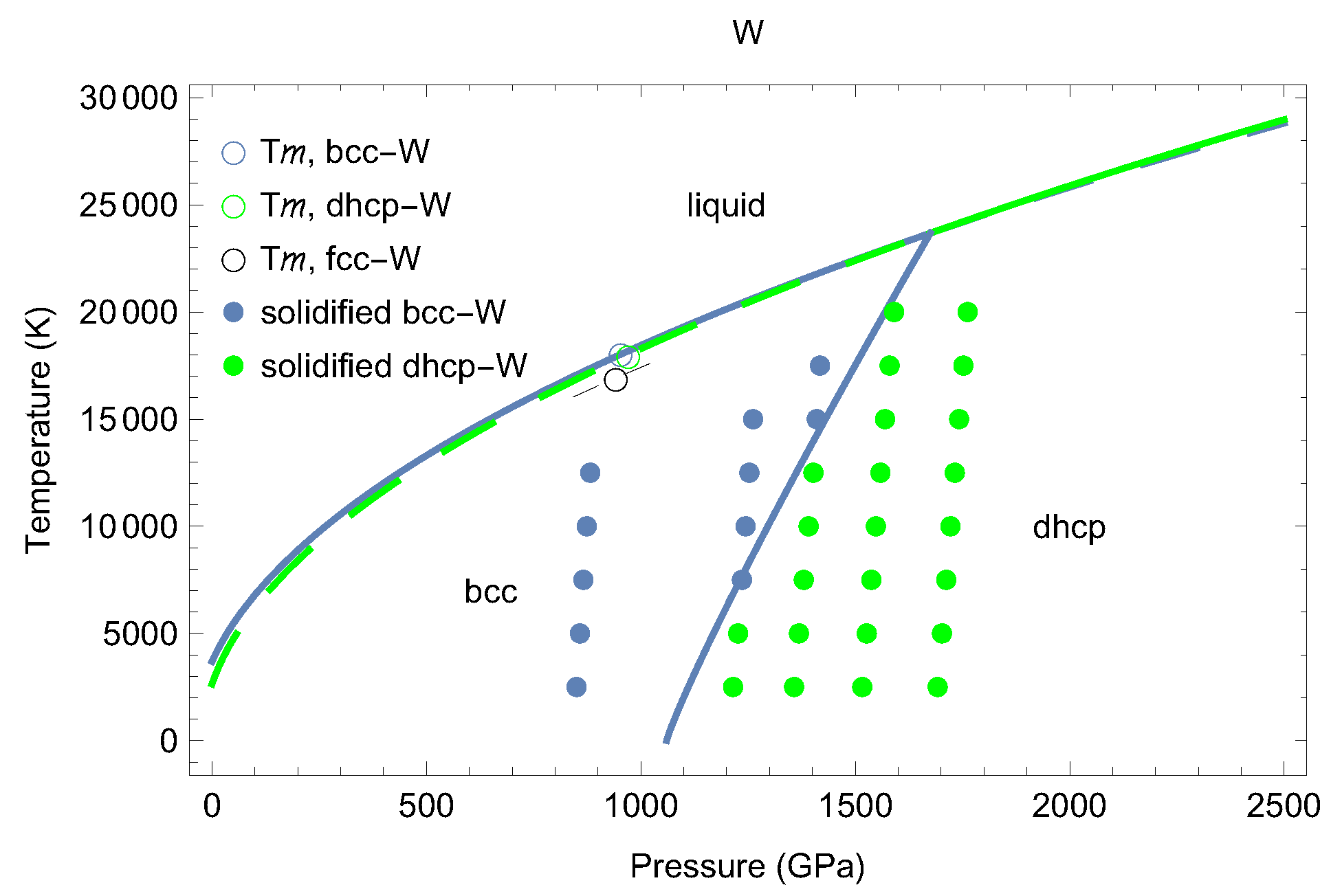
3. The Phase Diagram of W
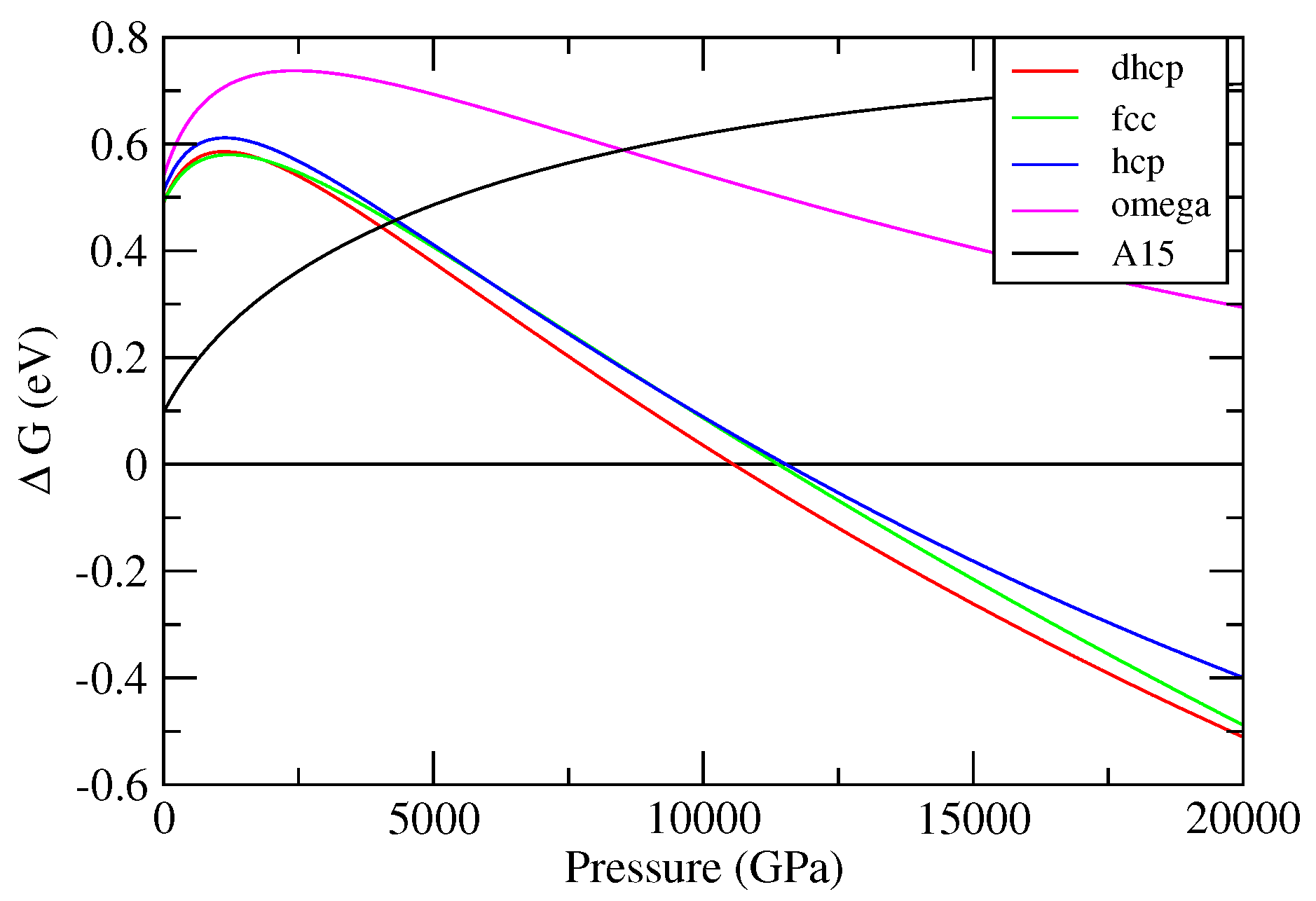
3.1. Cold Enthalpies of Different Solid Structures of W
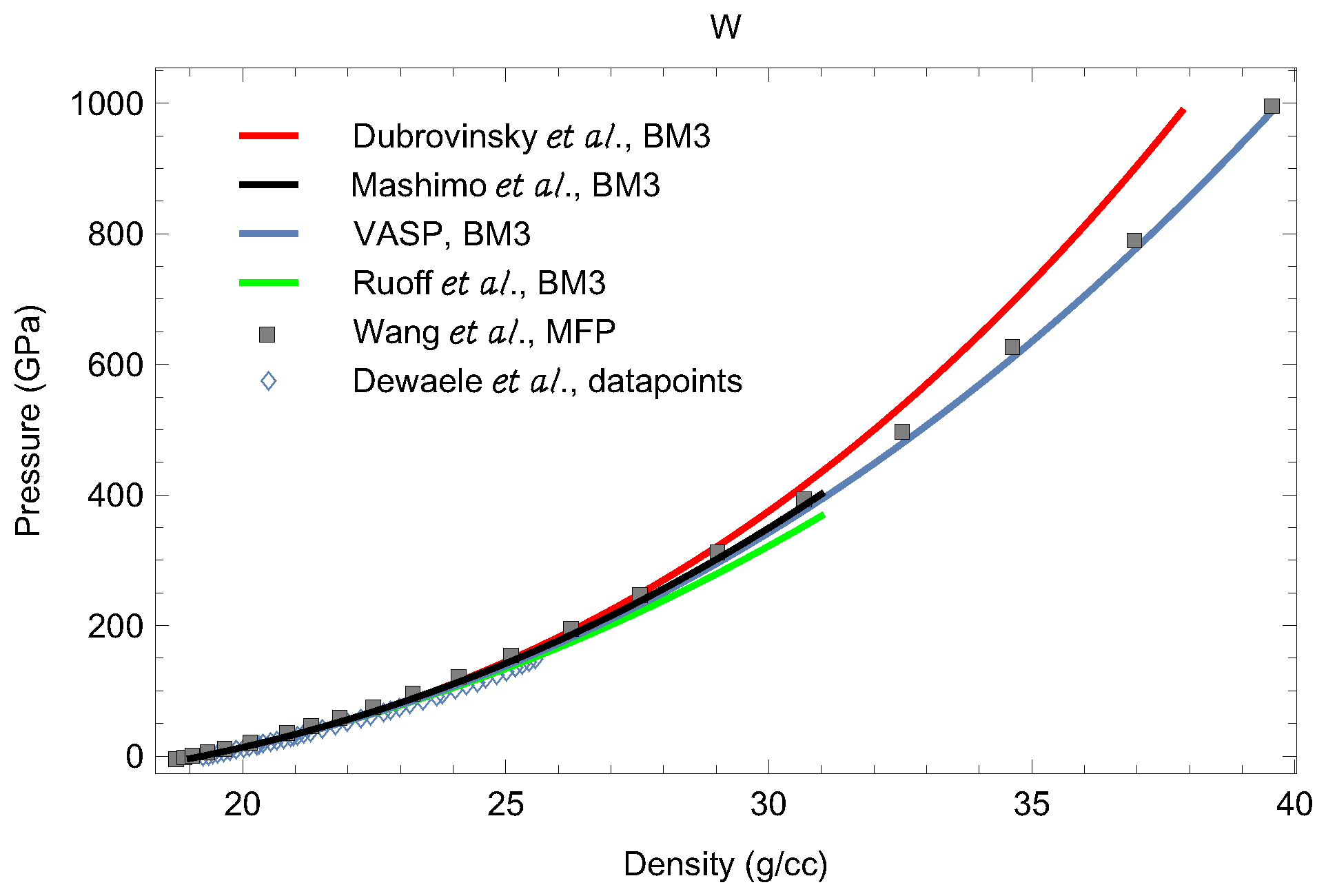
3.2. Equations of State of bcc-W and dhcp-W
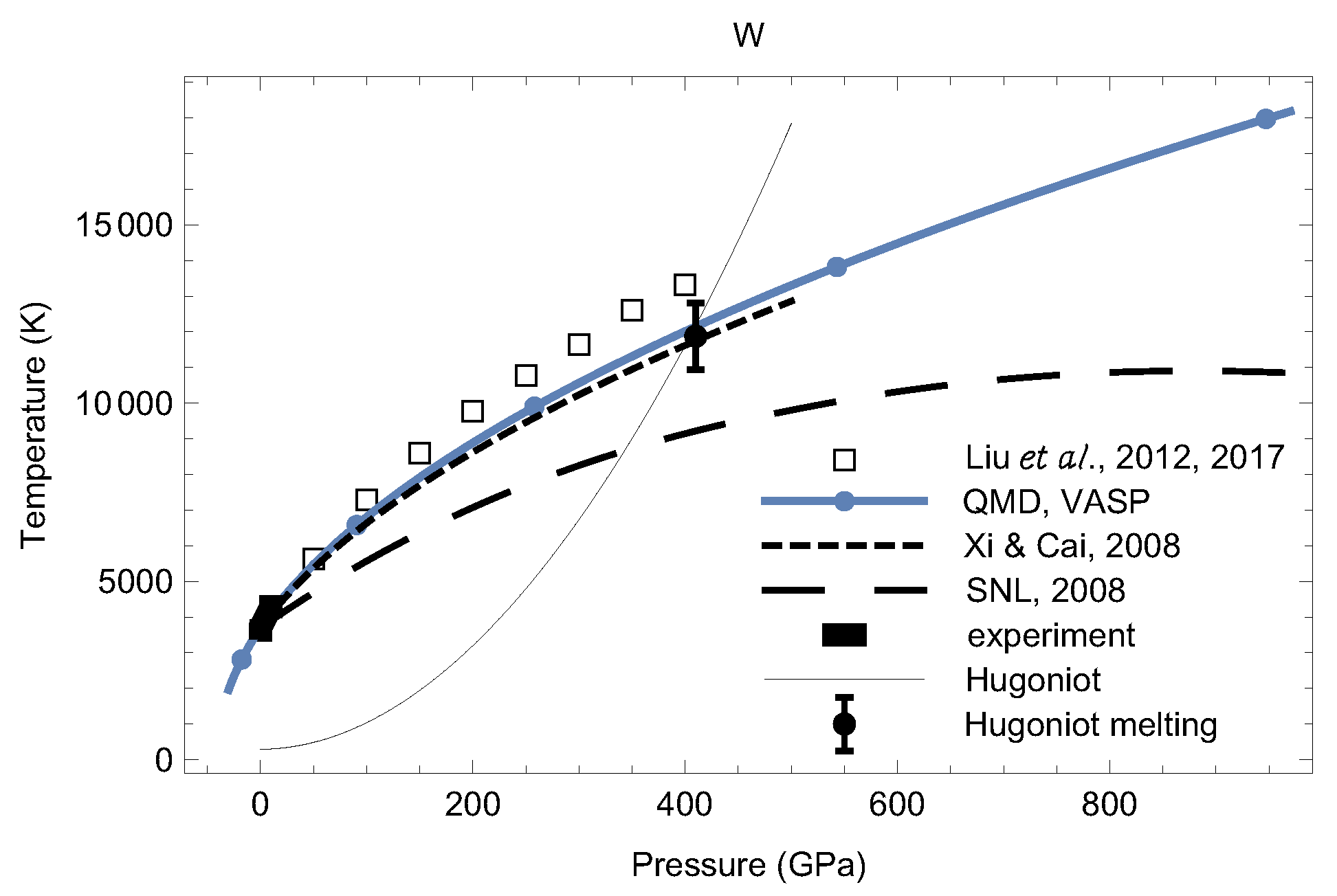
4. Melting Curves of Different Solid Structures of W
4.1. Ab Initio Melting Curve of bcc-W
4.2. Ab Initio Melting Curve of dhcp-W
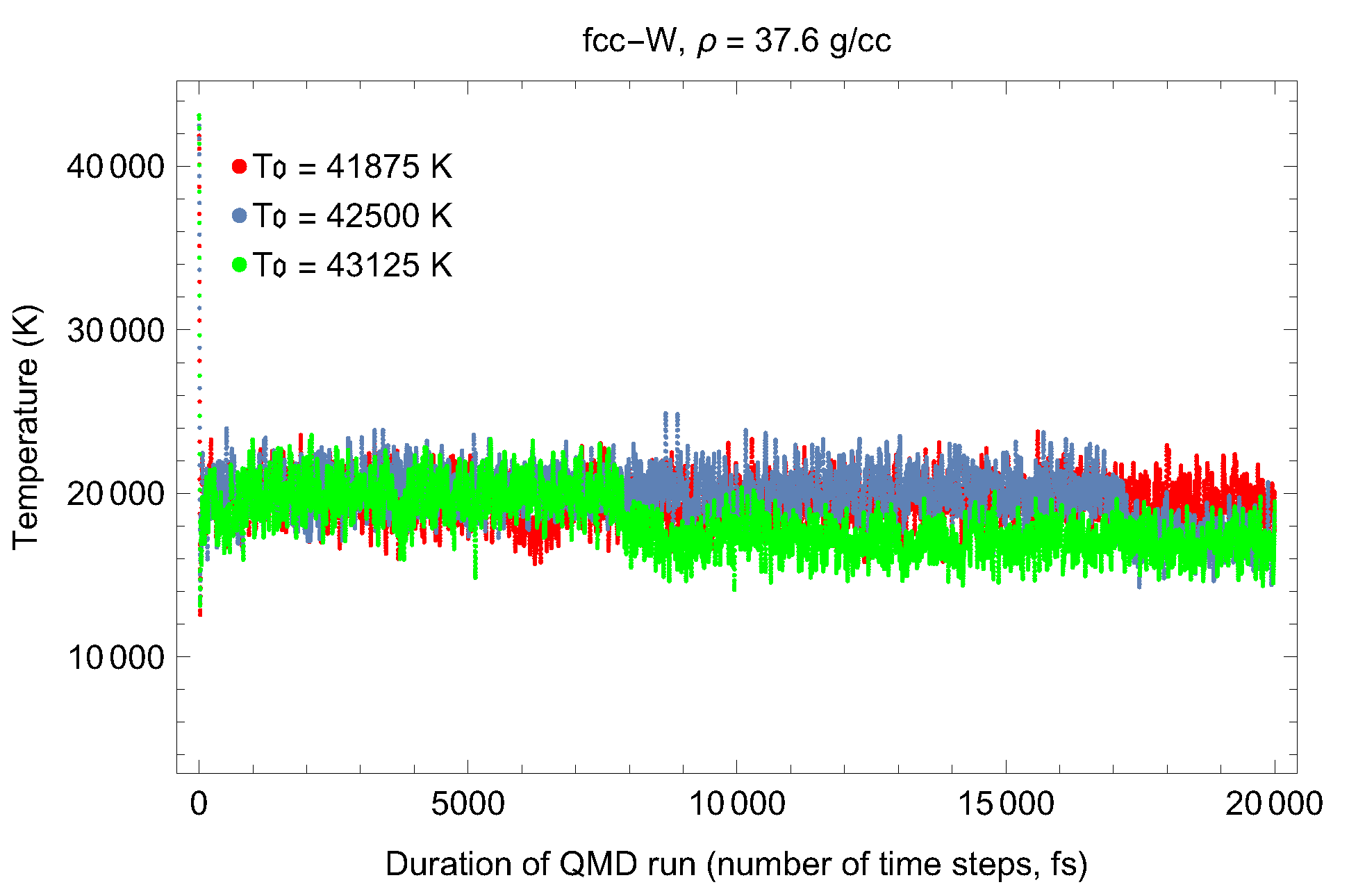
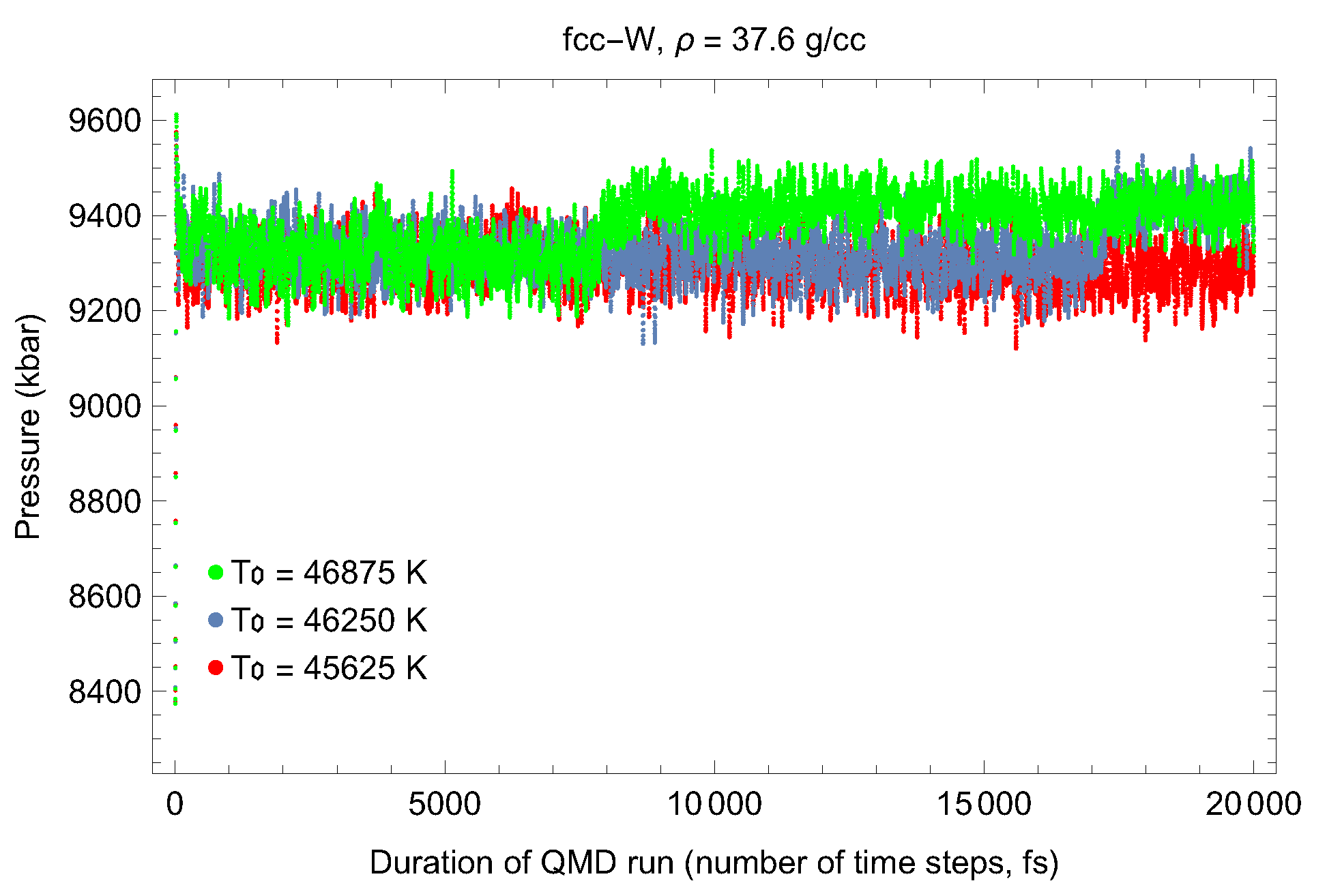
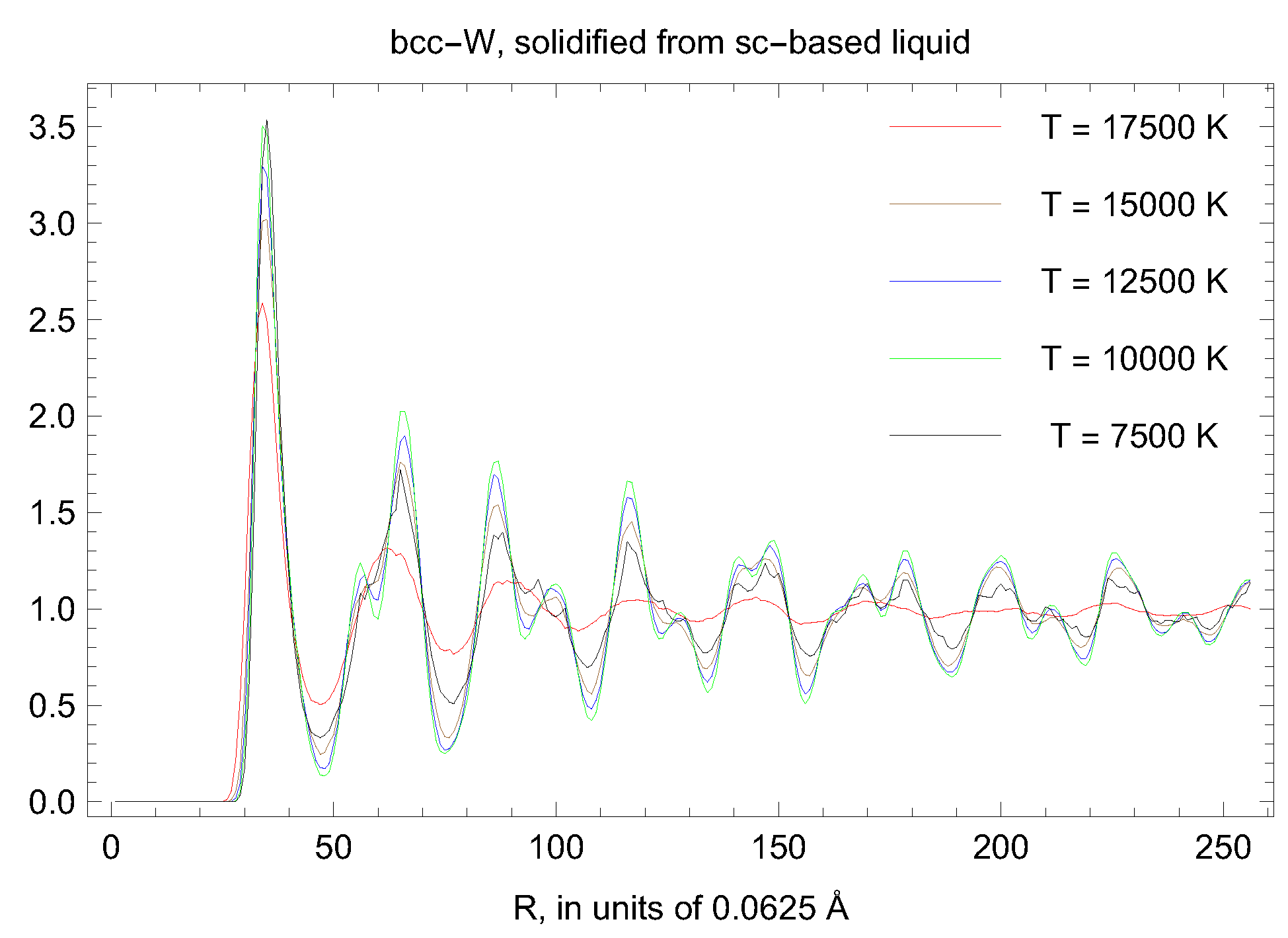
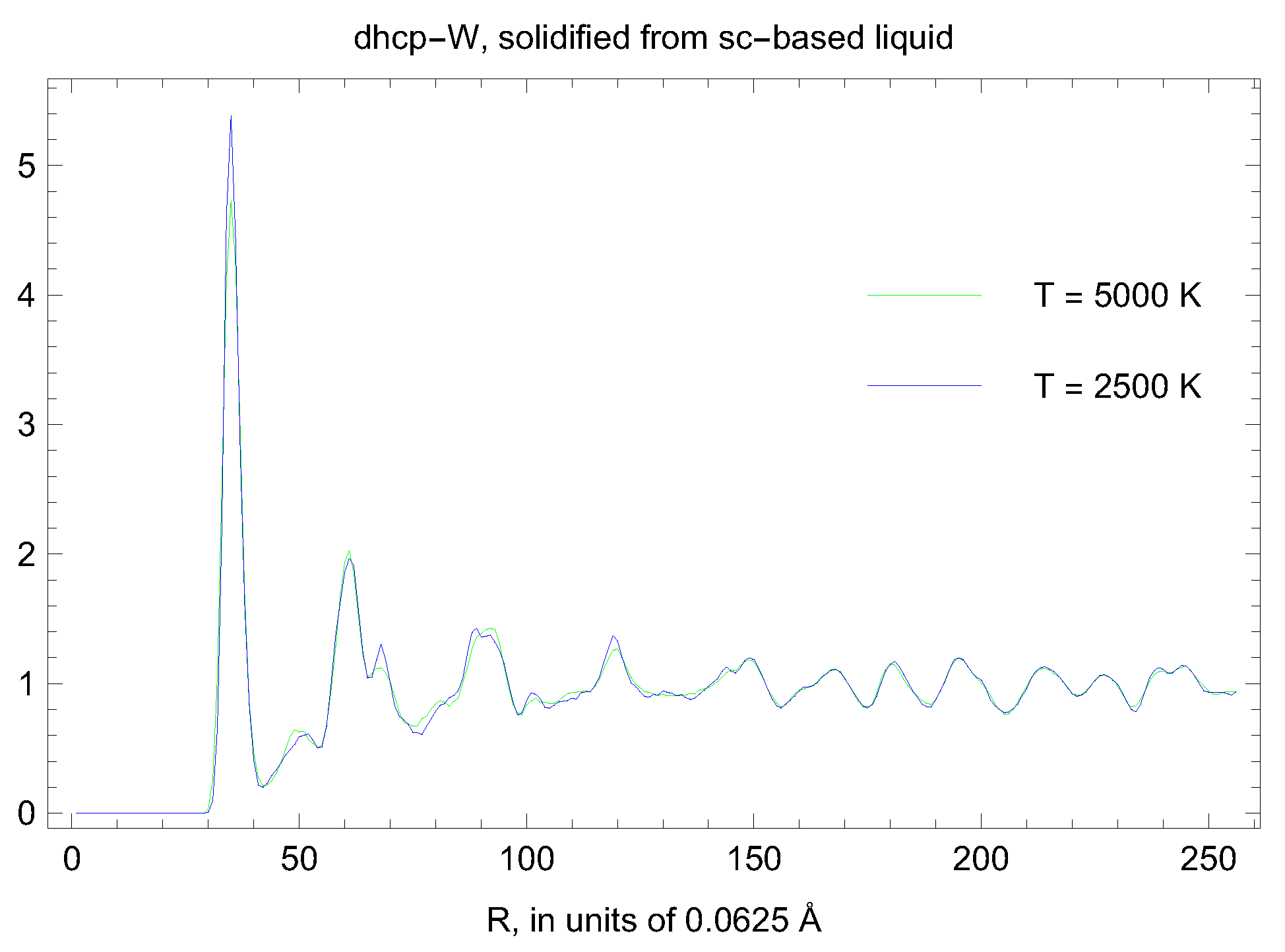
5. Inverse Z Solidification Simulations of Liquid W
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Belonoshko, A.B.; Burakovsky, L.; Chen, S.P.; Johansson, B.; Mikhaylushkin, A.S.; Preston, D.L.; Simak, S.I.; Swift, D.C. Molybdenum at high pressure and temperature: Melting from another solid phase. Phys. Rev. Lett. 2008, 100, 135701. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-L.; Cai, L.-C.; Chen, X.-R.; Jing, F.-Q. Molecular dynamics simulations of the melting curve of tantalum under pressure. Phys. Rev. B 2008, 77, 024103. [Google Scholar] [CrossRef]
- Burakovsky, L.; Chen, S.P.; Preston, D.L.; Belonoshko, A.B.; Rosengren, A.; Mikhaylushkin, A.S.; Simak, S.I.; Moriarty, J.A. High-pressure–high-temperature polymorphism in Ta: Resolving an ongoing experimental controversy. Phys. Rev. Lett. 2010, 104, 255702. [Google Scholar] [CrossRef] [PubMed]
- Haskins, J.; Moriarty, J.A.; Hood, R.Q. Polymorphism and melt in high-pressure tantalum. Phys. Rev. B 2012, 86, 224104. [Google Scholar] [CrossRef]
- Hu, J.; Dai, C.; Yu, Y.; Liu, Z.; Tan, Y.; Zhou, X.; Tan, H.; Cai, L.; Wu, Q. Sound velocity measurements of tantalum under shock compression in the 10–110 GPa range. J. Appl. Phys. 2012, 111, 033511. [Google Scholar] [CrossRef]
- Liu, C.M.; Chen, X.R.; Xu, C.; Cai, L.C.; Jing, F.Q. Melting curves and entropy of fusion of body-centered cubic tungsten under pressure. J. Appl. Phys. 2012, 112, 013518. [Google Scholar] [CrossRef]
- Yao, Y.; Klug, D. Stable structures of tantalum at high temperature and high pressure. Phys. Rev. B 2013, 88, 054102. [Google Scholar] [CrossRef]
- Pozzo, M.; Alfe, D. Melting curve of face-centered-cubic nickel from first-principles calculations. Phys. Rev. B 2013, 88, 024111. [Google Scholar] [CrossRef]
- Burakovsky, L.; Chen, S.P.; Preston, D.L.; Sheppard, D.G. Z methodology for phase diagram studies: Platinum and tantalum as examples. J. Phys. Conf. Ser. 2014, 500, 162001. [Google Scholar] [CrossRef]
- Burakovsky, L.; Burakovsky, N.; Preston, D.; Simak, S.I. Systematics of the third row transition metal melting: The hcp metals rhenium and osmium. Crystals 2018, 8, 243. [Google Scholar] [CrossRef]
- Lazor, P.; Shen, G.; Saxena, S.K. Laser-heated diamond anvil cell experiments at high pressure: Melting curve of nickel up to 700 kbar. Phys. Chem. Miner. 1993, 20, 86. [Google Scholar] [CrossRef]
- Kavner, A.; Jeanloz, R. High-pressure melting curve of platinum. J. App. Phys. 1998, 83, 7553. [Google Scholar] [CrossRef]
- Errandonea, D.; Schwager, B.; Ditz, R.; Gessmann, C.; Boehler, R.; Ross, M. Systematics of transition-metal melting. Phys. Rev. B 2001, 63, 132104. [Google Scholar] [CrossRef]
- Errandonea, D.; Somayazulu, M.; Häusermann, D.; Mao, H.K. Melting of tantalum at high pressure determined by angle dispersive x-ray diffraction in a double-sided laser-heated diamond-anvil cell. J. Phys. Cond. Mat. 2003, 15, 7635. [Google Scholar] [CrossRef]
- Boehler, R.; Santamaría-Perez, D.; Errandonea, D.; Mezouar, M. Melting, density, and anisotropy of iron at core conditions: New X-ray measurements to 150 GPa. J. Phys. Conf. Ser. 2008, 121, 022018. [Google Scholar] [CrossRef]
- Santamaría-Pérez, D.; Ross, M.; Errandonea, D.; Mukherjee, G.D.; Mezouar, M.; Boehler, R. X-ray diffraction measurements of Mo melting to 119 GPa and the high pressure phase diagram. J. Chem. Phys. 2009, 130, 124509. [Google Scholar] [CrossRef]
- Ruiz-Fuertes, J.; Karandikar, A.; Boehler, R.; Errandonea, D. Microscopic evidence of a flat melting curve of tantalum. Phys. Earth Planet. Inter. 2010, 181, 69. [Google Scholar] [CrossRef][Green Version]
- Yang, L.; Karandikar, A.; Boehler, R. Flash heating in the diamond cell: Melting curve of rhenium. Rev. Sci. Instrum. 2012, 83, 063905. [Google Scholar] [CrossRef]
- Dewaele, A.; Mezouar, M.; Guignot, N.; Loubeyre, P. High melting points of tantalum in a laser-heated diamond anvil cell. Phys. Rev. Lett. 2010, 104, 255701. [Google Scholar] [CrossRef]
- Errandonea, D. High-pressure melting curves of the transition metals Cu, Ni, Pd, and Pt. Phys. Rev. B 2013, 87, 054108. [Google Scholar] [CrossRef]
- Anzellini, S.; Dewaele, A.; Mezouar, M.; Loubeyre, P.; Morard, G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science 2013, 340, 464. [Google Scholar] [CrossRef] [PubMed]
- Lord, O.T.; Wood, I.G.; Dobson, D.P.; Vočadlo, L.; Wang, W.; Thomson, A.R.; Wann, E.T.; Morard, G.; Mezouar, M.; Walter, M.J. The melting curve of Ni to 1 Mbar. Earth Planet. Sci. Lett. 2014, 408, 226. [Google Scholar] [CrossRef]
- Hrubiak, R.; Meng, Y.; Shen, G. Microstructures define melting of molybdenum at high pressures. Nat. Commun. 2017, 8, 14562. [Google Scholar] [CrossRef] [PubMed]
- Anzellini, S. In situ characterization of the high pressure–high temperature melting curve of platinum. Sci. Rep. 2019, 9, 13034. [Google Scholar] [CrossRef] [PubMed]
- Errandonea, D.; MacLeod, S.G.; Burakovsky, L.; Santamaria-Perez, D.; Proctor, J.E.; Cynn, H.; Mezouar, M. Melting curve and phase diagram of vanadium under high-pressure and high-temperature conditions. Phys. Rev. B 2019, 100, 094111. [Google Scholar] [CrossRef]
- Shaner, J.W.; Gathers, G.R.; Minichino, C. A new apparatus for thermophysical measurements above 2500 K. High Temp.-High Pres. 1976, 8, 425. [Google Scholar]
- Hixson, R.S.; Fritz, J.N. Shock compression of tungsten and molybdenum. J. Appl. Phys. 1992, 71, 1721. [Google Scholar] [CrossRef]
- Musella, M.; Ronchi, C.; Sheindlin, M. Dependence of the melting temperature on pressure up to 2000 bar in uranium dioxide, tungsten, and graphite. Int. J. Thermophys. 1999, 20, 1177. [Google Scholar] [CrossRef]
- Kloss, A.; Hess, H.; Schneidenbach, H.; Grossjohann, R. Scanning the melting curve of tungsten by a submicrosecond wire-explosion experiment. Int. J. Thermophys. 1999, 20, 1199. [Google Scholar] [CrossRef]
- Gustafson, P. Evaluation of the thermodynamic properties of tungsten. Int. J. Thermophys. 1985, 6, 395. [Google Scholar] [CrossRef]
- Vereshchagin, L.F.; Fateeva, N.S. Melting curves of graphite, tungsten and platinum to 60 kbar. Sov. Phys. JETP 1969, 28, 597. [Google Scholar]
- Gorecki, T. Vacancies and melting curve of metals at high pressure. Z. Metallk. 1977, 68, 231. [Google Scholar]
- Gorecki, T. Vacancies and a generalised melting curve of metals. High Temp.-High Press. 1979, 11, 683. [Google Scholar]
- Arblaster, J.W. What is the true melting point of osmium? Platin. Met. Rev. 2005, 49, 166. [Google Scholar] [CrossRef]
- Zitserman, V.; (JIHT, Moscow). Personal communication. 2019. [Google Scholar]
- Burakovsky, L.; Burakovsky, N.; Preston, D.L. Ab initio melting curve of osmium. Phys. Rev. B 2015, 92, 174105. [Google Scholar]
- Burakovsky, L.; Preston, D.L. Shear moduli of silicon and germanium in semiconducting and metallic phases. Defect Diffus. Forum 2002, 210–212, 43. [Google Scholar] [CrossRef]
- Frohberg, M.G. Thirty years of levitation melting calorimetry-a balance. Thermochem. Acta 1999, 337, 7. [Google Scholar] [CrossRef]
- Burakovsky, L.; Lushcer, D.J.; Preston, D.; Sjue, S.; Vaughan, D. Generalization of the unified analytic melt-shear model to multi-phase materials: Molybdenum as an example. Crystals 2019, 9, 86. [Google Scholar] [CrossRef]
- Simon, F.; Glatzel, G. Bemerkungen zur Schmelzdruckkurve. Z. Anorg. Allgem. Chem. 1929, 178, 309. [Google Scholar] [CrossRef]
- Cazorla, C.; Gillan, M.J.; Taioli, S.; Alfè, D. Melting curve and Hugoniot of molybdenum up to 400 GPa by ab initio simulations. J. Phys. Conf. Ser. 2008, 121, 012009. [Google Scholar] [CrossRef]
- Shaner, J.W.; Gathers, G.R.; Minichino, C. Thermophysical properties of liquid tantalum and molybdenum. High Temp.-High Press. 1977, 9, 331. [Google Scholar]
- Ruoff, A.L.; Xia, H.; Xia, Q. The effect of a tapered aperture on x-ray diffraction from a sample with a pressure gradient: Studies on three samples with a maximum pressure of 560 GPa. Rev. Sci. Instrum. 1992, 63, 4342. [Google Scholar] [CrossRef]
- Dubrovinsky, L.; Dubrovinskaia, N.; Bykova, E.; Bykov, M.; Prakapenka, V.; Prescher, C.; Glazyrin, K.; Liermann, H.-P.; Hanfland, M.; Ekholm, M.; et al. The most incompressible metal osmium at static pressures above 750 gigapascals. Nature 2015, 525, 226. [Google Scholar] [CrossRef] [PubMed]
- Einarsdotter, K.; Sadigh, B.; Grimvall, G.; Ozoliņš, V. Phonon instabilities in fcc and bcc tungsten. Phys. Rev. Lett. 1997, 79, 2073. [Google Scholar] [CrossRef]
- Zhang, H.-Y.; Niu, Z.-W.; Cai, L.-C.; Chen, X.-R.; Xi, F. Ab initio dynamical stability of tungsten at high pressures and high temperatures. Comput. Mater. Sci. 2018, 144, 32. [Google Scholar] [CrossRef]
- Ruoff, A.L.; Rodriguez, C.O.; Christensen, N.E. Elastic moduli of tungsten to 15 Mbar, phase transition at 6.5 Mbar, and rheology to 6 Mbar. Phys. Rev. B 1998, 58, 2998. [Google Scholar] [CrossRef]
- Blöchl, P. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Ruoff, A.L.; Xia, H.; Luo, H.; Vohra, Y.K. Miniaturization techniques for obtaining static pressures comparable to the pressure at the center of the earth: X-ray diffraction at 416 GPa. Rev. Sci. Instrum. 1990, 61, 3830. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, D.; Zhang, X. Calculated equation of state of Al, Cu, Ta, Mo, and W to 1000 GPa. Phys. Rev. Lett. 2000, 84, 3220. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Mezouar, M. Equations of state of six metals above 94GPa. Phys. Rev. B 2004, 70, 094112. [Google Scholar] [CrossRef]
- Mashimo, T.; Liu, X.; Kodama, M.; Zaretsky, E.; Katayama, M.; Nagayama, K. Effect of shear strength on Hugoniot-compression curve and the equation of state of tungsten (W). J. Appl. Phys. 2016, 119, 035904. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Skorodumova, N.V.; Rosengren, A.; Johansson, B. Melting and critical superheating. Phys. Rev. B 2006, 73, 012201. [Google Scholar] [CrossRef]
- McQueen, R.G.; Marsh, S.P. Equation of state for nineteen metallic elements from shock-wave measurements to two megabars. J. Appl. Phys. 1960, 31, 1253. [Google Scholar] [CrossRef]
- Xi, F.; Cai, L. Theoretical study of melting curves on Ta, Mo, and W at high pressures. Phys. B 2008, 403, 2065. [Google Scholar] [CrossRef]
- Carpenter, J.H.; Desjarlais, M.P.; Mattsson, A.E.; Cochrane, K.R. A New Wide-Range Equation of State for Tungsten; SNL Report SAND2008-1415C; American Physical Society: Washington, DC, USA, 2008. [Google Scholar]
- Liu, C.M.; Xu, C.; Cheng, Y.; Chen, X.R.; Cai, L.C. Molecular dynamics studies of body-centered cubic tungsten during melting under pressure. Chin. J. Phys. 2017, 55, 2468. [Google Scholar] [CrossRef]
- Errandonea, D.; Burakovsky, L.; Preston, D.L.; MacLeod, S.G.; Santamaría-Perez, D.; Chen, S.P.; Cynn, H.; Simak, S.I.; McMahon, M.L.; Proctor, J.E.; et al. Niobium at High Pressure and High Temperature: Combined Experimental and Theoretical Study. 2019; submitted. [Google Scholar]
- Xie, Y.-Q.; Deng, Y.-P.; Liu, X.-B. Electroic structure and physical properties of pure Cr, Mo and W. Trans. Nonferrous Met. Soc. China 2003, 13, 5. [Google Scholar]
- Pure Chromium. Available online: https://icme.hpc.msstate.edu/mediawiki/index.php/Pure_Chromium (accessed on 30 December 2019).
- He, Y.; Xie, Y.-Q. Electroic structure and properties of V, Nb and Ta metals. J. Cent. South Univ. Technol. 2000, 7, 7. [Google Scholar] [CrossRef]
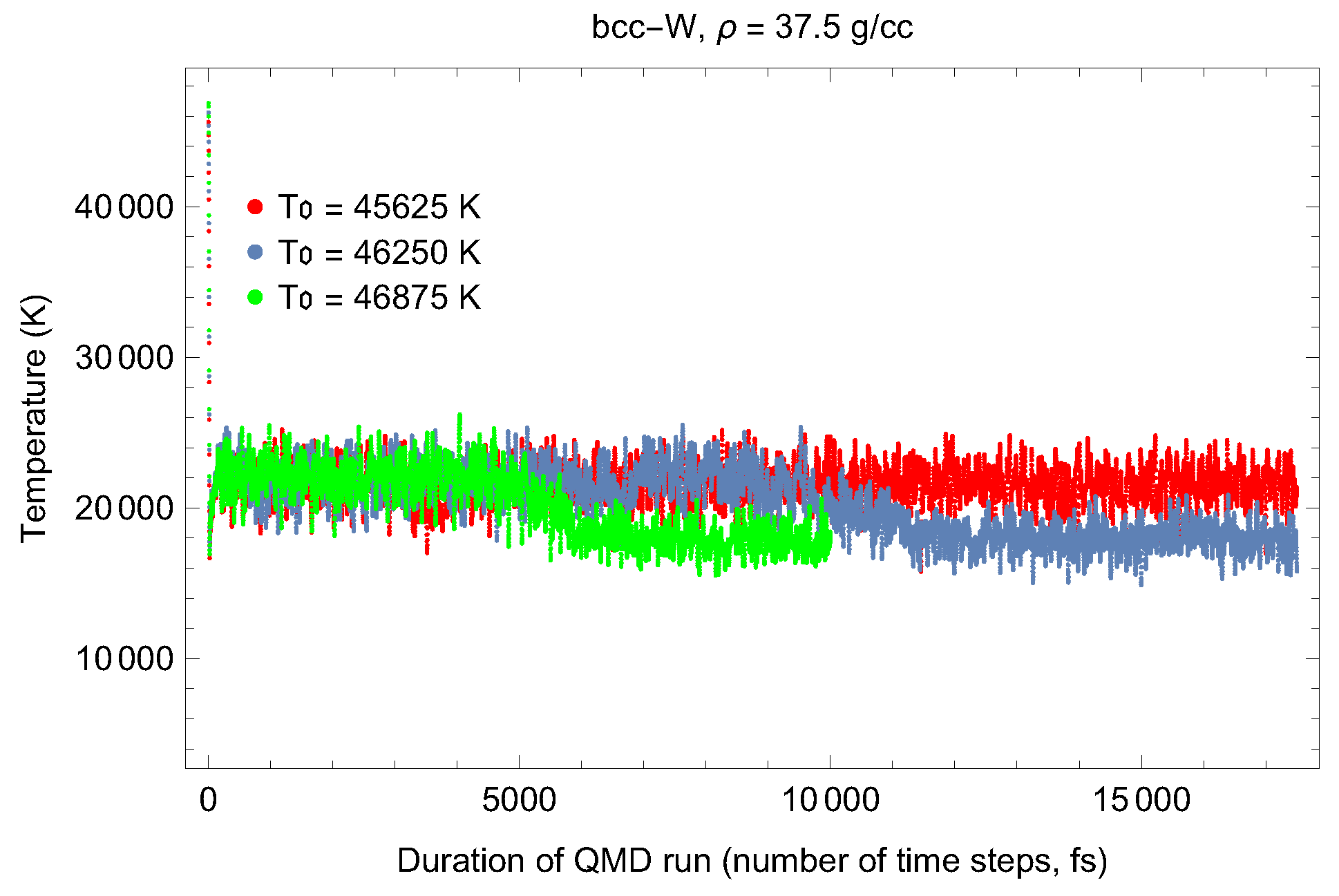
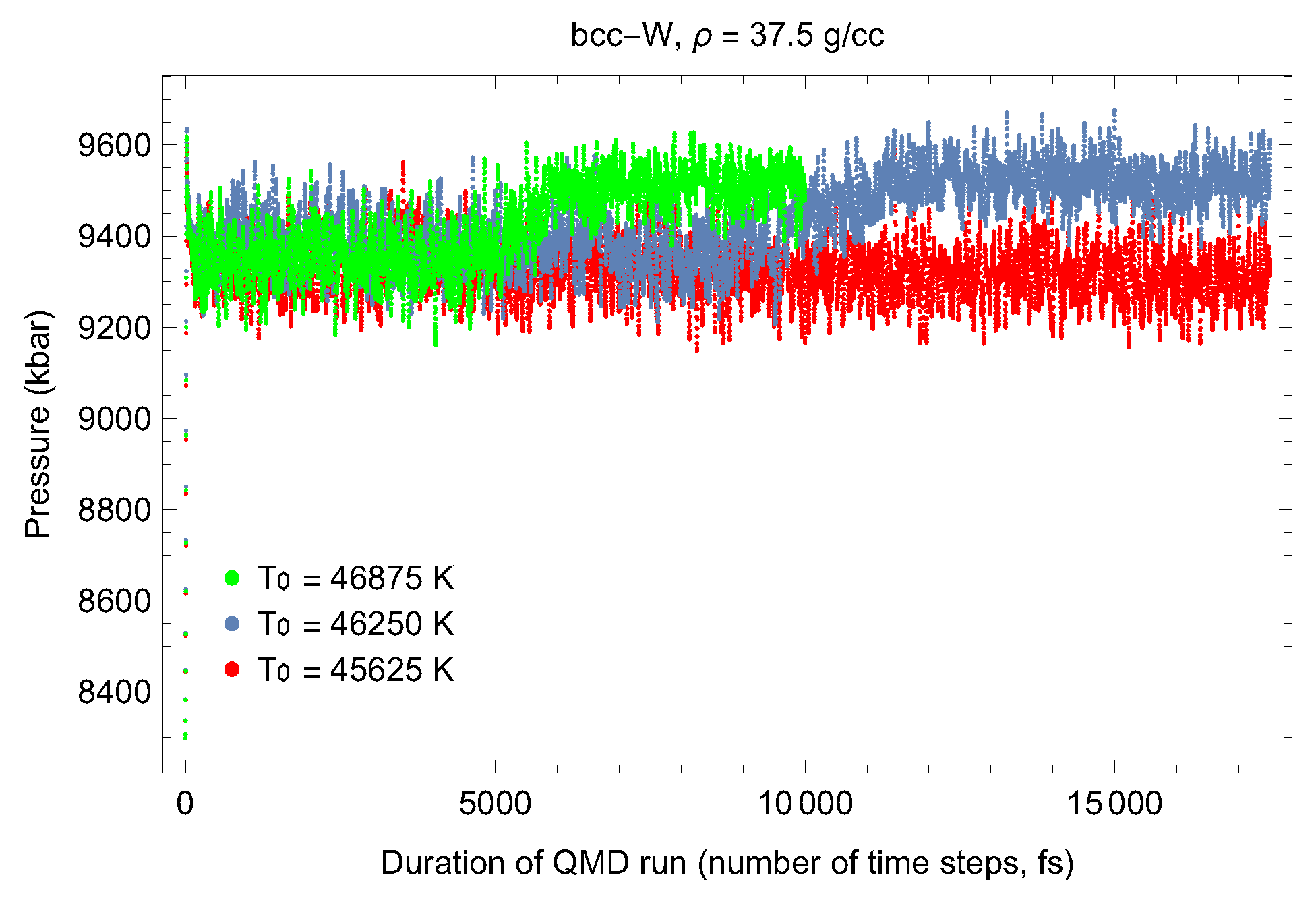
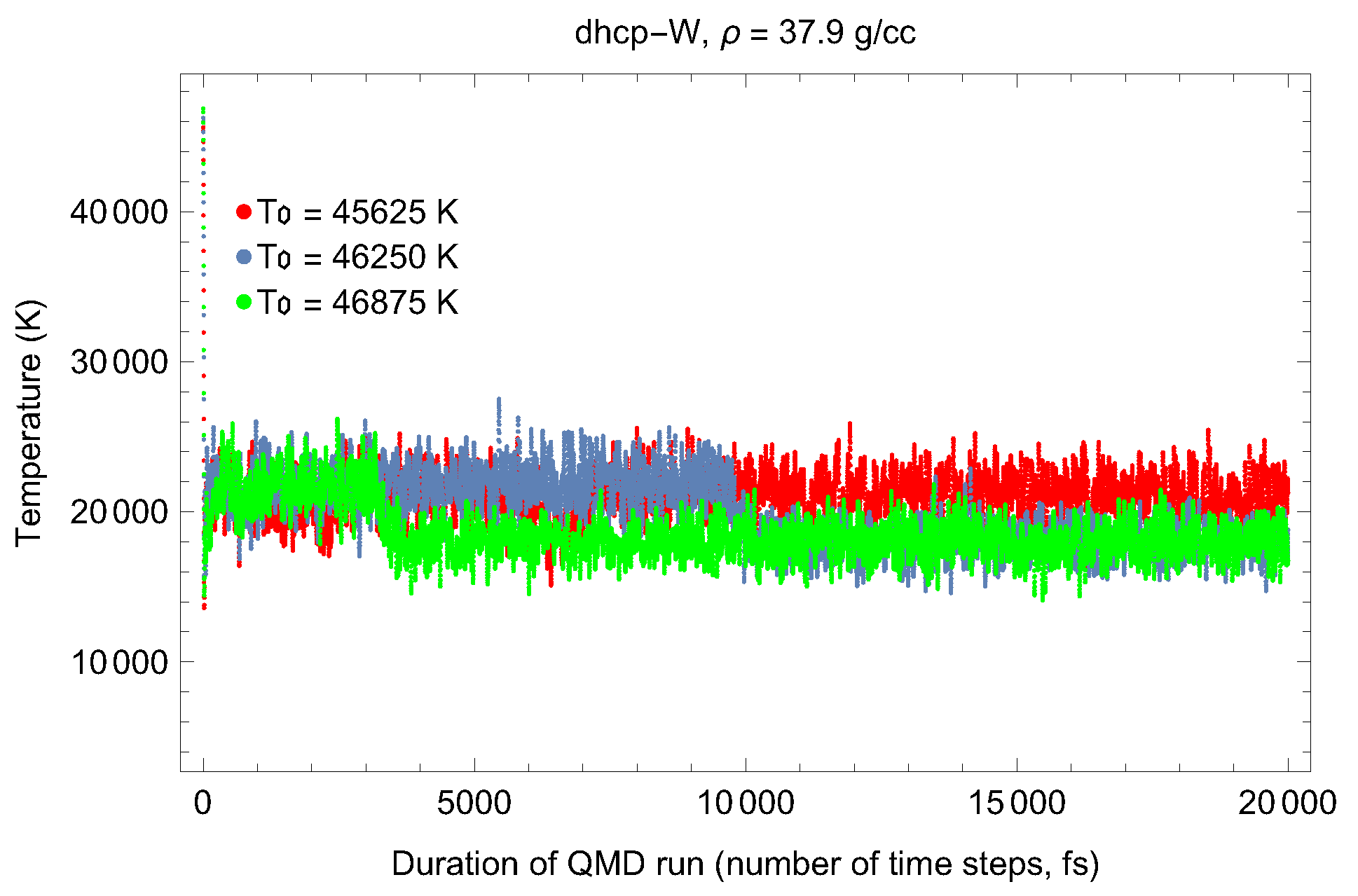
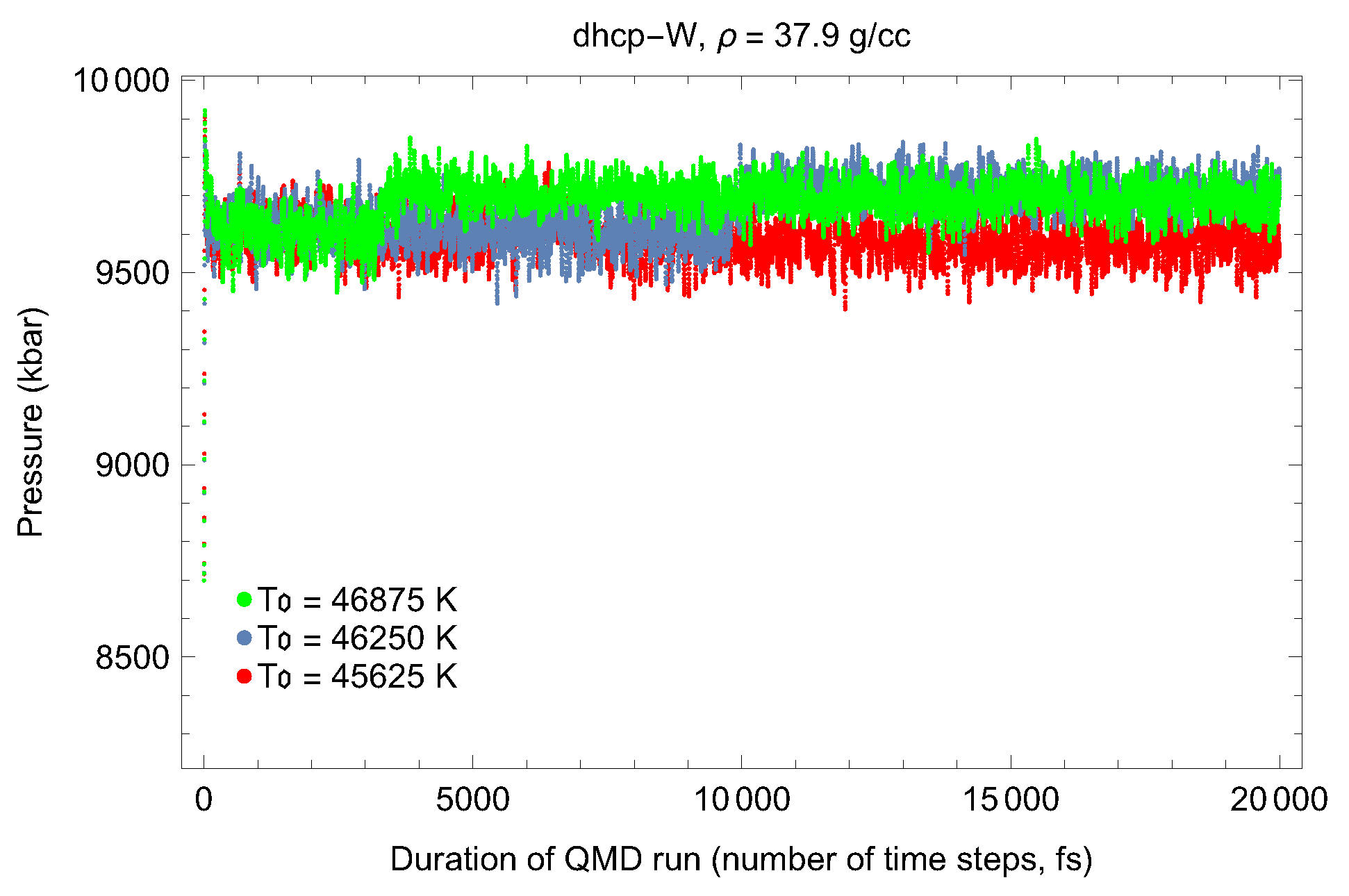
| Lattice Constant (Å) | Density (g/cm3) | (GPa) | (K) | (K) |
|---|---|---|---|---|
| 3.350 | 16.240 | −17.7 | 2800 | 125.0 |
| 3.050 | 21.519 | 90.6 | 6520 | 312.5 |
| 2.850 | 26.375 | 258 | 9840 | 312.5 |
| 2.675 | 31.897 | 543 | 13,760 | 312.5 |
| 2.535 | 37.479 | 947 | 18,070 | 312.5 |
| Lattice Constant (Å) | Density (g/cm3) | (GPa) | (K) | (K) |
|---|---|---|---|---|
| 2.90 | 17.702 | 8.1 | 3080 | 150.0 |
| 2.65 | 23.199 | 150 | 7380 | 312.5 |
| 2.40 | 31.230 | 510 | 13,110 | 312.5 |
| 2.25 | 37.902 | 970 | 18,000 | 312.5 |
| 2.15 | 43.440 | 1471 | 22,200 | 312.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baty, S.; Burakovsky, L.; Preston, D. Topological Equivalence of the Phase Diagrams of Molybdenum and Tungsten. Crystals 2020, 10, 20. https://doi.org/10.3390/cryst10010020
Baty S, Burakovsky L, Preston D. Topological Equivalence of the Phase Diagrams of Molybdenum and Tungsten. Crystals. 2020; 10(1):20. https://doi.org/10.3390/cryst10010020
Chicago/Turabian StyleBaty, Samuel, Leonid Burakovsky, and Dean Preston. 2020. "Topological Equivalence of the Phase Diagrams of Molybdenum and Tungsten" Crystals 10, no. 1: 20. https://doi.org/10.3390/cryst10010020
APA StyleBaty, S., Burakovsky, L., & Preston, D. (2020). Topological Equivalence of the Phase Diagrams of Molybdenum and Tungsten. Crystals, 10(1), 20. https://doi.org/10.3390/cryst10010020






