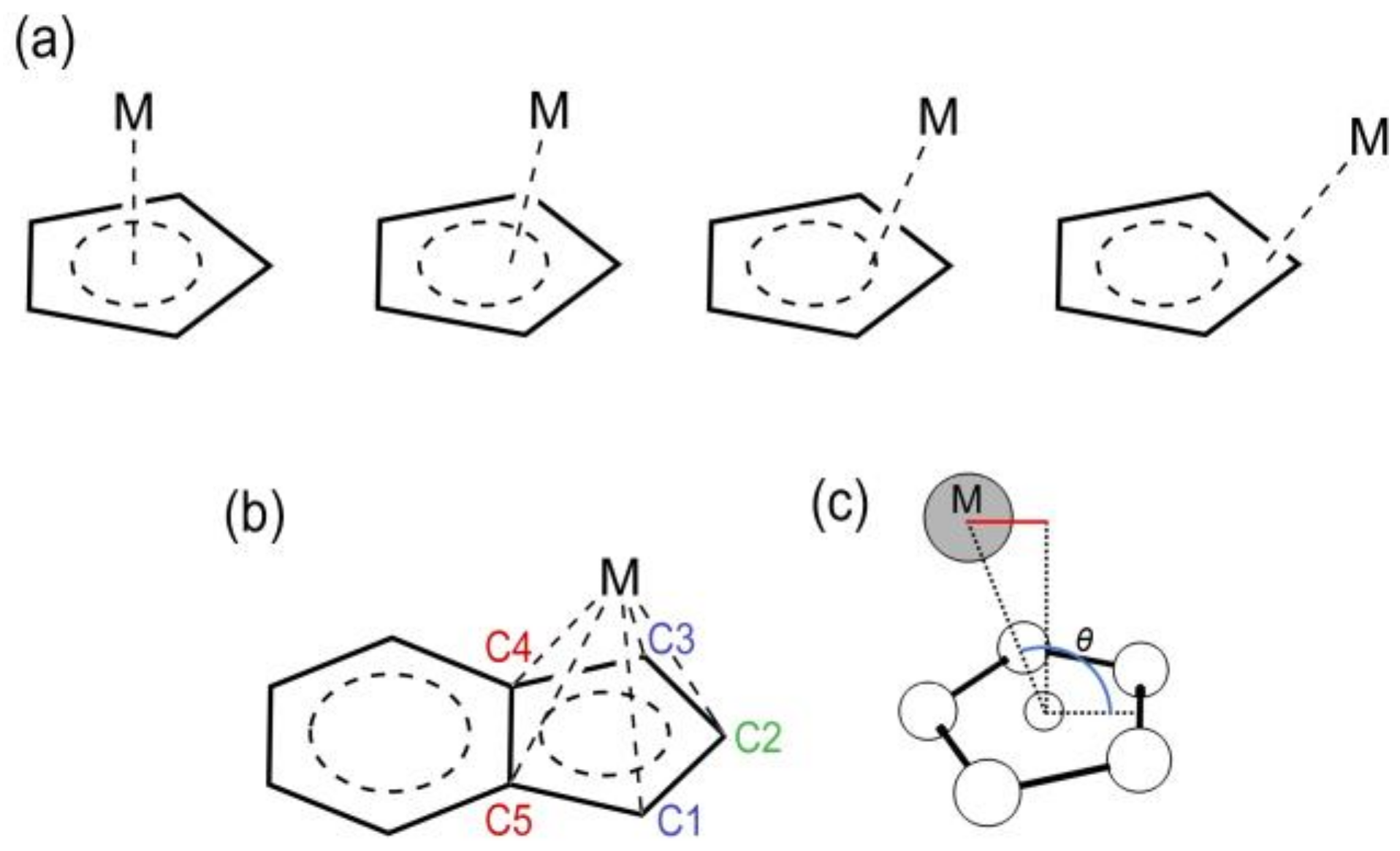
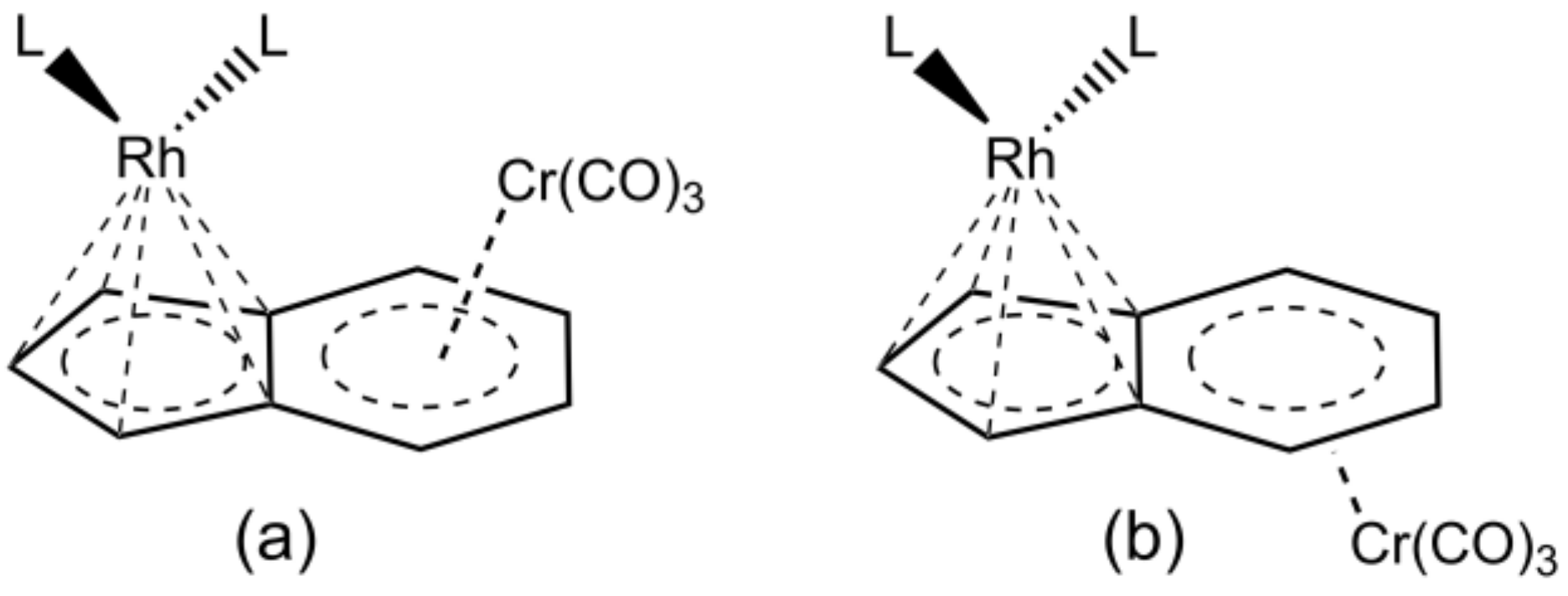
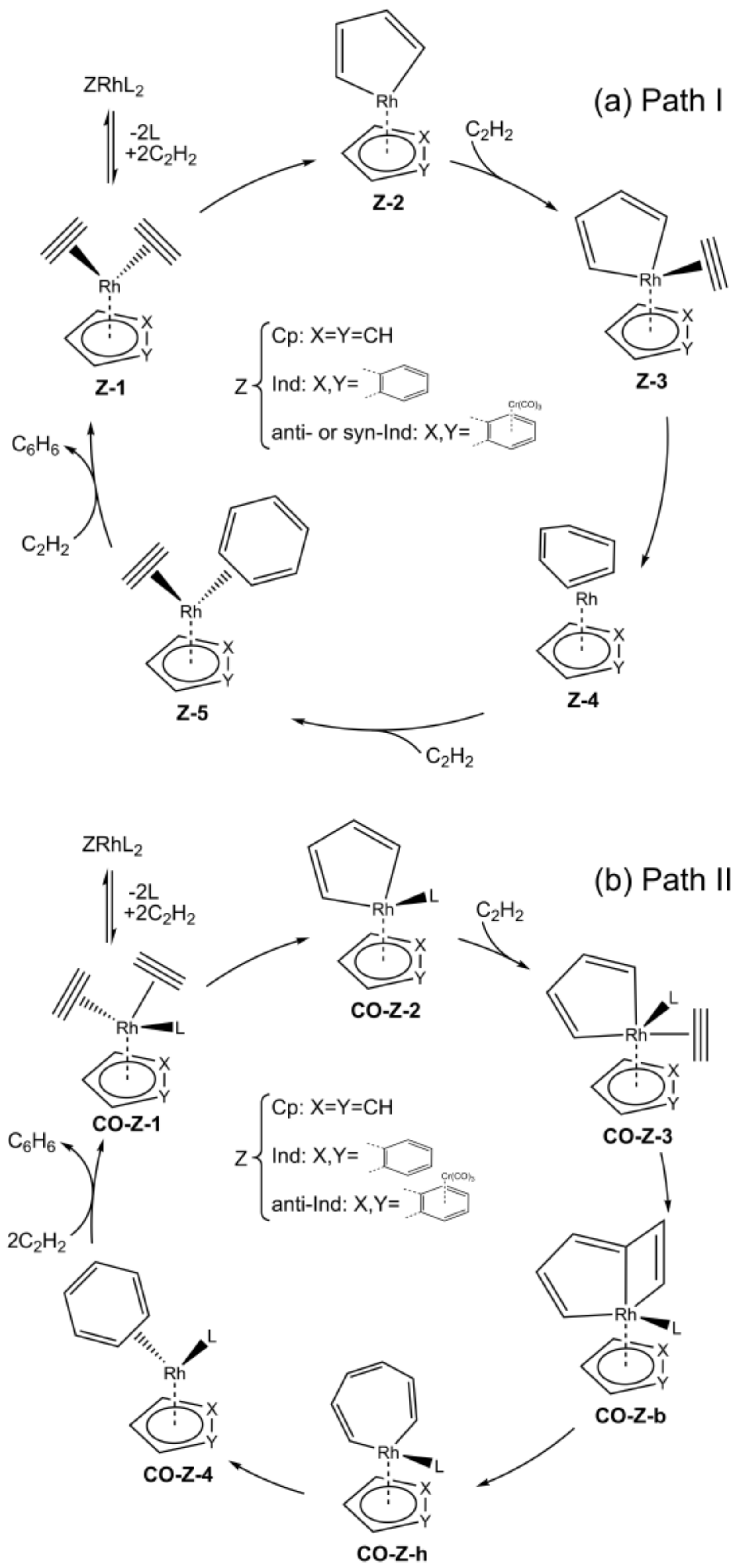
The computational mechanistic investigation of acetylene [2+2+2] cycloaddition to benzene catalyzed by the monometallic catalysts CpRh and IndRh was first reported in 2006 [
41]. In
Scheme 3a (Path I), the well-known and widely accepted mechanism, proposed by Albright for CpCo catalysis [
47,
48] is shown. The catalytic cycle begins with the replacement of the ancillary ligands L of the catalyst precursor, i.e., Cp-or Ind-RhL
2 (L = CO, PPh
3 or COD (1,5-cyclooctadiene)) by two molecules of acetylene, leading to the bis-acetylene complex
Z-1. The coordinated acetylene molecules undergo oxidative coupling and the unsaturated 16-electrons rhodacycle
Z-2 forms. This elementary step typically has the highest activation energy and was recently discussed in detail for group 9 metal-Cp fragments [
49]. The subsequent coordination of a third acetylene molecule occurs without an appreciable activation energy and leading to
Z-3, and, after its addition to the π-electron system of the rhodacycle, the intermediate
Z-4 is obtained, which is characterized by an unsaturated bent six-membered ring. By further stepwise addition of two acetylene molecules, the intermediate
Z-5 first forms and then the initial catalyst is regenerated with the cleavage of benzene.
2.1. Acetylene [2+2+2] Cycloaddition Catalyzed by Anti-[Cr(CO)3IndRh] Fragment: Reaction Mechanism and PES (Path I)
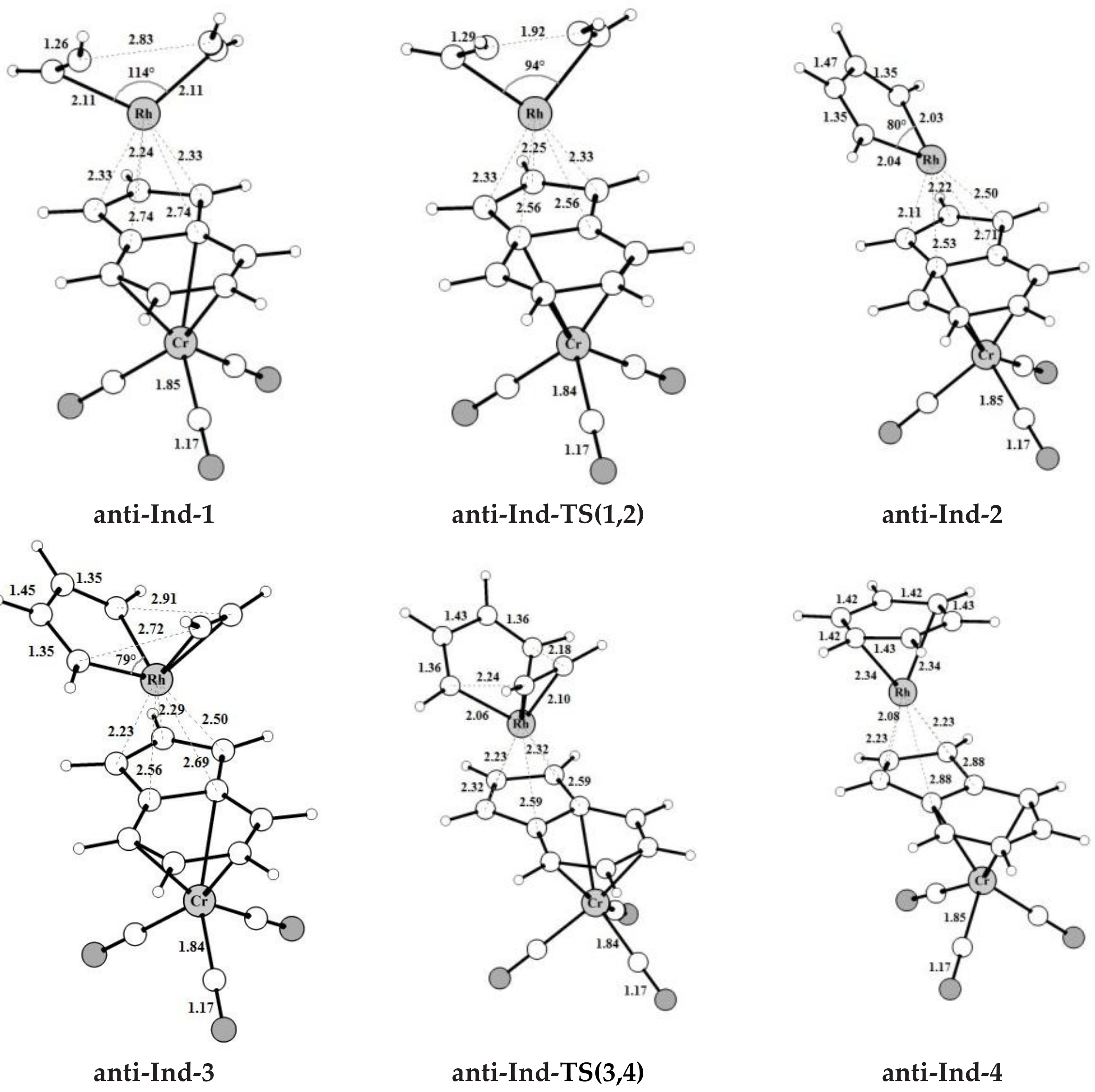
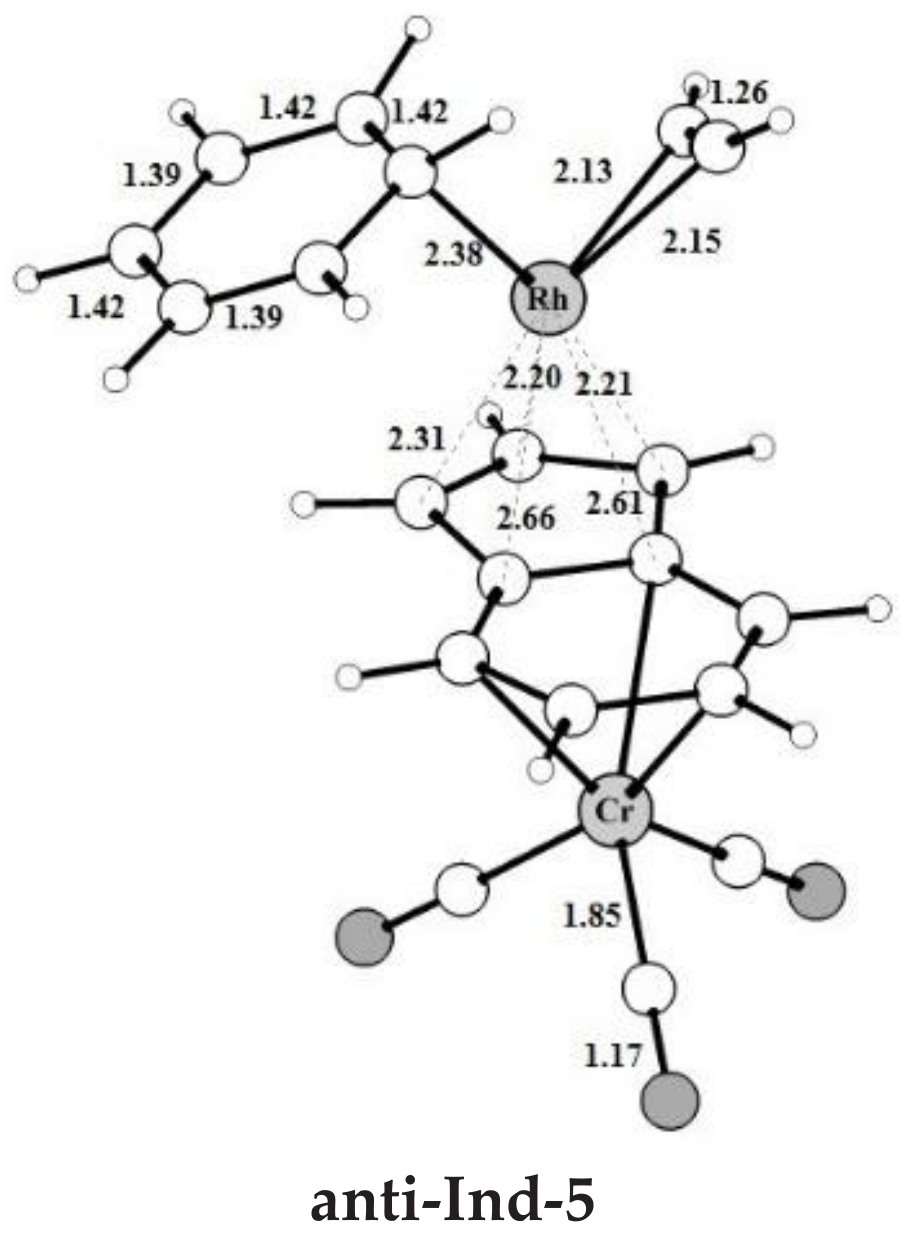
The intermediates and transition states found for acetylene [2+2+2] cycloaddition catalyzed by the bimetallic anti-IndRh along Path I (
Scheme 3a), are shown in
Figure 1. Those found on the PESs of the parent monometallic catalysts, i.e., CpRh and IndRh, are in
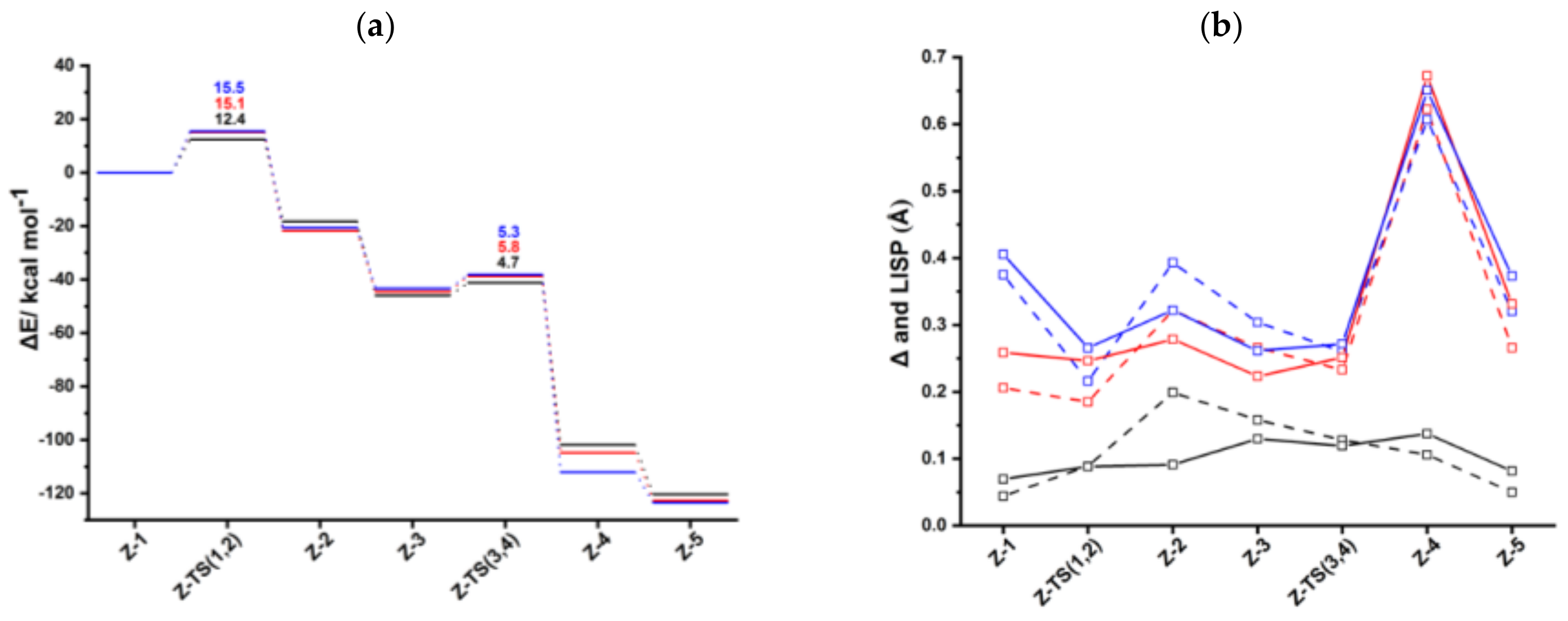
Figures S2 and S3, respectively. The computed energy profile for anti-RhInd is shown in
Figure 2a.
The catalytic cycle mediated by anti-IndRh is very similar to the cycle described for the monometallic parent catalysts CpRh and IndRh [
41] since the Cr(CO)
3 group is coordinated in anti, and thus there is no steric effect. It begins with replacement of the ancillary ligands L by two acetylene molecules to form a bis-acetylene complex labelled
anti-
Ind-1 (
Scheme 3a). This process usually occurs experimentally by thermal or photochemical activation and might be dissociative or associative depending on the nature of the metal, on the electrophilicity of the ligands and on the substituents on the Cp ring [
21,
28,
52]. In
anti-
Ind-1, the acetylene molecules are slanted with respect to the plane of the indenyl ring and the C-C bond length is 1.26 Å. The Rh-C
α and Rh-C
β bond lengths are 2.11 Å and 2.13 Å, respectively; they are shorter as compared to those of
Ind-1 (2.13 Å and 2.16 Å). This suggests that acetylene is more tightly bonded, likely due to the electron withdrawing effect of the second metal group Cr(CO)
3. Additionally, the Rh-Cp coordination is more distorted in
anti-Ind-1 than in the parent
Cp-1 and
Ind-1, as also quantified by the metal slippage parameters Δ and
, which were calculated for the intermediates and the transition states along the whole catalytic cycle (
Figure 2b).
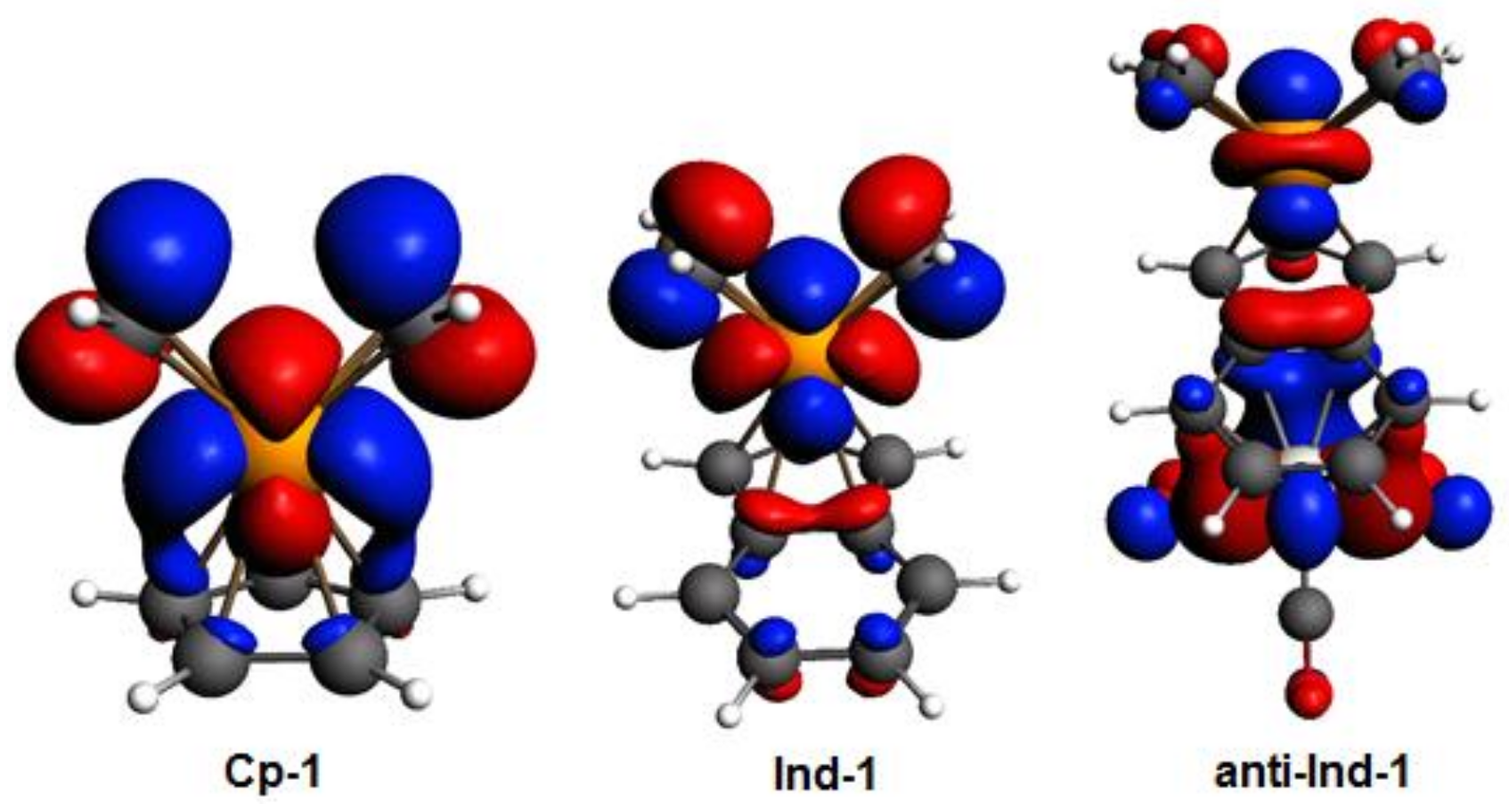
By inspecting the frontier molecular orbitals of
Cp-1,
Ind-1 and
anti-
Ind-1 shown in
Figure 3, the π-antibonding character between Cp’-π system and valence
d orbitals of Rh is found to increase in the order
Cp-1 <
Ind-1 <
anti-
Ind-1, leading to a corresponding increase of metal slippage. Calhorda et al. have reported the same observation in their pioneering work on the nature of indenyl effect, which was related to the nodal characteristics of Cp’-π orbitals of CpRh and IndRh [
19,
44]. Herein, it is found that the metal-π anti-bonding nature with Ind-π system is further enhanced in the presence of Cr(CO)
3 in
anti-
Ind-1 compared to the parent
Ind-1, leading to extra slippage of rhodium in the former.
The oxidative coupling of the two coordinated acetylene molecules in
anti-
Ind-1 leads to the 16-electrons unsaturated rhodacyclic intermediate
anti-
Ind-2 (
Figure 2), crossing an activation barrier of 15.5 kcal mol
−1, which is higher than those computed for the formation of
Ind-2 (15.1 kcal mol
−1) and
Cp-2 (12.4 kcal mol
−1). This reaction step is exothermic by 20.6 kcal mol
−1. These metallacycles are generally described by two resonating structures, i.e., a metallacyclopentadiene, as found for CpCo-(C
4H
4) [
37,
49] and CpRh-(C
4H
4) [
41,
49], and a metallacyclopentatriene, as for CpRuCl-(C
4H
4) [
38]. In
anti-
Ind-2, the C
α-C
β and C
β-C
β’ distances are 1.35 Å and 1.47 Å, respectively, which are rather well matched to the length of the ethylene double bond and to the length of the σ-bond between two carbon atoms, respectively. This suggests the character of rhodacyclopentadiene of
anti-Ind-2.
A third acetylene molecule easily coordinates to
anti-
Ind-2, which is converted into
anti-
Ind-3. This step is barrierless and exothermic by 22.8 kcal mol
−1, about 5 kcal mol
−1 less exothermic than the formation of
CpRh-3; this value is almost identical to the reaction energy computed for the formation of
IndRh-3. Subsequently, by Diels-Alder-like [4+2] addition of the coordinated acetylene to the rhodacycle,
anti-
Ind-4 forms, with an activation energy of 5.3 kcal mol
−1 (
Figure 2a). This step is strongly exothermic by 68.6 kcal mol
−1, 8.4 kcal mol
−1 more exothermic than the same step in the IndRh catalytic cycle; conversely, the energy barriers are very similar. Structurally,
anti-
Ind-4 (
Figure 1) is characterized by the presence of a six-carbon arene ring coordinated to rhodium in η
6 fashion, while η
3 coordination is found in the Cp-Rh moiety. A similar bonding mode of rhodium is found in
Ind-4; conversely, in
Cp-4, η
4 hapticity is observed with the arene ring and η
3 +η
2 coordination to Cp moiety. This pronounced slippage in
Ind-4 and
anti-Ind-4 explains the spikes in the profiles of Δ and
(
Figure 2b). The coordination of another acetylene leads to the formation of
anti-
Ind-5 (
Figure 2a), accompanied by a variation of hapticity from η
3 to η
3 + η
2 in the anti-IndRh fragment and by the release of 11.5 kcal mol
−1. The cleavage of benzene by the incoming second acetylene completes the cycle with the regeneration of the catalyst. The released energy is 16.4 kcal mol
−1. Summarizing, the η
3 + η
2 coordination is found along the whole cycle catalyzed by
anti-IndRh except in intermediate
anti-
Ind-4, where η
3 coordination is predicted.
Consistently with CpRh and IndRh catalysis, the first step
Z-1 → Z-2, that is the oxidative coupling of the acetylene molecules, has the highest energy barrier along the cycle (
Figure 2a). To gain insight on the origin of this barrier, an activation strain analysis (ASA) has been carried out and compared to those already reported for CpRh and IndRh [
49]. For this purpose, the complexes were divided into two fragments, i.e., Cp’Rh (Cp’ = Cp, Ind, and anti-[Cr(CO)
3Ind]) and the C
4H
4 moiety. Being an intramolecular reaction, the activation energy
is conveneintly given as the change, upon going from the reactant to the TS, in strain within the two fragments plus the change, upon going from the reactant to the TS, in the interaction between these two fragments [
53].
The results are shown in
Table 1. The
contributions increase from CpRh to IndRh and to anti-IndRh and are very similar for the Cp’Rh fragments (ranging from 2.4 to 2.7 kcal mol
−1), but increase significantly for the C
4H
4 fragment going from 33.2 to 37.0 and 37.3 kcal mol
−1, respectively. Since
are very similar, varying from -23.2 kcal mol
−1 (CpRh) to −24.6 kcal mol
−1 (IndRh) and −24.5 kcal mol
−1 (anti-IndRh), the increase of the barrier in the indenyl catalysts is mainly due to the strain effects localized on the bis-acetylene moiety. Based on the identical
for IndRh and anti-IndRh, no influence of the second metal of the latter is found in the barrier of this oxidative coupling.
We also examined
Z-4, which was found to be more stable in the case of anti-IndRh than in the cases of IndRh and CpRh. ASA was carried out on
Z-4, by considering these two fragments: Cp’Rh, where (Cp’ = Cp, Ind, and anti-[Cr(CO)
3Ind]) and the C
6H
6 moiety; the results are listed in
Table 2. A very high total
is found in
Cp-4 compared to
Ind-4 and
anti-Ind-4, which comes out from the benzene fragment and reflects the structural differences. In fact, benzene is bent in
Cp-4 with η
4 coordination (
Figure S2), while in
Ind-4 and
anti-Ind-4, the ring is almost planar and coordinated to rhodium in η
6 fashion and η
3 coordination is found for the Rh coordination to the Cp ring. On the other hand, the large
of
Cp-4 is well balanced by a large negative
, which leads to larger
by about 12.2 kcal/mol than
Ind-4 and
anti-Ind-4.
Although the catalytic center is rhodium, we also investigated the coordination of Cr(CO)
3 in all the intermediates and transition states of the anti-IndRh catalyzed cycle. ASA was carried out using as fragments Cr(CO)
3 and IndRhX
i (
Table 3). Significantly larger
values are found for
anti-Ind-TS (1,2) and
anti-Ind-TS (3,4); the biggest contribution comes from the IndRhL
n fragment, reflecting the changes occurring at the Rh center. The
of Cr(CO)
3 fragment remains almost equal along the path, reflecting the fact that no important structural changes occur within the Cr(CO)
3 moiety.
values fluctuate in the range~47–54 kcal mol
−1. In
anti-Ind-4, a sudden increase of
is computed. In fact, on the opposite side of the indenyl ligand, Rh-Cp coordination is highly slipped (
Figure 2). Therefore, in order to compensate for the weakening of Rh-Cp coordination, Cr(CO)
3 binds more tightly the benzene moiety of the aromatic ligand. In
anti-Ind-4, the increased
is due to a larger electrostatic contribution which is not sufficiently counterbalanced by an increase of
.
2.2. Acetylene [2+2+2] Cycloaddition Catalyzed by Syn-[Cr(CO)3IndRh] Fragment: Reaction Mechanism and PES (Path I)
As stated above, the coordination of the Cr(CO)
3 group to the benzene moiety of IndRh catalyst may occur in anti or syn conformation [
54]. Ceccon and co-workers have illuminated the stereochemistry of the syn catalyst, i.e., syn-[Cr(CO)
3IndRh], and found that it is kinetically more stable because of a Rh-Cr interaction.
First, we investigated the acetylene [2+2+2] cycloaddition to benzene catalyzed by syn-IndRh catalyst along Path I (
Scheme 3a). The structures of the intermediates and transition states found on the PES with their relevant parameters are shown in
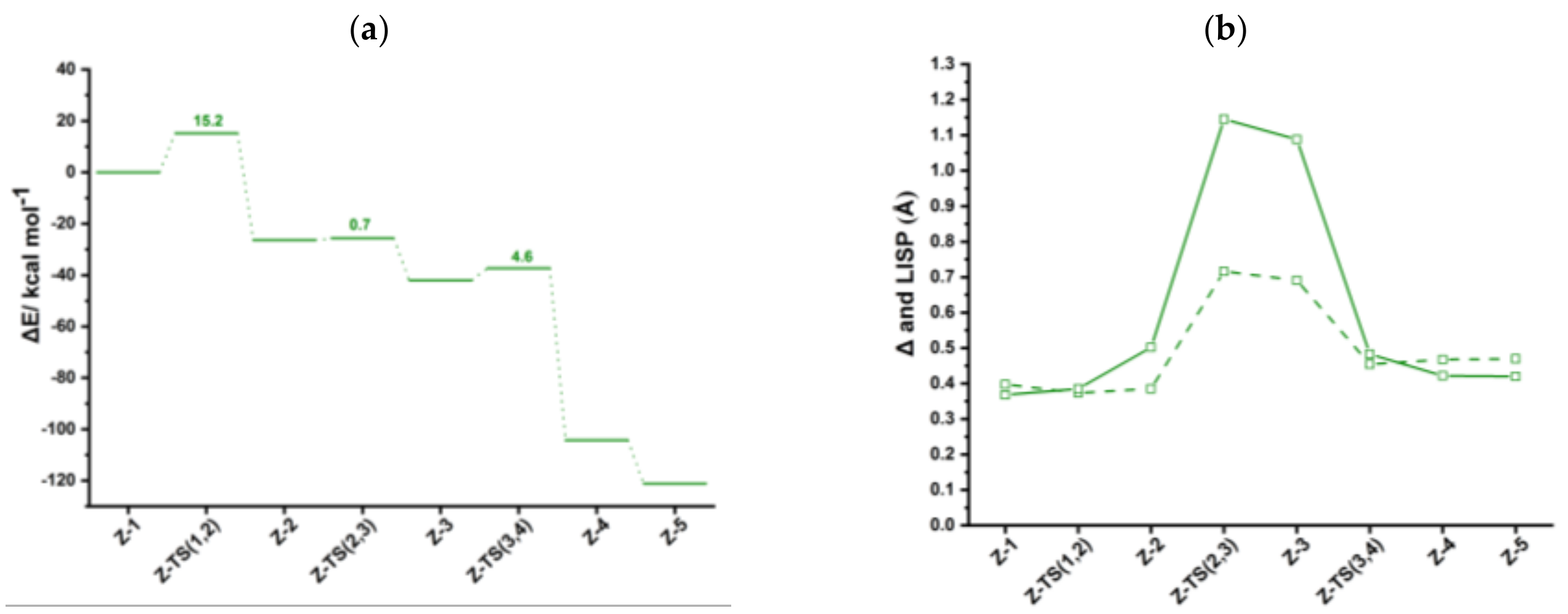
Figure S4, while the computed energy profile is in
Figure 4a. Like for anti-IndRh catalysis, at the beginning of the cycle, the ancillary ligands L are replaced by two molecules of acetylene, leading to the formation of the bis-acetylene complex
syn-
Ind-1 (
Figure S4). In
syn-
Ind-1, the Rh-C
α bond length is 2.15 Å, the distance C
β-C
β’ of two acetylenes coordinated to rhodium is 2.91 Å, and the angle C
α-Rh-C
α’ is 91°. To quantify the Rh-Cp slippage along the catalytic cycle, Δ and
parameters were computed for all the intermediates and transition states and are shown in
Figure 4b. In
syn-
Ind-1, their values are 0.40 Å and 0.37 Å, respectively, with no appreciable difference with respect to
anti-
Ind-1; this might be ascribed to Rh-Cr interaction, despite high steric effects are present.
The oxidative coupling in
syn-
Ind-1 leads to the formation of the five-membered ring rhodacycle
syn-
Ind-2 with an activation energy of 15.2 kcal mol
−1, nearly the same as found for anti-IndRh. Notably, in
syn-
Ind-2 complex, one CO of Cr(CO)
3 interacts with Rh. In fact, the distance between the CO ligand and rhodium is 2.30 Å, and the distance between Cr and Rh center is smaller by 0.34 Å than in
syn-
Ind-1, implying stabilization of
syn-
Ind-2. In this situation, the rhodacycle
syn-Ind-2 is a nearly 18-electron saturated complex, in contrast to
anti-Ind-2 and the parent
Ind-2 and
Cp-2. The conversion of
syn-
Ind-1 into
syn-
Ind-2 is exothermic by 26.4 kcal mol
−1, about 6 kcal mol
−1 more than in the anti-catalyst and in the parent IndRh (
Figure 3a). Finally, in this step, an hapticity shift from η
3+η
2 to η
3 occurs (
Figure 4b).
The coordination of the third acetylene to
syn-
Ind-2 occurs from the upper side with a low barrier of 0.7 kcal mol
−1, via
syn-
Ind-TS (2,3) (
Figure S4) and a large slippage variation (
changes by approximately 0.6 Å) leading to almost η
1 coordination. The conversion
syn-Ind-2 → syn-Ind-3 occurs only with a slight modification in the carbon-carbon bonds of the rhodacycle. The reaction is exothermic by 15.6 kcal mol
−1. In the next step,
syn-
Ind-4 forms, crossing a barrier of 4.6 kcal mol
−1. The
value drops from 1.09 Å to 0.42 Å (
Figure 4b).
syn-
Ind-4 has a six-carbon arene ring coordinated to rhodium in η
4 fashion, while in Rh-Cp the coordination is η
3 +η
2. Thus, the bonding mode of rhodium is different from
anti-
Ind-4 (
Figure 2), where η
6 coordination and η
3 coordination are found between the six-carbon arene ring and rhodium and the Cp ring and rhodium, respectively. However,
syn-Ind-4 resembles the case of the parent
Cp-4 [
41]. This step is exothermic by 62.3 kcal mol
−1.
Finally, the coordination of another acetylene leads to the formation of
syn-
Ind-5 with no appreciable activation energy and with the release of 16.8 kcal mol
−1 (
Figure 4a). It is less exothermic than the formation of
Ind-5 but more exothermic by 5 kcal/mol than the formation of
anti-Ind-5. The cleavage of benzene promoted by another acetylene completes the cycle and leads to the regeneration of the catalyst. The energy released in this last step is 18.8 kcal mol
−1. During the catalysis, the Rh-Cr distance varies in the range 3.05–3.51 Å, but remains close to the crystallographic value of 3.1 Å [
34].
The hapticity variations along the catalytic cycle are definitively more pronounced in syn-IndRh catalysis than in the anti-IndRh one.
By inspecting the energy profile (
Figure 4a), in the syn-IndRh catalyzed process the oxidative coupling
Z-1 → Z-2 has the highest energy barrier. From ASA (
Table 1), a very high ΔΔ
Estrain contribution to the barrier
has been found compared to anti-IndRh and also to the parent catalysts IndRh and CpRh. However,
is a pretty strongly stabilizing term and compensates for the strain, resulting in a lowering of
. In contrast to anti-IndRh, the strain arising from the Cp’Rh fragment is very high (
Table 1) because of the steric effects and because Cr(CO)
3 undergoes deformation to interact with the Rh center.
To further assess the interaction and the role of Cr(CO)
3 in the syn-IndRh catalyzed process, ASA was carried out for the intermediates and transition states of the whole catalytic cycle, considering Cr(CO)
3 and IndRhX
i fragments; the results are reported in
Table 4.
are in the range ~49–58 kcal mol
−1, larger than those computed for the anti-IndRh molecular species (
Table 3), suggesting Rh-Cr stabilizing interaction in the former case. On the other hand,
is also larger. This is mainly ascribed to steric factors. In particular, the contribution of Cr(CO)
3 to
in
syn-Ind-2, syn-Ind-TS (2,3) and
syn-Ind-3 is higher, suggesting some structural differences from the anti-analogous species. In fact, in these structures one carbonyl ligand is coordinated to Rh (
Figure S4). This feature also leads to larger
in syn-Ind-2.
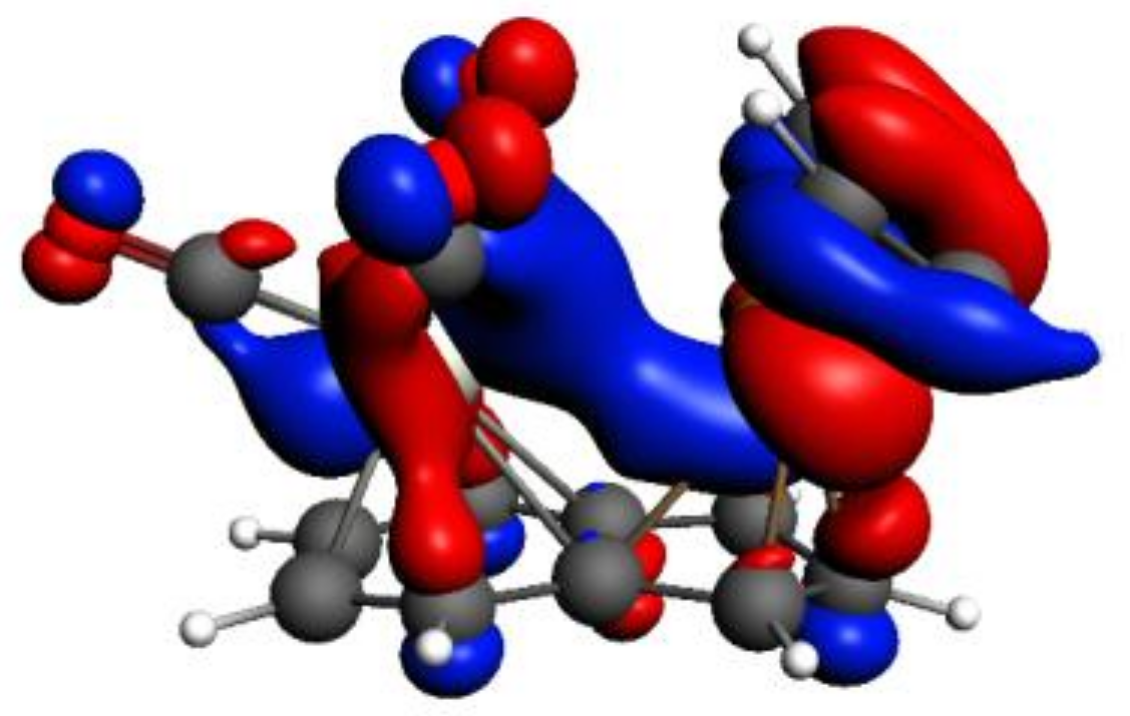
As an example of an existing favorable inter-metal interaction, in
Figure 5, we show HOMO-3 of
syn-Ind-1, which is formed by the contributions of the HOMOs of Cr(CO)
3 and IndRh(C
2H
2)
2 fragments, whose metal
d-based molecular orbitals (MOs) indicate stabilizing
d-d bonding between Rh-Cr.
2.3. Acetylene [2+2+2] Cycloaddition Catalyzed by Anti-[Cr(CO)3IndRh] Fragment: Reaction Mechanism and PES (Path II)
According to the alternative mechanistic path by Booth et al. [
26], an ancillary ligand of the catalyst precursor remains bonded to rhodium during the catalytic cycle; this mechanism is denoted Path II (
Scheme 3b). For CpRh(CO) and IndRh(CO), this path has been thoroughly explored, making it possible to give an interpretation of the higher efficiency of the indenyl catalyst observed in the experiment [
35]. Thus, here we considered the same hypothesis for anti-IndRh(CO) catalyzed acetylene [2+2+2] cycloaddition. The structures of the intermediates and transition states found on the PES with their relevant parameters are in
Figures S5–S7. The energy profile of the process is shown in
Figure 6a.
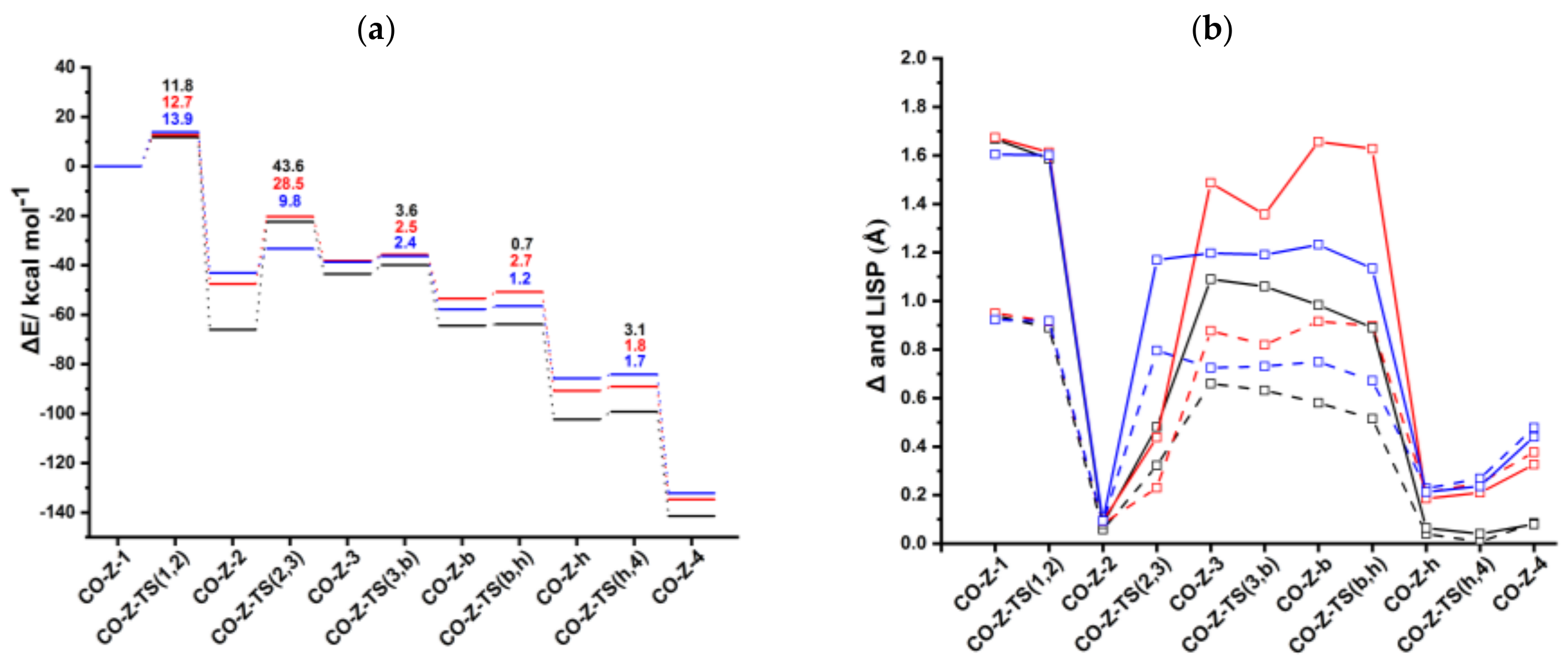
CO-
anti-
Ind-1 is characterized by η
1 coordination which is due to the presence of two acetylenes and the CO ligand, as observed for CpRh(CO) and IndRh(CO) catalysis [
43]. Δ and
values are 0.92 Å and 1.60 Å, respectively (
Figure 6b). The initial oxidative coupling leads to the formation of
CO-
anti-
Ind-2, in which rhodium is coordinatively saturated due to the presence of CO. The energy barrier required to cross
CO-anti-Ind-TS (1,2) is 13.9 kcal mol
−1 slightly higher if compared to those computed for CpRh(CO) and IndRh(CO) catalysis (by about 1–2 kcal mol
−1). This is the same energy trend observed along Path I. The conversion of
CO-
anti-
Ind-1 into
CO-
anti-
Ind-2 is accompanied by the hapticity change from η
1 to distorted η
5 and is exothermic by 43.1 kcal mol
−1 (
Figure 6a), 4.5 kcal mol
−1 and 23.0 kcal mol
−1 less than the analogous step in IndRh(CO) and CpRh(CO) catalysis, respectively. The addition of the third acetylene leads to the formation of the η
1 CO-
anti-
Ind-3 with an activation energy of 9.8 kcal mol
−1. The barriers for this step are much higher in the cases of IndRh(CO) and CpRh(CO) catalysis, i.e., 28.5 and 43.6 kcal mol
−1, respectively. Thus, this step is kinetically favored with the bimetallic anti-IndRh(CO). In addition, the formation of
CO-
anti-
Ind-3 is endothermic by 4.4 kcal mol
−1, that is overall less endothermic if compared to the same step in IndRh(CO) and CpRh(CO) catalysis, for which 9.3 kcal mol
−1 and 22.5 kcal mol
−1 are computed, respectively. Thus, the bimetallic catalyst has also a thermodynamic advantage. In the next step, the activation energy of 2.4 kcal mol
−1 is necessary to cross
CO-anti-Ind-TS (3,b) and generate the bicyclic intermediate
CO-
anti-
Ind-b (
Figure S7), with negligible difference from the IndRh(CO) catalyzed step and lower by 1.2 kcal mol
−1 than in CpRh(CO) catalyzed step. The formation of
CO-anti-Ind-b is accompanied by the release of 19.1 kcal mol
−1, being 3.8 kcal mol
−1 more exothermic than the formation of the parent
CO-
Ind-b but 1.8 kcal mol
−1 less exothermic than
CO-
Cp-b. One can notice that the bicyclic intermediate in CpRh(CO) catalysis has an higher energy while in bimetallic anti-IndRh(CO) and IndRh(CO) catalysis it lies at a lower energy (
Figure 6a), suggesting a better catalytic efficiency in these latter cases. By crossing a modest barrier of 1.2 kcal mol
−1, the bicyclic
CO-
anti-
Ind-b readily transforms into the heptacyclic intermediate
CO-
Ind-h; this step is accompanied by the haptotropic shift η
1 → distorted η
5 and by the release of 28.0 kcal mol
−1, a value lower than those computed for the parent catalysts, i.e., −37.4 kcal mol
−1 in the case of IndRh(CO) and −37.8 kcal mol
−1 in the case of CpRh(CO), respectively.
CO-
anti-
Ind-h undergoes reductive elimination with an activation energy of 1.7 kcal mol
−1.
CO-
anti-
Ind-4 forms and 46.4 kcal mol
−1 are released. Finally, benzene is cleaved from
CO-
anti-
Ind-4 by stepwise addition of two acetylene molecules and the catalyst is regenerated.
With the formation of the 18-electron intermediate
CO-Z-2, a rather flat portion of the PES begins (
Figure 6a). ASA was carried out on
CO-Z-2 considering CO-Cp’Rh (Cp’ = Cp, Ind and anti-[Cr(CO)
3Ind]) and the C
4H
4 moiety as fragments; the results are listed in
Table 5. The similar strain in fragment C
4H
4 computed for
CO-Cp-2,
CO-Ind-2, and
CO-anti-Ind-2 (
Table 5) revealed that the structure of this moiety is very similar in the three catalysts (see also
Figures S5–S7). The strain contribution of the fragment CO-Cp’Rh is much higher in
CO-anti-Ind-2 and
CO-Ind-2 than in
CO-Cp-2. This is related to the least slippage predicted for this last species. The stronger interaction Δ
Eint in
CO-Ind-2 and
CO-anti-Ind-2 does not counterbalance their strain term and thus
CO-Cp-2 results the most stabilized among the three.
In the subsequent step, i.e., the addition of third acetylene to the 18-electrons rhodacycle
CO-Z-2, an energy barrier is found along the catalytic Path II (
Figure 6a).
CO-Z-TS (2,3) was divided into two fragments, i.e., CO-Cp’Rh(C
4H
4) (Cp’ = Cp, Ind and anti-[Cr(CO)
3Ind] and acetylene and ASA was performed. The results are shown in
Table 6. The acetylene in all cases is only slightly deformed, whereas CO-Cp’Rh(C
4H
4) is highly strained.
To summarize, we found that most of the steps are kinetically as well as thermodynamically more favored in the bimetallic anti-IndRh(CO) catalysis. At a glance, this can be seen also from the energy profile (
Figure 6a), which is flatter in the case of anti-IndRh(CO) than in the parent IndRh(CO) and CpRh(CO) catalyzed processes. Alternatively, the slippage variations quantified with Δ and
(
Figure 6b) are less pronounced in anti-IndRh(CO) than those computed for the parent monometallic catalysts. Thus, the smaller slippage variations and the flatter potential energy profile of the bimetallic anti-IndRh(CO) suggest an higher catalytic efficiency than the monometallic IndRh(CO) and CpRh(CO), which is consistent with the experimental findings [
26]. The phenomena of
indenyl effect for IndRh and
extra-indenyl effect for the bimetallic anti-IndRh can be fully explained when considering the mechanism of path II.
Notably, path II has been excluded for syn-IndRh(CO) because in this particular case the rhodium center would be too much crowded.