Plasma Catalysis: Distinguishing between Thermal and Chemical Effects
Abstract
1. Introduction
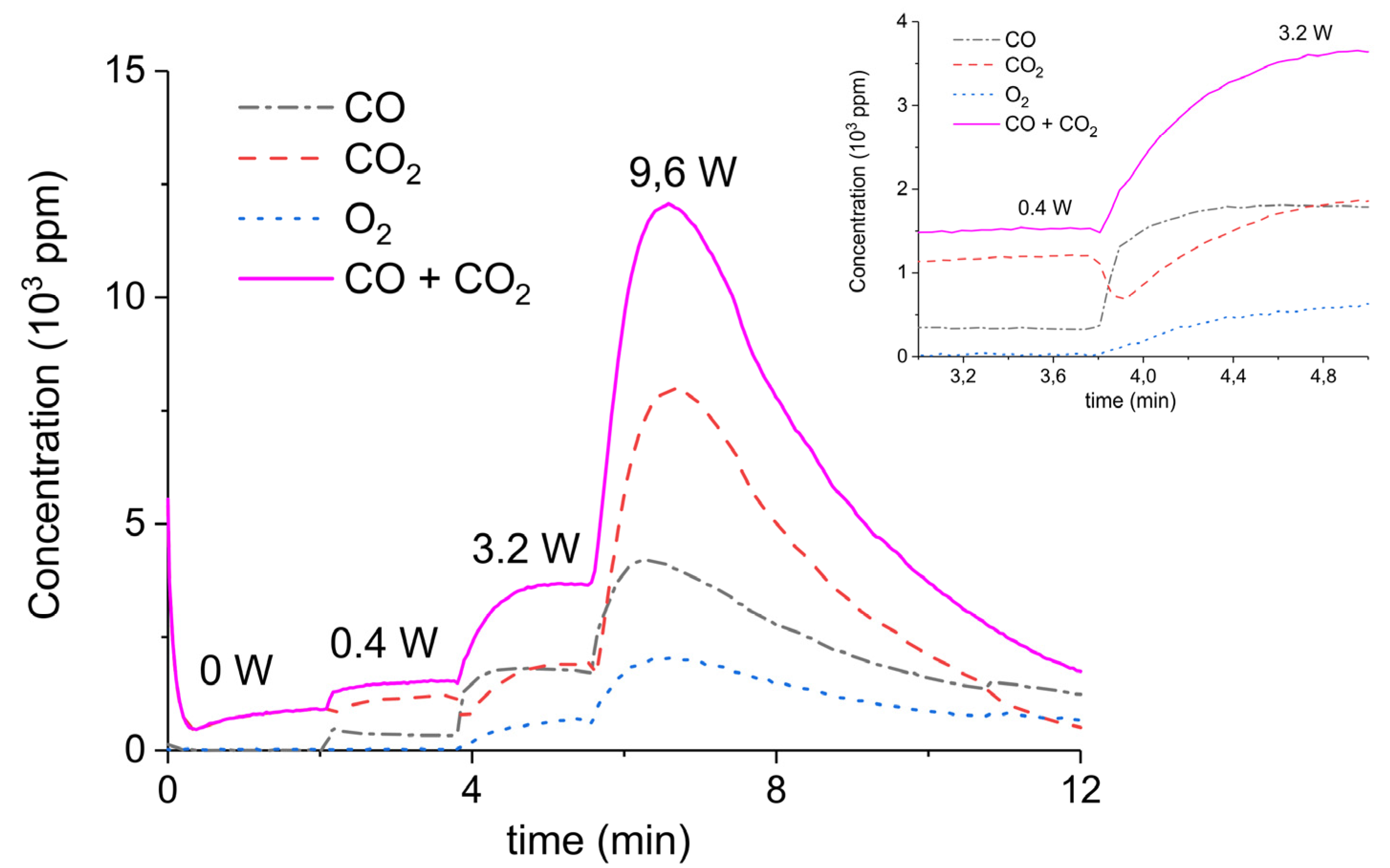
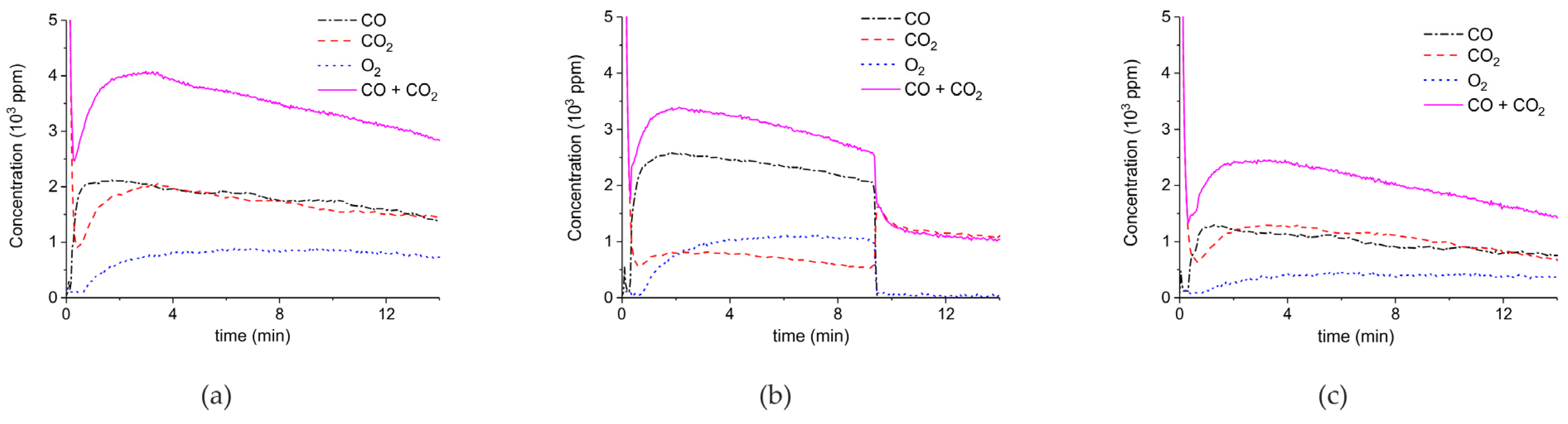
2. Results
3. Discussion
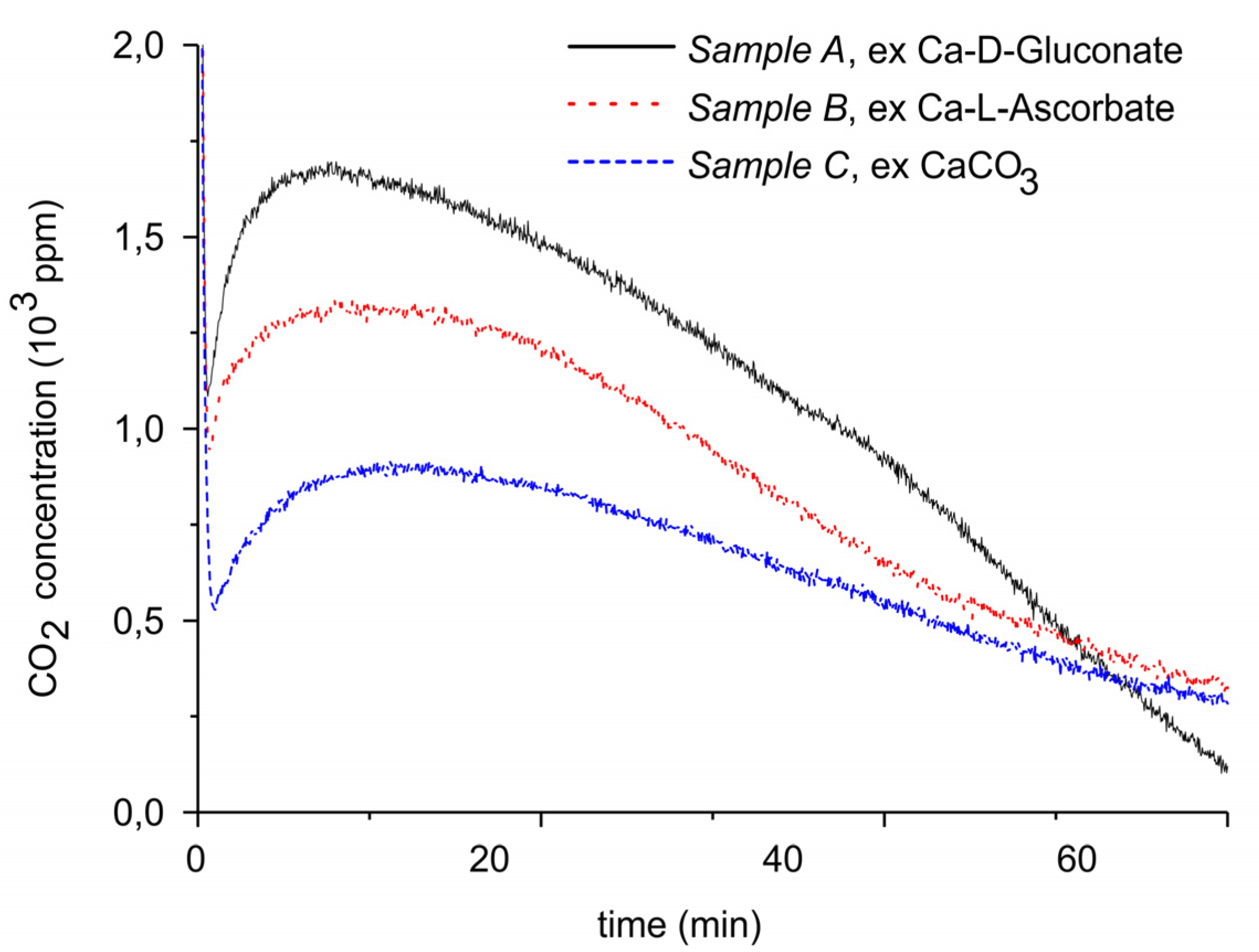
3.1. Formation of CO
3.2. Thermal Effect or Plasma Chemistry?
4. Materials and Methods
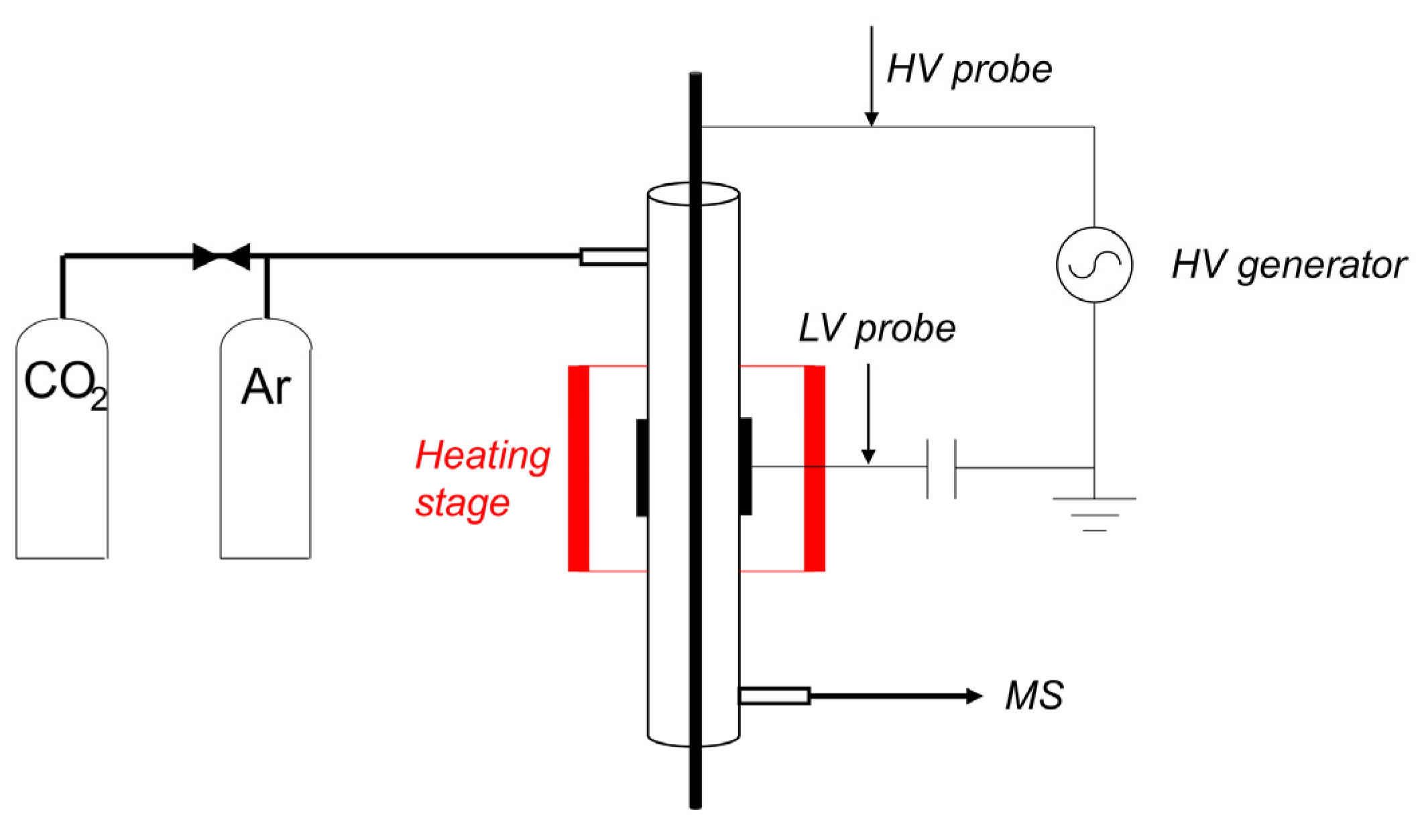
4.1. Plasma Reactor
4.2. Calcium Oxides Preparation
4.3. Carbonation
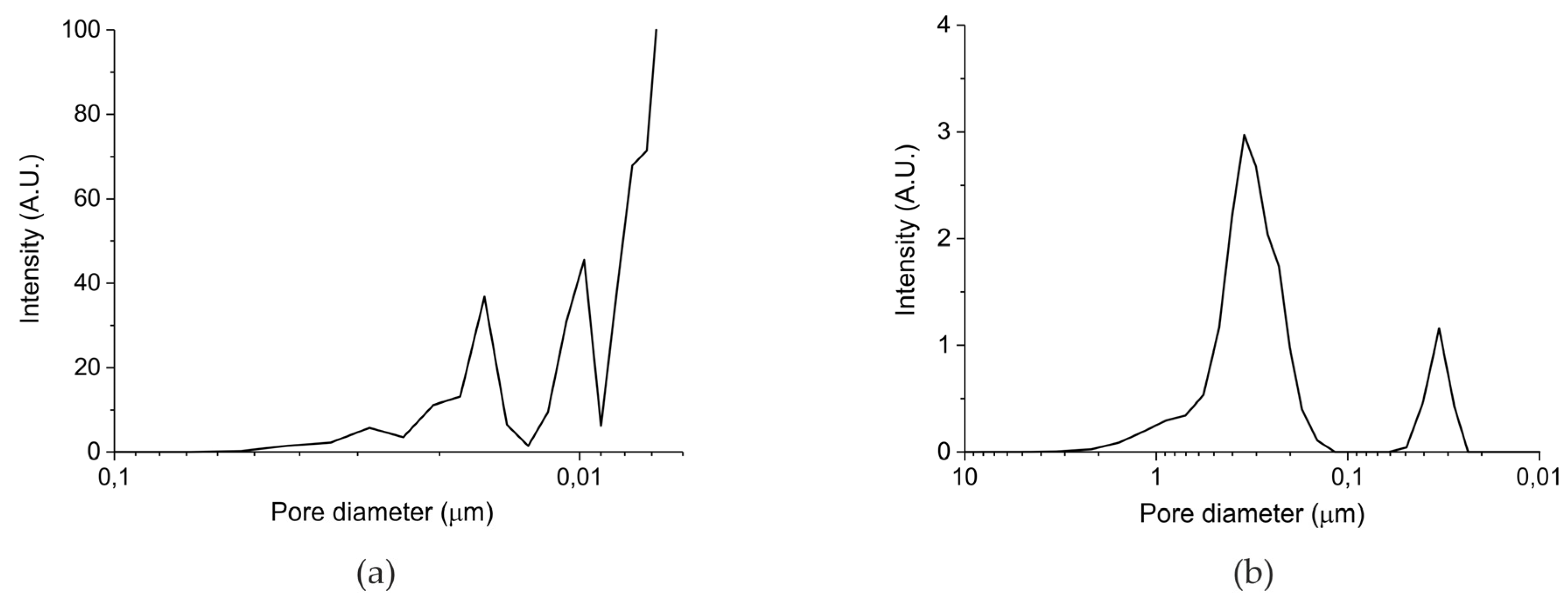
4.4. Characterization
4.5. Experimental Procedure
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Decomposition in Argon Plasma of All the Samples
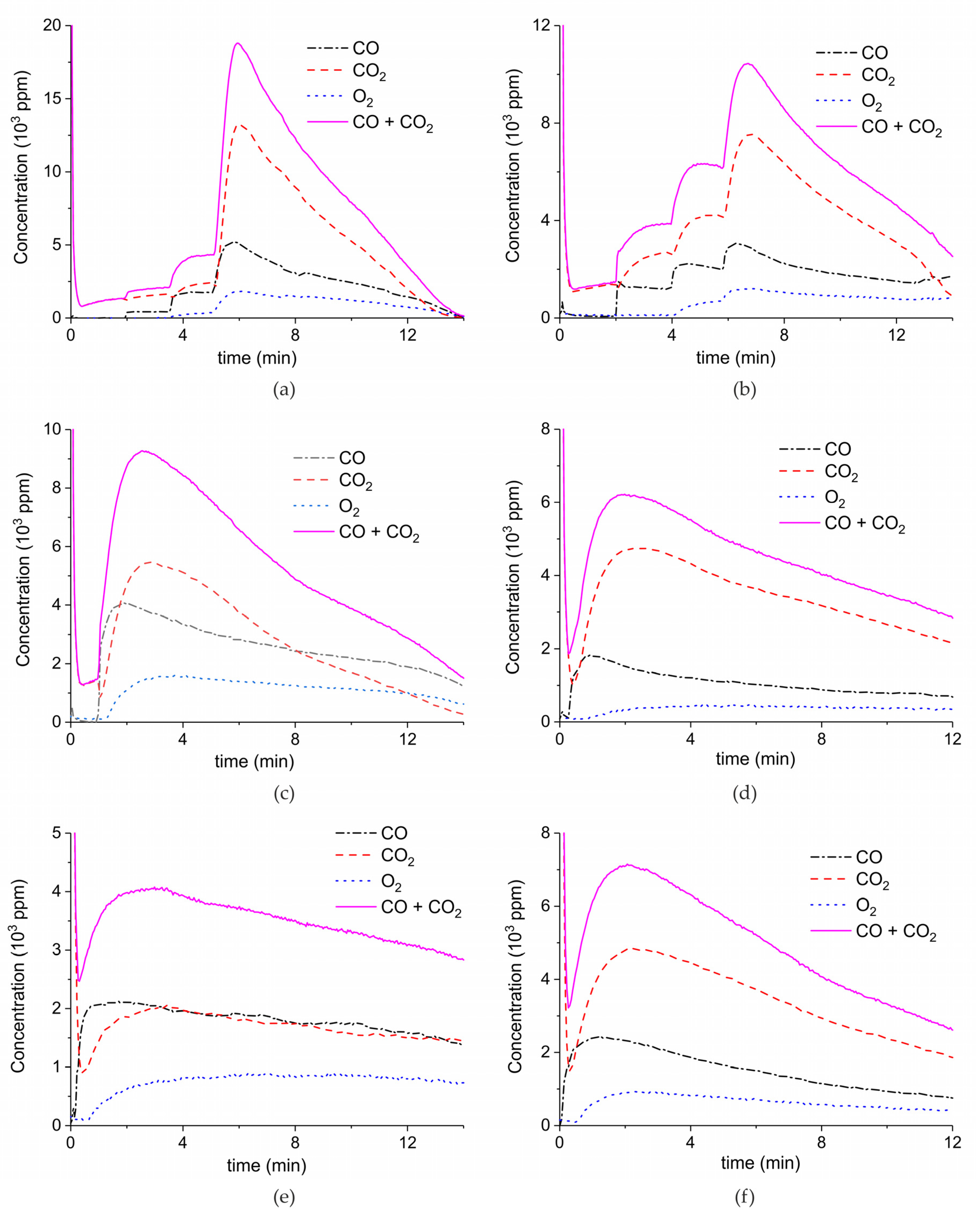
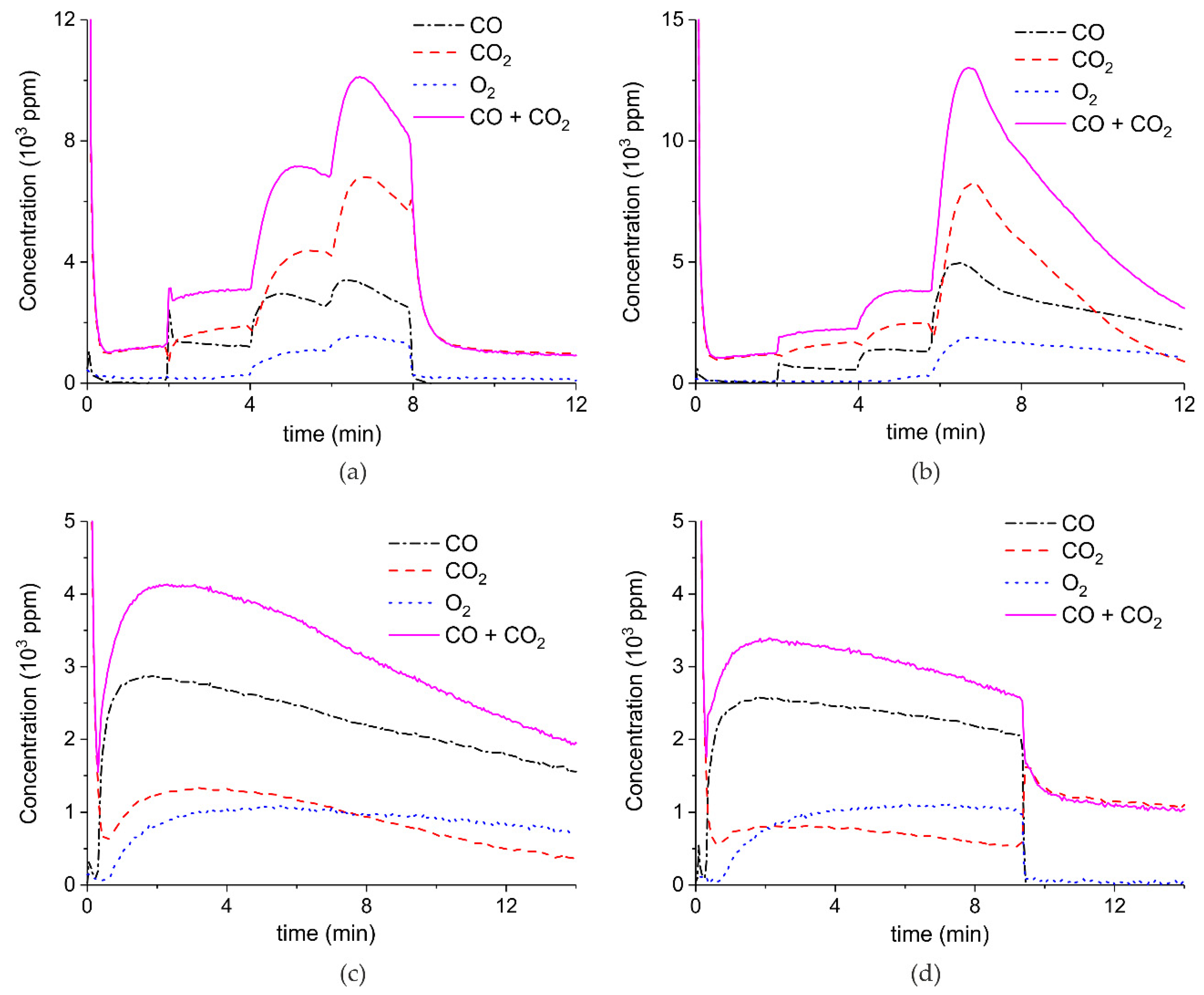
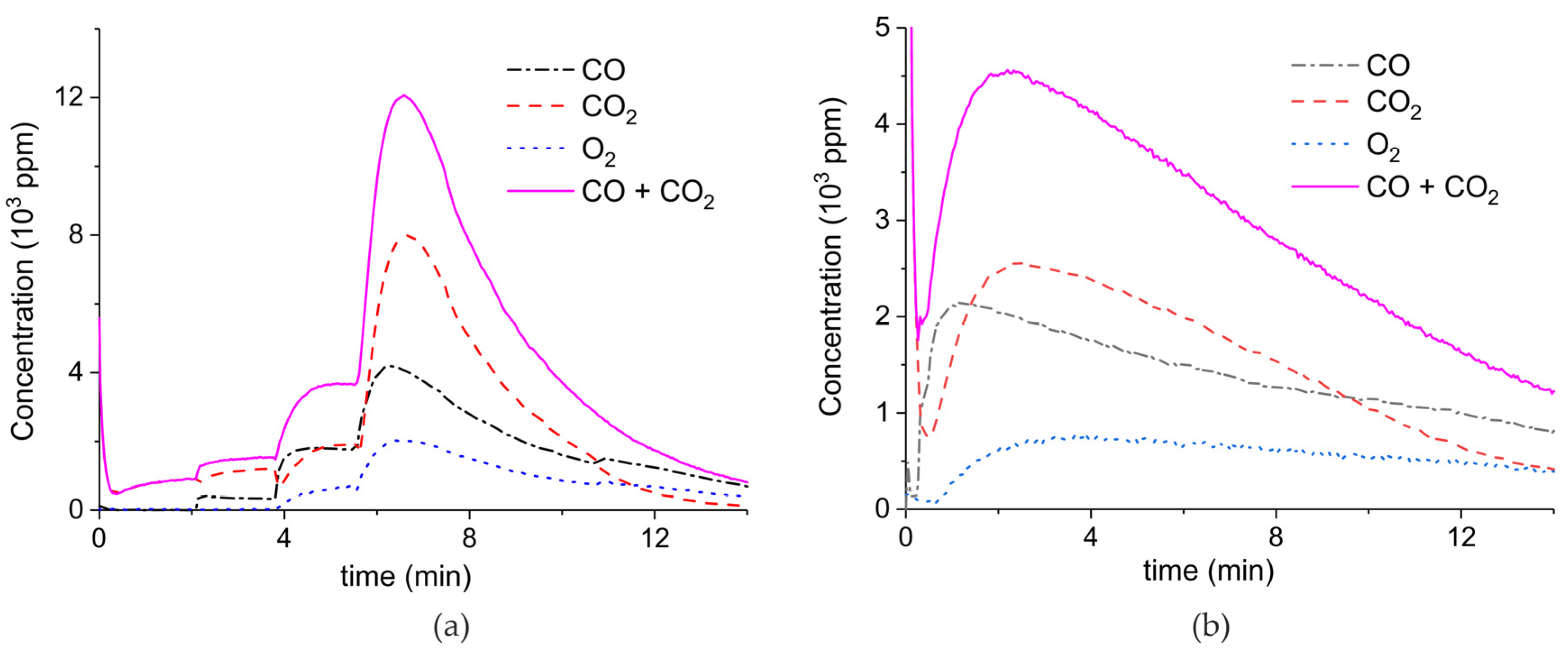
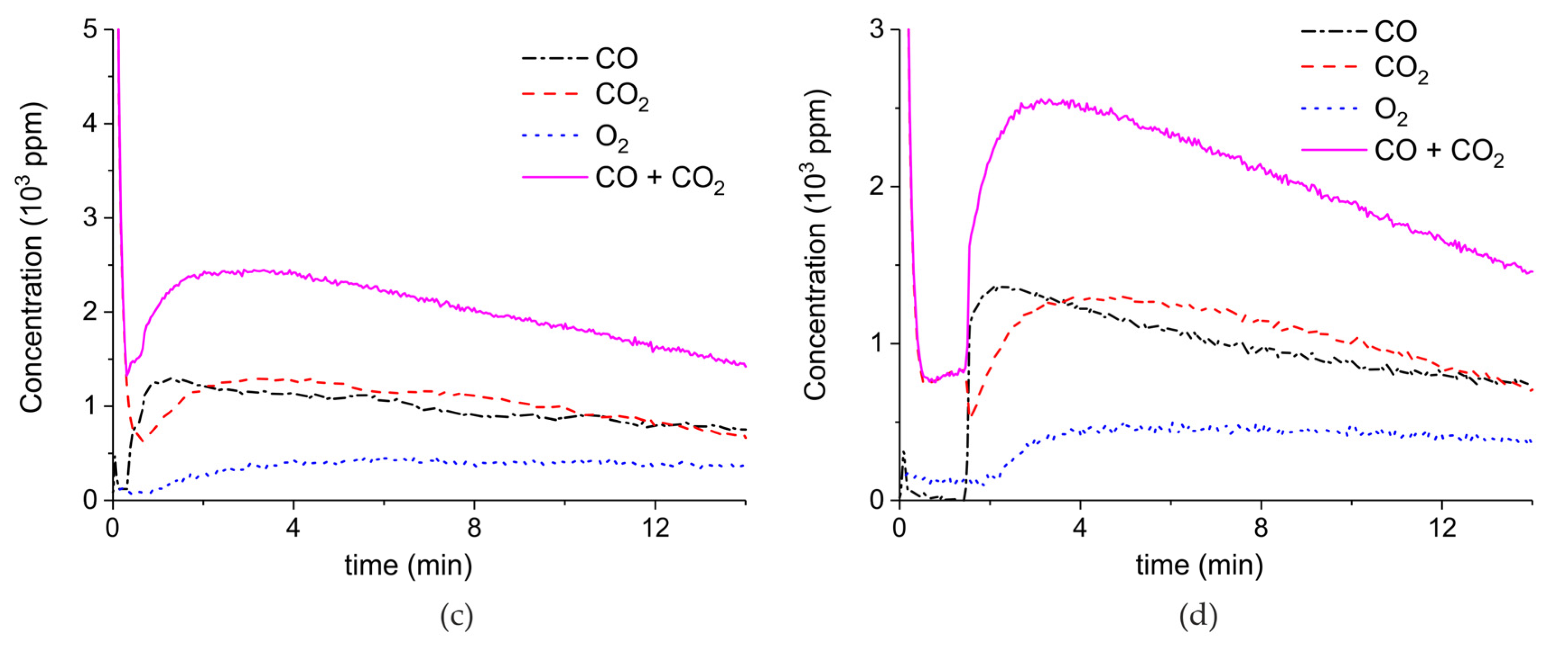
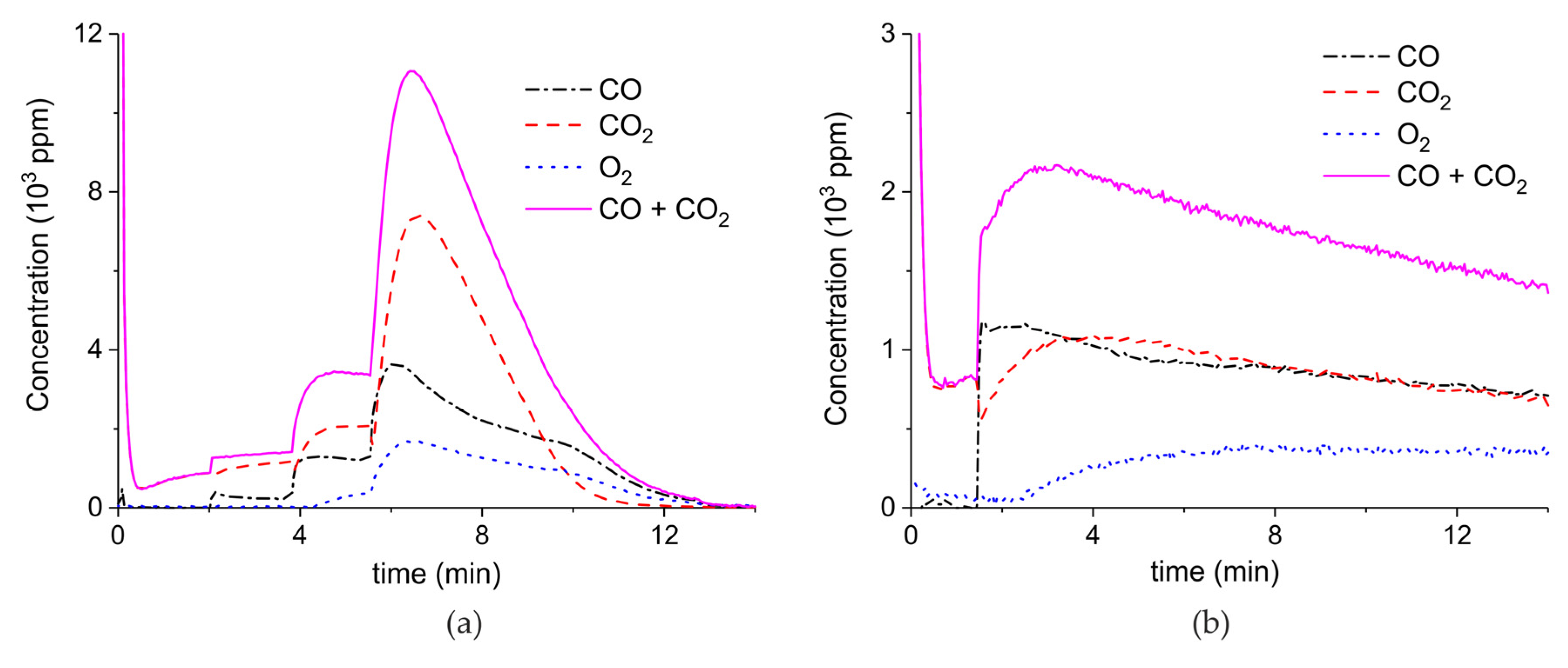
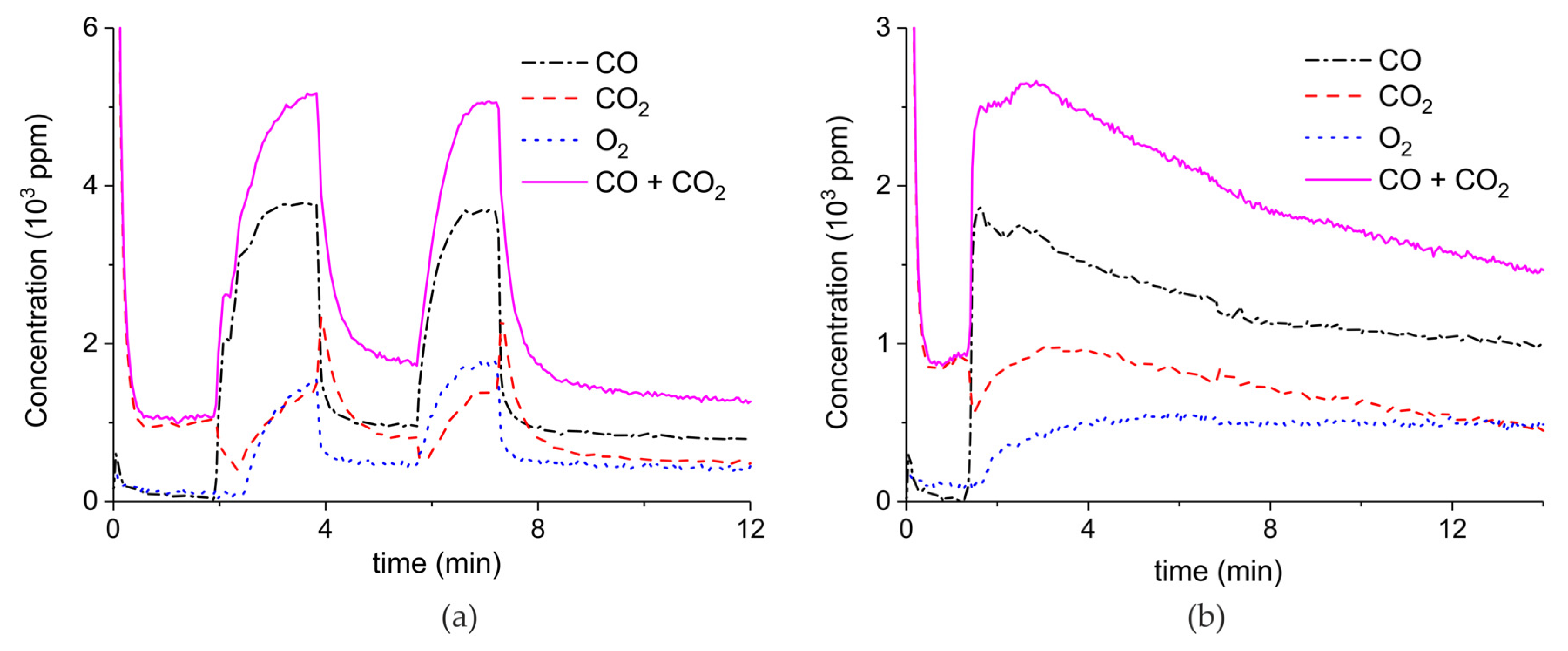
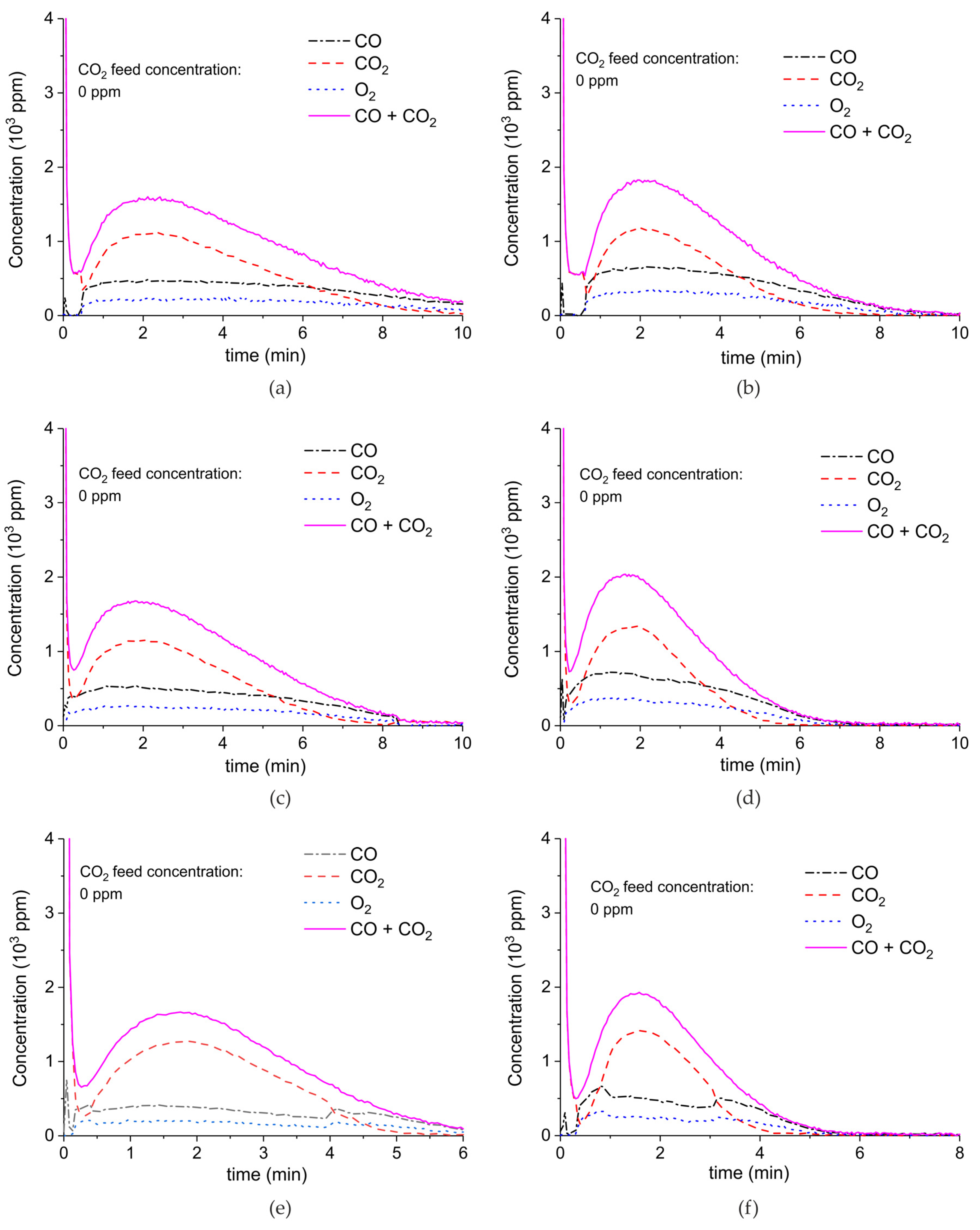
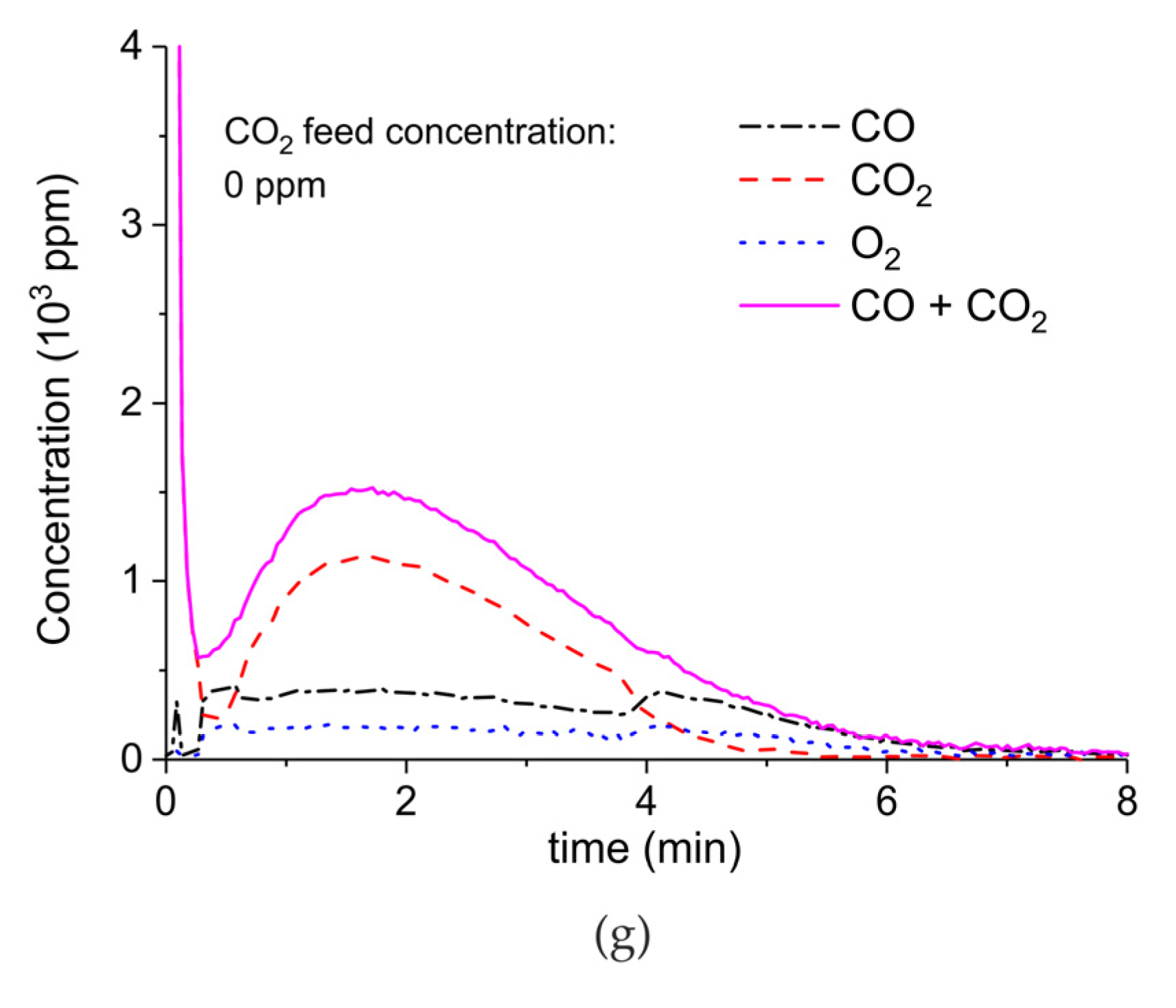
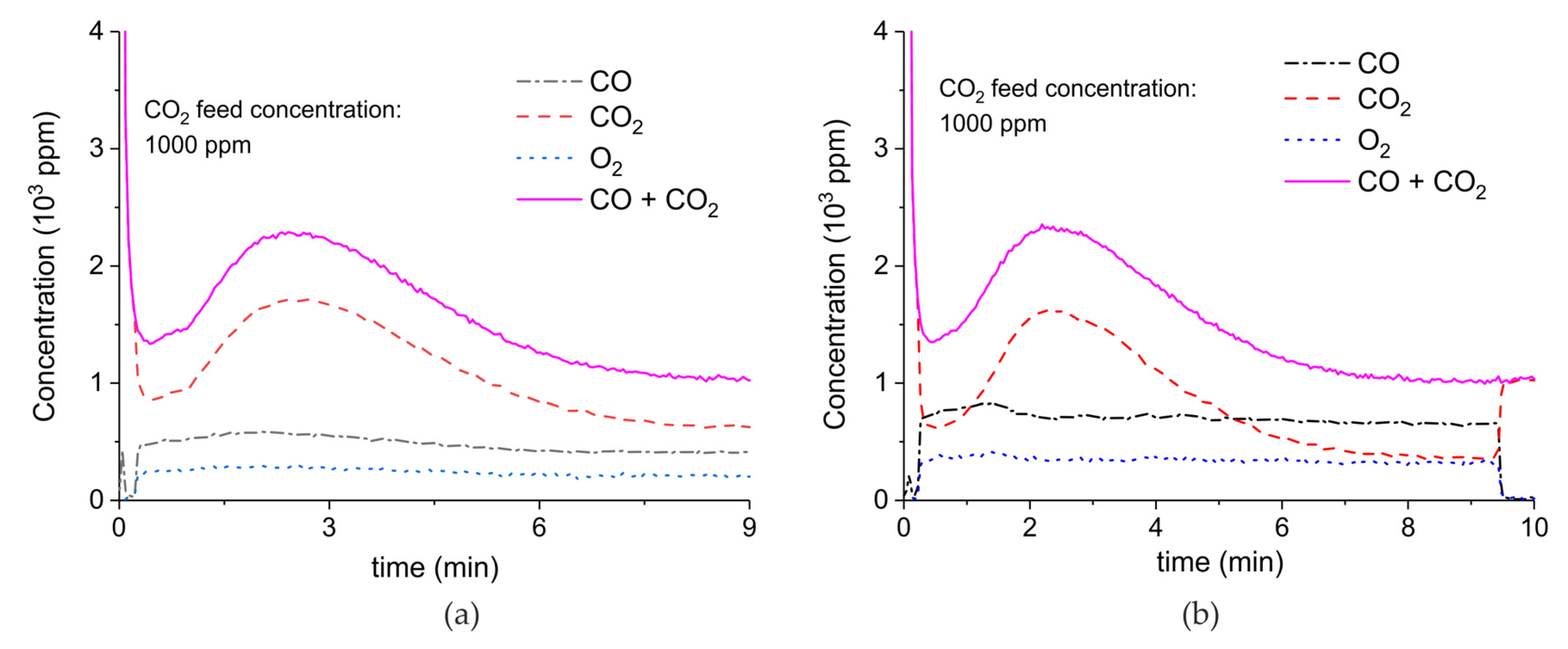
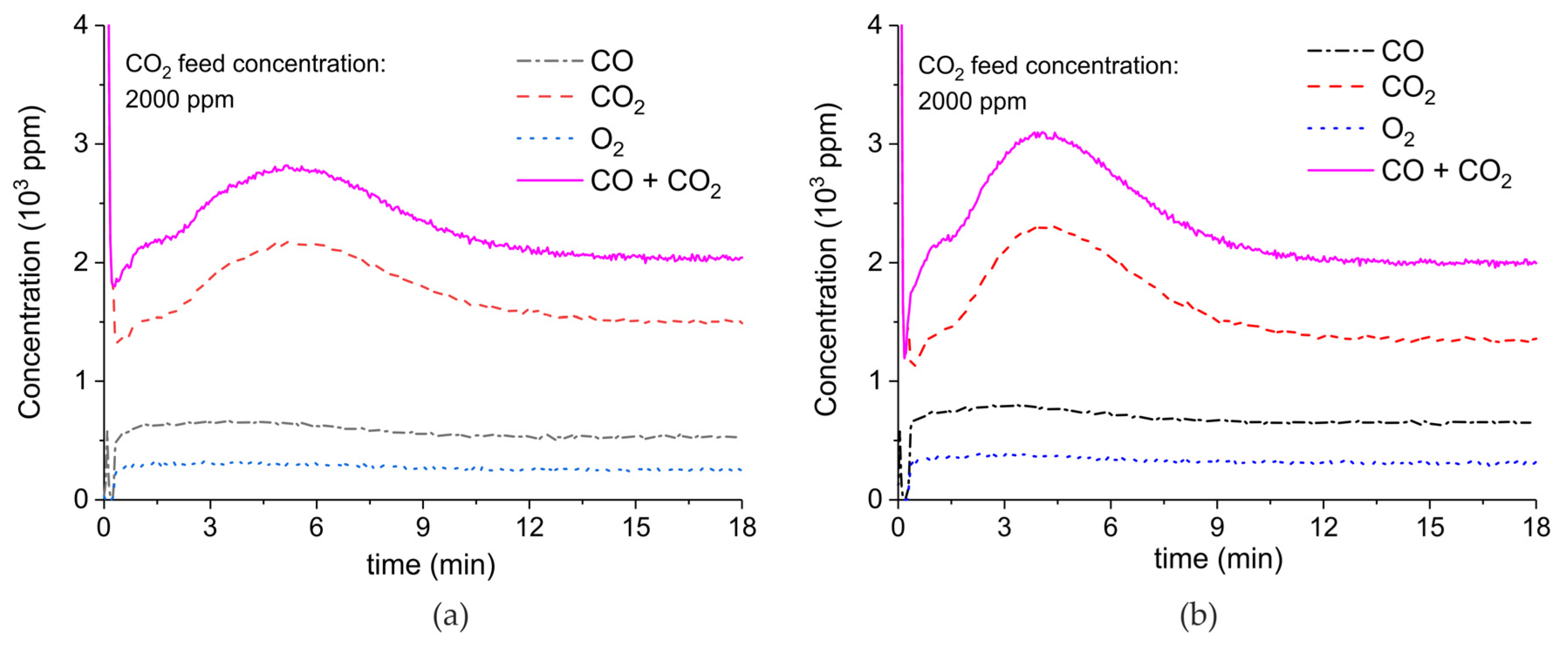
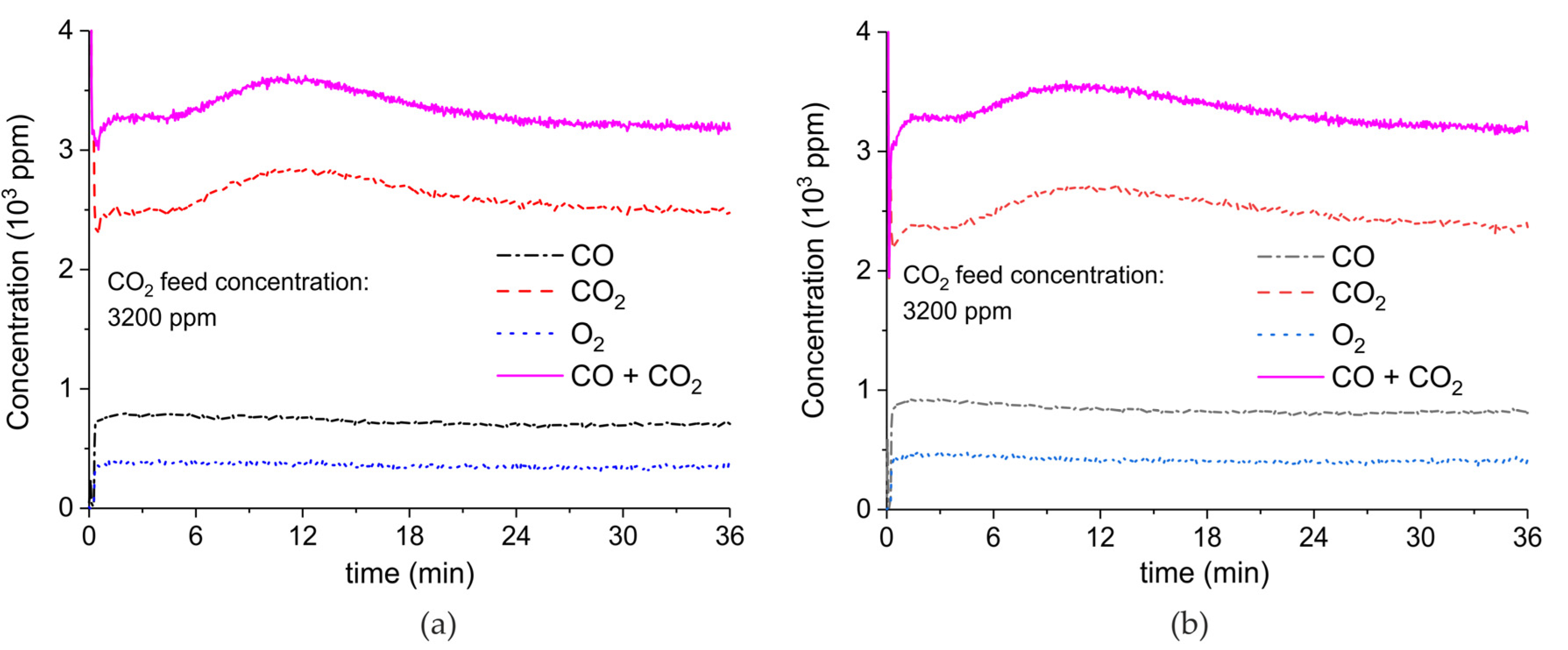
Appendix A.2. CO2 Dissociation with Only α-Al2O3
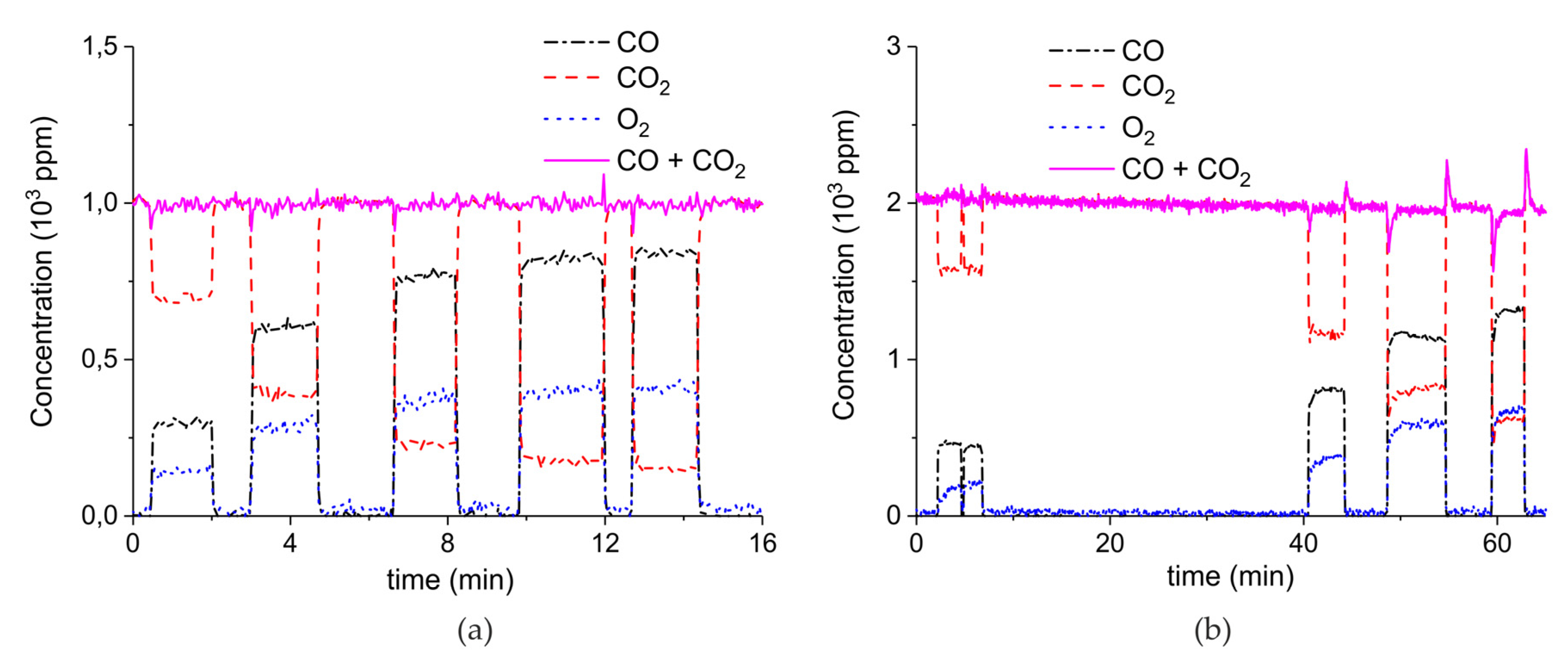
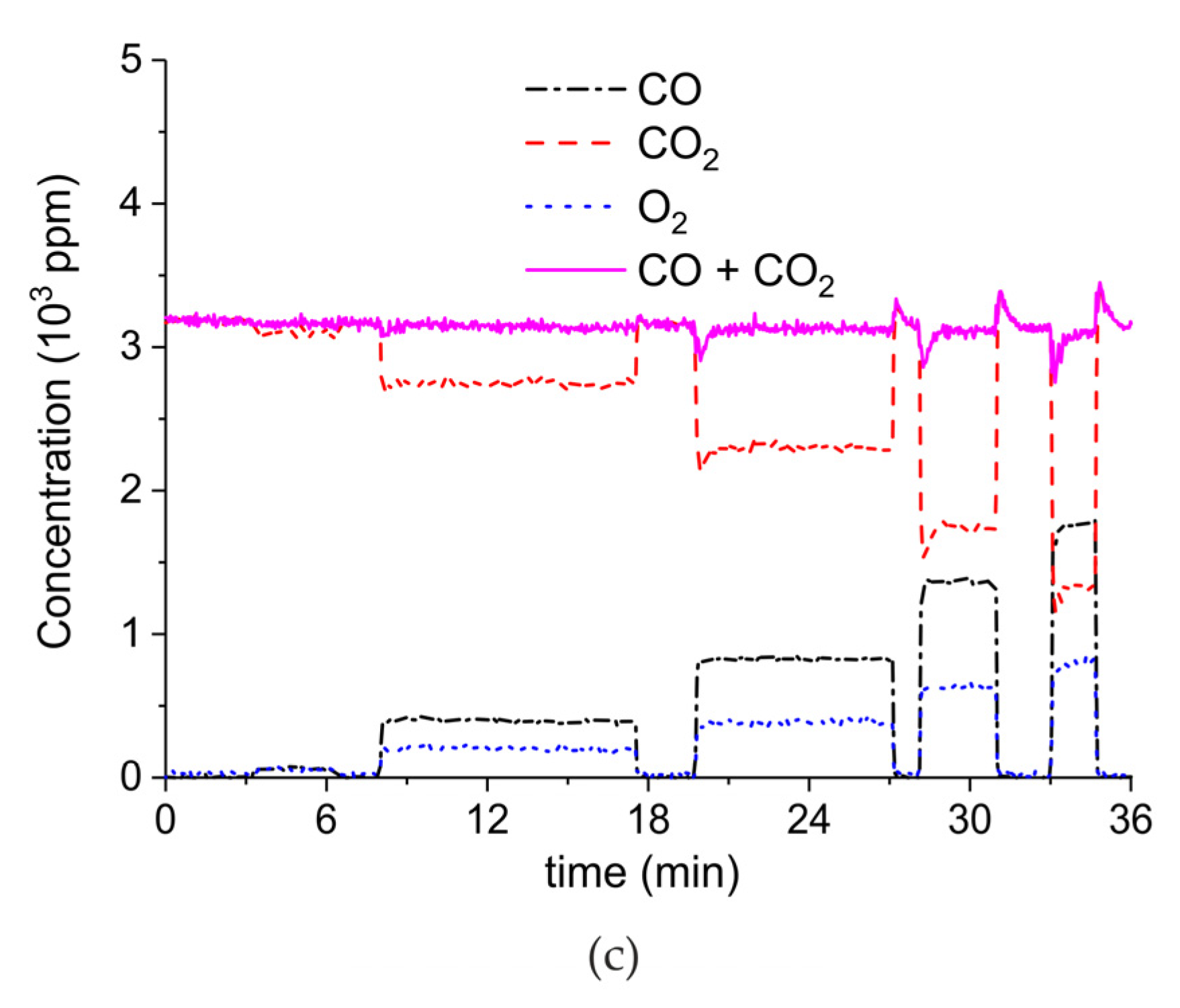
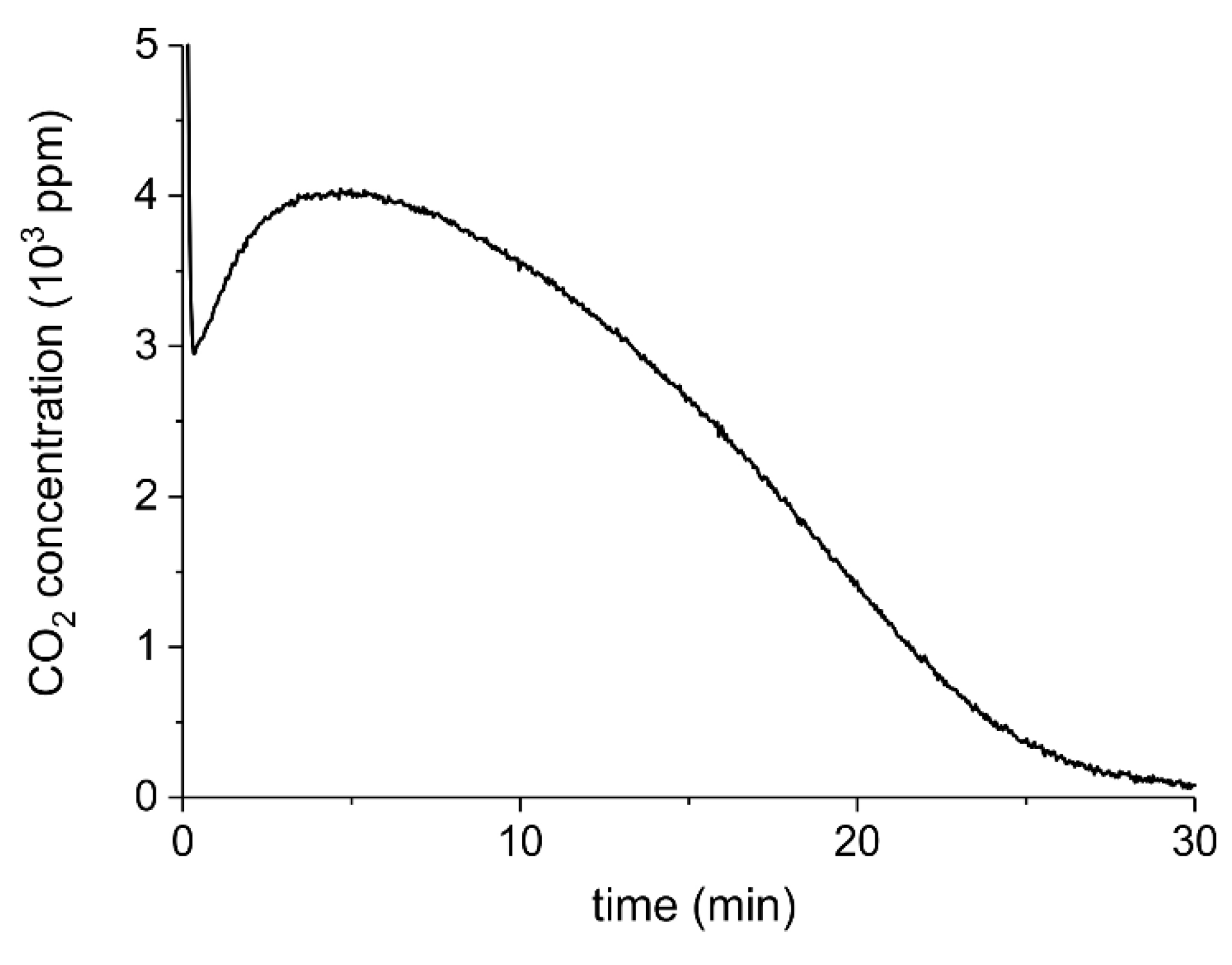
Appendix B
Appendix B.1. Determination of Plasma Power
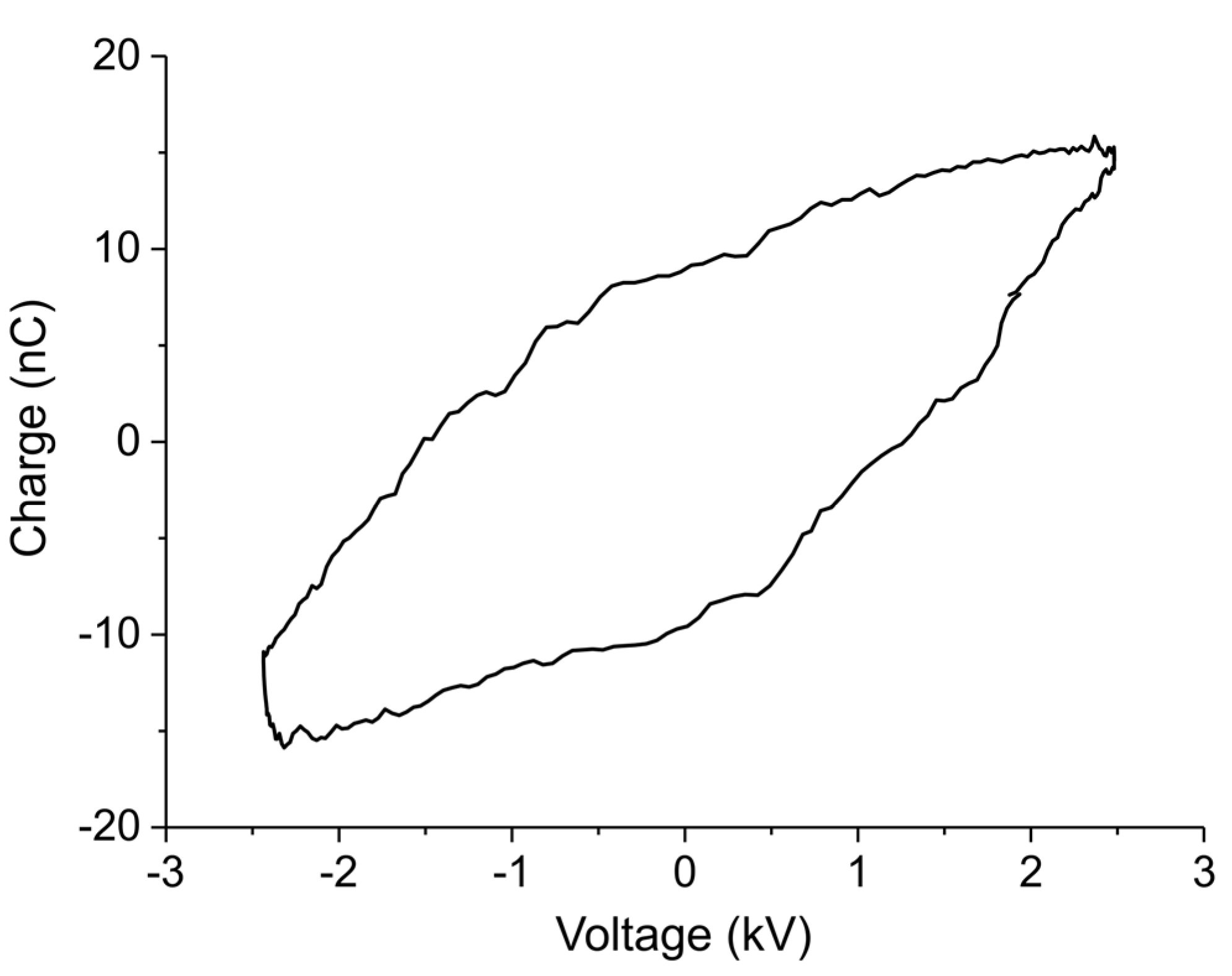
Appendix B.2. Method
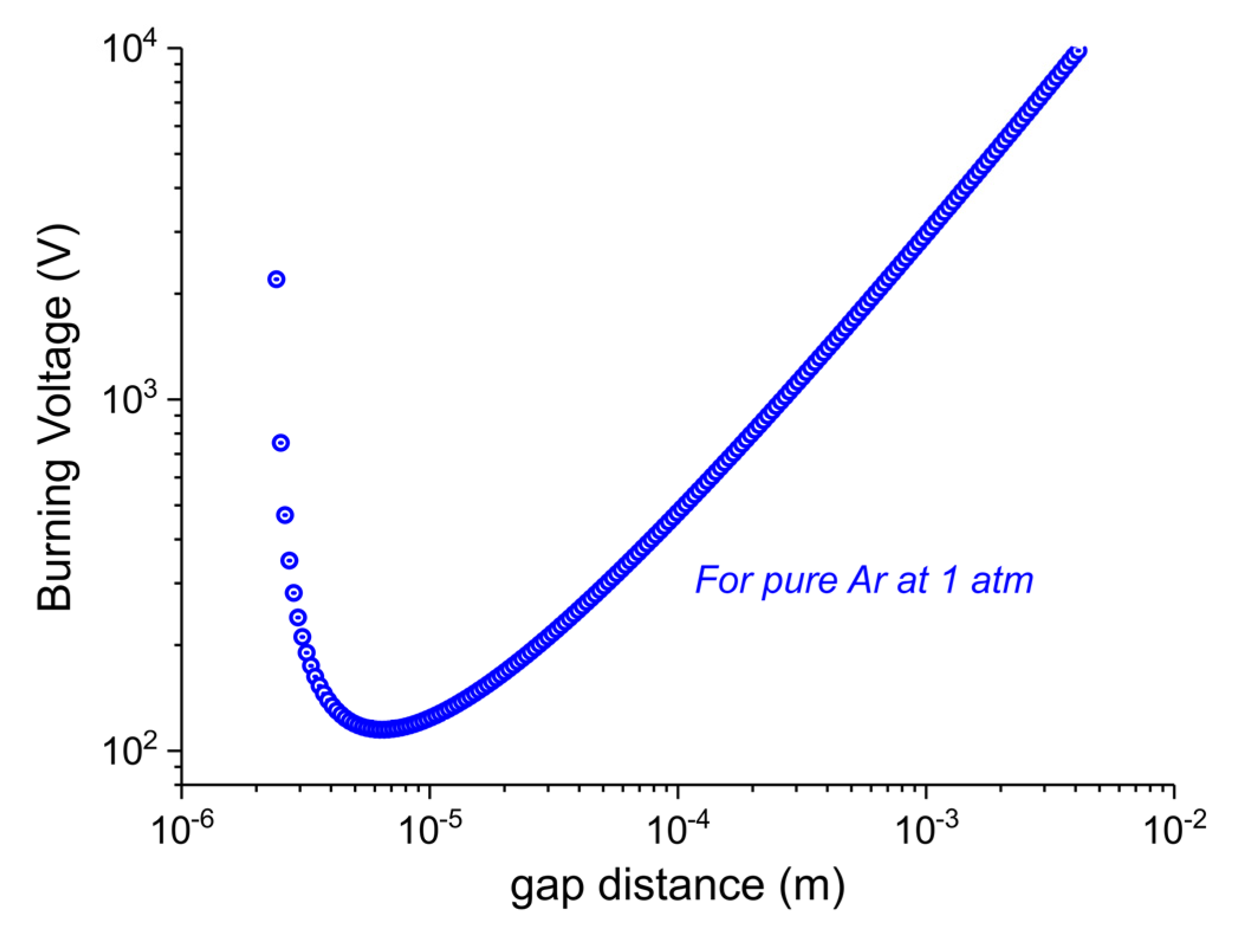
- According to the Paschen’s Law the electron filaments and active species cannot exist inside the pores of the carbonate particles, this is explained in the following paragraph.
- Temperature gradients between particles outer surface and inner core are minimized within much smaller times than the duration of the experiment, i.e., within 2 min, according to the Fourier time calculated in the specific case.
- dgap > 6μm: In order to generate a discharge (that is produced by an avalanche of ionizations of Argon atoms by high energy electrons), we need a minimum electric field that is able to accelerate electrons above the ionization energy of Ar atoms in the mean free path of electrons at that pressure (ca. 0.5 μm). Since the electric field is inversely proportional to dgap at constant voltage, Vb increases linearly with dgap.
- dgap < 6μm: the gap distance is comparable with the mean free path, so the probability of collisions that produce ionizations decreases. In order to have enough collisions to produce a discharge, the voltage has to be increased.
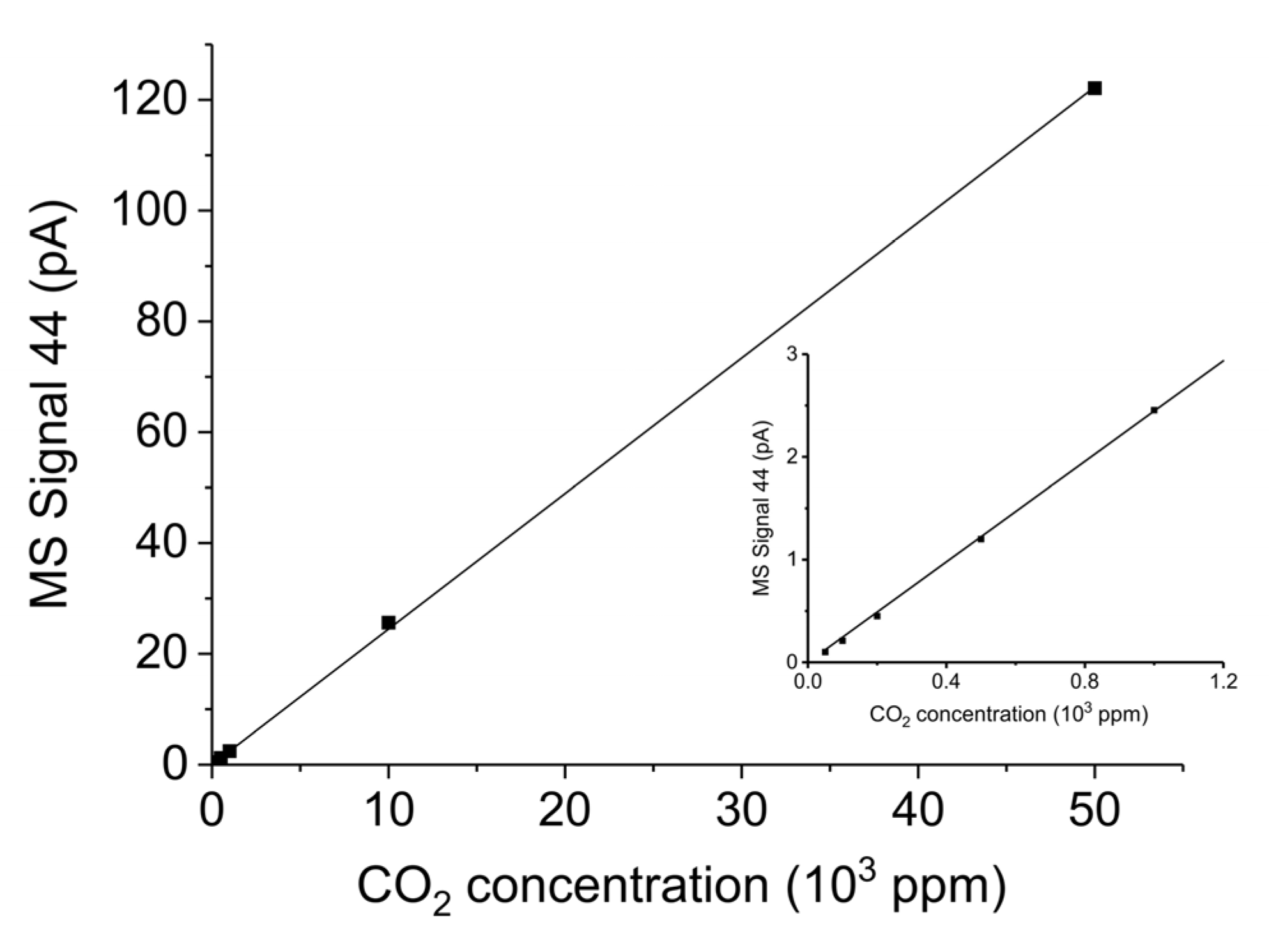
Appendix B.3. CO2 and CO and Calibration
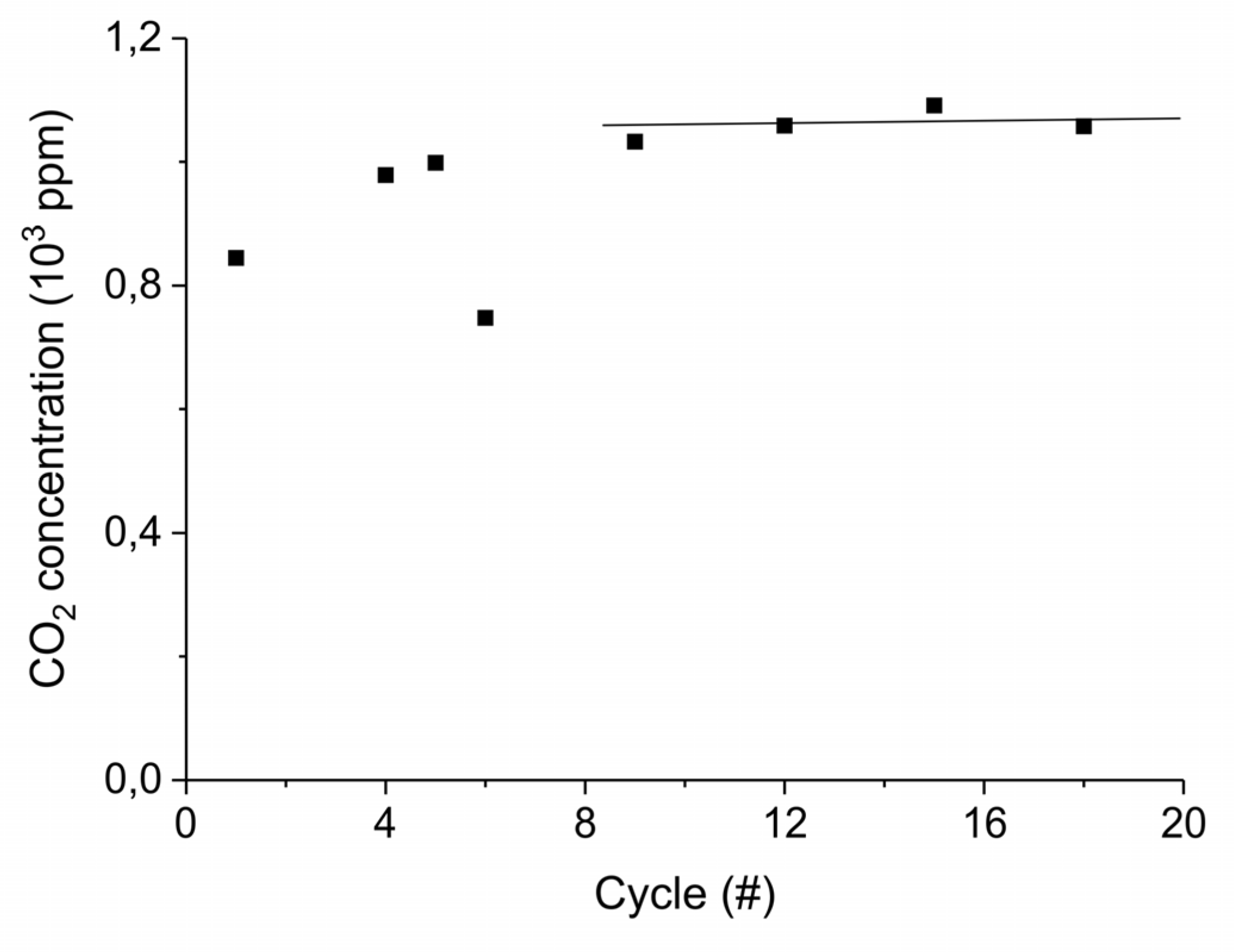
Appendix B.4. Sample Stability during Absorption–Desorption Cycles
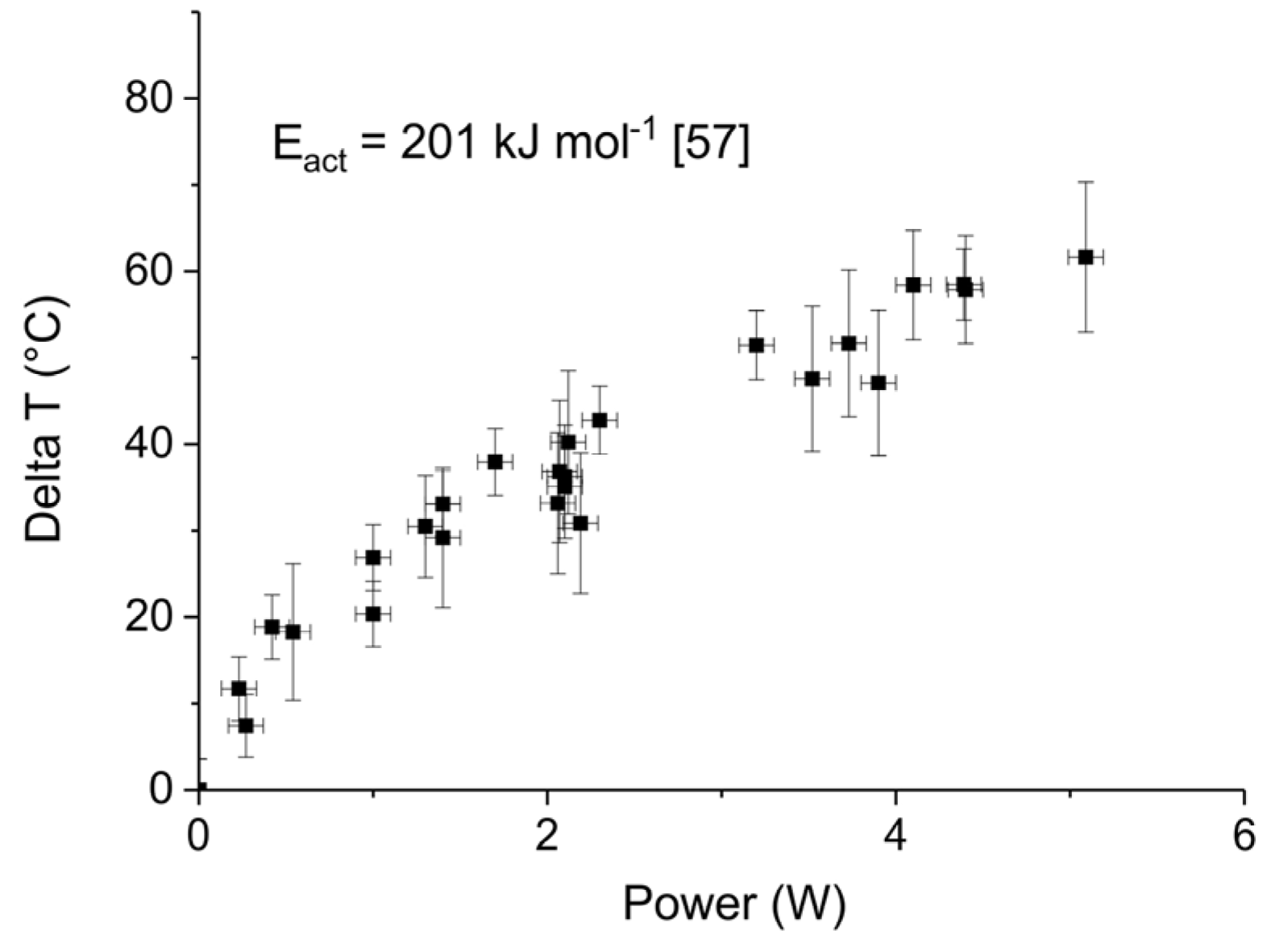
Appendix B.5. Heat Transfer in the Packed Bed
References
- Neyts, E.C.; Ostrikov, K.; Sunkara, M.K.; Bogaerts, A. Plasma Catalysis: Synergistic Effects at the Nanoscale. Chem. Rev. 2015, 115, 13408–13446. [Google Scholar] [CrossRef] [PubMed]
- Neyts, E.C.; Bogaerts, A. Understanding plasma catalysis through modelling and simulation—A review. J. Phys. D Appl. Phys. 2014, 47, 224010. [Google Scholar] [CrossRef]
- Neyts, E.C.; Ostrikov, K.; Sunkara, M.K.; Bogaerts, A. Plasma-Surface Interactions in Plasma Catalysis. Plasma Chem. Plasma Process. 2014, 36, 13408–13446. [Google Scholar] [CrossRef]
- Whitehead, J.C. Plasma-catalysis: The known knowns, the known unknowns and the unknown unknowns. J. Phys. D Appl. Phys. 2016, 49, 243001. [Google Scholar] [CrossRef]
- Chen, H.L.; Lee, H.M.; Chen, S.H.; Chang, M.B.; Yu, S.J.; Li, S.N. Removal of volatile organic compounds by single-stage and two-stage plasma catalysis systems: A review of the performance enhancement mechanisms, current status, and suitable applications. Environ. Sci. Technol. 2009, 43, 2216–2227. [Google Scholar] [CrossRef] [PubMed]
- Dobslaw, D.; Schulz, A.; Helbich, S.; Dobslaw, C.; Engesser, K.H. VOC removal and odor abatement by a low-cost plasma enhsnced biotrickling filter process. J. Environ. Chem. Eng. 2017, 5, 5501–5511. [Google Scholar] [CrossRef]
- Kozàk, T.; Bogaerts, A. Splitting of CO2 by vibrational excitation in non-equilibrium plasmas: A reaction kinetics model. Plasma Sources Sci. Technol. 2014, 23, 045004. [Google Scholar] [CrossRef]
- Ashford, B.; Tu, X. Non-thermal plasma technology for the conversion of CO2. Curr. Opin. Green Sustain. Chem. 2017, 3, 45–49. [Google Scholar] [CrossRef]
- Michielsen, I.; Uytdenhouwen, Y.; Pype, J.; Michielsen, B.; Mertens, J.; Reniers, F.; Meynen, V.; Bogaerts, A. CO2 dissociation in a packed bed DBD reactor: First steps towards a better understanding of plasma catalysis. Chem. Eng. J. 2017, 326, 477–488. [Google Scholar] [CrossRef]
- Grofulović, M.; Silva, T.; Klarenaar, B.L.; Morillo-Candas, A.S.; Guaitella, O.; Engeln, R.; Pintassilgo, C.D.; Guerra, V. Kinetic study of CO2 plasmas under non-equilibrium conditions. {I}. Relaxation of vibrational energy. Plasma Sources Sci. Technol. 2018, 27, 15019. [Google Scholar] [CrossRef]
- Sobacchi, M.G.; Saveliev, A.V.; Fridman, A.A.; Kennedy, L.A.; Ahmed, S.; Krause, T. Experimental assessment of a combined plasma/catalytic system for hydrogen production via partial oxidation of hydrocarbon fuels. Int. J. Hydrogen Energy 2002, 27, 635–642. [Google Scholar] [CrossRef]
- Tu, X.; Whitehead, J.C. Plasma-catalytic dry reforming of methane in an atmospheric dielectric barrier discharge: Understanding the synergistic effect at low temperature. Appl. Catal. B Environ. 2012, 125, 439–448. [Google Scholar] [CrossRef]
- Chung, W.C.; Chang, M.B. Review of catalysis and plasma performance on dry reforming of CH4 and possible synergistic effects. Renew. Sustain. Energy Rev. 2016, 62, 13–31. [Google Scholar] [CrossRef]
- Patil, B.S.; Wang, Q.; Hessel, V.; Lang, J. Plasma N2-fixation: 1900–2014. Catal. Today 2015, 256, 49–66. [Google Scholar] [CrossRef]
- Fridman, A. Plasma Chemistry; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Tendero, C.; Tixier, C.; Tristant, P.; Desmaison, J.; Leprince, P. Atmospheric pressure plasmas: A review. Spectrochim. Acta Part B At. Spectrosc. 2006, 61, 2–30. [Google Scholar] [CrossRef]
- Kim, H.H.; Teramoto, Y.; Negishi, N.; Ogata, A. A multidisciplinary approach to understand the interactions of nonthermal plasma and catalyst: A review. Catal. Today 2015, 256, 13–22. [Google Scholar] [CrossRef]
- Aerts, R.; Somers, W.; Bogaerts, A. Carbon Dioxide Splitting in a Dielectric Barrier Discharge Plasma: A Combined Experimental and Computational Study. ChemSusChem 2015, 8, 702–716. [Google Scholar] [CrossRef]
- Mei, D.; Zhu, X.; He, Y.L.; Yan, J.D.; Tu, X. Plasma-assisted conversion of CO2 in a dielectric barrier discharge reactor: Understanding the effect of packing materials. Plasma Sources Sci. Technol. 2015, 24, 015001. [Google Scholar]
- Nizio, M.; Albarazi, A.; Cavadias, S.; Amouroux, J.; Galvez, M.E.; da Costa, P. Hybrid plasma-catalytic methanation of CO2 at low temperature over ceria zirconia supported Ni catalysts. Int. J. Hydrogen Energy 2016, 41, 11584–11592. [Google Scholar] [CrossRef]
- Bogaerts, A.; Kozák, T.; van Laer, K.; Snoeckx, R. Plasma-based conversion of CO2: Current status and future challenges. Faraday Discuss. 2015, 183, 217–232. [Google Scholar] [CrossRef]
- van Laer, K.; Bogaerts, A. Improving the Conversion and Energy Efficiency of Carbon Dioxide Splitting in a Zirconia-Packed Dielectric Barrier Discharge Reactor. Energy Technol. 2015, 3, 1038–1044. [Google Scholar] [CrossRef]
- Brehmer, F.; Welzel, S.; van de Sanden, M.C.M.; Engeln, R. CO and byproduct formation during CO2 reduction in dielectric barrier discharges. J. Appl. Phys. 2014, 116, 123303. [Google Scholar] [CrossRef]
- Uytdenhouwen, Y.; van Alphen, S.; Michielsen, I.; Meynen, V.; Cool, P.; Bogaerts, A. A packed-bed DBD micro plasma reactor for CO2 dissociation: Does size matter? Chem. Eng. J. 2018, 348, 557–568. [Google Scholar] [CrossRef]
- Ramakers, M.; Michielsen, I.; Aerts, R.; Meynen, V.; Bogaerts, A. Effect of argon or helium on the CO2 conversion in a dielectric barrier discharge. Plasma Process. Polym. 2015, 12, 755–763. [Google Scholar] [CrossRef]
- Zeng, Y.; Tu, X. Plasma-catalytic hydrogenation of CO2 for the cogeneration of CO and CH4 in a dielectric barrier discharge reactor: Effect of argon addition. J. Phys. D Appl. Phys. 2017, 50, 184004. [Google Scholar] [CrossRef]
- Butterworth, T.; Elder, R.; Allen, R. Effects of particle size on CO2 reduction and discharge characteristics in a packed bed plasma reactor. Chem. Eng. J. 2016, 293, 55–67. [Google Scholar] [CrossRef]
- Kameshima, S.; Tamura, K.; Ishibashi, Y.; Nozaki, T. Pulsed dry methane reforming in plasma-enhanced catalytic reaction. Catal. Today 2015, 256, 67–75. [Google Scholar] [CrossRef]
- Kameshima, S.; Tamura, K.; Mizukami, R.; Yamazaki, T.; Nozaki, T. Parametric analysis of plasma-assisted pulsed dry methane reforming over Ni/Al2O3 catalyst. Plasma Process. Polym. 2017, 14, 1600096. [Google Scholar] [CrossRef]
- Ozkan, A.; Dufour, T.; Arnoult, G.; de Keyzer, P.; Bogaerts, A.; Reniers, F. CO2-CH4 conversion and syngas formation at atmospheric pressure using a multi-electrode dielectric barrier discharge. J. CO2 Util. 2015, 9, 78–81. [Google Scholar] [CrossRef]
- Tu, X.; Gallon, H.J.; Twigg, M.V.; Gorry, P.A.; Whitehead, J.C. Dry reforming of methane over a Ni/Al2O3 catalyst in a coaxial dielectric barrier discharge reactor. J. Phys. D Appl. Phys. 2011, 44, 274001. [Google Scholar] [CrossRef]
- Gallon, H.J.; Tu, X.; Whitehead, J.C. Effects of reactor packing materials on H2 production by CO2 reforming of CH4 in a dielectric barrier discharge. Plasma Process. Polym. 2012, 9, 90–97. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhu, X.; Mei, D.; Ashford, B.; Tu, X. Plasma-catalytic dry reforming of methane over γ-Al2O3 supported metal catalysts. Catal. Today 2015, 256, 80–87. [Google Scholar] [CrossRef]
- Zheng, X.; Tan, S.; Dong, L.; Li, S.; Chen, H. Silica-coated LaNiO3 nanoparticles for non-thermal plasma assisted dry reforming of methane: Experimental and kinetic studies. Chem. Eng. J. 2015, 265, 147–156. [Google Scholar] [CrossRef]
- Aerts, R.; Martens, T.; Bogaerts, A. Influence of vibrational states on CO2 splitting by dielectric barrier discharges. J. Phys. Chem. C 2012, 116, 23257–23273. [Google Scholar] [CrossRef]
- Bogaerts, A.; Wang, W.; Berthelot, A.; Guerra, V. Modeling plasma-based CO2 conversion: Crucial role of the dissociation cross section. Plasma Sources Sci. Technol. 2016, 25, 55016. [Google Scholar] [CrossRef]
- Pietanza, L.D.; Colonna, G.; D’Ammando, G.; Capitelli, M. Time-dependent coupling of electron energy distribution function, vibrational kinetics of the asymmetric mode of CO2 and dissociation, ionization and electronic excitation kinetics under discharge and post-discharge conditions. Plasma Phys. Control. Fusion 2017, 59, 14035. [Google Scholar] [CrossRef]
- Van Rooij, G.J.; van den Bekerom, D.C.; Den Harder, N.; Minea, T.; Berden, G.; Bongers, W.A.; Engeln, R.; Graswinckel, M.F.; Zoethout, E.; van de Sanden, M.C. Taming microwave plasma to beat thermodynamics in CO2 dissociation. Faraday Discuss. 2015, 183, 233–248. [Google Scholar] [CrossRef] [PubMed]
- Bongers, W.; Bouwmeester, H.; Wolf, B.; Peeters, F.; Welzel, S.; van den Bekerom, D.; den Harder, N.; Goede, A.; Graswinckel, M.; Groen, P.W.; et al. Plasma-driven dissociation of CO2 for fuel synthesis. Plasma Process. Polym. 2017, 14, 1600126. [Google Scholar] [CrossRef]
- Minea, T.; van den Bekerom, D.C.; Peeters, F.J.; Zoethout, E.; Graswinckel, M.F.; van de Sanden, M.C.; Cents, T.; Lefferts, L.; van Rooij, G.J. Non-oxidative methane coupling to C2 hydrocarbons in a microwave plasma reactor. Plasma Process. Polym. 2018, 15, 1800087. [Google Scholar] [CrossRef]
- Li, S.; Zheng, W.; Tang, Z.; Gu, F. Plasma heating and temperature difference between gas pellets in packed bed with dielectric barrier discharge under natural convection condition. Heat Transf. Eng. 2012, 33, 609–617. [Google Scholar] [CrossRef]
- Jidenko, N.; Bourgeois, E.; Borra, J.P. Temperature profiles in filamentary dielectric barrier discharges at atmospheric pressure. J. Phys. D Appl. Phys. 2010, 43, 295203. [Google Scholar] [CrossRef]
- Patil, B.S.; Cherkasov, N.; Lang, J.; Ibhadon, A.O.; Hessel, V.; Wang, Q. Low temperature plasma-catalytic NOx synthesis in a packed DBD reactor: Effect of support materials and supported active metal oxides. Appl. Catal. B Environ. 2016, 194, 123–133. [Google Scholar] [CrossRef]
- Nozaki, T.; Hiroyuki, T.; Okazaki, K. Hydrogen enrichment of low-calorific fuels using barrier discharge enhanced Ni/γ-Al2O3 bed reactor: Thermal and nonthermal effect of nonequilibrium plasma. Energy Fuels 2006, 20, 339–345. [Google Scholar] [CrossRef]
- Masoud, N.; Martus, K.; Figus, M.; Becker, K. Rotational and vibrational temperature measurements in a high-pressure cylindrical dielectric barrier discharge (C-DBD). Contrib. Plasma Phys. 2005, 45, 32–39. [Google Scholar] [CrossRef]
- Rajasekaran, P.; Opländer, C.; Hoffmeister, D.; Bibinov, N.; Suschek, C.V.; Wandke, D.; Awakowicz, P. Characterization of dielectric barrier discharge (DBD) on mouse and histological evaluation of the plasma-treated tissue. Plasma Process. Polym. 2011, 8, 246–255. [Google Scholar] [CrossRef]
- Du, Y.; Nayak, G.; Oinuma, G.; Ding, Y.; Peng, Z.; Bruggeman, P.J. Emission considering self-absorption of OH to simultaneously obtain the OH density and gas temperature: Validation, non-equilibrium effects and limitations. Plasma Sources Sci. Technol. 2017, 26, 095007. [Google Scholar] [CrossRef]
- Florian, J.; Merbahi, N.; Wattieaux, G.; Plewa, J.M.; Yousfi, M. Comparative Studies of Double Dielectric Barrier Discharge and Microwave Argon Plasma Jets at Atmospheric Pressure for Biomedical Applications. IEEE Trans. Plasma Sci. 2015, 43, 3332–3338. [Google Scholar] [CrossRef]
- Blamey, J.; Anthony, E.J.; Wang, J.; Fennell, P.S. The calcium looping cycle for large-scale CO2 capture. Prog. Energy Combust. Sci. 2010, 36, 260–279. [Google Scholar] [CrossRef]
- McBride, B.J.; Zehe, M.J.; Gordon, S. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species. In Technical Reports NASA; NASA: Washington, DC, USA, 2002; Volume 291, p. 211556. [Google Scholar]
- Fennell, P.S.; Pacciani, R.; Dennis, J.S.; Davidson, J.F.; Hayhurst, A.N. The effects of repeated cycles of calcination and carbonation on a variety of different limestones, as measured in a hot fluidized bed of sand. Energy Fuels 2007, 21, 2072–2081. [Google Scholar] [CrossRef]
- Lysikov, A.I.; Salanov, A.N.; Okunev, A.G. Change of CO2 carrying capacity of CaO in isothermal recarbonation-decomposition cycles. Ind. Eng. Chem. Res. 2007, 46, 4633–4638. [Google Scholar] [CrossRef]
- Borgwardt, R.H. Sintering of nascent calcium oxide. Chem. Eng. Sci. 1989, 44, 53–60. [Google Scholar] [CrossRef]
- Zhang, Y.R.; van Laer, K.; Neyts, E.C.; Bogaerts, A. Can plasma be formed in catalyst pores? A modeling investigation. Appl. Catal. B Environ. 2016, 185, 56–67. [Google Scholar] [CrossRef]
- Hensel, K.; Katsura, S.; Mizuno, A. DC Microdischarges inside porous ceramics. IEEE Trans. Plasma Sci. 2005, 33, 574–575. [Google Scholar] [CrossRef]
- Zhang, Q.Z.; Wang, W.Z.; Bogaerts, A. Importance of surface charging during plasma streamer propagation in catalyst pores. Plasma Sources Sci. Technol. 2018, 27, 065009. [Google Scholar] [CrossRef]
- Giammaria, G.; Lefferts, L. Catalytic Effect of Water on Calcium Carbonate Decomposition. Appl. Catal. B. unpublished.
- Peeters, F.J.J.; van de Sanden, M.C.M. The influence of partial surface discharging on the electrical characterization of DBDs. Plasma Sources Sci. Technol. 2015, 24, 15016. [Google Scholar] [CrossRef]
- Ghassemi, M.; Mohseni, H.; Niayesh, K.; Shayegani, A.A. Dielectric Barrier Discharge (DBD) Dynamic Modeling for High Voltage Insulation. In Proceedings of the 2011 Electrical Insulation Conference (EIC), Annapolis, MD, USA, 5–8 June 2011. [Google Scholar]
- Jess, A.; Wasserscheid, P. Chemical Technology; An Integrated Textbook; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Jacobs, G.K.; Kerrick, D.M.; Krupka, K.M. The High-Temperature Heat Capacity of Natural Calcite (CaCO3). Phys. Chem. Miner. 1981, 7, 55–59. [Google Scholar] [CrossRef]

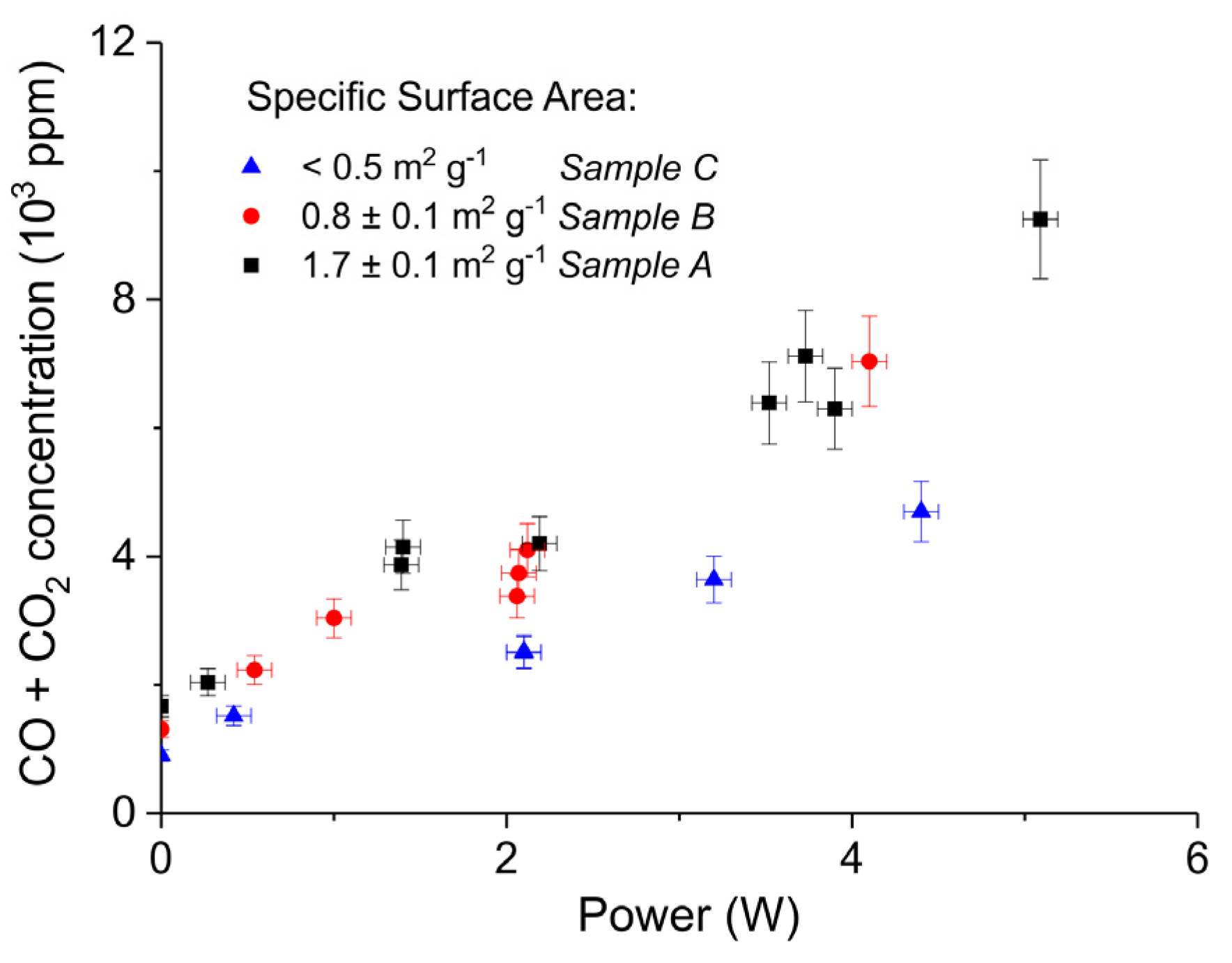
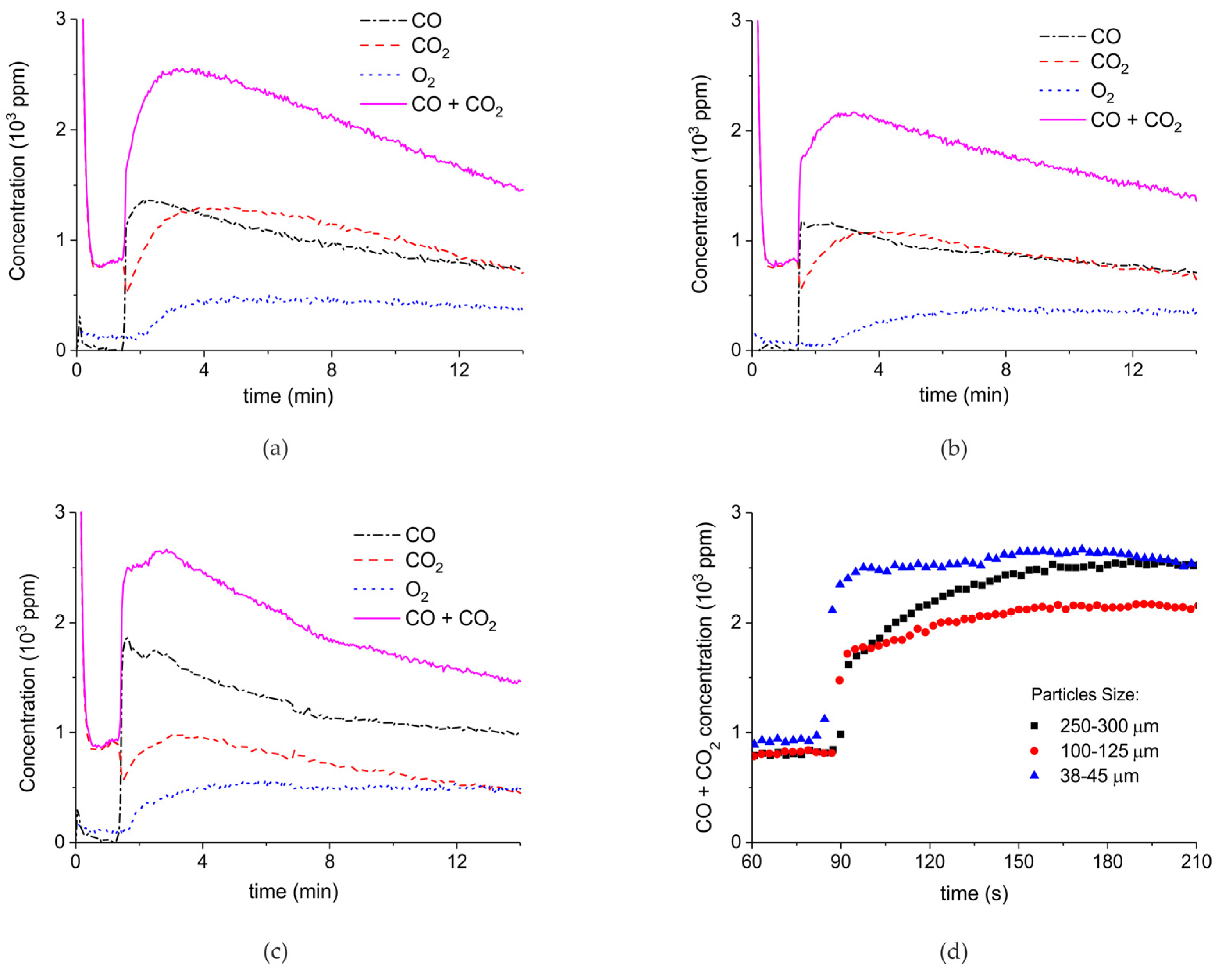
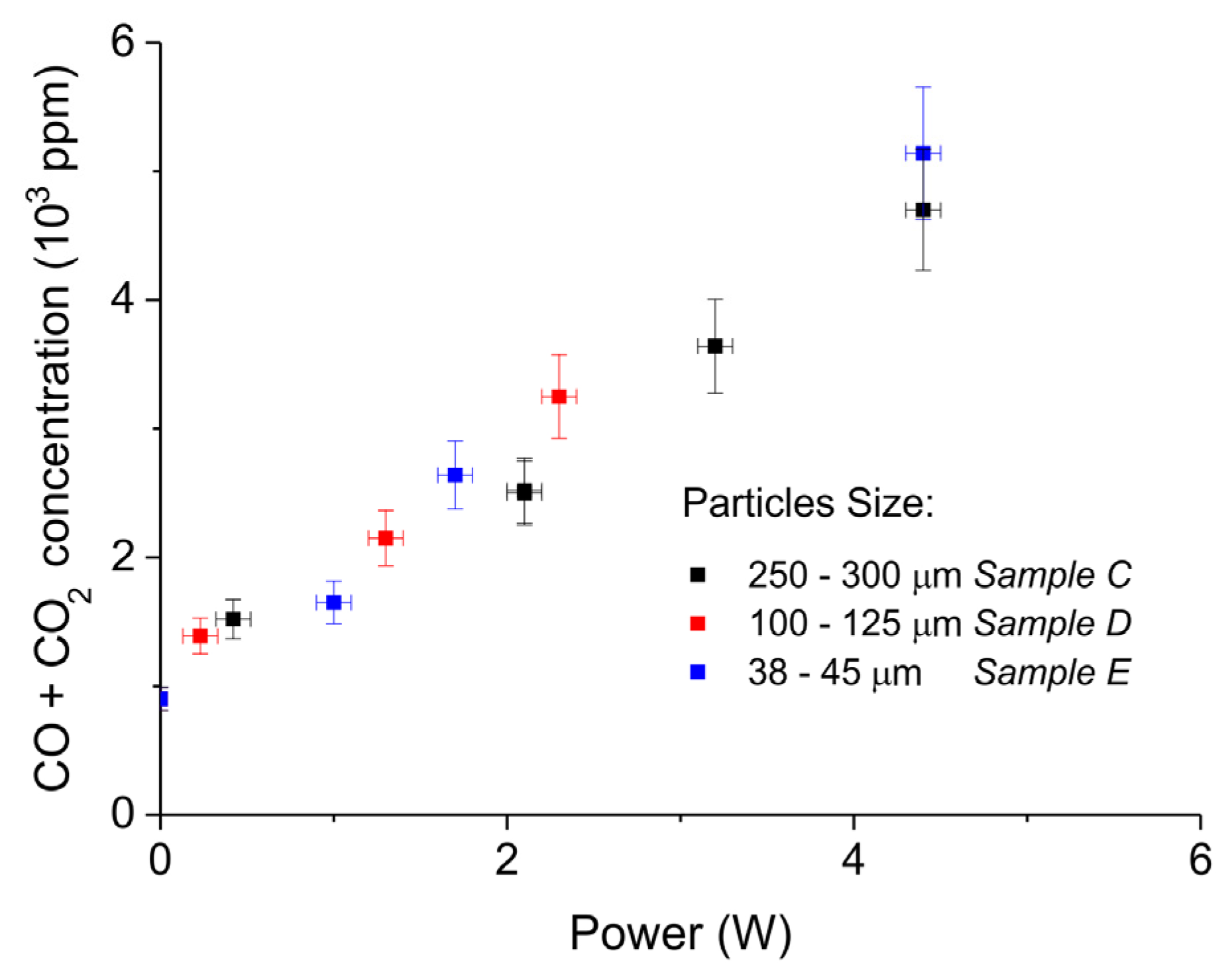
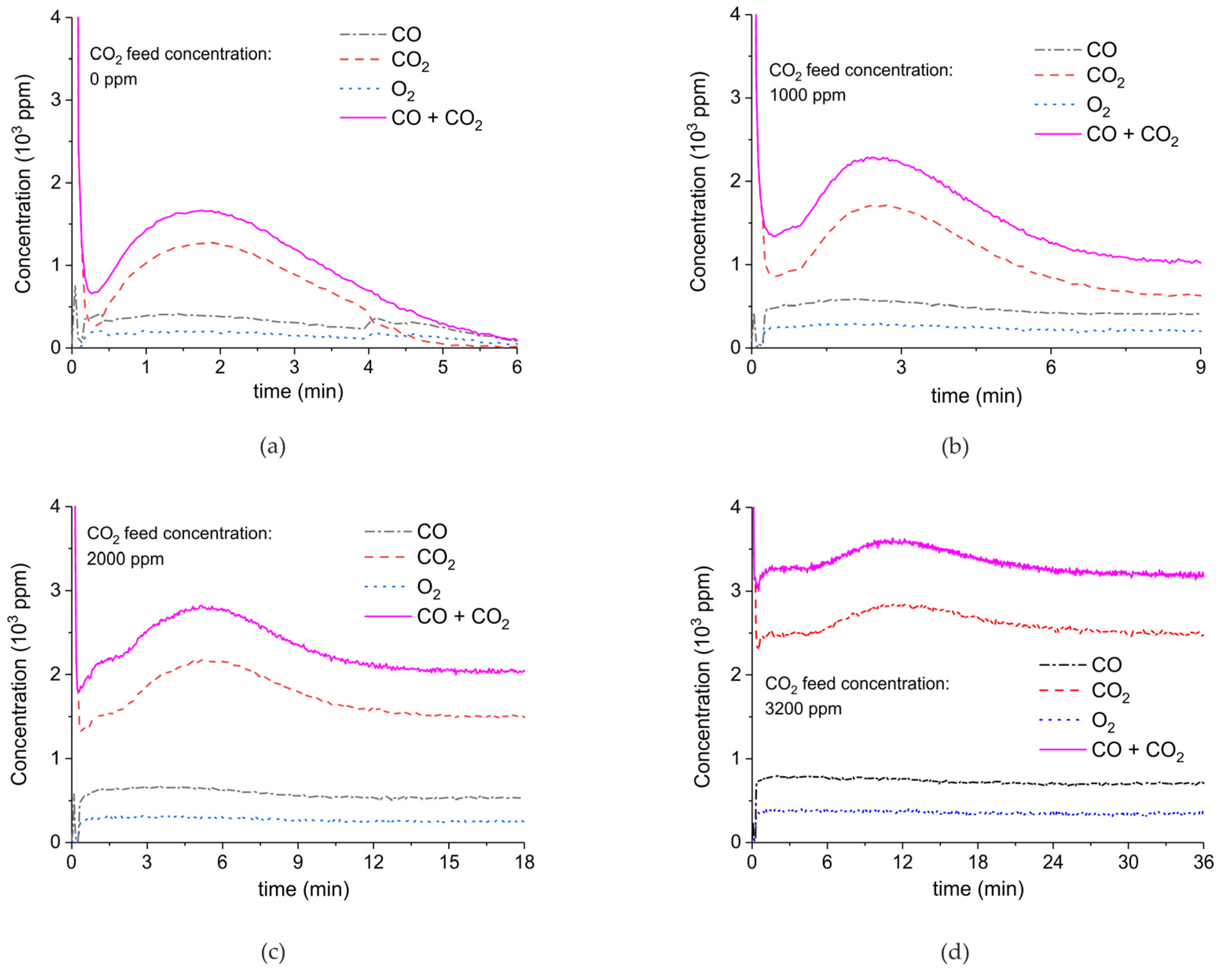
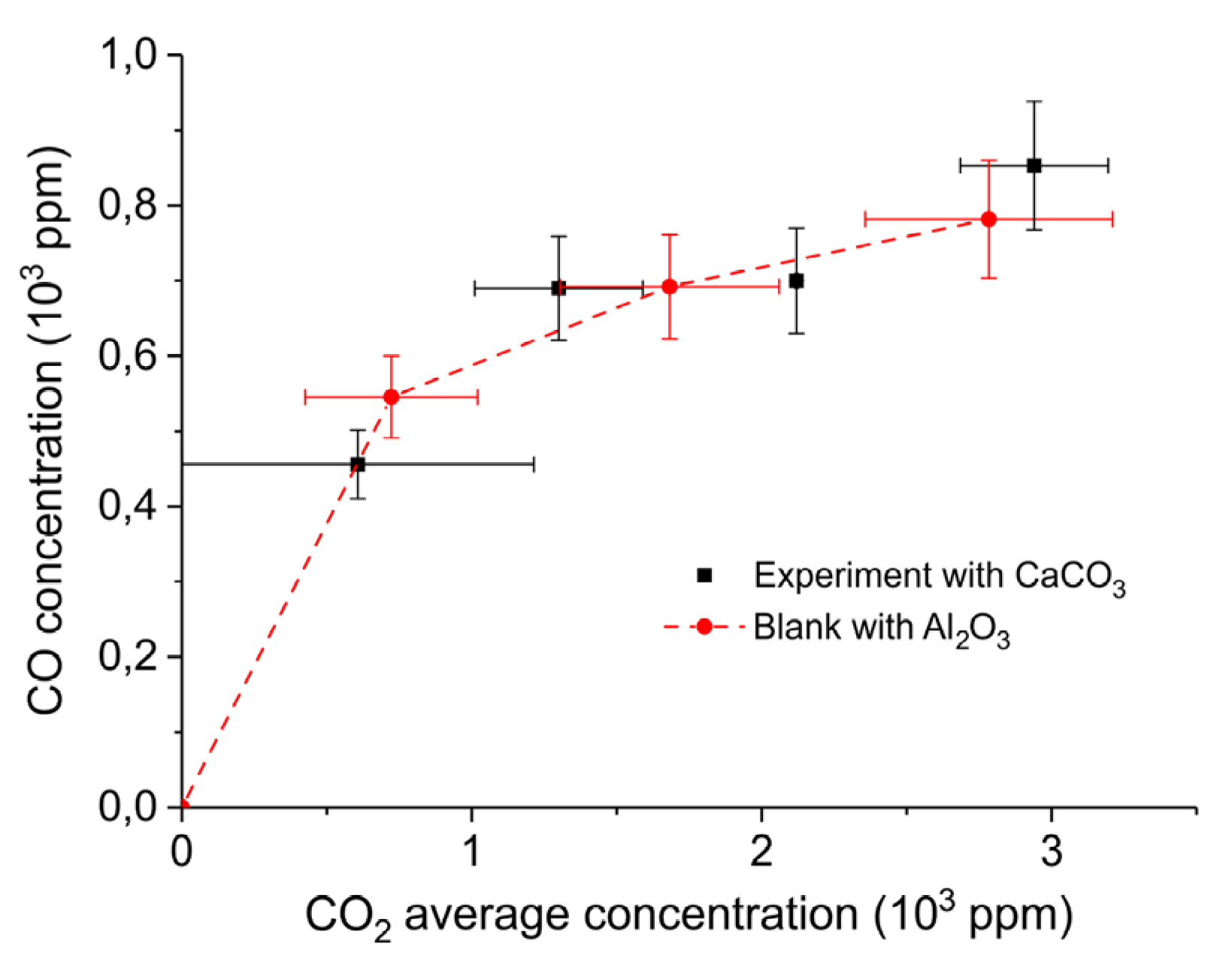
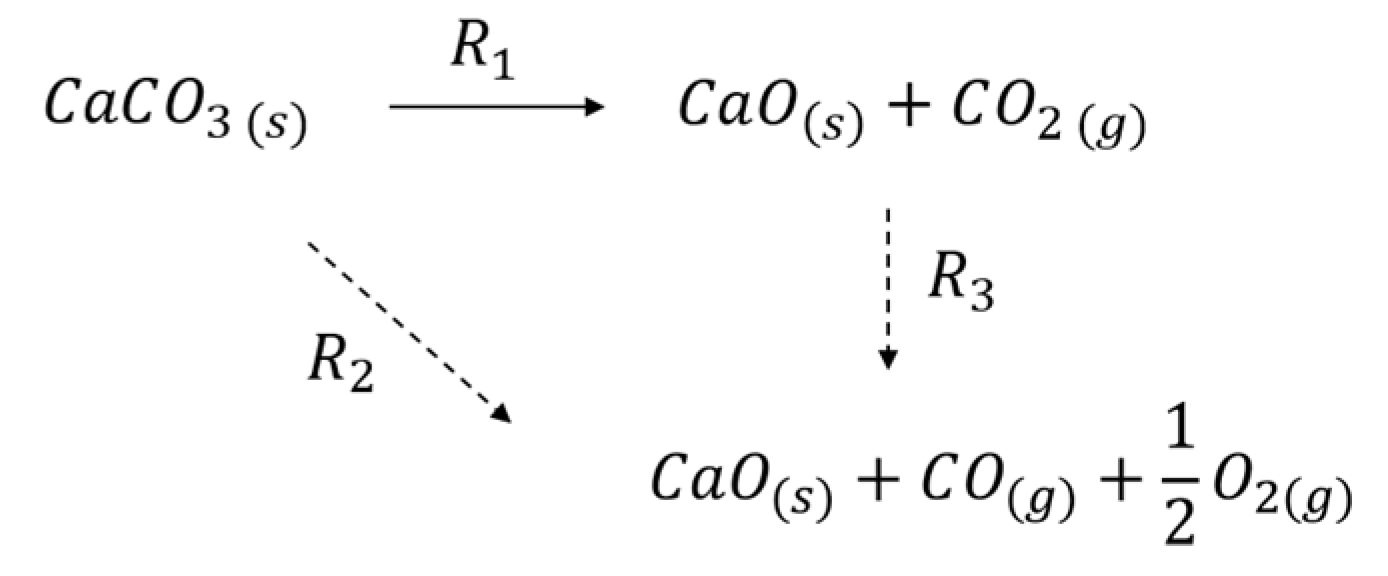
| Sample Code | Precursor (Batch #) | Carbonation Time at 630 °C (h) | Sintering Time at 900°C (h) | CaO S.S.A. (m2 g−1) | CaCO3 S.S.A. (m2 g−1) | Particles Diameter (µm) |
|---|---|---|---|---|---|---|
| A | Ca Gluconate (I) | 5 | 0 | 46.2 | 1.7 ± 0.1 | 250–300 |
| B | Ca Ascorbate (II) | 4 | 0 | 23.2 | 0.8 ± 0.1 | 250–300 |
| C | CaCO3 (III) | 5 | 24 | 10.1 | <0.5 | 250–300 |
| D | CaCO3 (III) | 5 | 24 | 10.1 | <0.5 | 100–125 |
| E | CaCO3 (III) | 5 | 24 | 10.1 | <0.5 | 38–45 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giammaria, G.; van Rooij, G.; Lefferts, L. Plasma Catalysis: Distinguishing between Thermal and Chemical Effects. Catalysts 2019, 9, 185. https://doi.org/10.3390/catal9020185
Giammaria G, van Rooij G, Lefferts L. Plasma Catalysis: Distinguishing between Thermal and Chemical Effects. Catalysts. 2019; 9(2):185. https://doi.org/10.3390/catal9020185
Chicago/Turabian StyleGiammaria, Guido, Gerard van Rooij, and Leon Lefferts. 2019. "Plasma Catalysis: Distinguishing between Thermal and Chemical Effects" Catalysts 9, no. 2: 185. https://doi.org/10.3390/catal9020185
APA StyleGiammaria, G., van Rooij, G., & Lefferts, L. (2019). Plasma Catalysis: Distinguishing between Thermal and Chemical Effects. Catalysts, 9(2), 185. https://doi.org/10.3390/catal9020185






