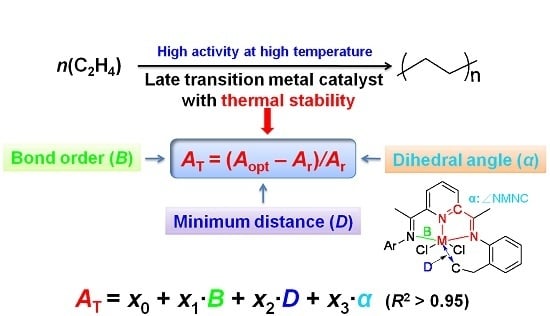
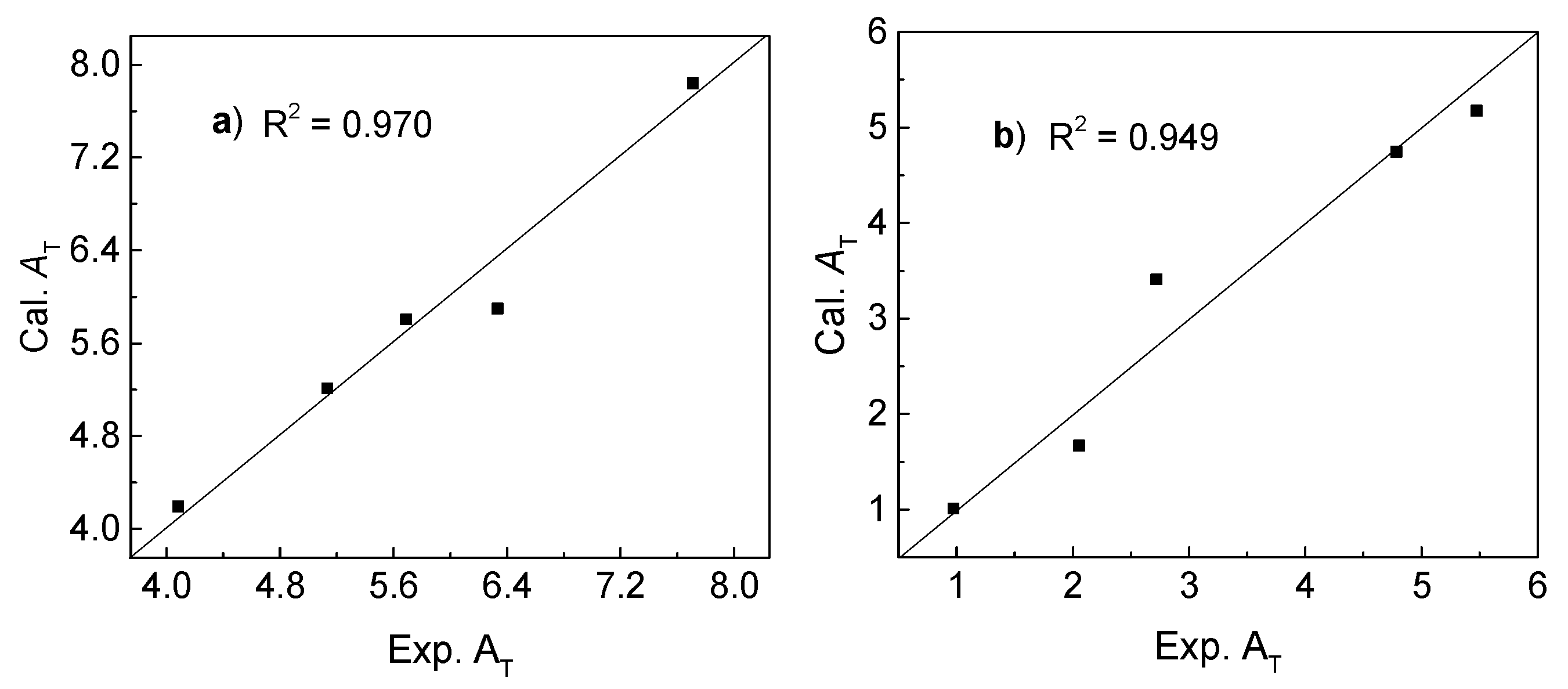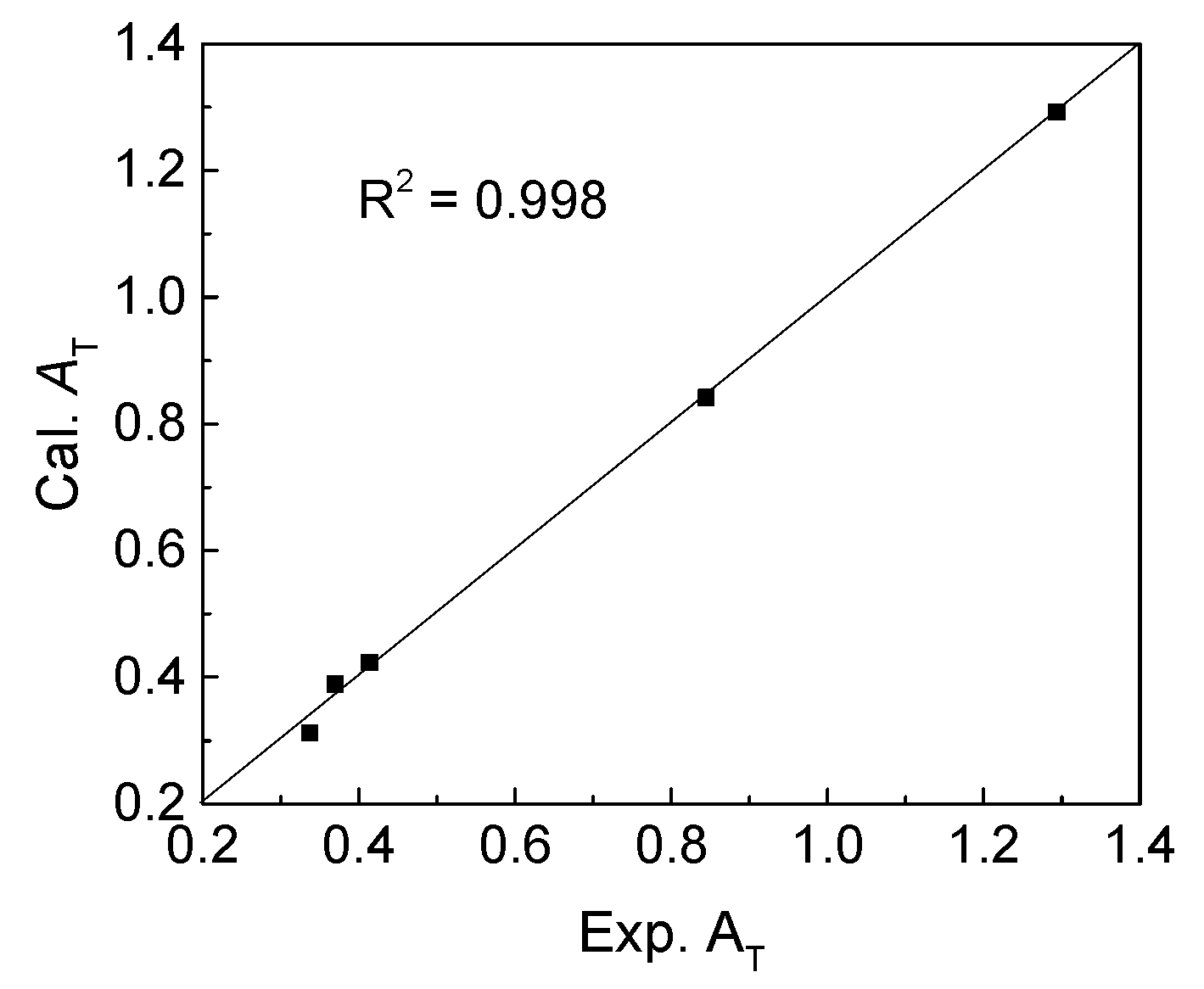2.1. Definition of the Parameters Related to Thermal Stability
In the present work, three parameters were chosen to characterize the thermal stability of late transition metal complex, including the bond order (
B), minimum distance (
D) and dihedral angle (
α). Regarding bond order (
B), it represents the strength of the bond between metal atoms and coordinated heteroatoms within ligands, which are nitrogen atoms for the modeled complexes. The bond strength of metal and nitrogen atoms (M–N) should be strong enough to prevent them from breaking (or decomposition) at high temperatures [
26]. Since there are usually two or three M–N bonds, the minimum value of bond order (
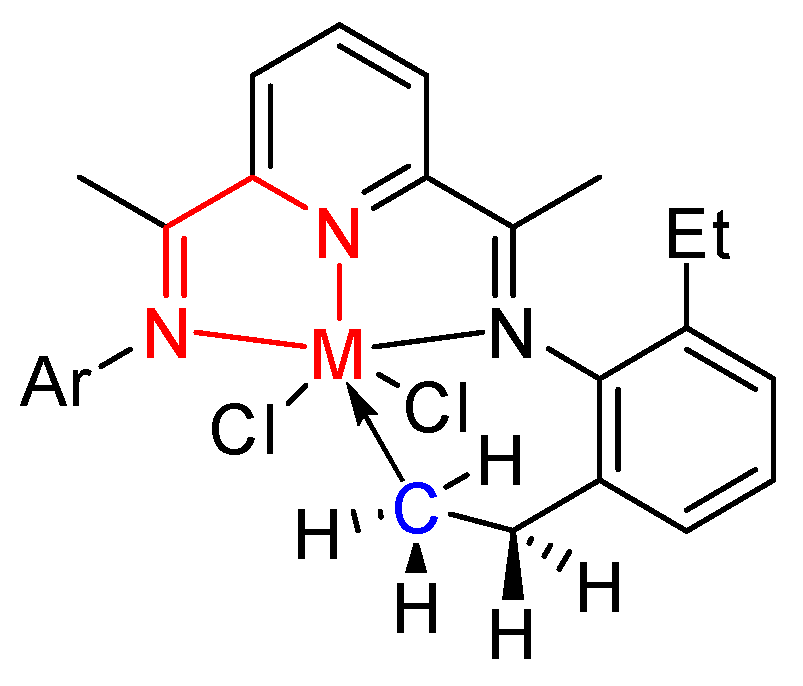
B) was chosen. According to previous research, the formation of the five- or six-membered metallacycle via intramolecular C–H activation demonstrated in
Scheme 2 may deactivate the catalyst, reducing the thermal stability of a catalyst [
19]. Therefore, the minimum distance (
D) between central metal and carbon atoms highlighted in blue (M–C) was calculated. The parameter
α is the dihedral angle of the central five-membered ring shown in the
Scheme 2 with the atoms in red. This factor indicates the stability of the complex due to the stress and strain of the central five-membered ring within a catalyst [
48]. For an N^N^N three chelated complex, the value of
α is the average data for two central five-membered rings.
To measure the thermal stability of different complexes, the variation values of catalytic activities at different reaction temperatures (
AT) were calculated by Equation (1):
where
Aopt and
Ar are the activities at optimum and room temperatures for each complex, respectively. Most of the model complexes in this work were taken from our previous experimental results, and the detailed values of activities at both optimum and room temperatures were provided in
Table S1 of Supplementary Materials.
The calculated parameters (
B,
D,
α) were related to the
AT by the MLRA Equation (2), which was resolved by the regression analysis based on the least squares method in Microsoft Excel [
49]. After fitting, the values of
x0,
x1,
x2 and
x3 were automatically obtained:
In order to analyze the contribution of each parameter to the thermal stability for each complex system, the values of
B,
D and
α were standardized using the
Z-Score method. Then, the contribution was calculated by the Equation (3) based on our previous works:
where
i is the serial number of parameter,
j is the order of the complex,
mij is the value of each parameter for each complex,
xi is the regression coefficient of each parameter, and
n is the total number of complexes.
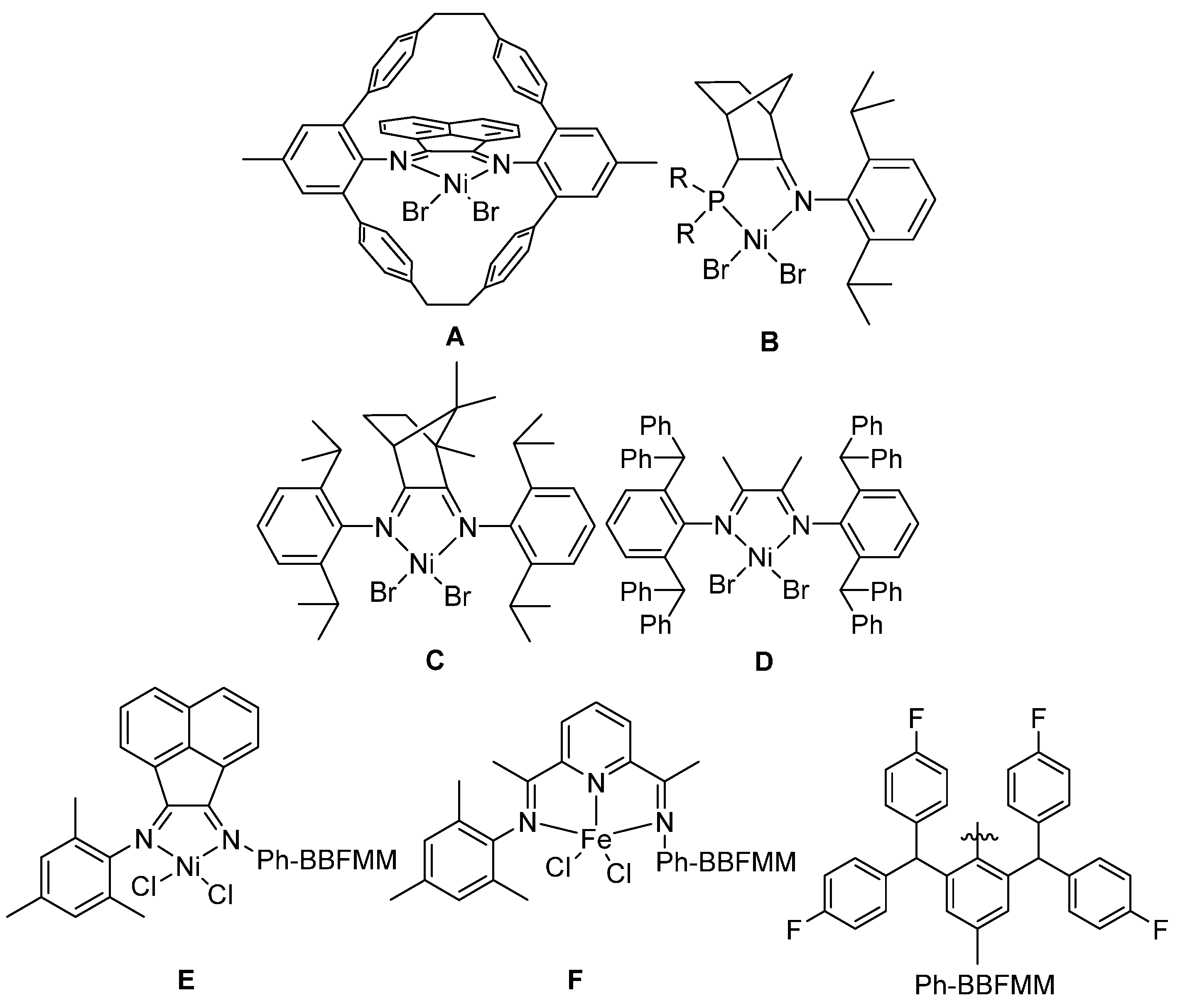
2.2. Thermal Stability of Bis(imino)pyridyliron(cobalt) Complexes
The main framework of the catalyst with thermal stability can be classified into two categories including the bis(imino)pyridyliron(cobalt) and the
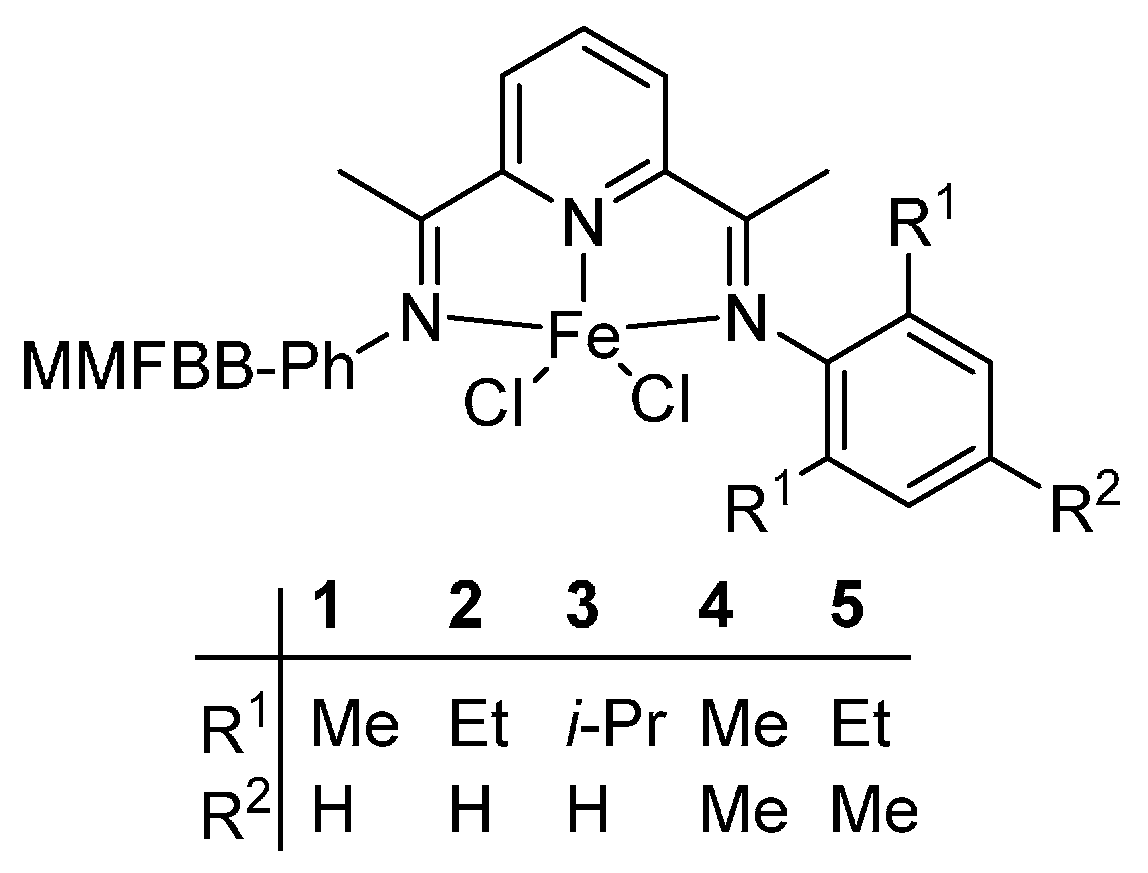
α-diiminenickel complexes. In this section, the bis(imino)pyridyliron(cobalt) complexes
1–
10 as showed in the
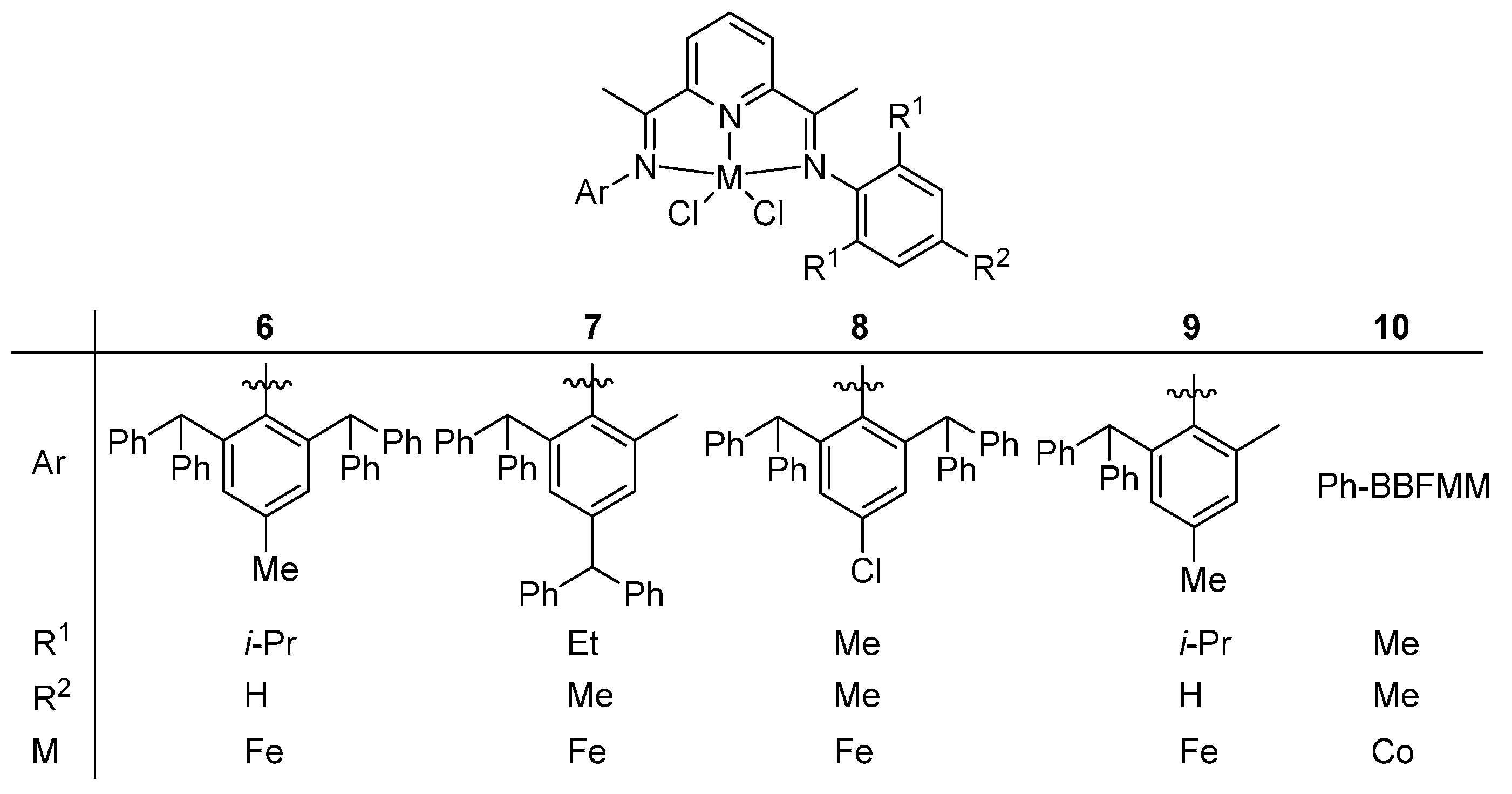
Scheme 3 and
Scheme 4 from previous reports [
31,
32,
33,
34,
35,
36] were selected to study the thermal stability. For the complexes
1–
5, the small variations of structures lie in the different substituents within the aryl moiety, while, for the complexes
6–
10, the differences are not only the substituents within the aryl moiety, but also the
Ar group. Furthermore, the experimental conditions were totally the same for complexes
1–
5, while, for complexes
6–
10, there was little difference. Therefore, the complexes were divided into two systems: complexes
1–
5 and complexes
6–
10.
In this study, the calculated three parameters (
B,
D,
α) are heavily dependent on the geometry structure, so the optimization of the complex structure was performed by the molecular mechanics (MM) method. The comparisons between calculated structure and experimental crystal data for the selected bond lengths and bond angles for complexes
1,
5 and
7 were listed in
Table 1. It is clearly seen that the values of standard deviation
δ for all three of these complexes are very small, indicating the reasonableness of the optimized structures. This guarantees a reliable relationship between structure parameters (
B,
D,
α) and the thermal stability.
Accordingly, the three structural parameters calculated were obtained and listed in
Table 2 for complexes
1–
5. Clearly, the variations of the three parameters as a function of substituents were very small. Regarding the bond order (
B), the values are from 0.1028 to 0.1048, meaning that there is little change in bond strength between iron and nitrogen with various substituents. For the minimum distance parameter (
D), all of the calculated results were above 2.0 Å, indicating no formation of an inter M–C bond, which improves the thermal stability of complex. As for a dihedral angle (
α), it is shown in
Table 2 that the obtained values of
α were from 7.839° to 8.627°. From previous study, it is indicated that the half-chair configuration (non plane form) of the central five-membered ring is helpful for the stability of the complex [
46]. Therefore, the bigger the value of
α, the more stable the complex is.
To quantitatively analyze the influence of catalyst structure on thermal stability, the relationship between
B,
D,
α and
AT was fitted using the multiple linear regression Equation (2). The regression and correlation coefficient values were obtained and listed in
Table 3. Then, the thermal stabilities were calculated by the fitting equation and compared with experimental results for the complexes
1–
5. The result shows that almost all points were in a diagonal line in
Figure 1a, suggesting that the calculated and experimental
AT values are very close. The obtained correlation coefficient value (
R2) is 0.970.
In the same manner, for complexes
6–
10, three parameters were obtained and listed in
Table 4. For bond order (
B), the calculated values were in the range of 0.0788 to 0.1031, which were smaller compared with the results of complexes
1–
5 (
Table 2), especially for complex
10, signifying the potential reduction of their thermal stabilities. For the minimum distance (
D), all of the data were over 2.00 Å, indicating that no metallacycle ring formed either. Regarding the dihedral angle (
α), the results ranged from 7.335° to 11.413°. From the variation of the structure parameters, the thermal stabilities of complexes
6–
10 should be lower than that of complexes
1–
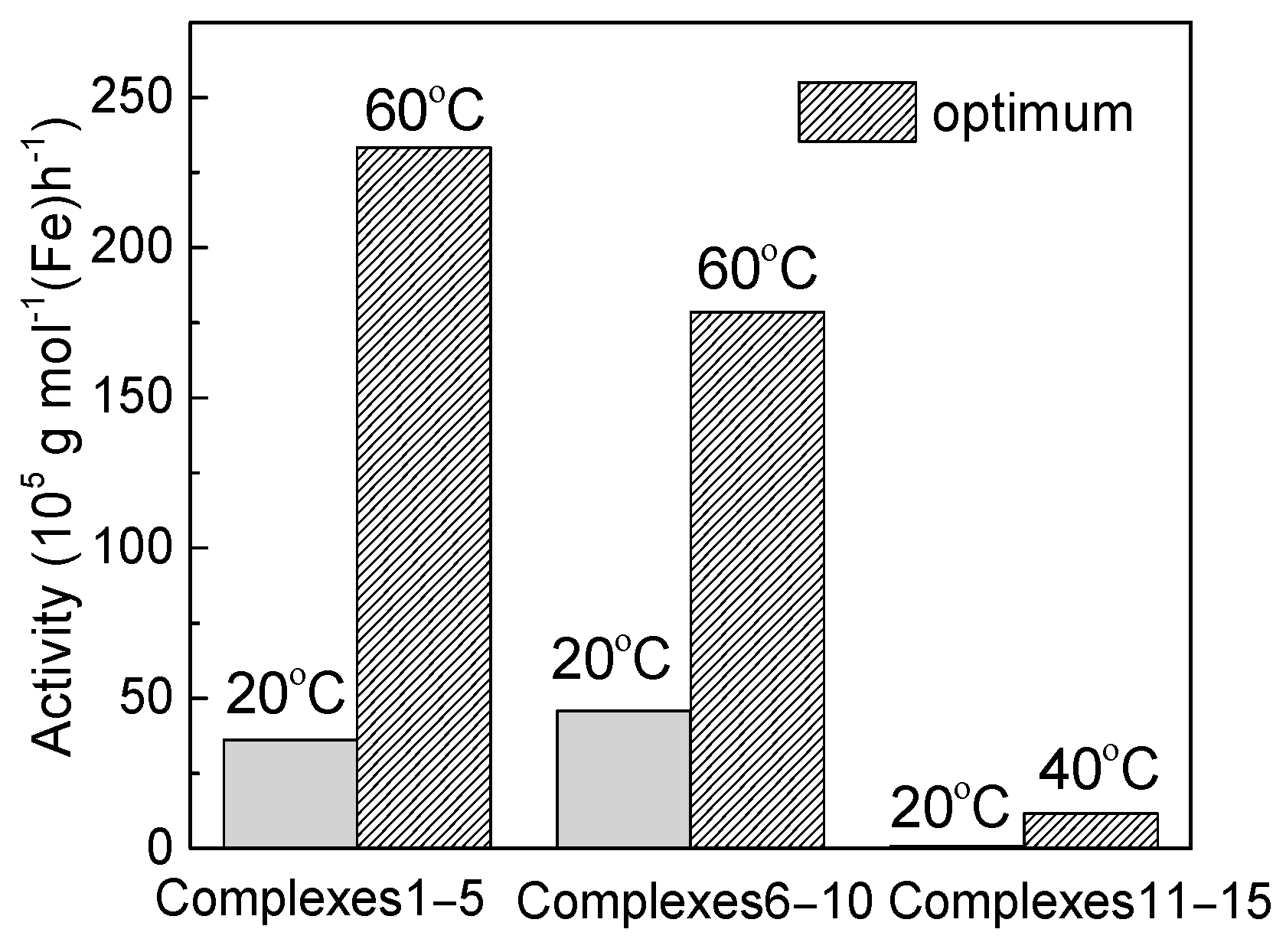
5. For clarity, the averaged values of the catalytic activities for complexes
1–
5 and
6–
10 were plotted in
Figure 2 at room and optimum temperatures. Obviously, the thermal stability of the former is better than the latter, although the catalytic activities at room temperature are almost the same.
Accordingly, from the values of
AT in
Table 2 and
Table 4, the thermal stabilities of complexes
6–
10 are lower than that of complexes
1–
5 correspondingly. This result is in agreement with the decrease of bond order (
B), suggesting that this parameter has an outstanding influence on the thermal stability of this series of complex system. By the MLRA method, the regression coefficients were obtained and showed in
Table 3. Then, the calculated values of thermal stabilities were obtained and compared with experimental results, which present good correlation with the
R2 value of 0.949 as showed in
Figure 1b.
In order to quantitatively investigate the influence of each parameter on the thermal stability, the values of three parameters and thermal stabilities were further standardized by the
Z-Score method. The obtained values of the
B,
D,
α,
AT were collected in
Table 2 and
Table 4 for complexes
1–
5 and complexes
6–
10, respectively, and the corresponding standard regression coefficients were obtained and listed in
Table 3. Then, using Equation (3), the contributions of each parameter were calculated. The obtained contribution values of the
B,
D and
α for the complexes
1–
5 are 48%, 26% and 26%, respectively. Therefore, it indicates that the bond order dominates the thermal stabilities of complexes
1–
5. Similarly, the contributions of the
B,
D and
α for the complexes
6–
10 are calculated and the results are 46%, 33% and 21%, respectively. It suggests that the bond order plays a predominant role in determining the thermal stabilities for complexes
6–
10 as well.
2.3. Thermal Stability of Phenanthrolinyliron Complexes
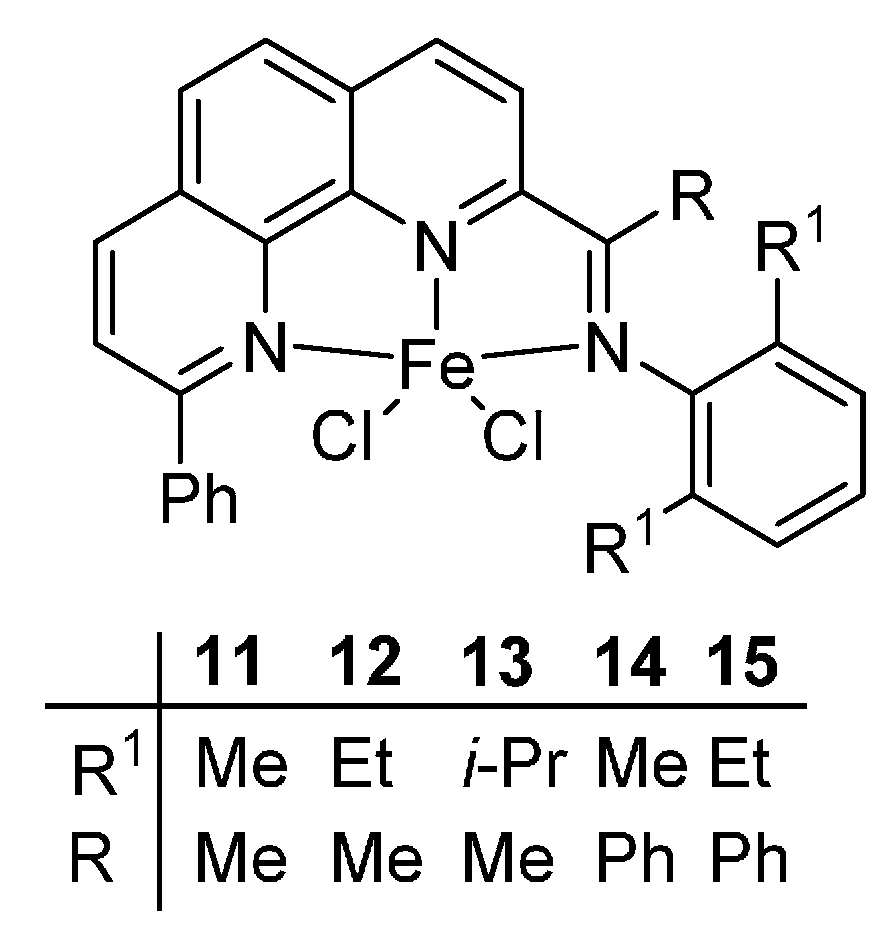
For the derivatives of bis(imino)pyridyline, the phenanthrolinyliron complexes also showed good thermal stability. Here, we selected a series of complexes
11–
15 from our previous reports [
47] with the structures showed in the
Scheme 5. In the same manner, the values of bond order (
B), minimum distance (
D) and dihedral angle (
α) as well as the results of the thermal stabilities (
AT), accordingly, were obtained and listed in
Table 5.
Compared with complexes
1–
10, the values of bond order (
B) and dihedral angle (
α) of complexes
11–
15 decreased obviously. To see the variation of the catalytic activities from experiments, the average values at room temperature and optimum temperature were showed in
Figure 2 for complexes
11–
15. It is clear that the average activities and thermal stabilities of complexes
11–
15 are obviously lower than that of complexes
1–
5 and
6–
10. These observations are in agreement with the decrease values of the calculated bond order (
B) and dihedral angle (
α) values within complexes
11–
15. On another side, the values of thermal stability (
AT) for complexes
11–
15 are large, as showed in
Table 5, especially for complexes
11 and
12. This can be explained by the very low catalytic activities at room temperature.
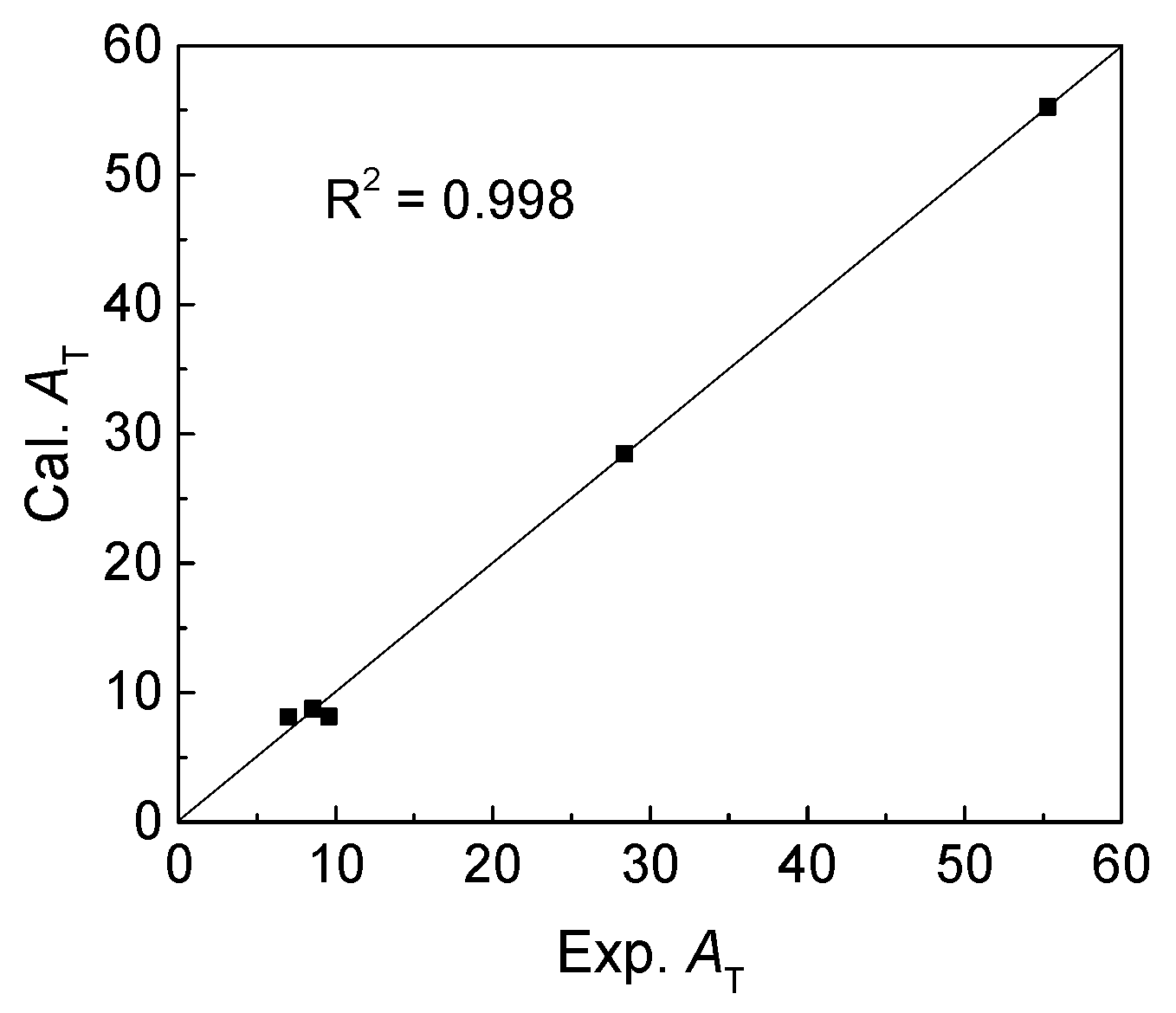
Then, the regression coefficients of fitting equation were calculated, and the values were listed in
Table 3. Comparison of calculated and experimental
AT was conducted as showed in
Figure 3. Obviously, there is a good correlation with the coefficient (
R2) value of 0.998, meaning that the thermal stabilities of complexes
11–
15 were reasonably investigated.
To further analyze the influence of each parameter on thermal stability, the
B,
D,
α and
AT values were standardized and the results were collected in
Table 5. Based on the standardized fitting equation, the contributions of each parameter were calculated accordingly. The obtained contribution of the dihedral angle (
α) is 78%, whereas those of bond order (
B) and minimum distance (
d) are 14% and 8%, respectively. These results reveal that, different from complexes
1–
5 and
6–
10, the dihedral angle became the major factor to determine the thermal stabilities of complexes
11–
15.
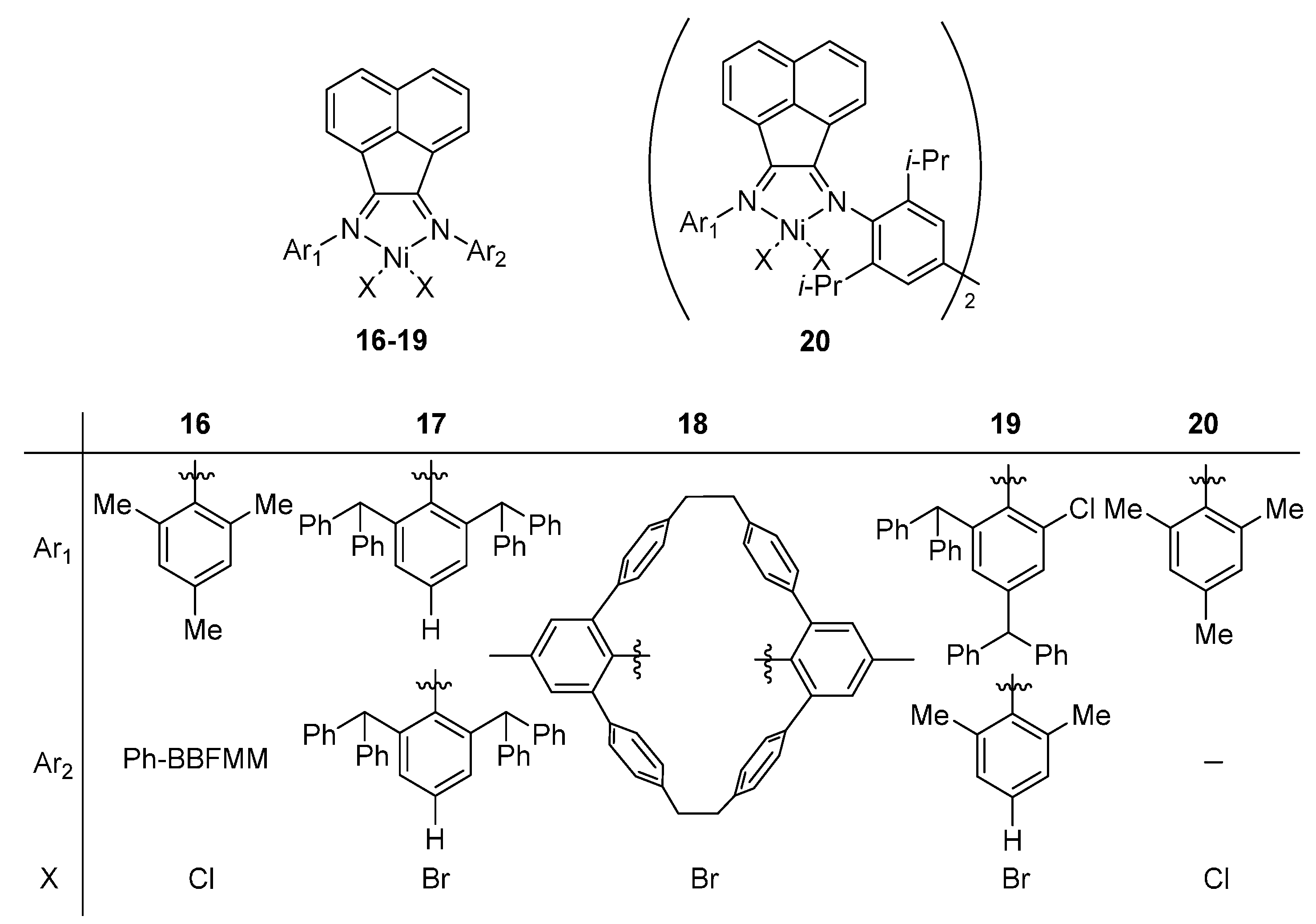
2.4. Thermal Stability of Acenaphthylnickel Complexes
As discussed in the introduction, besides the framework of bis(imino)pyridyline complex, the system with an acenaphthylene backbone also shows good thermal stability towards ethylene polymerization. In this section, a series of nickel complexes
16–
20 containing acenaphthylene ligands [
30,
43,
44,
45,
46] were investigated regarding the property of thermal stability. The structures of model complexes were showed in the
Scheme 6.
By the same method, three parameters (
B,
D,
α) were firstly obtained and listed in
Table 6 along with the values of thermal stabilities (
AT) for each complex. By the regression analysis method, the regression coefficients were obtained and showed in
Table 3. Then, the thermal stabilities were calculated and compared with experimental data. Results revealed in
Figure 4 that calculation values are in very agreement with experiments with the correlation coefficient (
R2) value of 0.998.
Based on standardized values of
B,
D,
α and
AT as well as the corresponding standard regression coefficients in
Table 3, the contributions of each factor were calculated accordingly, which showed the values of 49%, 22% and 29% for bond order (
B), minimum distance (
D) and dihedral angle (
α), respectively, signifying the dominant role of bond order in the thermal stabilities of complexes
16–
20.