Investigation of Structural Dynamics of Enzymes and Protonation States of Substrates Using Computational Tools
Abstract
:1. Introduction
2. Computational Tools
2.1. Atomistic Molecular Dynamics Simulations
2.2. Quantum Mechanics/Molecular Mechanics (QM/MM) Method
2.3. Combining Calculation, X-ray Crystallography and Solid-State NMR for Determining Protonation States
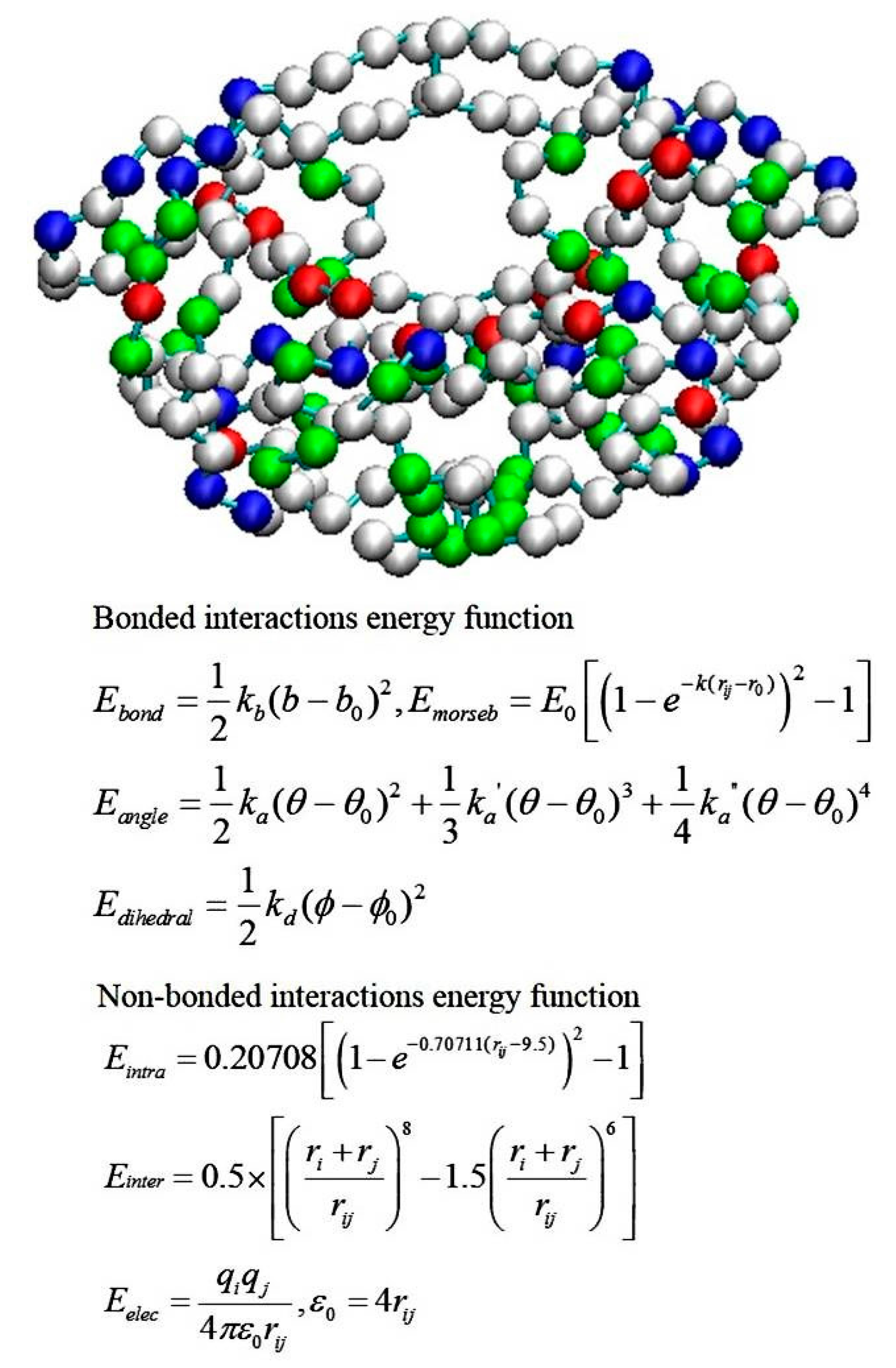
2.4. Coarse-Grained Brownian Dynamics Simulations
3. Examples of Modeling Enzymes and Substrates
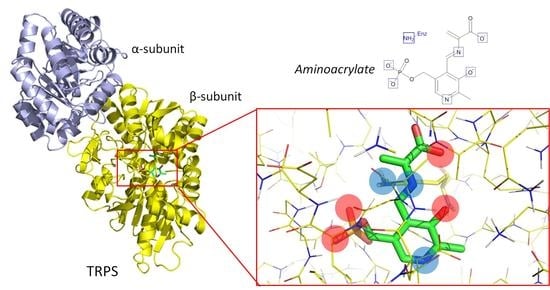
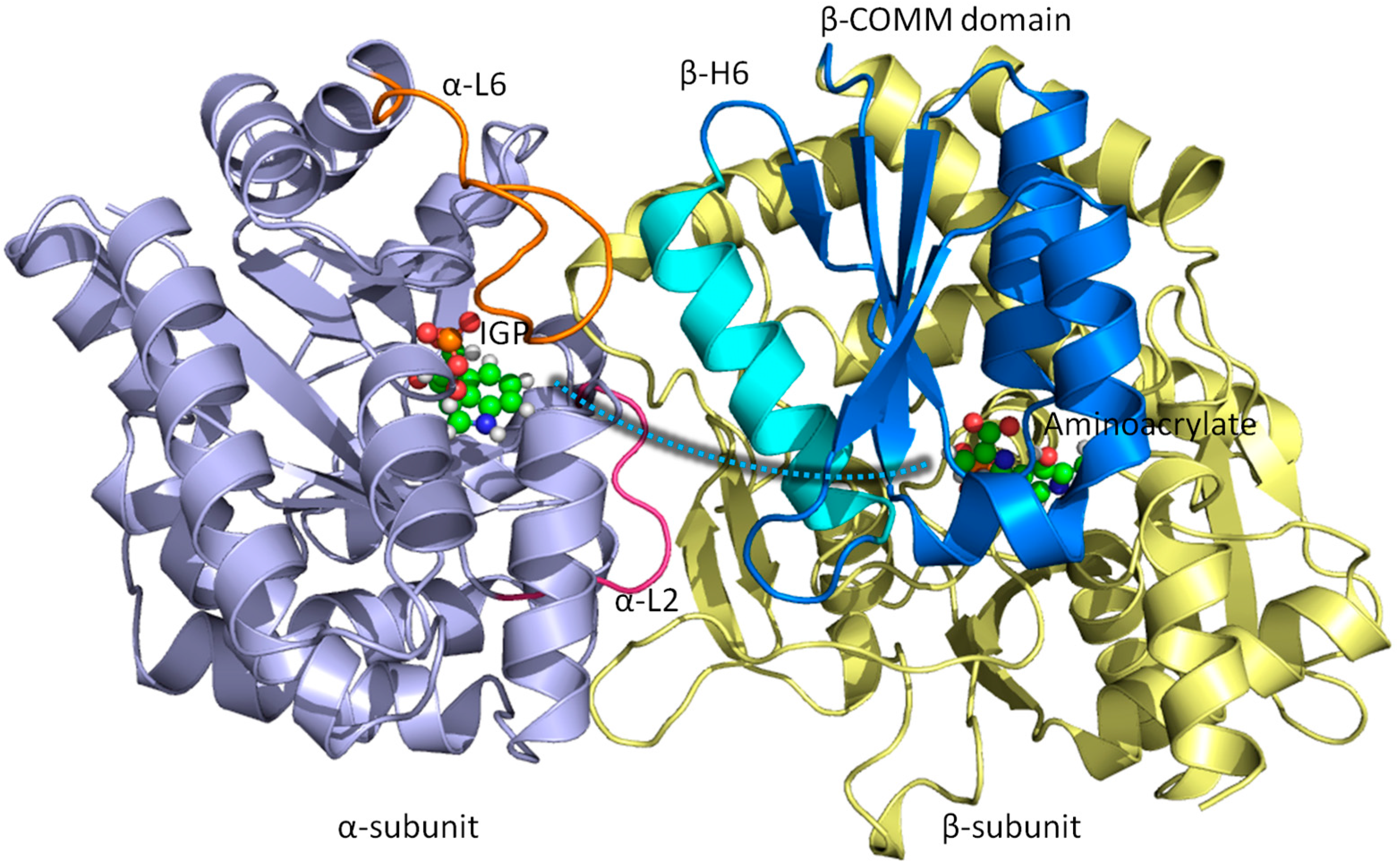
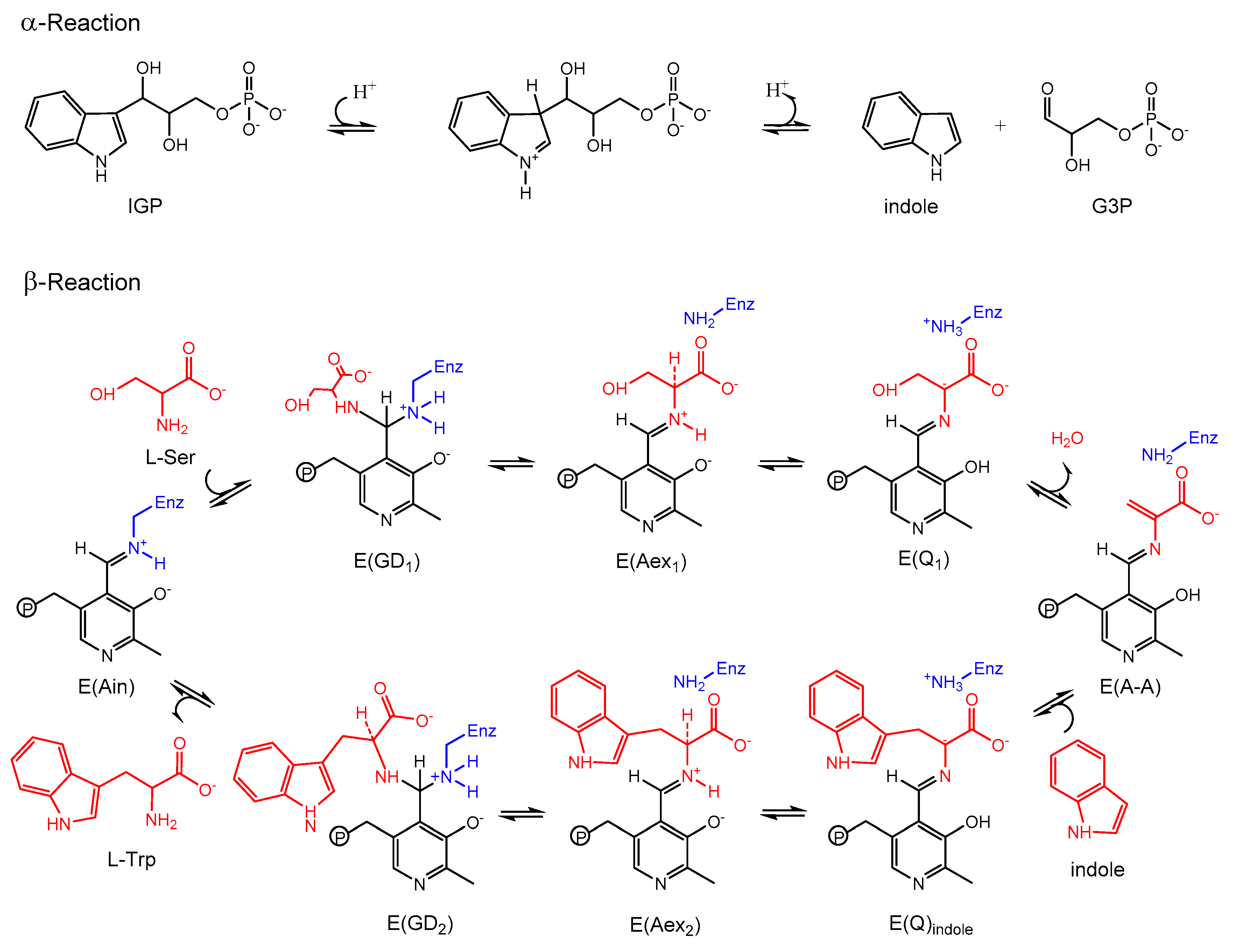
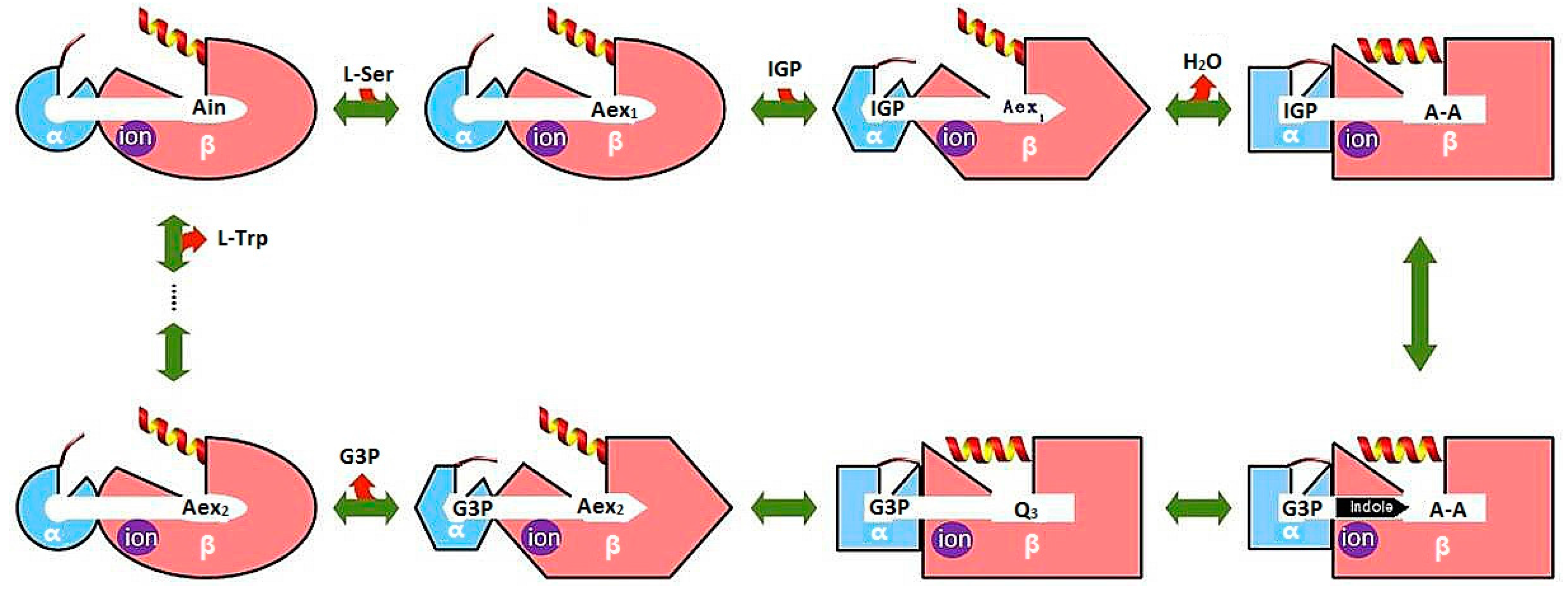
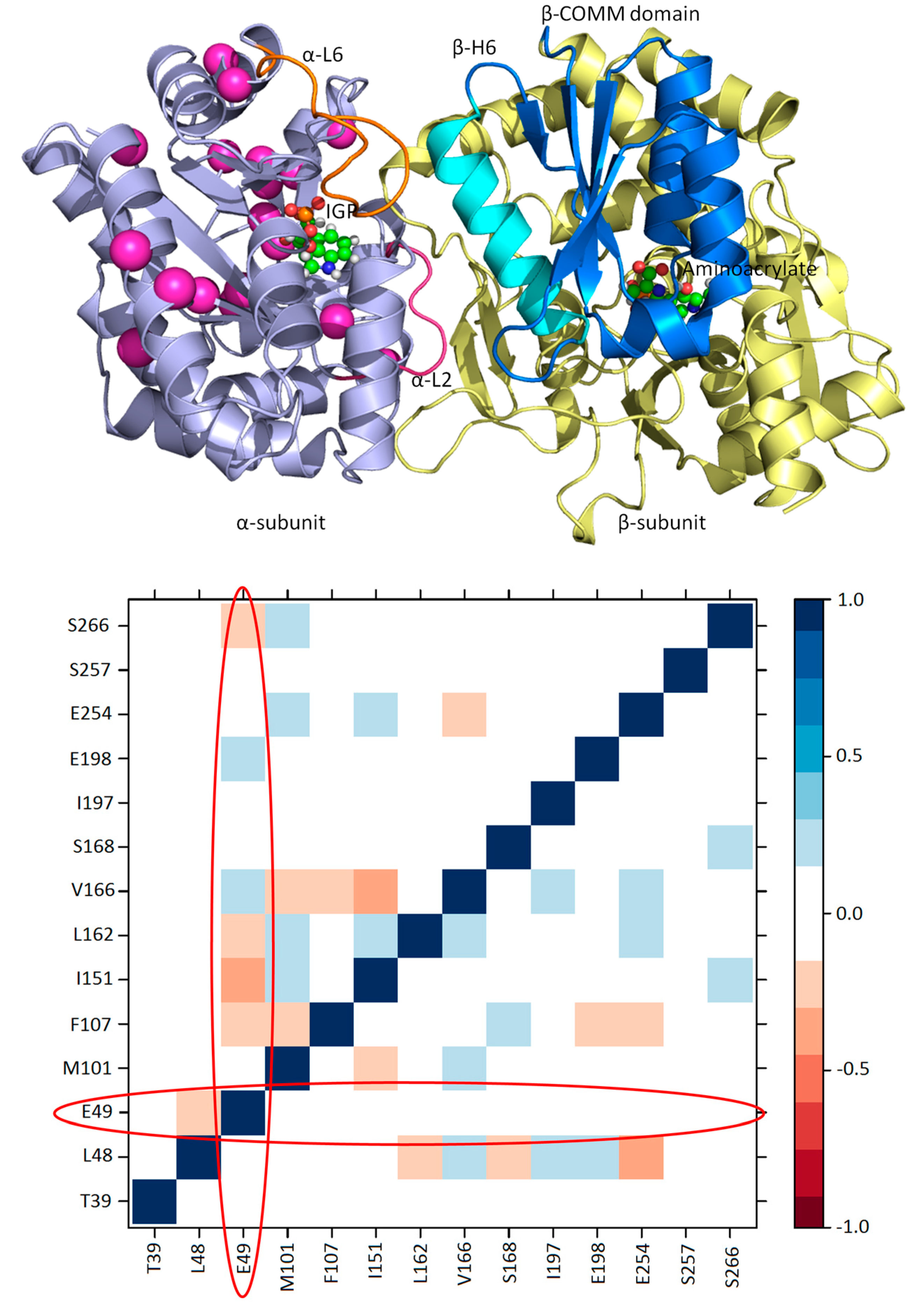
3.1. TRPS: A Model System for Allosteric and Network Regulation in Enzyme Catalysis
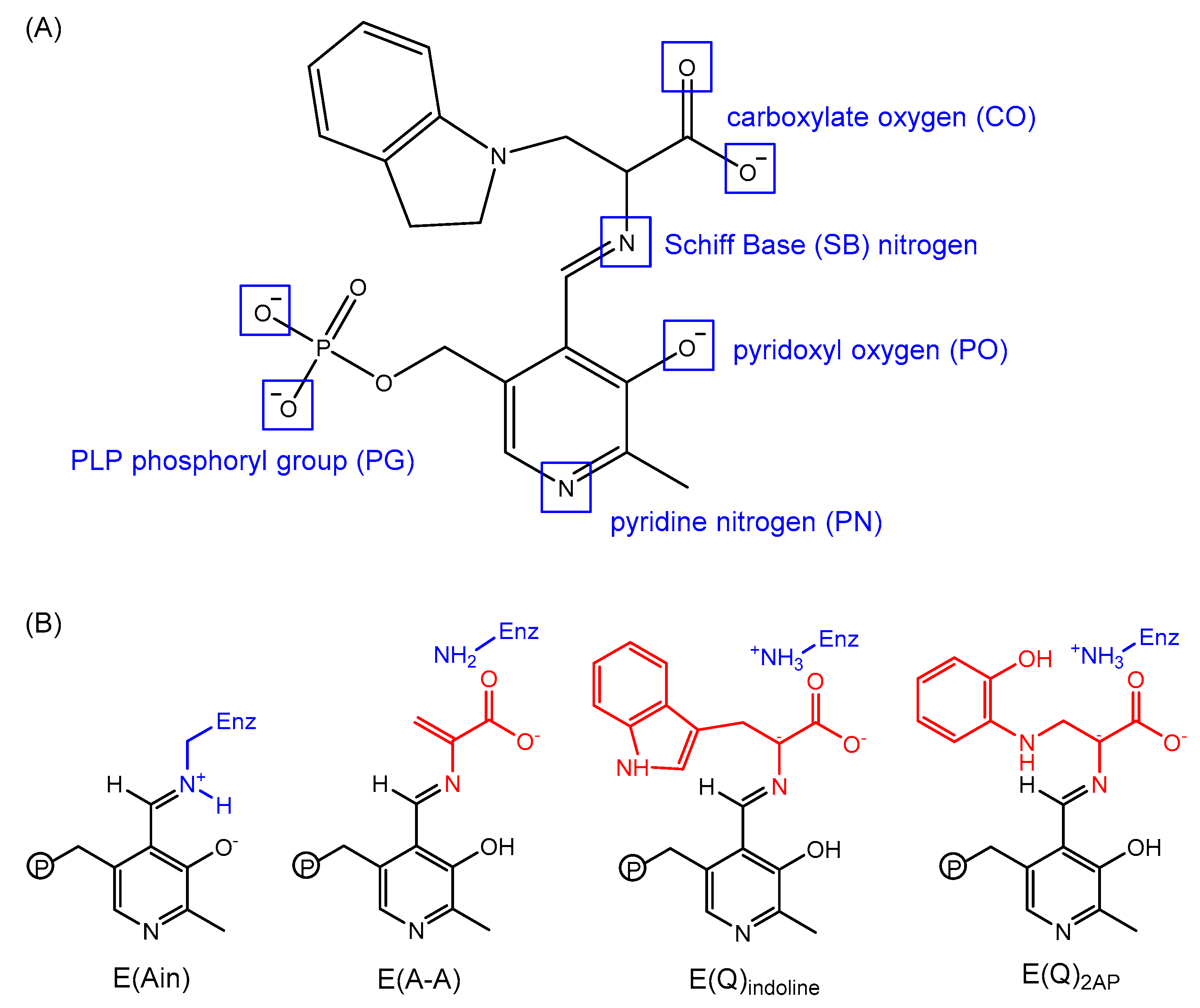
3.2. TRPS: How Protonation States Affect Protein Dynamics and Catalysis
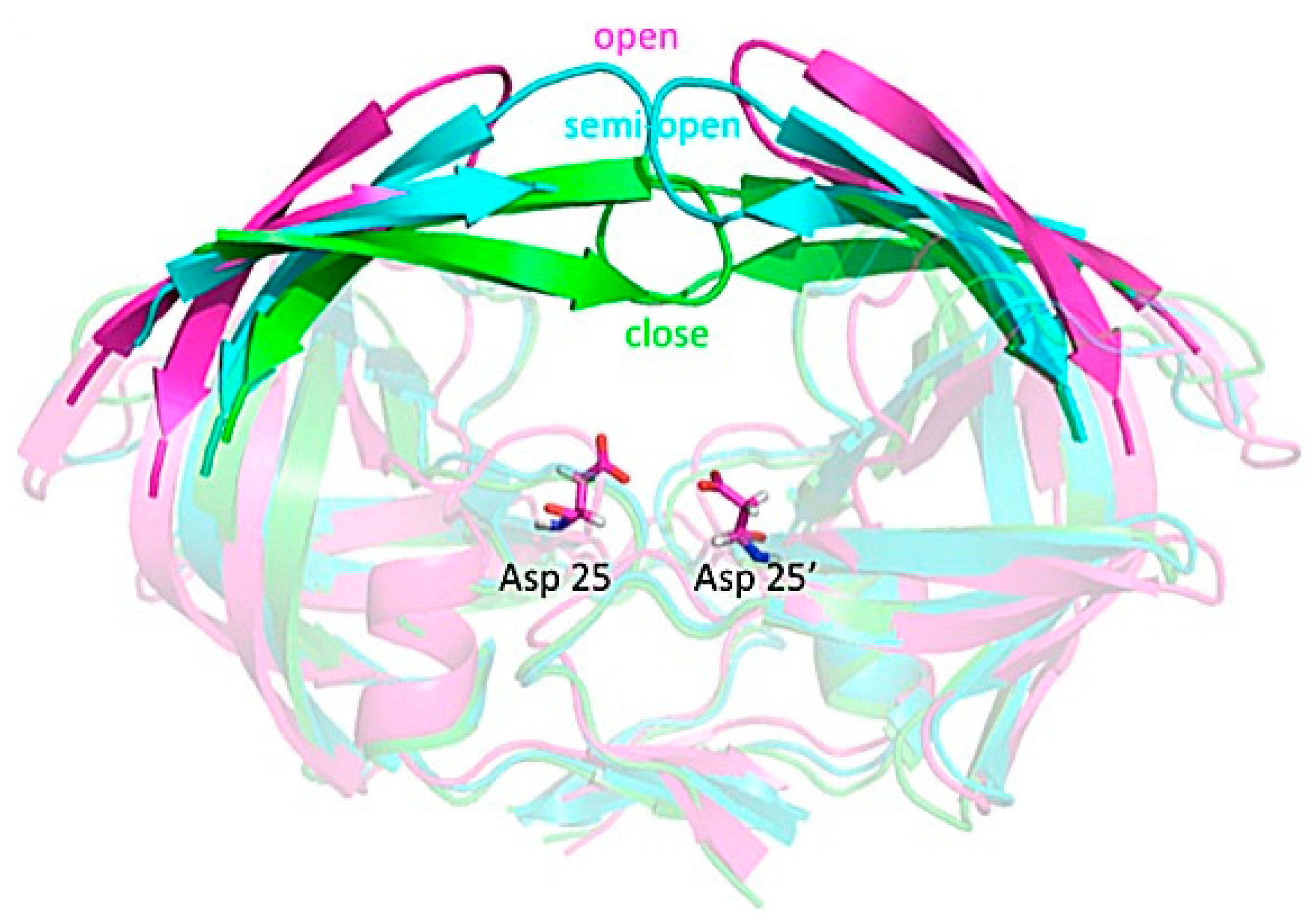
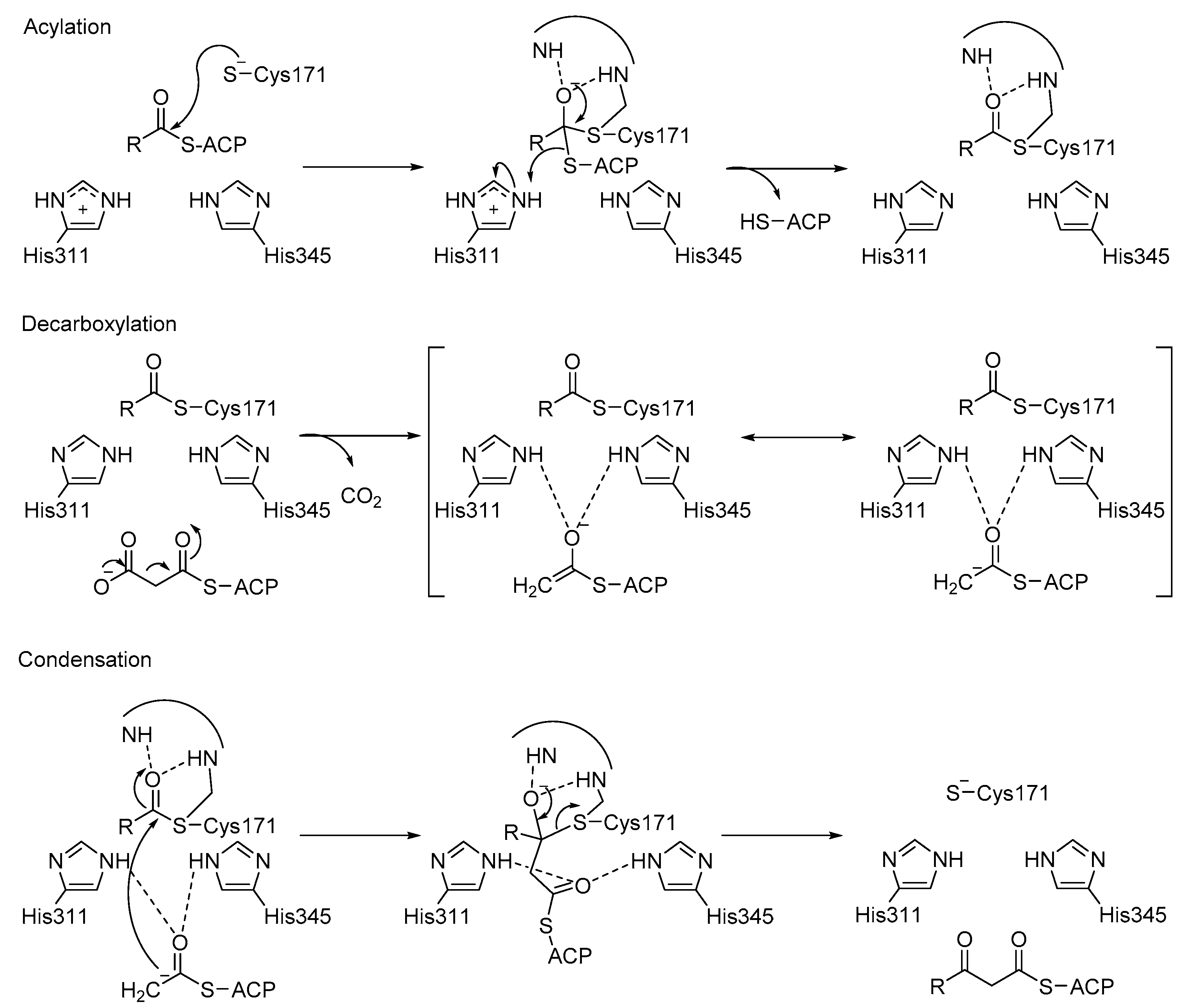
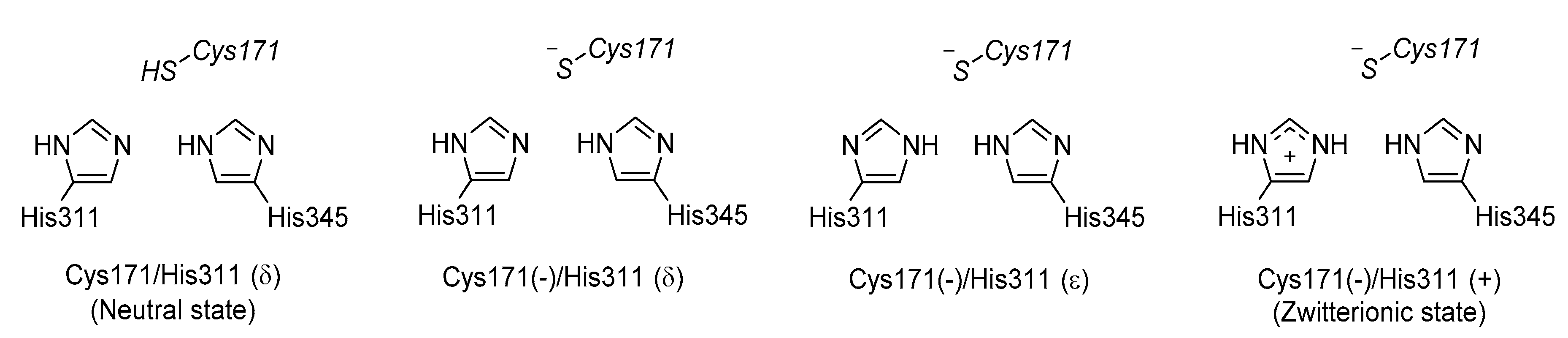
3.3. KaxA: Using QM/MM Methods to Determine Protonation States of Key Residues in Chemical Reactions
3.4. Investigating Large-Scale Conformational Changes in Enzymes: HIV-1 Protease
4. Outlook
Acknowledgments
Conflicts of Interest
References
- McCammon, J.A. Gated diffusion-controlled reactions. BMC Biophys. 2011, 4, 4. [Google Scholar] [CrossRef] [PubMed]
- Csermely, P.; Sandhu, K.S.; Hazai, E.; Hoksza, Z.; Kiss, H.J.; Miozzo, F.; Veres, D.V.; Piazza, F.; Nussinov, R. Disordered proteins and network disorder in network descriptions of protein structure, dynamics and function: Hypotheses and a comprehensive review. Curr. Protein Pept. Sci. 2012, 13, 19–33. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.J.; Del Sol, A.; Nussinov, R. Protein allostery, signal transmission and dynamics: A classification scheme of allosteric mechanisms. Mol. Biosyst. 2009, 5, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Kremer, L.; Dover, L.G.; Carrere, S.; Nampoothiri, K.M.; Lesjean, S.; Brown, A.K.; Brennan, P.J.; Minnikin, D.E.; Locht, C.; Besra, G.S. Mycolic acid biosynthesis and enzymic characterization of the beta-ketoacyl-ACP synthase A-condensing enzyme from Mycobacterium tuberculosis. Biochem. J. 2002, 364, 423–430. [Google Scholar] [CrossRef] [PubMed]
- White, S.W.; Zheng, J.; Zhang, Y.M.; Rock. The structural biology of type II fatty acid biosynthesis. Annu. Rev. Biochem. 2005, 74, 791–831. [Google Scholar] [CrossRef] [PubMed]
- Toney, M.D. Controlling reaction specificity in pyridoxal phosphate enzymes. Biochim. Biophys Acta 2011, 1814, 1407–1418. [Google Scholar] [CrossRef] [PubMed]
- Crugeiras, J.; Rios, A.; Riveiros, E.; Richard, J.P. Substituent effects on electrophilic catalysis by the carbonyl group: Anatomy of the rate acceleration for PLP-catalyzed deprotonation of glycine. J. Am. Chem. Soc. 2011, 133, 3173–3183. [Google Scholar] [CrossRef] [PubMed]
- Major, D.T.; Gao, J. A combined quantum mechanical and molecular mechanical study of the reaction mechanism and alpha-amino acidity in alanine racemase. J. Am. Chem. Soc. 2006, 128, 16345–16357. [Google Scholar] [CrossRef] [PubMed]
- Major, D.T.; Nam, K.; Gao, J. Transition state stabilization and alpha-amino carbon acidity in alanine racemase. J. Am. Chem. Soc. 2006, 128, 8114–8115. [Google Scholar] [CrossRef] [PubMed]
- Sachpatzidis, A.; Dealwis, C.; Lubetsky, J.B.; Liang, P.H.; Anderson, K.S.; Lolis, E. Crystallographic studies of phosphonate-based alpha-reaction transition-state analogues complexed to tryptophan synthase. Biochemistry 1999, 38, 12665–12674. [Google Scholar] [CrossRef] [PubMed]
- Drewe, W.F.; Dunn, M.F. Detection and identification of intermediates in the reaction of L-serine with escherichia-coli tryptophan synthase via rapid-scanning ultraviolet visible spectroscopy. Biochemistry 1985, 24, 3977–3987. [Google Scholar] [CrossRef] [PubMed]
- Drewe, W.F.; Dunn, M.F. Characterization of the reaction of L-serine and indole with Escherichia-coli tryptophan synthase via rapid-scanning ultraviolet visible spectroscopy. Biochemistry 1986, 25, 2494–2501. [Google Scholar] [CrossRef] [PubMed]
- Ngo, H.; Kimmich, N.; Harris, R.; Niks, D.; Blumenstein, L.; Kulik, V.; Barends, T.R.; Schlichting, I.; Dunn, M.F. Allosteric regulation of substrate channeling in tryptophan synthase: Modulation of the L-serine reaction in stage i of the ss-reaction by alpha-site ligands. Biochemistry 2007, 46, 7740–7753. [Google Scholar] [CrossRef] [PubMed]
- Lai, J.; Niks, D.; Wang, Y.; Domratcheva, T.; Barends, T.R.; Schwarz, F.; Olsen, R.A.; Elliott, D.W.; Fatmi, M.Q.; Chang, C.-E.A.; et al. X-ray and NMR crystallography in an enzyme active site: The indoline quinonoid intermediate in tryptophan synthase. J. Am. Chem. Soc. 2011, 133, 4–7. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, A.; Kremer, L.; Dai, A.Z.; Sacchettini, J.C.; Jacobs, W.R., Jr. Conditional depletion of KasA, a key enzyme of mycolic acid biosynthesis, leads to mycobacterial cell lysis. J. Bacteriol. 2005, 187, 7596–7606. [Google Scholar] [CrossRef] [PubMed]
- Debouck, C.; Gorniak, J.G.; Strickler, J.E.; Meek, T.D.; Metcalf, B.W.; Rosenberg, M. Human immunodeficiency virus protease expressed in Escherichia coli exhibits autoprocessing and specific maturation of the gag precursor. Proc. Natl. Acad. Sci. USA 1987, 84, 8903–8906. [Google Scholar] [CrossRef] [PubMed]
- Kohl, N.E.; Emini, E.A.; Schleif, W.A.; Davis, L.J.; Heimbach, J.C.; Dixon, R.A.; Scolnick, E.M.; Sigal, I.S. Active human immunodeficiency virus protease is required for viral infectivity. Proc. Natl. Acad. Sci. USA 1988, 85, 4686–4690. [Google Scholar] [CrossRef] [PubMed]
- Krausslich, H.G.; Ingraham, R.H.; Skoog, M.T.; Wimmer, E.; Pallai, P.V.; Carter, C.A. Activity of purified biosynthetic proteinase of human immunodeficiency virus on natural substrates and synthetic peptides. Proc. Natl. Acad. Sci. USA 1989, 86, 807–811. [Google Scholar] [CrossRef] [PubMed]
- Wlodawer, A.; Vondrasek, J. Inhibitors of HIV-1 protease: A major success of structure-assisted drug design. Annu. Rev. Biophys. Biomol. Struct. 1998, 27, 249–284. [Google Scholar] [CrossRef] [PubMed]
- Ishima, R.; Freedberg, D.I.; Wang, Y.X.; Louis, J.M.; Torchia, D.A. Flap opening and dimer-interface flexibility in the free and inhibitor-bound HIV protease, and their implications for function. Structure (London, England 1993) 1999, 7, 1047–1055. [Google Scholar] [CrossRef]
- Freedberg, D.I.; Ishima, R.; Jacob, J.; Wang, Y.X.; Kustanovich, I.; Louis, J.M.; Torchia, D.A. Rapid structural fluctuations of the free HIV protease flaps in solution: Relationship to crystal structures and comparison with predictions of dynamics calculations. Protein Sci. Publ. Protein Soc. 2002, 11, 221–232. [Google Scholar] [CrossRef] [PubMed]
- Adachi, M.; Ohhara, T.; Kurihara, K.; Tamada, T.; Honjo, E.; Okazaki, N.; Arai, S.; Shoyama, Y.; Kimura, K.; Matsumura, H.; et al. Structure of HIV-1 protease in complex with potent inhibitor KNI-272 determined by high-resolution X-ray and neutron crystallography. Proc. Natl. Acad. Sci. USA 2009, 106, 4641–4646. [Google Scholar] [CrossRef] [PubMed]
- McCammon, J.A.; Gelin, B.R.; Karplus, M. Dynamics of folded proteins. Nature 1977, 267, 585–590. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Orozco, M.; Orellana, L.; Hospital, A.; Naganathan, A.N.; Emperador, A.; Carrillo, O.; Gelpi, J.L. Coarse-grained representation of protein flexibility. Foundations, successes, and shortcomings. Adv. Protein Chem. Struct. Biol. 2011, 85, 183–215. [Google Scholar] [PubMed]
- Anandakrishnan, R.; Drozdetski, A.; Walker, R.C.; Onufriev, A.V. Speed of conformational change: Comparing explicit and implicit solvent molecular dynamics simulations. Biophys. J. 2015, 108, 1153–1164. [Google Scholar] [CrossRef] [PubMed]
- Bashford, D.; Case, D.A. Generalized born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 2000, 51, 129–152. [Google Scholar] [CrossRef] [PubMed]
- Haberthur, U.; Caflisch, A. Facts: Fast analytical continuum treatment of solvation. J. Comput. Chem. 2008, 29, 701–715. [Google Scholar] [CrossRef] [PubMed]
- Kleinjung, J.; Fraternali, F. Design and application of implicit solvent models in biomolecular simulations. Curr. Opin. Struct. Biol. 2014, 25, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Lazaridis, T.; Karplus, M. Effective energy function for proteins in solution. Proteins 1999, 35, 133–152. [Google Scholar] [CrossRef]
- Luchko, T.; Gusarov, S.; Roe, D.R.; Simmerling, C.; Case, D.A.; Tuszynski, J.; Kovalenko, A. Three-dimensional molecular theory of solvation coupled with molecular dynamics in amber. J. Chem. Theory Comput. 2010, 6, 607–624. [Google Scholar] [CrossRef] [PubMed]
- Orozco, M.; Luque, F.J. Theoretical methods for the description of the solvent effect in biomolecular systems. Chem. Rev. 2000, 100, 4187–4226. [Google Scholar] [CrossRef] [PubMed]
- Roux, B.; Simonson, T. Implicit solvent models. Biophys. Chem. 1999, 78, 1–20. [Google Scholar] [CrossRef]
- Vorobjev, Y.N. Advances in implicit models of water solvent to compute conformational free energy and molecular dynamics of proteins at constant ph. Adv. Protein Chem. Struct. Biol. 2011, 85, 281–322. [Google Scholar] [PubMed]
- Rueda, M.; Ferrer-Costa, C.; Meyer, T.; Perez, A.; Camps, J.; Hospital, A.; Gelpi, J.L.; Orozco, M. A consensus view of protein dynamics. Proc. Natl. Acad. Sci. USA 2007, 104, 796–801. [Google Scholar] [CrossRef] [PubMed]
- Perez, A.; Lankas, F.; Luque, F.J.; Orozco, M. Towards a molecular dynamics consensus view of b-DNA flexibility. Nucleic Acids Res. 2008, 36, 2379–2394. [Google Scholar] [CrossRef] [PubMed]
- Larsson, P.; Hess, B.; Lindahl, E. Algorithm improvements for molecular dynamics simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 93–108. [Google Scholar] [CrossRef]
- Case, D.A.; Babin, V.; Berryman, J.; Betz, R.M.; Cai, Q.; Cerutti, D.S.; Cheatham III, T.E.; Darden, T.A.; Duke, R.E.; Gohlke, H.; et al. Amber 14; University of California: San Francisco, CA, USA, 2014. [Google Scholar]
- Brooks, B.R.; Brooks, C.L., 3rd; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. Charmm: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. Gromacs 4: Algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Ponder, J.W.; Richards, F.M. An efficient newton-like method for molecular mechanics energy minimization of large molecules. J. Comput. Chem. 1987, 8, 1016–1024. [Google Scholar] [CrossRef]
- Harvey, M.J.; Giupponi, G.; Fabritiis, G.D. Acemd: Accelerating biomolecular dynamics in the microsecond time scale. J. Chem. Theory Comput. 2009, 5, 1632–1639. [Google Scholar] [CrossRef] [PubMed]
- Eastman, P.; Friedrichs, M.S.; Chodera, J.D.; Radmer, R.J.; Bruns, C.M.; Ku, J.P.; Beauchamp, K.A.; Lane, T.J.; Wang, L.P.; Shukla, D.; et al. OpenMM 4: A reusable, extensible, hardware independent library for high performance molecular simulation. J. Chem. Theory Comput. 2013, 9, 461–469. [Google Scholar] [CrossRef] [PubMed]
- Shaw, D.E.; Deneroff, M.M.; Dror, R.O.; Kuskin, J.S.; Larson, R.H.; Salmon, J.K.; Young, C.; Batson, B.; Bowers, K.J.; Chao, J.C.; et al. Anton, a special-purpose machine for molecular dynamics simulation. Commun. ACM 2008, 51, 91–97. [Google Scholar] [CrossRef]
- Shaw, D.E.; Grossman, J.P.; Bank, J.A.; Batson, B.; Butts, J.A.; Chao, J.C.; Deneroff, M.M.; Dror, R.O.; Even, A.; Fenton, C.H.; et al. Anton 2: Raising the bar for performance and programmability in a special-purpose molecular dynamics supercomputer. In Proceedings of the SC14: International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; pp. 41–53.
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y.; et al. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The martini force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, A.; Andersen, J.P.; Woolf, T.B. Coarse-grained simulations of transitions in the E2-to-E1 conformations for Ca ATPase (SERCA) show entropy-enthalpy compensation. J. Mol. Biol. 2012, 422, 575–593. [Google Scholar] [CrossRef] [PubMed]
- Tozzini, V. Coarse-grained models for proteins. Curr. Opin. Struct. Biol. 2005, 15, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Voter, A.F. Hyperdynamics: Accelerated molecular dynamics of infrequent events. Phys. Rev. Lett. 1997, 78, 3908–3911. [Google Scholar] [CrossRef]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef] [PubMed]
- Doshi, U.; Hamelberg, D. Achieving rigorous accelerated conformational sampling in explicit solvent. J. Phys. Chem. Lett. 2014, 5, 1217–1224. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Feher, V.A.; McCammon, J.A. Gaussian accelerated molecular dynamics: Unconstrained enhanced sampling and free energy calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. [Google Scholar] [CrossRef] [PubMed]
- Leech, J.; Prins, J.F.; Hermans, J. Smd: Visual steering of molecular dynamics for protein design. IEEE Comput. Sci. Eng. 1996, 3, 38–45. [Google Scholar] [CrossRef]
- Nicolini, P.; Frezzato, D.; Gellini, C.; Bizzarri, M.; Chelli, R. Toward quantitative estimates of binding affinities for protein-ligand systems involving large inhibitor compounds: A steered molecular dynamics simulation route. J. Comput. Chem. 2013, 34, 1561–1576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schlitter, J.; Engels, M.; Kruger, P. Targeted molecular-dynamics—A new approach for searching pathways of conformational transitions. J. Mol. Graph. 1994, 12, 84–89. [Google Scholar] [CrossRef]
- Wu, X.W.; Brooks, B.R. Self-guided langevin dynamics simulation method. Chem. Phys. Lett. 2003, 381, 512–518. [Google Scholar] [CrossRef]
- Wu, X.; Brooks, B.R.; Vanden-Eijnden, E. Self-guided langevin dynamics via generalized langevin equation. J. Comput. Chem. 2016, 37, 595–601. [Google Scholar] [CrossRef] [PubMed]
- Labute, P. Lowmodemd-implicit low-mode velocity filtering applied to conformational search of macrocycles and protein loops. J. Chem. Inform. Model. 2010, 50, 792–800. [Google Scholar] [CrossRef] [PubMed]
- Swenson, D.W.H.; Bolhuis, P.G. A replica exchange transition interface sampling method with multiple interface sets for investigating networks of rare events. J. Chem. Phys. 2014, 141. [Google Scholar] [CrossRef] [PubMed]
- Voter, A.F. Parallel replica method for dynamics of infrequent events. Phys. Rev. B 1998, 57, 13985–13988. [Google Scholar] [CrossRef]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Hu, H.; Yang, W. Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods. Annu. Rev. Phys. Chem. 2008, 59, 573–601. [Google Scholar] [CrossRef] [PubMed]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. (Int. Ed. Engl.) 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Van der Kamp, M.W.; Mulholland, A.J. Combined quantum mechanics/molecular mechanics (QM/MM) methods in computational enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef] [PubMed]
- Chatwin, S.L.; Davidson, M.G.; Doherty, C.; Donald, S.M.; Jazzar, R.F.R.; Macgregor, S.A.; McIntyre, G.J.; Mahon, M.F.; Whittlesey, M.K. H−X bond activation via hydrogen transfer to hydride in ruthenium N-heterocyclic carbene complexes: Density functional and synthetic studies. Organometallics 2006, 25, 99–110. [Google Scholar] [CrossRef]
- Genest, A.; Woiterski, A.; Krüger, S.; Shor, A.M.; Rösch, N. The imomm (integrated molecular orbitals/molecular mechanics) approach for ligand-stabilized metal clusters. Comparison to full density functional calculations for the model thiolate cluster Cu13(SCH2CH3)8. J. Chem. Theory Comput. 2006, 2, 47–58. [Google Scholar] [CrossRef] [PubMed]
- Shiota, Y.; Suzuki, K.; Yoshizawa, K. QM/MM study on the catalytic mechanism of benzene hydroxylation over fe−zsm-5. Organometallics 2006, 25, 3118–3123. [Google Scholar] [CrossRef]
- To, J.; Sherwood, P.; Sokol, A.A.; Bush, I.J.; Catlow, C.R.A.; van Dam, H.J.J.; French, S.A.; Guest, M.F. QM/MM modelling of the TS-1 catalyst using HPCx. J. Mater. Chem. 2006, 16, 1919–1926. [Google Scholar] [CrossRef]
- Gunaydin, H.; Acevedo, O.; Jorgensen, W.L.; Houk, K.N. Computation of accurate activation barriers for methyl-transfer reactions of sulfonium and ammonium salts in aqueous solution. J. Chem. Theory Comput. 2007, 3, 1028–1035. [Google Scholar] [CrossRef] [PubMed]
- Alexandrova, A.N.; Jorgensen, W.L. Why urea eliminates ammonia rather than hydrolyzes in aqueous solution. J. Phys. Chem. B 2007, 111, 720–730. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, Y.W.; Sanchez-Garcia, E.; Doerr, M.; Thiel, W. Quantum refinement of protein structures: Implementation and application to the red fluorescent protein dsred.M1. J. Phys. Chem. B 2010, 114, 15413–15423. [Google Scholar] [CrossRef] [PubMed]
- Ryde, U. Combined quantum and molecular mechanics calculations on metalloproteins. Curr. Opin. Chem. Biol. 2003, 7, 136–142. [Google Scholar] [CrossRef]
- Marti, S.; Moliner, V.; Tunon, I. Improving the QM/MM description of chemical processes: A dual level strategy to explore the potential energy surface in very large systems. J. Chem. Theory Comput. 2005, 1, 1008–1016. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, Y.W.; Drakenberg, T.; Ryde, U. NMR structure determination of proteins supplemented by quantum chemical calculations: Detailed structure of the Ca2+ sites in the EGF34 fragment of protein S. J. Biomol. NMR 2005, 31, 97–114. [Google Scholar] [CrossRef] [PubMed]
- Mueller, L.J.; Dunn, M.F. NMR crystallography of enzyme active sites: Probing chemically detailed, three-dimensional structure in tryptophan synthase. Acc. Chem. Res. 2013, 46, 2008–2017. [Google Scholar] [CrossRef] [PubMed]
- Clementi, C. Coarse-grained models of protein folding: Toy models or predictive tools? Curr. Opin. Struct. Biol. 2008, 18, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Gorfe, A.A.; Chang, C.E.A.; Ivanov, I.; McCammon, J.A. Dynamics of the acetylcholineasterase tetramer. Biophys. J. 2008, 94, 1144–1154. [Google Scholar] [CrossRef] [PubMed]
- Leonarski, F.; Trovato, F.; Tozzini, V.; Les, A.; Trylska, J. Evolutionary algorithm in the optimization of a coarse-grained force field. J. Chem. Theory Comput. 2013, 9, 4874–4889. [Google Scholar] [CrossRef] [PubMed]
- Tozzini, V.; McCammon, J.A. A coarse grained model for the dynamics of flap opening in HIV-1 protease. Chem. Phys. Lett. 2005, 413, 123–128. [Google Scholar] [CrossRef]
- Chang, C.E.; Shen, T.; Trylska, J.; Tozzini, V.; McCammon, J.A. Gated binding of ligands to HIV-1 protease: Brownian dynamics simulations in a coarse-grained model. Biophys. J. 2006, 90, 3880–3885. [Google Scholar] [CrossRef] [PubMed]
- Gorecki, A.; Szypowski, M.; Dlugosz, M.; Trylska, J. Redmd-reduced molecular dynamics package. J. Comput. Chem. 2009, 30, 2364–2373. [Google Scholar] [CrossRef] [PubMed]
- Davis, M.E.; Madura, J.D.; Luty, B.A.; McCammon, J.A. Electrostatics and diffusion of molecules in solution: Simulations with the university of houston brownian dynamics program. Comput. Phys. Commun. 1991, 62, 187–197. [Google Scholar] [CrossRef]
- Chang, C.-E.A.; Trylska, J.; Tozzini, V.; Andrew McCammon, J. Binding pathways of ligands to HIV-1 protease: Coarse-grained and atomistic simulations. Chem. Biol. Drug Des. 2007, 69, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Ermak, D.L.; McCammon, J.A. Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 1978, 69, 1352–1360. [Google Scholar] [CrossRef]
- Dunn, M.F. Allosteric regulation of substrate channeling and catalysis in the tryptophan synthase bienzyme complex. Arch. Biochem. Biophys. 2012, 519, 154–166. [Google Scholar] [CrossRef] [PubMed]
- Fatmi, M.Q.; Ai, R.; Chang, C.-E.A. Synergistic regulation and ligand-induced conformational changes of tryptophan synthase. Biochemistry 2009, 48, 9921–9931. [Google Scholar] [CrossRef] [PubMed]
- Fatmi, M.Q.; Chang, C.-E.A. The role of oligomerization and cooperative regulation in protein function: The case of tryptophan synthase. PLoS Comput. Biol. 2010, 6, e1000994. [Google Scholar] [CrossRef] [PubMed]
- Ai, R.; Qaiser Fatmi, M.; Chang, C.-E.A. T-analyst: A program for efficient analysis of protein conformational changes by torsion angles. J. Comput. Aided Mol. Des. 2010, 24, 819–827. [Google Scholar] [CrossRef] [PubMed]
- Grant, B.J.; Rodrigues, A.P.; ElSawy, K.M.; McCammon, J.A.; Caves, L.S. Bio3d: An R package for the comparative analysis of protein structures. Bioinformatics (Oxford, England) 2006, 22, 2695–2696. [Google Scholar] [CrossRef] [PubMed]
- Axe, J.M.; Yezdimer, E.M.; O’Rourke, K.F.; Kerstetter, N.E.; You, W.; Chang, C.-E.A.; Boehr, D.D. Amino acid networks in a (beta/alpha)(8) barrel enzyme change during catalytic turnover. J. Am. Chem. Soc. 2014, 136, 6818–6821. [Google Scholar] [CrossRef] [PubMed]
- Axe, J.M.; Boehr, D.D. Long-range interactions in the alpha subunit of tryptophan synthase help to coordinate ligand binding, catalysis, and substrate channeling. J. Mol. Biol. 2013, 425, 1527–1545. [Google Scholar] [CrossRef] [PubMed]
- Axe, J.M.; O’Rourke, K.F.; Kerstetter, N.E.; Yezdimer, E.M.; Chan, Y.M.; Chasin, A.; Boehr, D.D. Severing of a hydrogen bond disrupts amino acid networks in the catalytically active state of the alpha subunit of tryptophan synthase. Protein Sci. A Publ. Protein Soc. 2015, 24, 484–494. [Google Scholar] [CrossRef] [PubMed]
- Caulkins, B.G.; Bastin, B.; Yang, C.; Neubauer, T.J.; Young, R.P.; Hilario, E.; Huang, Y.-M.M.; Chang, C.-E.A.; Fan, L.; Dunn, M.F.; et al. Protonation states of the tryptophan synthase internal aldimine active site from solid-state NMR spectroscopy: Direct observation of the protonated schiff base linkage to pyridoxal-5′-phosphate. J. Am. Chem. Soc. 2014, 136, 12824–12827. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.-M.M.; You, W.; Caulkins, B.G.; Dunn, M.F.; Mueller, L.J.; Chang, C.-E.A. Protonation states and catalysis: Molecular dynamics studies of intermediates in tryptophan synthase. Protein Sci. A Publ. Protein Soc. 2016, 25, 166–183. [Google Scholar] [CrossRef] [PubMed]
- Schnackerz, K.D.; Andi, B.; Cook, P.F. P-31 NMR spectroscopy senses the microenvironment of the 5′-phosphate group of enzyme-bound pyridoxal 5′-phosphate. Biochim. Biophys. Acta Proteins Proteom. 2011, 1814, 1447–1458. [Google Scholar] [CrossRef] [PubMed]
- Eliot, A.C.; Kirsch, J.F. Pyridoxal phosphate enzymes: Mechanistic, structural, and evolutionary considerations. Annu. Rev. Biochem. 2004, 73, 383–415. [Google Scholar] [CrossRef] [PubMed]
- Fogle, E.J.; Liu, W.S.; Woon, S.T.; Keller, J.W.; Toney, M.D. Role of Q52 in catalysis of decarboxylation and transamination in dialkylglycine decarboxylase. Biochemistry 2005, 44, 16392–16404. [Google Scholar] [CrossRef] [PubMed]
- Sharif, S.; Fogle, E.; Toney, M.D.; Denisov, G.S.; Shenderovich, I.G.; Buntkowsky, G.; Tolstoy, P.M.; Huot, M.C.; Limbach, H.-H. NMR localization of protons in critical enzyme hydrogen bonds. J. Am. Chem. Soc. 2007, 129, 9558–9559. [Google Scholar] [CrossRef] [PubMed]
- Griswold, W.R.; Toney, M.D. Role of the pyridine nitrogen in pyridoxal 5′-phosphate catalysis: Activity of three classes of PLP enzymes reconstituted with deazapyridoxal 5′-phosphate. J. Am. Chem. Soc. 2011, 133, 14823–14830. [Google Scholar] [CrossRef] [PubMed]
- Shaw, J.P.; Petsko, G.A.; Ringe, D. Determination of the structure of alanine racemase from bacillus stearothermophilus at 1.9-angstrom resolution. Biochemistry 1997, 36, 1329–1342. [Google Scholar] [CrossRef] [PubMed]
- Tai, C.H.; Cook, P.F. Pyridoxal 5′-phosphate dependent alpha,beta-elimination reactions: Mechanism of O-acetylserine sulfhydrylase. Acc. Chem. Res. 2001, 34, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Luckner, S.R.; Kisker, C.; Tonge, P.J.; Engels, B. Elucidation of the protonation states of the catalytic residues in mtKasA: Implications for inhibitor design. Biochemistry 2011, 50, 5743–5756. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Engels, B. Clarification on the decarboxylation mechanism in KasA based on the protonation state of key residues in the acyl-enzyme state. J. Phys. Chem. B 2013, 117, 8095–8104. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.; Engels, B. The protonation state of catalytic residues in the resting state of KasA revisited: Detailed mechanism for the activation of KasA by its own substrate. Biochemistry 2014, 53, 919–931. [Google Scholar] [CrossRef] [PubMed]
- Karthik, S.; Senapati, S. Dynamic flaps in HIV-1 protease adopt unique ordering at different stages in the catalytic cycle. Proteins 2011, 79, 1830–1840. [Google Scholar] [CrossRef] [PubMed]
- Deng, N.J.; Zheng, W.; Gallicchio, E.; Levy, R.M. Insights into the dynamics of HIV-1 protease: A kinetic network model constructed from atomistic simulations. J. Am. Chem. Soc. 2011, 133, 9387–9394. [Google Scholar] [CrossRef] [PubMed]
- Hornak, V.; Okur, A.; Rizzo, R.C.; Simmerling, C. HIV-1 protease flaps spontaneously open and reclose in molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2006, 103, 915–920. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.M.; Kang, M.; Chang, C.-E.A. Switches of hydrogen bonds during ligand-protein association processes determine binding kinetics. J. Mol. Recognit. JMR 2014, 27, 537–548. [Google Scholar] [CrossRef] [PubMed]
- Kang, M.; Roberts, C.; Cheng, Y.; Chang, C.-E.A. Gating and intermolecular interactions in ligand-protein association: Coarse-grained modeling of HIV-1 protease. J. Chem. Theory Comput. 2011, 7, 3438–3446. [Google Scholar] [CrossRef] [PubMed]




© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.-e.A.; Huang, Y.-m.M.; Mueller, L.J.; You, W. Investigation of Structural Dynamics of Enzymes and Protonation States of Substrates Using Computational Tools. Catalysts 2016, 6, 82. https://doi.org/10.3390/catal6060082
Chang C-eA, Huang Y-mM, Mueller LJ, You W. Investigation of Structural Dynamics of Enzymes and Protonation States of Substrates Using Computational Tools. Catalysts. 2016; 6(6):82. https://doi.org/10.3390/catal6060082
Chicago/Turabian StyleChang, Chia-en A., Yu-ming M. Huang, Leonard J. Mueller, and Wanli You. 2016. "Investigation of Structural Dynamics of Enzymes and Protonation States of Substrates Using Computational Tools" Catalysts 6, no. 6: 82. https://doi.org/10.3390/catal6060082
APA StyleChang, C.-e. A., Huang, Y.-m. M., Mueller, L. J., & You, W. (2016). Investigation of Structural Dynamics of Enzymes and Protonation States of Substrates Using Computational Tools. Catalysts, 6(6), 82. https://doi.org/10.3390/catal6060082