Role of Conformational Motions in Enzyme Function: Selected Methodologies and Case Studies
Abstract
:1. Introduction
2. Selected Experimental and Computational Approaches for Sampling Conformational Motions in Proteins
3. Case Studies
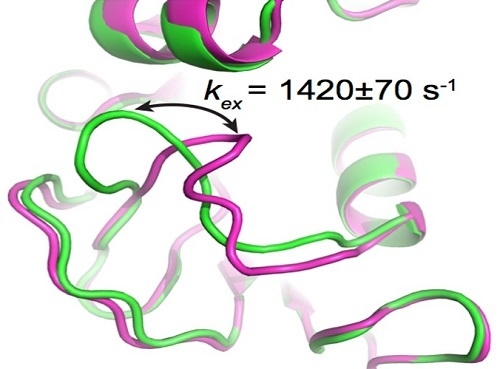
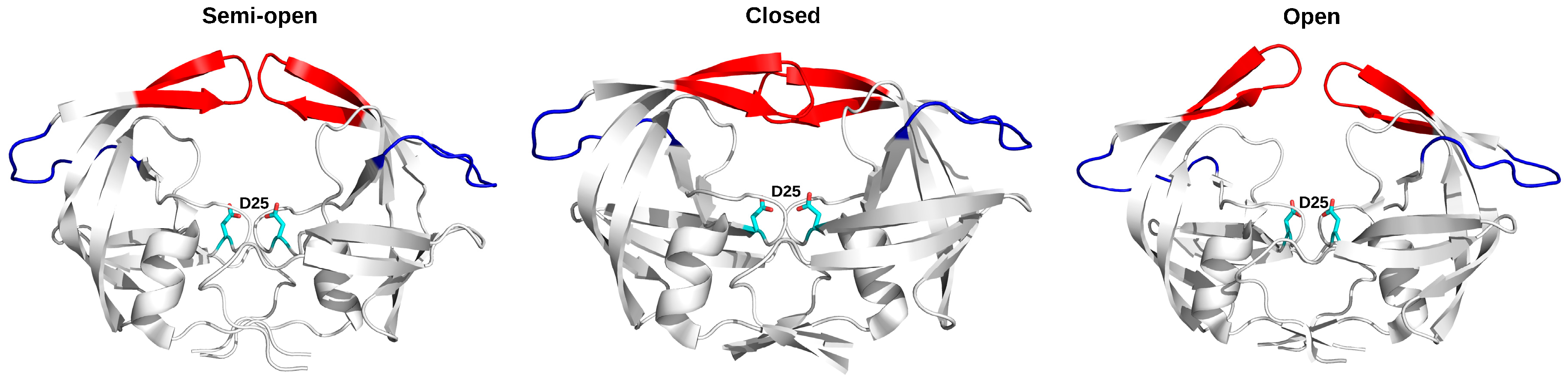
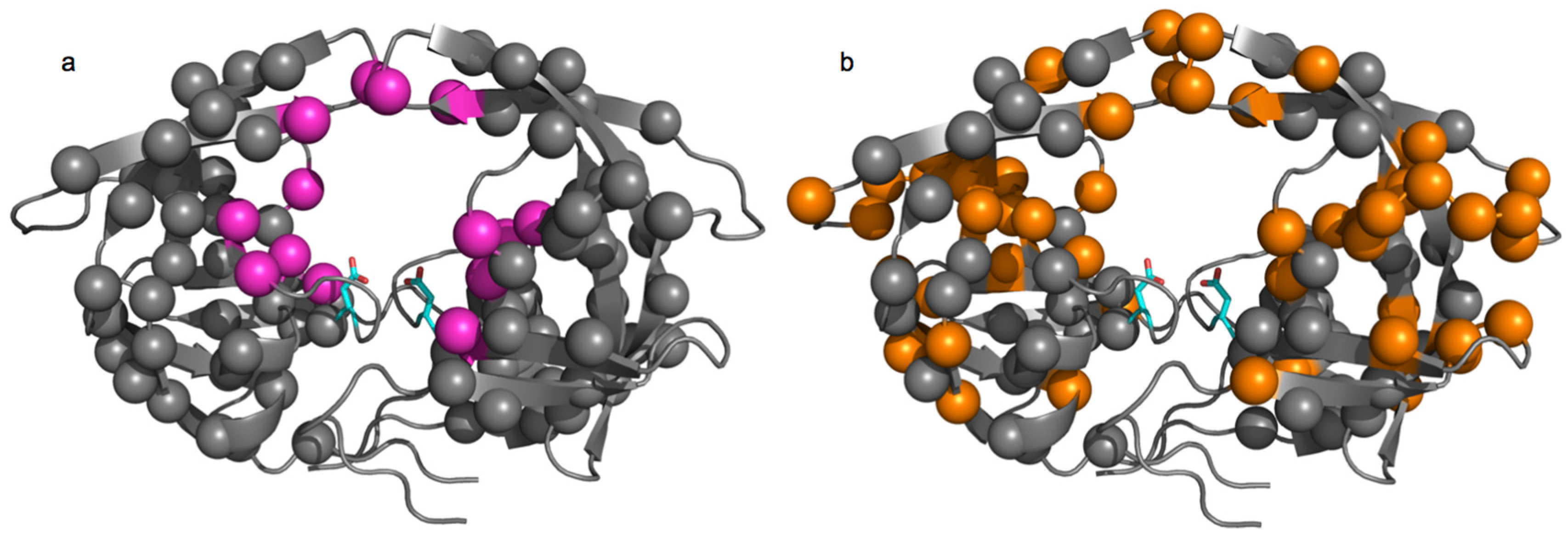
3.1. HIV Protease
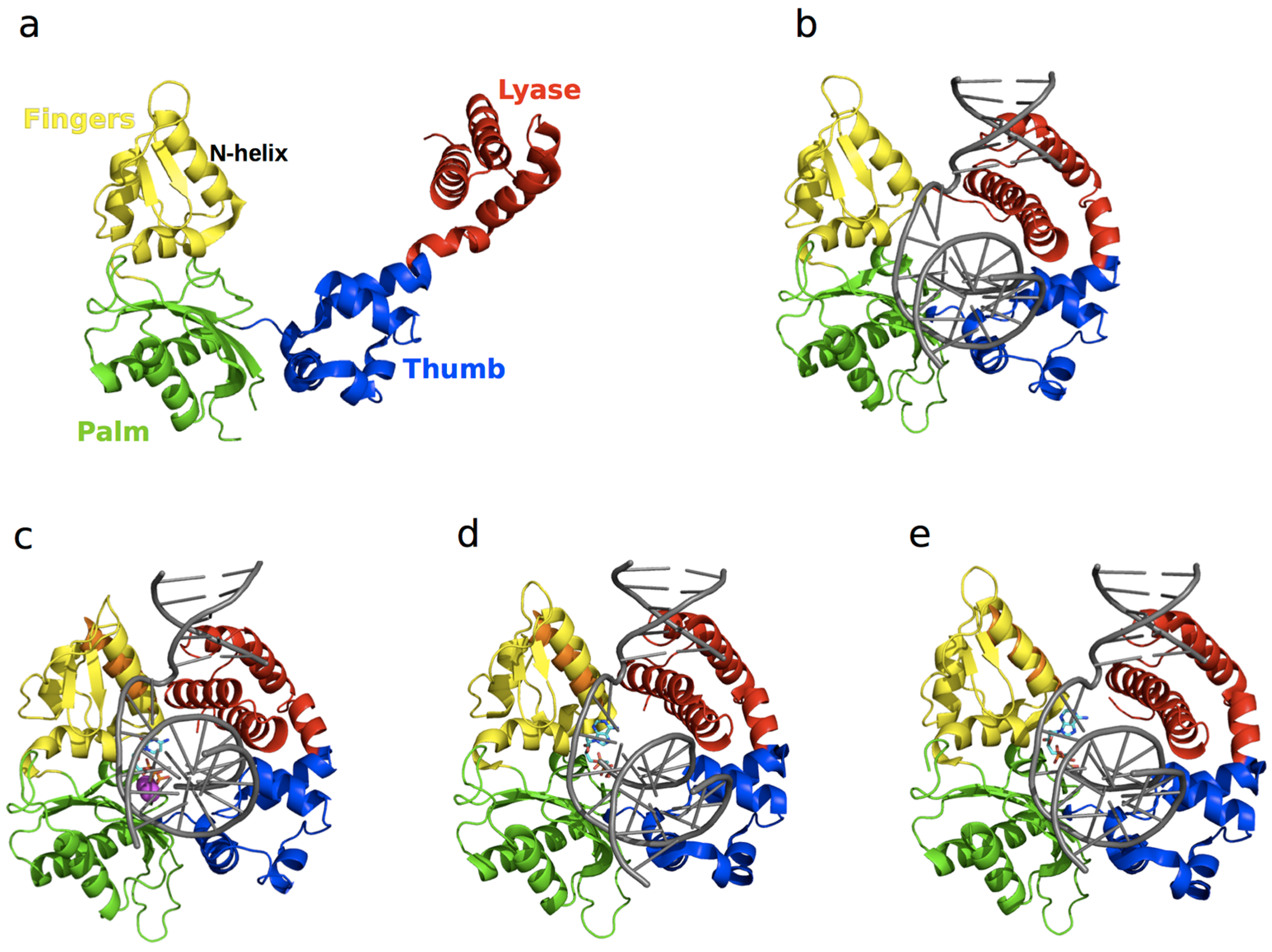
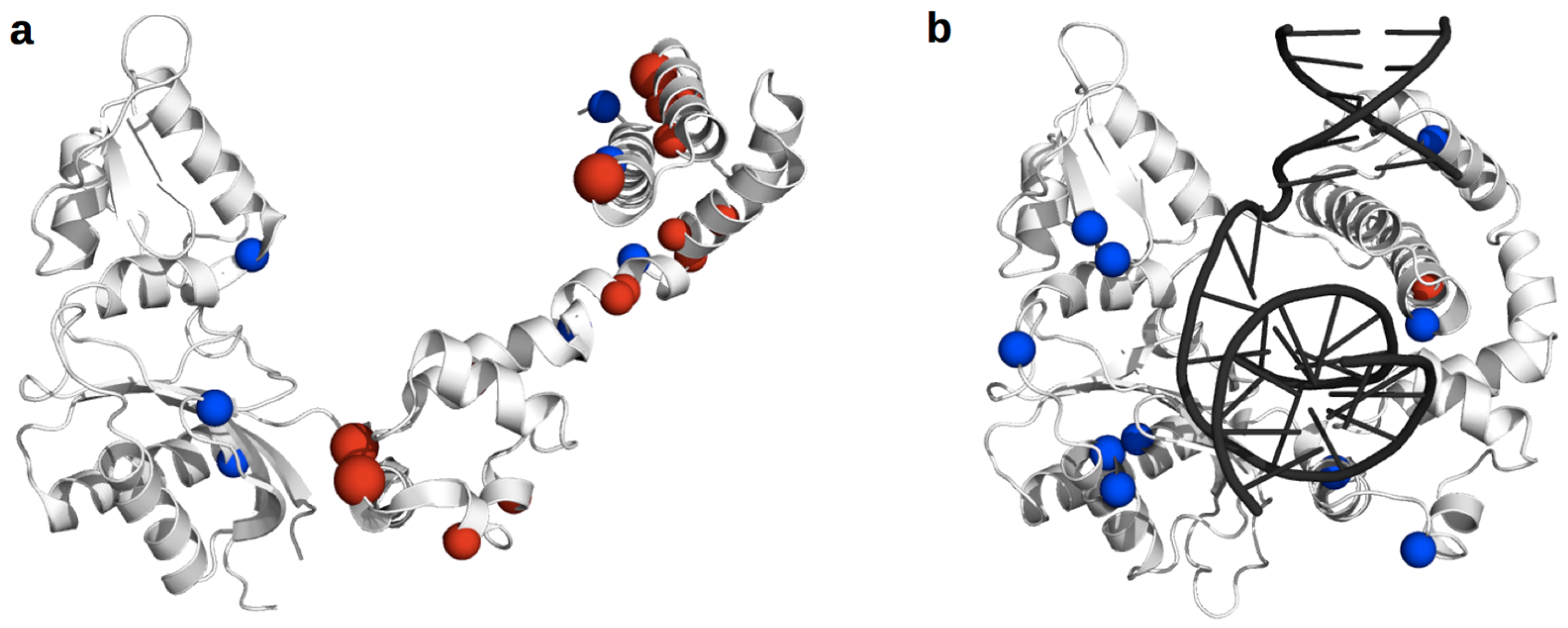
3.2. DNA Polymerase β
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Garcia-Viloca, M.; Gao, J.; Karplus, M.; Truhlar, D.G. How enzymes work: Analysis by modern rate theory and computer simulations. Science 2004, 303, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Wolfenden, R. Degrees of difficulty of water-consuming reactions in the absence of enzymes. Chem. Rev. 2006, 106, 3379–3396. [Google Scholar] [CrossRef] [PubMed]
- Hammes, G.G.; Chang, Y.C.; Oas, T.G. Conformational selection or induced fit: A flux description of reaction mechanism. Proc. Natl. Acad. Sci. USA 2009, 106, 13737–13741. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Watt, E.D.; Shimada, H.; Kovrigin, E.L.; Loria, J.P. The mechanism of rate-limiting motions in enzyme function. Proc. Natl. Acad. Sci. USA 2007, 104, 11981–11986. [Google Scholar] [CrossRef] [PubMed]
- Venkitakrishnan, R.P.; Zaborowski, E.; McElheny, D.; Benkovic, S.J.; Dyson, H.J.; Wright, P.E. Conformational changes in the active site loops of dihydrofolate reductase during the catalytic cycle. Biochemistry 2004, 43, 16046–16055. [Google Scholar] [CrossRef] [PubMed]
- Boehr, D.D. Promiscuity in protein-RNA interactions: Conformational ensembles facilitate molecular recognition in the spliceosome. Bioessays 2012, 34, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Berlow, R.B.; Swain, M.; Dalal, S.; Sweasy, J.B.; Loria, J.P. Substrate-dependent millisecond domain motions in DNA polymerase β. J. Mol. Biol. 2012, 419, 171–182. [Google Scholar] [CrossRef] [PubMed]
- Kay, L.E. NMR studies of protein structure and dynamics. J. Magn. Reson. 2005, 173, 193–207. [Google Scholar] [CrossRef] [PubMed]
- Vallurupalli, P.; Hansen, D.F.; Kay, L.E. Structures of invisible, excited protein states by relaxation dispersion NMR spectroscopy. Proc. Natl. Acad. Sci. USA 2008, 105, 11766–11771. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, A.; Savol, A.; Burger, V.; Chennubhotla, C.S.; Agarwal, P.K. Protein conformational populations and functionally relevant substates. Acc. Chem. Res. 2014, 47, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Vanwart, A.T.; Eargle, J.; Luthey-Schulten, Z.; Amaro, R.E. Exploring residue component contributions to dynamical network models of allostery. J. Chem. Theory Comput. 2012, 8, 2949–2961. [Google Scholar] [CrossRef] [PubMed]
- Gagné, D.; Charest, L.A.; Morin, S.; Kovrigin, E.L.; Doucet, N. Conservation of flexible residue clusters among structural and functional enzyme homologues. J. Biol. Chem. 2012, 287, 44289–44300. [Google Scholar] [CrossRef] [PubMed]
- Eisenmesser, E.Z.; Millet, O.; Labeikovsky, W.; Korzhnev, D.M.; Wolf-Watz, M.; Bosco, D.A.; Skalicky, J.J.; Kay, L.E.; Kern, D. Intrinsic dynamics of an enzyme underlies catalysis. Nature 2005, 438, 117–121. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, P.K.; Geist, A.; Gorin, A. Protein dynamics and enzymatic catalysis: Investigating the peptidyl-prolyl cis-trans isomerization activity of cyclophilin A. Biochemistry 2004, 43, 10605–10618. [Google Scholar] [CrossRef] [PubMed]
- Goodey, N.M.; Benkovic, S.J. Allosteric regulation and catalysis emerge via a common route. Nat. Chem. Biol. 2008, 4, 474–482. [Google Scholar] [CrossRef] [PubMed]
- Suel, G.M.; Lockless, S.W.; Wall, M.A.; Ranganathan, R. Evolutionarily conserved networks of residues mediate allosteric communication in proteins. Nat. Struct. Biol. 2003, 10, 59–69. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, K.A.; McLaughlin, R.N.; Ranganathan, R. Hot spots for allosteric regulation on protein surfaces. Cell 2011, 147, 1564–1575. [Google Scholar] [CrossRef] [PubMed]
- Cole, R.; Loria, J.P. Evidence for flexibility in the function of ribonuclease A. Biochemistry 2002, 41, 6072–6081. [Google Scholar] [CrossRef] [PubMed]
- Gagné, D.; Doucet, N. Structural and functional importance of local and global conformational fluctuations in the RNase A superfamily. FEBS J. 2013, 280, 5596–5607. [Google Scholar] [CrossRef] [PubMed]
- Pareek, V.; Samanta, M.; Joshi, N.V.; Balaram, H.; Murthy, M.R.; Balaram, P. Connecting active site loop conformations and catalysis in triosephosphate isomerase: Insights from a rare variation at residue 96 in the plasmodial enzyme. Chembiochem 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Torbeev, V.Y.; Raghuraman, H.; Hamelberg, D.; Tonelli, M.; Westler, W.M.; Perozo, E.; Kent, S.B. Protein conformational dynamics in the mechanism of HIV-1 protease catalysis. Proc. Natl. Acad. Sci. USA 2011, 108, 20982–20987. [Google Scholar] [CrossRef] [PubMed]
- Kar, G.; Keskin, O.; Gursoy, A.; Nussinov, R. Allostery and population shift in drug discovery. Curr. Opin. Pharmacol. 2010, 10, 715–722. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, P.K. Enzymes: An integrated view of structure, dynamics and function. Microb. Cell Fact. 2006, 5, 2. [Google Scholar] [CrossRef] [PubMed]
- Kohen, A. Role of dynamics in enzyme catalysis: Substantial versus semantic controversies. Acc. Chem. Res. 2015, 48, 466–473. [Google Scholar] [CrossRef] [PubMed]
- Kamerlin, S.C.; Warshel, A. At the dawn of the 21st century: Is dynamics the missing link for understanding enzyme catalysis? Proteins 2010, 78, 1339–1375. [Google Scholar] [CrossRef] [PubMed]
- Nagel, Z.D.; Klinman, J.P. A 21st century revisionist's view at a turning point in enzymology. Nat. Chem. Biol. 2009, 5, 543–550. [Google Scholar] [CrossRef] [PubMed]
- Hanoian, P.; Liu, C.T.; Hammes-Schiffer, S.; Benkovic, S. Perspectives on electrostatics and conformational motions in enzyme catalysis. Acc. Chem. Res. 2015, 48, 482–489. [Google Scholar] [CrossRef] [PubMed]
- Grutsch, S.; Bruschweiler, S.; Tollinger, M. NMR methods to study dynamic allostery. PLoS Comput. Biol. 2016, 12, e1004620. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.G., 3rd. Chemical exchange in biomacromolecules: Past, present, and future. J. Magn. Reson. 2014, 241, 3–17. [Google Scholar] [CrossRef] [PubMed]
- Kleckner, I.R.; Foster, M.P. An introduction to NMR-based approaches for measuring protein dynamics. Biochim. Biophys. Acta 2011, 1814, 942–968. [Google Scholar] [CrossRef] [PubMed]
- Loria, J.P.; Rance, M.; Palmer, A.G., 3rd. A trosy cpmg sequence for characterizing chemical exchange in large proteins. J. Biomol. NMR 1999, 15, 151–155. [Google Scholar] [CrossRef] [PubMed]
- Loria, J.P.; Rance, M.; Palmer, A.G. A relaxation-compensated carr-purcell-meiboom-gill sequence for characterizing chemical exchange by NMR spectroscopy. J. Am. Chem. Soc. 1999, 121, 2331–2332. [Google Scholar] [CrossRef]
- Oyen, D.; Fenwick, R.B.; Stanfield, R.L.; Dyson, H.J.; Wright, P.E. Cofactor-mediated conformational dynamics promote product release from Escherichia Coli dihydrofolate reductase via an allosteric pathway. J. Am. Chem. Soc. 2015, 137, 9459–9468. [Google Scholar] [CrossRef] [PubMed]
- Bhabha, G.; Biel, J.T.; Fraser, J.S. Keep on moving: Discovering and perturbing the conformational dynamics of enzymes. Acc. Chem. Res. 2015, 48, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Doucet, N. Can enzyme engineering benefit from the modulation of protein motions? Lessons learned from NMR relaxation dispersion experiments. Protein Pept. Lett. 2011, 18, 336–343. [Google Scholar] [CrossRef] [PubMed]
- Palmer, A.G., 3rd. NMR probes of molecular dynamics: Overview and comparison with other techniques. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 129–155. [Google Scholar] [PubMed]
- Palmer, A.G., 3rd. NMR characterization of the dynamics of biomacromolecules. Chem. Rev. 2004, 104, 3623–3640. [Google Scholar] [CrossRef] [PubMed]
- Manley, G.; Loria, J.P. NMR insights into protein allostery. Arch. Biochem. Biophys. 2012, 519, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Luk, L.Y.; Loveridge, E.J.; Allemann, R.K. Protein motions and dynamic effects in enzyme catalysis. Phys. Chem. Chem. Phys. 2015, 17, 30817–30827. [Google Scholar] [CrossRef] [PubMed]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982, 104, 4546–4559. [Google Scholar] [CrossRef]
- Lipari, G.; Szabo, A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982, 104, 4559–4570. [Google Scholar] [CrossRef]
- Morin, S. A practical guide to protein dynamics from 15N spin relaxation in solution. Prog. Nucl. Magn. Reson. Spectrosc. 2011, 59, 245–262. [Google Scholar] [CrossRef] [PubMed]
- Fisette, O.; Lagüe, P.; Gagné, S.; Morin, S. Synergistic applications of MD and NMR for the study of biological systems. J. Biomed. Biotechnol. 2012, 2012, 254208. [Google Scholar] [CrossRef] [PubMed]
- Mandel, A.M.; Akke, M.; Palmer, A.G., 3rd. Backbone dynamics of Escherichia Coli Ribonuclease HI: Correlations with structure and function in an active enzyme. J. Mol. Biol. 1995, 246, 144–163. [Google Scholar] [CrossRef] [PubMed]
- Stephenson, J.D.; Kenyon, J.C.; Symmons, M.F.; Lever, A.M. Characterizing 3D RNA structure by single molecule FRET. Methods 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; de Vera, I.M.; Veloro, A.M.; Blackburn, M.E.; Kear, J.L.; Carter, J.D.; Rocca, J.R.; Simmerling, C.; Dunn, B.M.; Fanucci, G.E. Inhibitor-induced conformational shifts and ligand-exchange dynamics for HIV-1 protease measured by pulsed epr and NMR spectroscopy. J. Phys. Chem. B 2012, 116, 14235–14244. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Britto, M.D.; Kear-Scott, J.L.; Boone, C.D.; Rocca, J.R.; Simmerling, C.; McKenna, R.; Bieri, M.; Gooley, P.R.; Dunn, B.M.; et al. The role of select subtype polymorphisms on HIV-1 protease conformational sampling and dynamics. J. Biol. Chem. 2014, 289, 17203–17214. [Google Scholar] [CrossRef] [PubMed]
- Jeschke, G.; Polyhach, Y. Distance measurements on spin-labelled biomacromolecules by pulsed electron paramagnetic resonance. Phys. Chem. Chem. Phys. 2007, 9, 1895–1910. [Google Scholar] [CrossRef] [PubMed]
- Boehr, D.D.; McElheny, D.; Dyson, H.J.; Wright, P.E. Millisecond timescale fluctuations in dihydrofolate reductase are exquisitely sensitive to the bound ligands. Proc. Natl. Acad. Sci. USA 2010, 107, 1373–1378. [Google Scholar] [CrossRef] [PubMed]
- Boehr, D.D.; Liu, X.; Yang, X. Targeting structural dynamics of the RNA-dependent RNA polymerase for anti-viral strategies. Curr. Opin. Virol. 2014, 9, 194–200. [Google Scholar] [CrossRef] [PubMed]
- Voelz, V.A.; Bowman, G.R.; Beauchamp, K.; Pande, V.S. Molecular simulation of ab initio protein folding for a millisecond folder NTL9(1–39). J. Am. Chem. Soc. 2010, 132, 1526–1528. [Google Scholar] [CrossRef] [PubMed]
- Bowman, G.R.; Voelz, V.A.; Pande, V.S. Atomistic folding simulations of the five-helix bundle protein λ6–85. J. Am. Chem. Soc. 2011, 133, 664–667. [Google Scholar] [CrossRef] [PubMed]
- Voelz, V.A.; Jager, M.; Yao, S.; Chen, Y.; Zhu, L.; Waldauer, S.A.; Bowman, G.R.; Friedrichs, M.; Bakajin, O.; Lapidus, L.J.; et al. Slow unfolded-state structuring in Acyl-coA binding protein folding revealed by simulation and experiment. J. Am. Chem. Soc. 2012, 134, 12565–12577. [Google Scholar] [CrossRef] [PubMed]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y.; et al. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Bucher, D.; Grant, B.J.; Markwick, P.R.; McCammon, J.A. Accessing a hidden conformation of the maltose binding protein using accelerated molecular dynamics. PLoS Comput. Biol. 2011, 7, e1002034. [Google Scholar] [CrossRef] [PubMed]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef] [PubMed]
- Wojtas-Niziurski, W.; Meng, Y.; Roux, B.; Berneche, S. Self-learning adaptive umbrella sampling method for the determination of free energy landscapes in multiple dimensions. J. Chem. Theory Comput. 2013, 9, 1885–1895. [Google Scholar] [CrossRef] [PubMed]
- Da, L.T.; Wang, D.; Huang, X. Dynamics of pyrophosphate ion release and its coupled trigger loop motion from closed to open state in RNA polymerase II. J. Am. Chem. Soc. 2012, 134, 2399–2406. [Google Scholar] [CrossRef] [PubMed]
- Tagle, A.M. Percutaneous encoscopic gastrostomy. Rev. Gastroenterol. Peru 1998, 18, 56–61. [Google Scholar]
- Sutto, L.; Gervasio, F.L. Effects of oncogenic mutations on the conformational free-energy landscape of EGFR kinase. Proc. Natl. Acad. Sci. USA 2013, 110, 10616–10621. [Google Scholar] [CrossRef] [PubMed]
- Abrams, C.; Bussi, G. Enhanced sampling in molecular dynamics using metadynamics, replica-exchange, and temperature-acceleration. Entropy 2014, 16, 163–199. [Google Scholar] [CrossRef]
- Doshi, U.; Hamelberg, D. Towards fast, rigorous and efficient conformational sampling of biomolecules: Advances in accelerated molecular dynamics. Biochim. Biophys. Acta 2015, 1850, 878–888. [Google Scholar] [CrossRef] [PubMed]
- Doshi, U.; McGowan, L.C.; Ladani, S.T.; Hamelberg, D. Resolving the complex role of enzyme conformational dynamics in catalytic function. Proc. Natl. Acad. Sci. USA 2012, 109, 5699–5704. [Google Scholar] [CrossRef] [PubMed]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in monte carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Camilloni, C.; Schaal, D.; Schweimer, K.; Schwarzinger, S.; De Simone, A. Energy landscape of the prion protein helix 1 probed by metadynamics and NMR. Biophys. J. 2012, 102, 158–167. [Google Scholar] [CrossRef] [PubMed]
- Andersen, O.J.; Grouleff, J.; Needham, P.; Walker, R.C.; Jensen, F. Toward an enhanced sampling molecular dynamics method for studying ligand-induced conformational changes in proteins. J. Phys. Chem. B 2015, 119, 14594–14603. [Google Scholar] [CrossRef] [PubMed]
- Singhal, N.; Snow, C.D.; Pande, V.S. Using path sampling to build better markovian state models: Predicting the folding rate and mechanism of a tryptophan zipper β hairpin. J. Chem. Phys. 2004, 121, 415–425. [Google Scholar] [CrossRef] [PubMed]
- Bowman, G.R.; Beauchamp, K.A.; Boxer, G.; Pande, V.S. Progress and challenges in the automated construction of Markov state models for full protein systems. J. Chem. Phys. 2009, 131, 124101. [Google Scholar] [CrossRef] [PubMed]
- Noé, F.; Fischer, S. Transition networks for modeling the kinetics of conformational change in macromolecules. Curr. Opin. Struct. Biol. 2008, 18, 154–162. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, A.; Agarwal, P.K. Evolutionarily conserved linkage between enzyme fold, flexibility, and catalysis. PLoS Biol. 2011, 9, e1001193. [Google Scholar] [CrossRef] [PubMed]
- Shukla, D.; Hernandez, C.X.; Weber, J.K.; Pande, V.S. Markov state models provide insights into dynamic modulation of protein function. Acc. Chem. Res. 2015, 48, 414–422. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Noe, F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Morcos, F.; Chatterjee, S.; McClendon, C.L.; Brenner, P.R.; Lopez-Rendon, R.; Zintsmaster, J.; Ercsey-Ravasz, M.; Sweet, C.R.; Jacobson, M.P.; Peng, J.W.; et al. Modeling conformational ensembles of slow functional motions in Pin1-WW. PLoS Comput. Biol. 2010, 6, e1001015. [Google Scholar] [CrossRef] [PubMed]
- Ramanathan, A.; Savol, A.J.; Langmead, C.J.; Agarwal, P.K.; Chennubhotla, C.S. Discovering conformational sub-states relevant to protein function. PLoS ONE 2011, 6, e15827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gagné, D.; French, R.L.; Narayanan, C.; Simonovic, M.; Agarwal, P.K.; Doucet, N. Perturbation of the conformational eynamics of an active-site loop alters enzyme activity. Structure 2015, 23, 2256–2266. [Google Scholar] [CrossRef] [PubMed]
- Camilloni, C.; Robustelli, P.; De Simone, A.; Cavalli, A.; Vendruscolo, M. Characterization of the conformational equilibrium between the two major substates of RNase A using NMR chemical shifts. J. Am. Chem. Soc. 2012, 134, 3968–3971. [Google Scholar] [CrossRef] [PubMed]
- De Simone, A.; Montalvao, R.W.; Dobson, C.M.; Vendruscolo, M. Characterization of the interdomain motions in hen lysozyme using residual dipolar couplings as replica-averaged structural restraints in molecular dynamics simulations. Biochemistry 2013, 52, 6480–6486. [Google Scholar] [CrossRef] [PubMed]
- Camilloni, C.; Cavalli, A.; Vendruscolo, M. Assessment of the use of NMR chemical shifts as replica-averaged structural restraints in molecular dynamics simulations to characterize the dynamics of proteins. J. Phys. Chem. B 2013, 117, 1838–1843. [Google Scholar] [CrossRef] [PubMed]
- Sundquist, W.I.; Krausslich, H.G. HIV-1 assembly, budding, and maturation. Cold Spring Harb. Perspect. Med. 2012, 2, a006924. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.K.; Osswald, H.L.; Prato, G. Recent progress in the development of HIV-1 protease inhibitors for the treatment of HIV/AIDS. J. Med. Chem. 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Spinelli, S.; Liu, Q.Z.; Alzari, P.M.; Hirel, P.H.; Poljak, R.J. The three-dimensional structure of the aspartyl protease from the HIV-1 isolate BRU. Biochimie 1991, 73, 1391–1396. [Google Scholar] [CrossRef]
- Pastor, N.; Amero, C. Information flow and protein dynamics: The interplay between nuclear magnetic resonance spectroscopy and molecular dynamics simulations. Front. Plant Sci. 2015, 6, 306. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, L.K.; Yamazaki, T.; Torchia, D.A.; Grzesiek, S.; Bax, A.; Stahl, S.J.; Kaufman, J.D.; Wingfield, P.T.; Lam, P.Y.; Jadhav, P.K.; et al. Flexibility and function in HIV-1 protease. Nat. Struct. Biol. 1995, 2, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Ishima, R.; Louis, J.M. A diverse view of protein dynamics from NMR studies of HIV-1 protease flaps. Proteins 2008, 70, 1408–1415. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Deng, N.J.; Levy, R.M. NMR relaxation in proteins with fast internal motions and slow conformational exchange: Model-free framework and Markov state simulations. J. Phys. Chem. B 2013, 117, 6625–6634. [Google Scholar] [CrossRef] [PubMed]
- Ishima, R.; Torchia, D.A.; Lynch, S.M.; Gronenborn, A.M.; Louis, J.M. Solution structure of the mature HIV-1 protease monomer: Insight into the tertiary fold and stability of a precursor. J. Biol. Chem. 2003, 278, 43311–43319. [Google Scholar] [CrossRef] [PubMed]
- Deng, N.J.; Zheng, W.; Gallicchio, E.; Levy, R.M. Insights into the dynamics of HIV-1 protease: A kinetic network model constructed from atomistic simulations. J. Am. Chem. Soc. 2011, 133, 9387–9394. [Google Scholar] [CrossRef] [PubMed]
- Shukla, D.; Meng, Y.; Roux, B.; Pande, V.S. Activation pathway of SRC kinase reveals intermediate states as targets for drug design. Nat. Commun. 2014, 5, 3397. [Google Scholar] [CrossRef] [PubMed]
- Roche, J.; Louis, J.M.; Bax, A. Conformation of inhibitor-free HIV-1 protease derived from nmr spectroscopy in a weakly oriented solution. Chembiochem 2015, 16, 214–218. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, T.; Hinck, A.P.; Wang, Y.X.; Nicholson, L.K.; Torchia, D.A.; Wingfield, P.; Stahl, S.J.; Kaufman, J.D.; Chang, C.H.; Domaille, P.J.; et al. Three-dimensional solution structure of the HIV-1 protease complexed with DMP323, a novel cyclic urea-type inhibitor, determined by nuclear magnetic resonance spectroscopy. Protein Sci. 1996, 5, 495–506. [Google Scholar] [CrossRef] [PubMed]
- Leonis, G.; Steinbrecher, T.; Papadopoulos, M.G. A contribution to the drug resistance mechanism of darunavir, amprenavir, indinavir, and saquinavir complexes with HIV-1 protease due to flap mutation I50V: A systematic MM-PBSA and thermodynamic integration study. J. Chem. Inf. Model. 2013, 53, 2141–2153. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Jamal, S.; Goyal, S.; Jain, R.; Wahi, D.; Grover, A. Structural studies on molecular mechanisms of nelfinavir resistance caused by non-active site mutation V77I in HIV-1 protease. BMC Bioinform. 2015, 16, S10. [Google Scholar] [CrossRef] [PubMed]
- Mittal, S.; Cai, Y.; Nalam, M.N.; Bolon, D.N.; Schiffer, C.A. Hydrophobic core flexibility modulates enzyme activity in HIV-1 protease. J. Am. Chem. Soc. 2012, 134, 4163–4168. [Google Scholar] [CrossRef] [PubMed]
- Goldfarb, N.E.; Ohanessian, M.; Biswas, S.; McGee, T.D., Jr.; Mahon, B.P.; Ostrov, D.A.; Garcia, J.; Tang, Y.; McKenna, R.; Roitberg, A.; et al. Defective hydrophobic sliding mechanism and active site expansion in HIV-1 protease drug resistant variant Gly48Thr/Leu89Met: Mechanisms for the loss of saquinavir binding potency. Biochemistry 2015, 54, 422–433. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Goodey, N.M. Catalytic contributions from remote regions of enzyme structure. Chem. Rev. 2011, 111, 7595–7624. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.D.; Schiffer, C.A.; Gonzales, M.J.; Taylor, J.; Kantor, R.; Chou, S.; Israelski, D.; Zolopa, A.R.; Fessel, W.J.; Shafer, R.W. Mutation patterns and structural correlates in human immunodeficiency virus type 1 protease following different protease inhibitor treatments. J. Virol. 2003, 77, 4836–4847. [Google Scholar] [CrossRef] [PubMed]
- Ragland, D.A.; Nalivaika, E.A.; Nalam, M.N.; Prachanronarong, K.L.; Cao, H.; Bandaranayake, R.M.; Cai, Y.; Kurt-Yilmaz, N.; Schiffer, C.A. Drug resistance conferred by mutations outside the active site through alterations in the dynamic and structural ensemble of HIV-1 protease. J. Am. Chem. Soc. 2014, 136, 11956–11963. [Google Scholar] [CrossRef] [PubMed]
- Tzoupis, H.; Leonis, G.; Avramopoulos, A.; Mavromoustakos, T.; Papadopoulos, M.G. Systematic molecular dynamics, MM-PBSA, and ab initio approaches to the saquinavir resistance mechanism in HIV-1 PR due to 11 double and multiple mutations. J. Phys. Chem. B 2014, 118, 9538–9552. [Google Scholar] [CrossRef] [PubMed]
- Carter, J.D.; Gonzales, E.G.; Huang, X.; Smith, A.N.; de Vera, I.M.; D'Amore, P.W.; Rocca, J.R.; Goodenow, M.M.; Dunn, B.M.; Fanucci, G.E. Effects of pre and post therapy drug-pressure selected mutations on HIV-1 protease conformational sampling. FEBS Lett. 2014, 588, 3123–3128. [Google Scholar] [CrossRef] [PubMed]
- Kunze, J.; Todoroff, N.; Schneider, P.; Rodrigues, T.; Geppert, T.; Reisen, F.; Schreuder, H.; Saas, J.; Hessler, G.; Baringhaus, K.H.; et al. Targeting dynamic pockets of HIV-1 protease by structure-based computational screening for allosteric inhibitors. J. Chem. Inf. Model. 2014, 54, 987–991. [Google Scholar] [CrossRef] [PubMed]
- Ung, P.M.; Dunbar, J.B., Jr.; Gestwicki, J.E.; Carlson, H.A. An allosteric modulator of HIV-1 protease shows equipotent inhibition of wild-type and drug-resistant proteases. J. Med. Chem. 2014, 57, 6468–6478. [Google Scholar] [CrossRef] [PubMed]
- Beard, W.A.; Wilson, S.H. Structure and mechanism of DNA polymerase β. Chem. Rev. 2006, 106, 361–382. [Google Scholar] [CrossRef] [PubMed]
- Barnes, D.E.; Lindahl, T. Repair and genetic consequences of endogenous DNA base damage in mammalian cells. Annu. Rev. Genet. 2004, 38, 445–476. [Google Scholar] [CrossRef] [PubMed]
- Starcevic, D.; Dalal, S.; Sweasy, J.B. Is there a link between DNA polymerase β and cancer? Cell Cycle 2004, 3, 998–1001. [Google Scholar] [CrossRef] [PubMed]
- Loeb, L.A.; Monnat, R.J., Jr. DNA polymerases and human disease. Nat. Rev. Genet. 2008, 9, 594–604. [Google Scholar] [CrossRef] [PubMed]
- Beard, W.A.; Shock, D.D.; Yang, X.P.; DeLauder, S.F.; Wilson, S.H. Loss of DNA polymerase β stacking interactions with templating purines, but not pyrimidines, alters catalytic efficiency and fidelity. J. Biol. Chem. 2002, 277, 8235–8242. [Google Scholar] [CrossRef] [PubMed]
- Towle-Weicksel, J.B.; Dalal, S.; Sohl, C.D.; Doublie, S.; Anderson, K.S.; Sweasy, J.B. Fluorescence resonance energy transfer studies of DNA polymerase β: The critical role of fingers domain movements and a novel non-covalent step during nucleotide selection. J. Biol. Chem. 2014, 289, 16541–16550. [Google Scholar] [CrossRef] [PubMed]
- Moscato, B.; Swain, M.; Loria, J.P. Induced fit in the selection of correct versus incorrect nucleotides by DNA polymerase β. Biochemistry 2016, 55, 382–395. [Google Scholar] [CrossRef] [PubMed]
- Sawaya, M.R.; Pelletier, H.; Kumar, A.; Wilson, S.H.; Kraut, J. Crystal structure of rat DNA polymerase β: Evidence for a common polymerase mechanism. Science 1994, 264, 1930–1935. [Google Scholar] [CrossRef] [PubMed]
- Sawaya, M.R.; Prasad, R.; Wilson, S.H.; Kraut, J.; Pelletier, H. Crystal structures of human DNA polymerase β complexed with gapped and nicked DNA: Evidence for an induced fit mechanism. Biochemistry 1997, 36, 11205–11215. [Google Scholar] [CrossRef] [PubMed]
- Batra, V.K.; Beard, W.A.; Shock, D.D.; Krahn, J.M.; Pedersen, L.C.; Wilson, S.H. Magnesium-induced assembly of a complete DNA polymerase catalytic complex. Structure 2006, 14, 757–766. [Google Scholar] [CrossRef] [PubMed]
- Batra, V.K.; Beard, W.A.; Shock, D.D.; Pedersen, L.C.; Wilson, S.H. Structures of DNA polymerase β with active-site mismatches suggest a transient abasic site intermediate during misincorporation. Mol. Cell. 2008, 30, 315–324. [Google Scholar] [CrossRef] [PubMed]
- Freudenthal, B.D.; Beard, W.A.; Wilson, S.H. Structures of dNTP intermediate states during DNA polymerase active site assembly. Structure 2012, 20, 1829–1837. [Google Scholar] [CrossRef] [PubMed]
- Freudenthal, B.D.; Beard, W.A.; Shock, D.D.; Wilson, S.H. Observing a DNA polymerase choose right from wrong. Cell 2013, 154, 157–168. [Google Scholar] [CrossRef] [PubMed]
- Donigan, K.A.; Sun, K.W.; Nemec, A.A.; Murphy, D.L.; Cong, X.; Northrup, V.; Zelterman, D.; Sweasy, J.B. Human POLB gene is mutated in high percentage of colorectal tumors. J. Biol. Chem. 2012, 287, 23830–23839. [Google Scholar] [CrossRef] [PubMed]
- Beard, W.A.; Shock, D.D.; Batra, V.K.; Prasad, R.; Wilson, S.H. Substrate-induced DNA polymerase β activation. J. Biol. Chem. 2014, 289, 31411–31422. [Google Scholar] [CrossRef] [PubMed]
- Bakhtina, M.; Lee, S.; Wang, Y.; Dunlap, C.; Lamarche, B.; Tsai, M.D. Use of viscogens, dNTPαS, and rhodium(III) as probes in stopped-flow experiments to obtain new evidence for the mechanism of catalysis by DNA polymerase β. Biochemistry 2005, 44, 5177–5187. [Google Scholar] [CrossRef] [PubMed]
- Arora, K.; Beard, W.A.; Wilson, S.H.; Schlick, T. Mismatch-induced conformational distortions in polymerase β support an induced-fit mechanism for fidelity. Biochemistry 2005, 44, 13328–13341. [Google Scholar] [CrossRef] [PubMed]
- Kirmizialtin, S.; Nguyen, V.; Johnson, K.A.; Elber, R. How conformational dynamics of DNA polymerase select correct substrates: Experiments and simulations. Structure 2012, 20, 618–627. [Google Scholar] [CrossRef] [PubMed]
- Zhong, X.; Patel, S.S.; Werneburg, B.G.; Tsai, M.D. DNA polymerase β: Multiple conformational changes in the mechanism of catalysis. Biochemistry 1997, 36, 11891–11900. [Google Scholar] [CrossRef] [PubMed]
- Balbo, P.B.; Wang, E.C.; Tsai, M.D. Kinetic mechanism of active site assembly and chemical catalysis of DNA polymerase β. Biochemistry 2011, 50, 9865–9875. [Google Scholar] [CrossRef] [PubMed]
- Williamson, M.P. Using chemical shift perturbation to characterise ligand binding. Prog. Nucl. Magn. 2013, 73, 1–16. [Google Scholar] [CrossRef] [PubMed]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narayanan, C.; Bernard, D.N.; Doucet, N. Role of Conformational Motions in Enzyme Function: Selected Methodologies and Case Studies. Catalysts 2016, 6, 81. https://doi.org/10.3390/catal6060081
Narayanan C, Bernard DN, Doucet N. Role of Conformational Motions in Enzyme Function: Selected Methodologies and Case Studies. Catalysts. 2016; 6(6):81. https://doi.org/10.3390/catal6060081
Chicago/Turabian StyleNarayanan, Chitra, David N. Bernard, and Nicolas Doucet. 2016. "Role of Conformational Motions in Enzyme Function: Selected Methodologies and Case Studies" Catalysts 6, no. 6: 81. https://doi.org/10.3390/catal6060081
APA StyleNarayanan, C., Bernard, D. N., & Doucet, N. (2016). Role of Conformational Motions in Enzyme Function: Selected Methodologies and Case Studies. Catalysts, 6(6), 81. https://doi.org/10.3390/catal6060081