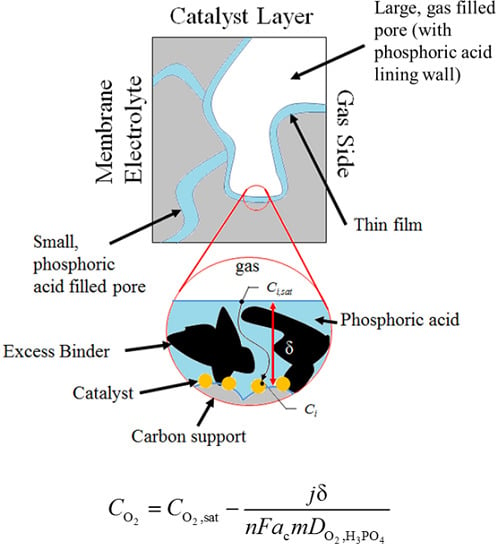
Application of a Coated Film Catalyst Layer Model to a High Temperature Polymer Electrolyte Membrane Fuel Cell with Low Catalyst Loading Produced by Reactive Spray Deposition Technology
Abstract
:1. Introduction
2. Results and Discussion
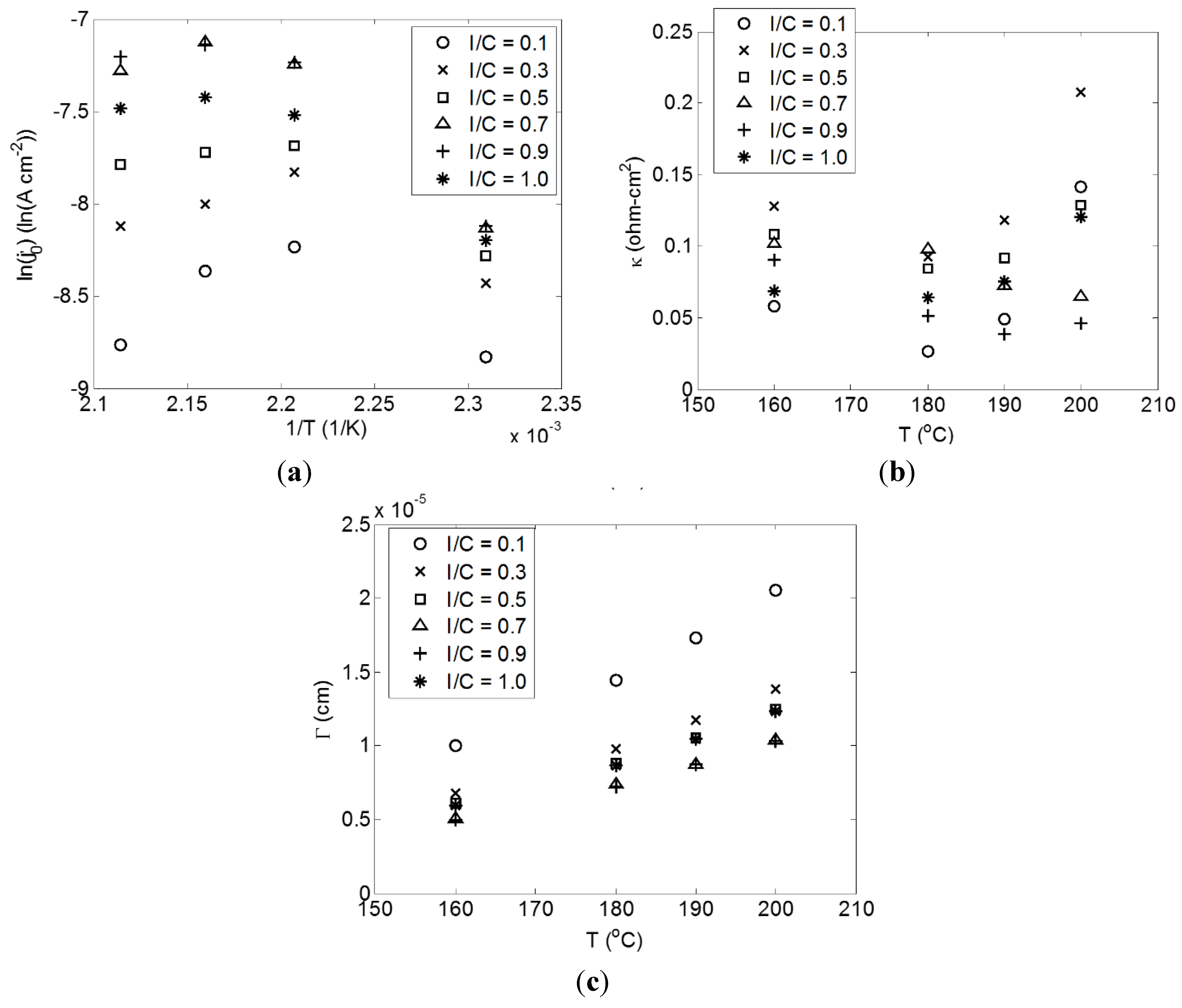
2.1. Correlation of Model and Experimental Data
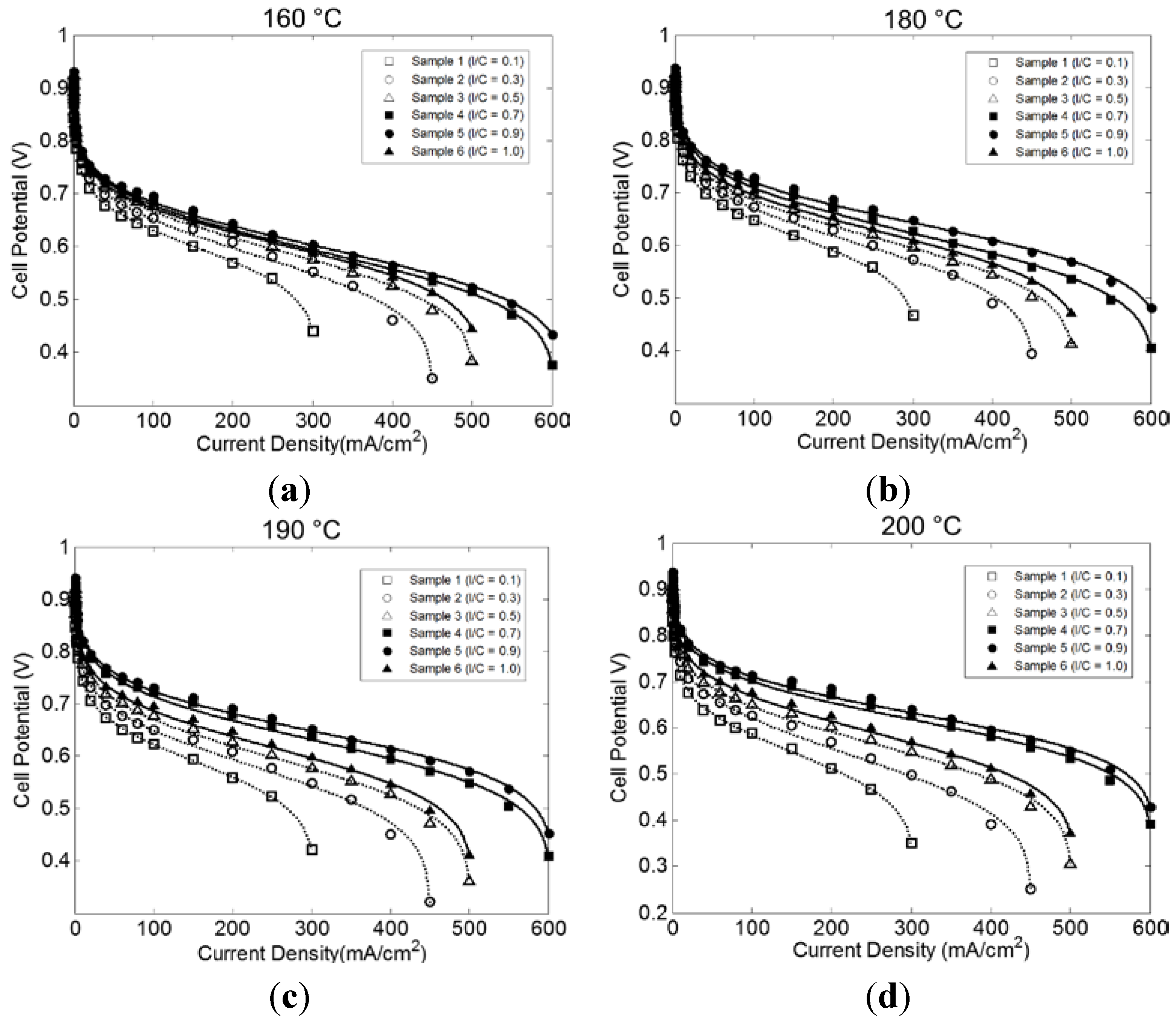

2.2. Effect of I/C Ratio
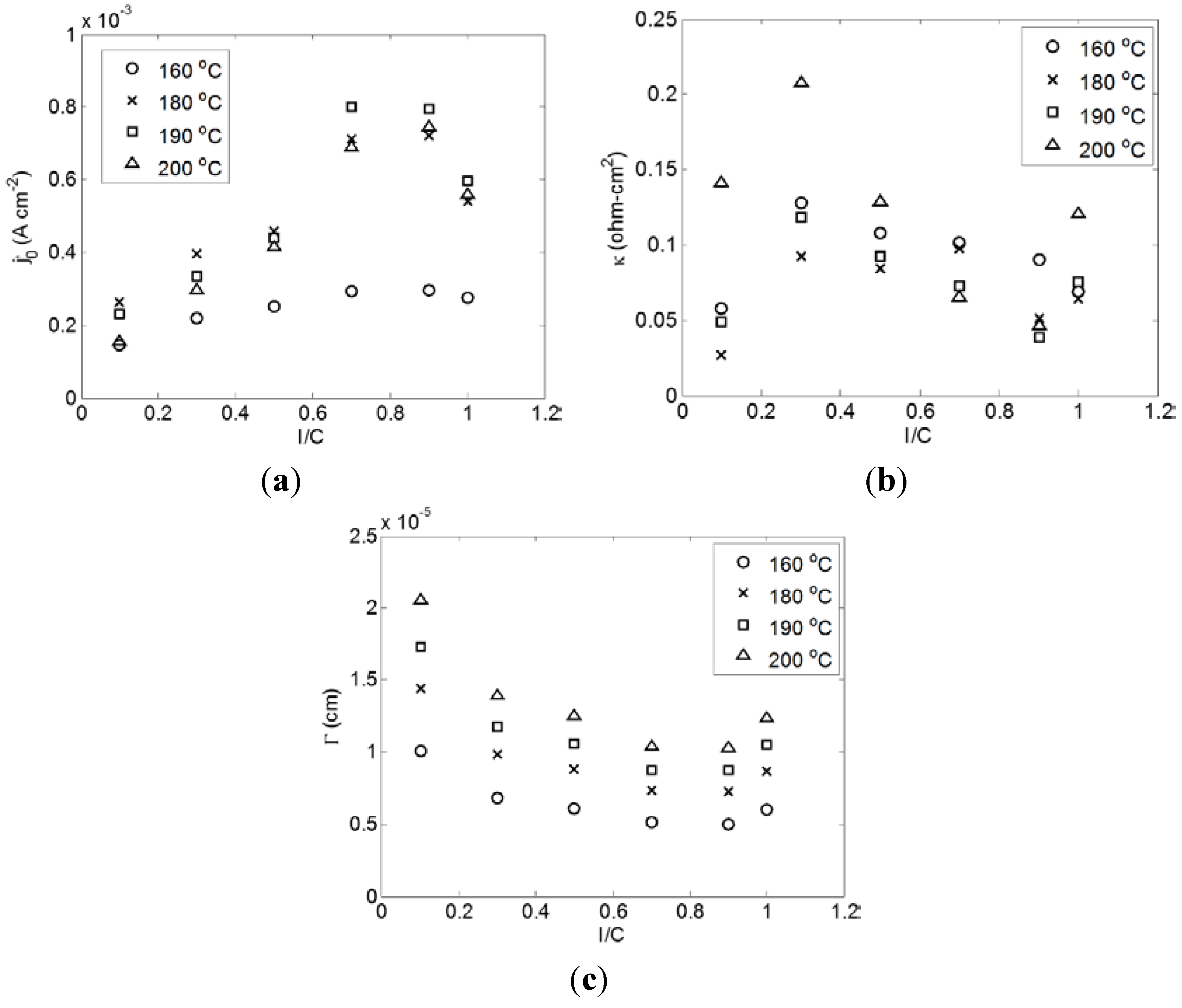
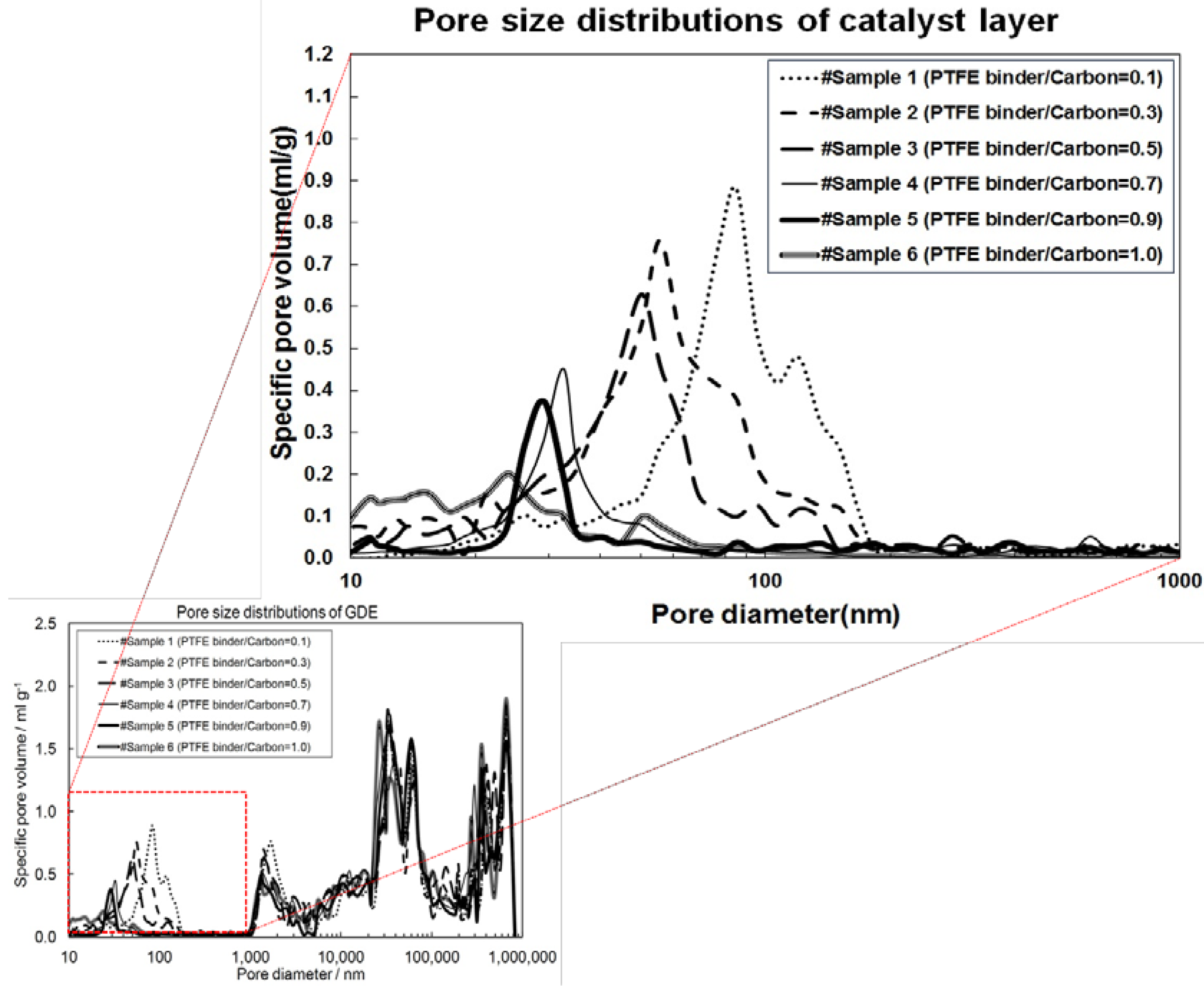
2.3. Effect of Temperature
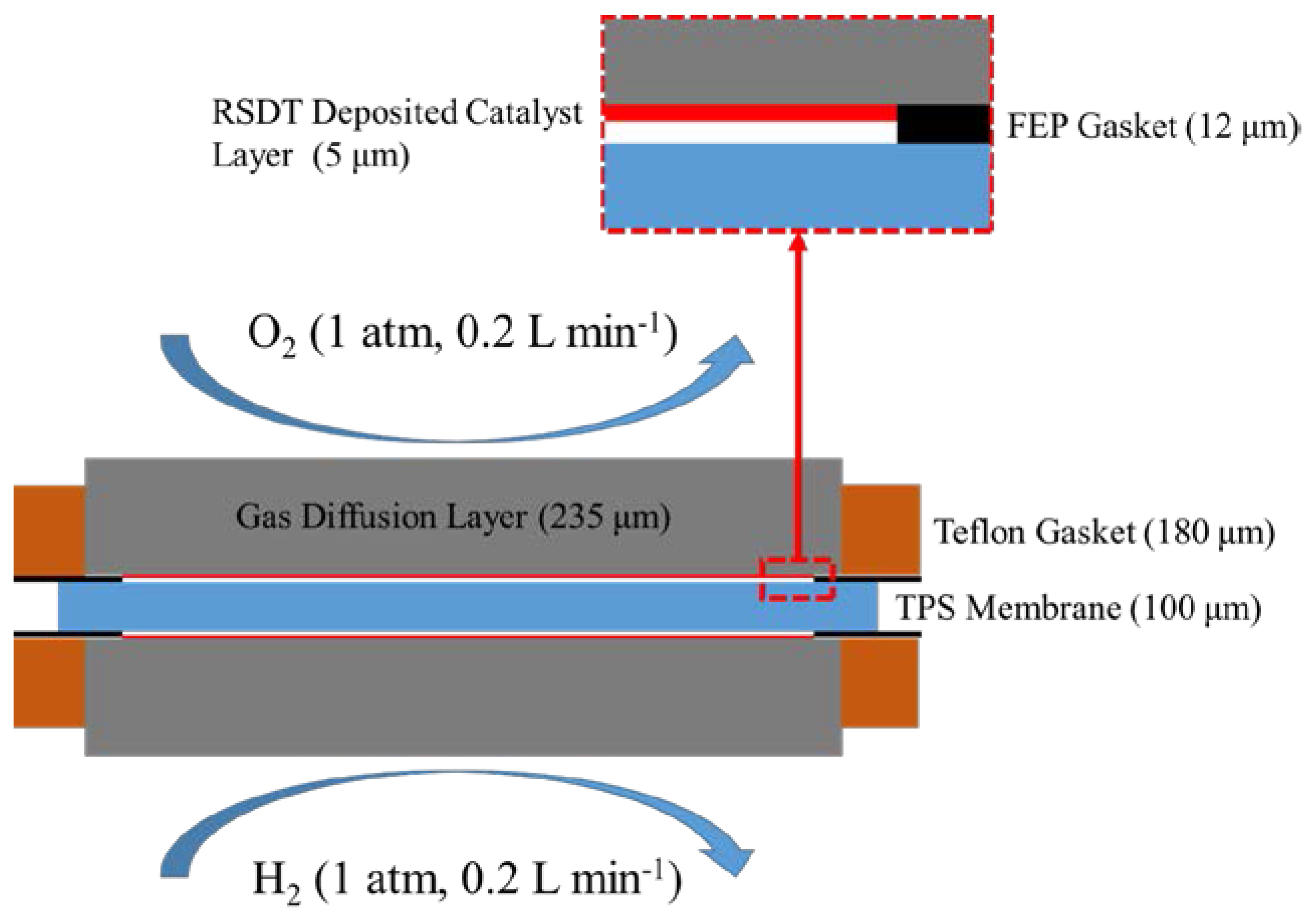
3. Methods
3.1. Experimental Section
3.2. Performance Model
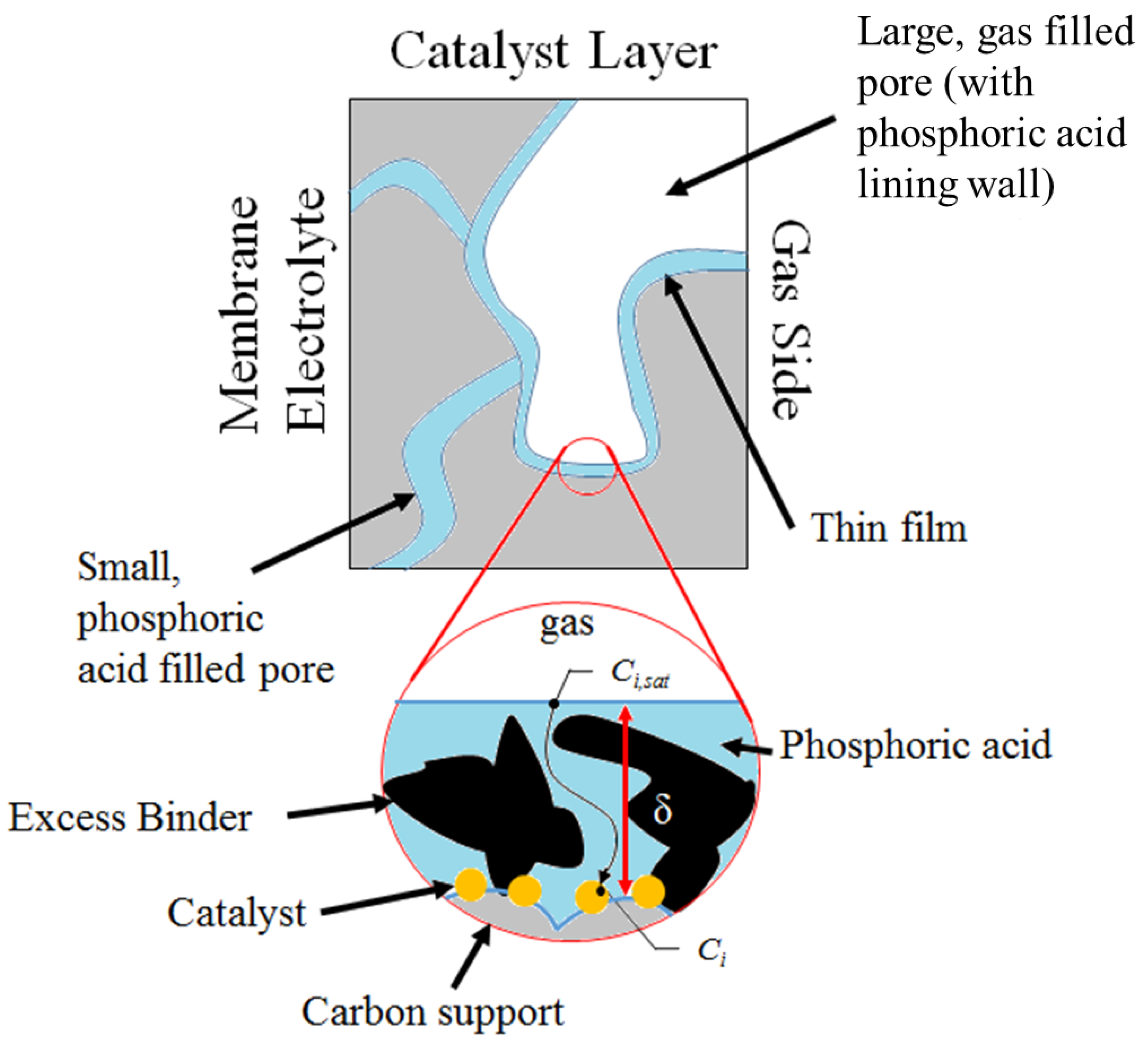
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Catalyst surface roughness factor (catalyst surface area/electrode geometric area) | |
| Molar concentration of species i at the catalyst surface (mol·cm−3) | |
| Saturation concentration of species i (mol·cm−3) | |
| Diffusivity of species i in phosphoric acid (cm2·s−1) | |
| Activation energy (kJ·mol−1) | |
| Cell potential (V) | |
| Open circuit potential (V) | |
| Faraday’s constant (C·mol−1) | |
| Current density (A·cm−2) | |
| Exchange current density (A·cm−2) | |
| Reference exchange current density (A·cm−2) | |
| Parameter defined by Equation (3) (A·cm−2) | |
| Thickness of catalyst layer (cm) | |
| Thickness of membrane electrolyte (cm) | |
| Diffusivity correction factor | |
| Number of transfer electrons | |
| Ideal gas constant (kJ·mol−1·K−1) | |
| Contact resistance (Ω·cm2) | |
| Operating temperature (K) | |
| Reference temperature (K) | |
| Greek | |
| Transfer coefficient | |
| Pressure coefficient | |
| Parameter defined by Equation (6) (cm) | |
| Film thickness (cm) | |
| Cell potential drop (V) | |
| Change in Nernst potential (V) | |
| Anode activation overpotential (V) | |
| Cathode activation overpotential (V) | |
| Parameter defined by Equation (4) (Ω·cm2) | |
| Conductivity of the catalyst layer (S·cm−1) | |
| Conductivity of the membrane electrolyte (S·cm−1) | |
References
- Asensio, J.A.; Sanchez, E.M.; Gomez-Romero, P. Proton-conducting Membranes Based on Benzimidazole Polymers for High-temperature PEM Fuel Cells. A Chemical Quest. Chem. Soc. Rev. 2010, 39, 3210–3239. [Google Scholar] [CrossRef] [PubMed]
- Chandan, A.; Hattenberger, M.; El-kharouf, A.; Du, S.; Dhir, A.; Self, V.; Pollet, B.G.; Ingram, A.; Bujalski, W. High Temperature (HT) Polymer Electrolyte Membrane Fuel Cells (PEMFC)—A Review. J. Power Sources 2013, 231, 264–278. [Google Scholar] [CrossRef]
- Costamagna, P.; Yang, C.; Bocarsly, A.B.; Srinivasan, S. Nafion® 115/Zirconium Phosphate Composite Membranes for Operation of PEMFCs above 100 °C. Electrochim. Acta 2002, 47, 1023–1033. [Google Scholar] [CrossRef]
- Reichman, S.; Ulus, A.; Peled, E. PTFE-Based Solid Polymer Electrolyte Membrane for High-Temperature Fuel Cell Applications. J. Electrochem. Soc. 2007, 154, B327–B333. [Google Scholar] [CrossRef]
- Rikukawa, M.; Sanui, K. Proton-Conducting Polymer Electrolyte Membranes Based on Hydrocarbon Polymers. Prog. Polym. Sci. 2000, 25, 1463–1502. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Z.; Zhang, J.; Tang, Y.; Song, C.; Navessin, T.; Shi, Z.; Song, D.; Wang, H.; Wilkinson, D.P.; et al. High Temperature PEM Fuel Cells. J. Power Sources 2006, 160, 872–891. [Google Scholar] [CrossRef]
- Ahluwalia, R.K.; Doss, E.D.; Kumar, R. Performance of High Temperature Polymer Electrolyte Fuel Cell Systems. J. Power Sources 2003, 117, 45–60. [Google Scholar] [CrossRef]
- Parthasarathy, A.; Srinivasan, A.; Appleby, A.J.; Martin, C.R. Temperature Dependence of the Electrode Kinetics of Oxygen Reduction at the Platinum/Nafion® Interface—A Microelectrode Investigation. J. Electrochem. Soc. 1992, 139, 2530–2537. [Google Scholar] [CrossRef]
- Pan, C.; He, R.; Li, Q.; Jensen, J.O.; Bjerrum, N.J.; Hjulmand, H.A.; Jensen, A.B. Integration of High Temperature PEM Fuel Cells with a Methanol Reformer. J. Power Sources 2005, 145, 392–398. [Google Scholar] [CrossRef]
- Li, Q.; He, R.; Gao, J.-A.; Jensen, J.O.; Bjerrum, N.J. The CO Poisoning Effect in PEMFCs Operational at Temperatures up to 200 °C. J. Electrochem. Soc. 2003, 150, A1599–A1605. [Google Scholar] [CrossRef]
- Li, Q.; He, R.; Jensen, J.O.; Bjerrum, N.J. PBI-Based Polymer Membranes for High Temperature Fuel Cells—Preparation, Characterization and Fuel Cell Demonstration. Fuel Cells 2004, 4, 147–159. [Google Scholar] [CrossRef]
- Li, Q.; Hjuler, H.A.; Bjerrum, N.J. Phosphoric Acid Doped Polybenzimidazole Membranes: Physiochemical Characterization and Fuel Cell Applications. J. Appl. Electrochem. 2001, 31, 773–779. [Google Scholar] [CrossRef]
- Hasiotis, C.; Li, Q.; Deimede, V.; Kallistis, J.K.; Kontoyannis, C.G.; Bjerrum, N.J. Development and Characterization of Acid-Doped Polybenzimidazole/Sulfonated Polysulfone Blend Polymer Electrolytes for Fuel Cells. J. Electrochem. Soc. 2001, 148, A513–A519. [Google Scholar] [CrossRef]
- Kim, H.-J.; An, S.J.; Kim, J.-Y.; Moon, J.K.; Cho, S.Y.; Eun, Y.C.; Yoon, H.-K.; Park, Y.; Kweon, H.-J.; Shin, E.-M. Polybenzimidazoles for High Temperature Fuel Cell Applications. Macromol. Rapid Commun. 2004, 25, 1410–1413. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Wainright, J.S.; Litt, M.H.; Savinell, R.F. Study of the Oxygen Reduction Reaction (ORR) at Pt Interfaced with Phosphoric Acid Doped Polybenzimidazole at Elevated Temperature and Low Relative Humidity. Electrochim. Acta 2006, 51, 3914–3923. [Google Scholar] [CrossRef]
- Lobato, J.; Cañizares, P.; Rodrigo, M.A.; Linares, J.J. Study of Different Bimetallic Anodic Catalysts Supported on Carbon for a High Temperature Polybenzimidazole-Based Direct Ethanol Fuel Cell. Appl. Catal. B 2009, 91, 269–274. [Google Scholar] [CrossRef]
- Savadogo, O.; Varela, F.J.R. Low-Temperature Direct Propane Polymer Electrolyte Membranes Fuel Cell (DPFC). J. New Mater. Electrochem. Syst. 2001, 4, 93–97. [Google Scholar]
- Wainright, J.S.; Wang, J.-T.; Weng, D.; Savinell, R.F.; Litt, M. Acid Doped Polybenzimidazoles, A New Polymer Electrolyte. J. Electrochem. Soc. 1995, 142, L121–L123. [Google Scholar] [CrossRef]
- Wang, J.T.; Lin, W.F.; Weber, M.; Wasmus, S.; Savinell, R.F. Trimethoxymethane as an Alternative Fuel for a Direct Oxidation PBI Polymer Electrolyte Fuel Cell. Electrochim. Acta 1998, 43, 3821–3828. [Google Scholar] [CrossRef]
- Wang, J.T.; Savinell, R.F.; Wainright, J.S.; Litt, M.; Yu, H. A H2/O2 Fuel Cell using Acid Doped Polybenzimidazoles as a Polymer Electrolyte. Electrochim. Acta 1996, 41, 193–197. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H.; Zhai, Y.; Liu, G.; Hu, J.; Yi, B. Performance Degradation studies on PBI/H3PO4 High Temperature PEMFC and One-dimensional numerical analysis. Electrochim. Acta 2006, 52, 394–401. [Google Scholar] [CrossRef]
- Liao, J.H.; Li, Q.F.; Rudbeck, H.C.; Jensen, J.O.; Chromik, A.; Bjerrum, N.J.; Kerres, J.; Xing, W. Oxidative Degradation of Polybenzimidazole Membranes as Electrolytes for High Temperature Proton Exchange Membrane Fuel Cells. Fuel Cells 2011, 11, 745–755. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, H.; Hu, J.; Zhai, Y.; Xu, D.; Shao, Z.G. Studies of Performance Degradation of a High Temperature PEMFC Based on H3PO4-doped PBI. J. Power Sources 2006, 162, 547–552. [Google Scholar] [CrossRef]
- Modestov, A.D.; Tarasevich, M.R.; Filimonov, V.Y.; Zagudaeva, N.M. Degradation of High Temperature MEA with PBI-H3PO4 Membrane in a Life Test. Electrochim. Acta 2009, 54, 7121–7127. [Google Scholar] [CrossRef]
- Ubeda, D.; Canizares, P.; Rodrigo, M.A.; Pinar, F.J.; Lobato, J. Durability Study of HTPEMFC Through Current Distribution Measurements and the Application of a Model. Int. J. Hydrogen Energy 2014, 39, 21678–21687. [Google Scholar] [CrossRef]
- Mench, M.M. Other Fuel Cells. In Fuel Cell Engines; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2008; p. 410. [Google Scholar]
- Yu, H.; Roller, J.; Kim, S.; Wang, Y.; Kwak, D.; Maric, R. One-Step Deposition of Catalyst Layers for High Temperature Proton Exchange Membrane Fuel Cells (PEMFC). J. Electrochem. Soc. 2014, 161, F622–F627. [Google Scholar] [CrossRef]
- Kim, S.; Myles, T.D.; Kunz, H.R.; Kwak, D.; Wang, Y.; Maric, R. The Effect of Binder Content on the Performance of a High Temperature Polymer Electrolyte Membrane Fuel Cell Produced with Reactive Spray Deposition Technology. Electrochim. Acta 2015, 177, 190–200. [Google Scholar] [CrossRef]
- Dale, M.K.; Geomezi, M.; Vogli, E.; Voyiatzis, G.A.; Neophytides, S.G. The Interaction of H3PO4 and Steam with PBI and TPS Polymeric Membranes. A TGA and Raman Study. J. Mater. Chem. A 2014, 2, 1117–1127. [Google Scholar]
- Berning, T.; Lu, D.M.; Djilali, N. Three-Dimensional Computational Analysis of Transport Phenomena in a PEM Fuel Cell. J. Power Sources 2002, 106, 284–294. [Google Scholar] [CrossRef]
- Harvey, D.; Pharoah, J.G.; Karen, K. A Comparison of Different Approaches to Modelling the PEMFC Catalyst Layer. J. Power Sources 2008, 179, 209–219. [Google Scholar] [CrossRef]
- Sousa, T.; Mamlouk, M.; Scott, K. An Isothermal Model of a Laboratory Intermediate Temperature Fuel Cell Using PBI Doped Phosphoric Acid Membranes. Chem. Eng. Sci. 2010, 65, 2513–2530. [Google Scholar] [CrossRef]
- Bernardi, D.M.; Verbrugge, M.W. Mathematical Model of a Gas Diffusion Electrode Bonded to a Polymer Electrolyte. AIChE J. 1991, 37, 1151–1163. [Google Scholar] [CrossRef]
- Marr, C.; Li, X. Composition and Performance Modelling of Catalyst Layer in a Proton Exchange Membrane Fuel Cell. J. Power Sources 1999, 77, 17–27. [Google Scholar] [CrossRef]
- Song, D.; Wang, Q.; Liu, Z.; Navessin, T.; Eikerling, M.; Holdcraft, S. Numerical Optimization Study of the Catalyst Layer of PEM Fuel Cell Cathode. J. Power Sources 2004, 126, 104–111. [Google Scholar] [CrossRef]
- Eikerling, M.; Kornyshev, A.A. Modelling the Performance of the Cathode Catalyst Layer of Polymer Electrolyte Fuel Cells. J. Electroanal. Chem. 1998, 453, 89–106. [Google Scholar] [CrossRef]
- Bevers, D.; Wohr, M.; Yasuda, K.; Oguro, K. Simulation of Polymer Electrolyte Fuel Cell Electrode. J. Appl. Electrochem. 1997, 27, 1254–1264. [Google Scholar]
- Kulikovsky, A.A.; Divisek, J.; Kornyshev, A.A. Modeling Cathode Compartment of Polymer Electrolyte Fuel Cells: Dead and Active Reaction Zones. J. Electrochem. Soc. 1999, 146, 3981–3991. [Google Scholar] [CrossRef]
- You, L.; Liu, H. A Parametric Study of the Cathode Catalyst Layer of PEM Fuel Cells using a Pseudo-homogeneous Model. Int. J. Hydrogen Energy 2001, 26, 991–999. [Google Scholar] [CrossRef]
- Li, Q.; Xiao, G.; Hjuler, H.A.; Berg, R.W.; Bjerrum, N.J. Limiting Current of Oxygen Reduction on Gas-Diffusion Electrodes for Phosphoric Acid Fuel Cells. J. Electrochem. Soc. 1994, 141, 3114–3119. [Google Scholar]
- Scott, K.; Mamlouk, M. A Cell Voltage Equation for an Intermediate Temperature Proton Exchange Membrane Fuel Cell. Int. J. Hydrogen Energy 2009, 34, 9195–9202. [Google Scholar] [CrossRef]
- Scott, K.; Pilditch, S.; Mamlouk, M. Modelling and Experimental Validation of a High Temperature Polymer Electrolyte Fuel Cell. J. Appl. Electrochem. 2007, 37, 1245–1259. [Google Scholar] [CrossRef]
- Broka, K.; Ekdunge, P. Modelling the PEM Fuel Cell Cathode. J. Appl. Electrochem. 1997, 27, 281–289. [Google Scholar] [CrossRef]
- Cetinbas, F.C.; Advani, S.G.; Prasad, A.K. A Modified Agglomerate Model with Discrete Catalyst Particles for the PEM Fuel Cell Catalyst Layer. J. Electrochem. Soc. 2013, 160, F750–F756. [Google Scholar] [CrossRef]
- Sun, W.; Peppley, B.A.; Karan, K. An Improved Two-Dimensional Agglomerate Cathode Model to Study the Influence of Catalyst Layer Structural Parameters. Electrochim. Acta 2005, 50, 3359–3374. [Google Scholar] [CrossRef]
- Moein-Jahromi, M.; Kermani, M.J. Performance Prediction of PEM Fuel Cell Cathode Catalyst Layer Using Agglomerate Model. Int. J. Hydrogen Energy 2012, 37, 17954–17966. [Google Scholar] [CrossRef]
- Roa, R.M.; Rengaswamy, R. Optimization Study of an Agglomerate Model for Platinum Reduction and Performance in PEM Fuel Cell Cathode. Chem. Eng. Res. Des. 2006, 84, 952–964. [Google Scholar]
- Wang, Q.; Eikerling, M.; Song, D.; Liu, Z. Structure and Performance of Different Types of Agglomerates in Cathode Catalyst Layers of PEM Fuel Cells. J. Electroanal. Chem. 2004, 573, 61–69. [Google Scholar] [CrossRef]
- Lobato, J.; Cañizares, P.; Rodrigo, M.A.; Linares, J.J.; Pinar, F.J. Study of the Influence of the Amount of PBI-H3PO4 in the Catalytic Layer of a High Temperature PEMFC. Int. J. Hydrogen Energy 2010, 35, 1347–1355. [Google Scholar] [CrossRef]
- Lobato, J.; Cañizares, P.; Rodrigo, M.A.; Úbeda, D.; Pinar, F.J.; Linares, J.J. Optimisation of the Microporous Layer for a Polybenzimidazole-Based High Temperature PEMFC—Effect of Carbon Content. Fuel Cells 2010, 10, 770–777. [Google Scholar] [CrossRef]
- Roller, J.M.; Arellano-Jiménez, M.J.; Jain, R.; Yu, H.; Carter, C.B.; Maric, R. Oxygen Evolution duringWater Electrolysis from Thin Films Using Bimetallic Oxides of Ir–Pt and Ir–Ru. J. Electrochem. Soc. 2013, 160, F716–F730. [Google Scholar] [CrossRef]
- Roller, J.M.; Renner, J.; Yu, H.; Capuano, C.; Kwak, T.; Wang, Y.; Carter, C.B.; Ayers, K.; Mustain, W.E.; Maric, R. Flame-Based Processing as a Practical Approach for Manufacturing Hydrogen Evolution Electrodes. J. Power Sources 2014, 271, 366–376. [Google Scholar] [CrossRef]
- Korsgaard, A.R.; Refshauge, R.; Nielsen, M.P.; Bang, M.; Kaer, S.K. Experimental Characterization and Modeling of Commercial Polybenzimidazole-Based MEA Performance. J. Power Sources 2006, 162, 239–245. [Google Scholar] [CrossRef]
- Mamlouk, M.; Sousa, T.; Scott, K. A High Temperature Polymer Electrolyte Membrane Fuel Cell Model for Reformate Gas. Int. J. Electrochem. 2011, 2011, 1–18. [Google Scholar] [CrossRef]
- Kunz, H.R.; Gruver, G.A. The Catalytic Activity of Platinum Supported on Carbon for Electrochemical Oxygen Reduction in Phosphoric Acid. J. Electrochem. Soc. 1975, 122, 1279–1287. [Google Scholar] [CrossRef]
- Klinedinst, K.; Bett, J.A.S.; Macdonald, J.; Stonehart, P. Oxygen Solubility and Diffusivity in Hot Concentrated H3PO4. J. Electroanal. Chem. Interfacial Electrochem. 1974, 57, 281–289. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Myles, T.D.; Kim, S.; Maric, R.; Mustain, W.E. Application of a Coated Film Catalyst Layer Model to a High Temperature Polymer Electrolyte Membrane Fuel Cell with Low Catalyst Loading Produced by Reactive Spray Deposition Technology. Catalysts 2015, 5, 1673-1691. https://doi.org/10.3390/catal5041673
Myles TD, Kim S, Maric R, Mustain WE. Application of a Coated Film Catalyst Layer Model to a High Temperature Polymer Electrolyte Membrane Fuel Cell with Low Catalyst Loading Produced by Reactive Spray Deposition Technology. Catalysts. 2015; 5(4):1673-1691. https://doi.org/10.3390/catal5041673
Chicago/Turabian StyleMyles, Timothy D., Siwon Kim, Radenka Maric, and William E. Mustain. 2015. "Application of a Coated Film Catalyst Layer Model to a High Temperature Polymer Electrolyte Membrane Fuel Cell with Low Catalyst Loading Produced by Reactive Spray Deposition Technology" Catalysts 5, no. 4: 1673-1691. https://doi.org/10.3390/catal5041673
APA StyleMyles, T. D., Kim, S., Maric, R., & Mustain, W. E. (2015). Application of a Coated Film Catalyst Layer Model to a High Temperature Polymer Electrolyte Membrane Fuel Cell with Low Catalyst Loading Produced by Reactive Spray Deposition Technology. Catalysts, 5(4), 1673-1691. https://doi.org/10.3390/catal5041673