First Principles Evaluation of Platinum Cluster Metal–Support Interactions on Nitrogen-Doped Carbon Supports
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Systems with Single Pt Atom Catalyst
3.1.1. Adsorption
3.1.2. Charge Transfer
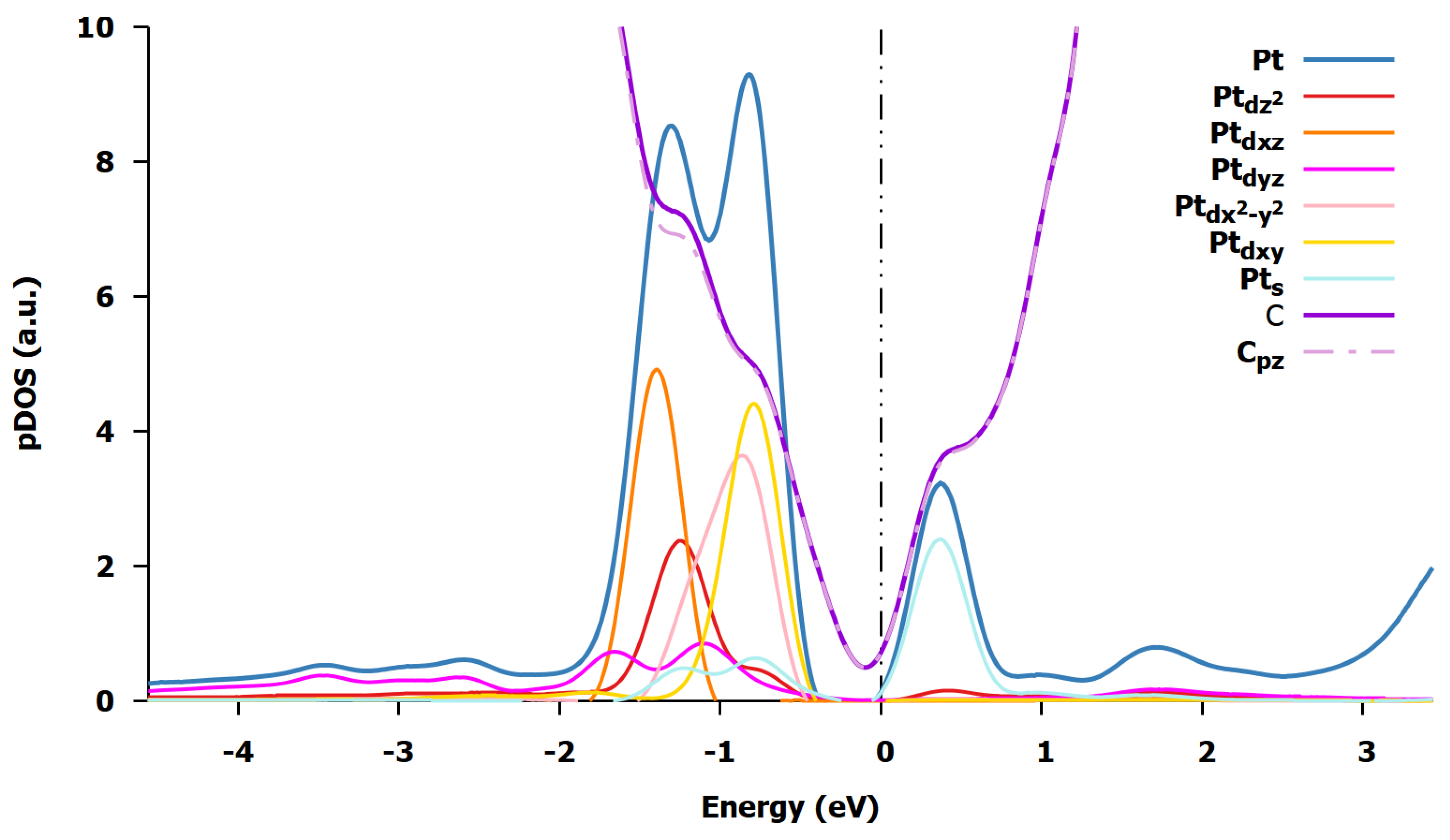
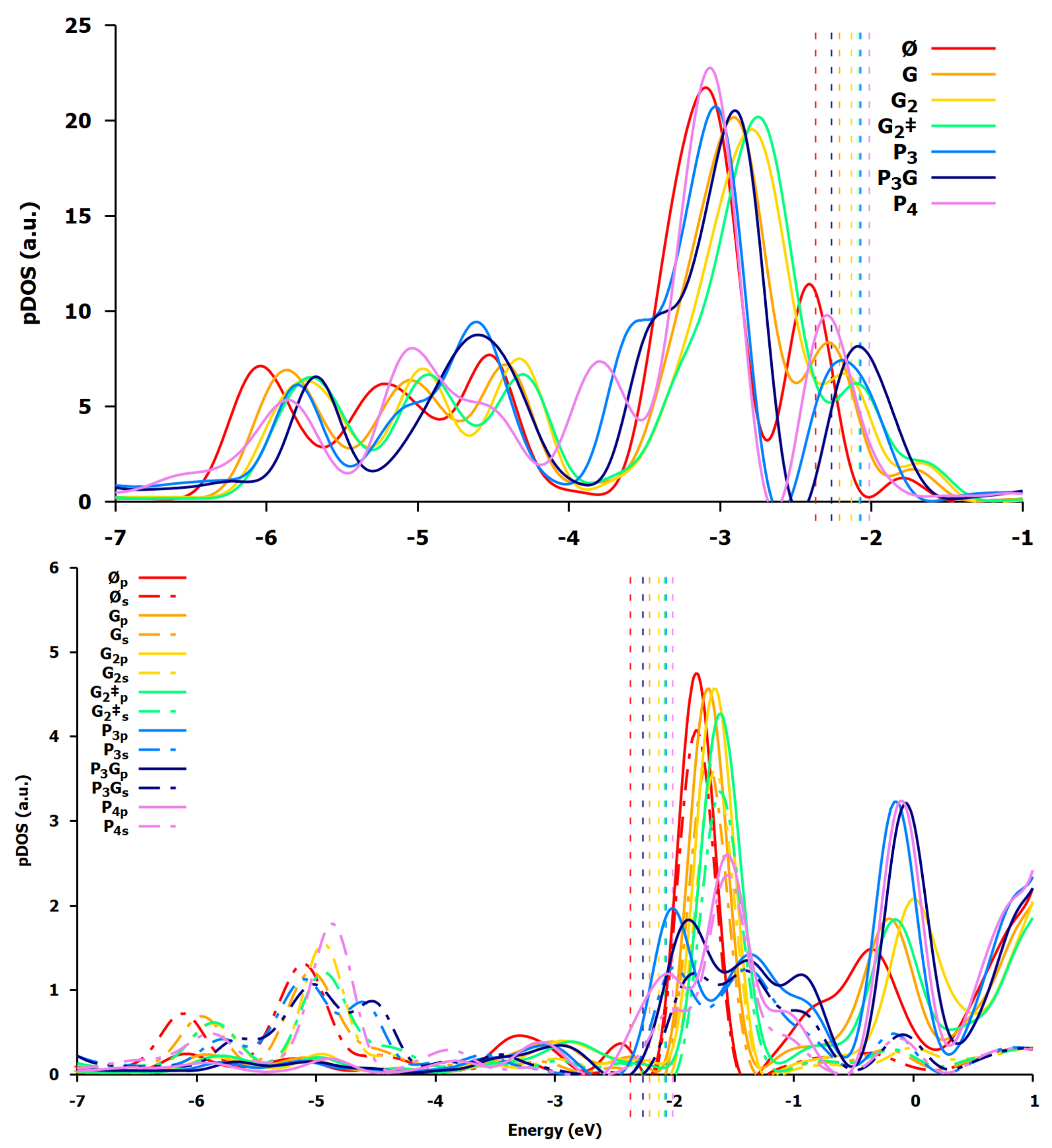
3.1.3. Electronic Rearrangement
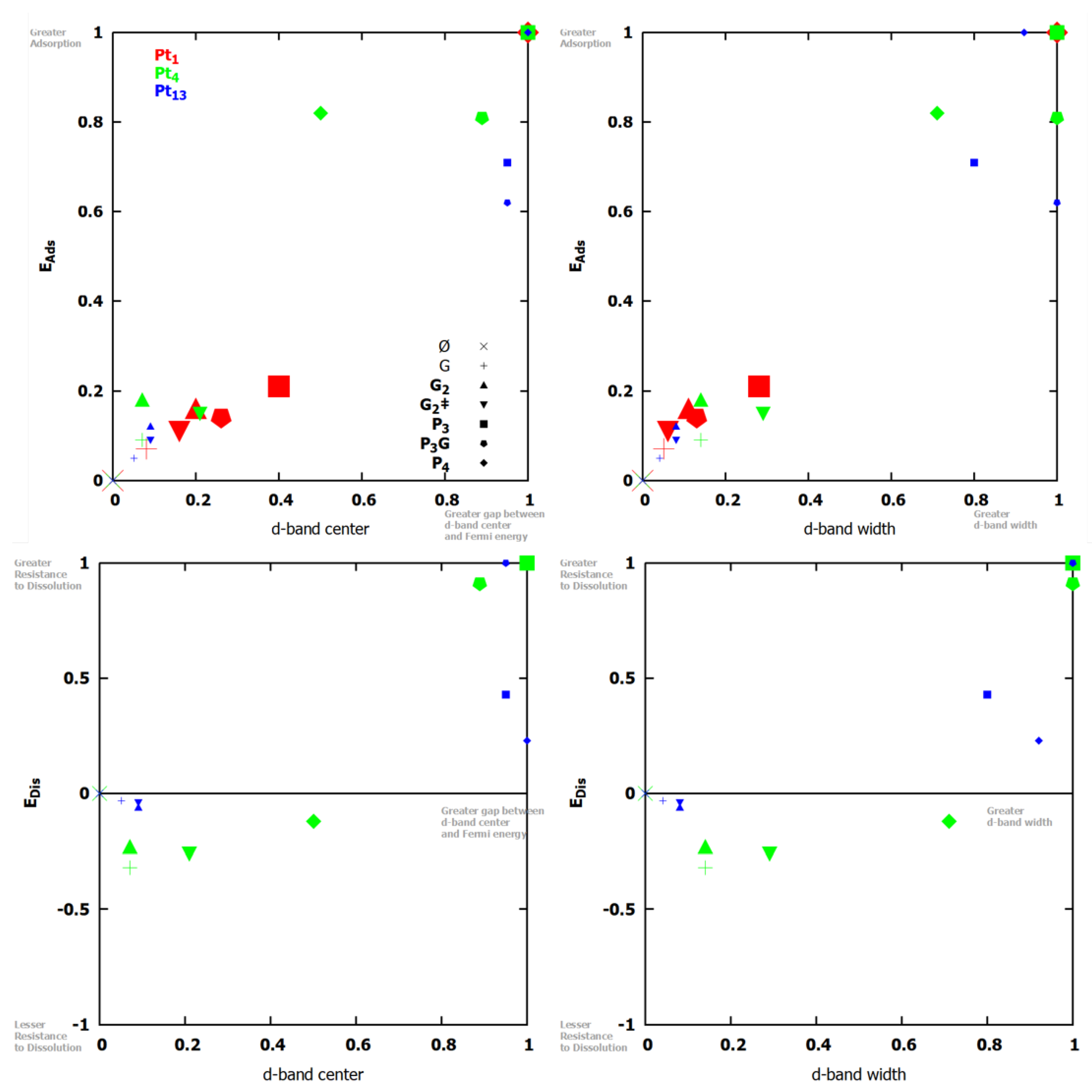
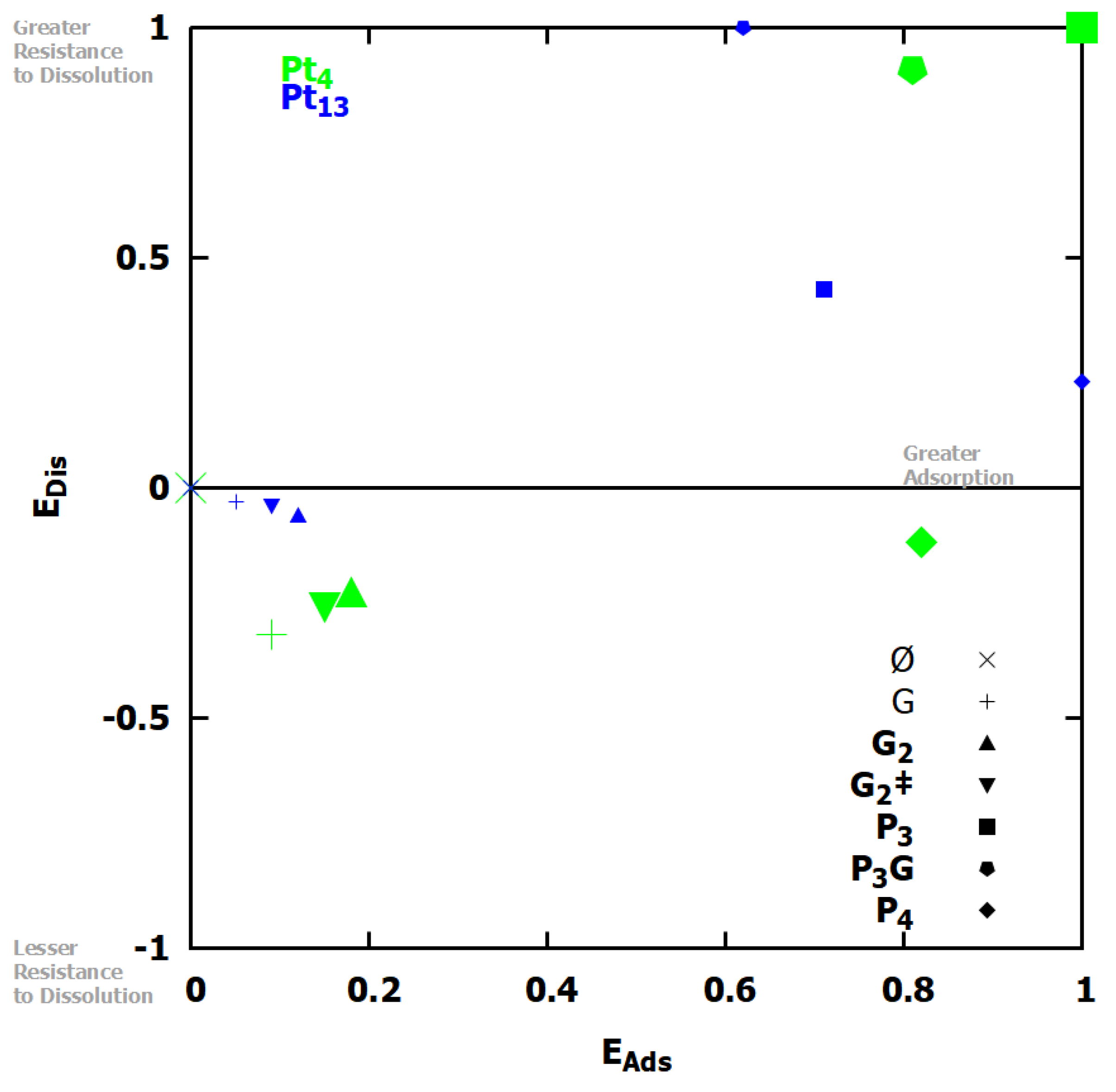
3.2. Platinum Nanoclusters
3.3. Larger Platinum Nanocluster
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| pDOS | Partial Density of States |
| MOA | Mode of Adsorption |
| BL | Bond Length |
| CN | Coordination Number |
References
- Kaiser, S.K.; Chen, Z.; Faust Akl, D.; Mitchell, S.; Pérez-Ramírez, J. Single-Atom Catalysts across the Periodic Table. Chem. Rev. 2020, 120, 11703–11809. [Google Scholar] [CrossRef] [PubMed]
- Zhuo, H.Y.; Zhang, X.; Liang, J.X.; Yu, Q.; Xiao, H.; Li, J. Theoretical Understandings of Graphene-based Metal Single-Atom Catalysts: Stability and Catalytic Performance. Chem. Rev. 2020, 120, 12315–12341. [Google Scholar] [CrossRef] [PubMed]
- Nakatsuka, K.; Yoshii, T.; Kuwahara, Y.; Mori, K.; Yamashita, H. Controlled synthesis of carbon-supported Co catalysts from single-sites to nanoparticles: Characterization of the structural transformation and investigation of their oxidation catalysis. Phys. Chem. Chem. Phys. 2017, 19, 4967–4974. [Google Scholar] [CrossRef] [PubMed]
- Zhou, M.; Zhang, A.; Dai, Z.; Zhang, C.; Feng, Y.P. Greatly enhanced adsorption and catalytic activity of Au and Pt clusters on defective graphene. J. Chem. Phys. 2010, 132, 194704. [Google Scholar] [CrossRef]
- Yumura, T.; Awano, T.; Kobayashi, H.; Yamabe, T. Platinum clusters on vacancy-type defects of nanometer-sized graphene patches. Molecules 2012, 17, 7941–7960. [Google Scholar] [CrossRef]
- Shao, Y.; Yin, G.; Gao, Y. Understanding and approaches for the durability issues of Pt-based catalysts for PEM fuel cell. J. Power Sources 2007, 171, 558–566. [Google Scholar] [CrossRef]
- Alia, S.M.; Ngo, C.; Shulda, S.; Ha, M.A.; Dameron, A.A.; Weker, J.N.; Neyerlin, K.C.; Kocha, S.S.; Pylypenko, S.; Pivovar, B.S. Exceptional Oxygen Reduction Reaction Activity and Durability of Platinum-Nickel Nanowires through Synthesis and Post-Treatment Optimization. ACS Omega 2017, 2, 1408–1418. [Google Scholar] [CrossRef]
- Holme, T.; Zhou, Y.; Pasquarelli, R.; O’Hayre, R. First principles study of doped carbon supports for enhanced platinum catalysts. Phys. Chem. Chem. Phys. 2010, 12, 9461–9468. [Google Scholar] [CrossRef]
- Marshall-Roth, T.; Libretto, N.J.; Wrobel, A.T.; Anderton, K.J.; Pegis, M.L.; Ricke, N.D.; Voorhis, T.V.; Miller, J.T.; Surendranath, Y. A pyridinic Fe-N4 macrocycle models the active sites in Fe/N-doped carbon electrocatalysts. Nat. Commun. 2020, 11, 5283. [Google Scholar] [CrossRef]
- Zhao, L.; He, R.; Rim, K.T.; Schiros, T.; Kim, K.S.; Zhou, H.; Gutiérrez, C.; Chockalingam, S.P.; Arguello, C.J.; Pálová, L.; et al. Visualizing individual nitrogen dopants in monolayer graphene. Science 2011, 333, 999–1003. [Google Scholar] [CrossRef]
- Rangel, E.; Magana, L.F.; Sansores, L.E. A theoretical study of the interaction of hydrogen and oxygen with palladium or gold adsorbed on pyridine-like nitrogen-doped graphene. ChemPhysChem 2014, 15, 4042–4048. [Google Scholar] [CrossRef]
- Xin, L.; Yang, F.; Rasouli, S.; Qiu, Y.; Li, Z.F.; Uzunoglu, A.; Sun, C.J.; Liu, Y.; Ferreira, P.; Li, W.; et al. Understanding Pt Nanoparticle Anchoring on Graphene Supports through Surface Functionalization. ACS Catal. 2016, 6, 2642–2653. [Google Scholar] [CrossRef]
- Antolini, E. Graphene as a new carbon support for low-temperature fuel cell catalysts. Appl. Catal. Environ. 2012, 123, 52–68. [Google Scholar] [CrossRef]
- Artyushkova, K.; Serov, A.; Rojas-Carbonell, S.; Atanassov, P. Chemistry of Multitudinous Active Sites for Oxygen Reduction Reaction in Transition Metal-Nitrogen-Carbon Electrocatalysts. J. Phys. Chem. C 2015, 119, 25917–25928. [Google Scholar] [CrossRef]
- Singh, S.K.; Takeyasu, K.; Nakamura, J. Active Sites and Mechanism of Oxygen Reduction Reaction Electrocatalysis on Nitrogen-Doped Carbon Materials. Adv. Mater. 2019, 31, 1804297. [Google Scholar] [CrossRef]
- Campisi, S.; Chan-Thaw, C.E.; Villa, A. Understanding heteroatom-mediated metal-support interactions in functionalized carbons: A perspective review. Appl. Sci. 2018, 8, 1159. [Google Scholar] [CrossRef]
- Meng, Y.; Huang, X.; Lin, H.; Zhang, P.; Gao, Q.; Li, W. Carbon-Based Nanomaterials as Sustainable Noble-Metal-Free Electrocatalysts. Front. Chem. 2019, 7, 759. [Google Scholar] [CrossRef]
- Han, H.; Noh, Y.; Kim, Y.; Park, S.; Yoon, W.; Jang, D.; Choi, S.M.; Kim, W.B. Selective electrochemical CO2 conversion to multicarbon alcohols on highly efficient N-doped porous carbon-supported Cu catalysts. Green Chem. 2020, 22, 71–84. [Google Scholar] [CrossRef]
- Dzara, M.J.; Artyushkova, K.; Shulda, S.; Strand, M.B.; Ngo, C.; Crumlin, E.J.; Gennett, T.; Pylypenko, S. Characterization of Complex Interactions at the Gas-Solid Interface with in Situ Spectroscopy: The Case of Nitrogen-Functionalized Carbon. J. Phys. Chem. C 2019, 123, 9074–9086. [Google Scholar] [CrossRef]
- Xu, Y.; Dzara, M.J.; Kabir, S.; Pylypenko, S.; Neyerlin, K.; Zakutayev, A. X-ray photoelectron spectroscopy and rotating disk electrode measurements of smooth sputtered Fe-N-C films. Appl. Surf. Sci. 2020, 515, 146012. [Google Scholar] [CrossRef]
- Martinez, U.; Komini Babu, S.; Holby, E.F.; Zelenay, P. Durability challenges and perspective in the development of PGM-free electrocatalysts for the oxygen reduction reaction. Curr. Opin. Electrochem. 2018, 9, 224–232. [Google Scholar] [CrossRef]
- Ramos-Sanchez, G.; Praserthdam, S.; Godinez-Salomon, F.; Barker, C.; Moerbe, M.; Calderon, H.A.; Lartundo, L.A.; Leyva, M.A.; Solorza-Feria, O.; Balbuena, P.B. Challenges of modelling real nanoparticles: Ni@Pt electrocatalysts for the oxygen reduction reaction. Phys. Chem. Chem. Phys. 2015, 17, 28286–28297. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.W.; Xu, L.; Mavrikakis, M. Computational Methods in Heterogeneous Catalysis. Chem. Rev. 2021, 121, 1007–1048. [Google Scholar] [CrossRef] [PubMed]
- Pylypenko, S.; Borisevich, A.; More, K.L.; Corpuz, A.R.; Holme, T.; Dameron, A.A.; Olson, T.S.; Dinh, H.N.; Gennett, T.; O’Hayre, R. Nitrogen: Unraveling the secret to stable carbon-supported Pt-alloy electrocatalysts. Energy Environ. Sci. 2013, 6, 2957–2964. [Google Scholar] [CrossRef]
- Calle-Vallejo, F.; Martínez, J.I.; Rossmeisl, J. Density functional studies of functionalized graphitic materials with late transition metals for oxygen reduction reactions. Phys. Chem. Chem. Phys. 2011, 13, 15639–15643. [Google Scholar] [CrossRef]
- Hossain, M.D.; Liu, Z.; Zhuang, M.; Yan, X.; Xu, G.L.; Gadre, C.A.; Tyagi, A.; Abidi, I.H.; Sun, C.J.; Wong, H.; et al. Rational Design of Graphene-Supported Single Atom Catalysts for Hydrogen Evolution Reaction. Adv. Energy Mater. 2019, 9, 1803689. [Google Scholar] [CrossRef]
- Kropp, T.; Mavrikakis, M. Transition Metal Atoms Embedded in Graphene: How Nitrogen Doping Increases CO Oxidation Activity. ACS Catal. 2022, 58, 24. [Google Scholar] [CrossRef]
- Nguyen, V.; Etz, B.D.; Pylypenko, S.; Vyas, S. Periodic Trends behind the Stability of Metal Catalysts Supported on Graphene with Graphitic Nitrogen Defects. ACS Omega 2021, 6, 28215–28228. [Google Scholar] [CrossRef]
- Perazzolo, V.; Brandiele, R.; Durante, C.; Zerbetto, M.; Causin, V.; Rizzi, G.A.; Cerri, I.; Granozzi, G.; Gennaro, A. Density Functional Theory (DFT) and Experimental Evidences of Metal-Support Interaction in Platinum Nanoparticles Supported on Nitrogen- and Sulfur-Doped Mesoporous Carbons: Synthesis, Activity, and Stability. ACS Catal. 2018, 8, 1122–1137. [Google Scholar] [CrossRef]
- Myshlyavtsev, A.V.; Stishenko, P.V.; Svalova, A.I. A systematic computational study of the structure crossover and coordination number distribution of metallic nanoparticles. Phys. Chem. Chem. Phys. 2017, 19, 17895–17903. [Google Scholar] [CrossRef]
- Kong, F.; Ren, Z.; Norouzi Banis, M.; Du, L.; Zhou, X.; Chen, G.; Zhang, L.; Li, J.; Wang, S.; Li, M.; et al. Active and Stable Pt-Ni Alloy Octahedra Catalyst for Oxygen Reduction via Near-Surface Atomical Engineering. ACS Catal. 2020, 10, 4205–4214. [Google Scholar] [CrossRef]
- Imaoka, T.; Toyonaga, T.; Morita, M.; Haruta, N.; Yamamoto, K. Isomerizations of a Pt4 cluster revealed by spatiotemporal microscopic analysis. Chem. Commun. 2019, 55, 4753–4756. [Google Scholar] [CrossRef] [PubMed]
- Lou, Y.; Xu, J.; Zhang, Y.; Pan, C.; Dong, Y.; Zhu, Y. Metal-support interaction for heterogeneous catalysis: From nanoparticles to single atoms. Mater. Today Nano 2020, 12, 100093. [Google Scholar] [CrossRef]
- Aprà, E.; Fortunelli, A. Density-functional calculations on platinum nanoclusters: Pt 13, Pt 38, and Pt 55. J. Phys. Chem. A 2003, 107, 2934–2942. [Google Scholar] [CrossRef]
- Demiroglu, I.; Yao, K.; Hussein, H.A.; Johnston, R.L. DFT Global Optimization of Gas-Phase Subnanometer Ru-Pt Clusters. J. Phys. Chem. C 2017, 121, 10773–10780. [Google Scholar] [CrossRef]
- Parreira, R.L.; Caramori, G.F.; Galembeck, S.E.; Huguenin, F. The nature of the interactions between Pt4 cluster and the adsorbates H, OH, and H2O. J. Phys. Chem. A 2008, 112, 11731–11743. [Google Scholar] [CrossRef]
- Gao, Z.; Li, A.; Liu, X.; Ma, C.; Li, X.; Yang, W.; Ding, X. Density functional study of the adsorption of NO on Ni n (n = 1, 2, 3 and 4) clusters doped functionalized graphene support. Appl. Surf. Sci. 2019, 481, 940–950. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Quantum Espresso. 2017. Available online: https://iopscience.iop.org/article/10.1088/1361-648X/aa8f79 (accessed on 20 March 2025).
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum Espresso. 2009. Available online: https://iopscience.iop.org/article/10.1088/0953-8984/21/39/395502 (accessed on 20 March 2025). [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Fitzgerald, M.A.; Ibbotson, D.; Foster, J.; Dzara, M.J.; Zaccarine, S.F.; Vyas, S.; Pylypenko, S. Effects of Graphitic and Pyridinic Nitrogen Defects on Transition Metal Nucleation and Nanoparticle Formation on N-Doped Carbon Supports: Implications for Catalysis. ACS Appl. Nano Mater. 2022, 5, 14922–14933. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 1989, 40, 3616. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Sohier, T.; Calandra, M.; Mauri, F. Density functional perturbation theory for gated two-dimensional heterostructures: Theoretical developments and application to flexural phonons in graphene. Phys. Rev. B 2017, 96, 075448. [Google Scholar] [CrossRef]
- Wood, K.N.; O’Hayre, R.; Pylypenko, S. Recent progress on nitrogen/carbon structures designed for use in energy and sustainability applications. Energy Environ. Sci. 2014, 7, 1212–1249. [Google Scholar] [CrossRef]
- Vojvodic, A.; Nørskov, J.K.; Abild-Pedersen, F. Electronic structure effects in transition metal surface chemistry. Top. Catal. 2014, 57, 25–32. [Google Scholar] [CrossRef]
- Inoǧlu, N.; Kitchin, J.R. Simple model explaining and predicting coverage-dependent atomic adsorption energies on transition metal surfaces. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 045414. [Google Scholar] [CrossRef]
- Sanville, E.; Kenny, S.D.; Smith, R.; Henkelman, G. Improved grid-based algorithm for Bader charge allocation. J. Comput. Chem. 2007, 28, 899–908. [Google Scholar] [CrossRef]
- Matanovic, I.; Artyushkova, K.; Strand, M.B.; Dzara, M.J.; Pylypenko, S.; Atanassov, P. Core Level Shifts of Hydrogenated Pyridinic and Pyrrolic Nitrogen in the Nitrogen-Containing Graphene-Based Electrocatalysts: In-Plane vs Edge Defects. J. Phys. Chem. C 2016, 120, 29225–29232. [Google Scholar] [CrossRef]
- Chen, Y.; Ji, S.; Chen, C.; Peng, Q.; Wang, D.; Li, Y. Single-Atom Catalysts: Synthetic Strategies and Electrochemical Applications. Joule 2018, 2, 1242–1264. [Google Scholar] [CrossRef]
- Muhich, C.L.; Westcott, J.Y.; Morris, T.C.; Weimer, A.W.; Musgrave, C.B. The effect of N and B doping on graphene and the adsorption and migration behavior of Pt atoms. J. Phys. Chem. C 2013, 117, 10523–10535. [Google Scholar] [CrossRef]
- Groves, M.N.; Chan, A.S.; Malardier-Jugroot, C.; Jugroot, M. Improving platinum catalyst binding energy to graphene through nitrogen doping. Chem. Phys. Lett. 2009, 481, 214–219. [Google Scholar] [CrossRef]
- Usachov, D.; Vilkov, O.; Grüneis, A.; Haberer, D.; Fedorov, A.; Adamchuk, V.K.; Preobrajenski, A.B.; Dudin, P.; Barinov, A.; Oehzelt, M.; et al. Nitrogen-doped graphene: Efficient growth, structure, and electronic properties. Nano Lett. 2011, 11, 5401–5407. [Google Scholar] [CrossRef] [PubMed]
- Wickramaratne, N.P.; Xu, J.; Wang, M.; Zhu, L.; Dai, L.; Jaroniec, M. Nitrogen enriched porous carbon spheres: Attractive materials for supercapacitor electrodes and CO2 adsorption. Chem. Mater. 2014, 26, 2820–2828. [Google Scholar] [CrossRef]

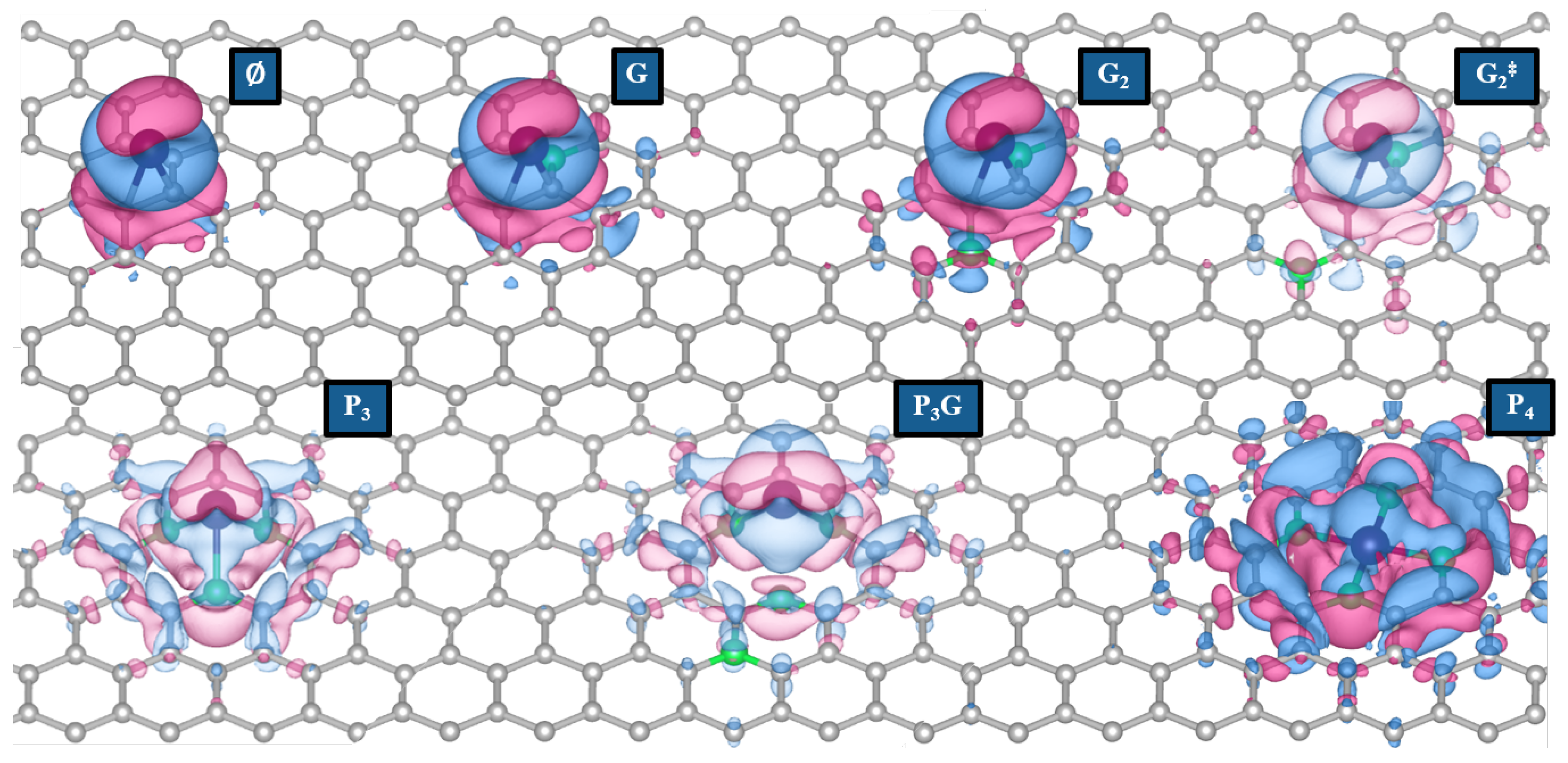



| Defect | ∅ | G | |||||
|---|---|---|---|---|---|---|---|
| (eV) | −1.85 | −2.26 | −2.81 | −2.51 | −3.13 | −2.70 | −8.06 |
| MOA | CC | CC | CC | CC | V | V | V |
| Bader Charge | ∅ | G | |||||
|---|---|---|---|---|---|---|---|
| Pt | 0.04 | −0.03 | −0.10 | −0.10 | 0.50 | 0.38 | 1.06 |
| N#1 | −0.58 | −0.67 | −0.60 | −0.56 | −0.54 | −0.50 | |
| N#2 | −0.17 | −0.63 | −0.53 | −0.55 | −0.55 | ||
| N#3 | −0.53 | −0.95 | −0.55 | ||||
| N#4 | −0.68 | −0.51 |
| Defects | ∅ | G | |||||
|---|---|---|---|---|---|---|---|
| −2.44 | −2.32 | −2.27 | −2.21 | −2.54 | −2.24 | −2.35 | |
| −3.80 | −3.78 | −3.88 | −3.76 | −4.39 | −3.92 | −4.93 | |
| −1.36 | −1.46 | −1.61 | −1.55 | −1.85 | −1.68 | −2.58 | |
| 1.05 | 1.09 | 1.14 | 1.10 | 1.29 | 1.16 | 1.90 |
| Defects | ∅ | G | |||||
|---|---|---|---|---|---|---|---|
| −1.82 | −2.10 | −2.38 | −2.30 | −5.04 | −4.42 | −4.47 | |
| 4.12 | 4.01 | 4.04 | 4.03 | 4.48 | 4.45 | 4.08 | |
| Average Bond Length of (Å) | 2.61 ± 0.02 | 2.62 ± 0.02 | 2.64 ± 0.05 | 2.63 ± 0.02 | 2.57 ± 0.03 | 2.54 ± 0.01 | 2.58 ± 0.01 |
| Coordination Number of (Å) | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 |
| Average Bond Length Between (Å) | 2.56 ± 0.00 | 2.56 ± 0.00 | 2.56 ± 0.01 | 2.56 ± 0.01 | 2.59± 0.00 | 2.59 ± 0.01 | 2.58 ± 0.01 |
| Average Coordination Number of (Å) | 3.00 ± 0.00 | 3.00 ± 0.00 | 3.00 ± 0.00 | 3.00 ± 0.00 | 3.00 ± 0.00 | 3.00 ± 0.00 | 3.00 ± 0.00 |
| −2.37 | −2.21 | −2.13 | −2.08 | −2.07 | −2.01 | −2.27 | |
| −4.11 | −3.97 | −3.89 | −3.88 | −4.09 | −4.00 | −4.15 | |
| −1.74 | −1.76 | −1.76 | −1.80 | −2.02 | −1.99 | −1.88 | |
| 1.37 | 1.38 | 1.38 | 1.39 | 1.44 | 1.44 | 1.42 |
| Defects | ∅ | G | |||||
|---|---|---|---|---|---|---|---|
| −2.03 | −2.39 | −2.82 | −2.65 | −6.83 | −6.19 | −8.75 | |
| 4.66 | 4.62 | 4.58 | 4.60 | 5.27 | 6.08 | 4.98 | |
| Average Bond Length of (Å) | 2.80 ± 0.09 | 2.80 ± 0.08 | 2.79 ± 0.08 | 2.80 ± 0.08 | 2.58 ± 0.02 | 2.67 ± 0.10 | 2.77 |
| Coordination Number of (Å) | 6.00 | 6.00 | 6.00 | 6.00 | 3.00 | 4.00 | 1.00 |
| Average Bond Length Between (Å) | 2.72 ± 0.07 | 2.72 ± 0.07 | 2.72 ± 0.07 | 2.72 ± 0.07 | 2.64 ± 0.07 | 2.65 ± 0.06 | 2.65 ± 0.08 |
| Average Coordination Number of (Å) | 6.00 ± 0.00 | 6.00 ± 0.00 | 6.00 ± 0.00 | 6.00 ± 0.00 | 4.36 ± 1.12 | 4.91 ± 0.54 | 4.73 ± 0.90 |
| −2.23 | −2.07 | −1.98 | −1.94 | −1.94 | −1.97 | −1.98 | |
| −4.01 | −3.87 | −3.80 | −3.76 | −4.14 | −4.17 | −4.20 | |
| −1.78 | −1.80 | −1.82 | −1.82 | −2.20 | −2.20 | −2.22 | |
| 1.46 | 1.47 | 1.48 | 1.48 | 1.66 | 1.71 | 1.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.; Vyas, S. First Principles Evaluation of Platinum Cluster Metal–Support Interactions on Nitrogen-Doped Carbon Supports. Catalysts 2025, 15, 635. https://doi.org/10.3390/catal15070635
Nguyen V, Vyas S. First Principles Evaluation of Platinum Cluster Metal–Support Interactions on Nitrogen-Doped Carbon Supports. Catalysts. 2025; 15(7):635. https://doi.org/10.3390/catal15070635
Chicago/Turabian StyleNguyen, Vu, and Shubham Vyas. 2025. "First Principles Evaluation of Platinum Cluster Metal–Support Interactions on Nitrogen-Doped Carbon Supports" Catalysts 15, no. 7: 635. https://doi.org/10.3390/catal15070635
APA StyleNguyen, V., & Vyas, S. (2025). First Principles Evaluation of Platinum Cluster Metal–Support Interactions on Nitrogen-Doped Carbon Supports. Catalysts, 15(7), 635. https://doi.org/10.3390/catal15070635







