Abstract
Pharmaceutical residues are emerging contaminants of growing concern due to their persistence and poor removal efficiency in conventional wastewater treatment plants. This study evaluates UVC photolysis with type C ultraviolet radiation (UVC) and UVC/TiO2 photocatalysis of a mixture of four pharmaceuticals—atenolol (ATL), acetaminophen (ACM), clofibric acid (CLA), and antipyrine (ANT)—commonly found in treated urban wastewater. A comprehensive kinetic model was developed to describe their degradation, taking into account the generation of reactive oxygen species (ROS): hydroxyl (HO●), superoxide ion (O2●−) radicals, and singlet oxygen (1O2), along with their reactions with both the pharmaceuticals and dissolved organic matter. Direct quantum yields were determined as 8.05 × 10−3 mol·Einstein−1 for ATL, 1.93 × 10−3 for ACM, 3.12 × 10−1 for CLA, and 5.12 × 10−2 for ANT. In addition, rate constants of the reactions between singlet oxygen and pharmaceuticals were 9.93, 1.3 × 106, 1.18 × 102, and 1.14 × 104 M−1s−1 for ATL, ACM, CLA, and ANT, respectively. Scavenger experiments confirmed the key role of the ROS involved. The model reproduces the inhibitory effect of natural organic matter in secondary effluent and, in most cases, treated, accurately predicts the concentration profiles of the pharmaceuticals. Under photocatalytic conditions (0.10 g·L−1 TiO2), all compounds were completely degraded in less than 15 min. This validated model provides a useful tool for understanding the degradation mechanisms of pharmaceutical mixtures and for supporting the design of effective water strategies based on photochemical processes.
1. Introduction
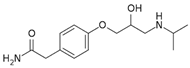
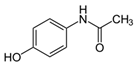
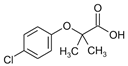
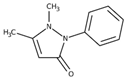
The detection of pharmaceutical residues in aquatic environments has emerged as a matter of growing environmental concern [1,2,3,4]. Conventional wastewater treatment processes are often inadequate for removing these contaminants, allowing pharmaceutical substances such as atenolol (ATL), acetaminophen (ACM), clofibric acid (CLA), and antipyrine (ANT) (see Table 1) to remain in aquatic environments. Even though the concentrations of these compounds in the environment are significantly lower than therapeutic doses, it is recognized that some substances can interfere with vital processes in non-target and sensitive organisms, including vulnerable human populations like children and pregnant women [5]. These compounds, widely used in medical treatments, pose serious ecological and public health risks when released into natural water systems.

Table 1.
Main physicochemical characteristics of the pharmaceuticals used in this study.
Atenolol, a beta-blocker prescribed for hypertension management, is frequently detected in surface waters and wastewater effluents. Concentrations ranging from 7 to 6897 ng·L−1 have been reported, with studies identifying levels up to 2300 ng·L−1 in urban water systems [6] or as high as 2346 ng·L−1 and 1707 ng·L−1 in influents and effluents, respectively [7]. ATL has also been widely detected in hospital sewage and wastewater in concentrations ranging from about 780 ng·L−1 to 6600 ng·L−1 [8]. Persistence of ATL is attributed to its resistance to conventional chlorination processes, while its ability to bioaccumulate in aquatic organisms raises additional ecological concerns [9].
Acetaminophen, a widely used analgesic and antipyretic, is another significant contaminant. Studies have reported variable concentrations across different types of water sources. For example, ACM levels of up to 500 ng·L−1 in Lagos and Ologe Lagoons [10] have been identified, and in treated wastewater effluents, concentrations from 8.1 ng·L−1 to 11,730 ng·L−1 have been measured [11]. Additionally, extreme values of 1.33 × 1010 ng·L−1 during periods of high usage in Aksaray, Turkey, have been reported [12], whereas an average concentration of 44,000 ng·L−1 in wastewater from San Marcos, Texas, has been observed [6]. Pozdnyakov et al. reported that irradiation at 254 nm leads to the disappearance of ACM with a ϕ254 = 1.4 × 10−3 mol·Einstein−1 quantum yield [13]. The limited efficiency of traditional wastewater treatments to effectively remove ACM contributes to its accumulation in natural water systems, with potential adverse ecotoxicological impacts.
Antipyrine, used for its analgesic properties, has been studied less extensively but remains a persistent contaminant in aquatic environments. Roveri et al. detected ATN in river systems, highlighting its environmental persistence and potential for bioaccumulation [14]. In China, the concentration of ANT in the influent of a drinking water treatment plant was found to range from 1.34 to 2.22 ng·L−1 [15]. These characteristics underscore the importance of monitoring its impact on aquatic life and ecosystems.
Clofibric acid, a metabolite of lipid-regulating drugs, is another compound of concern due to its persistence in water. Concentrations ranging from 200 to 500 ng·L−1 have been reported in wastewater effluents [16]. Its resistance to conventional treatment methods and tendency to accumulate in aquatic organisms highlight the need to develop more effective removal strategies.
The available literature does not include studies reporting the UVC photolysis or photocatalytic removal of a mixture comprising the four selected contaminants using TiO2 P25, nor the development of a kinetic model describing their simultaneous degradation. However, several works have investigated the individual direct photolysis and photocatalytic removal of these compounds using TiO2 or TiO2-based materials. Table S1 summarizes the experimental conditions and removal efficiencies reported for each contaminant.
To address the challenges posed by these contaminants, advanced treatment methods have been explored. Traditional processes, such as activated sludge systems, often fail to achieve adequate removal [17]. Advanced oxidation processes (AOPs), including ozonation and photocatalysis, have demonstrated significant potential in degrading pharmaceuticals. For instance, Lu et al. found that laccase-mediated oxidative coupling effectively removed ACM from water [18]. Floating treatment wetlands have also been shown to reduce organic contaminants, including ACM [19]. Bioremediation, leveraging microorganisms, represents another promising approach. Qutob et al. investigated the degradation of ACM and hydroxychloroquine, achieving substantial removal in controlled settings [20]. Similarly, adsorption techniques using natural materials like modified Moringa oleifera seed husks have shown potential for cost-effective removal [21]. Numerous AOPs have been explored for the removal of various pharmaceutical active compounds (PhACs) from water [22,23,24,25,26]. However, many studies have focused on the degradation of individual pharmaceuticals dissolved in water, often overlooking the influence of PhAC mixtures on treatment efficiency [27]. Photolysis, induced by ultraviolet (UV) radiation, plays a central role in photo-irradiated AOPs and can also be employed as a standalone process for wastewater treatment or sterilization. Despite its potential, the effectiveness of UV photolysis in treating water and effluents is often constrained by low photon absorption or limited quantum yields. However, when contaminants efficiently absorb UV radiation, photolysis can become a highly efficient treatment method [28].
Kinetic models have been developed to predict the degradation of these compounds under various treatment conditions. For instance, the degradation of pharmaceuticals in aqueous solutions often follows pseudo-first-order kinetics, as demonstrated in studies involving advanced oxidation processes (AOPs) [29]. The reaction rate constants for the degradation of specific pharmaceuticals have been reported, with ATL exhibiting a reaction rate constant with hydroxyl radicals (HO●) of approximately 1.1 × 109 M−1·s−1 [30]. Similarly, ACM has been shown to react with HO● at a rate constant of 1.4 × 109 M−1·s−1 [31]. ANT and CLA also exhibit significant reactivity, with reported rate constants of 1.2 × 109 M−1·s−1 and 7.5 × 108 M−1·s−1, respectively [32,33]. The reaction rate constant of ATL with singlet oxygen (1O2) was determined as 7.0 × 105 M−1·s−1 in D2O, 8.0 × 106 M−1·s−1 in acetonitrile, and 8.4 × 105 M−1·s−1 in ethanol, highlighting the influence of solvent polarity and hydrogen donating ability on the reaction kinetics [34]. According to pulse radiolysis measurements and competitive kinetic approaches, the bimolecular reaction rate constants for HO● and 1O2 with CLA were found to be 8.47(±0.33) × 109 M−1·s−1 and 6.6(±0.37) × 106 M−1·s−1, respectively [35]. However, in another study on the kinetics and mechanism of CLA photodegradation under simulated sunlight irradiation, using the competition kinetic method, the bimolecular reaction rate constants with HO● and 1O2 were determined as 3.93(±0.20) × 108 and 2.38(±0.12) × 106 M−1·s−1, respectively [36]. Literature provides limited information on the reaction rate constants of these contaminants with the superoxide ion radical, though values for other organics are between 105 and 108 M−1s−1 [37].
Novelty and main objectives of this study are as follows:
- (a)
- Investigate the photolytic and photocatalytic degradation kinetics of a mixture comprising four pharmaceuticals, proposing a generic kinetic model to address the complexity of simultaneously removing multiple compounds, considering the formation of reactive oxygen species (ROS),
- (b)
- Determination of the actual quantum yield at 254 nm of each pharmaceutical and identification of the specific ROS generated during their photolysis.
- (c)
- Determination of the reaction rate constant of each pharmaceutical with 1O2 to elucidate the role of this species in the photolysis of photosensitizing agents.
- (d)
- Check the influence of TiO2 concentration incorporated into the kinetic model in order to simulate the photocatalytic degradation of the four pharmaceuticals as a mixture, as well as the evolution of the ROS involved throughout the process.
2. Results and Discussion
2.1. UVC Photolysis
2.1.1. Effects of Scavengers
Several studies have shown that certain antibiotics (e.g., fluoroquinolones) and other organic compounds exhibit photosensitizing properties [38,39,40]. When exposed to light in aqueous solutions, these compounds can produce ROS, primarily 1O2, O2●−, and HO●, through mechanisms involving excitation to a triplet state. This process not only facilitates their photolysis but also accelerates the degradation of other substances present in the solution, a phenomenon known as indirect photolysis.
For this reason, in the present study, direct photolysis experiments are individually conducted for each of the selected pharmaceuticals in phosphate buffered ultrapure water at pH 7, both in the presence and absence of t-butanol (TBA), TIRON, and sodium azide (NaN3), to determine whether HO●, O2●− and 1O2 are formed and influence the degradation of each pharmaceutical when treated as a mixture. Figure 1 presents the results from the aforementioned experiments, illustrating the influence of these ROS on the photolytic degradation of the pharmaceuticals.
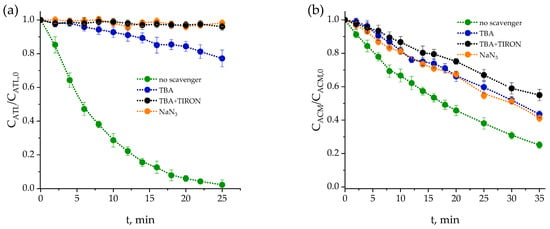
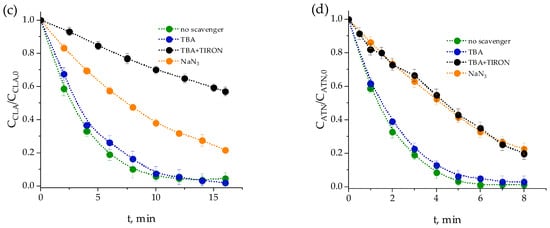
Figure 1.
Impact of scavengers on the individual photolytic degradation of pharmaceuticals: (a) ATL, (b) ACM, (c) CLA, (d) ANT. Conditions: Initial concentration: 0.5 mg·L−1, CTBA,0 = 0.01 M, CTIRON,0 = 0.001 M, CNaN3,0 = 0.01 M, pH0 = 7. I0 = 3.99 × 10−6 Einstein L−1·s−1.
Figure 1 shows that the degradation rate varies depending on the scavenger used. The curve without scavenger (green line) represents the results of scavenger-free photolysis of the contaminant, where direct photolysis due to light absorption is likely combined with indirect photolysis mediated by ROS, such as HO●, O2●−, and 1O2, which are likely generated from the excited state of the contaminant. Subsequently, scavengers were used to determine which reactive species dominate in each case.
In the case of ATL, the addition of TBA (blue line), a selective scavenger of HO●, significantly reduces the degradation rate compared to the green curve. This indicates that HO● plays an essential role in the degradation of this contaminant. The presence of NaN3 (orange line), which eliminates both HO● and 1O2, produces a result almost identical to that obtained with TBA+TIRON (black line), which removes HO● and O2●−. The similarity between the orange and black lines suggests that both ROS could also be responsible for part of the ATL inhibition rate. However, as shown later (see Section 2.1.3), the low-rate constant of the 1O2-ATL reaction seems to confirm that, in addition to HO●, the second most relevant ROS influencing ATL removal is O2●−.
In the case of ACM, the addition of TBA reduces the degradation rate, confirming that HO● is involved in the process, though the inhibition is less pronounced than in ATL. The use of NaN3 produces a similar inhibitory effect to that of TBA, confirming the important involvement of HO●, with no contribution from 1O2. However, the fact that the presence of TIRON leads to greater inhibition also indicates that O2●− participates to some extent.
The addition of TBA practically has little influence on the CLA reaction rate, indicating low participation of HO●. Inhibition is more pronounced with NaN3, suggesting a possible contribution from 1O2, although this ROS does not appear to be the predominant species. The combination of TBA+TIRON causes the greatest inhibition, with the curve above that corresponding to NaN3. This behavior indicates that O2●− plays a more significant role in CLA degradation than 1O2, since, when HO● and O2●− radicals are removed, the degradation is reduced more than when HO● and 1O2 are eliminated. In the case of ANT, the addition of TBA slightly inhibits the degradation rate, confirming that HO● is not significantly involved. The curve corresponding to TBA+TIRON is practically identical to that obtained with NaN3, as is also seen for the case of ATL. For a similar reason (low-rate constant of 1O2-ANT reaction, see Section 2.1.3). O2●− could be a more relevant species in the degradation of ANT. Based on these results, it is concluded that the dominant species in these processes are, to a greater or lesser extent, HO● and O2●−. This does not imply that 1O2 fails to contribute to indirect photolysis, but rather that it may react more slowly with pharmaceuticals or be produced in a lower proportion [41,42]. In any case, considering the photolysis of the mixture of these pharmaceuticals, these three ROS will be formed, and their reactions need to be considered when modelling the kinetics (see Section 2.2.3).
2.1.2. Comparison with Photolysis Results from Literature
Table S1 lists conditions and removal results of the few literature reports on the UVC photolysis of the pharmaceuticals studied that used similar photochemical equipment (UVC lamps emitting at 254 nm with similar intensity of radiation). For instance, Katsumata et al. [43] worked on the photolysis of ATL and ACM, among other pharmaceuticals. These authors found removals of 62% and 54%, respectively, of ATL and ACM after 1 h of treatment, while in the present study, complete removal of these compounds was achieved in less than 30 min. This difference can be mainly attributed to the initial concentration of the compounds, 5 mg·L−1 against 0.5 mg·L−1 used in this work. Also, Li et al. [44] have reported 92% removal of CLA after 1 h photolysis using an initial concentration of 2.14 mg·L−1. However, in the present study, almost complete removal was achieved within just 15 min, which can also be attributed to the difference in CLA initial concentration used. Finally, Tan et al. [45] reported 40% ANT removal after 1 h, which negatively compares with the complete removal achieved in this work in just 5 min reaction. Once again, the initial concentration applied can be the reason for this difference.
2.1.3. Apparent and Actual Direct Quantum Yields
To determine the quantum yield of pharmaceuticals, the equation describing the mass balance of a compound undergoing photolysis is used [40], as follows:
where ϕi represents the quantum yield of component i, eia corresponds to the photon absorption rate, I0 is the volumetric incident radiation, L is the effective path length of radiation (see Section 3.2. for further information), Abs254 is the absorbance of solution at 254 nm, and Fi the fraction of incident radiation species i absorbs:
where εi is the molar extinction or absorptivity coefficient of i at 254 nm. It should be noted that Abs254 varies depending on the species present in the reaction medium, scavengers included, especially NaN3 and TIRON, which absorb a significant fraction of 254 nm radiation (see Figure S1). However, when considering the transmittance of these compounds, it becomes clear that, although they absorb substantial amounts of radiation, they also allow a significant fraction to pass through (see Table 2). This ensures that the available radiation remains sufficient for the contaminants to undergo direct photolysis, while the scavenging function of both NaN3 and TIRON is still preserved.

Table 2.
Molar absorptivity coefficient, concentration of each pharmaceutical and scavenger used, absorbance at 254 nm, and transmittance at this concentration at pH 7.
For the integration of Equation (1), a constant value can be assumed for Abs254, as it does not vary by more than 10% during the photolysis reaction (see Figure S2). Then, analytical integration of Equation (1) yields the following:
By applying Equation (3) to the experimental results in the presence and absence of the scavenger (TBA+TIRON), both direct and apparent quantum yields of each pharmaceutical, respectively, can be determined from the slopes of the straight lines representing Equation (3), as shown in Figure S3. Table 3 presents the quantum yield values obtained for each case. The apparent quantum yields were determined from scavenger-free photolysis experiments of each pharmaceutical.

Table 3.
Apparent (ϕapp) and direct (ϕd) quantum yields of pharmaceuticals studied.
The results of Table 3 show that ATL and ACM are the compounds with the lowest direct quantum yields. This explains why their removal requires the longest time, and their photodegradation rates were affected when scavengers were added. On the other hand, as expected, CLA and ANT exhibit higher quantum yields, which aligns with the fact that these were the compounds that degraded most rapidly. However, it can be observed that, although ANT is removed in under 10 min, its quantum yield is lower than that of CLA, which is completely degraded in approximately 30 min in the presence of TBA+TIRON. This apparent discrepancy is explained by the fact that ANT has a molar absorptivity coefficient of 8890.6 M−1·cm−1, while CLA has a coefficient of only 251.2 M−1·cm−1.
2.1.4. Determination of the Reaction Rate Constant with Singlet Oxygen
The influence of singlet oxygen is generally considered less significant than that of HO● and O2●−. However, due to the limited availability of data in the literature, the second-order reaction rate constant of singlet oxygen with the pharmaceuticals (k1O2) was also determined in this work. For this purpose, the competitive kinetic method reported by Gao et al. [46] was used to determine these rate constants, employing Rose Bengal as a singlet oxygen generator and using furfural (F) as a reference compound, in accordance with Equation (4).
where CP0 and CF0 represent the initial concentration of the pharmaceutical and furfural, respectively, and CP and CF are their corresponding concentrations at time t. Figure S4 confirms Equation (4), and Table 4 presents the results.

Table 4.
Calculated rate constants of the reaction of singlet oxygen and pharmaceuticals were studied.
According to the rate constant data of Table 4, ATL exhibits the lowest reactivity towards singlet oxygen, showing an almost negligible reaction rate constant. This supports the earlier conclusion regarding the limited role of ROS in the indirect photolysis of ATL. A similar observation applies to singlet oxygen during CLA and ANT photolysis. ACM, by contrast, shows the highest value among the four compounds. However, according to results from Figure 1, formation of singlet oxygen from ACM photolysis does not seem important, and overall, it appears to be considerably less reactive than the hydroxyl radical and the superoxide ion radical as widely described in the literature [41,42]. Nonetheless, the influence of singlet oxygen must be considered when treating the UVC photolysis of an aqueous mixture of the four pharmaceuticals, as it could be mainly generated from CLA and/or ANT.
2.2. UVC Photolysis in Effluent of Urban Wastewater
The presence of dissolved organic matter (DOM) in water may have a significant impact on photochemical processes, as it could also generate ROS considered in this work (O2●−, 1O2, HO●). The production of these species varies depending on the source and composition of the DOM. For instance, humic and fulvic substances found in natural waters produce superoxide ion radicals (O2●−) and hydrogen peroxide (H2O2), with reaction rates influenced by the molecular composition of the DOM [47]. Moreover, the aqueous matrix influences reaction kinetics, as natural organic matter (NOM) can modify both the generation and decay of ROS. Indicators such as specific ultraviolet absorbance (SUVA) are useful for predicting these kinetics [48]. These processes may involve direct photolysis, where a molecule absorbs light and undergoes transformation, or indirect photochemistry, mediated by photosensitizers that generate transient species. The presence of NOM can alter these mechanisms, influencing reaction kinetics and the formation of intermediates [49]. Based on these considerations, a study was conducted to determine the influence of organic matter in the wastewater used.
2.2.1. Determination of ROS Involved in the Photolysis of Secondary Effluent
Photolysis experiments were subsequently conducted to investigate the role of secondary effluent (WWEf) in generating ROS during photolytic processes. The focus was on the potential of this water matrix to absorb radiation and its ability to form ROS. To explore these mechanisms, direct photolysis experiments of WWEf were performed, both in the absence and presence of scavengers [40].
The results are presented in Figure 2, which shows the evolution of absorbance at 254 nm and total organic carbon (TOC) over time. An initial absorbance of 0.160 was recorded, indicating the presence of compounds that can absorb UVC radiation. In all cases, the absorbance attributable to the scavengers was subtracted to ensure that the absorbance loss was only due to the secondary effluent. While this value is relatively low, it is significant enough to compete for the radiation required for the photolytic degradation of contaminants. In contrast, TOC remained constant throughout the experiments, suggesting that the photolytic processes were insufficient to achieve significant mineralization of organic matter within the timeframe of the tests.
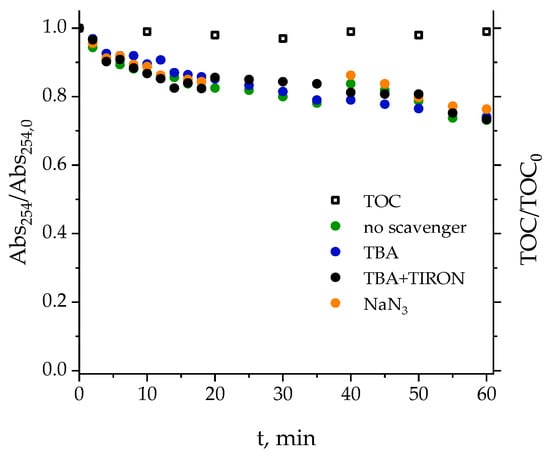
Figure 2.
Impact of scavengers on the photolysis of pharmaceutical-free WWEf. Conditions: AbsWWEf,0= 0.160 a.u., AbsWWEf+TBA,0 = 0.163 a.u., AbsWWEf+NaN3,0 = 0.213 a.u., AbsWWEf+TIRON,0 = 0.604 a.u., TOC0 = 7.3 mg·L−1, CTBA, 0 = 0.01 M, CTIRON, 0 = 0.001 M, CNaN3, 0 = 0.01 M, pH0 = 7.
The results revealed no significant differences between the photolysis curves obtained under different scavenger conditions. This suggests that the water matrix used does not generate substantial amounts of ROS capable of influencing the degradation kinetics of the pharmaceuticals. Moreover, the absence of pronounced differences in the degradation behavior suggests that the effluent contains minimal photosensitizing compounds. If ROS were formed, their concentration and reactivity would likely be too low to significantly impact the degradation of any pharmaceutical.
The use of absorbance at 254 nm proved to be a valuable parameter for assessing the composition of the effluent. This measurement correlates with the presence of aromatic and unsaturated compounds, which are known to absorb radiation at this wavelength. The stability of TOC alongside changes in absorbance further supports the notion that photolysis predominantly induces structural modifications rather than complete mineralization of the organic matter present in the water. However, DOM would compete for ROS generated in the photolysis of the water matrix in the presence of pharmaceuticals studied, thereby hindering their indirect photolysis. Since the absorbance results of Figure 2 are similar regardless of the presence and absence of scavengers, there appears to be no significant role of ROS. Then, it can be inferred that only direct photolysis of the organic matter is occurring. Therefore, the quantum yield of the secondary effluent was also determined. As in the previous section, the variation in absorbance over time would be as follows:
In this case, the term Fi is assumed to be unity, as it refers to the naturally occurring matter in water capable of absorbing radiation. This matter will be treated as a single entity, and thus the product ΣεjCj will correspond to the absorbance value of the water at each time point when measured in a 1 cm path length cell. The analytical solution of Equation (5) is as follows:
A quantum yield value of 5.53 a.u.·L−1·Einstein−1 was obtained from the experimental data using Equation (6) (see Figure S2).
2.2.2. Effect of the Aqueous Matrix on the Photolysis of Pharmaceuticals
Photolysis experiments were performed with a mixture of four pharmaceuticals in the secondary effluent to evaluate the effect of the aqueous matrix, particularly the presence of natural organic matter (NOM). The main characteristics of WWEf are described in Table S4 of Supplementary information.
The degradation kinetics of the pharmaceuticals were significantly slower in secondary effluent compared to ultrapure water, as shown in Figure 3 compared to Figure 1. This decrease in photolytic efficiency is attributable to the presence of NOM, which, as expected, influences both radiation absorption and the dynamics of reactive species formation. NOM absorbs radiation at 254 nm, reducing the fraction available for direct photolysis of the pharmaceuticals. This competitive light absorption limits the energy reaching the pharmaceuticals, thereby reducing their photodegradation rate. Although photolysis does achieve a certain degree of contaminant removal in secondary effluent (as shown in Figure 3), the extent of mineralization is not significant. The total organic carbon (TOC) remains practically constant throughout the process, with a maximum mineralization of only 4%, as illustrated in Figure S5.
Figure 3.
Experimental variation of the normalized concentrations of pharmaceuticals over time during the photolysis of the mixture in (a) ultrapure water and (b) secondary effluent. Conditions: CPharm,0 = 0.5 mg·L−1, pH0 = 7, I0 = 3.99 × 10−6 Einstein L−1·s−1.
At first, NOM competes for UV radiation and ROS pharmaceuticals generated. However, the fact that scavengers practically have no influence on 254 nm absorbance suggests that NOM of wastewater is preferentially altered through direct photolysis. Thus, the decrease in pharmaceutical degradation rates in wastewater is mainly attributed to the photolysis of NOM, in contrast to what occurs in ultrapure water.
2.2.3. Kinetic Model of Photolysis
Ultrapure Water
The mechanism of direct photolysis involves both direct photon absorption and subsequent reaction of ROS with pharmaceuticals, including hydrogen peroxide generated during the process. In this mechanism, hydroxyl radicals are assumed to be generated from photolysis of ATL and ACM and singlet oxygen from that of CLA and ANT, as experimental results suggest (see Section 2.1.1). It is also assumed that the formation of superoxide ion radical results from the reactions involving hydroxyl radical and singlet oxygen with pharmaceuticals [39,40]:
where M and P represent any pharmaceutical initially present in water and any product formed, respectively, and α and β are the stoichiometric ratios for HO• and 1O2 formation, respectively.
The hydroperoxide ion radical, HO2., is in equilibrium with the superoxide ion radical (Equation (11)), but this equilibrium is completely shifted towards the formation of the latter since pH was 7 and pK = 4.8. Hence, any hydroperoxide ion radical instantaneously becomes a superoxide ion radical [50]:
As a result, in reaction (9), the superoxide ion radical is effectively formed instead of the hydroperoxide radical.
The recombination of free radicals occurs via the following reaction [51]:
and reactions with the participation of hydrogen peroxide, including its direct photolysis, are as follows [52,53]:
and termination reactions [54].
where
and
It should be noted that there are other reactions involving hydroxyl radicals and primary intermediates that could also undergo photolysis, that have not been considered due to insufficient data. Reactions of superoxide ion radical with pharmaceuticals have also been considered as termination reactions:
According to experimental results, the photolysis kinetic model for pharmaceuticals is based on mol balance equations of participating species, including both molecular species (pharmaceuticals and hydrogen peroxide) and ROS. All these equations follow a general form corresponding to the design equation for a perfectly mixed batch reactor for liquid phase reactions [55]:
The reaction rate term, ri, for any participating species, i, takes the form presented below:
- (a)
- For any pharmaceutical, the reaction rate comprises four contributions: direct photolysis and reactions with HO●, O2●−, and 1O2:where [56]:here, ϕi represents the quantum yield of species i, and eia its volumetric photon absorption rate, kHO·i, kO2·−ii and k1O2i denote the rate constants for reactions with HO●, O2●−, and 1O2, respectively, and CHO·, CO2·−, and C1O2 represent the concentrations of these reactive oxygen species.
- (b)
- For hydrogen peroxide, the net reaction rate is given by the following:where,with ϕH and εH as the quantum yield and absorptivity coefficient of hydrogen peroxide at 254 nm, respectively.
- (c)
- For the hydroxyl radical:where,
- (d)
- For the superoxide ion radical:
- (e)
- For singlet oxygen:
Secondary Effluent Water
When reactions occur in secondary effluent, the photolysis of natural organic matter (NOM) is incorporated into the mechanism:
A new balance equation corresponding to reaction (35) must then be considered. The absorbance of the water at 254 nm is used as a parameter to represent NOM so that its photolysis reaction rate is as follows:
where
with AbsWWEf representing the absorbance of the secondary effluent at 254 nm, excluding contributions of pharmaceuticals. Moreover, the NOM absorbance influences the photolysis reaction rates of pharmaceuticals (Equation (25)) and hydrogen peroxide (Equation (30)), which are now as follows:
where i refers to any pharmaceutical or hydrogen peroxide.
Finally, the reaction rates of H2O2, HO•, O2•−, and 1O2 remain as defined in Equations (29), (31), (33), and (34), respectively.
The kinetic model comprising Equations (20)–(34) describes the photolysis of a mixture of the four pharmaceuticals in ultrapure buffered water (pH = 7) was first solved with the initial conditions:
For the kinetic model applied to the effluent wastewater, the following condition for water absorbance was added to Equation (39):
The kinetic models were solved using the Ode23s MATLAB 2024b code, incorporating the values of quantum yields and absorptivity coefficients given in Table 2 and Table 3. For the rate constant of hydroxyl radical reactions, initial values were taken from the literature, as also referenced in the Section 1. For superoxide ion radical reaction rate constants a general value of 5 × 106 M−1s−1 was initially taken for all pharmaceuticals while for the case of singlet oxygen reactions, values were experimentally determined and are shown in Table 4. Definitive rate constants for hydroxyl radical and superoxide ion radical reactions are provided in Table S2 along with others also used and present in the reaction rates of species. The used pharmaceutical-ROS reaction rate constants are of the expected order of magnitude for these kinds of processes [37,57].
Figure 4 presents the evaluation of the kinetic model applied to both ultrapure water (UP) and secondary effluent (WWEf).
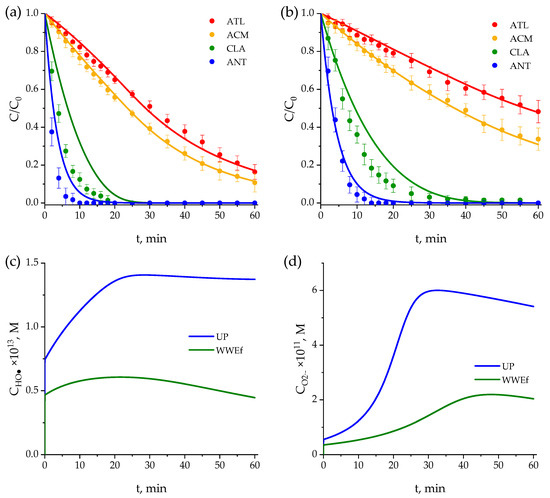
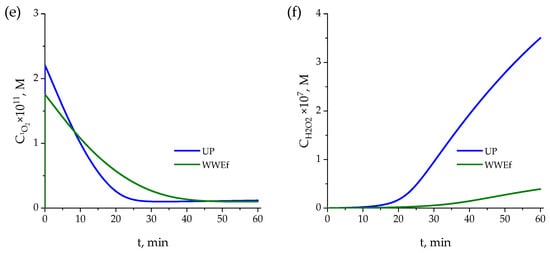
Figure 4.
Evaluation of the kinetic model in (a) ultrapure water and (b) secondary effluent. Variation of normalized concentrations of pharmaceuticals over time: Symbols: experimental data; curves: calculated values. Evolution of the concentration of (c) hydroxyl radicals, (d) superoxide ion radical, (e) singlet oxygen, (f) hydrogen peroxide in ultrapure water (blue lines) and secondary effluent (green lines). Conditions: CPharm0 = 0.5 mg·L−1, pH0 = 7. Other conditions, as in Figure 2.
As observed in Figure 4a,b, experimental and calculated results for ATL and ACM are in close agreement, while those for CLA and ANT (especially in UP water) present the greatest discrepancies, although their temporal evolution follows the same trend as the experimental results. These discrepancies are most likely attributable to the lack of data about the kinetics of intermediates formed (see Section 2.4). Moreover, the higher degradation rates of both compounds complicate the fitting of the model to the experimental results and the high number of parameters influencing the kinetic model (see Table S2). In any case, as observed in Figure 4, the fundamentals for establishing molar balances in the completely mixed batch photochemical reactor are valuable tools for predicting experimental results of processes such as photolysis. As also shown in Figure 4, the kinetic model provides a good fit for explaining differences due to the water content. As can be seen, the kinetic model predicts, even with higher precision, the concentrations in the effluent wastewater and the slower reaction rates observed in wastewater effluent compared to those in UP water. This is particularly clear in the case of the more refractory reacting compounds: ATL and ACM.
On the other hand, Figure 4c,d depict the calculated concentrations of HO● and O2●− over time, highlighting notable differences between the two water matrices. In ultrapure water, hydroxyl radicals increase steadily, indicating continuous generation with minimal interference, eventually reaching a near-plateau value. This behavior corresponds to the faster degradation of the compounds, as a higher concentration of reactive species is available. However, in secondary effluent, the concentration of hydroxyl radicals remains consistently lower and more stable. This can be explained by parallel reactions with NOM in the effluent, which limit the accumulation of radicals and reduce their overall effectiveness in degrading the compounds. During approximately the first 23 min, the formation trends of HO● are similar in both ultrapure water and effluent wastewater. However, beyond this point, hydroxyl radical formation declines (more slowly in UP water), likely due to the generation of reaction intermediates that interact with these radicals [58] and with the NOM present in the water [59,60,61]. These interactions may inhibit further radical generation, leading to a slower degradation process in secondary effluent compared to ultrapure water [62].
Figure 4e shows the trend with time followed for the calculated concentration of singlet oxygen, which continuously decreases due to the consumption of CLA and ANT, whose photolysis generates this ROS. Singlet oxygen disappears after 20–25 min, which is approximately the time required for complete elimination of CLA and ANT.
Finally, Figure 4f shows the predicted hydrogen peroxide concentration over time. Experimental values could not be obtained due to the detection limits of the analytical method, which was unable to measure such low concentrations. Once again, concentrations in ultrapure water were higher than in wastewater, likely due to the greater presence of compounds (including NOM) that scavenge free radicals, thereby leading to lower concentrations of hydrogen peroxide.
2.3. UVC TiO2 Photocatalysis
A series of TiO2 photocatalytic reactions in secondary effluent wastewater was carried out using a mixture of the four pharmaceuticals, with the main objective of developing and validating a kinetic model. Figure 5 shows the results obtained at different catalyst concentrations. Adsorption experiments also indicated that none of the pharmaceuticals adhered to the catalyst surface, thereby reducing the complexity of the kinetic model, as surface-bound reactions can be disregarded.
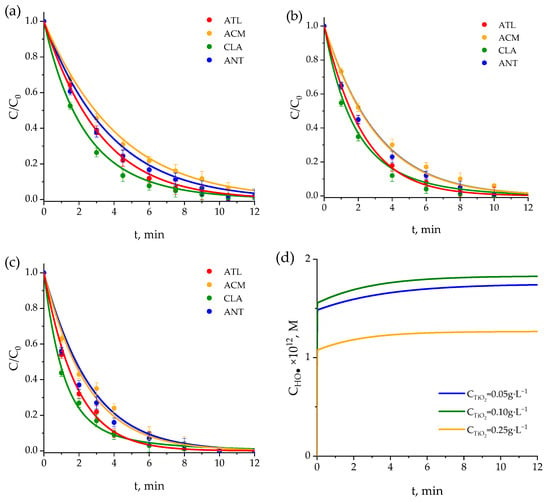
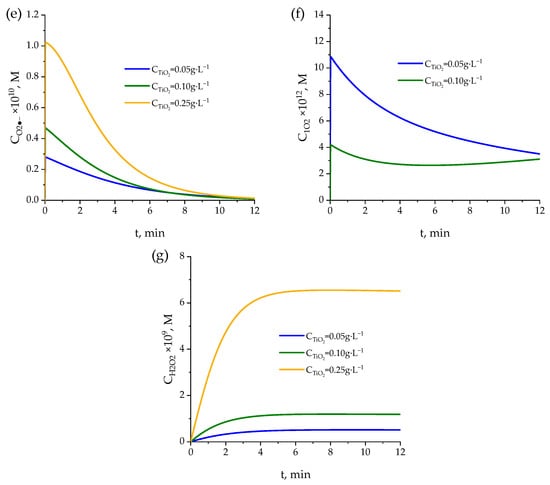
Figure 5.
Evaluation of the kinetic model in TiO2 photocatalytic experiments. Time evolution of the normalized concentration of pharmaceuticals for different TiO2 concentrations: (a) 0.05 g·L−1, (b) 0.10 g·L−1, and (c) 0.25 g·L−1. Evolution of reactive species: (d) hydroxyl radicals (HO•), (e) superoxide radical (O2•−), (f) singlet oxygen (1O2), and (g) hydrogen peroxide (H2O2). Conditions: CPharmac,0 = 0.5 mg·L−1, pH = 7.
Comparing Figure 4 and Figure 5 reveals that the photocatalytic process significantly increases the degradation rates of pharmaceuticals, achieving complete removal in under 15 min while much longer times are needed in the absence of the catalyst, especially for ATL and ACM.
For different catalyst concentrations (see Figure 5a,b,d) beyond a certain threshold, increasing the TiO2 concentration did not improve efficiency and, in some cases, even reduced it. This effect can be attributed to light shading and scattering [63,64,65], particle aggregation [66,67,68], electron-hole recombination [69], and limitations in the diffusion of reactants [70,71]. As in the case of photolysis, dissolved TOC was also monitored during the photocatalytic experiments. The results show that mineralization of the solution increases with higher catalyst concentrations (see Figure S5). Although complete removal of the parent compounds is achieved at early stages, the reduction in TOC does not follow the same trend. Specifically, TOC removal rates of 13%, 28%, and 51% were observed for catalyst concentrations of 0.05, 0.1, and 0.25 g·L−1, respectively, which is consistent with findings reported by other authors (see Table S1). These observations clearly highlight the importance of accounting for the formation of reaction intermediates, as well as the need to include an inhibition factor in the kinetic model (kT in hydroxyl radical molar balance Equation (31)) to reflect the presence of species that terminate the radical chains and hence slow down the degradation of the target pollutants.
2.3.1. Comparison with Photocatalytic Results from Literature
The photocatalytic degradation results obtained in this study are consistent with trends previously reported in the literature (see Table S1). For instance, the rapid and nearly complete removal of all compounds within 15 min under optimized TiO2 conditions aligns with the high efficiencies reported for ATL and CLA using visible or UV-based photocatalysis. In particular, ATL removal values of 75–82% after 60 min have been observed with both UV (60 W) and visible light sources at higher catalyst doses (1.5–3.0 g·L−1) [72], while our system achieves full removal in a significantly shorter time with a lower dose. Similarly, although TOC reduction in our system remains moderate (13–51% depending on catalyst load), it matches or exceeds the values reported in pilot-scale studies such as that of TiO2 P25 under solar CPCs (TOC removal of 40%) [73], or CLA degradation with Pd-doped TiO2 under UV-A (TOC reductions of 32–65%) [74]. These comparisons confirm that the enhanced performance observed here may be attributed not only to the catalyst’s activity, but also to optimized operational parameters such as pollutant concentration, mixing, and reactor design.
2.3.2. Mechanism and Kinetic Model
The photocatalytic kinetic model builds upon the photolysis reaction mechanism and incorporates additional steps arising from radiation absorption by the catalyst. First of the steps to add is the formation of charges (positive holes, h+, and electrons, e−) caused by excitation from the valence to the conduction band of TiO2, due to the high energy associated to 254 nm wavelength (4.89 eV) that vastly exceeds the band gap of the catalyst (3.2 eV) [75]:
Oxidizing holes, h+, subsequently react with water or hydroxyl ions adsorbed on the catalyst surface, producing adsorbed hydroxyl radicals that can subsequently react with pharmaceuticals [76]:
and
In turn, the electrons react with oxygen to generate adsorbed superoxide ion radicals [77]:
Finally, recombination of charges regenerates the catalyst surface, releasing energy [75]:
Also, hydrogen peroxide formed from free radical recombination, Equations (12) and (13), reacts with electrons to form more hydroxyl radicals [77]:
As described in the photolysis section, the photocatalysis kinetic model also requires solving a system of first-order ordinary differential equations of mass balances of species participating in the reacting system Equations (23) – (40). Now, to the reaction rate of the photolysis kinetic model, ri, the following terms were added:
- (a)
- For the balance of pharmaceuticals (Equation (24)):where kHOMs and CHOs are the rate constants of the reaction between any pharmaceutical M and adsorbed hydroxyl radicals and the concentration of the latter, respectively. However, adsorbed hydroxyl radicals are in equilibrium with hydroxyl radicals in solutions, that is, CHOs = KHO· CHO· [76], so that Equation (47) can be expressed as follows:with kHOs-M = kHO-M KHO·, the latter being the equilibrium constant [76].Initial values of kHOs-M for the photocatalytic kinetic model at TiO2 concentration of 0.1 g·L−1 were adopted from previous work [76] and initially considering the proportionality with TiO2 concentration for other catalyst concentrations. Table S3 shows the final optimized values of kHOs-M applied in the kinetic model. A proportional relationship between kHOs-M and catalyst concentration was ultimately observed. For instance, with some exception, kHOs-M values for 0.1 g·L−1 TiO2 concentration are twice the values for a 0.05 g·L−1 TiO2 concentration, and the corresponding proportionality was found for 0.25 g·L−1 catalyst concentration. Something similar was applied in the case of reactions of pharmaceuticals with adsorbed superoxide ion radical. Nevertheless, the contribution of these reactions was found to be negligible, so that only the superoxide ion radical reactions in solution, as in the photolysis kinetic model, were considered.
- (b)
- For the balance of hydroxyl radicals:where Ch+ and Ce− are the concentrations of holes and electrons, which are considered equal [78] and expressed as follows:wherewith k1s being a function of the rate constant of reaction (42), equilibrium constant between adsorbed and non-adsorbed hydroxyl radicals and catalyst concentration [76] and r0 is the TiO2 photon absorption rate calculated by solving the radiative transfer balance using the Six Flux Model (SFM) [79] (see Table S3 for r0 values). It has to be noted that for 0.25 g·L−1 catalyst concentration, the r0 value obtained from SFM was higher than the incident intensity of radiation, so this latter rate was taken as the photon absorption rate for this catalyst concentration. Therefore, at this catalyst concentration, the direct photolysis rate of pharmaceuticals, hydrogen peroxide, and WWEf was not included in the kinetic model. As a result, the participation of singlet oxygen was not considered either.
- (c)
- For the balance of total hydrogen peroxide:
- (d)
- For the balance of superoxide ion radical [76]:wherewith C*O2 as oxygen solubility in water.
The kinetic model was then solved with initial conditions (39) and (40) with the Ode23s code of MATLAB 2024b and rate constants shown in Tables S2 and S3. Figure 5 also presents kinetic model calculated results of the photocatalytic degradation of the mixture of pharmaceuticals using different concentrations of TiO2 (0.05, 0.10, and 0.25 g·L−1). Figure 5a–c show the temporal evolution of the dimensionless concentrations (C/C0) of the pharmaceuticals, while Figure 5d–g display the simulated evolution of the main reactive species concentrations: HO•, O2•−, 1O2, and H2O2, respectively.
As shown in Figure 5a–c, increasing the TiO2 concentration slightly enhances the degradation rate of all four pharmaceuticals. The fastest degradation occurs with 0.25 g·L−1 (Figure 5c), as indicated by the steeper decline in C/C0 values relative to the other two concentrations. This behavior is attributed to the greater availability of active sites. However, the generation of hydroxyl radicals, which can be considered as the main oxidizing ROS, increases for 0.05 to 0.1 g·L−1 but it decreases at the highest photocatalyst concentration tested, 0.25 g·L−1, which can be due to light attenuation at high TiO2 concentrations (Figure 5d). Also, likely for similar reason, the degradation curves tend to converge after 10 min, irrespective of the TiO2 concentration applied.
The kinetic model accurately captures the degradation kinetics of the four pharmaceuticals, especially during the initial stages of the process, where differences among compounds are more evident. In later stages, slight deviations may be attributed to experimental limitations, the accumulation of intermediates, or partial deactivation of the photocatalyst. Nevertheless, overall agreement between experimental and simulated data confirms the ability of the model to accurately describe the system behavior under various operating conditions.
On the other hand, the evolution of O2•−, 1O2, and H2O2 concentration (Figure 5e–g) with time shows what seems to be a logical trend: the increase in catalyst concentration leads to an increase in these species concentrations. An opposite trend is observed in the case of hydroxyl radical concentration, which can explain the slight differences observed in pharmaceutical concentrations (both calculated and experimental) with varying TiO2 concentrations.
In summary, the results confirm that increasing TiO2 concentration improves photocatalytic performance up to a certain point. Beyond this threshold, excess TiO2 may cause light scattering or shielding effects, which reduce process efficiency. The simulated ROS concentrations provide further insight into the degradation mechanisms, highlighting the predominant role of hydroxyl radicals and the complementary roles of other species, including the superoxide ion radical, singlet oxygen, and hydrogen peroxide.
2.4. Importance of End Radical Reactions
The comparison between experimental and simulated degradation curves in secondary effluent when intermediate reactions are not considered in the kinetic model (shown in Figure S6) highlights the importance of their inclusion in the model. Nonetheless, in UVC photolysis, from Figure S6a, it is seen that for the first 10–15 min, there is an acceptable agreement between experimental and calculated concentrations, even for the case of CLA and ANT. However, at higher reaction times, when these two compounds have already been completely removed, the deviation between experimental and calculated concentrations of ATL and ACM starts to be of increasing importance. There are two possible explanations for this behavior: (a) It is likely that due to the faster reaction rates of CLA and ANT, competition of intermediates could be negligible during the time these compounds need to be removed. The results obtained from the kinetic model when intermediate reactions (18) and (20) were not considered support this fact. (see Section 2.4 and Figure S6a,b. (b) The rate-terminating term (kT for hydroxyl radicals and kTT for superoxide ion radicals) should be a function of time, of practically negligible value during the initial minutes, as intermediates at such low concentrations do not yet compete for free radicals and radiation. The situation changes at higher reaction times, where competition becomes important as calculated concentrations of ACM and ATL start to be much lower than the experimental ones. However, during UVC photocatalysis, for kT and kTT = 0 (reactions (18) and (20)), removal of pharmaceuticals is almost instantaneous, highlighting the importance of free radical termination reactions. This indicates a higher formation of intermediate and end products in UVC photocatalytic oxidation.
3. Materials and Methods
3.1. Chemicals
The pharmaceuticals ATL (CAS 29122-68-7, 99%), CLA (CAS 882-09-7, >99.5%), ACM (CAS 103-90-2, 99%), and ANT (CAS 60-80-0, >99.5%) were purchased from Sigma-Aldrich (Burlington, MA, USA). Sodium hydroxide (CAS 1310-73-2, 99.5%) and hydrogen peroxide (CAS 7722-84-1, 30%) were purchased from PanReac AppliChem (Barcelona, Spain). Titanium (IV) oxysulfate (CAS 123334-00-9, >29%), sodium azide (CAS 26628-22-8, >99.5%), and tert-butanol (CAS 75-65-0, 99.5%), TIRON (4,5-Dihydroxy-1,3-benzenedisulfonic acid disodium salt monohydrate, CAS:270573-71-2, Sigma-Aldrich, 99%) were also obtained from Sigma-Aldrich, Furfural (Fischer Scientific, Waltham, MA, USA, CAS: 98-01-1), Rose Bengal (4,5,6,7-Tetrachloro-2′,4′,5′,7′-tetraiodofluorescein disodium salt, Sigma-Aldrich, CAS: 632-69-9). Ortho-phosphoric acid (PanReac AppliChem, CAS 7664-38-2) and acetonitrile (PanReac AppliChem, CAS 75-05-8). TiO2 P25 Aeroxide® was supplied by Evonik Industries (Essen, Germany). This photocatalyst is widely used in photocatalytic studies due to its well-known physicochemical properties, including a high surface area (~50 m2/g), average particle size of 30 nm, and a mixed-phase composition of approximately 70% anatase and 30% rutile [80]. Ultrapure water was sourced from a Milli-Q system with a resistivity of 18.2 MΩ·cm.
The wastewater effluent (WWEf) from a municipal wastewater treatment plant (WWTP) was used as the matrix to evaluate the process’s performance. This effluent was pre-filtered using an S-PAC filter with a pore size of 0.45 µm (Merck, Darmstadt, Germany) to remove solid particles and stored in a refrigerator at 5 °C. The pre-treated effluent was used within five days of collection to ensure sample integrity. The physicochemical characterization of the WWEf is presented in Table S4 of the Supplementary section.
3.2. Photochemical Experiments
The photochemical experiments were performed in an 800 mL cylindrical glass reactor equipped with a 15 W low-pressure mercury vapor UVC lamp (Heraeus, model TNN 15–32) emitting mainly at 254 nm. The lamp was placed in the middle of the reactor inside a quartz sleeve provided with a cooling jacket. The incident radiation (I0) and the effective light path length of the reactor (L) were determined using hydrogen peroxide as an actinometer following standard procedures described elsewhere [81]. Values of 3.99 × 10−6 Einstein·L−1·s−1 and 1.81 cm were found for I0 and L, respectively. The apparent and direct quantum yields of the pharmaceuticals at 254 nm were determined by photolysis experiments under UVC radiation in the absence and presence of t-butanol (TBA) (0.01 M), TIRON, and sodium azide (NaN3) (0.01 M) [40].
Simple photolysis experiments were conducted for each pharmaceutical individually and for a mixture of the four pharmaceuticals collectively, using both ultrapure water and wastewater buffered in advance with phosphate buffer at pH 7 (2 mM). The initial concentration of each pharmaceutical was set at 0.5 mg·L−1. Photocatalytic experiments were carried out following the same procedure, with TiO2 P25 being added beforehand in varying concentrations ranging from 0.05 to 0.25 g·L−1. The aqueous mixture containing the pharmaceuticals and the powdered catalyst was kept under stirring in the dark for 30 min using a magnetic stirrer to allow the potential adsorption of the contaminants on the surface of the catalyst.
Before the experiment started, the UVC lamp was turned on to stabilize the emission and ensure consistent irradiance at the beginning of the test. After the stabilization period, the lamp was turned off, and the solution containing the pharmaceutical, with or without the catalyst, was introduced. The cooling system for the lamp was activated, and the lamp was switched on again, marking the start of the experiment. Samples were collected at intervals during the experiment and filtered (using 0.45 µm syringe filters, Millex-HA®, Millipore, Darmstadt, Germany) if TiO2 P25 was present for subsequent analysis.
3.3. Analytical Methods
The absorption spectra of pharmaceuticals were recorded from 200 to 400 nm using a spectrophotometer (Thermo Scientific UV-Vis Evolution 201, Waltham, MA, USA) and a quartz cuvette (1 cm path length). The molar absorption coefficient was determined at 254 nm after applying the Beer–Lambert law to spectrometric measurements of stock solutions of the pharmaceuticals at different concentrations at pH 7. A TOC-VSCH analyzer (Shimadzu, Kyoto, Japan) was used to determine the dissolved organic carbon. The concentrations of pharmaceuticals in water were analyzed using an HPLC-DAD (Hitachi, Elite LaChrom, San Jose, CA, USA), using a C-18 Phenomenex column (3 × 150 mm, 5 μm) provided with a degassing unit, an automatic injector, an oven, and a diode array detector. The analysis was performed using a gradient method with a mixture of acidified ultrapure water (H3PO4 0.1% v/v) and acetonitrile at 0.6 mL·min−1. The method started with 5 min of initial stabilization with a water (A) and acetonitrile (B) ratio of 95:5. A linear gradient for 5 min to reach 80:20 A:B followed, and this ratio was maintained for 4 min. Subsequently, a second linear gradient for 8 min up to 5:95 A:B was applied; this ratio was maintained for 1 min. Finally, in order to return to the initial conditions, a 1 min linear gradient is applied to achieve a 95:5 initial ratio of A to B, which is then maintained for 6 min The pharmaceutical concentrations were measured at the following wavelengths and retention times: ATL (λ = 230 nm, tr = 3.00 min), ACM (λ = 250 nm, tr = 5.10 min), ANT (λ = 250 nm, tr = 13.40 min), CLA (λ = 230 nm, tr = 21.80 min). The concentration of hydrogen peroxide was tried to be spectrophotometrically evaluated following the formation of the yellowish pertitanic acid at 405 nm [82]. For the determination of the second-order rate constant of each pharmaceutical with singlet oxygen, the same HPLC analytical method was used, where F was detected at λ = 278 nm with a retention time (tr) of 4.8 min.
4. Conclusions
This study proposes a comprehensive kinetic modeling approach for the UVC photolysis and UVC/TiO2 photocatalysis of a mixture of four representative pharmaceuticals (ATL, ACM, CLA, and ANT) in aqueous media. Experimental results confirmed the generation of hydroxyl and, to a lesser extent, superoxide ion radicals and singlet oxygen during photolysis. Determination of quantum yields and scavenger experiments enables ROS identification of the reactive oxygen species (ROS) involved in each case.
The validated kinetic model, incorporating ROS generation and reaction pathways, demonstrated strong predictive capabilities, especially for a secondary effluent matrix. The presence of natural organic matter in the effluent reduced photodegradation efficiency by competing for radiation and reactive species. This matrix effect was successfully integrated into the model by accounting for effluent absorbance and ROS quenching reactions.
Under photocatalytic conditions, significant enhancement of degradation rates was observed, particularly for slower-reacting compounds (ATL and ACM). The model also captured the influence of catalyst concentration on ROS evolution and degradation kinetics, identifying an optimal TiO2 loading beyond which performance declined due to scattering and recombination effects.
In summary, the proposed kinetic framework provides a detailed mechanistic understanding of pharmaceutical degradation in complex water matrices and offers a reliable tool for designing and optimizing advanced treatment processes under both photolytic and photocatalytic conditions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/catal15050471/s1, Figure S1. Comparison of initial scavenger and pharmaceutical absorbance at 254 nm. Conditions: CPharm = 0.5 ppm, CTBA,0 = 0.01 M, CNAN3,0 = 0.01 M. Figure S2. Fit of absorbance at 254 nm of wastewater effluent with time using the analytical solution of Equation (5), employing the quantum yield value calculated from experiments with TBA and TIRON. Initial conditions: Abs2540 = 0.160 a.u., CTiron0 = 0.001 M, CTBA,0 = 0.01 M pH0 = 7. Figure S3. Fitting Equation (3) to the experimental photolysis data: (a) ATL, (b) ACM, (c) CLA, (d) ANT. Conditions as in Figure 2. Green line: without scavengers; black line: with TBA and TIRON. Figure S4. Evaluation of Equation (4) based on the experiments with Rose Bengal. ATL, (b) ACM, (c) CLA, (d) ANT. Determination of the singlet oxygen-pharmaceutical reaction rate constant. Figure S5. Total organic carbon (TOC) removal during photolysis and photocatalysis of the mixture of pharmaceuticals in effluent wastewater: experimental results. Conditions: CPharm0 = 0.5 mg·L−1, pH0 = 7, Io = 3.99 × 10−6 Einstein·L−1s−1, TOC0 = 8.52 mg·L−1. Figure S6. Experimental degradation profiles (symbols) in secondary effluent under (a) photolytic (UVC) and (b) photocatalytic (UVC/TiO2) conditions. Solid lines represent simulation results obtained without including termination and intermediate degradation reactions in the kinetic model. Table S1. Key results and experimental conditions from references related to the UVC photolysis and TiO2-photocatalytic removal of the selected compounds. Table S2. Kinetic parameters and rate constants used in the photolysis modela. Table S3. Kinetic parameters and rate constants used in the photocatalysis modela. Table S4. Chemical characterization of secondary effluent. References [83,84,85,86] are cited in the Supplementary Materials.
Author Contributions
Conceptualization, M.A.J.-L. and F.J.B.; methodology, M.A.J.-L.; software, F.J.B.; validation, M.A.J.-L. and M.C.R.-G.; formal analysis, M.A.J.-L. and M.C.R.-G.; investigation, M.A.J.-L. and M.C.R.-G.; resources, F.J.B.; data curation, M.A.J.-L. and M.C.R.-G.; writing—original draft preparation, M.A.J.-L. and F.J.B.; writing—review and editing, M.A.J.-L. and F.J.B.; visualization, M.A.J.-L.; supervision, F.J.B.; project administration, F.J.B.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Ministerio de Ciencia e Innovación and Agencia Estatal de Investigación Grant PID2023-149919OB-I00 funded by MCIN/AEI/ 10.13039/501100011033 and by ESF+.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Acknowledgments
The authors gratefully acknowledge financial support from Grant PID2023-149919OB-I00 funded by MCIN/AEI/ 10.13039/501100011033 and by ESF+. M.A. Jiménez-López thanks the Ministry of Science, Innovation, and Universities for granting the FPI PRE2020-091840 research training scholarship.
Conflicts of Interest
The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Kanakaraju, D.; Glass, B.D.; Oelgemöller, M. Advanced Oxidation Process-Mediated Removal of Pharmaceuticals from Water: A Review. J. Environ. Manag. 2018, 219, 189–207. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Sarmah, A.K.; Padhye, L.P. Fate of Pharmaceuticals and Personal Care Products in a Wastewater Treatment Plant with Parallel Secondary Wastewater Treatment Train. J. Environ. Manag. 2019, 233, 649–659. [Google Scholar] [CrossRef]
- Peña-Guzmán, C.; Ulloa-Sánchez, S.; Mora, K.; Helena-Bustos, R.; Lopez-Barrera, E.; Alvarez, J.; Rodriguez-Pinzón, M. Emerging Pollutants in the Urban Water Cycle in Latin America: A Review of the Current Literature. J. Environ. Manag. 2019, 237, 408–423. [Google Scholar] [CrossRef]
- Rivera-Utrilla, J.; Sánchez-Polo, M.; Ferro-García, M.Á.; Prados-Joya, G.; Ocampo-Pérez, R. Pharmaceuticals as Emerging Contaminants and Their Removal from Water. A Review. Chemosphere 2013, 93, 1268–1287. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Senn, D.B.; Moran, R.E.; Shine, J.P. Prioritizing Environmental Risk of Prescription Pharmaceuticals. Regul. Toxicol. Pharmacol. 2013, 65, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Oates, R.P.; Longley, G.; Hamlett, P.; Klein, D. Pharmaceutical and Endocrine Disruptor Compounds in Surface and Wastewater in San Marcos, Texas. Water Environ. Res. 2017, 89, 2021–2030. [Google Scholar] [CrossRef]
- Haro, N.K.; Del Vecchio, P.; Marcilio, N.R.; Féris, L.A. Removal of Atenolol by Adsorption—Study of Kinetics and Equilibrium. J. Clean Prod. 2017, 154, 214–219. [Google Scholar] [CrossRef]
- Papageorgiou, M.; Kosma, C.; Lambropoulou, D. Seasonal Occurrence, Removal, Mass Loading and Environmental Risk Assessment of 55 Pharmaceuticals and Personal Care Products in a Municipal Wastewater Treatment Plant in Central Greece. Sci. Total Environ. 2016, 543, 547–569. [Google Scholar] [CrossRef]
- Ulvi, A.; Aydın, S.; Aydın, M.E. Fate of Selected Pharmaceuticals in Hospital and Municipal Wastewater Effluent: Occurrence, Removal, and Environmental Risk Assessment. Environ. Sci. Pollut. Res. 2022, 29, 75609–75625. [Google Scholar] [CrossRef]
- Folarin, O.S.; Otitoloju, A.A.; Amaeze, N.H.; Saliu, J.K. Occurrence of Acetaminophen, Amoxicillin, Diclofenac and Methylparaben in Lagos and Ologe Lagoons, Lagos, Nigeria. J. Appl. Sci. Environ. Manag. 2019, 23, 2143–2149. [Google Scholar] [CrossRef]
- McLain, N.K.; Gomez, M.Y.; Gachomo, E.W. Acetaminophen Levels Found in Recycled Wastewater Alter Soil Microbial Community Structure and Functional Diversity. Microb. Ecol. 2023, 85, 1448–1462. [Google Scholar] [CrossRef]
- Ayman, Z.; Işik, M. Pharmaceutically Active Compounds in Water, Aksaray, Turkey. Clean 2015, 43, 1381–1388. [Google Scholar] [CrossRef]
- Pozdnyakov, I.P.; Zhang, X.; Maksimova, T.A.; Yanshole, V.V.; Wu, F.; Grivin, V.P.; Plyusnin, V.F. Wavelength-Dependent Photochemistry of Acetaminophen in Aqueous Solutions. J. Photochem. Photobiol. A Chem. 2014, 274, 117–123. [Google Scholar] [CrossRef]
- Roveri, V.; Guimarães, L.L.; Toma, W.; Correia, A.T. Occurrence, Ecological Risk Assessment and Prioritization of Pharmaceuticals and Abuse Drugs in Estuarine Waters along the São Paulo Coast, Brazil. Environ. Sci. Pollut. Res. 2022, 29, 89712–89726. [Google Scholar] [CrossRef] [PubMed]
- Cai, M.; Zhang, L.; Qi, F.; Feng, L. Influencing Factors and Degradation Products of Antipyrine Chlorination in Water with Free Chlorine. J. Environ. Sci. 2013, 25, 77–84. [Google Scholar] [CrossRef]
- Gomes, I.B.; Simões, L.C.; Simões, M. The Effects of Emerging Environmental Contaminants on Stenotrophomonas Maltophilia Isolated from Drinking Water in Planktonic and Sessile States. Sci. Total Environ. 2018, 643, 1348–1356. [Google Scholar] [CrossRef]
- Benotti, M.J.; Trenholm, R.A.; Vanderford, B.J.; Holady, J.C.; Stanford, B.D.; Snyder, S.A. Pharmaceuticals and Endocrine Disrupting Compounds in U.S. Drinking Water. Environ. Sci. Technol. 2009, 43, 597–603. [Google Scholar] [CrossRef]
- Lu, J.; Huang, Q.; Mao, L. Removal of Acetaminophen Using Enzyme-Mediated Oxidative Coupling Processes: I. Reaction Rates and Pathways. Environ. Sci. Technol. 2009, 43, 7062–7067. [Google Scholar] [CrossRef]
- Hwang, J.I.; Li, Z.; Andreacchio, N.; Ordonez Hinz, F.; Wilson, P.C. Potential Use of Floating Treatment Wetlands Established with Canna Flaccida for Removing Organic Contaminants from Surface Water. Int. J. Phytoremediat. 2020, 22, 1304–1312. [Google Scholar] [CrossRef]
- Qutob, M.; Hussein, M.A.; Alamry, K.A.; Rafatullah, M. A Review on the Degradation of Acetaminophen by Advanced Oxidation Process: Pathway, by-Products, Biotoxicity, and Density Functional Theory Calculation. RSC Adv. 2022, 12, 18373–18396. [Google Scholar] [CrossRef]
- Quesada, H.B.; Cusioli, L.F.; de O Bezerra, C.; Baptista, A.T.A.; Nishi, L.; Gomes, R.G.; Bergamasco, R. Acetaminophen Adsorption Using a Low-Cost Adsorbent Prepared from Modified Residues of Moringa Oleifera Lam. Seed Husks. J. Chem. Technol. Biotechnol. 2019, 94, 3147–3157. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, X.; Liu, Y. New Insights into the Primary Phototransformation of Acetaminophen by UV/H2O2: Photo-Fries Rearrangement versus Hydroxyl Radical Induced Hydroxylation. Water Res. 2015, 86, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Rivas, J.; Gimeno, O.; Borralho, T.; Sagasti, J. UV-C and UV-C/Peroxide Elimination of Selected Pharmaceuticals in Secondary Effluents. Desalination 2011, 279, 115–120. [Google Scholar] [CrossRef]
- Ioannou, L.A.; Hapeshi, E.; Vasquez, M.I.; Mantzavinos, D.; Fatta-Kassinos, D. Solar/TiO2 Photocatalytic Decomposition of β-Blockers Atenolol and Propranolol in Water and Wastewater. Sol. Energy 2011, 85, 1915–1926. [Google Scholar] [CrossRef]
- Salgado, R.; Pereira, V.J.; Carvalho, G.; Soeiro, R.; Gaffney, V.; Almeida, C.; Cardoso, V.V.; Ferreira, E.; Benoliel, M.J.; Ternes, T.A.; et al. Photodegradation Kinetics and Transformation Products of Ketoprofen, Diclofenac and Atenolol in Pure Water and Treated Wastewater. J. Hazard. Mater. 2013, 244–245, 516–527. [Google Scholar] [CrossRef] [PubMed]
- Su, C.C.; Bellotindos, L.M.; Chang, A.T.; Lu, M.C. Degradation of Acetaminophen in an Aerated Fenton Reactor. J. Taiwan Inst. Chem. Eng. 2013, 44, 310–316. [Google Scholar] [CrossRef]
- Dewil, R.; Mantzavinos, D.; Poulios, I.; Rodrigo, M.A. New Perspectives for Advanced Oxidation Processes. J. Environ. Manag. 2017, 195, 93–99. [Google Scholar] [CrossRef]
- Parsons, S. Advanced Oxidation Processes for Water and Wastewater Treatment. Water Intell. Online 2005, 4, 9781780403076. [Google Scholar] [CrossRef]
- Xiao, R.; Wei, Z.; Chen, D.; Weavers, L.K. Kinetics and Mechanism of Sonochemical Degradation of Pharmaceuticals in Municipal Wastewater. Environ. Sci. Technol. 2014, 48, 9675–9683. [Google Scholar] [CrossRef]
- Tang, Y.; Li, X.M.; Xu, Z.C.; Guo, Q.W.; Hong, C.Y.; Bing, Y.X. Removal of Naproxen and Bezafibrate by Activated Sludge under Aerobic Conditions: Kinetics and Effect of Substrates. Biotechnol. Appl. Biochem. 2014, 61, 333–341. [Google Scholar] [CrossRef]
- Moreno, A.d.H.; Salgado, H.R.N. Stability Study and Degradation Kinetics of Ceftazidime in Pharmaceutical Preparations. Adv. Anal. Chem. 2012, 2, 1–5. [Google Scholar] [CrossRef]
- Tazesh, S.; Tamizi, E.; Siahi Shadbad, M.; Mostaghimi, N.; Monajjemzadeh, F. Comparative Stability of Two Anti-Hyperpigmentation Agents: Kojic Acid as a Natural Metabolite and Its Di-Palmitate Ester, Under Oxidative Stress; Application to Pharmaceutical Formulation Design. Adv. Pharm. Bull. 2022, 12, 329–335. [Google Scholar] [CrossRef] [PubMed]
- Bhangare, D.; Rajput, N.; Jadav, T.; Sahu, A.K.; Tekade, R.K.; Sengupta, P. Systematic Strategies for Degradation Kinetic Study of Pharmaceuticals: An Issue of Utmost Importance Concerning Current Stability Analysis Practices. J. Anal. Sci. Technol. 2022, 13, 1–13. [Google Scholar] [CrossRef]
- Wang, C.; Xiong, M.C.; Zhao, X.; Liu, K.H. Kinetics Study on Reaction of Atenolol with Singlet Oxygen by Directly Monitoring the 1O2 Phosphorescence. Chin. J. Chem. Phys. 2021, 34, 406–412. [Google Scholar] [CrossRef]
- Chen, P.; Wang, F.; Zhang, Q.; Su, Y.; Shen, L.; Yao, K.; Chen, Z.F.; Liu, Y.; Cai, Z.; Lv, W.; et al. Photocatalytic Degradation of Clofibric Acid by G-C3N4/P25 Composites under Simulated Sunlight Irradiation: The Significant Effects of Reactive Species. Chemosphere 2017, 172, 193–200. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Kong, Q.; Liu, G.; Lv, W.; Li, F.; Lin, X. Aquatic Photodegradation of Clofibric Acid under Simulated Sunlight Irradiation: Kinetics and Mechanism Analysis. RSC Adv. 2018, 8, 27796–27804. [Google Scholar] [CrossRef] [PubMed]
- Bielski, B.H.J.; Cabelli, D.E.; Arudi, R.L.; Ross, A.B. Reactivity of HO2/O−2 Radicals in Aqueous Solution. J. Phys. Chem. Ref. Data 1985, 14, 1041–1100. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Fan, L.; Su, L.; Zhao, Y. Photolysis Mechanism of Eleven Insecticides under Simulated Sunlight Irradiation: Kinetics, Pathway and QSAR. Chemosphere 2023, 334, 138968. [Google Scholar] [CrossRef]
- Rodríguez, E.M.; Márquez, G.; Tena, M.; Álvarez, P.M.; Beltrán, F.J. Determination of Main Species Involved in the First Steps of TiO2 Photocatalytic Degradation of Organics with the Use of Scavengers: The Case of Ofloxacin. Appl. Catal. B 2015, 178, 44–53. [Google Scholar] [CrossRef]
- Beltrán, F.J.; Chávez, A.M.; Jiménez-López, M.A.; Álvarez, P.M. Kinetic Modelling of UVC and UVC/H2O2 Oxidation of an Aqueous Mixture of Antibiotics in a Completely Mixed Batch Photoreactor. Environ. Sci. Pollut. Res. 2024, 31, 55222–55238. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, K.; Zhao, H. The Debatable Role of Singlet Oxygen in Persulfate-Based Advanced Oxidation Processes. Water Res. 2023, 235, 119925. [Google Scholar] [CrossRef]
- Nidheesh, P.V.; Boczkaj, G.; Ganiyu, S.O.; Oladipo, A.A.; Fedorov, K.; Xiao, R.; Dionysiou, D.D. Generation, Properties, and Applications of Singlet Oxygen for Wastewater Treatment: A Review. Environ. Chem. Lett. 2025, 23, 195–240. [Google Scholar] [CrossRef]
- Katsumata, C.P.; Parizi, M.P.S.; Lastre-Acosta, A.M.; Teixeira, A.C.S.C. Low Pressure UV Photolysis of the Pharmaceutical Compounds Acetaminophen, Atenolol, Bezafibrate, Diclofenac and Ibuprofen. Water 2022, 14, 3165. [Google Scholar] [CrossRef]
- Li, W.; Lu, S.; Qiu, Z.; Lin, K. Clofibric Acid Degradation in UV254/H2O2 Process: Effect of Temperature. J. Hazard. Mater. 2010, 176, 1051–1057. [Google Scholar] [CrossRef]
- Tan, C.; Gao, N.; Deng, Y.; Zhang, Y.; Sui, M.; Deng, J.; Zhou, S. Degradation of Antipyrine by UV, UV/H2O2 and UV/PS. J. Hazard Mater. 2013, 260, 1008–1016. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Guo, Y.; Zhan, J.; Yu, G.; Wang, Y. Assessment of the Validity of the Quenching Method for Evaluating the Role of Reactive Species in Pollutant Abatement during the Persulfate-Based Process. Water Res. 2022, 221, 118730. [Google Scholar] [CrossRef]
- Du, C.; Cheng, D.; Dai, J.; Du, Q.; Shao, A. Differences in the Ability of Dissolved Organic Matter from Different Sources to Produce Reactive Oxygen Species under Light Irradiation. Huanjing Kexue Xuebao/Acta Sci. Circumstantiae 2019, 39, 2279–2287. [Google Scholar] [CrossRef]
- Fujii, M.; Otani, E. Photochemical Generation and Decay Kinetics of Superoxide and Hydrogen Peroxide in the Presence of Standard Humic and Fulvic Acids. Water Res. 2017, 123, 642–654. [Google Scholar] [CrossRef]
- Vione, D.; Scozzaro, A. Photochemistry of Surface Fresh Waters in the Framework of Climate Change. Environ. Sci. Technol. 2019, 53, 7945–7963. [Google Scholar] [CrossRef]
- Westerhoff, P.; Song, R.; Amy, G.; Minear, R. Applications of Ozone Decomposition Models. Ozone Sci. Eng. 1997, 19, 55–73. [Google Scholar] [CrossRef]
- Rabani, J.; Matheson, M.S. The Pulse Radiolysis of Aqueous Solutions of Potassium Ferrocyanide. J. Phys. Chem. 1966, 70, 761–769. [Google Scholar] [CrossRef]
- Baxendale, J.H.; Wilson, J.A. The Photolysis of Hydrogen Peroxide at High Light Intensities. Trans. Faraday Soc. 1957, 53, 344–356. [Google Scholar] [CrossRef]
- Christensen, H.; Sehested, K.; Corfitzen, H. Reactions of Hydroxyl Radicals with Hydrogen Peroxide at Ambient and Elevated Temperatures. J. Phys. Chem. 1982, 86, 1588–1590. [Google Scholar] [CrossRef]
- Staehelln, J.; Hoigne, J. Decomposition of Ozone in Water in the Presence of Organic Solutes Acting as Promoters and Inhibitors of Radical Chain Reactions. Environ. Sci. Technol. 1985, 19, 1206–1213. [Google Scholar] [CrossRef]
- Fogler, H.S. Elements of Chemical Reaction Engineering; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1999; ISBN 0135317088. [Google Scholar]
- Leifer, A. The Kinetics of Environmental Aquatic Photochemistry American Chemical Society. In ACS Professional and Reference Book; Oxford University Press: New York, NY, USA, 1988. [Google Scholar]
- Buxton, G.V.; Greenstock, C.L.; Helman, W.P.; Ross, A.B. Critical Review of Rate Constants for Reactions of Hydrated Electrons, Hydrogen Atoms and Hydroxyl Radicals (·OH/·O− in Aqueous Solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. [Google Scholar] [CrossRef]
- Brame, J.; Long, M.; Li, Q.; Alvarez, P. Trading Oxidation Power for Efficiency: Differential Inhibition of Photo-Generated Hydroxyl Radicals versus Singlet Oxygen. Water Res. 2014, 60, 259–266. [Google Scholar] [CrossRef]
- Ahn, Y.; Lee, D.; Kwon, M.; Choi, I.h.; Nam, S.N.; Kang, J.W. Characteristics and Fate of Natural Organic Matter during UV Oxidation Processes. Chemosphere 2017, 184, 960–968. [Google Scholar] [CrossRef]
- Song, C.; Zhang, K.X.; Wang, X.J.; Zhao, S.; Wang, S.G. Effects of Natural Organic Matter on the Photolysis of Tetracycline in Aquatic Environment: Kinetics and Mechanism. Chemosphere 2021, 263, 128338. [Google Scholar] [CrossRef]
- Fu, H.; Zheng, W.; Duan, W.; Fang, G.; Duan, X.; Wang, S.; Feng, C.; Zhu, S. Overlooked Roles and Transformation of Carbon-Centered Radicals Produced from Natural Organic Matter in a Thermally Activated Persulfate System. Environ. Sci. Technol. 2024, 58, 14949–14960. [Google Scholar] [CrossRef]
- Qin, W.; Wang, Y.; Fang, G.; Wu, T.; Liu, C.; Zhou, D. Evidence for the Generation of Reactive Oxygen Species from Hydroquinone and Benzoquinone: Roles in Arsenite Oxidation. Chemosphere 2016, 150, 71–78. [Google Scholar] [CrossRef]
- Calza, P.; Minella, M.; Demarchis, L.; Sordello, F.; Minero, C. Photocatalytic Rate Dependence on Light Absorption Properties of Different TiO2 Specimens. Catal. Today 2020, 340, 12–18. [Google Scholar] [CrossRef]
- Yang, Q.; Ling Ang, P.; Ray, M.B.; Pehkonen, S.O. Light Distribution Field in Catalyst Suspensions within an Annular Photoreactor. Chem. Eng. Sci. 2005, 60, 5255–5268. [Google Scholar] [CrossRef]
- Minero, C.; Vione, D. A Quantitative Evalution of the Photocatalytic Performance of TiO2 Slurries. Appl. Catal. B 2006, 67, 257–269. [Google Scholar] [CrossRef]
- Pellegrino, F.; Pellutiè, L.; Sordello, F.; Minero, C.; Ortel, E.; Hodoroaba, V.D.; Maurino, V. Influence of Agglomeration and Aggregation on the Photocatalytic Activity of TiO2 Nanoparticles. Appl. Catal. B 2017, 216, 80–87. [Google Scholar] [CrossRef]
- Luo, B.; Song, R.; Jing, D. Particle Aggregation Behavior during Photocatalytic Ethanol Reforming Reaction and Its Correlation with the Activity of H2 Production. Colloids Surf A Physicochem. Eng. Asp. 2017, 535, 114–120. [Google Scholar] [CrossRef]
- Ren, Y.; Jing, D. Study on Particle and Photonic Flux Distributions in a Magnetically Stirred Photocatalytic Reactor. J. Photonics Energy 2015, 5, 052097. [Google Scholar] [CrossRef]
- Wang, X.; Shui, M.; Li, R.; Song, Y. Correlation of Lattice Distortion with Photocatalytic Activity of Titanium Dioxide. Mater. Res. Bull. 2008, 43, 2476–2484. [Google Scholar] [CrossRef]
- Roushenas, P.; Ong, Z.C.; Ismail, Z.; Majidnia, Z.; Ang, B.C.; Asadsangabifard, M.; Onn, C.C.; Tam, J.H. Operational Parameters Effects on Photocatalytic Reactors of Wastewater Pollutant: A Review. Desalin. Water Treat. 2018, 120, 109–118. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Tao, Y.; Shen, L.; Xu, Z.; Bian, Z.; Li, H. Challenges of Photocatalysis and Their Coping Strategies. Chem. Catal. 2022, 2, 1315–1345. [Google Scholar] [CrossRef]
- Mehrabadi, Z.; Faghihian, H. Comparative Photocatalytic Performance of TiO2 Supported on Clinoptilolite and TiO2/Salicylaldehyde-NH2-MIL-101(Cr) for Degradation of Pharmaceutical Pollutant Atenolol under UV and Visible Irradiations. J. Photochem. Photobiol. A Chem. 2018, 356, 102–111. [Google Scholar] [CrossRef]
- Radjenović, J.; Sirtori, C.; Petrović, M.; Barceló, D.; Malato, S. Solar Photocatalytic Degradation of Persistent Pharmaceuticals at Pilot-Scale: Kinetics and Characterization of Major Intermediate Products. Appl Catal. B 2009, 89, 255–264. [Google Scholar] [CrossRef]
- Harja, M.; Sescu, A.M.; Favier, L.; Lutic, D. Doping Titanium Dioxide with Palladiun for Enhancing the Photocatalytic Decontamination and Mineralization of a Refractory Water Pollutant. Rev. Chim. 2020, 71, 145–152. [Google Scholar] [CrossRef]
- Turchi, C.S.; Ollis, D.F. Photocatalytic Degradation of Organic Water Contaminants: Mechanisms Involving Hydroxyl Radical Attack. J. Catal. 1990, 122, 178–192. [Google Scholar] [CrossRef]
- Beltrán, F.J.; Jiménez-López, M.A.; Álvarez, P.M.; Rivas, F.J. Kinetic Modeling of Photocatalytic Oxidation-Ozonation of Metronidazole Removal from Water. J. Environ. Chem. Eng. 2025, 13, 115869. [Google Scholar] [CrossRef]
- Milosavijević, B.H.; Mićić, O.I. Solvated Electron Reactions in Water—Alcohol Solutions. J. Phys. Chem. 1978, 82, 1359–1362. [Google Scholar] [CrossRef]
- Tolosana-Moranchel, A.; Casas, J.A.; Carbajo, J.; Faraldos, M.; Bahamonde, A. Influence of TiO2 Optical Parameters in a Slurry Photocatalytic Reactor: Kinetic Modelling. Appl. Catal. B 2017, 200, 164–173. [Google Scholar] [CrossRef]
- Beltrán, F.J.; Rivas, F.J.; García-araya, J.F. Six Flux Model for the Central Lamp Reactor Applied to an External Four-lamp Reactor. Catalysts 2021, 11, 1190. [Google Scholar] [CrossRef]
- Wong, C.C.; Chu, W. The Hydrogen Peroxide-Assisted Photocatalytic Degradation of Alachlor in TiO2 Suspensions. Environ. Sci. Technol. 2003, 37, 2310–2316. [Google Scholar] [CrossRef]
- Rabani, J.; Mamane, H.; Pousty, D.; Bolton, J.R. Practical Chemical Actinometry—A Review. Photochem. Photobiol. 2021, 97, 873–902. [Google Scholar] [CrossRef]
- O’Sullivan, D.W.; Tyree, M. The Kinetics of Complex Formation between Ti(IV) and Hydrogen Peroxide. Int. J. Chem. Kinet. 2007, 39, 457–461. [Google Scholar] [CrossRef]
- Dalida, M.L.P.; Amer, K.M.S.; Su, C.C.; Lu, M.C. Photocatalytic Degradation of Acetaminophen in Modified TiO2 under Visible Irradiation. Environ. Sci. Pollut. Res. 2014, 21, 1208–1216. [Google Scholar] [CrossRef] [PubMed]
- Shahabi, H.; Allahrasani, A.; Naghizadeh, A. Photocatalytic Degradation of Acetaminophen in Aqueous Solution in the Presence of Montmorillonite Nanosheets Modified with Titanium Dioxide. Desalin. Water Treat. 2019, 149, 164–170. [Google Scholar] [CrossRef]
- Silva, C.G.; Faria, J.L. Anatase vs Rutile Efficiency on the Photocatalytic Degradation of Clofibric Acid under near UV to Visible Irradiation. Photochem. Photobiol. Sci. 2009, 8, 705–711. [Google Scholar] [CrossRef]
- Peñas-Garzón, M.; Gómez-Avilés, A.; Álvarez-Conde, J.; Bedia, J.; García-Frutos, E.M.; Belver, C. Azaindole Grafted Titanium Dioxide for the Photodegradation of Pharmaceuticals under Solar Irradiation. J. Colloid Interface Sci. 2023, 629, 593–603. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).