Integrating Density Functional Theory Calculations and Machine Learning to Identify Conduction Band Minimum as a Descriptor for High-Efficiency Hydrogen Evolution Reaction Catalysts in Transition Metal Dichalcogenides
Abstract
1. Introduction
2. Results and Discussion
2.1. Crystal Structure
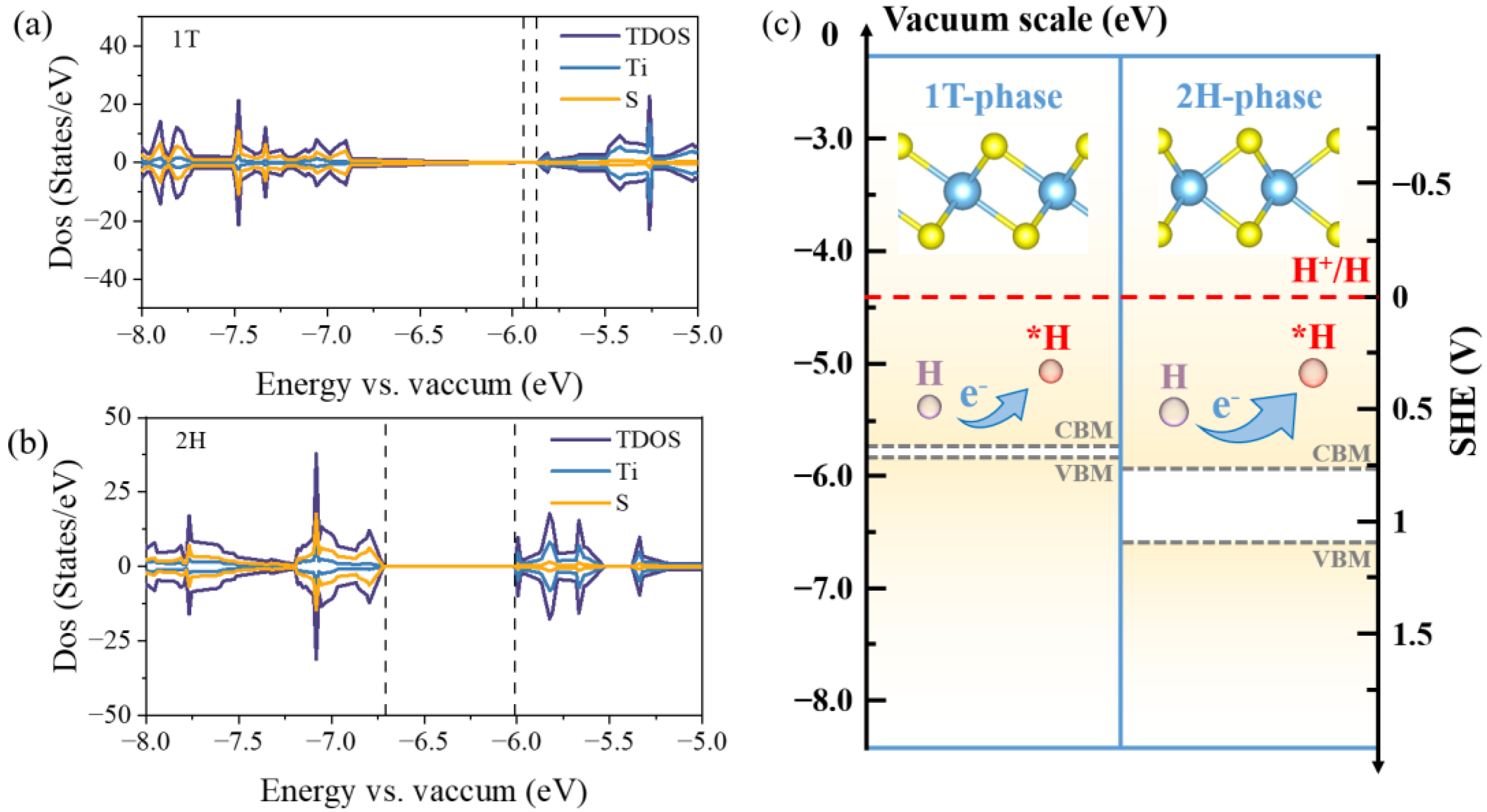
2.2. HER Activity on the Nanostructured TMDs
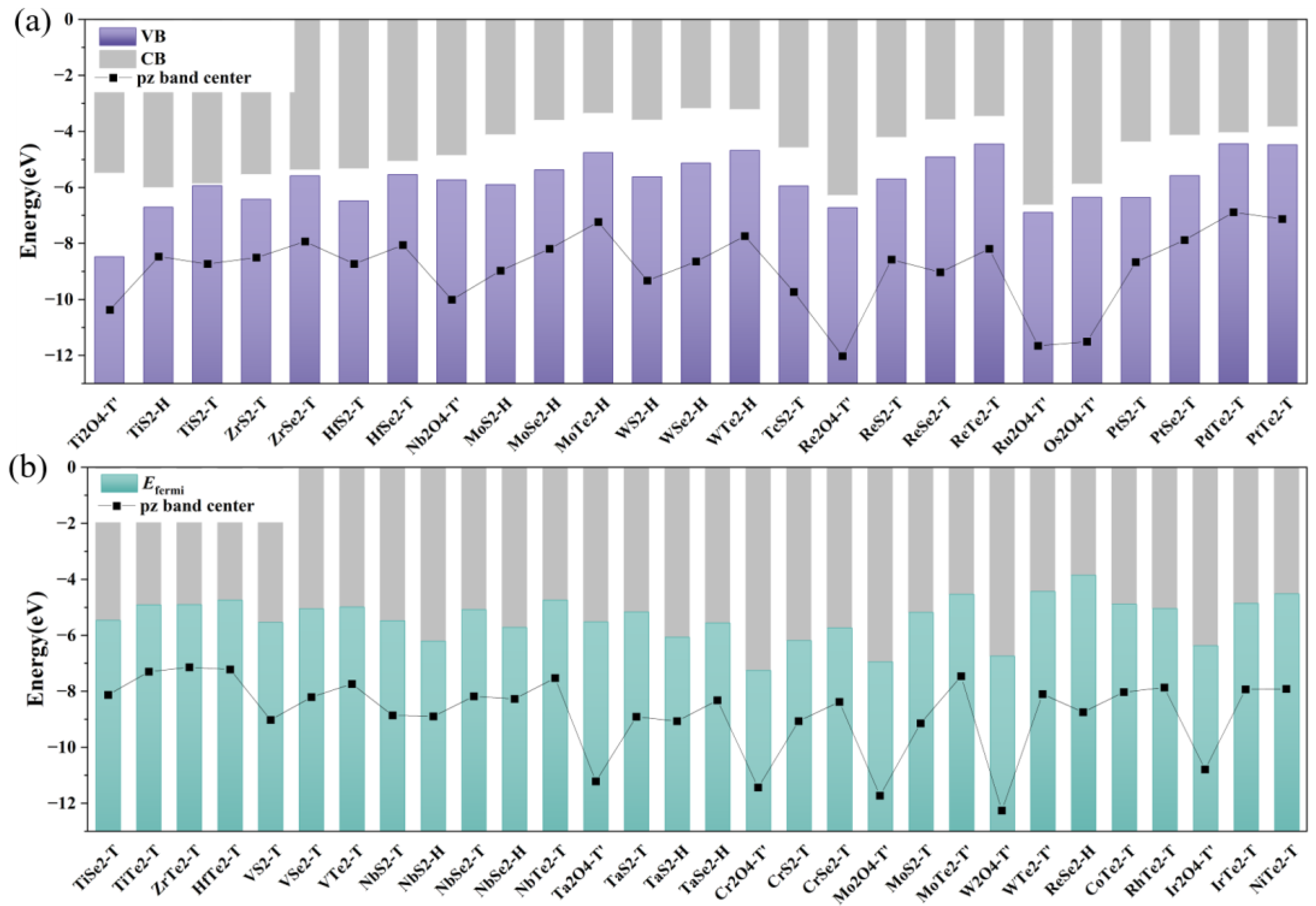
2.3. CB, VB, and pz Band Center of TMDs
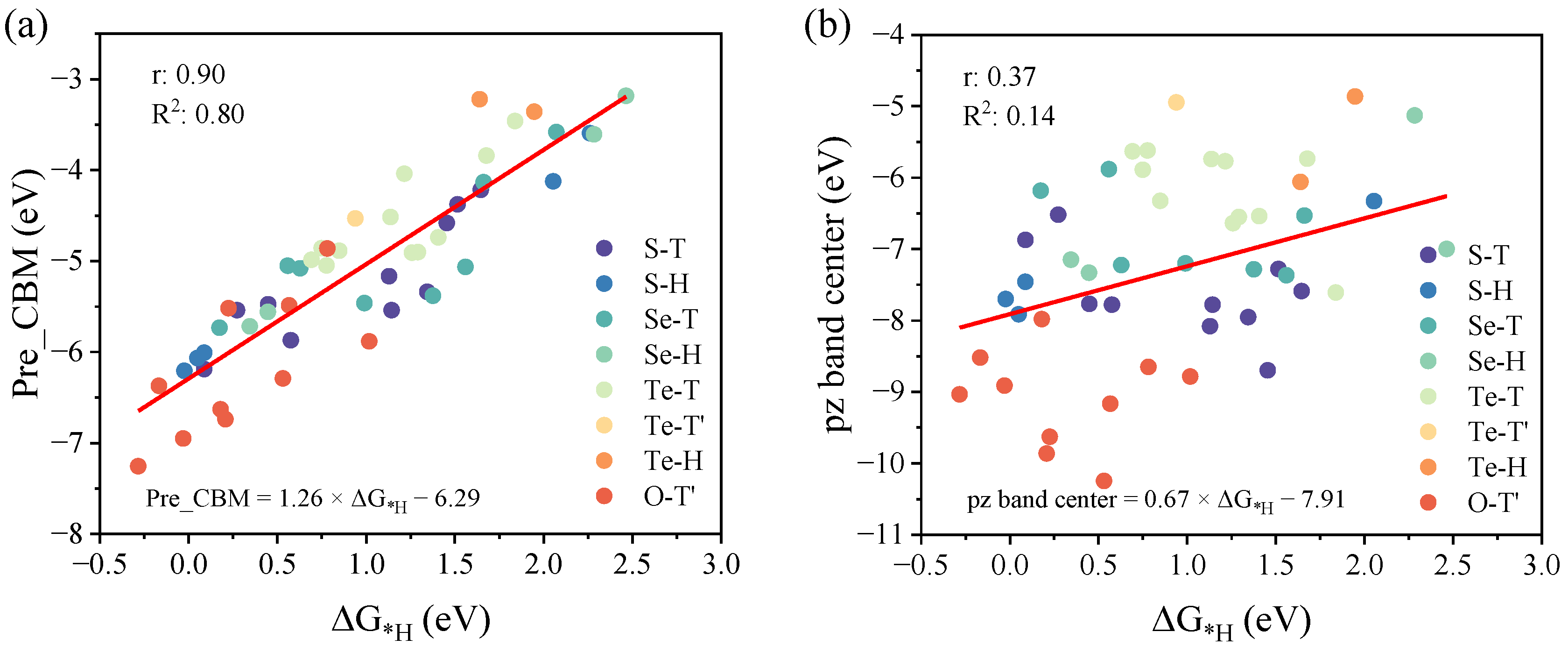
2.4. Selection and Analysis of HER Descriptors
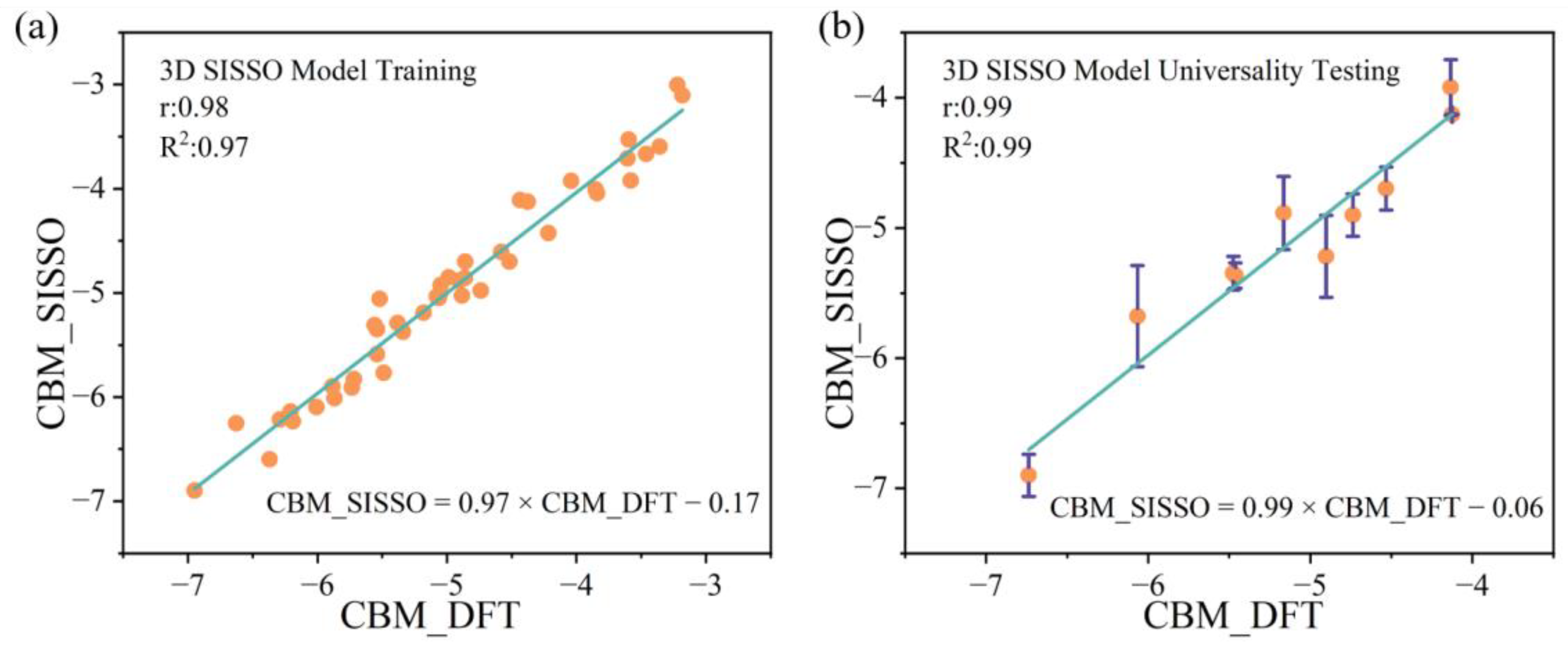
2.5. Construction of a 3D Descriptor for Predicting CBM Through Machine Learning
3. Computational Method
3.1. DFT Calculation and Parameters
3.2. Machine Learning Model and Performance Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, A.; Sun, Y.; Yao, T.; Han, H. Earth-Abundant Transition-Metal-Based Electrocatalysts for Water Electrolysis to Produce Renewable Hydrogen. Chem. A Eur. J. 2018, 24, 18334–18355. [Google Scholar] [CrossRef]
- Yan, Y.; Xia, B.Y.; Zhao, B.; Wang, X. A Review on Noble-Metal-Free Bifunctional Heterogeneous Catalysts for Overall Electrochemical Water Splitting. J. Mater. Chem. A 2016, 4, 17587–17603. [Google Scholar] [CrossRef]
- Suen, N.-T.; Hung, S.-F.; Quan, Q.; Zhang, N.; Xu, Y.-J.; Chen, H.M. Electrocatalysis for the Oxygen Evolution Reaction: Recent Development and Future Perspectives. Chem. Soc. Rev. 2017, 46, 337–365. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; Zhang, Y. Noble Metal-Free Hydrogen Evolution Catalysts for Water Splitting. Chem. Soc. Rev. 2015, 44, 5148–5180. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Lu, X.F.; Zang, S.; Lou, X.W. Non-Noble-Metal-Based Electrocatalysts toward the Oxygen Evolution Reaction. Adv. Funct. Mater. 2020, 30, 1910274. [Google Scholar] [CrossRef]
- Fabbri, E.; Schmidt, T.J. Oxygen Evolution Reaction—The Enigma in Water Electrolysis. ACS Catal. 2018, 8, 9765–9774. [Google Scholar] [CrossRef]
- Yu, F.; Yu, L.; Mishra, I.K.; Yu, Y.; Ren, Z.F.; Zhou, H.Q. Recent Developments in Earth-Abundant and Non-Noble Electrocatalysts for Water Electrolysis. Mater. Today Phys. 2018, 7, 121–138. [Google Scholar] [CrossRef]
- Liu, Z.; Nie, K.; Yuan, Y.; Li, B.; Liu, P.; Chong, S.; Du, Y.; Huang, W. Crystalline/Amorphous Heterophase with Self-Assembled Hollow Structure for Highly Efficient Electrochemical Hydrogen Production. CCS Chem. 2022, 4, 3391–3401. [Google Scholar] [CrossRef]
- Nie, K.; Qu, X.; Gao, D.; Li, B.; Yuan, Y.; Liu, Q.; Li, X.; Chong, S.; Liu, Z. Engineering Phase Stability of Semimetallic MoS2 Monolayers for Sustainable Electrocatalytic Hydrogen Production. ACS Appl. Mater. Interfaces 2022, 14, 19847–19856. [Google Scholar] [CrossRef]
- Liu, Z.; Nie, K.; Qu, X.; Li, X.; Li, B.; Yuan, Y.; Chong, S.; Liu, P.; Li, Y.; Yin, Z.; et al. General Bottom-Up Colloidal Synthesis of Nano-Monolayer Transition-Metal Dichalcogenides with High 1T′-Phase Purity. J. Am. Chem. Soc. 2022, 144, 4863–4873. [Google Scholar] [CrossRef]
- Tan, C.; Zhang, H. Two-Dimensional Transition Metal Dichalcogenide Nanosheet-Based Composites. Chem. Soc. Rev. 2015, 44, 2713–2731. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Han, J.; Wang, X.; Xu, P.; Yao, T.; Zhong, J.; Zhong, W.; Liu, S.; Gao, T.; Zhang, Z.; et al. 2D Transition Metal Dichalcogenides: Design, Modulation, and Challenges in Electrocatalysis. Adv. Mater. 2021, 33, 1907818. [Google Scholar] [CrossRef]
- Chia, X.; Pumera, M. Characteristics and Performance of Two-Dimensional Materials for Electrocatalysis. Nat. Catal. 2018, 1, 909–921. [Google Scholar] [CrossRef]
- Huang, H.H.; Fan, X.; Singh, D.J.; Zheng, W.T. Recent Progress of TMD Nanomaterials: Phase Transitions and Applications. Nanoscale 2020, 12, 1247–1268. [Google Scholar] [CrossRef]
- Voiry, D.; Yang, J.; Chhowalla, M. Recent Strategies for Improving the Catalytic Activity of 2D TMD Nanosheets Toward the Hydrogen Evolution Reaction. Adv. Mater. 2016, 28, 6197–6206. [Google Scholar] [CrossRef] [PubMed]
- Dai, B.; Su, Y.; Guo, Y.; Wu, C.; Xie, Y. Recent Strategies for the Synthesis of Phase-Pure Ultrathin 1T/1T′ Transition Metal Dichalcogenide Nanosheets. Chem. Rev. 2024, 124, 420–454. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Gao, D.; Ding, J.; Chao, D.; Wang, J. TMD-Based Highly Efficient Electrocatalysts Developed by Combined Computational and Experimental Approaches. Chem. Soc. Rev. 2018, 47, 4332–4356. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Sun, Z.; Hu, Y.H. 1T Phase Transition Metal Dichalcogenides for Hydrogen Evolution Reaction. Electrochem. Energ. Rev. 2021, 4, 194–218. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Kou, L.; Gu, Y. Mechanism Exploration and Catalyst Design for Hydrogen Evolution Reaction Accelerated by Density Functional Theory Simulations. ACS Sustain. Chem. Eng. 2023, 11, 467–481. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, W.; Jiang, Q. A Machine Learning Scheme for the Catalytic Activity of Alloys with Intrinsic Descriptors. J. Mater. Chem. A 2020, 8, 17507–17515. [Google Scholar] [CrossRef]
- Ran, N.; Qiu, W.; Song, E.; Wang, Y.; Zhao, X.; Liu, Z.; Liu, J. Bond Electronegativity as Hydrogen Evolution Reaction Catalyst Descriptor for Transition Metal (TM = Mo, W) Dichalcogenides. Chem. Mater. 2020, 32, 1224–1234. [Google Scholar] [CrossRef]
- Wexler, R.B.; Martirez, J.M.P.; Rappe, A.M. Chemical Pressure-Driven Enhancement of the Hydrogen Evolving Activity of Ni2 P from Nonmetal Surface Doping Interpreted via Machine Learning. J. Am. Chem. Soc. 2018, 140, 4678–4683. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Wang, J.; Liu, J.; Zhang, L.; Wan, H.; Miao, L.; Jiang, J. Dual-Descriptor Tailoring: The Hydroxyl Adsorption Energy-Dependent Hydrogen Evolution Kinetics of High-Valance State Doped Ni3 N in Alkaline Media. ACS Catal. 2019, 9, 9332–9338. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, L.; Liu, Y.; Xu, J.; Zhu, H.; Guo, W. Enhancing Hydrogen Evolution Activity by Doping and Tuning the Curvature of Manganese-Embedded Carbon Nanotubes. Catal. Sci. Technol. 2019, 9, 5301–5314. [Google Scholar] [CrossRef]
- Dong, Y.; Dang, J.; Wang, W.; Yin, S.; Wang, Y. First-Principles Determination of Active Sites of Ni Metal-Based Electrocatalysts for Hydrogen Evolution Reaction. ACS Appl. Mater. Interfaces 2018, 10, 39624–39630. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.T.; Saidi, W.A. Graphene Activation Explains the Enhanced Hydrogen Evolution on Graphene-Coated Molybdenum Carbide Electrocatalysts. J. Phys. Chem. Lett. 2020, 11, 2759–2764. [Google Scholar] [CrossRef]
- Sun, X.; Zheng, J.; Gao, Y.; Qiu, C.; Yan, Y.; Yao, Z.; Deng, S.; Wang, J. Machine-Learning-Accelerated Screening of Hydrogen Evolution Catalysts in MBenes Materials. Appl. Surf. Sci. 2020, 526, 146522. [Google Scholar] [CrossRef]
- Krishnamurthy, D.; Sumaria, V.; Viswanathan, V. Maximal Predictability Approach for Identifying the Right Descriptors for Electrocatalytic Reactions. J. Phys. Chem. Lett. 2018, 9, 588–595. [Google Scholar] [CrossRef]
- Tang, Q.; Jiang, D. Mechanism of Hydrogen Evolution Reaction on 1T-MoS2 from First Principles. ACS Catal. 2016, 6, 4953–4961. [Google Scholar] [CrossRef]
- Ge, L.; Yuan, H.; Min, Y.; Li, L.; Chen, S.; Xu, L.; Goddard, W.A. Predicted Optimal Bifunctional Electrocatalysts for the Hydrogen Evolution Reaction and the Oxygen Evolution Reaction Using Chalcogenide Heterostructures Based on Machine Learning Analysis of in Silico Quantum Mechanics Based High Throughput Screening. J. Phys. Chem. Lett. 2020, 11, 869–876. [Google Scholar] [CrossRef]
- Ling, C.; Shi, L.; Ouyang, Y.; Wang, J. Searching for Highly Active Catalysts for Hydrogen Evolution Reaction Based on O-Terminated MXenes through a Simple Descriptor. Chem. Mater. 2016, 28, 9026–9032. [Google Scholar] [CrossRef]
- Wei, C.; Sun, Y.; Scherer, G.G.; Fisher, A.C.; Sherburne, M.; Ager, J.W.; Xu, Z.J. Surface Composition Dependent Ligand Effect in Tuning the Activity of Nickel–Copper Bimetallic Electrocatalysts toward Hydrogen Evolution in Alkaline. J. Am. Chem. Soc. 2020, 142, 7765–7775. [Google Scholar] [CrossRef]
- Zhang, Q.; Jiang, Z.; Tackett, B.M.; Denny, S.R.; Tian, B.; Chen, X.; Wang, B.; Chen, J.G. Trends and Descriptors of Metal-Modified Transition Metal Carbides for Hydrogen Evolution in Alkaline Electrolyte. ACS Catal. 2019, 9, 2415–2422. [Google Scholar] [CrossRef]
- Wang, A.; Shen, L.; Zhao, M.; Wang, J.; Zhou, W.; Li, W.; Feng, Y.; Liu, H. Tungsten Boride: A 2D Multiple Dirac Semimetal for the Hydrogen Evolution Reaction. J. Mater. Chem. C 2019, 7, 8868–8873. [Google Scholar] [CrossRef]
- Ouyang, R.; Curtarolo, S.; Ahmetcik, E.; Scheffler, M.; Ghiringhelli, L.M. SISSO: A Compressed-Sensing Method for Identifying the Best Low-Dimensional Descriptor in an Immensity of Offered Candidates. Phys. Rev. Mater. 2018, 2, 083802. [Google Scholar] [CrossRef]
- Jain, A.; Hautier, G.; Moore, C.J.; Ping Ong, S.; Fischer, C.C.; Mueller, T.; Persson, K.A.; Ceder, G. A High-Throughput Infrastructure for Density Functional Theory Calculations. Comput. Mater. Sci. 2011, 50, 2295–2310. [Google Scholar] [CrossRef]
- Papadimitriou, I.; Gialampoukidis, I.; Vrochidis, S.; Kompatsiaris, I. AI Methods in Materials Design, Discovery and Manufacturing: A Review. Comput. Mater. Sci. 2024, 235, 112793. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Z.; Sundmacher, K. Big Data Creates New Opportunities for Materials Research: A Review on Methods and Applications of Machine Learning for Materials Design. Engineering 2019, 5, 1017–1026. [Google Scholar] [CrossRef]
- Jablonka, K.M.; Ongari, D.; Moosavi, S.M.; Smit, B. Big-Data Science in Porous Materials: Materials Genomics and Machine Learning. Chem. Rev. 2020, 120, 8066–8129. [Google Scholar] [CrossRef]
- Ratcliff, L.E.; Mohr, S.; Huhs, G.; Deutsch, T.; Masella, M.; Genovese, L. Challenges in Large Scale Quantum Mechanical Calculations. WIREs Comput. Mol. Sci. 2017, 7, e1290. [Google Scholar] [CrossRef]
- Pollice, R.; Dos Passos Gomes, G.; Aldeghi, M.; Hickman, R.J.; Krenn, M.; Lavigne, C.; Lindner-D’Addario, M.; Nigam, A.; Ser, C.T.; Yao, Z.; et al. Data-Driven Strategies for Accelerated Materials Design. Acc. Chem. Res. 2021, 54, 849–860. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Sun, Z.; Yin, H.; Liu, X.; Wang, J.; Zhao, H.; Pang, C.H.; Wu, T.; Li, S.; Yin, Z.; et al. Data-Driven Materials Innovation and Applications. Adv. Mater. 2022, 34, 2104113. [Google Scholar] [CrossRef] [PubMed]
- Bradley, W.; Kim, J.; Kilwein, Z.; Blakely, L.; Eydenberg, M.; Jalvin, J.; Laird, C.; Boukouvala, F. Perspectives on the Integration between First-Principles and Data-Driven Modeling. Comput. Chem. Eng. 2022, 166, 107898. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T.; Logadottir, A.; Kitchin, J.R.; Chen, J.G.; Pandelov, S.; Stimming, U. Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc. 2005, 152, J23. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Zhang, B.; Ji, X.; Xu, K.; Chen, C.; Miao, L.; Jiang, J. The Mechanism of Hydrogen Adsorption on Transition Metal Dichalcogenides as Hydrogen Evolution Reaction Catalyst. Phys. Chem. Chem. Phys. 2017, 19, 10125–10132. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab. Initio Molecular Dynamics for Open-Shell Transition Metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab. Initio Molecular-Dynamics Simulation of the Liquid-Metal–Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab. Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Ruzsinszky, A.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Wu, X.; et al. Accurate First-Principles Structures and Energies of Diversely Bonded Systems from an Efficient Density Functional. Nat. Chem. 2016, 8, 831–836. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Kitchaev, D.A.; Yang, J.; Chen, T.; Dacek, S.T.; Sarmiento-Pérez, R.A.; Marques, M.A.L.; Peng, H.; Ceder, G.; Perdew, J.P.; et al. Efficient First-Principles Prediction of Solid Stability: Towards Chemical Accuracy. npj Comput. Mater. 2018, 4, 9. [Google Scholar] [CrossRef]
- Ke, D.; Sun, J.; Zhang, Y. Accurate DFT Simulation of Complex Functional Materials: Synergistic Enhancements Achieved by SCAN Meta-GGA. J. Chem. Phys. 2025, 162, 014107. [Google Scholar] [CrossRef] [PubMed]
- Saßnick, H.-D.; Cocchi, C. Electronic Structure of Cesium-Based Photocathode Materials from Density Functional Theory: Performance of PBE, SCAN, and HSE06 Functionals. Electron. Struct. 2021, 3, 027001. [Google Scholar] [CrossRef]
- Chakraborty, A.; Dixit, M.; Aurbach, D.; Major, D.T. Predicting Accurate Cathode Properties of Layered Oxide Materials Using the SCAN Meta-GGA Density Functional. npj Comput. Mater. 2018, 4, 60. [Google Scholar] [CrossRef]
- Sun, J.; Remsing, R.C.; Zhang, Y.; Sun, Z.; Peng, H.; Yang, Z.; Paul, A.; Waghmare, U.; Klein, M.L.; Perdew, J.P. SCAN: An Efficient Density Functional Yielding Accurate Structures and Energies of Diversely-Bonded Materials. arXiv 2015, arXiv:1511.01089. [Google Scholar]
- Bengtsson, L. Dipole Correction for Surface Supercell Calculations. Phys. Rev. B 1999, 59, 12301–12304. [Google Scholar] [CrossRef]
- Yu, L.; Ranjan, V.; Lu, W.; Bernholc, J.; Nardelli, M.B. Equivalence of Dipole Correction and Coulomb Cutoff Techniques in Supercell Calculations. Phys. Rev. B 2008, 77, 245102. [Google Scholar] [CrossRef]
- Zheng, Y.; Jiao, Y.; Jaroniec, M.; Qiao, S.Z. Advancing the Electrochemistry of the Hydrogen-Evolution Reaction through Combining Experiment and Theory. Angew. Chem. Int. Ed. 2015, 54, 52–65. [Google Scholar] [CrossRef]
- Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. Crystal Orbital Hamilton Population (COHP) Analysis as Projected from Plane-Wave Basis Sets. J. Phys. Chem. A 2011, 115, 5461–5466. [Google Scholar] [CrossRef] [PubMed]
- Maintz, S.; Deringer, V.L.; Tchougréeff, A.L.; Dronskowski, R. LOBSTER: A Tool to Extract Chemical Bonding from Plane-wave Based DFT. J. Comput. Chem. 2016, 37, 1030–1035. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Yan, Q.; Ruzsinszky, A. Key Role of Antibonding Electron Transfer in Bonding on Solid Surfaces. Phys. Rev. Mater. 2019, 3, 092801. [Google Scholar] [CrossRef]
- Guo, X.; Gu, J.; Hu, X.; Zhang, S.; Chen, Z.; Huang, S. Coordination Tailoring towards Efficient Single-Atom Catalysts for N2 Fixation: A Case Study of Iron-Nitrogen-Carbon (Fe@N-C) Systems. Catal. Today 2020, 350, 91–99. [Google Scholar] [CrossRef]
- Ling, C.; Shi, L.; Ouyang, Y.; Chen, Q.; Wang, J. Transition Metal-Promoted V2 CO2 (MXenes): A New and Highly Active Catalyst for Hydrogen Evolution Reaction. Adv. Sci. 2016, 3, 1600180. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Yuan, J.; Wu, P.; Zhou, W. Scaling Law of Hydrogen Evolution Reaction for InSe Monolayer with 3d Transition Metals Doping and Strain Engineering. J. Energy Chem. 2020, 41, 107–114. [Google Scholar] [CrossRef]
- Liu, X.; Jiao, Y.; Zheng, Y.; Jaroniec, M.; Qiao, S.-Z. Building Up a Picture of the Electrocatalytic Nitrogen Reduction Activity of Transition Metal Single-Atom Catalysts. J. Am. Chem. Soc. 2019, 141, 9664–9672. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer Topics in Signal Processing; Springer Berlin Heidelberg: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. ISBN 978-3-642-00295-3. [Google Scholar]
- Hernandez, H. Replacing the R2 Coefficient in Model Analysis. ForsChem Res. Rep. 2023, 8, 2023-10. [Google Scholar] [CrossRef]





| Category | Feature | Abbreviation |
|---|---|---|
| Cation | d-electron number | Cde |
| Valence electron number | CVe | |
| Pauling electronegativity | Cχ | |
| 1st ionization energy | CI | |
| Covalent radius | Crc | |
| Atomic radius | Cra | |
| Anion | d-electron number | Ade |
| Pauling electronegativity | Aχ | |
| 1st ionization energy | AI | |
| Covalent radius | Arc | |
| Atomic radius | Ara | |
| Numbers of anions | Ana |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Liu, G.; Zhang, L.; Hu, Z. Integrating Density Functional Theory Calculations and Machine Learning to Identify Conduction Band Minimum as a Descriptor for High-Efficiency Hydrogen Evolution Reaction Catalysts in Transition Metal Dichalcogenides. Catalysts 2025, 15, 309. https://doi.org/10.3390/catal15040309
Jiang X, Liu G, Zhang L, Hu Z. Integrating Density Functional Theory Calculations and Machine Learning to Identify Conduction Band Minimum as a Descriptor for High-Efficiency Hydrogen Evolution Reaction Catalysts in Transition Metal Dichalcogenides. Catalysts. 2025; 15(4):309. https://doi.org/10.3390/catal15040309
Chicago/Turabian StyleJiang, Xiaolin, Guanqi Liu, Lifu Zhang, and Zhenpeng Hu. 2025. "Integrating Density Functional Theory Calculations and Machine Learning to Identify Conduction Band Minimum as a Descriptor for High-Efficiency Hydrogen Evolution Reaction Catalysts in Transition Metal Dichalcogenides" Catalysts 15, no. 4: 309. https://doi.org/10.3390/catal15040309
APA StyleJiang, X., Liu, G., Zhang, L., & Hu, Z. (2025). Integrating Density Functional Theory Calculations and Machine Learning to Identify Conduction Band Minimum as a Descriptor for High-Efficiency Hydrogen Evolution Reaction Catalysts in Transition Metal Dichalcogenides. Catalysts, 15(4), 309. https://doi.org/10.3390/catal15040309






