Theoretical Insights into Methanol Electro-Oxidation on NiPd Nanoelectrocatalysts: Investigating the Carbonate–Palladium Oxide Pathway and the Role of Water and OH Adsorption

Abstract

We conducted a theoretical and experimental study on the electro-oxidation of methanol (MOR) on Ni_xPd_y nanoparticles. The results are presented in terms of kinetic parameters, surface concentrations, and peak currents, showing significant differences between three main compositions: Ni₃Pd₁, Ni₁Pd₁, and Ni₁Pd₃. The kinetic mechanism adopted for accounting the linear voltammetry experiments performed follows the carbonate–palladium oxide pathway of the MOR. Numerical simulations of the kinetic equations, fitted to experimental data obtained at varying methanol concentrations, allowed us to distinguish the adsorption contributions of methanol, water, and OH ions from the nonlinear contribution associated with palladium oxide and carbon dioxide production. The synergistic effects of Ni:Pd nanoalloys on the MOR were then assessed by analyzing the behavior and tendencies of the reaction rate constants for different bulk methanol concentrations. Our results suggest that a higher Pd content favors more efficient oxidation mechanisms by reducing the formation of intermediate products that cause surface poisoning, such as CO, carbonates, or palladium oxide. However, as the proportion of Ni increases, an increase in the concentration of adsorbed OH is observed, which dominates the blocking of active sites even greater than the palladium oxide blocking.

1. Introduction

Fuel cells are a specialized electrochemical device that convert the stored chemical energy of a fuel into electrical energy. During the process, the anode receives a continuous fuel supply, and the cathode is fed with an oxidant [1]. These fuel cells can produce electrical energy continuously if supplied constantly. Due to their absence of intermediate heat-producing steps or thermodynamic limitations for mechanical work [1], in addition to their low contamination due to a lack of a combustion process [2,3], the fuel cells are advantaged over other electrochemical cells like batteries and even engines and devices that employ fossil fuels.

Reducing the size of the electrocatalysts to the nanoparticle scale significantly alters their thermodynamic and transport properties. The large relative fraction of surface atoms in nanoparticles determines the size dependencies of the melting temperature and pressure and, therefore, it has an impact on heat capacity, thermal and electrical conductivity, and, most importantly for this work, chemical potential [4,5,6,7,8,9,10]. For instance, quantum confinement modifies the band structure of metallic nanoparticles and nanocrystals, affecting their electronic, conductive, and optical properties. This modification induces anomalous behaviors of the band gap energy at different temperatures [7,8]. In addition, the chemical potential of a nanoparticle is influenced by the surface energy and the surface structure [11]. As nanoparticles have a much larger surface area to volume ratio compared to bulk materials, their chemical affinity increases and, therefore, the nanoparticles are more reactive [4,5,7,12,13,14,15,16,17,18]. Notably, the classical equations of chemical kinetics can be used to describe the processes on the surface of nanoparticles [7].

In recent years, considerable progress has been made in developing nanoelectrocatalysts and their synthesis techniques over the past few decades [19,20,21]. Many efforts have been focused on optimizing their performance for alcohol oxidation (methanol, ethanol) and oxygen reduction; see, for instance, [21,22,23,24,25,26,27,28].

In the present study, we are interested in the methanol oxidation reaction (MOR), which involves the oxidation of methanol (CH₃OH) into carbon dioxide (CO₂) as a final product [28,29,30]. However, in the case of Pd-based nanocatalysts, their sensitivity to CO or palladium oxide poisoning can significantly degrade their catalytic performance [19,25]. Hence, it is of primary importance to develop and understand the performance of Pd-based catalysts combined with other metals like Ni or Cu, since the addition of Ni to Pd can significantly enhance the catalytic activity towards MOR and reduces significantly the costs of practical implementation [19,29,30,31,32].

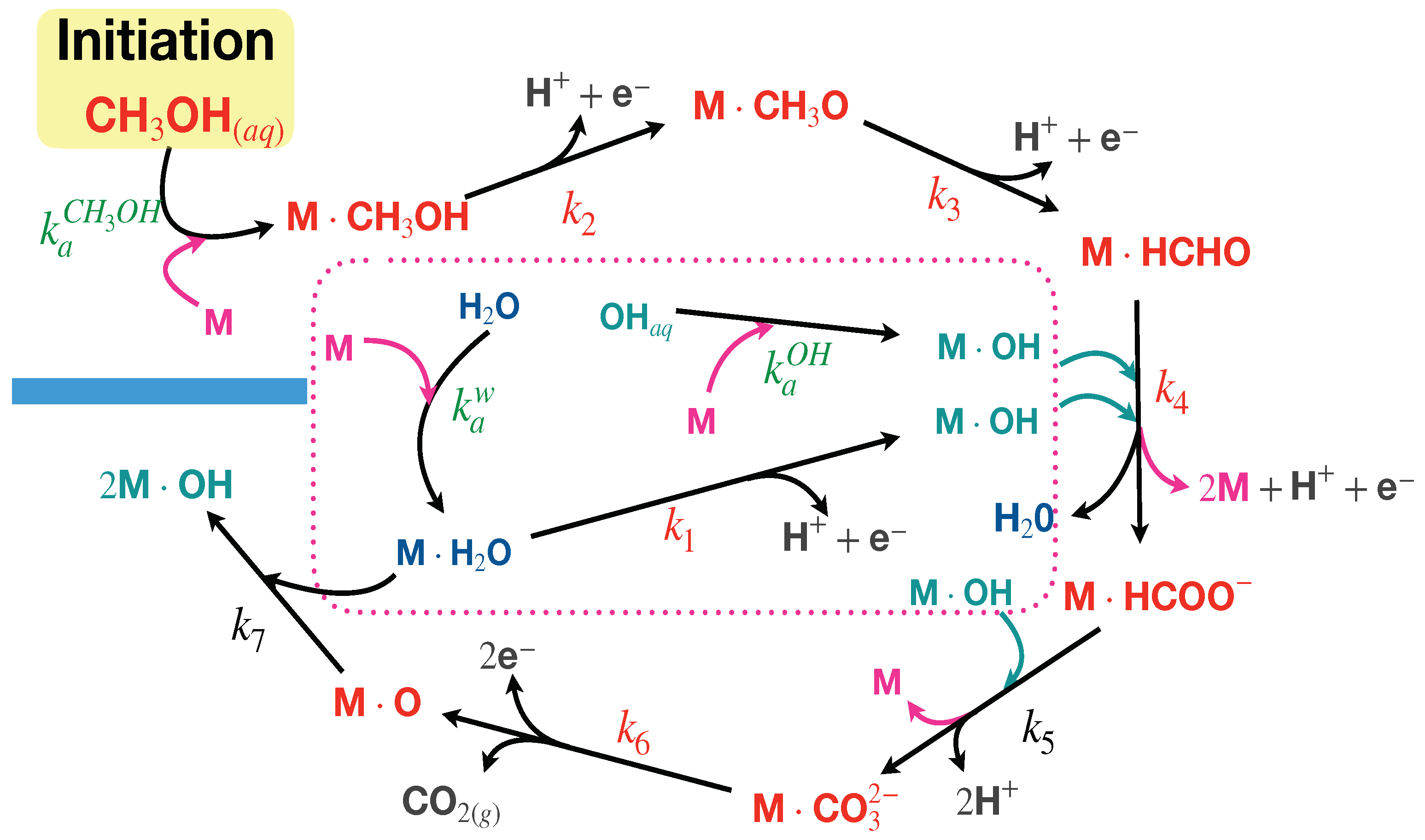
In the case of bimetallic particles like the NiPd nanoalloys that we will study here, the evolution of the reactions takes place, apparently, along a bifunctional mechanism [19,29,31,33]. This mechanism is characterized by the synergistic effect of the NiPd composition, which leads to the enhanced catalytic performance of NiPd nanocatalysts compared to the monometallic Pd case [29,31].

According to this mechanism, methanol is adsorbed at Pd sites and first dehydrogenated to methoxy. Then, formaldehyde and subsequently formate are then oxidized with the help of adsorbed OH⁻ ions. OH⁻ ions have, in general, two sources: one by direct adsorption from the solution, and, complementary, as a product of the hydrolysis of previously adsorbed water molecules [19,21,25,29,31,32]. Therefore, the oxidation steps run simultaneously with the hydrolysis of water molecules and the adsorption of OH⁻ radicals at the Ni sites. Notice that these processes compete for the active sites over the nanoparticle’s surface. The last step suggested is the oxidation of adsorbed carbonate, which decomposes in carbon dioxide (instantaneously released to the solution), producing two electrons and protons. This step also yields an oxidation of an active site, therefore having a poisoning effect over the surface [29,31,34].

In this work, we conduct a combined theoretical and experimental investigation of MOR on nickel–palladium electrocatalysts. Using linear voltammetry in an alkaline medium, we examine the performance of catalysts with varying Ni:Pd ratios (3:1, 1:1, 1:3). Our approach aims to elucidate the synergistic effects of nickel and palladium on MOR activity by systematically probing different nanoalloy compositions and analyzing the results obtained through the comparison with a kinetic model of the mechanism. Hence, the synergistic effects are then assessed by analyzing the behavior and tendencies of the reaction rate constants for different bulk methanol concentrations.

Concerning experiments, our work builds upon the findings of Araujo et al. (2020) [33], highlighting the crucial role of Pd-Ni interactions in enhancing MOR performance on Pd-based electrocatalysts. By systematically varying the Ni:Pd ratio, we aim to gain deeper insights into the underlying mechanisms and the optimal nanoparticle composition for maximizing methanol oxidation activity. This mesoscopic study of the chemical mechanisms could be complemented by molecular-level studies such as SEM, XRD, and XPS, as well as heuristic DFT and molecular dynamics studies that would deepen our understanding of the relationship between the electronic structure of nanoparticles and their efficiency [35]. However, the present study, based primarily on theoretical modeling of electrochemical measurements, seems to be sufficient to explain the differentiated performance of the cell as a function of the nickel-to-palladium ratio.

Our theoretical analysis of the oxidation curves is based on the proposal of a reaction mechanism of the MOR that approximately follows the mechanisms reported in the literature [19,25,29,31,32], as already discussed in previous paragraphs. Specifically, in the model mechanism we presented in Ref. [25], the process begins with water and methanol molecules diffusing into the electrode’s pores with a limited number of active sites. Methanol adsorbs onto active metal sites independently of voltage, forming neutral layers. The chemical potentials determine the adsorption affinity and Gibbs energy. Using irreversible thermodynamics, the dynamics are proposed to follow a Langmuir–Hinshelwood-like equation. At equilibrium, the Nernst relation adjusts the affinity based on the external potential. This affinity, linked to reaction rates via flow–force relationships, leads to the Butler–Volmer equation, describing current as a function of concentrations and the applied voltage. In this work, we will follow a similar thermodynamic strategy, but instead applying it to the chemical mechanism of the new catalyst. In the present case, direct adsorption of OH ions is also included, as suggested in the literature, and the path followed differs from others since it is assumed that bimetallic nanoparticles promote the formation of formate and carbonate as intermediates and, therefore, the poisoning of the active sites occurs by direct oxidation of palladium atoms and not by the formation of carbon monoxide molecules, as assumed in the case of pure Pd-based catalysts [25].

The article is organized as follows: Section 3 describes the experimental procedure from synthesis to linear voltammetry followed to obtain the oxidation curves. Then, Section 4 presents the theoretical model starting from the postulation of the mechanism to the formulation of the corresponding set of kinetic equations. Section 5 is then devoted to presenting our results and their discussion in terms of the comparison with the theoretical model. Finally, the conclusions Section 2 summarizes our results and contextualizes this study.

2. Results and Discussion

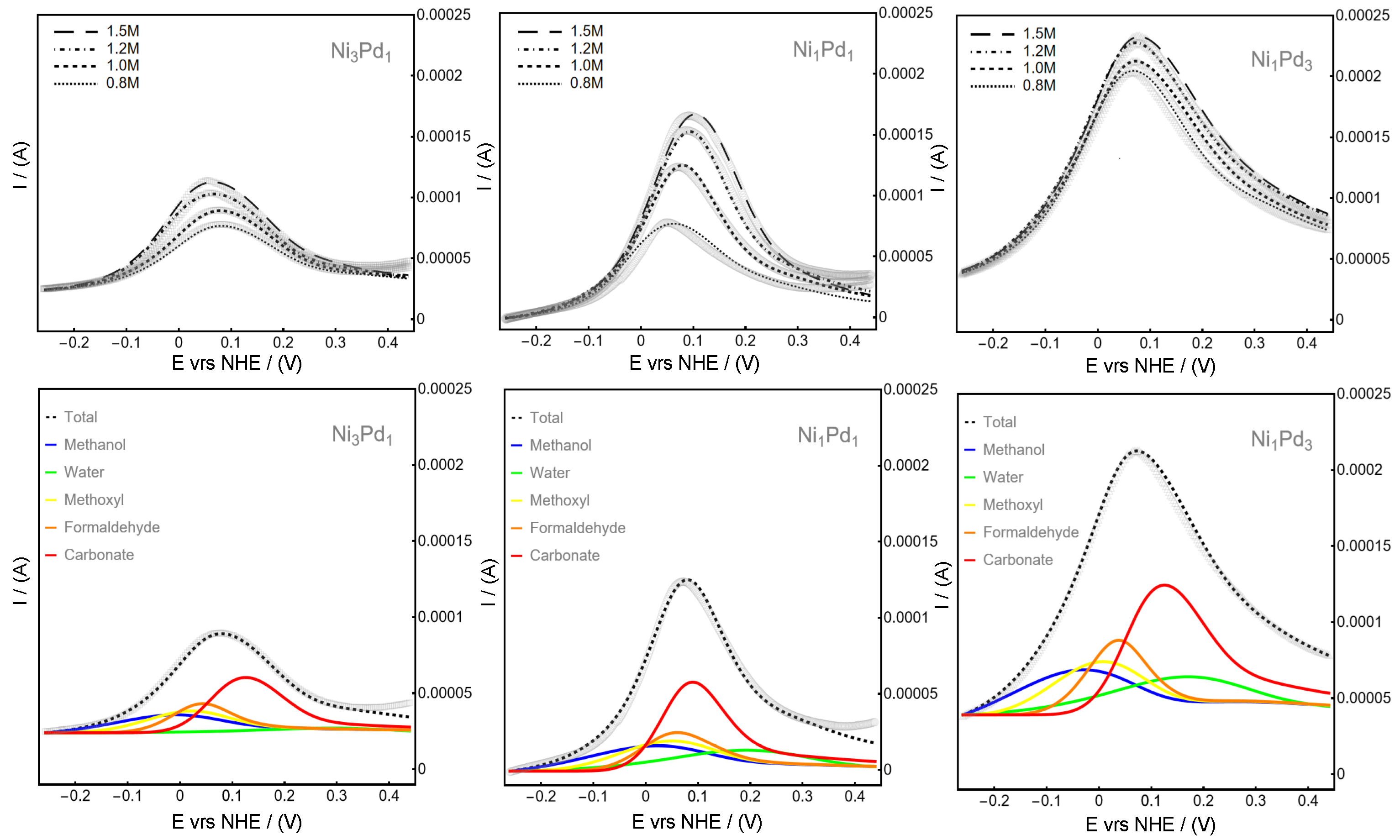
Figure 1 presents the fit (lines) of the experimental data (symbols) obtained using our synthesized Ni_xPd_y catalysts (see Section 3). Subplots illustrate results for specific compositions: (a) Ni₃Pd₁, (b) Ni₁Pd₁, and (c) Ni₁Pd₃. The data indicate that nanoparticles with a higher relative proportion of Pd (Ni₁Pd₃) exhibit superior oxidation performance compared to those with higher Ni content.

The numerical procedure for constructing Figure 1 involves solving the differential Equations (11)–(17) and (23) with a fourth-order Runge–Kutta method, followed by the calculation of the total oxidation current using Equation (22). The dependent variables include the concentrations $S^w$, $S^{OH}$, $S^{\theta }$, $S^{\beta }$, $S^{\gamma }$, $S^{\delta }$, $S^{ϵ}$, $S^{MO}$, $S^{C{O}_2}$, and $\eta$. These equations are solved parametrically over a wide range of fitting parameters: $k_a$, $k_a^w$, $k_d$, $k_d^w$, $k_a^{OH}$, $k_d^{OH}$, and $k_1$–$k_7$. The total simulation time is 35 s, with a maximum time step of $5·{10}^{-3}$ s. Initial conditions are set to zero for all variables except $S^w\left(0\right)=S^{OH}\left(0\right)=S^{\theta }\left(0\right)={10}^{-4}$.

In the top row of Figure 1, we show the fits for different methanol concentrations, from 0.8 to 1.5, ranging from lowest to highest. The peak current for the Ni₃Pd₁ case shifts towards lower overpotential values, contrasting with the behavior observed in the other two cases. However, this shift is relatively minor across all cases studied. Notably, for potentials exceeding 0.3 V, the Ni₁Pd₃ material does not exhibit a significant increase in oxidation, facilitating the alignment of experimental results with the proposed model. This absence of higher-potential oxidation appears linked to a delay in water hydrolysis for materials with higher Ni content.

To confirm this observation, the bottom row of Figure 1 details the contributions of each reactant to the total oxidation current. The reaction involving water, depicted by the green line, demonstrates the delayed production and depletion of water relative to other intermediates contributing to the overall current, as outlined in Equation (22). The green line for water hydrolysis peaks at different potentials depending on the material composition: 0.31 V for Ni₃Pd₁, 0.22 V for Ni₁Pd₁, and 0.185 V for Ni₁Pd₃. This trend suggests that the delay in water hydrolysis decreases as the oxidation activity increases.

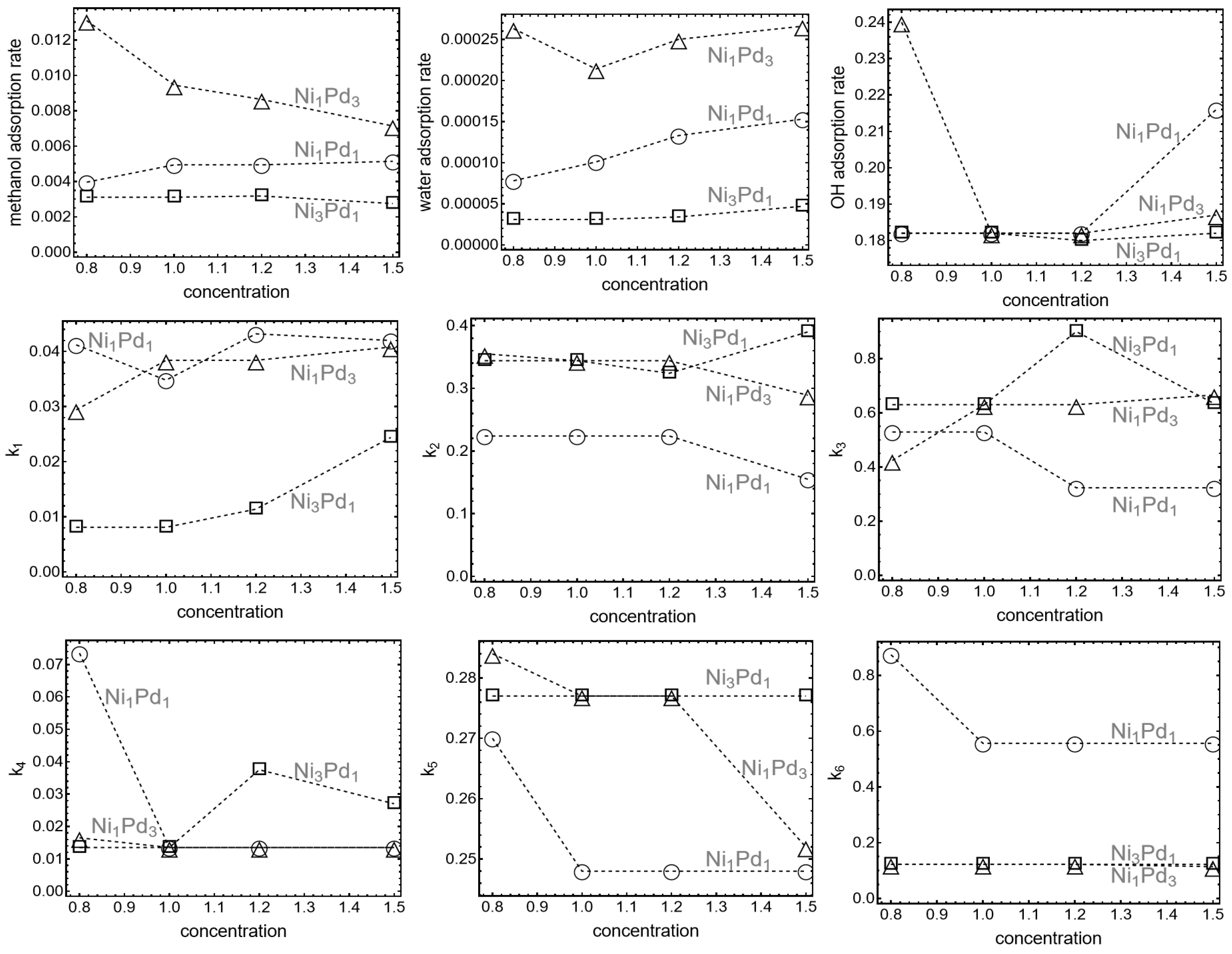
To better understand the progression of key reaction steps in the oxidation process including the role played by hydrolysis it is important to compare the reaction rates in the different processes. Figure 2 displays the adsorption and reaction rate constants used for the fit: in the first row, the adsorption rate constants for surface reactants: methanol, water and OH in $k_a^{\theta }$, $k_a^w$, and $k_a^{OH}$, respectively; in the second row the reaction constants for water hydrolysis $k_1$, methanol oxidation $k_2$, and methoxy oxidation $k_3$ and finally, in the third row, constants for formaldehyde oxidation $k_4$, carbonate formation $k_5$, and carbonate oxidation $k_6$. The value of the fitting parameters is plotted against methanol concentration to show possible trends.

The second row of Figure 2 shows that the water hydrolysis rate constant $k_1$ for Ni₃Pd₁ is four times smaller than the corresponding constants for Ni₁Pd₁ and Ni₁Pd₃, which exhibit similar maxima positions. The green curve heights also align with the first-row results in Figure 2, where the methanol and water adsorption rates for Ni₁Pd₃ are higher than for the other two cases. Besides, regarding adsorption rate constants, $k_a^w$ for Ni₃Pd₁ is nearly double that of Ni₁Pd₁ but approximately one-third of the value for Ni₁Pd₃. This allows to conclude that the influence of water depends crucially on the characteristic time dictated fundamentally by hydrolysis on the constant $k_1$ rather than by adsorption, and that this time is fundamentally affected by the nickel/palladium ratio.

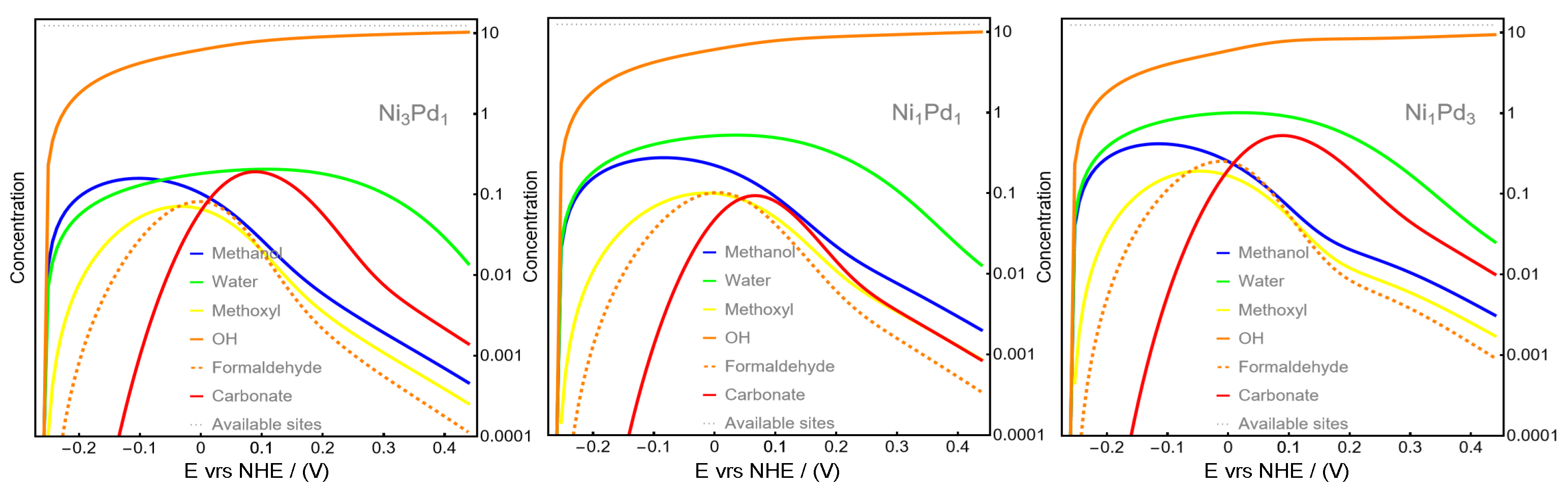
Figure 3 illustrates the surface concentration evolution of all species involved in the methanol oxidation reaction (MOR) as a function of applied voltage. The green line, representing water surface concentration, confirms that Ni₃Pd₁ nanoparticles adsorb considerably less water than the other two compositions. This observation supports the conclusion that a higher proportion of Pd atoms on the nanoparticle surface enhances water adsorption and accelerates its oxidation rate.

Additionally, this finding suggests that, at lower Ni content, the dominant mechanism, characterized by direct OH adsorption (depicted by the orange line in Figure 3, representing OH surface concentration), may compete with the mechanism described in Ref. [25]. In that study, direct OH adsorption was not considered, and surface poisoning was attributed to adsorbed CO formation rather than the formation of palladium oxides or the overpopulation of adsorbed OH. Here, it could be useful to delve deeper into the comparison between both mechanisms. The mechanism proposed in [25] was based on the assumption that, in an aqueous solution of 0.3 M KOH, water molecules generally adsorb more strongly onto Pd than OH ions. This assumption arises from the fact that water molecules, despite being present at a much higher concentration, are less charged and experience weaker repulsive forces from the negatively charged Pd surface. This allows for water molecules to compete more effectively for adsorption sites on the Pd surface compared to OH ions. Additionally, the high concentration of OH ions in the solution can lead to strong electrostatic repulsion between the negatively charged Pd surface (due to adsorbed OH species) and incoming OH ions, further hindering their adsorption. According to this mechanism, water hydrolysis becomes a relevant factor during the MOR on pure Pd catalysts, as it becomes noticeable even at low applied potentials and reaches a maximum of around 0.06 V (see Figure 3 in Ref. [25]). This behavior contrasts with the results obtained in the mechanism proposed here, where the water hydrolysis maxima occur at potentials higher than 1.5 V (see Figure 1). Therefore, water hydrolysis seems to be significantly delayed in NiPd catalysts compared to pure Pd. Water adsorption on Pd catalysts has been related to d-orbitals through first-principles calculations [36,37]. Furthermore, in this pathway in the former mechanism, the oxidation of methanol and its intermediates over Pd proceeds directly toward the formation of adsorbed CO without the necessity of OH ions, which only participate in the slow formation of COOH before the final production of CO₂. This highlights CO as the primary poisoning species.

In contrast, the presence of Ni on the surface of NiPd alloys modifies the adsorption properties of the nanoparticles, as Ni exhibits stronger adsorption of OH ions compared to Pd, which has a higher affinity for water, but is now less abundant on the surface. Since Ni is more electropositive than Pd, it tends to have a higher electron density at the surface due to its electronic structure and higher d-band center. This increased electron density can stabilize and interact more effectively with the negatively charged OH species, leading to stronger adsorption. Therefore, Ni generally exhibits a stronger affinity for OH compared to Pd. Hence, due to its higher affinity for OH ions and the competitive adsorption effects in the presence of high OH concentrations, OH ions are likely to adsorb more strongly onto Ni than onto Pd. Consequently, in the present study, both OH and water adsorption have been considered to account for these two sources of surface OH. This, along with the high binding energy of OH on Ni and Pd [34,38], results in OH ions contributing earlier and more significantly than water to the oxidation of intermediates in the MOR (see Figure 3), thereby favoring the alternative pathway described in this work. Increasing the proportion of Pd reduces the surface concentration of OH, as observed in Figure 3. In this pathway, OH ions are required for the formation of formate from formaldehyde (the rate-determining step, see Figure 1) and for the conversion of formate to carbonate (steps 4 and 5 of the mechanism). The combination of OH adsorption and production via water hydrolysis significantly increases the surface coverage by OH ions, making them the primary poisoning species, in contrast to pure Pd catalysts. Further research is necessary to determine the relative contribution of each mechanism to MOR activity and how it relates to the detailed structure of the catalyst surfaces. To conclude this discussion, it is worth mentioning that the presence of OH can be confirmed, for example, through Fourier-transform infrared spectroscopy (FTIR) [35,39].

Consistent with previous observations, the rate constants in Figure 2 further clarify the influence of Pd content on methanol adsorption and oxidation. For example, it is clear that, for nanoparticles with higher Pd content (Ni₁Pd₃), methanol adsorption rates are strongly dependent on methanol bulk concentration. Below 1 M, the adsorption rate is approximately three times larger compared to the other two compositions, but it decreases by nearly half when the concentration reaches 1.5 M. In contrast, Ni₃Pd₁ and Ni₁Pd₁ nanoparticles exhibit only a minor increase in adsorption rates with methanol concentration, suggesting a less dynamic response. In the case of OH adsorption rates, Ni₃Pd₁ nanoparticles remain constant at $k_a^{OH}$∼0.182, independent of methanol concentration. However, for Ni₁Pd₃ nanoparticles, the rate starts higher at 0.24 and decreases rapidly to converge with the rate of Ni₃Pd₁.

The methanol oxidation rate ($k_2$) is comparable for Ni₃Pd₁ and Ni₁Pd₃ nanoparticles, both exceeding the rate observed for Ni₁Pd₁. This highlights the efficiency of these two compositions in oxidizing methanol. For carbonate oxidation, remarkably, Ni₁Pd₁ nanoparticles exhibit a significantly faster oxidation rate of adsorbed carbonate ($k_6$), approximately three times higher than in the other two cases (as can be seen in Figure 1, second row, red lines). The maximum of the red line for Ni₁Pd₁ appears at lower voltages, contributing to a more symmetric oxidation peak compared to the other compositions. The oxidation steps for methanol ($k_2$), methoxy ($k_3$), and formaldehyde ($k_4$) are similar across all compositions. However, nickel carbonate is more readily oxidized than palladium carbonate, as evidenced by the general trends in the data.

To further clarify the role of OH in relation to other intermediates, including metal oxides, Figure 4 presents the surface concentrations of formate (magenta), metal oxide (brown), and the combined concentration of all other species (orange), and, as observed in Figure 3, these other species are predominantly constituted by OH. Figure 4 reveals a continuous increase in OH surface concentration, underscoring its significant role in surface poisoning during the anodic reaction. This finding highlights the critical influence of OH adsorption on the reaction’s efficiency and mechanism. Additionally, the presence of palladium oxides shows a slight increase from left to right, suggesting that their contribution to surface poisoning does not significantly impair cell efficiency. Interestingly, a higher Ni content inhibits palladium oxide formation while promoting an increase in OH concentration, which emerges as the primary blocker of active sites due to its high binding energy. This strong binding leads to an excessive amount of adsorbed OH on the surface, blocking active sites and preventing the adsorption of other reactants (such as methanol, in this case) necessary for the reaction to proceed. This conclusion aligns with the finding of Ref. [34]. From a microscopic perspective, several mechanisms can influence the adsorption and binding process. In bimetallic systems such as Ni-Pd catalysts, the d-band center can be modulated through alloying, strain engineering, or surface modifications. For instance, modifying the d-band center of Pd using ethylene glycol has been shown to enhance catalytic performance by altering hydrogen adsorption characteristics [40]. Furthermore, the increased binding energy can be attributed to a ligand effect, as the presence of Ni in the alloy can alter the electronic structure of Pd. Being more electropositive than Pd, Ni can donate electrons to Pd, weaken the Pd-O bond, and facilitate OH adsorption while simultaneously increasing site poisoning due to the relatively high OH binding energy [38,40]. Another possible factor that can be considered involves strain effects. Incorporating Ni into the Pd lattice can induce strain, altering the adsorption energies of reaction intermediates. Strain can modify bond lengths and bond angles on the surface, impacting the interaction between the catalyst and adsorbates [41]. Further analysis, such as ab initio computational studies to determine OH binding energies on Ni and Pd sites, could help to elucidate the optimal OH binding strength and the spatial distribution of species during adsorption and OH production in this NiPd catalyst system. However, these studies fall beyond the scope of the present work.

This equilibrium differs from the mechanism proposed in Ref. [25], where surface poisoning was attributed to CO formation rather than OH adsorption or palladium oxide formation. This difference arises from the fact that, the in direct pathway for the CO-CO₂ formation mechanism [25], it seems that water adsorption is predominant compared to OH adsorption. Dominant CO formation in MOR against OH adsorption and Pd·O formation, as suggested by the mechanism analyzed in this study, has been recently reported in a study analyzing the role of Sb in mitigating CO poisoning in Pd-based MOR catalysts [42]. The authors concluded that, by modifying the electronic properties of Pd and potentially facilitating the removal of adsorbed CO through interactions with adsorbed OH and alkali metal cations, like in the mechanism proposed in [25], the Sb-Pd catalyst demonstrates enhanced activity and durability [42]. For the present study, we may conclude that the balance between Ni and Pd plays a pivotal role in modulating the reaction pathway and efficiency.

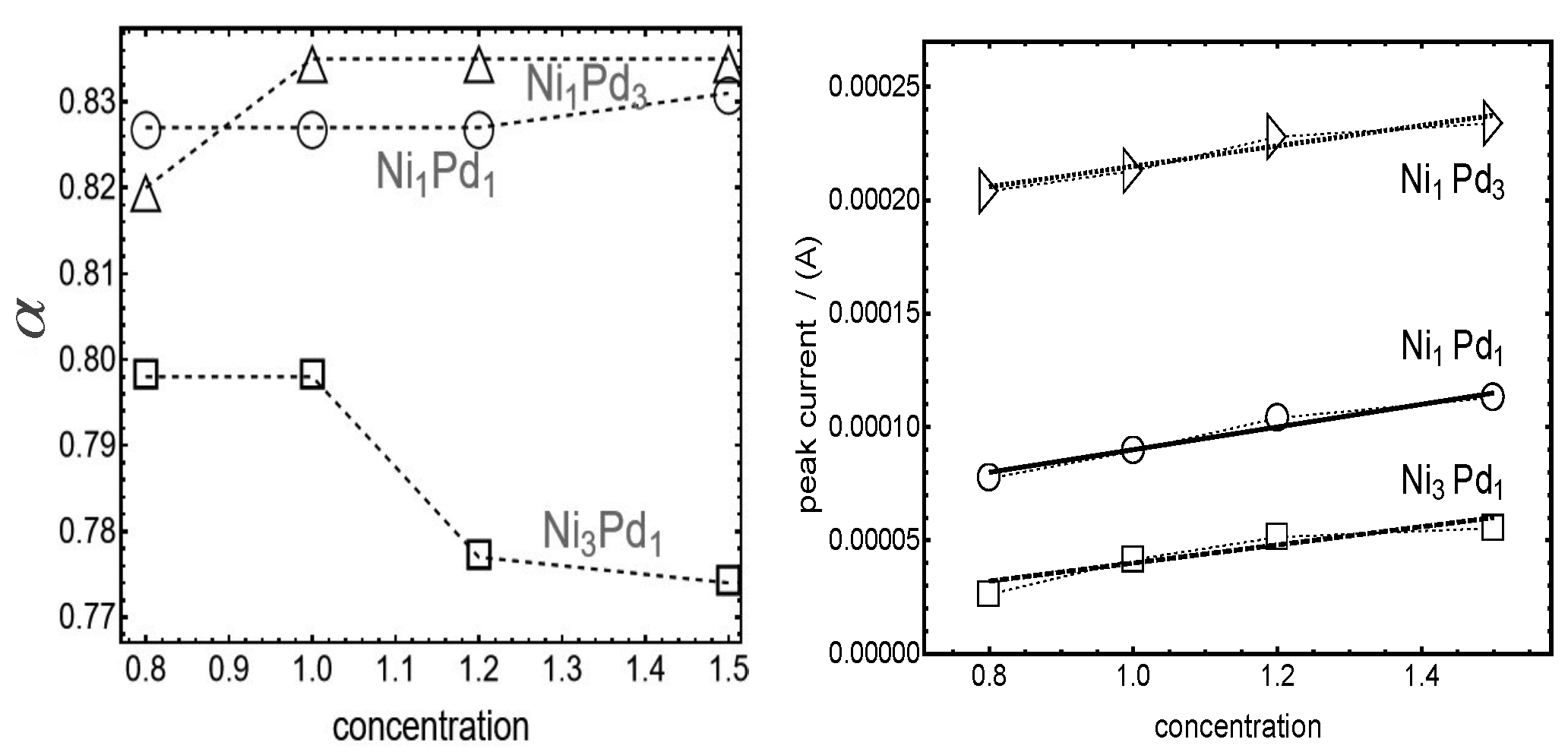
The most significant differences arising from varying proportions of Nickel (Ni) and Palladium (Pd) are highlighted in Figure 5, which displays the transfer parameter ($\alpha$) and the peak current for the three types of nanoparticles. Two notable results are evident from the figure.

As first result at the left of Figure 5 we can see that the different Ni/Pd ratios during nanoparticle synthesis lead to distinct energy barrier asymmetries. For Ni₃Pd₁ nanoparticles, the transfer parameter $\alpha$ is notably larger than 0.5, indicating that the energy barrier for the oxidation reaction surpasses that of the reduction reaction. However, the value of $\alpha$ for Ni₃Pd₁ (${\alpha }_{31}$∼0.77–0.8) is lower than the nearly constant $\alpha$∼0.83 observed for both Ni₁Pd₁ and Ni₁Pd₃. This suggests that higher Ni proportions on the nanoparticle surface enhance the asymmetry of the oxidation energy barrier compared to nanoparticles with higher Pd proportions. Moreover, the transfer factor of the Ni₃Pd₁ alloy exhibits greater sensitivity to the surrounding methanol concentration, decreasing as methanol bulk concentration increases.

The second result concerns the linear relationship between the peak current and methanol concentration, confirming that the adsorption mechanism we adopted is valid in the range of methanol and OH concentrations used (see [43]). Furthermore, the slope of this linear trend correlates with the surface energy of the nanoparticles, as detailed in Ref. [43]. This finding supports the notion that variations in surface composition significantly influence the nanoparticles’ catalytic activity and adsorption behavior.

More quantitatively, from Figure 5, it is possible to observe that the peak current for Ni₁Pd₃ is higher, with fluctuations among the four maxima remaining within ±20% of the average peak current, $\langle i_p^{1:3}\rangle$∼2.375 $·{10}^{-4}$ A. In contrast, Ni₁Pd₁ shows greater variability in peak current, reaching up to ±33% around the average value $\langle i_p^{1:1}\rangle$∼2.375 $·{10}^{-4}$ A. For Ni₃Pd₁, the average peak current is significantly lower, at $\langle i_p^{3:1}\rangle$∼9.55 $·{10}^{-5}$ A, but the variations are similar to Ni₁Pd₃, around ±20%. These findings suggest that the current variability increases when the relative proportions of Ni and Pd approach equimolar ratios.

3. Experiments

3.1. Materials

Nickel(II)sulfate hexahydrate (99%, Sigma-Aldrich, Darmstadt, Germany), potassium tetrachloropalladate(II) (99%, Sigma-Aldrich, Darmstadt, Germany), polyvinylpyrrolidone (PVP, MW 40,000, Sigma-Aldrich, Darmstadt, Germany), sodium borohydride (98%, Sigma-Aldrich, Darmstadt, Germany), ethylene glycol (99.8%, Sigma-Aldrich, Darmstadt, Germany), Vulcan carbon XC-72R (Cabot, Boston, MA, USA), isopropyl alcohol (96% industrial grade), ethanol (99.7%, Sigma-Aldrich, Darmstadt, Germany), Nafion® (5 wt.% in isopropanol, Sigma-Aldrich, Darmstadt, Germany), potassium chloride (99.7%, Sigma-Aldrich, Darmstadt, Germany), and potassium hydroxide (85%, Sigma-Aldrich, Darmstadt, Germany) were used as received.

3.2. Synthesis

Ni_x-Pd_y/C electrocatalysts were synthesized in two steps:

• Synthesis of Ni nuclei. The Ni component was prepared by adding 4 mL of distilled water to a three-necked round-bottom flask equipped with a condenser. While stirring at room temperature, 3 mL, 2 mL, and 1 mL of aqueous NiSO₄$·$6H₂O (50 mM) and their corresponding volumes of aqueous PVP (100 mM) surfactant were added. Subsequently, aqueous NaBH₄ (100 mM) was added dropwise at a rate of 25 $\mathsf{\mu }$L/min to induce a slow Ni synthesis reaction. After completing NaBH₄ addition, the solution was stirred at room temperature for an additional hour.
• Formation of Ni_x-Pd_y alloy nanoparticles. After adding 4 mL of ethylene glycol (EG) to the flask, it was immersed in a 180 °C silicon oil bath with constant stirring. To synthesize various Ni_x-Pd_y/C nanoparticle alloys, a mixture of 1 mL, 2 mL, and 3 mL of K₂PdCl₄ (50 mM) and their corresponding volumes of PVP (100 mM) surfactant, both dissolved in EG, were added to the stirred solution at a rate of 25 $\mathsf{\mu }$L/min. The reaction mixture was maintained at 180 °C while stirring for 1 h, and then was quenched to room temperature in a cold bath. The resulting solutions were washed repeatedly with isopropyl alcohol. To prepare the powder, 0.4 mg of a highly concentrated nanoparticle solution and 1.6 mg of Vulcan carbon were combined in a beaker with a few drops of isopropyl alcohol and sonicated. The mixture was then allowed to dry at room temperature.

3.3. Electrochemical Measurements

The electrochemical properties and electrocatalytic activity of the methanol electrooxidation reaction in alkaline media were investigated using linear sweep voltammetry (LSV). A BioLogic (Seyssinet-Pariset, France) VSP Potentiostat/Galvanostat, served as the electrochemical workstation. The experiments employed a three-electrode electrochemical cell configuration. A glassy carbon electrode (Basi®, West Lafayette, IN, USA, 0.0769 cm²) served as the working electrode. A calomel electrode saturated with KCl (SCE) acted as the reference electrode, and a graphite rod was used as the counter electrode. The catalytic inks were prepared by mixing 1 mg of catalyst powder with 73 $\mathsf{\mu }$L of isopropyl alcohol (dispersant) and 7 $\mathsf{\mu }$L of Nafion®(5 wt.% in isopropyl alcohol, Sigma-Aldrich, Darmstadt, Germany) (binder). After stirring, 10 $\mathsf{\mu }$L of the ink was pipetted on the working electrode to ensure complete coverage of the glassy carbon surface. Prior to each experiment, the electrolyte solutions were purged with nitrogen gas (Infra, 99.999%) for 10 min.

MOR tests were carried out using 0.3 M KOH solution with varying ethanol concentrations (0.8 M, 1.0 M, 1.2 M, and 1.5 M). Linear voltammograms were recorded in a potential range of −0.6 V–0.8 V vs. NHE (normal hydrogen electrode; referenced to SCE + 0.241 V). A scan rate of 20 mV/s was employed for the electrocatalytic evaluation. Prior to each experiment, the electrolyte solutions were purged with nitrogen gas (Infra, Edo. de México, México 99.999%) for 10 min.

4. A Model Mechanism for the Methanol Oxidation Reaction over NiPd

The mechanism proposed here for MOR on NiPd-based catalysts in alkaline conditions corresponds to a bifunctional mechanism that tries to capture the essential steps reported in the literature [29,31,34] and can be summarized as follows: Methanol molecules adsorb onto the Ni_xPd_y surface and then undergo methanol dehydrogenation at the Pd sites, forming methoxy and releasing a proton (${\mathrm{H}}^{+}$) and an electron (e⁻). Then, the methoxy intermediate is oxidized to formaldehyde by the intermediation of adsorbed hydroxide ions. Formaldehyde is subsequently oxidized to formate and then to carbonate, from which the desorption of ${\mathrm{CO}}_{2\left(g\right)}$ is assumed as a direct step accompanied by the formation of palladium oxide and the recovery of a free active site. In chemical notation, the assumed steps are the following:

For the adsorption of methanol, water, and OH ions, we have the following three reactions:

$$\mathrm{C}{\mathrm{H}}_3\mathrm{O}{\mathrm{H}}_{\left(aq\right)}+\mathrm{M}\underset{k_d}{\stackrel{k_a}{\rightleftharpoons }}\mathrm{M}·\mathrm{C}{\mathrm{H}}_3\mathrm{O}\mathrm{H}$$

(1)

$${\mathrm{H}}_2\mathrm{O}+\mathrm{M}\underset{k_d^w}{\stackrel{k_a^w}{\rightleftharpoons }}\mathrm{M}·{\mathrm{H}}_2\mathrm{O}$$

(2)

$$\mathrm{O}{\mathrm{H}}_{\left(aq\right)}+\mathrm{M}\underset{k_d^{OH}}{\stackrel{k_a^{OH}}{\rightleftharpoons }}\mathrm{M}·\mathrm{O}\mathrm{H}.$$

(3)

In these reactions, we denote the adsorbed molecules B by M·B. The adsorption and desorption rate constants are $k_a$ and $k_d$ for methanol, $k_a^w$ and $k_d^w$ for water, and $k_a^{OH}$ and $k_d^{OH}$ for OH ions. Then we have the following:

• 1. Adsorbed water hydrolysis:

  $$\mathrm{M}·{\mathrm{H}}_2\mathrm{O}\stackrel{k_1}{\to }\mathrm{M}·\mathrm{O}\mathrm{H}+{\mathrm{H}}^{+}+{\mathrm{e}}^{-}$$

  (4)
• 2. Methanol dehydrogenation to methoxy ($\beta$):

  $$\mathrm{M}·\mathrm{C}{\mathrm{H}}_3\mathrm{O}\mathrm{H}\stackrel{k_2}{\to }\mathrm{M}·\mathrm{C}{\mathrm{H}}_3\mathrm{O}+{\mathrm{H}}^{+}+{\mathrm{e}}^{-}$$

  (5)
• 3. Further dehydrogenation to formaldehyde ($\gamma$):

  $$\mathrm{M}·\mathrm{C}{\mathrm{H}}_3\mathrm{O}\stackrel{k_3}{\to }\mathrm{M}·\mathrm{H}\mathrm{C}\mathrm{H}\mathrm{O}+{\mathrm{H}}^{+}+{\mathrm{e}}^{-}$$

  (6)
• 4. Oxidation of formaldehyde ($\gamma$) to formate ($\delta$):

  $$\mathrm{M}·\mathrm{H}\mathrm{C}\mathrm{H}\mathrm{O}+2\mathrm{M}·\mathrm{O}\mathrm{H}\stackrel{k_4}{\to }\mathrm{M}·\mathrm{H}\mathrm{C}\mathrm{O}{\mathrm{O}}^{-}+{\mathrm{H}}_2\mathrm{O}+2\mathrm{M}+{\mathrm{H}}^{+}+{\mathrm{e}}^{-}$$

  (7)
• 5. Oxidation of formate ($\delta$) to carbonate ($ϵ$):

  $$\mathrm{M}·\mathrm{H}\mathrm{C}\mathrm{O}{\mathrm{O}}^{-}+\mathrm{M}·\mathrm{O}\mathrm{H}\stackrel{k_5}{\to }\mathrm{M}·\mathrm{C}{\mathrm{O}}_3^{2-}+\mathrm{M}+2{\mathrm{H}}^{+}$$

  (8)
• 6. Decomposition of carbonate ($ϵ$) to carbon dioxide:

  $$\mathrm{M}·\mathrm{C}{\mathrm{O}}_3^{2-}\stackrel{k_6}{\rightleftharpoons }\mathrm{C}{\mathrm{O}}_{2\left(g\right)}+\mathrm{M}·\mathrm{O}+2{\mathrm{e}}^{-}$$

  (9)
• 7. Regeneration of Pd active sites:

  $$\mathrm{M}·\mathrm{O}+\mathrm{M}·{\mathrm{H}}_2\mathrm{O}\stackrel{k_7}{\rightleftharpoons }2\mathrm{M}·\mathrm{O}\mathrm{H}$$

  (10)

In this set of Equations (4)–(10), the subindexes in the velocity rate constant indicate the number of the oxidation reaction. Thus, $k_1$ corresponds to water hydrolysis and $k_2$ and $k_3$ are the rate constants associated with the methanol and methoxy oxidation steps. $k_4$ and $k_5$ correspond to the rate constants for carbonate formation. $k_6$ is the oxidation of carbonate giving ${\mathrm{CO}}_{2\left(g\right)}$ and, finally, $k_7$ is the rate constant associated with the regeneration of Pd active sites. It is worth emphasizing that, in the present model reaction, the poisoning of the nanoparticles occurs due to the formation of palladium oxide, in contrast with what was proposed for pure palladium nanocatalysts [25,29,31,34]. A schematic diagram of the mechanism is shown in Figure 6.

5. Kinetics for Linear Voltammetry and Oxidation Current

From the previous mechanism, it is possible to obtain a set of differential equations for the surface concentration by following the laws of non-equilibrium thermodynamics [25]. Surface concentrations will be denoted by $S\left(t\right)$ in Mol/m², and the set of reactions in (1)–(10) leads to the following set of equations. From the reactions accounting for adsorption processes, we have that the change in time of the surface concentration of water, with notation $S^w\equiv S^{H_{2}O}$ for shortness, is

$${\displaystyle \frac{d{S}^w}{dt}}=k_a^w{C}^w{S}_M-k_d^w{S}^w-e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left\{k_1{S}^w+k_7{S}^{MO}{S}^w\right\},$$

(11)

whereas for the surface concentration the methanol, $S^{\theta }\equiv S^{C{H}_{3}OH}$, is given by

$${\displaystyle \frac{d{S}^{\theta }}{dt}}=k_a{C}^{\theta }{S}_M-k_d{S}^{\theta }-k_2{e}^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}{S}^{\theta },$$

(12)

The time evolution of the surface OH⁻ is given by

$$\begin{array}{c}\hfill \frac{d{S}^{OH}}{dt}=k_a^{OH}{C}^{OH}{S}_M-k_d^{OH}{S}^{OH}\\ \hfill +e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left\{k_1{S}^w-k_4{S}^{\gamma }{\left[S^{OH}\right]}^2-k_5{S}^{\delta }{S}^{OH}+2k_7{S}^{MO}{S}^w\right\}.\end{array}$$

(13)

In these equations, the first two terms at the right-hand side (RHS) represent the adsorption and desorption of bulk methanol, water, and hydroxyl, having bulk concentrations of $C^{\theta }$, $C^w$ and $C^{OH}$, respectively. $S_M$ counts the number of active sites not occupied by the reacting species, and its explicit dependence will be given later. The respective adsorption velocity constants were discussed above. The third terms at the RHS correspond to the first oxidation step of the mechanism, being $k_1$ and $k_w$, or the oxidation constants of surface-adsorbed methanol and water. The hydrolysis reaction leads to the formation of surface ${\mathrm{OH}}^{-1}$ with the rate $k_1$. Additionally, (13) contains two terms corresponding to the oxidation of formaldehyde $S^{\gamma }\equiv S^{HCHO}$ and formate $S^{\delta }\equiv S^{HCOO}$. The surface concentration of palladium oxide is denoted by $S^{MO}$. The oxidation processes are induced by an over-potential $\eta \left(t\right)$ and are modulated by the transfer coefficient $\alpha$. Finally, F is the Faraday constant and $RT$ is the molar thermal energy of the system.

Denoting by $S^{\beta }$ the surface concentration of CH₃O, we have

$${\displaystyle \frac{d{S}^{\beta }}{dt}}=e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left(k_2{S}^{\theta }-k_3{S}^{\beta }\right),$$

(14)

where $k_3$ is the oxidation velocity constant of CH₃O. The following steps are as follows:

$${\displaystyle \frac{d{S}^{\gamma }}{dt}}=e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left(k_3{S}^{\beta }-k_4{S}^{\gamma }{\left[S^{OH}\right]}^2\right),$$

(15)

with $S^{\gamma }$ being the surface concentration of formaldehyde (HCHO) and $k_4$ being its oxidation velocity constant. Then, we have

$${\displaystyle \frac{d{S}^{\delta }}{dt}}=e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left(k_4{S}^{\gamma }{\left[S^{OH}\right]}^2-k_5{S}^{\delta }{S}^{OH}\right),$$

(16)

where $S^{\delta }$ is the surface concentration of HCOO⁻ concentration and $k_5$ the corresponding reaction constant. Carbonate (${\mathrm{CO}}_3^{2-}$) surface concentration is $S^{ϵ}$, and therefore is as follows:

$${\displaystyle \frac{d{S}^{ϵ}}{dt}}=e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left(k_5{S}^{\delta }{S}^{OH}-k_6{S}^{ϵ}\right).$$

(17)

The subsequent reaction is the regeneration of active sites from palladium oxide (M·O) $S^{MO}$:

$${\displaystyle \frac{d{S}^{MO}}{dt}}=e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left(k_6{S}^{ϵ}-k_7{S}^{MO}{S}^w\right).$$

(18)

Carbon dioxide gas production is, therefore,

$${\displaystyle \frac{d{C}^{C{O}_2}}{dt}}=e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}{k}_6{S}^{ϵ}.$$

(19)

In the previous reaction mechanism, the oxidation contributions finish at Equation (17), in which the six electrons produced by methanol oxidation are completed [25]. The subsequent reactions do not influence the oxidation peak and will not be taken into account in the following analysis, since they took place in the cathodic part of the cyclic voltammetry.

In the adsorption steps of methanol, water, and OH⁻ ions, the concentration of free surface active sites, $S_M$, is given by a Langmuir–Hinshelwood-like term:

$$S_M=S_M^0-\left(S^{\theta }+S^w+S^{OH}+S^{\beta }+S^{\gamma }+S^{\delta }+S^{ϵ}+S^{MO}\right).$$

(20)

The last term in the previous equation is likely responsible for surface poisoning because of the existence of adsorbed OH ions and the specific formation of palladium oxides (MO). These poisoning effects differ from the one previously considered during MOR on pure Pd nanoparticles, in which the formation of adsorbed CO was responsible for the blocking of active sites [25].

Although we have called it a Langmuir–Hinshelwood-like model for the reader’s reference, it is convenient to clarify here that our adsorption model, represented by the set of Equations (11)–(13) and (20), in fact goes beyond the classical LH model since the standard LH model assumes that the availability of free sites is determined solely by the total number of sites and the fractional coverage of a single adsorbate (methanol, water, or OH). It does not explicitly consider the influence of multiple adsorbed species on the availability of free sites (in our case, all of the intermediates of the mechanism). Therefore, although competitive adsorption among three bulk species can still be considered a classical LH model, our description cannot be considered to be the same rigorous type, since it incorporates surface interactions and competitive adsorption through Equation (20). Our kinetic model, by incorporating Equation (20) (implying that several species compete for adsorption sites on the surface) into three different adsorption kinetic equations with different adsorption rates (and, implicitly, different adsorption energies), couples the whole mechanism into the adsorption kinetics, giving rise to a highly non-linear feedback that is not accounted for in the classical LH case. Thus, despite the apparent simple form of the equations, a highly competitive adsorption and intermediate occupancy of active sites implicitly incorporates lateral interactions and surface heterogeneity in an averaged form. What is not directly incorporated in our model is the lateral diffusion of the species over the surface of the catalyst. However, we believe that, in the case of nanoscale catalysts, this effect is not too relevant due to the small characteristic size of the system. Finally, we want to add that, despite the possible limitations of the LH model and our more general approach, some reports suggest that the use of the LH model for methanol adsorption can still be quantitatively acceptable [44,45].

The total current observed in a methanol oxidation reaction (MOR) is the result of multiple individual oxidation reactions occurring simultaneously or sequentially at the electrode surface. Each of these steps involves an oxidation reaction, and each oxidation reaction contributes to the overall current. This electrochemical current $i_{ox}$ can be written as the sum of the contributions of the oxidation reactions in the mechanism:

$${\displaystyle \frac{i_{ox}}{E_{A}F}}=\sum _j{\left[{\displaystyle \frac{d{S}_i}{dt}}\right]}_{ox}$$

(21)

where $E_A$ is the electrode area. In the present case, the current is given by

$${\displaystyle \frac{i_{ox}}{AF}}=e^{(1-\alpha )\frac{F\eta \left(t\right)}{RT}}\left\{k_1{S}^w+k_2{S}^{\theta }+k_3{S}^{\beta }+k_4{S}^{\gamma }{\left[S^{OH}\right]}^2+2k_6{S}^{ϵ}\right\}.$$

(22)

Using the previous relations and the evolution equation for the applied voltage:

$${\displaystyle \frac{d}{dt}}\eta \left(t\right)=\nu ,$$

(23)

with $\nu$ being the sweep rate satisfying $\nu \left(0\right)={\mathcal{E}}_{eq}$, one can calculate how the current changes with time and applied voltage during a linear voltammetry experiment.

6. Conclusions

This study analyzes the impact of the relative proportion of nickel (Ni) and palladium (Pd) in catalytic nanoparticles on the methanol oxidation reaction (MOR). The results are presented in terms of kinetic parameters, surface concentrations, and peak currents, showing significant differences between three main compositions: Ni₃Pd₁, Ni₁Pd₁, and Ni₁Pd₃.

It is observed that a higher Pd content on the surface promotes water adsorption and increases its oxidation rate, thereby reducing the need for direct OH adsorption. This trend is evident in the lower concentration of water adsorbed on Ni₃Pd₁ nanoparticles compared to the other two compositions. Furthermore, the increase in Pd favors mechanisms in which the formation of Pd oxides plays a minor role in surface poisoning, unlike Ni, which increases the concentrations of adsorbed OH, contributing significantly to the blocking of active sites.

The analysis of the rate constants shows that, for Ni₁Pd₃, the adsorption of methanol depends markedly on its concentration in the medium, being approximately three times higher for concentrations lower than 1 M, compared to the other two compositions. In contrast, the adsorption rate of OH on Ni₃Pd₁ remains constant. These results suggest that the predominant presence of Pd favors the oxidation of water and reduces the dependence on OH-based mechanisms. On the other hand, nanoparticles with equimolar proportions (Ni₁Pd₁) stand out for oxidizing adsorbed carbonates approximately three times faster than the other two compositions, which influences the symmetry of the oxidation peaks. Regarding the transfer parameter, Ni₃Pd₁ shows a higher degree of asymmetry in the oxidation energy barrier, while Ni₁Pd₁ and Ni₁Pd₃ have more constant values and closer to 0.83.

The results suggest that a higher Pd content favors more efficient oxidation mechanisms by reducing the formation of intermediate products that cause surface poisoning, such as CO, carbonates, or palladium oxide. However, as the proportion of Ni increases, an increase in the concentration of adsorbed OH is observed, which dominates the blocking of active sites even above from the palladium oxide blocking. This behavior clearly differs from the that observed in the direct methanol–CO mechanism in which carbonate formation is avoided in Pd-dominant alloys. This relationship suggests that the surface composition can be tuned to optimize catalytic performance, depending on the desired dominant mechanism.

Finally, this study highlights how the relative proportion of Ni and Pd affects both the kinetic characteristics and the intermediate products, providing a basis for the rational design of catalysts in methanol oxidation applications.