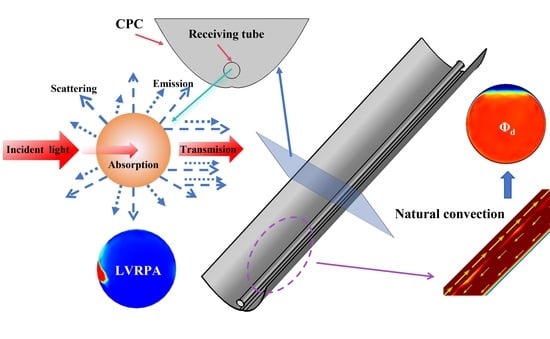
A Numerical Case Study of Particle Flow and Solar Radiation Transfer in a Compound Parabolic Concentrator (CPC) Photocatalytic Reactor for Hydrogen Production
Abstract
Highlights
- A comprehensive simulation model including particle flow and radiation transfer was developed for a CPC photocatalytic reactor.
- The ray tracing method was utilized to determine the radiation reaching the surface of the receiving tube, while the discrete ordinates method (DOM) was also employed to solve the radiative transfer equation (RTE), which shows the complete process of solar energy transfer.
- Local volume radiative power absorption (LVRPA) and total radiative power absorption (TRPA) inside the receiving tube was obtained by this study, which is critical data for the photocatalytic reactor.
- Natural convection with intermittent disturbances is demonstrated to be effective operating mode for the CPC photocatalytic reactor.
Abstract
1. Introduction
2. Results and Discussion
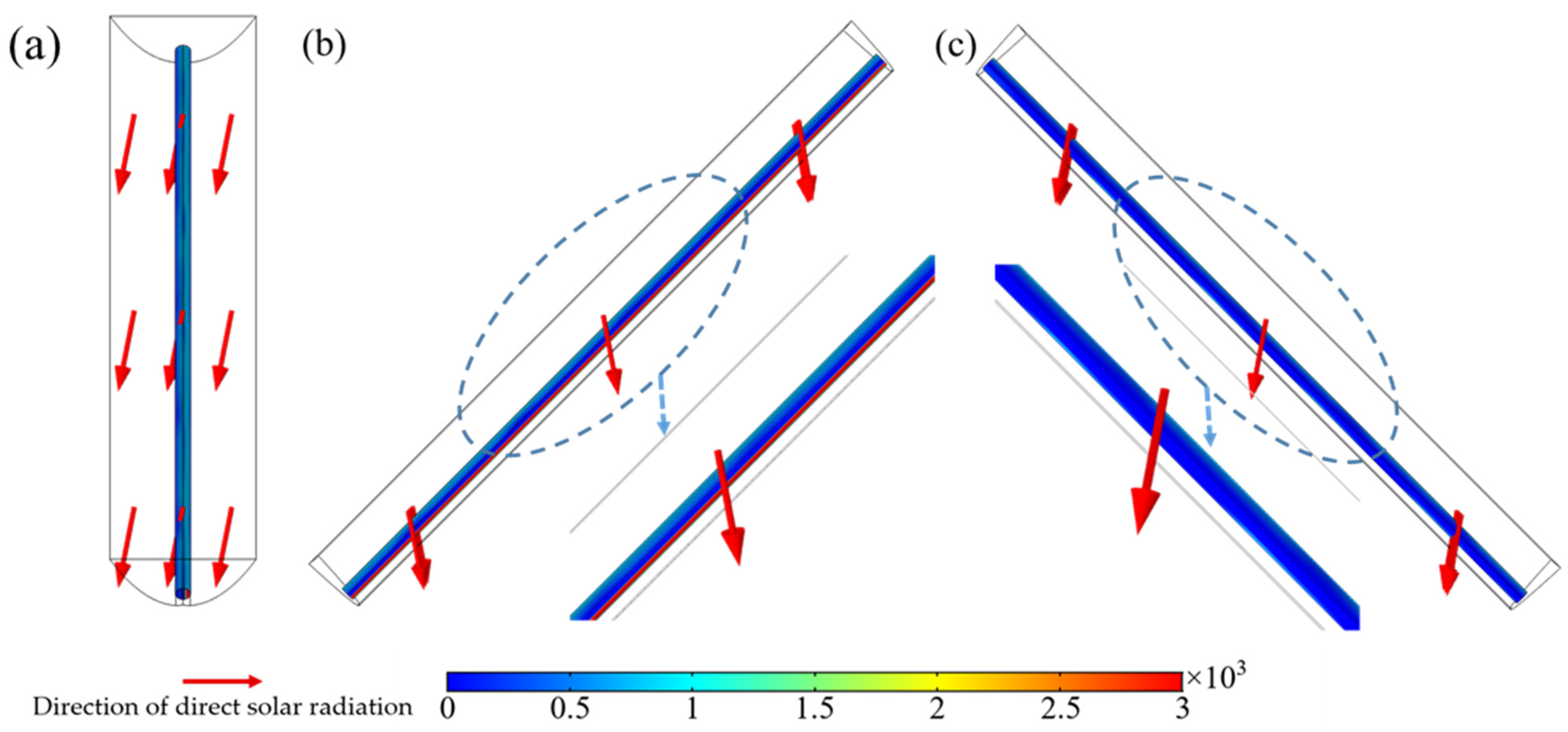
2.1. The Distribution of Radiation on the Surface of Receiving Tube
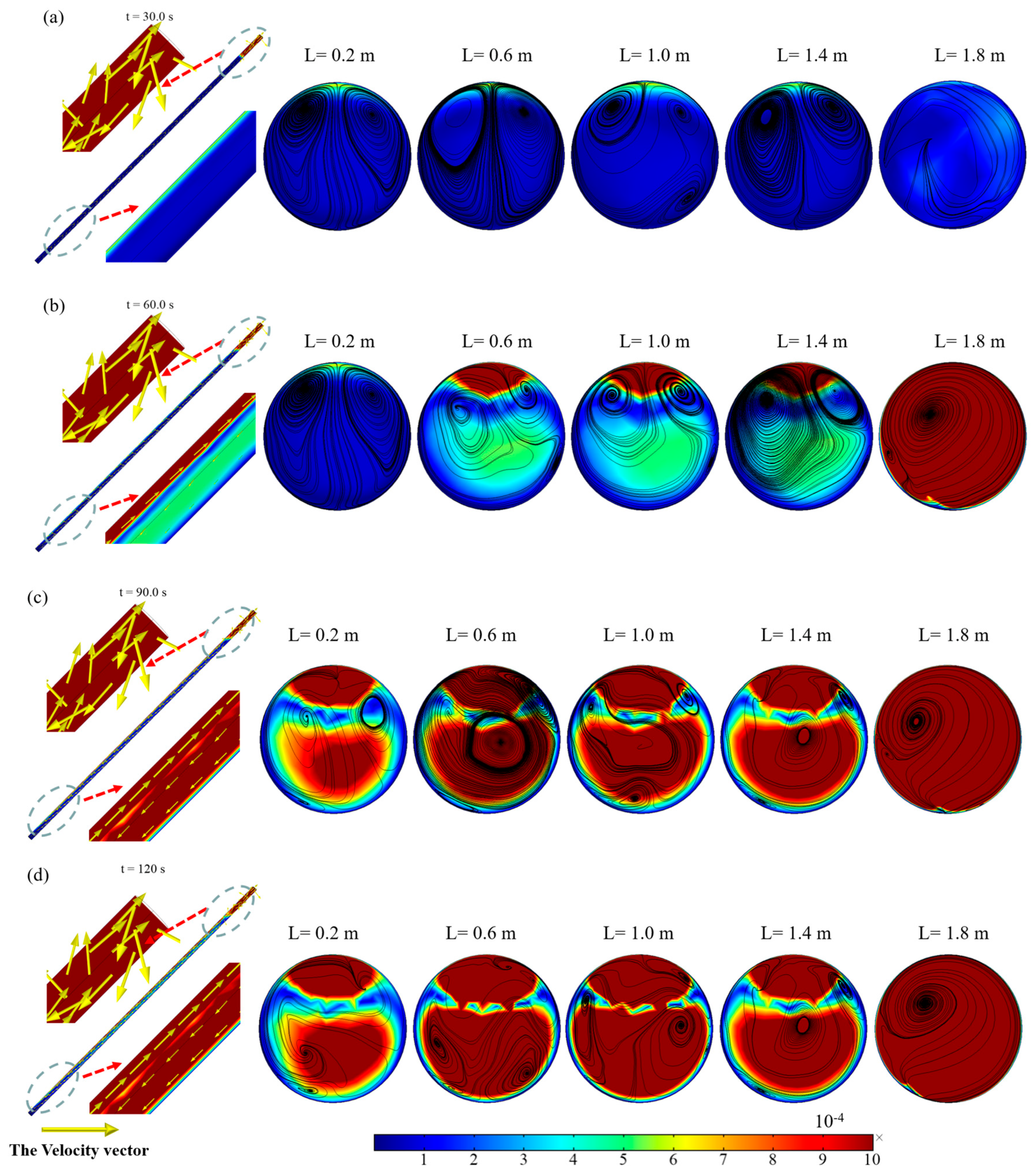
2.2. Natural Circulation Flow in the Receiving Tube
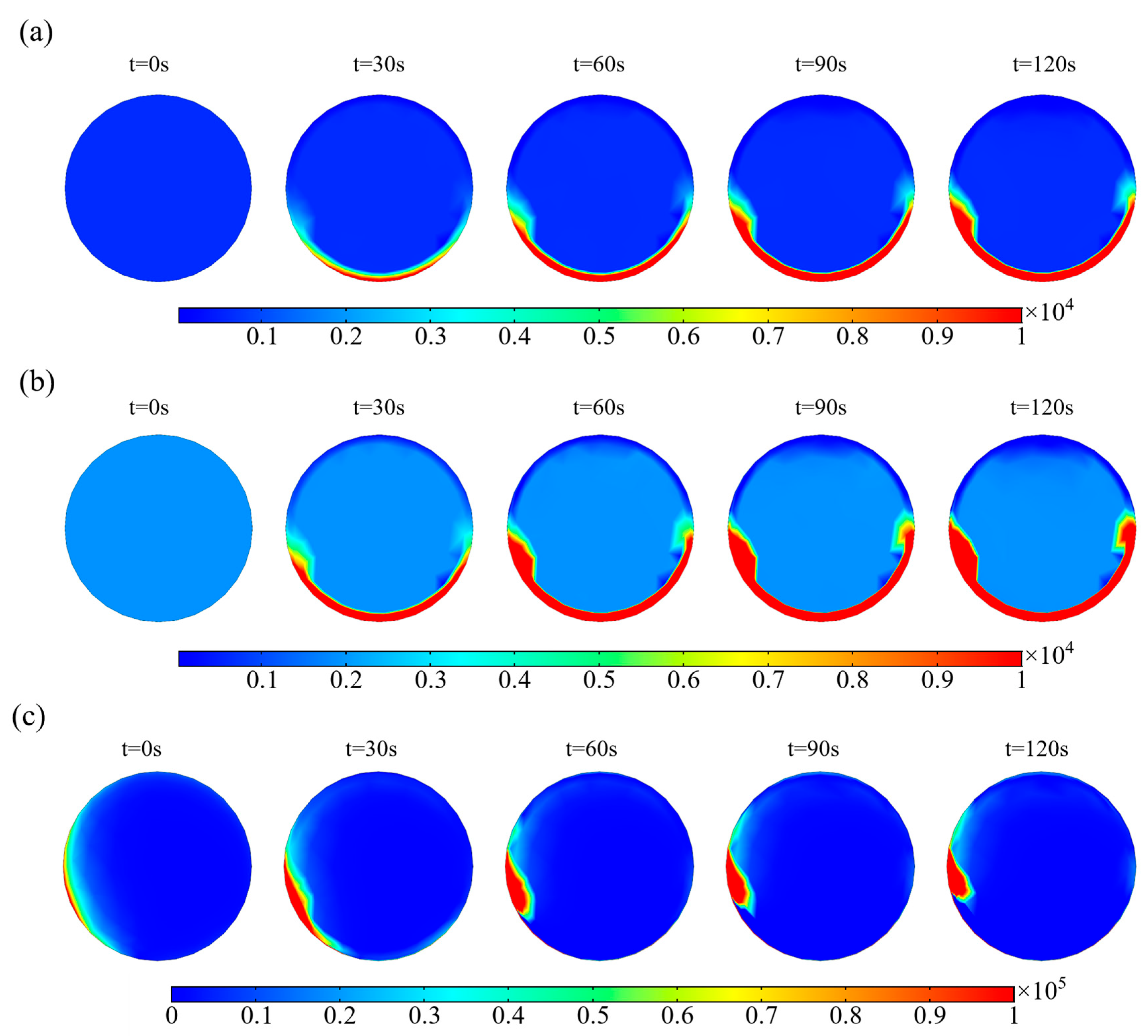
2.3. The Phase Volume Fraction of the Photocatalysts in the Receiving Tube
2.4. Radiation Transfer Characteristics in the Receiving Tube
3. Mathematical Model
3.1. Physical Model
3.1.1. Ray Tracing Approach
3.1.2. Euler–Euler Two-Fluid Flow Model
3.1.3. Discrete Ordinates Method
3.1.4. Simulation Method and Process
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| c | Speed of light |
| ccat | Concentration of the photocatalyst |
| cp | Specific heat capacity |
| dR | Diameter of the receiving tube |
| Gap | Gap between CPC and receiving tube |
| k | Heat conductivity coefficient |
| lR | Length of the receiving tube |
| n | Refractive index |
| p | Pressure |
| rB | Radius of the base circle of the CPC |
| CD | Drag coefficient |
| I | Radiation density |
| T | Temperature |
| Q | Quantity of heat |
| Abbreviations | |
| CPC | Compound parabolic concentrator |
| CFD | Computational fluid dynamics |
| DOM | Discrete ordinates method |
| LVRPA | Local volume radiative power absorption, W·m−3 |
| RTE | Radiative transfer equation |
| TRPA | Total radiative power absorption, W |
| UV | Ultraviolet |
| Vectors and tensors | |
| F | Volume forces, N·m−3 |
| Fm | Interphase interaction force, N·m−3 |
| g | Gravitational acceleration vector |
| I | Unit tensor |
| k | Wave vector |
| q | Position vector of the ray |
| r | Position vector of the space |
| s | Spatial angle vector |
| u | Velocity vector |
| K | Viscous stress tensor, Pa |
| S | Strain rate tensor |
| Greek letters | |
| αht | Efficiency of solar-to-thermal conversion |
| αp | Thermal diffusion coefficient |
| ε | Emission coefficient |
| θa | Maximum acceptance half angle, ° |
| θt | Truncation angle, ° |
| κ | Absorption coefficient in aqueous medium, m−1 |
| ρ | Density, kg·m−3 |
| σ | Scattering coefficient, m−1 |
| τ | Viscous stress tensor |
| φ | Azimuth angle in spherical coordinates |
| Ψ | Polar angle in spherical coordinates |
| φ | Phase volume fraction |
| φS | Scattering phase function |
| Ω | , sr |
| Superscripts and subscripts | |
| c | Continuous phase |
| d | Discrete phase |
| m | Mixed phase |
| p | Particle |
References
- Xia, B.; He, B.; Zhang, J.; Li, L.; Zhang, Y.; Yu, J.; Ran, J.; Qiao, S.Z. TiO2/FePS3 S-Scheme Heterojunction for Greatly Raised Photocatalytic Hydrogen Evolution. Adv. Energy Mater. 2022, 12, 2201449. [Google Scholar] [CrossRef]
- Xiang, X.; Zhang, L.; Luo, C.; Zhang, J.; Cheng, B.; Liang, G.; Zhang, Z.; Yu, J. Ultrafast electron transfer from CdS quantum dots to atomically-dispersed Pt for enhanced H2 evolution and value-added chemical synthesis. Appl. Catal. B Environ. 2024, 340, 123196. [Google Scholar] [CrossRef]
- Jing, D.W.; Guo, L.J.; Zhao, L.; Zhang, X.M.; Liu, H.; Li, M.T.; Shen, S.H.; Liu, G.J.; Hu, X.W.; Zhang, X.H. Efficient solar hydrogen production by photocatalytic water splitting: From fundamental study to pilot demonstration. Int. J. Hydrogen Energy 2010, 35, 7087–7097. [Google Scholar] [CrossRef]
- Guo, P.; Xiong, Z.; Yuan, S.; Xie, K.; Wang, H.; Gao, Y. The synergistic effect of Co/CoO hybrid structure combined with biomass materials promotes photocatalytic hydrogen evolution. Chem. Eng. J. 2021, 420, 130372. [Google Scholar] [CrossRef]
- Nandal, V.; Shoji, R.; Matsuzaki, H.; Furube, A.; Lin, L.; Hisatomi, T.; Kaneko, M.; Yamashita, K.; Domen, K.; Seki, K. Unveiling charge dynamics of visible light absorbing oxysulfide for efficient overall water splitting. Nat. Commun. 2021, 12, 7055. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y.; Dong, C.; Meng, F.; Huang, Y.; Zhang, Q.; Gu, L.; Liu, L.; Shen, S. Electron-Deficient Zn-N6 Configuration Enabling Polymeric Carbon Nitride for Visible-Light Photocatalytic Overall Water Splitting. Nano-Micro Lett. 2022, 14, 223. [Google Scholar] [CrossRef] [PubMed]
- Kumaravel, V.; Mathew, S.; Bartlett, J.; Pillai, S.C. Photocatalytic hydrogen production using metal doped TiO2: A review of recent advances. Appl. Catal. B Environ. 2019, 244, 1021–1064. [Google Scholar] [CrossRef]
- Hamd, W.; Daher, E.A.; Tofa, T.S.; Dutta, J. Recent Advances in Photocatalytic Removal of Microplastics: Mechanisms, Kinetic Degradation, and Reactor Design. Front. Mar. Sci. 2022, 9, 885614. [Google Scholar] [CrossRef]
- Grao, M.; Ratova, M.; Kelly, P. Design and optimisation of a low-cost titanium dioxide-coated stainless steel mesh photocatalytic water treatment reactor. J. Clean Prod. 2021, 297, 126641. [Google Scholar] [CrossRef]
- Mei, J.; Gao, X.; Zou, J.; Pang, F. Research on Photocatalytic Wastewater Treatment Reactors: Design, Optimization, and Evaluation Criteria. Catalysts 2023, 13, 974. [Google Scholar] [CrossRef]
- Abdel-Maksoud, Y.; Imam, E.; Ramadan, A. TiO2 Solar Photocatalytic Reactor Systems: Selection of Reactor Design for Scale-up and Commercialization—Analytical Review. Catalysts 2016, 6, 138. [Google Scholar] [CrossRef]
- Keller, N.; Ivanez, J.; Highfield, J.; Ruppert, A.M. Photo-/thermal synergies in heterogeneous catalysis: Towards low-temperature (solar-driven) processing for sustainable energy and chemicals. Appl. Catal. B Environ. 2021, 296, 120320. [Google Scholar] [CrossRef]
- Jebasingh, V.K.; Herbert, G.M.J. A review of solar parabolic trough collector. Renew. Sustain. Energy Rev. 2016, 54, 1085–1091. [Google Scholar] [CrossRef]
- Martínez-García, A.; Vincent, M.; Rubiolo, V.; Domingos, M.; Canela, M.C.; Oller, I.; Fernández-Ibáñez, P.; Polo-López, M.I. Assessment of a pilot solar V-trough reactor for solar water disinfection. Chem. Eng. J. 2020, 399, 125719. [Google Scholar] [CrossRef]
- Fendrich, M.; Quaranta, A.; Orlandi, M.; Bettonte, M.; Miotello, A. Solar Concentration for Wastewaters Remediation: A Review of Materials and Technologies. Appl. Sci. 2019, 9, 118. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Chen, J.; Chen, F. Preliminary investigation on optical performance of linear fresnel lens coupled compound parabolic concentrator. Energy 2023, 278, 127910. [Google Scholar] [CrossRef]
- Sichel, C.; Blanco, J.; Malato, S.; Fernández-Ibáñez, P. Effects of experimental conditions on E. coli survival during solar photocatalytic water disinfection. J. Photochem. Photobiol. A Chem. 2007, 189, 239–246. [Google Scholar] [CrossRef]
- Nchikou, C.; Loredo-Medrano, J.Á.; Hernández-Ramírez, A.; Colina-Marquez, J.Á.; Mueses, M.Á. Estimation of the radiation field for CPC photocatalytic reactors using a novel six-flux model in two dimensions (SFM-2D). J. Environ. Chem. Eng. 2021, 9, 106392. [Google Scholar] [CrossRef]
- García-Montaño, J.; Pérez-Estrada, L.; Oller, I.; Maldonado, M.I.; Torrades, F.; Peral, J. Pilot plant scale reactive dyes degradation by solar photo-Fenton and biological processes. J. Photochem. Photobiol. A Chem. 2008, 195, 205–214. [Google Scholar] [CrossRef]
- Monteagudo, J.M.; Duran, A.; Aguirre, M.; Martin, I.S. Photodegradation of Reactive Blue 4 solutions under ferrioxalate-assisted UV/solar photo-Fenton system with continuous addition of H2O2 and air injection. Chem. Eng. J. 2010, 162, 702–709. [Google Scholar] [CrossRef]
- Jing, D.; Liu, H.; Zhang, X.; Zhao, L.; Guo, L. Photocatalytic hydrogen production under direct solar light in a CPC based solar reactor: Reactor design and preliminary results. Energy Conv. Manag. 2009, 50, 2919–2926. [Google Scholar] [CrossRef]
- Wei, Q.Y.; Yang, Y.; Hou, J.Y.; Liu, H.; Cao, F.; Zhao, L. Direct solar photocatalytic hydrogen generation with CPC photoreactors: System development. Sol. Energy 2017, 153, 215–223. [Google Scholar] [CrossRef]
- Hu, X.W.; Guo, L.J. Numerical investigations of catalyst–liquid slurry flow in the photocatalytic reactor for hydrogen production based on algebraic slip model. Int. J. Hydrogen Energy 2010, 35, 7065–7072. [Google Scholar]
- Geng, J.; Tang, J.; Wang, Y.; Huang, Z.; Jing, D.; Guo, L. Attenuated Periodical Oscillation Characteristics in a Nanoscale Particle-Laden Laminar Flow. Ind. Eng. Chem. Res. 2020, 59, 8018–8027. [Google Scholar] [CrossRef]
- Geng, J.F.; Wang, Y.C.; Hu, X.W.; Jing, D.W. Insights into the hydrodynamic properties of slurry flow in a tubular photocatalytic reactor by PIV combined with LSIA. Chem. Eng. Sci. 2016, 152, 127–139. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, Q.; Hou, J.; Liu, H.; Zhao, L. Solar concentrator with uniform irradiance for particulate photocatalytic hydrogen production system. Int. J. Hydrogen Energy 2016, 41, 16040–16047. [Google Scholar] [CrossRef]
- Wei, Q.; Yang, Y.; Liu, H.; Hou, J.; Liu, M.; Cao, F.; Zhao, L. Experimental study on direct solar photocatalytic water splitting for hydrogen production using surface uniform concentrators. Int. J. Hydrogen Energy 2018, 43, 13745–13753. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, Q.; Liu, H.; Zhao, L. Optimization of the radiation absorption for a scaled-up photocatalytic hydrogen production system. Sol. Energy 2018, 160, 168–177. [Google Scholar] [CrossRef]
- Hou, J.; Liu, H.; Zhao, L. Optimization of radiation absorption model in solar photocatalytic reactors: Coupling photocatalyst concentration distribution. Appl. Therm. Eng. 2019, 160, 114090. [Google Scholar] [CrossRef]
- Ren, Y.; Zhao, L.; Jing, D.; Guo, L. Investigation and modeling of CPC based tubular photocatalytic reactor for scaled-up hydrogen production. Int. J. Hydrogen Energy 2016, 41, 16019–16031. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, Y.; Dai, B.; Yang, Y.; Liu, H.; Yuan, H.; Jing, D.; Zhao, L. Theoretical study on flow and radiation in tubular solar photocatalytic reactor. Front. Energy 2021, 15, 687–699. [Google Scholar] [CrossRef]
- Moreira, R.P.M.; Puma, G.L. Multiphysics Computational Fluid-Dynamics (CFD) Modeling of Annular Photocatalytic Reactors by the Discrete Ordinates Method (DOM) and the Six-Flux Model (SFM) and Evaluation of the Contaminant Intrinsic Kinetics Constants. Catal. Today 2021, 361, 77–84. [Google Scholar] [CrossRef]
- Tolosana-Moranchel, A.; Casas, J.A.; Carbajo, J.; Faraldos, M.; Bahamonde, A. Influence of TiO2 optical parameters in a slurry photocatalytic reactor: Kinetic modelling. Appl. Catal. B Environ. 2017, 200, 164–173. [Google Scholar] [CrossRef]
- Di Felice, R. The pseudo-fluid model applied to three-phase fluidisation. Chem. Eng. Sci. 2000, 55, 3899–3906. [Google Scholar] [CrossRef]
- Enwald, H.; Peirano, E.; Almstedt, A.E. Eulerian two-phase flow theory applied to fluidization. Int. J. Multiph. Flow 1996, 22, 21–66. [Google Scholar] [CrossRef]



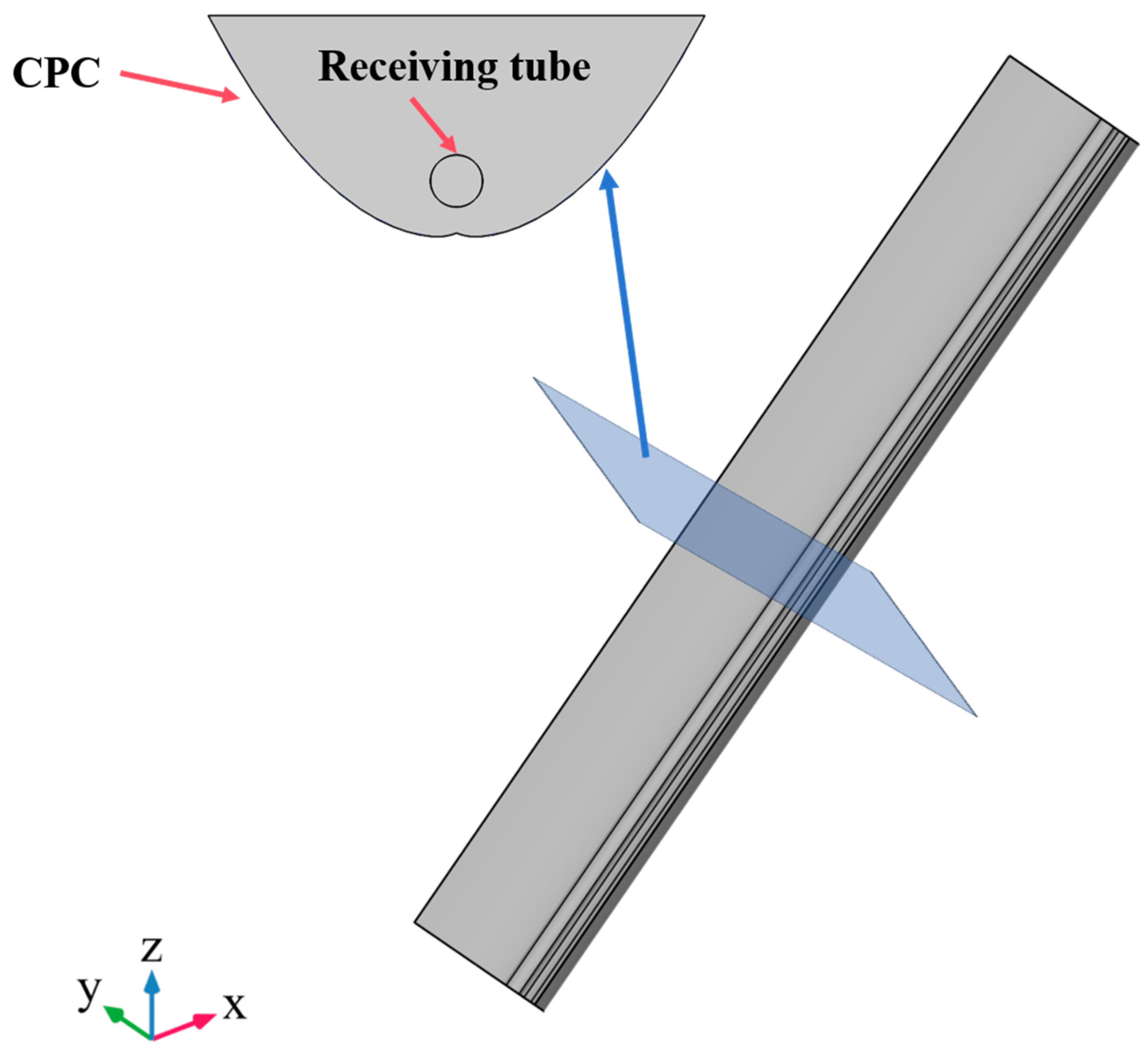
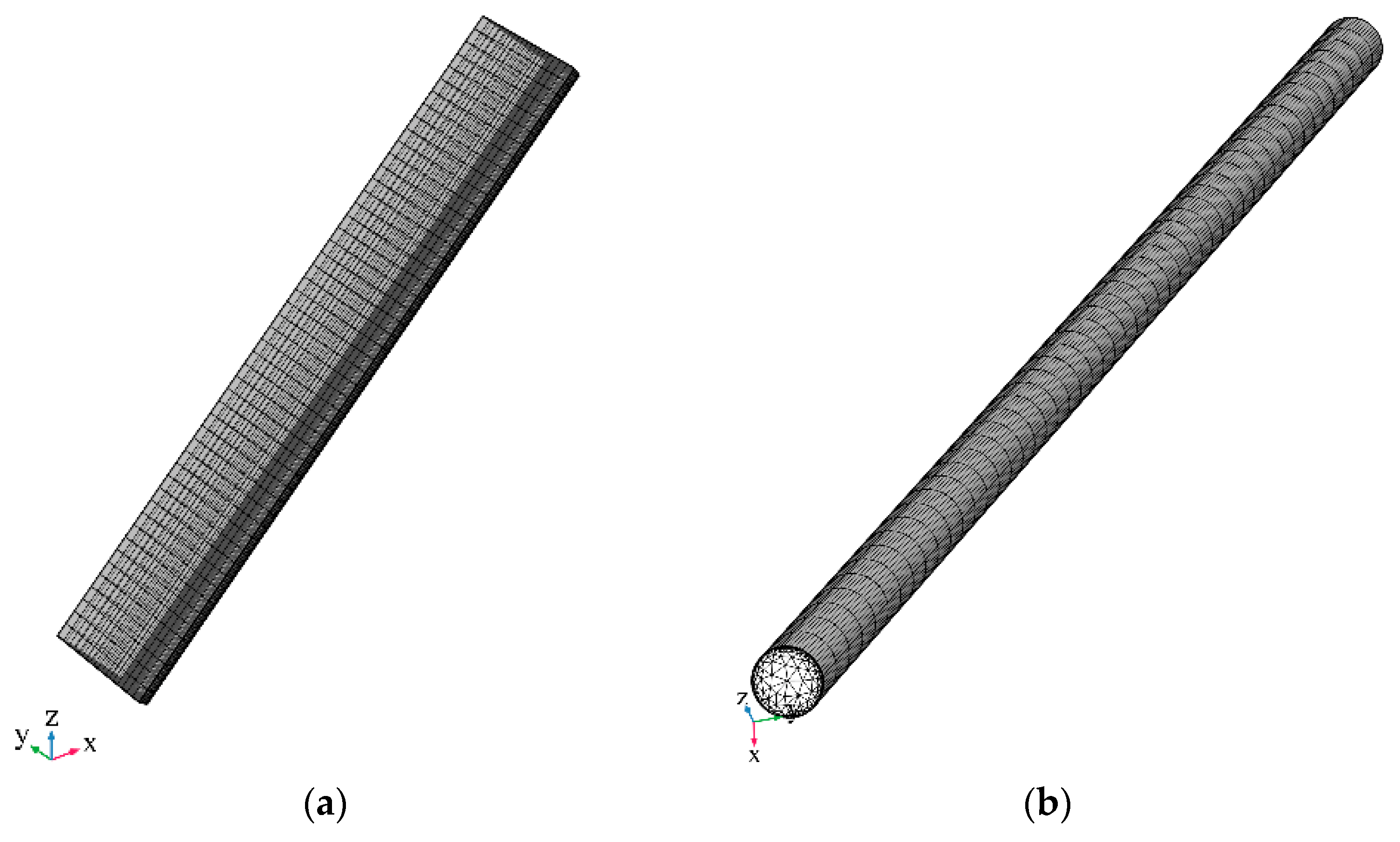

| Parameters | Numerical Value |
|---|---|
| dR/mm | 30 |
| lR/m | 2 |
| rB/mm | 15 |
| Gap/mm | 25 |
| θa/° | 5 |
| θt/° | 60 |
| Coefficient | Numerical Value/m2·kg−1 |
|---|---|
| κ*UVA | 189.9 |
| σ*UVA | 1175.1 |
| κ*UVB | 508.5 |
| σ*UVB | 1016.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, J.; Wei, Q.; Luo, B.; Zong, S.; Ma, L.; Luo, Y.; Zhou, C.; Deng, T. A Numerical Case Study of Particle Flow and Solar Radiation Transfer in a Compound Parabolic Concentrator (CPC) Photocatalytic Reactor for Hydrogen Production. Catalysts 2024, 14, 237. https://doi.org/10.3390/catal14040237
Geng J, Wei Q, Luo B, Zong S, Ma L, Luo Y, Zhou C, Deng T. A Numerical Case Study of Particle Flow and Solar Radiation Transfer in a Compound Parabolic Concentrator (CPC) Photocatalytic Reactor for Hydrogen Production. Catalysts. 2024; 14(4):237. https://doi.org/10.3390/catal14040237
Chicago/Turabian StyleGeng, Jiafeng, Qingyu Wei, Bing Luo, Shichao Zong, Lijing Ma, Yu Luo, Chunyu Zhou, and Tongkun Deng. 2024. "A Numerical Case Study of Particle Flow and Solar Radiation Transfer in a Compound Parabolic Concentrator (CPC) Photocatalytic Reactor for Hydrogen Production" Catalysts 14, no. 4: 237. https://doi.org/10.3390/catal14040237
APA StyleGeng, J., Wei, Q., Luo, B., Zong, S., Ma, L., Luo, Y., Zhou, C., & Deng, T. (2024). A Numerical Case Study of Particle Flow and Solar Radiation Transfer in a Compound Parabolic Concentrator (CPC) Photocatalytic Reactor for Hydrogen Production. Catalysts, 14(4), 237. https://doi.org/10.3390/catal14040237