Abstract
Chalcogen-nitrogen chemistry deals with systems in which sulfur, selenium, or tellurium is linked to a nitrogen nucleus. This chemical motif is a key component of different functional structures, ranging from inorganic materials and polymers, to rationally designed catalysts, to bioinspired molecules and enzymes. The formation of a selenium–nitrogen bond, typically occurring upon condensation of an amine and the unstable selenenic acid, often leading to intramolecular cyclizations, and its disruption, mainly promoted by thiols, are rather common events in organic Se-catalyzed processes. In this work, focusing on examples taken from selenium organic chemistry and biochemistry, the selenium–nitrogen bond is described, and its strength and reactivity are quantified using accurate computational methods applied to model molecular systems. The intermediate strength of the Se–N bond, which can be tuned to necessity, gives rise to significant trends when comparing it to the stronger S– and weaker Te–N bonds, reaffirming also in this context the peculiar and valuable role of selenium in chemistry and life.
1. Introduction
The chalcogen–nitrogen bond (X–N, X = S, Se, Te) is an important motif in chemistry and is present in many different structures, ranging from inorganic and organic materials, catalysts, protein mimics, and drugs [1,2,3,4]. In the lab, the formation of a X–N bond is typically obtained from benzanilide, using ortholithiation, chalcogen insertion, and oxidative cyclization [5,6,7,8], and by intramolecular cyclocondensation of chalcogenic acids [9,10,11].
The Se–N bond is present in the isoselenazole ring of ebselen (2-phenyl-1,2-benzisoselenazol-3(2H)-one, which is described as the first and most popular glutathione peroxidase (GPx) mimic [12,13]. This compound is endowed with antimicrobic and cytoprotective activities. In addition, it has the potential of modulating seleno(thio)proteins, gene expression, epigenetics, immune system, and antioxidant defenses. In general, ebselen is reported to interact with targets from several biological pathways, including oxidative enzymes involved in inflammatory reactions [14]. So far, the mechanistic details of its catalytic activity have not been fully elucidated [14,15,16,17,18], although a nice computational investigation has provided an exhaustive picture of the possible paths [19], disclosing that the chemistry of the Se–N bond plays a crucial role in triggering the antioxidant effects [3,20].
According to the results of clinical studies, ebselen administration is well tolerated. This molecule is characterized by satisfying metabolic profile and safety, and limited side effects have been reported [21,22].
In this connection, and in light of its several macromolecular interactors, ebselen represents an example of a multi-target drug. It is currently being studied for the prevention of noise-induced hearing loss in a phase 2 trial [22]. Moreover, this compound is under investigation for the potential beneficial effects on bipolar disorder as it targets inositol monophosphatase (IMPase) [23,24].
Importantly, ebselen was recently highlighted in the context of a structure-based virtual screening as a putative inhibitor of the SARS-CoV-2 main protease (Mpro), suggesting its potential therapeutic use for COVID-19. Ebselen activity against this cysteine protease was also confirmed experimentally (IC50 = 0.67 μM) and in a cell-based antiviral assay [25]. The reaction between the thiol moiety from the cysteine residue of Mpro active site and the isoselenazole ring can break the Se–N bond, leading to the formation of a Se–S bond and subsequent enzyme inhibition [26]. Nevertheless, a contribution of non-covalent binding of ebselen to antiviral activity cannot be ruled out [25]. Computational studies have recently been enrolled to investigate the mechanism of action, at the molecular levels, of small molecules interfering with SARS-CoV-2 targets [27]. Concerning the binding of ebselen to Mpro, Menéndez and colleagues reported the presence of a second, high-affinity allosteric site, which would be involved in catalytic site access regulation by surface–loop interactions [28]. In addition, ebselen is also a multi-target agent for contrasting SARS-CoV-2, as it has been reported to inhibit papain-like protease (PLpro), another cysteine-containing enzyme [29]. Notably, Mpro and PLpro inhibition is abolished by the addition of the reducing agent 1,4-dithiothreitol (DTT) [30].
It must be also pointed out that this is not the first time that ebselen is being studied as an antiviral agent. This compound was previously reported to be a human immunodeficiency virus type 1 (HIV-1) capsid assembly inhibitor [31] and to prevent hepatitis C virus replication by interfering with NS3 helicase binding to nucleic acid [32].
An early overview on the structure and on the electronic as well as steric features of Se–N and Te–N bonds was reported by Bjorgvinsson and Roesky three decades ago [33]. In this contribution, the authors provided interesting comments on stability issues of the compounds and their precursors, highlighting that simple classes of molecules such as amides or imides of selenium and tellurium were almost unknown at that time. The structures of several X–N bond-containing heterocycles were also reported. Mahmudov and colleagues provided an updated perspective on the relevance of covalent and non-covalent chalcogen bonding in several trending branches of modern solid state and solution chemistry. Organic and inorganic synthesis, catalysis, material sciences, and molecular recognition are just some of the fields in which X–N bond can direct and assist chemical reactivity [34].
In biochemistry and medicinal chemistry, besides ebselen and other GPx mimics, compounds based on heterocyclic scaffolds containing one or multiple Se–N bonds are being studied as antibiotic, antifungal, antiproliferative, anti-inflammatory, analgesic, and antimicrobial agents [1,3,17]. Particularly, selenazolinium salts appear as promising candidates in light of their good reactivity and selectivity toward thiol groups in peptides, proteins, and enzymes [35].
In nature, along the mechanistic path of GPx, evidence of the formation of a cyclic intermediate characterized by the presence of a Se–N bond in highly oxidizing conditions has been reported and interpreted as a strategy to protect the selenoenzyme by overoxidation [36]. Similarly, the redox regulation of protein tyrosine phosphatase 1B (PTP1B) involves the formation of a sulfenamide intermediate (S–N bond), from the attack of amide nitrogen on the sulfenic acid sulfur of Cys residue [37,38,39]. Similar examples have been observed for the transcriptional regulator OhrR from Bacillus subtilis [40] and the murine receptor-like protein tyrosine phosphatase [41]. In addition, the formation of Se–N bond might be involved in the δ-aminolevulinic acid dehydratase enzyme inhibition by organoselenium compounds [42].
Another important field dealing with structures characterized by the X–N bond motif is represented by binary chalcogen-nitrogen and ternary S, N, P molecules with intriguing future applications for fingerprint detection, optoelectronic devices, and as hydrogen-storage materials [4]. Finally, taking into account the importance of the supramolecular chemistry, 1,2,5-chalcogenadiazoles are promising building blocks for the development of conductors, optical devices, and self-assembled materials [43,44,45].
It is worth to mention that Tsuzuki and Sato explored in detail the features of intermolecular X–N (X = S, Se, Te) bonds in chalcogenadiazole dimers. [46] Their study, performed employing coupled cluster (CCSD(T)) calculations at the basis set limit, disclosed how intermolecular X–N bonds behave similarly to halogen bonds, displaying moderately weak interaction energies (−3 to −12 kcal mol−1) that become more negative, increasing the size of the chalcogen. Particularly, the stabilization comes almost exclusively from dispersion and electrostatic interactions, with the latter being responsible for the stronger interaction displayed by Te–N bonds with respect to S/Se–N. A similar trend has been observed by some of us when investigating the chalcogen-π interaction [47]. This agreement between structurally different systems confirms the fact that accurate knowledge of the intrinsic atomistic properties of S, Se, or Te is crucial to obtain a set of principles that can be applied across a whole range of different partner molecules.
This brief overview highlights the importance of the chalcogen–nitrogen bond in many areas of chemistry. In this work, the X–N bond (X = S, Se, Te) is not only described, but its strength and reactivity changes upon varying the chalcogen and substituents are also quantified using accurate computational methods applied to model molecular systems. Going beyond the mere description provides us with conclusions of general validity for the very different systems presented above and move the first steps toward a systematic way of improving their chemical properties through rational design.
The manuscript is organized as follows. First, the molecular geometries, charge distributions, and interaction energies calculated for the investigated compounds are presented. Then, the discussion is focused on an in-depth analysis of such interaction energies accompanied by a detailed orbital analysis with the aim of understanding how the X–N bond strength can be related to the intrinsic atomistic properties of the different chalcogen and how the surrounding chemical environment will modify its strength.
2. Results
The model chosen for the analysis of the chalcogen–nitrogen bonds had general formula RX–NR’2, in which X can be S, Se, or Te and R and R’ were chosen among H, CH3, and CF3. A representative sample of optimized geometries of the structures is reported in Figure 1. Structures of the compounds with S and Te are shown in the Supplementary Materials (Table S1).
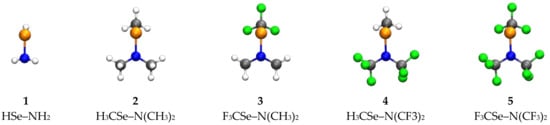
Figure 1.
Optimized geometries of selected model molecules of general formula RX–NR’ (X = Se). Level of theory: ZORA-BLYP-D3(BJ)/TZ2P.
Analysis of the geometries optimized at the ZORA-BLYP-D3(BJ)/TZ2P level of theory showed how the X–N bond length varied upon changing the chalcogen or the substituents R and R’ (Table 1). Particularly, descending along the group there was a lengthening of the bond with all substituents, caused by the increase of the van der Waals radius of the increasingly bigger chalcogen. The variations upon modification of the substituents in series with the same chalcogens were smaller and did not follow the same trend for all the chalcogens. However, the structures that showed the longest and shortest bond length were the same for all the chalcogens, with the combination having CF3 on the chalcogen and CH3 on the nitrogen, displaying the shortest bond length, whereas the alternative combination, i.e., R,R’ = CH3,CF3, showed the longest bond length

Table 1.
X–N bond length of optimized geometries of model molecules. Structure definitions are reported in Figure 1. Level of theory: ZORA-BLYP-D3(BJ)/TZ2P.
The Mulliken charge distributions, also calculated at the BLYP-QZ and M06-2X-QZ levels of theory (see Section 4 for a complete explanation of the employed levels of theory and their short notation), show how the X–N charge gap increased as we moved from S to Te (Table 2). The effect of the substituent within the same chalcogen was in agreement with the nature of the substituent itself, i.e., going from the small H to CH3 we saw that the charge got more delocalized and, therefore, the value on the X and N atoms was found to be, in absolute value, smaller in structure 2 than in structure 1 for all the chalcogens at the BLYP-QZ level of theory. An exception was found at the M06-2X-QZ level of theory, as both for S and Se the atomic charge was smaller on the chalcogen in the H-substituted structure. The presence of the strong electron withdrawing CF3 groups made the atomic charge become more positive both on the X and N atoms as more electronic density was shifted toward the highly electronegative fluorine atoms. This effect did not involve only the atom to which the CF3 group was directly bonded to but also the partner in the X–N bond, as we can see in structures 3 and 4 compared to their analogues with CH3.

Table 2.
Mulliken charges of the investigated compounds. Structure definitions are reported in Figure 1. Levels of theory: BLYP-QZ=ZORA-BLYP-D3(BJ)/QZ4Pae//ZORA-BLYP-D3(BJ)/TZ2P; M06-2X-QZ=ZORA-M06-2X/QZ4Pae //ZORA-BLYP-D3(BJ)/TZ2P.
To get a more exhaustive picture on the variation of the X–N bond strength upon changing the chalcogen or substituent, an accurate analysis on the interaction energy existing between the two molecular fragments obtained by homolytic cleavage of the X–N bond was carried out at two different levels of theory. Results, reported in Table 3, showed how the interaction diminished as the chalcogen atom increased in size. For example, at the BLYP-QZ level of theory with R,R’ = CH3 it went from −59.0 kcal mol−1 of sulfur to −47.5 of tellurium. The same trend was found for all the substituents’ combination, and also when the M06-2X functional was employed in the analysis (Table 3).

Table 3.
The ∆Eint for the model molecules. Structure definitions are reported in Figure 1. Levels of theory: BLYP = ZORA-BLYP-D3(BJ)/QZ4P ae // ZORA-BLYP-D3(BJ)/TZ2P; M06 = ZORA-M06-2X/QZ4Pae // ZORA-BLYP-D3(BJ)/TZ2P; CC = DLPNO-CCSD(T)/aug-cc-pVTZ-DK// ZORA-BLYP-D3(BJ)/TZ2P.
If we focus on the effect of the substituent effect instead, results show how the level of theory affects how different substituents modulate interaction energy changes. Using the M06-2X functional, a clear trend was found that was common for all the chalcogens. The interaction energy was, in fact, seen to become less negative in the sequence 4 < 5 < 1 < 3 < 2 (Figure 2). When we used BLYP-QZ to calculate interaction instead, structures having R,R’ = H occupied different positions in the series depending on the chalcogen. To clarify this behavior, a series of coupled cluster calculations were run on the ZORA-BLYP-D3(BJ)/TZ2P geometries to obtain highly accurate interaction energies (Figure 2 and Table 3). Results showed that the M06-2X-QZ interaction energy trend showed the best accordance with the post Hartree-Fock (HF) calculations as the compounds with H, as substituent were found to lie at relatively less negative interaction energy values when compared to the density functional theory (DFT) ones. In addition, the ab initio results agreed completely with the general trend in interaction energies found with the DFT calculations for compounds 2 to 5.
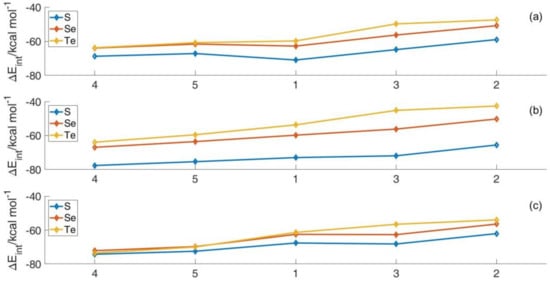
Figure 2.
Eint upon substituent variation. Level of theory: BLYP-QZ (a), M06-2X-QZ (b), and DLPNO-CCSD(T) (c).
3. Discussion
The energetic analysis of the homolytic cleavage of the X–N bond (RX–NR’2 → RX• + •NR’2) showed the presence of interesting trends (Table 3). To elucidate these behaviors, a quantitative energy decomposition analysis (EDA) was conducted through the activation strain model [48,49] at the BLYP-QZ (Table 4) and at the M06-2X-QZ (Supplementary Material Table S2) levels of theory. First, focus was centered on the effect of the chalcogen. Results highlighted how the decrease of total orbital interactions (∆EOI), as we moved down in the group, was the main factor that caused a diminished ∆Eint.

Table 4.
EDA for the investigated compounds (energies in kcal mol−1). Level of theory BLYP-QZ.
Taking compound 1 as the simplest example, an accurate analysis on its frontier orbitals and on those of the radical fragments with all three chalcogens was conducted. Particularly, from the orbital diagram for the radical fragments (Figure 3), it was clear that the orbitals that accommodated the unpaired electrons were of p type and were located mainly on the X and N atoms, respectively. The energies of these singly occupied molecular orbitals (SOMOs) had a clear behavior upon variation of the chalcogen: The •NH2 fragments remained almost unmodified in the three molecules, making the energy of their SOMOs almost constant. On the contrary, the SOMOs centered on X were found at higher energies as we moved from S to Se and Te (they were from −9.14 to −8.56 and −7.93 eV in HS•, HSe•, and HTe•, respectively). This destabilization was mainly due to the decrease in interaction energy. A similar behavior can be predicted also for the compounds with the other substituents, as the trends that result from those calculations are analogous.
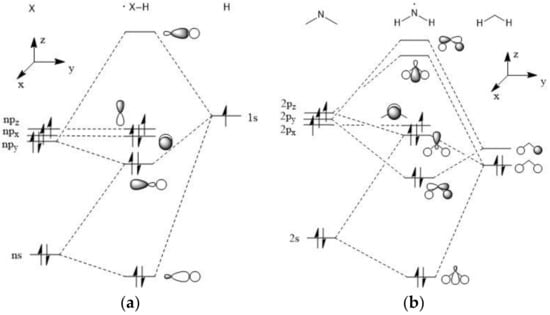
Figure 3.
Orbital diagram for the radical fragments HX• (a) and •NH2 (b).
Another factor that reinforces this observation was found in the energies of the orbitals that were responsible for the presence of the X–N bond in the HX–NH2 compound (Figure 4). The calculation results showed that they were located in the range HOMO-2 to HOMO-4 as the outermost HOMO and HOMO-1 orbitals had a prevalent non-bonding character. These three highest occupies molecular orbitals (HOMO-2 to HOMO-4) were computed to become increasingly higher in energy going from HS–NH2 to Te–NH2 (for example, HOMO-2 went from −8.73 of HS–NH2 to −8.47 HSe–NH2 to −7.97 eV of HTe–NH2), effectively resulting in a diminished interaction and in a subsequently weaker X–N bond.
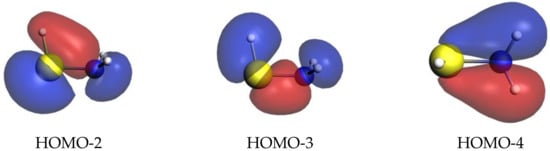
Figure 4.
Molecular orbitals of HS–NH2 mainly responsible for the formation of the S–N bond. Isosurface value 0.03 a.u. Level of theory M06-2X-QZ.
Second, the effect of the variation of the substituent on the interaction energy within the same chalcogen was analyzed. The effects that the different moieties had on the interaction energy within the same chalcogen series were overall weaker than the change of the chalcogen itself, as changing the substituents did not involve the atoms directly participating in the chalcogen–nitrogen bond. In this instance, the more subtle variations in the electronic environment around the X–N bond, which translated to a different weight of the EDA contributions, resulted in a trend that did not depend mainly on the magnitude of the orbital interaction. In fact, (Table 4) shows how ∆Eoi followed a clearly increasing trend in all the chalcogens going from 2 to 5. However, total interaction did not mirror this behavior. The ∆Eoi definitely played an important part in the strength of the X–N bond of CH3X–N(CH3)2 compounds as its value was the principal reason for its weak total interaction energy. Conversely, the relative strength of the chalcogen–nitrogen bond in compounds 3, 4, and 5 was determined by the value of the Pauli repulsion as it overweighed the stabilizing effect of ∆Eint and ∆Velstat. Therefore, compound 4, the one that showed the lowest ∆EPauli, was also found to be the most stable, followed by 5 and, finally, 3. These results were valid for all three chalcogens also with the meta hybrid functional M06-2X (see Supplementary Material Table S2), with the only difference of the absolute magnitude of the different contributions. A somewhat different situation was found for compound 1 with S whose relative position in the substituents’ series was found to depend on the functional employed. A comparison with highly accurate coupled cluster calculations showed that the higher interaction found by the BLYP-QZ calculation for 1 was somewhat overestimated relative to compounds 2 to 5. This was most probably due, again, to the values of ∆EPauli, which were seen to be quite higher in compounds 2 to 5 in comparison to those calculated at the M06-2X-QZ level of theory for the same compounds, while the other contributions were computed to be much more similar between the two functionals. Nonetheless, the trend that the GGA functional returned for compounds 2 to 5 was completely in agreement with the meta-hybrid and the post-HF methods, which ensured a suitable description of the substituent effect.
Both the chalcogen and the substituent effects on the interaction energy magnitude can be rationalized by the quantitative energy decomposition analysis conducted, aided by an accurate orbital inspection. This can be regarded as a starting point for rational design, aiming at fine tuning the X–N bond strength to have the best performance in the desired application.
4. Methods
DFT calculations were performed with the Amsterdam Density Functional (ADF) program [50,51]. Geometry optimizations were performed with the GGA BLYP functional [52,53,54,55] in conjunction with a triple-ζ slater basis set with a double set of polarization functions (TZ2P). Core electrons were kept frozen: up to 1s for C and N, up to 2p for S, up to 3p for Se, and up to 4p for Te, and the zeroth-order regular approximation (ZORA) was used to take relativistic effects into account [56,57,58,59]. Grimme’s empirical dispersion correction with Becke-Johnson damping was added to correct the underestimation of non-bonded forces by this functional [60]. This level of theory will be referred as ZORA-BLYP-D3(BJ)/TZ2P. This level of theory has been thoroughly benchmarked [61] and successfully applied to structure and reactivity studies on mono- and dichalcogenides [62,63] and to analyze the chalcogen-π interaction [47], proving its accuracy and reliability. For the bonding analysis, based on the activation strain model [48,49], a more accurate level of theory was employed, i.e., using a full electron quadruple-ζ slater basis set (QZ4Pae). This level of theory (ZORA-BLYP-D3(BJ)/QZ4P ae // ZORA-BLYP-D3(BJ)/TZ2P) will be referred henceforth as BLYP-QZ. Moreover the bonding analysis was also carried out with the meta-hybrid M06-2X functional [64,65] due to its excellent performance with radical systems [66]. Single points calculation done with this level of theory (ZORA-M06-2X/QZ4Pae // ZORA-BLYP-D3(BJ)/TZ2P) are referred as M06-2X-QZ. The X–N bond strength was computed with the activation strain model. [48,49] This model partitions the total energy of a molecule into two terms:
in which ∆Eint arises from the interaction of a pair of molecular fragments in which the structure of interest can be partitioned. In this work, we selected the radicals RX• and •NR’2 as the starting fragments and, since our interest was quantifying the strength of the chalcogen–nitrogen bond, we did not relax the radicals’ geometries and so did not compute the strain contribution. Conversely, ∆Eint was subsequently analyzed through the energy decomposition analysis (EDA) to identify the physical terms of its origin:
where ∆Velstat is the Coulomb interaction of the unrelaxed electron densities of the fragments, ∆EPauli is the repulsion arising from the pairwise interactions of filled orbitals on the two fragments, and ∆Eoi is the stabilizing energy obtained from the mixing of pairs of a filled and an empty orbital on different fragments. Finally, if an empirical correction for dispersion is added to the functional (as is the case with BLYP-D3(BJ)) a fourth term including this contribution (∆Edisp) is added.
Coupled cluster energies were obtained using the domain-based local pair natural orbital coupled cluster singles and doubles with perturbative triples (DLPNO-CCSD(T)) method [67] as implemented in the ORCA suite [67,68,69]. All electron relativistic contracted basis set aug-cc-pVTZ-DK with Douglas-Kroll-Hess (DKH) scalar relativistic Hamiltonians [70] were used.
5. Conclusions
In this work, we analyzed the nitrogen–chalcogen bond using energy decomposition analysis and molecular orbital theory based on accurate quantum chemistry calculations. The results showed that sulfur has a better interaction with nitrogen than selenium or tellurium due to a stronger interaction energy deriving from the lower energy of sulfur p orbitals with respect to selenium and tellurium. Particularly, our calculations confirmed how N–S bond displays the strongest character, while N–Se and N–Te are much weaker and similar, with N–Te bond being the least stable and selenium holding an intermediate position. Besides, a correlation between the magnitude of the Pauli repulsion between the radical fragments constituting the bond can explain the different effect each substituent has on the interaction. In fact, by an accurate tuning of the substituents, even a relatively weak N–Se bond can be strengthened, reaching in the most stable system, 4, a similar stability to the N–S bond of 2, which, in turn, displayed the weakest character in the sulfur series. Generally speaking, electron donating groups decrease bond stability, while electron withdrawing groups lead to more stabilizing interaction energies, with differences between the strongest and the weakest bond along N–X series of about 10–20 kcal mol−1, which are expected to impact on the N–X bond reactivity, particularly for N–Se in virtue of its intermediate stability.
These results can open new perspectives on the fine tuning of the chalcogen–nitrogen bond, with a particular attention to the Se–N bond, which can be applied in many biological and pharmaceutical applications targeted toward the development of novel bio-active compounds, catalysts, and antioxidant drugs.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4344/11/1/114/s1. Table S1: Optimized geometries of compounds of general formula RX-NR’ (X = S, Te). Table S2: EDA for the investigated compounds (energies in kcal mol-1). Level of theory ZORA-M06-2X/QZ4Pae // ZORA-BLYP-D3(BJ)/TZ2P. Table S3: Coordinates and energies of optimized structures. Level of theory ZORA-BLYP-D3(BJ)/TZ2P.
Author Contributions
Conceptualization, supervision, validation, and project administration, L.O. and J.B.T.R.; methodology, L.O. and M.B.; formal analysis, investigation, and data curation, A.M., D.Z., and F.B.O.; writing—original draft preparation, M.B., L.O., G.R., and P.A.N.; writing—review and editing, M.B., G.R., L.O., and J.B.T.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Università degli Studi di Padova, thanks to the P-DiSC (BIRD2018-UNIPD) project MAD3S (Modeling Antioxidant Drugs: Design and Development of computer-aided molecular Systems). P.I., L.O., and L.O. contributed to this research as part of the scientific activity of the international multidisciplinary network ‘‘SeS Redox and Catalysis’’. P.A.N. and J.B.T.R. were funded by CAPES (Edital 09-88887.505377/2020-00). F.B.O. was funded by CAPES (Edital 88887.354370/2019-00).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the article or in the Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Joshi, P.; More, M.; Jadhav, A.; Khanna, P. Materials and biological applications of 1,2,3-selenadiazoles: A review. Mater. Today Chem. 2020, 16, 100255. [Google Scholar] [CrossRef]
- Alberto, E.E.; Nascimento, V.D.; Braga, A.L. Catalytic application of selenium and tellurium compounds as glutathione peroxidase enzyme mimetics. J. Braz. Chem. Soc. 2010, 21, 2032–2041. [Google Scholar] [CrossRef]
- Barbosa, N.V.; Nogueira, C.W.; Nogara, P.A.; De Bem, A.F.; Aschner, M.; Barbosa, N.B.D.V. Organoselenium compounds as mimics of selenoproteins and thiol modifier agents. Metallomics 2017, 9, 1703–1734. [Google Scholar] [CrossRef]
- Chivers, T.; Laitinen, R.S. Neutral binary chalcogen–nitrogen and ternary S,N,P molecules: New structures, bonding insights and potential applications. Dalton Trans. 2020, 49, 6532–6547. [Google Scholar] [CrossRef]
- Engman, L.; Hallberg, A. Expedient synthesis of ebselen and related compounds. J. Org. Chem. 1989, 54, 2964–2966. [Google Scholar] [CrossRef]
- Sarma, B.K.; Manna, D.; Minoura, M.; Mugesh, G. Synthesis, Structure, Spirocyclization Mechanism, and Glutathione Peroxidase-like Antioxidant Activity of Stable Spirodiazaselenurane and Spirodiazatellurane. J. Am. Chem. Soc. 2010, 132, 5364–5374. [Google Scholar] [CrossRef]
- Zade, S.S.; Panda, S.; Tripathi, S.K.; Singh, H.B.; Wolmershäuser, G. Convenient Synthesis, Characterization and GPx-Like Catalytic Activity of Novel Ebselen Derivatives. Eur. J. Org. Chem. 2004, 2004, 3857–3864. [Google Scholar] [CrossRef]
- Kersting, B.; DeLion, M. Synthesis of Benzisochalcogenol and -azole Derivatives via ortho Metalation of Isophthalamides. Zeitschrift für Naturforschung B 1999, 54, 1042–1047. [Google Scholar] [CrossRef]
- Bhowmick, D.; Mugesh, G. Introduction of a catalytic triad increases the glutathione peroxidase-like activity of diaryl diselenides. Org. Biomol. Chem. 2015, 13, 9072–9082. [Google Scholar] [CrossRef]
- Sarma, B.K.; Mugesh, G. Antioxidant Activity of the Anti-Inflammatory Compound Ebselen: A Reversible Cyclization Pathway via Selenenic and Seleninic Acid Intermediates. Chem. A Eur. J. 2008, 14, 10603–10614. [Google Scholar] [CrossRef]
- Singh, V.P.; Singh, H.B.; Butcher, R.J. Synthesis and Glutathione Peroxidase-Like Activities of Isoselenazolines. Eur. J. Org. Chem. 2011, 2011, 5485–5497. [Google Scholar] [CrossRef]
- Orian, L.; Toppo, S. Organochalcogen peroxidase mimetics as potential drugs: A long story of a promise still unfulfilled. Free. Radic. Biol. Med. 2014, 66, 65–74. [Google Scholar] [CrossRef]
- Wolters, L.P.; Orian, L. Peroxidase Activity of Organic Selenides: Mechanistic Insights from Quantum Chemistry. Curr. Org. Chem. 2015, 20, 189–197. [Google Scholar] [CrossRef]
- Azad, G.K.; Tomar, R.S. Ebselen, a promising antioxidant drug: Mechanisms of action and targets of biological pathways. Mol. Biol. Rep. 2014, 41, 4865–4879. [Google Scholar] [CrossRef]
- Müller, A.; Cadenas, E.; Graf, P.; Sies, H. A novel biologically active seleno-organic compound-1. Glutathione peroxidase-like activity in vitro and antioxidant capacity of PZ 51 (Ebselen). Biochem. Pharm. 1984, 33, 3235–3239. [Google Scholar] [CrossRef]
- Sies, H. Ebselen, a selenoorganic compound as glutathione peroxidase mimic. Free. Radic. Biol. Med. 1993, 14, 313–323. [Google Scholar] [CrossRef]
- Nogueira, C.W.; Rocha, J.B. Toxicology and pharmacology of selenium: Emphasis on synthetic organoselenium compounds. Arch. Toxicol. 2011, 85, 1313–1359. [Google Scholar] [CrossRef]
- Zhao, R.; Holmgren, A. A Novel Antioxidant Mechanism of Ebselen Involving Ebselen Diselenide, a Substrate of Mammalian Thioredoxin and Thioredoxin Reductase. J. Biol. Chem. 2002, 277, 39456–39462. [Google Scholar] [CrossRef]
- Antony, S.; Bayse, C.A. Modeling the Mechanism of the Glutathione Peroxidase Mimic Ebselen. Inorg. Chem. 2011, 50, 12075–12084. [Google Scholar] [CrossRef]
- Ribaudo, G.; Orian, L. Organodiselenides: Organic Catalysis and Drug Design Learning from Glutathione Peroxidase. Curr. Org. Chem. 2019, 23, 1381–1402. [Google Scholar] [CrossRef]
- Wendel, A.; Fausel, M.; Safayhi, H.; Tiegs, G.; Otter, R. A novel biologically active seleno-organic compound—II. Biochem. Pharmacol. 1984, 33, 3241–3245. [Google Scholar] [CrossRef]
- Kil, J.; Lobarinas, E.; Spankovich, C.; Griffiths, S.K.; Antonelli, P.J.; Lynch, E.D.; Le Prell, C.G. Safety and efficacy of ebselen for the prevention of noise-induced hearing loss: A randomised, double-blind, placebo-controlled, phase 2 trial. Lancet 2017, 390, 969–979. [Google Scholar] [CrossRef]
- Singh, N.; Halliday, A.C.; Thomas, J.M.; Kuznetsova, O.V.; Baldwin, R.; Woon, E.C.Y.; Aley, P.K.; Antoniadou, I.; Sharp, T.; Vasudevan, S.R.; et al. A safe lithium mimetic for bipolar disorder. Nat. Commun. 2013, 4, 1–7. [Google Scholar] [CrossRef]
- Singh, N.; Sharpley, A.L.; Emir, U.E.; Masaki, C.; Herzallah, M.M.; Gluck, M.A.; Sharp, T.; Harmer, C.J.; Vasudevan, S.R.; Cowen, P.J.; et al. Effect of the Putative Lithium Mimetic Ebselen on Brain Myo-Inositol, Sleep, and Emotional Processing in Humans. Neuropsychopharmacol 2015, 41, 1768–1778. [Google Scholar] [CrossRef]
- Jin, Z.; Du, X.; Xu, Y.; Deng, Y.; Liu, M.; Zhao, Y.; Zhang, B.; Li, X.; Zhang, L.; Peng, C.; et al. Structure of Mpro from SARS-CoV-2 and discovery of its inhibitors. Nature 2020, 582, 289–293. [Google Scholar] [CrossRef]
- Sies, H.; Parnham, M.J. Potential therapeutic use of ebselen for COVID-19 and other respiratory viral infections. Free. Radic. Biol. Med. 2020, 156, 107–112. [Google Scholar] [CrossRef]
- Ribaudo, G.; Ongaro, A.; Oselladore, E.; Zagotto, G.; Memo, M.; Gianoncelli, A. A computational approach to drug repurposing against SARS-CoV-2 RNA dependent RNA polymerase (RdRp). J. Biomol. Struct. Dyn. 2020, 1–8. [Google Scholar] [CrossRef]
- Menéndez, C.A.; Byléhn, F.; Perez-Lemus, G.R.; Alvarado, W.; De Pablo, J.J. Molecular characterization of ebselen binding activity to SARS-CoV-2 main protease. Sci. Adv. 2020, 6, eabd0345. [Google Scholar] [CrossRef]
- Sargsyan, K.; Lin, C.-C.; Chen, T.; Grauffel, C.; Chen, Y.-P.; Yang, W.-Z.; Yuan, H.S.; Lim, C. Multi-targeting of functional cysteines in multiple conserved SARS-CoV-2 domains by clinically safe Zn-ejectors. Chem. Sci. 2020, 11, 9904–9909. [Google Scholar] [CrossRef]
- Ma, C.; Hu, Y.; Townsend, J.A.; Lagarias, P.I.; Marty, M.T.; Kolocouris, A.; Wang, J. Ebselen, Disulfiram, Carmofur, PX-12, Tideglusib, and Shikonin Are Nonspecific Promiscuous SARS-CoV-2 Main Protease Inhibitors. Acs Pharm. Transl. Sci. 2020, 3, 1265–1277. [Google Scholar] [CrossRef]
- Thenin-Houssier, S.; De Vera, I.M.S.; Pedro-Rosa, L.; Brady, A.; Richard, A.; Konnick, B.; Opp, S.; Buffone, C.; Fuhrmann, J.; Kota, S.; et al. Ebselen, a Small-Molecule Capsid Inhibitor of HIV-1 Replication. Antimicrob. Agents Chemother. 2016, 60, 2195–2208. [Google Scholar] [CrossRef]
- Mukherjee, S.; Weiner, W.S.; Schroeder, C.E.; Simpson, D.S.; Hanson, A.M.; Sweeney, N.L.; Marvin, R.K.; Ndjomou, J.; Kolli, R.; Isailovic, D.; et al. Ebselen Inhibits Hepatitis C Virus NS3 Helicase Binding to Nucleic Acid and Prevents Viral Replication. ACS Chem. Biol. 2014, 9, 2393–2403. [Google Scholar] [CrossRef]
- Björgvinsson, M.; Roesky, H.W. The structures of compounds containing selenium-nitrogen and tellurium-nitrogen bonds. Polyhedron 1991, 10, 2353–2370. [Google Scholar] [CrossRef]
- Mahmudov, K.T.; Kopylovich, M.N.; Da Silva, M.F.C.G.; Pombeiro, A.J.L. Chalcogen bonding in synthesis, catalysis and design of materials. Dalton Trans. 2017, 46, 10121–10138. [Google Scholar] [CrossRef]
- Rendeková, J.; Vlasáková, D.; Arsenyan, P.; Vasiljeva, J.; Nasim, M.J.; Witek, K.; Domínguez-Álvarez, E.; Żesławska, E.; Mániková, D.; Tejchman, W.; et al. The Selenium-Nitrogen Bond as Basis for Reactive Selenium Species with Pronounced Antimicrobial Activity. Curr. Org. Synth. 2018, 14, 1082–1090. [Google Scholar] [CrossRef]
- Orian, L.; Mauri, G.; Roveri, A.; Toppo, S.; Benazzi, L.; Bosello-Travain, V.; De Palma, A.; Maiorino, M.; Miotto, G.; Zaccarin, M.; et al. Selenocysteine oxidation in glutathione peroxidase catalysis: An MS-supported quantum mechanics study. Free. Radic. Biol. Med. 2015, 87, 1–14. [Google Scholar] [CrossRef]
- Salmeen, A.; Andersen, J.N.; Myers, M.P.; Meng, T.-C.; Hinks, J.A.; Tonks, N.K.; Barford, D. Redox regulation of protein tyrosine phosphatase 1B involves a sulphenyl-amide intermediate. Nature 2003, 423, 769–773. [Google Scholar] [CrossRef]
- Montfort, R.L.M.; Van Congreve, M.; Tisi, D.; Carr, R.; Jhoti, H. Reduction of the sulphenyl-amide bond. Nature 2003, 423, 773–777. [Google Scholar] [CrossRef]
- Poole, L.B.; Nelson, K.J. Discovering mechanisms of signaling-mediated cysteine oxidation. Curr. Opin. Chem. Biol. 2008, 12, 18–24. [Google Scholar] [CrossRef]
- Lee, J.-W.; Soonsanga, S.; Helmann, J.D. A complex thiolate switch regulates the Bacillus subtilis organic peroxide sensor OhrR. Proc. Natl. Acad. Sci. USA 2007, 104, 8743–8748. [Google Scholar] [CrossRef]
- Yang, J.; Groen, A.; Lemeer, S.; Jans, A.; Slijper, M.; Roe, S.M.; Hertog, J.D.; Barford, D. Reversible Oxidation of the Membrane Distal Domain of Receptor PTPα Is Mediated by a Cyclic Sulfenamide†. Biochemistry 2007, 46, 709–719. [Google Scholar] [CrossRef]
- Nogara, P.A.; Orian, L.; Rocha, J.B. The Se S/N interactions as a possible mechanism of δ-aminolevulinic acid dehydratase enzyme inhibition by organoselenium compounds: A computational study. Comput. Toxicol. 2020, 15, 100127. [Google Scholar] [CrossRef]
- Cozzolino, A.F.; Vargas-Baca, I. The supramolecular chemistry of 1,2,5-chalcogenadiazoles. J. Organomet. Chem. 2007, 692, 2654–2657. [Google Scholar] [CrossRef]
- Cozzolino, A.F.; Yang, Q.; Vargas-Baca, I. Engineering Second-Order Nonlinear Optical Activity by Means of a Noncentrosymmetric Distortion of the [Te−N]2 Supramolecular Synthon. Cryst. Growth Des. 2010, 10, 4959–4964. [Google Scholar] [CrossRef]
- Suturina, E.A.; Semenov, N.A.; Lonchakov, A.V.; Bagryanskaya, I.Y.; Gatilov, Y.V.; Irtegova, I.G.; Vasilieva, N.V.; Lork, E.; Mews, R.; Gritsan, N.P.; et al. Interaction of 1,2,5-Chalcogenadiazole Derivatives with Thiophenolate: Hypercoordination with Formation of Interchalcogen Bond versus Reduction to Radical Anion. J. Phys. Chem. A 2011, 115, 4851–4860. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Sato, N. Origin of Attraction in Chalgogen–Nitrogen Interaction of 1,2,5-Chalcogenadiazole Dimers. J. Phys. Chem. B 2013, 117, 6849–6855. [Google Scholar] [CrossRef]
- Bortoli, M.; Ahmad, S.M.; Hamlin, T.A.; Bickelhaupt, F.M.; Orian, L. Nature and strength of chalcogen–π bonds. Phys. Chem. Chem. Phys. 2018, 20, 27592–27599. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Baerends, E.J. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. In Reviews in Computational Chemistry; Lipkovitz, K.B., Boyd, D.B., Eds.; Wiley-VCH: New York, NY, USA, 2000; Volume 15, pp. 1–86. ISBN 9780470125922. [Google Scholar]
- Bickelhaupt, F.M.; Houk, K.N. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem. Int. Ed. 2017, 56, 10070–10086. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; Van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- ADF, version 103; SCM, Theoretical Chemistry; Vrije Universiteit: Amsterdam, The Netherlands, 2019.
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colic-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Johnson, B.G.; Gill, P.M.W.; Pople, J.A. The performance of a family of density functional methods. J. Chem. Phys. 1993, 98, 5612–5626. [Google Scholar] [CrossRef]
- Russo, T.V.; Martin, R.L.; Hay, P.J. Density functional calculations on first-row transition metals. J. Chem. Phys. 1994, 101, 7729–7737. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J.; Snijders, J.G. Relativistic total energy using regular approximations. J. Chem. Phys. 1994, 101, 9783–9792. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Snijders, J.G.; Baerends, E.J. The zero-order regular approximation for relativistic effects: The effect of spin–orbit coupling in closed shell molecules. J. Chem. Phys. 1996, 105, 6505–6516. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Ehlers, A.; Baerends, E.-J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Zaccaria, F.; Wolters, L.P.; Guerra, C.F.; Orian, L. Insights on selenium and tellurium diaryldichalcogenides: A benchmark DFT study. J. Comput. Chem. 2016, 37, 1672–1680. [Google Scholar] [CrossRef]
- Bortoli, M.; Bruschi, M.; Swart, M.; Orian, L. Sequential oxidations of phenylchalcogenides by H2O2: Insights into the redox behavior of selenium via DFT analysis. New J. Chem. 2020, 44, 6724–6731. [Google Scholar] [CrossRef]
- Bortoli, M.; Zaccaria, F.; Tiezza, M.D.; Bruschi, M.; Guerra, C.F.; Bickelhaupt, F.M.; Orian, L. Oxidation of organic diselenides and ditellurides by H2O2 for bioinspired catalyst design. Phys. Chem. Chem. Phys. 2018, 20, 20874–20885. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Accounts 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. How Well Can New-Generation Density Functionals Describe the Energetics of Bond-Dissociation Reactions Producing Radicals? J. Phys. Chem. A 2008, 112, 1095–1099. [Google Scholar] [CrossRef]
- Liakos, D.G.; Guo, Y.; Neese, F. Comprehensive Benchmark Results for the Domain Based Local Pair Natural Orbital Coupled Cluster Method (DLPNO-CCSD(T)) for Closed- and Open-Shell Systems. J. Phys. Chem. A 2019, 124, 90–100. [Google Scholar] [CrossRef]
- Neese, F. The ORCA Program System: Software Update—Version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Neese, F.; Wolf, A.; Fleig, T.; Reiher, M.; Hess, B.A. Calculation of electric-field gradients based on higher-order generalized Douglas-Kroll transformations. J. Chem. Phys. 2005, 122, 204107. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).