Coordination and Private Information Revelation

Abstract

This paper examines a persuasion game between two agents with one-sided asymmetric information, where the informed agent can reveal her private information prior to playing a Battle-of-the-Sexes coordination game. There is a close connection between the extent of information revelation and the possibility of coordination failure; while, in the absence of any coordination failure, there exist equilibria with full disclosure, in the presence of strategic uncertainty in coordination there exists an equilibrium with no information revelation. We provide a purification argument for the non-existence result, as well demonstrate that it is robust to several extensions, including both-sided asymmetric information and imprecise information revelation.

1. Introduction

This paper examines the interaction between information revelation and coordination. To this end, we consider a variant of the persuasion game: following the disclosure stage, agents decide whether to coordinate or not. As with persuasion games, the central issue is whether agents with private information have an incentive to reveal their information. We find that the extent of information revelation has close connections with the possibility of strategic uncertainty regarding coordination possibilities (motivating our investigation into mixed-strategy equilibria), thereby providing some interesting insights regarding the connections between these two issues that add to the literature (in particular to the seminal contributions by [1,2]).

Coordination is, of course, central to much of economics. Beginning with the compelling example of [3] on coordination among two agents, various sub-disciplines of economics has investigated coordination games and their applications. Examples can be drawn from fields as diverse as industrial organization (e.g., agents coordinating on various actions like technology, entry, mergers and joint ventures); political economy (e.g., lobbying and coalitional politics) and growth and development. Interestingly, even in games where the equilibria are Pareto-ranked, ref [4] claim that coordination failures occur using experiments.

Take the case of joint ventures and mergers. These phenomena have to contend with coordination issues such as strategic uncertainty and have been analyzed in detail in the literature on antitrust. For instance, for research joint ventures, ref [5] finds that ignoring costs of coordination in the formation of joint ventures incorrectly inflates the value of the partnership and that competition in R&D might yield a welfare enhancing outcome.

Coordination games are discussed extensively in the macroeconomics literature dealing with excessive aggregate responses to shocks. Ref [6] provides a summary of macroeconomic models where strategic complementarities arise due to peculiarities in the production and demand functions, as well as models where the presence of private information and search costs result in coordination failures and over-reactions to aggregative shocks. Ref [7] discusses strategic complementarities in a multi-sector imperfectly competitive economy resulting in coordination failure.

Turning to the formal model, we consider a framework with two agents, call them A and B, with both having an “idea” of their own. They obtain a payoff from their own idea, as well as an additional amount in case there is coordination on a single idea. Furthermore, the type of one of the agents, say agent A, is private information. We consider a two stage game where, in Stage 1, agent A can reveal her type1, and then in Stage 2 they play a battle-of-the sexes game where they decide on which idea to adopt. In line with much of the literature on persuasion games, information is taken to be hard.

Our central result is that disclosure of private information is linked with the possibility of coordination failure–to wit, equilibria with full disclosure exist in the absence of any coordination failure; whereas in the presence of coordination failure, there exists an equilibrium with no information revelation. We begin by examining two different scenarios where there is complete information disclosure. In the first, the agents play a pure strategy equilibrium, coordinating on A if agent A’s type had been revealed to be ‘sufficiently high’, and coordinating on B otherwise. In the second, we allow for correlated equilibria in the coordination stage. In neither of these cases are there coordination failures, and, consistent with our intuition, there exist equilibria with full disclosure.

We next examine equilibria with coordination failure in Stage 2, with this failure being captured by the fact that while agent A plays a cut-off strategy, adopting A if and only if her type is ‘sufficiently high’, agent B plays a completely mixed strategy. We find that in the presence of such strategic uncertainty A never reveals her own type.

This non-revelation result is in contrast to the early literature on persuasion games which uses an unraveling argument to demonstrate that there would be full disclosure. Our analysis traces the non-revelation result to the possibility of strategic uncertainty over coordination possibilities. Thus this result adds to the subsequent literature that examines economic environments where the revelation argument needs to be qualified. One can mention, among others, ref [8], who finds partial revelation in the presence of costly revelation of private information; ref [9], who argue that in the presence of asymmetric information over the preference of the information providers there is no information revelation; and [10], who study sufficient conditions for complete revelation of private information, when such disclosure is a strategic choice. However, the latter rule out strategic uncertainty in coordination by abstracting from ‘coordination equilibria’, whereby there can be multiple pure strategy equilibria in the stage following information communication.

The intuition for the non-revelation result has to do with coordination possibilities in the second stage game. Why, for example, should an agent with a valuable private idea not want to reveal? We find that the non-revelation argument holds whenever the continuation game in the coordination stage involves strategic uncertainty, formalized through a mixed-strategy equilibrium. An important aspect of the mixed-strategy equilibrium in a coordination game is that, in order to keep the opponent indifferent between her two actions, a player has to play the action associated with a lower-payoff coordinated outcome with a higher probability than the action associated with a higher-payoff coordinated outcome. Letting $\theta$ denote the value of her own idea to agent A, if agent A reveals a relatively high $\theta$, agent B becomes more aggressive in adopting his own idea and choosing B with a relatively high probability in the ensuing coordination game. Thus, if an agent A with high valuation reveals her type, agent B will respond much more aggressively compared to the case when agent A does not (since in this case agent B’s response will be based on the expected average value of agent A’s type). For such an agent A, non-revelation is optimal. Whereas if agent A has a relatively ‘bad’ idea, then agent A is more interested in coordination itself, rather than the identity of the idea on which coordination takes place. Therefore, agent A has little to gain by revealing information and ensuring coordination on her own idea. She would rather ensure that coordination takes place on agent B’s idea (B) and still gain through a higher payoff due to the higher probability associated with coordination on B. So, agent A with ‘bad’ idea (low values of $\theta$) would also prefer not to reveal.

Please note that the non-revelation outcome involves agent B playing a completely mixed strategy in the coordination stage, with B’s adoption of a mixed strategy reflecting his lack of knowledge regarding both A’s type as well as action. It has been argued, most notably by [11], that in the presence of coordination uncertainties, mixed strategies can help capture such uncertainties. In a similar vein, ref [12] argues that randomization in mixed strategies reflects the uncertainty in the mind of a player about the opponent’s strategy, rather than a deliberate mixing of pure strategies.

It is natural to ask, however, if the non-revelation result is critically dependent on the fact that agent B plays a completely mixed strategy in equilibrium. To that end we adopt a purification argument akin to Harsanyi’s defense of mixed-strategy equilibria [13], and examine a modified version of our baseline framework where agent B’s type is also private information (though agent B cannot reveal his type as hard information). We find that the coordination game has an equilibrium where each B-type plays a pure strategy, with each B-type opting for technology B iff his valuation exceeds a critical cut-off. Interestingly, this strategy generates the same probability distribution over agent B’s actions, as that under the mixed-strategy equilibrium in our baseline framework. We use this equilibrium to demonstrate that the non-revelation result holds in the purification setup as well, even though the coordination game does not involve any type of agent B playing mixed strategies.

Finally, we go on to examine several extensions of the baseline model. We allow for both sided asymmetric information (where both agents can reveal hard information) as well as the possibility of imprecise information revelation. The non-revelation result is robust to these extensions. Furthermore, in case of mandatory disclosure of information, we find that the overall probability of coordination (on either A or B) may or may not exceed that in the absence of such mandatory disclosure, with the result depending on the nature of the distribution of $\theta$.

In line with the literature on persuasion games, this paper restricts itself to revelation of hard evidence. With soft information, we would be in the realm of signaling games (cheap talk games, to be precise). It is well-known that in this class of games a babbling equilibrium necessarily exists, but equilibria with partial information revelation also exist as demonstrated by [14] in their path-breaking contribution.2 Our result is different in that we show, modulo there being strategic uncertainty in the coordination continuation game, non-revelation or babbling follows as the unique outcome. It would, however, be of interest to examine if the results are robust to allowing for soft information. We conjecture that the equilibrium set would be enlarged with the introduction of cheap talk, making the selection of equilibrium a more difficult task. Our analysis ignores equilibria with cheap talk, as well the possibility of side-payments between agents (and therefore, mechanism design issues). In future work we would like to extend our framework to allow for both these aspects. Games with cheap talk or side payments would be relevant in the context of firm entry with underlying conditions of natural monopoly, as discussed in [15,16].

The paper is structured as follows: Section 2 provides a brief review of the literature, Section 3 discusses the model with the detailed analysis in Section 4. We provide a purification argument for the mixed-strategy equilibrium in Section 5, Section 6 discusses some extensions of the model with two-sided private information, imprecise information revelation and mandatory disclosure. Section 7 concludes.

2. Literature Review

The early literature on voluntary disclosure of private information discusses complete unraveling of private information. Ref [1], for instance, demonstrates full disclosure in a persuasion game involving a privately informed seller and an informed buyer. Similarly, ref [2] finds that unraveling holds for a single seller with private information and no reputational concerns when facing many buyers with no prior experience of the good, as long as the seller makes ex post verifiable claims (or can offer warranties), and beliefs are skeptical.

However, there are many environments where the incentive to reveal private information is limited. In the context of a buyer-seller exchange [8] shows that the unraveling result fails to hold in monopolistically competitive markets with costly disclosure of private information. Ref [17] obtains a similar result when buyers are unsure about the existence of private information in the market. Furthermore, ref [18,19] note that competition increases the amount of private information disclosed in market exchange. Ref [20] observe that intermediary agents in agricultural markets with limited competition do not voluntarily reveal private information. Ref [21] mentions that there is no voluntary disclosure in the market for insurance plans offered by Health Maintenance Organizations despite competition.

Reference [9] qualifies the unraveling result in the context of an uninformed decision-maker, who has to rely on information provided by interested parties. If the decision maker is fully informed, competition is not necessary for complete information revelation. However, in case the preference of the interested party is private information, competition itself is not sufficient for full disclosure. Finally, for accounting disclosures, ref [22] shows that the context decides whether revelation will be complete or incomplete.

None of these papers marry the problem of information revelation to the presence of strategic uncertainty in coordination. This is the precise problem investigated in our paper, which is closest in spirit to [11,23]. We examine an asymmetric private information version of the complete information committee standardization game in [11]. Ref [23] study a related framework with symmetric private information among all agents in the context of a war-of-attrition game. In both these papers, however, the focus is on the issue of standardization, rather than on information revelation. We, on the other hand, analyze the interaction between coordination uncertainty and private information.

Some papers, such as [24,25], show that even when there is a unique equilibrium in the second stage, unraveling fails. This paper contributes to the literature on both revelation of private information, as well as coordination games, the central contribution being the identification of strategic uncertainty in coordination as a reason for non-disclosure and the finding that complete non-revelation can obtain in a robust fashion. In our paper, the conditions in [24,25,26] for a “worst case type” supporting full disclosure equilibrium is not satisfied by the continuation equilibrium payoffs of player A, given that player B randomizes in the second stage.

3. The Model

Two agents A and B each have an idea/technology of their own, denoted A and B respectively. There is one-sided asymmetric information: agent A has some private information regarding her own payoff from adopting A. We analyze a two stage game with an initial information revelation stage, where agent A may or may not reveal her private information. This is followed by a version of the battle-of-the sexes game, where both the agents choose, simultaneously, whether to adopt their own idea, or to switch to the idea of the other agent. The outcome in Stage 2 of course depends on the information revealed earlier, if any, in Stage 1.

In case an agent adopts her own idea, she obtains a private benefit. She also obtains an additional coordination benefit in case the other agent coordinates on the same idea as well. In case she switches to the idea of the other agent, she obtains no private benefit, but will obtain the coordination benefit in case both choose the same idea.

Formally, agent A’s private benefit from adopting A, denoted $\theta$, is distributed over the compact, continuous type space $\Theta$, where $\Theta =[{\theta }_l,{\theta }_h]\subset {\mathbb{R}}_{+}$, with distribution $F\left(\theta \right)$, with $F\left(\theta \right)$ being non-degenerate and strictly increasing. The exact realization of $\theta$ is however private information of agent A. Agent B’s benefit from operating B, denoted b, is however deterministic. Furthermore, both agents obtain a coordination benefit c in case they both choose the same idea.

The timing of the game is as follows:

• Stage 1: Revelation: Agent A decides whether or not to reveal her type $\theta$. Agent A can either reveal her exact type by providing hard information, or decline to offer any information. The message space of a type $\theta$ agent A is, therefore, $M\left(\theta \right)=\left\{\theta \right\}\cup${Not Reveal her Type}3. Thus, the set of random messages of agent A of type $\theta$ is given by $\Delta \left(M\right(\theta \left)\right)$, where $\Delta \left(M\right(\theta \left)\right)=\left\{m\right|m\mathrm{is}\mathrm{a}\mathrm{probability}\mathrm{distribution}\mathrm{over}M\left(\theta \right)\}$. We define $M={\cup }_{\theta }M\left(\theta \right)=[{\theta }_l,{\theta }_h]\cup${Not Reveal her Type}.
• Stage 2: Coordination: The agents play a coordination game, where agent i chooses an action from {Adopt i, Switch to j, $i,j\in \{A,B\},j\ne i\}$. If both the agents choose to adopt their own idea, there is no coordination: agent A obtains $\theta$ and agent B obtains b. On the other hand, if both the agents switch to the other’s idea, then they both have a payoff of 0. If they coordinate on A, then the payoff vector is $(\theta +c,c)$, whereas it is $(c,b+c)$ if they coordinate on B.4

The payoff matrix for the Stage 2 game is given in

Table 1. Payoff matrix for the one-shot game.

	Switch to A	Adopt B
Adopt A	$\theta +c$, c	$\theta$, b
Switch to B	0, 0	c, $b+c$

below:

Assumption 1 below allows us to focus on the interesting case where coordination benefits are large enough such that the possibility of coordination failure is a significant strategic consideration. In Remark 2 later, we briefly examine the outcome for other parameter values.

Assumption 1.

$c>max\{{\theta }_h,b\}$.

We need some notations:

• The strategy of a type $\theta$ agent A in the revelation stage, i.e., Stage 1, denoted by ${\alpha }^I\left(\theta \right)$, is a probability distribution over $M\left(\theta \right)$.
• The strategies of the agents A and B in Stage 2, i.e., the coordination stage, are:

  -

  The strategy of a type $\theta$ agent A in the coordination stage is a mapping ${\alpha }^C\left(\theta \right)$ from her decision in Stage 1 to a probability distribution over the action space $\{adoptA,switchtoB\}$, i.e., ${\alpha }^C\left(\theta \right):M\left(\theta \right)\to [0,1].$

  -

  Following a history where, in Stage 1, agent A revealed her type to be $\theta$, let $q_R\left(\theta \right)$ denote a mixed strategy of agent B where he plays “Adopt B” with probability $q_R\left(\theta \right)$.

  -

  Similarly, following a history where agent A played “Not Reveal $\theta$” in Stage 1, $q_{NR}$ denotes a mixed strategy of agent B, where he plays “Adopt B” with probability $q_{NR}$.

• The belief of agent B at the coordination stage, i.e., Stage 2, is a mapping $\overline{B}$ from the message sent by agent A in the revelation stage to a probability distribution over agent A’s type space $[{\theta }_l,{\theta }_h]$, i.e., $\overline{B}:M\to \Delta [{\theta }_l,{\theta }_h]$5.
• Finally, agent A’s strategy in Stage 2 is said to be a cut-off strategy iff there is some $\widehat{\theta }\in [{\theta }_l,{\theta }_h]$ such that she adopts A iff $\theta \ge \widehat{\theta }$.

Given these notations on strategies and beliefs, the perfect Bayesian equilibria of this game can be defined in a routine fashion.

We say that a perfect Bayesian equilibrium is efficient if the outcome involves both agents choosing A when $\theta \ge b$, and both agents choosing B otherwise.

4. The Analysis

We next solve for the perfect Bayesian equilibria of this game. The focus is on understanding whether, in equilibrium, there will be information revelation or not. We shall find that the underlying strategic uncertainty regarding coordination failure plays a central role in the analysis.

4.1. Full Disclosure Equilibria in the Absence of Coordination Failure

We begin by examining two scenarios such that the coordination stage exhibits no coordination failure, demonstrating that information revelation is possible in such cases.

We first consider a scenario where the agents play a pure strategy equilibrium in Stage 2. In particular, depending on whether the $\theta$ revealed in Stage 1 is ‘sufficiently high’ or not, they coordinate on either A or B in the coordination stage.

Proposition 1.

There exists perfect Bayesian equilibria with no coordination failure in Stage 2 and complete information revelation in Stage 1.

(a) 

In this equilibrium, in Stage 1, all A agents reveal their own types. In Stage 2:

(i) 

In case of non-revelation by the A agent in Stage 1, agent B believes that agent A is of type ${\theta }_h$.

(ii) 

Fix ${\theta }^{\prime }$, where ${\theta }^{\prime }\in [{\theta }_l,{\theta }_h]$. The agents coordinate on A if $\theta \ge {\theta }^{\prime }$, and on B if $\theta <{\theta }^{\prime }$.

(b) 

For ${\theta }^{\prime }=b$, the equilibrium so described is efficient.

Proof. 

(a)

Clearly, the Stage 2 strategies constitute an equilibrium, so that it is sufficient to examine whether agent A’s revelation strategy is optimal or not.

Please note that following disclosure of her type, agent A’s payoff is at least c since disclosure ensures coordination in Stage 2. Whereas in case agent A opts not to disclose, then given the belief, agent B plays a completely mixed strategy, adopting B with probability $\frac{{\theta }_h+c}{2c}$. It is straightforward to check that for all $\theta$, it is optimal for agent A to switch to B, so that her payoff is $\frac{{\theta }_h+c}{2}$, which is less than her payoff from revealing her type (which is at least c).

(b)

Please note that there is coordination on A iff $\theta \ge b$, which is efficient.

☐

Please note that the equilibrium involves complete information revelation. This corroborates our central intuition that the issue of information revelation is intimately tied to the possibility of coordination failure.6 Furthermore, there exists an equilibrium which achieves efficiency in the coordination stage.

Turning to the second scenario, we demonstrate that in case one allows for correlated equilibria in the coordination continuation game, one can again sustain equilibria with full disclosure. Since, in the main text, we restrict attention to Bayesian equilibria, the details for this case have been placed in Appendix A.

4.2. Non-Revelation Equilibria in the Presence of Coordination Failure

We now turn to equilibria where there is coordination failure in Stage 2, focusing on equilibria where agent B plays a completely mixed strategy in the coordination stage. Our investigation is in line with many papers investigating coordination problems, e.g., ref [27] on corporate take-overs, ref [28] on repeated coordination games, as well as [29] on international environment agreements for addressing greenhouse gas emissions (modeled as a participation game). Ref [29], for example, defend their investigation of mixed strategy equilibria on the grounds that it captures the uncertainty of countries in coordinating an effective climate change treaty.7

We begin by examining equilibria in the coordination stage with the following definition.

Definition 1.

A PBEM denotes a perfect Bayesian equilibrium where agent B plays a completely mixed strategy in the coordination stage, i.e., Stage 2.

We begin by examining equilibria in the coordination stage. We first examine A’s strategy following non-revelation of her own type.

Lemma 1.

Consider the Stage 2 continuation game where agent A does not reveal her type in Stage 1. In any PBEM, agent A plays a cut-off strategy in Stage 2.

Proof. 

Consider the Stage 2 continuation game following non-revelation of her type by agent A in Stage 1. Consider a PBEM where, in Stage 2, agent B plays adopt B with probability $q_{NR}$, $0<q_{NR}<1$.

Next, note that the payoff to agent A in this continuation game from adopting A (call it ${\pi }_A\left(\mathrm{Not}\mathrm{Reveal}\mathrm{and}\mathrm{Adopt}\mathrm{A}\right)$) is increasing in her type $\theta$. Thus,

$${\pi }_A\left(\mathrm{Not} \mathrm{Reveal} \mathrm{and} \mathrm{Adopt} \mathrm{A}\right)=(1-q_{NR})c+\theta .$$

(1)

Similarly,

$${\pi }_A\left(\mathrm{Not}\mathrm{Reveal}\mathrm{and}\mathrm{Switch}\mathrm{to}\mathrm{B}\right)={\mathrm{q}}_{\mathrm{NR}}\mathrm{c}.$$

(2)

Let $\widehat{\theta }$ be the minimum of all $\theta \in [{\theta }_l,{\theta }_h]$ such that ${\pi }_A\left(\mathrm{Not}\mathrm{Reveal}\mathrm{and}\mathrm{Adopt}\mathrm{A}\right)\le {\pi }_A(\mathrm{Not}\mathrm{Reveal}\mathrm{and}\mathrm{Switch}\mathrm{to}\mathrm{B})$. Hence, for all types $\theta \ge (<)\widehat{\theta }$, it is optimal to adopt A (switch to B) following non-revelation, given that $0<q_{NR}<1$. ☐

In Lemma 2 below we consider the equilibrium outcome in Stage 2 following revelation of her type by agent A in Stage 1. Given that we have a standard Battle-of-the-Sexes game, we omit the proof (which is routine).

Lemma 2.

Consider any candidate PBEM such that agent A reveals her type θ in Stage 1. In Stage 2, agent B plays “Adopt B” with probability $q_R\left(\theta \right)=\frac{\theta +c}{2c}$, and has a payoff of $\frac{b+c}{2}$, whereas agent A of type θ plays “Adopt A” with probability $\frac{b+c}{2c}$ and has a payoff of $\frac{\theta +c}{2}$.

From Lemma 2 note that $q_R\left(\theta \right)$ is increasing in $\theta$, so that agent B becomes more aggressive in adopting his own idea as $\theta$ increases. This follows from the intuition of mixed strategies itself, which requires the choice of $q_R\left(\theta \right)$ to be such that A is indifferent between her two pure strategies.

If agent A with high $\theta$ reveals her type, agent B will respond much more aggressively compared to the case when agent A does not (since in this case agent B’s response will be based on the expected value of $\theta$). This intuition has important implications for the coordination possibilities in the second stage game, and, as we shall find, plays an important role in Proposition 2 (to follow).

Proposition 2 is the central result of this section, showing that in the presence of coordination issues there is no information revelation by agent A (except possibly by a single type), providing a new insight as to why ‘unraveling’ may not occur.

Proposition 2.

Consider any PBEM. In Stage 1, all types of agent A, with the possible exception of one type, strictly prefer non-revelation to revelation.

Proof. 

Recall from Lemma 2 that if an agent A of type $\theta$ reveals her type in Stage 1, then her payoff in any PBEM is $\frac{\theta +c}{2}$. Therefore for such revelation to be optimal for agent A, it must be that

$$\frac{\theta +c}{2}\ge \mathrm{Max}[q_{NR}c,\theta +c-q_{NR}c].$$

(3)

However, we note that

$$\frac{\theta +c}{2}>q_{NR}c\Rightarrow \frac{\theta +c}{2}<\theta +c-q_{NR}c.$$

(4)

Therefore, $\frac{\theta +c}{2}$ cannot be bigger than both $q_{NR}c$ and $\theta +c-q_{NR}c$. Thus, for information revelation to be optimal it must be that

$$\frac{\theta +c}{2}=q_{NR}c.$$

(5)

Given that $q_{NR}$ is independent of $\theta$, (5) can hold for at most one $\theta$, so that the probability of revelation is zero.8 ☐

The intuition for non-revelation has to do with coordination possibilities in the second stage game. As argued earlier, for an agent A with a high realization of $\theta$, non-revelation followed by choosing to adopt A is optimal. This follows as revelation would lead the other agent to follow extremely aggressive strategies.

Whereas, if $\theta$ is low, then agent A’s private benefit from adopting A itself is low compared to the possible coordination benefits from c. Consequently, agent A is more interested in coordination itself rather than the identity of the idea on which coordination takes place. Furthermore, given that b is large relative to $\theta$, agent B will put a relatively ‘large’ probability on adopting B in case of information revelation, even if the revealed $\theta$ turns out to be small. Therefore, agent A has little to gain by revealing information so as to encourage coordination on A. She would rather ensure that coordination takes place on B, since while she loses because agent B’s idea is selected, she more than makes up for it because the probability associated with coordination on B is larger.

We now characterize the equilibrium, showing that there is a ‘unique’ PBEM.9

Proposition 3.

A unique PBEM exists. In this equilibrium, there is no information revelation in Stage 1. In Stage 2:

(i) 

Agent A adopts her own idea, i.e., A, if and only if $\theta \ge \widehat{\theta }$, where $\widehat{\theta }=F^{-1}\left(\frac{c-b}{2c}\right)$ and ${\theta }_l<\widehat{\theta }<{\theta }_h$, and switches to B otherwise.

(ii) 

Agent B adopts her own idea, i.e., B, with probability $\frac{1}{2}+\frac{F^{-1}\left(\frac{c-b}{2c}\right)}{2c}$.

(iii) 

In case agent A does not reveal her type in Stage 1, agent B believes that the type of agent A is distributed over $[{\theta }_l,{\theta }_h]$ with distribution $F\left(\theta \right)$. In case agent A does reveal her type to be θ, say, the belief of agent B puts probability 1 on agent A being of type θ.

(iv) 

In this PBEM, a type θ agent A has an expected payoff of:

$${\pi }_A\left(\theta \right)=\left\{\begin{array}{c}\theta +\frac{c-\widehat{\theta }}{2},if\theta >\widehat{\theta },\hfill \\ \frac{c+\widehat{\theta }}{2},\mathit{otherwise},\hfill \end{array}\right.$$

and agent B has an expected payoff of $\frac{b+c}{2}$.

Proof. 

From Proposition 2, we know that with probability 1 there will be no revelation in the first stage.

Next consider Stage 2. Given Lemma 1, we know that agent A will be playing a simple cut-off strategy where she adopts A if and only if her type is larger than some cut-off value, call it $\widehat{\theta }$. The value of this cut-off $\widehat{\theta }$, given that agent B is playing a completely mixed strategy, must make agent B indifferent between adopting B and switching to A, so that

$$(1-F\left(\widehat{\theta }\right))c=(1-F\left(\widehat{\theta }\right))b+F\left(\widehat{\theta }\right)(b+c)=b+F\left(\widehat{\theta }\right)c.$$

(6)

This yields $\widehat{\theta }=F^{-1}\left(\frac{c-b}{2c}\right)$, where $\widehat{\theta }$ is well defined since $0<\frac{c-b}{2c}<1$ (given that $c>b$). Furthermore, given that agent B adopts B with probability $q_{NR}$, the cut-off strategy of agent A in the coordination stage will be optimal if, at $\widehat{\theta }$, we get the following expression for $q_{nr}$:

$$\frac{\widehat{\theta }+c}{2c}=q_{nr}.$$

(7)

Given that $\widehat{\theta }=F^{-1}\left(\frac{c-b}{2c}\right)$, the result follows.

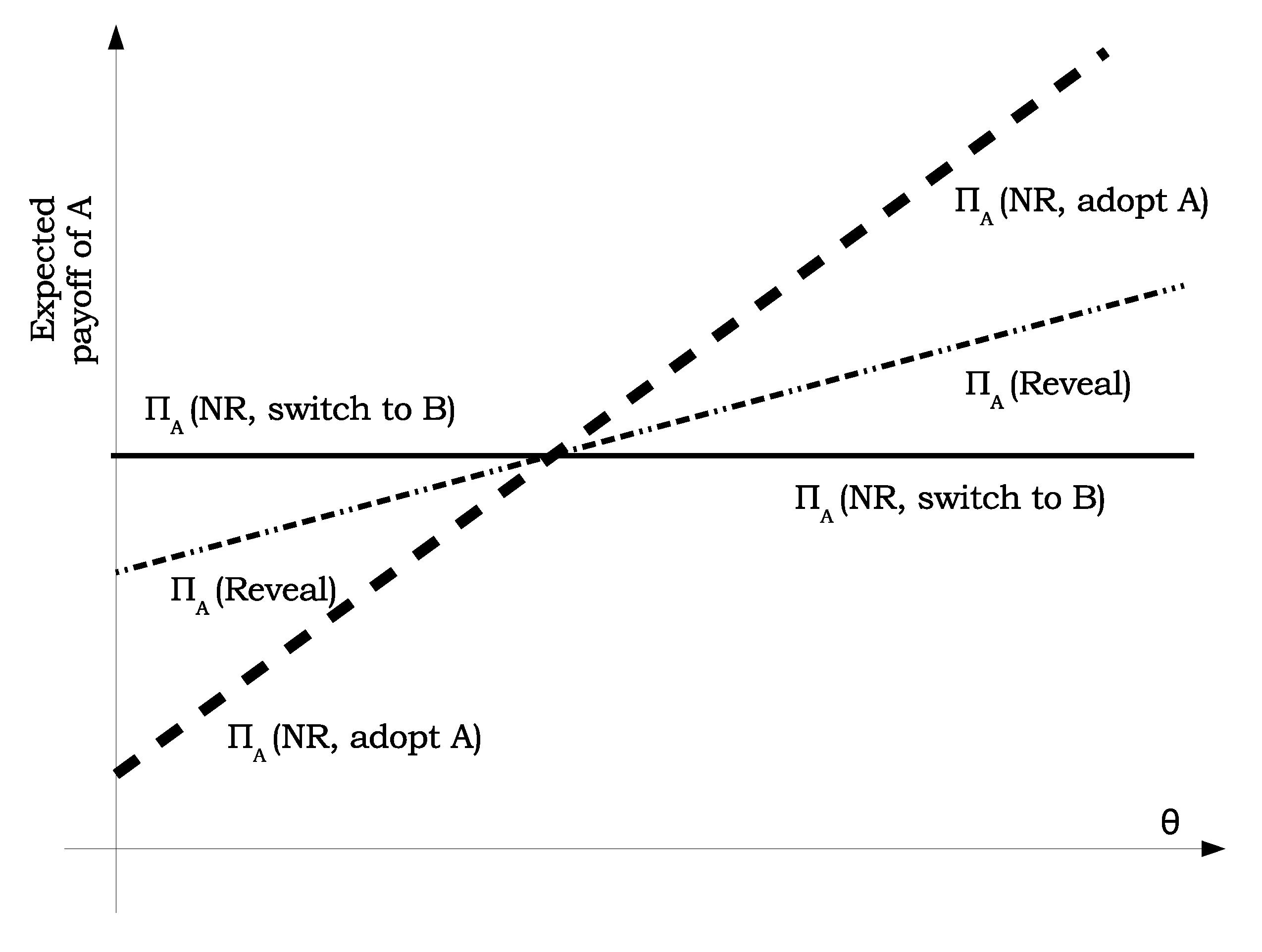
Figure 1 provides a graphical representation of agent A’s payoffs under the three strategic options, not revealing her information, revealing her information and then playing “Adopt A”, and revealing her information and then playing “Switch to B”. ☐

We next examine efficiency properties of this PBEM.

Proposition 4.

The PBEM discussed in Propositions 2 and 3 is inefficient.

Proof. 

Since agent B plays a completely mixed strategy, there is a positive probability that agent B will choose B even when $\theta \ge b$, as well as choose A even when $\theta <b$. ☐

At this point a few remarks would be useful.

Remark 1.

We find that the full disclosure results in Section 4.1, together with the non-revelation results in Section 4.2, jointly suggest that it is the presence, or absence of strategic uncertainty that determines whether there is information non-revelation or not. Thus, both sets of results are of interest. Even so, in future work we plan to examine if one can use some selection mechanism to isolate the non-revelation equilibrium.

One strand of the literature on equilibrium selection considers global games and the role of higher order beliefs. The global games framework, as proposed by [30], has been extensively used to study, among others, equilibrium selection in coordination games arising in the pricing of debt ([31]), and to problems of stochastic common learning ([32]). In this context, ref [33] examines the role of higher order beliefs and the precision of signals about private vs. public information in equilibrium selection. However, note that in the coordination continuation game, not only are the pure strategy equilibria strict, they are also not dominance solvable. Hence, we cannot use the method of global games for selecting any one of the pure strategy equilibria over the other.

Remark 2.

We next examine scenarios where the parameter values do not satisfy Assumption 1. Please note that if $b>c$, then adopting B is a dominant strategy for agent B. Similarly, if $c<{\theta }_l$, then adopting A is a dominant strategy for agent A. In either of these cases, the coordination problem disappears, and agent A’s payoff is the same irrespective of whether she reveals her own type in Stage 1 or not. Thus, the interesting case is if $b<c$ and ${\theta }_l<c<{\theta }_h$. In this case there is an equilibrium with partial information revelation. Let $\tilde{F}\left(\theta \right)$ denote the probability distribution derived from $F\left(\theta \right)$ conditional on θ being less than c. It is now straightforward to construct an equilibrium where all A agents with $\theta \ge c$ reveal their type and choose A in the coordination stage, whereas the other A agents do not reveal their type. In particular, we can mimic the argument in Propositions 2 and 3 (replacing $F\left(\theta \right)$ with $\tilde{F}\left(\theta \right)$), to construct equilibrium strategies for all A agents with $\theta <c$. Interestingly, as discussed earlier in the introduction, ref [8] also demonstrates the existence of equilibrium with partial disclosure in the presence of hard information.

5. Purification of Agent B’s Mixed Strategies

The non-revelation result in Propositions 2 and 3 are open to the critique that we examine equilibria where agent B plays a completely mixed strategy whenever A reveals her private information about her own type. In an effort to address this issue, we next argue that there exists a natural extension of our framework such that sustaining the non-revelation result does not require the B agent to play mixed strategies in the coordination stage.

To this end, we extend the baseline framework to allow for a unit mass of B-agents with different realizations over their private benefit b, where the exact realization of b for any given B agent is private information. We then argue that a version of Harsanyi’s purification theorem goes through: following type revelation by the A agent, the continuation pure strategy played by the B-type agents generates the same probability distribution as the mixed-strategy equilibrium in the baseline model (see Lemma 3 later). Subsequently, we use this result to demonstrate (in Proposition 5 later on), that the non-revelation results goes through under this re-formulation. Formally, the B agents’ private benefit from adopting B is distributed over the compact, continuous type space $\mathsf{\Xi }$, where $\mathsf{\Xi }=[b_l,b_h]\subset {\mathbb{R}}_{+}$, with distribution $G\left(b\right)$, where $b_l<b_h$, and $G\left(b\right)$ is non-degenerate and strictly increasing. Furthermore, for this section we assume that an analogue of Assumption 1 goes through, i.e., $c>max\{{\theta }_h,b_h\}$.

We next turn to modeling the coordination benefits in this setup. The coordination benefit on technology i, $i\in \{A,B\}$, arises if and only if the A agent, as well as a positive measure of B-agents adopt this technology. Thus, conditional on the A agent adopting technology i, the total coordination benefit from i is given by $c.x$, where x denotes the fraction of B-agents opting for this technology. The modified payoff matrix in this new game is shown in

Table 2. Modified payoff matrix for the one-shot game.

	Switch	Adopt B
Adopt A	$\theta +c(1-l)$, $c(1-l)$	$\theta +c(1-l)$, b
Switch	$cl$, 0	$cl$, $b+cl$

.

We next introduce some definitions that we need for the analysis:

• The strategy of a type $\theta$ agent A in Stage 1, denoted ${\beta }^I\left(\theta \right)$, is a probability distribution over $M\left(\theta \right)$.
• Strategies of the agents in Stage 2, i.e., the coordination stage, are:

  -

  In Stage 2, the strategy of a type $\theta$ agent A, i.e., ${\beta }_A^C\left(\theta \right)$, maps from her message is Stage 1, to the set of probability distributions over her action space. Hence, ${\beta }_A^C\left(\theta \right):M\left(\theta \right)\to [0,1]$.

  -

  In Stage 2, agent B’s strategy is a mapping from his own type space $\mathsf{\Xi }$, and the disclosure made by A in Stage 1, to the set probability distributions over his own actions. Hence, ${\beta }_B^C:\mathsf{\Xi }\times M\to [0,1]$.

  -

  Agent A’s strategy in Stage 2 is said to be a cut-off strategy if there exists $\widehat{\theta }\in \Theta$ such that A adopts A iff $\theta \ge \widehat{\theta }$.

  -

  Agent B’s strategy in Stage 2, ${\beta }_B^C$, is said to be a cut-off strategy if there exists $\widehat{b}\in \mathsf{\Xi }$ such that B adopts B iff $b\ge \widehat{b}$.

• The belief of a type b agent B at the coordination stage, i.e., Stage 2, is a mapping ${\overline{B}}_b$ from the message sent by agent A in the revelation stage to a probability distribution over agent A’s type space $[{\theta }_l,{\theta }_h]$, i.e., ${\overline{B}}_b:M\to \Delta [{\theta }_l,{\theta }_h]$10.

One can define a perfect Bayesian equilibrium of this game in the usual manner.

5.1. Analysis: Non-Revelation by the A Agent in Stage 1

Given the complementarities inherent in this game, cut-off strategies arise naturally for all types of A, as well as the B-agents. In the continuation game following type revelation by the A agent, we, therefore, focus on equilibria where the B-agents play a cut-off strategy with a cut-off of $\widehat{b}$. Next, consider the continuation game following non-revelation by agent A. Let ${\widehat{\theta }}_{NR}$ denote the cut-off for agent A and ${\widehat{b}}_{NR}$ denote the cut-off for the B-agents in the subsequent coordination stage.

Definition 2.

A PBEC for the modified game is a perfect Bayesian equilibrium where, in every continuation game, the B-agents play cut-off strategies with strictly interior cut-offs in the coordination stage of the game.

We first argue that in the unique PBEC for the continuation game following type revelation by agent A, the probability that the B-agents adopt B is the same as that under the PBEM equilibrium where agent B plays a completely mixed strategy (see Lemma 1).

Lemma 3.

Consider the Stage 2 continuation game where agent A reveals her type θ in Stage 1.

(a) 

In any PBEC of this continuation game, the cut-off for agent B ($\widehat{b}\left(\theta \right)$) and the probability that agent A adopts A, i.e., $\alpha \left(\theta \right)$, solves:

$$\begin{array}{ccc}\hfill \widehat{b}\left(\theta \right)& =& (\alpha -\frac{c+\theta }{2c})c,\hfill \\ \hfill \alpha \left(\theta \right)& =& \frac{(c+\theta )}{2c}+\frac{G^{-1}((c-\theta )/2c)}{c}.\hfill \end{array}$$

(b) 

A θ-type A-agent’s payoff from revealing her type is $\frac{c+\theta }{2}$.

(c) 

The equilibrium cut-off for the B-types is unique and interior, i.e., $0<\widehat{b}<1$. Moreover, it generates the same probability distribution over the two choices, i.e., A and B, as that under the PBEM equilibrium following type revelation by agent A in the baseline model.

Proof. 

(a)

Consider the continuation game following the A agent revealing her type to be $\theta$. Let the B-agents adopt a cut-off strategy involving a cut-off of $\widehat{b}\left(\theta \right)$. Let $l\left(\theta \right)$ be the fraction of B-agents that adopt B with $l\left(\theta \right)\equiv 1-G\left(\widehat{b}\left(\theta \right)\right)$. Let $\alpha \left(\theta \right)$ be the probability that the A-agent adopts A.

First, consider the decision problem facing a B-agent with private valuation b. His expected payoff when he switches to B, is:

$${\pi }_B\left(B\right)=(1-\alpha ).(b+cl)+\alpha .b,$$

(8)

whereas his expected payoff when he adopts A, is:

$${\pi }_B\left(A\right)=\alpha .c(1-l).$$

(9)

For the indifferent type $\widehat{b}$, Equating (8) and (9), we get:

$$\widehat{b}=(\alpha -l)c.$$

(10)

Next consider the decision problem facing the A-agent with private valuation $\theta$. Her expected payoff from adopting A is:

$${\pi }_A\left(A\right)=\theta +c(1-l),$$

(11)

whereas her expected payoff from switching to B:

$${\pi }_A\left(B\right)=c.l.$$

(12)

For the A-agent of type $\theta$ to be indifferent between A and B, Equations (11) and (12) have to yield

$$l\left(\theta \right)=\frac{c+\theta }{2c}.$$

(13)

Given that $c>{\theta }_h\ge \theta$, it is straightforward to check that $0<l\left(\theta \right)<1$. Therefore, $\widehat{b}\left(\theta \right)=(\alpha -\frac{c+\theta }{2c})c$.

Solving (10) and (13) simultaneously, we find that

$$\alpha =l\left(\theta \right)+\frac{\widehat{b}}{c}=\frac{(c+\theta )}{2c}+\frac{G^{-1}((c-\theta )/2c)}{c}>0,$$

(14)

using the fact that $l\left(\theta \right)=\frac{c+\theta }{2}$ (from (13)), and $G\left(\widehat{b}\left(\theta \right)\right)=1-l\left(\theta \right)=\frac{c-\theta }{2c}$.11

(b)

Using (13), the A-agent’s expected payoff is given by $cl\left(\theta \right)=\frac{c+\theta }{2}$.

(c)

Please note that $G\left(\widehat{b}\right)=1-l\left(\theta \right)=\frac{c-\theta }{2c}$. Given that $G\left(b\right)$ is strictly increasing, $\widehat{b}$ is unique. Given that $c>{\theta }_h\ge \theta$, it is straightforward to check that $0<G\left(\widehat{b}\right)<1$, so that $b_l<\widehat{b}<b_h$.

Next observe that the fraction of B-agents adopting B, i.e., $l\left(\theta \right)=1-G\left(\widehat{b}\right)=\frac{\theta +c}{2c}$ (from (11)). From Lemma 1, recall that $q_R\left(\theta \right)=\frac{\theta +c}{2c}$, where $q_R\left(\theta \right)$ is the probability with which B adopts B in the our baseline model for the continuation game where agent A reveals her type to be $\theta$. Thus, $l\left(\theta \right)=q_R\left(\theta \right)$. ☐

Proposition 5 below is the central result in this section. We find that in the revelation stage of the modified game, agent A does not reveal her type, showing that the non-revelation result is robust to this modification.

Proposition 5.

Consider any PBEC of the modified game.

(a) 

Consider the Stage 2 continuation game where agent A does not reveal her type in Stage 1. In any PBEC, agent A plays a cut-off strategy in Stage 2.

(b) 

In Stage 1, all types of agent A, with the possible exception of one type, strictly prefer non-revelation to revelation.

(c) 

If $F\left(\theta \right)+\frac{\theta }{2c}+\frac{G^{-1}((c-\theta )/2c)}{c}$ is monotonic in θ, then this game has a unique PBEC.

Proof. 

(a)

The proof mimics that of Lemma 1 earlier.

(b)

Given Proposition 5(a), we restrict attention to PBEC where, following non-revelation the A agent plays a cut-off strategy. Let the cut-offs following non-revelation be ${\widehat{\theta }}_{NR}$ for the A, and ${\widehat{b}}_{NR}$ for the B agents. Equating the payoffs from switching to A and adopting B for the indifferent B agent, i.e., of type ${\widehat{b}}_{NR}$, we have that

$${\widehat{b}}_{NR}=(G\left({\widehat{b}}_{NR}\right)-F\left({\widehat{\theta }}_{NR}\right))c.$$

(15)

Similarly, equating the payoffs from A and B for the indifferent A agent, i.e., of type ${\widehat{\theta }}_{NR}$, we have that

$$G\left({\widehat{b}}_{NR}\right)=\frac{c-{\widehat{\theta }}_{NR}}{2c}.$$

(16)

Given that $c>{\theta }_h\ge \widehat{\theta }$, it follows that $0<G\left({\widehat{b}}_{NR}\right)<1$, so that $b_l<{\widehat{b}}_{NR}<b_h$.

Next, from Equations (15) and (16), we have that

$$F\left({\widehat{\theta }}_{NR}\right)=\frac{(c-{\widehat{\theta }}_{NR})}{2c}-\frac{G^{-1}((c-{\widehat{\theta }}_{NR})/2c)}{c}.$$

(17)

It is straightforward to check that $F\left({\widehat{\theta }}_{NR}\right)<1$, so that ${\widehat{\theta }}_{NR}<{\theta }_h$.12 Given ${\widehat{\theta }}_{NR}$, ${\widehat{b}}_{NR}$ can then be solved using Equation (15). Furthermore, if ${\widehat{\theta }}_{NR}={\theta }_l$, then from Equation (15), ${\widehat{b}}_{NR}=c.G\left({\widehat{b}}_{NR}\right)$. In all cases, for all $\theta \ge {\widehat{\theta }}_{NR}$, A adopts A and for all $\theta <{\widehat{\theta }}_{NR}$, A switches to B upon non-revelation of $\theta$ in Stage 1.

Please note that for ${\widehat{\theta }}_{NR}>{\theta }_l$, the expected payoff for A, denoted ${\pi }_A\left(NR\right)$, is:

$${\pi }_A\left(NR\right)=\left\{\begin{array}{c}\theta +c.G\left({\widehat{b}}_{NR}\right),\mathrm{if}\theta \ge \widehat{\theta },\hfill \\ c[1-G\left({\widehat{b}}_{NR}\right)],\mathrm{if}\theta <\widehat{\theta }.\hfill \end{array}\right.$$

(18)

Whereas, if ${\widehat{\theta }}_{NR}={\theta }_l$, then from Equations (16) and (18), the expected payoff for A is:

$${\pi }_A\left(NR\right)=\theta +\frac{c-{\theta }_l}{2},\forall \theta .$$

(19)

We first consider ${\widehat{\theta }}_{NR}>{\theta }_l$:

• At $\theta ={\widehat{\theta }}_{NR}$, ${\pi }_A\left(NR\right)={\widehat{\theta }}_{NR}+c.G\left({\widehat{b}}_{NR}\right)={\widehat{\theta }}_{NR}+c.\left(\frac{c-{\widehat{\theta }}_{NR}}{2c}\right)=\frac{{\widehat{\theta }}_{NR}+c}{2}={\pi }_A\left(R\right)$.
• For all types of $\theta >{\widehat{\theta }}_{NR}$, ${\pi }_A\left(NR\right)-{\pi }_A\left(R\right)=\frac{\theta }{2}-c[\frac{1}{2}-G\left({\widehat{b}}_{NR}\right)]$. Please note that $\frac{\partial [{\pi }_A\left(NR\right)-{\pi }_A\left(R\right)]}{\partial {\theta }_{NR}}=1/2>0$, and at $\theta ={\theta }_h$, this difference ${\pi }_A\left(NR\right)-{\pi }_A\left(R\right)=\frac{{\theta }_h}{2}-c[\frac{1}{2}-G\left({\widehat{b}}_{NR}\right)]$. This expression is positive, iff ${\widehat{b}}_{NR}>G^{-1}\left(\frac{c-{\theta }_h}{2c}\right)$. Finally, from Equation (16), ${\widehat{b}}_{NR}=G^{-1}\left(\frac{c-{\widehat{\theta }}_{NR}}{2c}\right)>G^{-1}\left(\frac{c-{\theta }_h}{2}\right)$, since ${\widehat{\theta }}_{NR}<{\theta }_h$ and $G\left(B\right)$ is strictly increasing. As discussed earlier, ${\pi }_A\left(R\right)={\pi }_A\left(NR\right)$ at $\theta ={\widehat{\theta }}_{NR}$.Therefore, in the range $({\widehat{\theta }}_{NR},{\theta }_h]$, ${\pi }_A\left(R\right)<{\pi }_A\left(NR\right)$.
• Next, consider $\theta$ in the range $[{\theta }_l,\widehat{\theta })$. Over this range ${\pi }_A\left(NR\right)$ is independent of $\theta$, whereas ${\pi }_A\left(R\right)$ is strictly decreasing in $\theta$. Given that ${\pi }_A\left(NR\right)$ equals ${\pi }_A\left(R\right)$ at ${\widehat{\theta }}_{NR}$, it follows that ${\pi }_A\left(NR\right)>{\pi }_A\left(R\right),\forall \theta \in [{\theta }_l,{\widehat{\theta }}_{NR})$.

Therefore, whenever ${\widehat{\theta }}_{NR}>{\theta }_l$, A’s expected payoff from non-revelation is greater than that from revelation $\forall \theta \in [{\theta }_l,{\theta }_h]$, except for $\theta ={\widehat{\theta }}_{NR}$, where these payoffs are equal. Finally, consider the case where ${\widehat{\theta }}_{NR}={\theta }_l$ in the non-revelation equilibrium. Please note that for any $\theta \in \Theta$, ${\pi }_A\left(R\right)=\frac{\theta +c}{2}<\theta +\frac{c-{\theta }_l}{2}={\pi }_A\left(NR\right)$.

(c)

Given that $F\left(\theta \right)+\frac{\theta }{2c}+\frac{g^{-1}((c-\theta )/2c)}{c}$ is monotonic in $\theta$, from (17) it follows that ${\widehat{\theta }}_{NR}$ is unique. This in turn ensures that ${\widehat{b}}_{NR}$ is unique.

☐

6. Extensions

In this section, we consider three extensions of the baseline model. In the first two, we argue that the non-revelation result is robust to (a) two-sided private information and (b) imprecise information disclosure. Finally, we examine if mandatory disclosure of information can improve coordination probability.

6.1. Two-Sided Private Information

Consider the case where both the agents have private information about their own types, with agent A’s (respectively B’s) type being denoted by ${\theta }_A$ (respectively ${\theta }_B$). For simplicity, let ${\theta }_A$ and ${\theta }_B$ be identically and independently distributed with distribution function $F\left(\theta \right)$ (assumed to be strictly monotonic) with support $[{\theta }_l,{\theta }_h]$. While agent $i,i\in \{A,B\},$ knows her own type, she only knows the distribution of agent $j\ne i$, i.e., $F\left(\theta \right)$. Consider a simple modification of the earlier game whereby, in Stage 1, both the agents simultaneously choose whether to reveal their type, or to reveal nothing. Thus, agent ${\theta }_A$ chooses an element from $\left\{{\theta }_A\right\}\cup${Not Reveal her Type}, whereas agent ${\theta }_B$ chooses an element from $\left\{{\theta }_A\right\}\cup${Not Reveal her Type}.

Let ${\pi }_i(i=X,j=Y)$ denote the payoff of agent i in case in Stage 1 she selects X and agent j selects $Y,$ where $X,Y\in M_i=[{\theta }_l,{\theta }_h]\cup \{$Not Reveal ${\theta }_i\}$. We show that even with two-sided private information, a version of the earlier non-revelation result in Proposition 1 goes through.

Proposition 6.

Consider any perfect Bayesian equilibria where, in Stage 2, an agent uses cut-off strategies, in case she has not revealed her type, and completely mixed strategies, in case she has. In any such equilibrium, all θ types lower than a cut-off $\widehat{\theta }$ are indifferent between revealing and not revealing her type. All types higher than this cut-off type prefer not to reveal. Thus, there exists a PBEM where there is no information revelation.

Proof. 

Step (i). We first prove that in case agent j reveals her type, at most one type of agent i, $i\ne j$, will reveal her type. We know from our earlier results that if both the agents reveal their types, then the expected payoff for agent i in the completely mixed-strategy equilibrium is $\frac{{\theta }_i+c}{2c}$.

Suppose that agent i decides not to reveal her type, given that j has revealed her type. Clearly, the mixed-strategy equilibrium in the second stage game is identical to that under the unique PBEM characterized in Propositions 2 and 3. Thus the payoff of agent i is:

$$\begin{array}{c}\hfill {\pi }_i(i=\mathrm{Not}\mathrm{reveal}{\theta }_i|j=\mathrm{Reveal}{\theta }_j)=\left\{\begin{array}{c}{\theta }_i+(1-\frac{c+\widehat{\theta }}{2c}).c,\mathrm{if}{\theta }_i>\widehat{\theta },\hfill \\ \frac{c+\widehat{\theta }}{2c}.c,\mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

The difference between the expected equilibrium payoff to i from not revealing and revealing, given that j reveals, is strictly positive for all values of $\theta$ as shown below:

$$\begin{array}{ccc}\hfill {\pi }_i(i=\mathrm{Not}\mathrm{Reveal}{\theta }_i|j=\mathrm{Reveal}{\theta }_j)& -& {\pi }_i(i=\mathrm{Reveal}{\theta }_i|j=\mathrm{Reveal}{\theta }_j)=\hfill \\ & & \left\{\begin{array}{c}\frac{{\theta }_i-\widehat{\theta }}{2}>0,\mathrm{if}{\theta }_i>\widehat{\theta },\hfill \\ \frac{\widehat{\theta }-{\theta }_i}{2}>0,\mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

Given that j reveals, i would therefore prefer to not reveal and adopt for ${\theta }_i>\widehat{\theta }$ and not reveal and switch for $\theta <\widehat{\theta }$. Only the type $\widehat{\theta }$ is indifferent.

Step (ii) We argue that in case agent j does not reveal her type, all types lower than $\widehat{\theta }$ are indifferent between revelation and non-revelation, whereas all types higher than this cut-off strictly prefer non-revelation to revelation.

In this case, if agent i does not reveal, the coordination cut-off $\widehat{\theta }$ ensures that she is indifferent between adopting and switching, so that

$$\widehat{\theta }+F\left(\widehat{\theta }\right)c=(1-F\left(\widehat{\theta }\right))c.$$

(20)

As $F\left(\theta \right)$ is strictly monotonic, $\widehat{\theta }$ exists in the interior of the type space and is unique. The expected payoff of agent i from not revealing, given that j has not revealed her type is

$${\pi }_i(i=\mathrm{Not}\mathrm{Reveal}{\theta }_i|j=\mathrm{Not}\mathrm{Reveal}{\theta }_j)=\left\{\begin{array}{c}{\theta }_i+\frac{c-\widehat{\theta }}{2},\mathrm{if}{\theta }_i>\widehat{\theta },\hfill \\ \frac{c+\widehat{\theta }}{2},\mathrm{otherwise}\hfill \end{array}\right.$$

where, $F\left(\widehat{\theta }\right)=\frac{c-\widehat{\theta }}{2c}$.

Now, consider the case where agent i reveals her information, given that j does not. From our earlier analysis of one-sided asymmetric information case, the expected mixed strategy payoff for agent i is $\frac{c+\widehat{\theta }}{2}$.

Hence, we have

$$\begin{array}{cc}& {\pi }_i(i=\mathrm{Not}\mathrm{Reveal}{\theta }_i|j=\mathrm{Not}\mathrm{Reveal}{\theta }_j)-{\pi }_i(i=\mathrm{Reveal}{\theta }_i|j=\mathrm{Not}\mathrm{Reveal}{\theta }_j)\hfill \\ =& \left\{\begin{array}{c}{\theta }_i-\widehat{\theta }>0,\mathrm{if}{\theta }_i>\widehat{\theta },\hfill \\ 0,\mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(21)

Thus, all types with $\theta \le \widehat{\theta }$ are indifferent about revealing or not revealing, if j does not reveal. All types strictly greater than $\widehat{\theta }$ prefer non-revelation to revelation.

Finally, taking steps (i) and (ii) together, the proposition follows.13 ☐

Remark 3.

The characterization of this equilibrium, in terms of $\widehat{\theta }$, is as follows: In Stage 1, there is no information revelation. In Stage 2: agent i adopts her own idea, ${\theta }_i$, if and only if ${\theta }_i\ge \widehat{\theta }$, where $\widehat{\theta }=F^{-1}\left(\frac{c-\widehat{\theta }}{2c}\right)$ and ${\theta }_l<\widehat{\theta }<{\theta }_h$, and switches to the other agent’s idea otherwise.

6.2. Imprecise Information Revelation

Please note that the informed agent can either reveal her own type truthfully, or can refuse to reveal. This message space does not allow for imprecise disclosures, unlike e.g., ref [10] who not only allows for imprecise revelation, but also cheap talk.

Given that strategic uncertainty in coordination is at the heart of this paper, in this sub-section we allow for imprecise information revelation though in the presence of strategic uncertainty, showing that the non-revelation equilibrium does survive.

Consider a scenario where agent A is allowed to report that her type lies within a set, rather than the exact value. Information is still assumed to be hard however, so that agent A can only make truthful claims.14 For technical reasons, we restrict attention to disclosures within closed sets only. In Stage 1, agent A chooses an element from $\overline{\Theta }$, where $\overline{\Theta }$ is the set of all closed subsets of $[{\theta }_l,{\theta }_h]$. However information is hard in the sense that if an agent of type $\theta$ chooses $\Theta \left(\theta \right)\in \overline{\Theta }$ in Stage 1, then it must be the case that $\theta \in \Theta \left(\theta \right)$. Please note that since $[{\theta }_l,{\theta }_h]\in \overline{\Theta }$, revealing no information is also an option.

Consider the PBEM of the baseline model described in Propositions 1 and 2. Define $q_{NR}^{*}$ (respectively $q_R^{*}\left(\theta \right)$) to be the probability that agent B adopts B in the second stage, given that agent A chooses not to reveal any information (respectively reveals her type $\theta$). Recall that

$$q_{NR}^{*}=\frac{1}{2}+\frac{F^{-1}\left(\frac{c-b}{2c}\right)}{2c},\mathrm{and}{q}_R^{*}\left(\theta \right)=\frac{1}{2}+\frac{\theta }{2c}.$$

Furthermore, (a) $q_{NR}^{*}>q_R^{*}\left(\theta \right)$ if and only if $\theta <\widehat{\theta }$, and (b) $q_R^{*}\left(\theta \right)$ intersects $q_{NR}^{*}$ from below at the coordination cut-off point $\widehat{\theta }$.

We then prove that there exists an equilibrium where there is no information revelation by agent A.

Proposition 7.

There exists an equilibrium where there is no information revelation by agent A in Stage 1 (except possibly by a single type).

Proof. 

The argument is by construction. Consider the following strategies:

In Stage 1, agent A reveals no information. In case agent A selects any other ${\Theta }^{\prime }\in \overline{\Theta }$ instead, then agent B believes that A’s type is $sup{\Theta }^{\prime }.$

In Stage 2, the agents play completely mixed strategies with agent B’s beliefs described above.

It remains to check if any type A agent has an incentive to deviate and reveal her type in Stage 1. Suppose an agent of type ${\theta }^{\prime }$ deviates and chooses ${\Theta }^{\prime }\in \overline{\theta }$, where ${\theta }^{\prime }\in {\Theta }^{\prime }$. Let ${\theta }^{″}=sup{\Theta }^{\prime }$. Recall that agent A’s payoff from selecting ${\Theta }^{\prime }$, is ${\theta }^{\prime }+c-q_R^{*}\left({\theta }^{″}\right)c$, where $q_R^{*}\left({\theta }^{″}\right)=\frac{1}{2}+\frac{{\theta }^{″}}{2c}$. Given agent B’s belief, and the fact that agent A’s payoff is decreasing in $q_R^{*}\left(\theta \right)$, agent A cannot do any better than to announce ${\theta }^{\prime }$ itself (more generally announce a set with ${\theta }^{\prime }$ as its supremum). However, if ${\theta }^{\prime }>\widehat{\theta }$, then agent A would prefer not to reveal and adopt, rather than reveal, since $({\theta }^{\prime }+c)-q_{NR}^{*}c>({\theta }^{\prime }+c)-q_R^{*}\left({\theta }^{\prime }\right)c$. This is because $q_{NR}^{*}<q_R^{*}\left(\theta \right)$ for all $\theta >\widehat{\theta }$. If ${\theta }^{\prime }<\widehat{\theta }$, then type ${\theta }^{\prime }$ would prefer not to reveal and switch, getting a payoff of $q_{NR}^{*}c$, as opposed to $q_R^{*}\left(\theta \right)c$ if she revealed her type, since $q_{N{R}^{*}}>q_R^{*}\left(\theta \right)$ for all $\theta <\widehat{\theta }$. ☐

6.3. Mandatory Disclosure

We now compare the coordination probability under the PBEM vis-a-vis that under mandatory information revelation followed by a play of completely mixed strategies.

Fixing $\theta$, let ${\psi }_R\left(\theta \right)$ denote the coordination probability on either one of the two ideas, either A or B, under mandatory disclosure (full revelation) followed by completely mixed strategies in the coordination phase. Similarly, let ${\varphi }_{NR}$ denote the coordination probabilities under the unique PBEM. With complete revelation, the coordination probability in the completely mixed-strategy equilibrium is

$${\psi }_R\left(\theta \right)=(1-p_R)q_R+(1-q_R)p_R=\frac{c^2-b\theta }{2c^2},$$

(22)

where $p_R$ and $q_R$ are the probabilities with which agents A and B adopt their own ideas respectively, $0<p_R,q_R<1$. In contrast, the coordination probability under the unique PBEM is

$${\psi }_{NR}=(1-F\left(\widehat{\theta }\right))(1-q_{NR})+F\left(\widehat{\theta }\right)q_{NR}=\frac{c^2-b\widehat{\theta }}{2c^2},$$

(23)

recalling that $q_{NR}$ is the probability with which B adopts own idea and A plays a simple cut-off strategy at $\widehat{\theta }$. Thus, the difference in expected probability of coordination is

$${\int }_{{\theta }_l}^{{\theta }_h}\psi d\left(F\left(\theta \right)\right)={\int }_{{\theta }_l}^{{\theta }_h}[{\psi }_R\left(\theta \right)-{\psi }_{NR}]d\left(F\left(\theta \right)\right)=\frac{b}{2c^2}(\overline{\theta }-\widehat{\theta }),$$

(24)

where, $\overline{\theta }$ is the average value of $\theta$.

Proposition 8.

The overall expected coordination probability through mandatory information disclosure is greater than or equal to that with the non-revelation equilibrium iff $\overline{\theta }\ge \widehat{\theta }$.

It is interesting to note, therefore, that mandatory disclosure need not improve coordination probability in the game. This follows directly from the fact that revelation makes the opponent more aggressive. Recall that $q_R\left(\theta \right)$ is increasing in $\theta$, whereas $q_{NR}$ is independent of $\theta$. For all types $\theta$ higher than $\widehat{\theta }$, $q_{NR}$ is greater than $q_R\left(\theta \right)$. Consequently, agent B is more aggressive without mandated disclosure than with mandated disclosure. For all types lower than $\widehat{\theta }$, agent B is less aggressive without mandated disclosure and the converse holds.

Example 1.

If θ is uniformly distributed over $[0,1]$, $c=2$ and $b=1$, with $\widehat{\theta }=\frac{c-b}{2c}=\frac{1}{4}$ and $\overline{\theta }=\frac{1}{2}$, ${\int }_{{\theta }_l}^{{\theta }_h}\psi d\left(F\left(\theta \right)\right)=\frac{1}{4}>0$ leading to lower overall expected coordination probability with mandated disclosure in comparison with the no disclosure equilibrium. On the other hand, if the support of the distribution changes to $[0,\frac{1}{2}]$, mandated disclosure and no disclosure equilibria achieve the same expected probability of coordination, as $\overline{\theta }=\widehat{\theta }=\frac{1}{4}$. If we change the support of the distribution to $[0,\frac{1}{4}]$, expected coordination probability is higher with mandated disclosure than no disclosure, as the mean of the distribution falls to $\frac{1}{8}<\widehat{\theta }$.

7. Conclusions

We examine the issue of information revelation in an asymmetric information Battle-of-the-Sexes game with one-sided asymmetric information. The analysis unearths a link between strategic uncertainty in coordination and the extent of information revelation, which is new in the literature. We find that while, in the absence of any coordination failure, there exist equilibria with full disclosure, in the presence of strategic uncertainty in coordination there exists an equilibrium with no information revelation. The latter requires an application of mixed strategies, which acts as an equilibrium selection device and results in non-revelation of information in the unique equilibrium. We provide a purification argument for the non-existence result, as well demonstrate that it is robust to several extensions, including both-sided asymmetric information, imprecise information revelation and mandatory disclosure. Our analysis suggests avenues for further research in terms of optimal design of mandatory disclosure rules, such as those applicable for patent pools. We also plan to extend the basic model to address problems of commitment and externalities such as coordination benefits correlated with private benefits.