The Patron Game: the Individual Provision of a Public Good

Abstract

The Patron Game studies the individual provision of a public good, i.e., a situation in which the cost of contributing exceeds by construction its private return (e.g., volunteering, Open Collaboration projects). We test the Patron Game in the lab finding that contributions are high, though significantly lower than in a classic Public Good Game. Results show that demand effects and the warm glow of giving account almost entirely for the contributions, with the former playing the most prominent role. The social nature of the individual provision of a public good is confirmed by the fact that, even when the efficiency multiplier is removed, contributions are higher than in comparable Dictator Games.

I’m a scheming, conniving bastard who doesn’t care for any hurt feelings or lost hours of work, if it just results in what I consider to be a better system.

(Linus Torvalds, 2000)

1. Introduction

This paper investigates the individual provision of a public good by means of a game, that we call the Patron Game, in which only one player per group, the patron, chooses how much to contribute to the public good knowing that the other players benefit from the public good without contributing. We have chosen to name the game “Patron” because it appropriately captures the role played by a person called upon to use his wealth or to exert some effort to advance a social goal. The decision to contribute does not rely upon the prospect of a private return. At the same time, the contribution does not correspond to a simple transfer of resources as it would be in a dictator game. The public good benefits the contributor, too, but the return is by construction lower than the cost of its provision.

The Patron Game captures in a stylized manner some key features of philanthropic activities undertaken in a direct manner to advance social goals.1 Another distinguishing characteristic of the Patron Game is that the contribution is not a mere transfer of resources, because the patron receives a benefit from his activity although lower than the cost to generate it. Hence, the Patron Game consistently replicates the incentives underlying voluntary activities, particularly when the volunteer enjoys an improvement at the community (or social) level in exchange for his costly effort.

The Patron Game mimics a wide range of situations in which the costly individual effort is helpful to others more than to oneself and in which the patron is the bearer of the required skills. For instance, it is suitable to analyze the early stage of development of Open Collaboration projects, defined as a system that relies on loosely coordinated participants, who interact to create products (or services) of economic value, which are then made available to contributors and non-contributors alike [2]. This definition encompasses a wide range of activities of growing importance, such as crowdsourcing, open source, as well as copyleft projects, and it is similar to that of a public good apart from the qualification about the “loosely coordinated participants”. Linux or Wikipedia now share the nature of a classic public good, but what about the countless number of projects that do not share a similar story of success? Crosetto [3] reports that in the SourceForge development community the density of projects is exponentially decreasing in the number of developers. More than 80% of the projects feature only one developer.

Despite the countless number of contributions in the literature studying the provision of public goods, no attention has been paid up to our knowledge to the special case of its individual rather than joint provision. This finding is even more striking given the relevance of the activities potentially involved. More than 60 million people volunteer in the U.S according to the Bureau of Labor Statistics. More than a hundred thousand projects in SourceForge feature only the project owner. The Patron Game provides a stylized framework reproducing such an interaction-free environment in the laboratory, abstracting from considerations about the uncertainty of the outcome as well as from non-monetary return such as social image. Using the Patron Game allows us to address two research questions: First, how does the level of the contributions compare with that in a classic Voluntary Contribution Mechanism (VCM)? Second, what are the motivations behind the choice of volunteering or starting a project when the likelihood of sharing the burden of the provision of the public good is negligible and the private return lower than the cost?

Positive contributions in the Patron Game cannot be rationalized by conditional cooperation and reciprocity simply because there is no other active opponent whose behavior can be used to condition a player’s contribution, unlike in a classic VCM [4,5,6].2 Another crucial difference compared to the VCM is that the Patron Game removes the potential to achieve a Pareto improvement through cooperation and therefore the element of common interest. More generally, the Patron Game removes any reason to contribute that relies upon strategic interaction.3

What drives the individual provision of a public good must therefore be found at the individual level. Does the patron receive positive utility from the mere act of giving? Is the behavior driven by the expectations one feels about having to contribute his fair share towards building a better society? Of course, it is difficult to reproduce such complicate motivations in the lab. As commonly done in experimental economics, the Patron Game tries to answer these questions in an artificial environment inducing individual preferences through monetary incentives. Moreover, we borrow from the literature (mostly from the strand on VCM) to classify the individual determinants and to find experimental manipulations to assess their importance.

Our paper provides evidence concerning the individual determinants to contributions thanks to an element of methodological originality represented by how our experimental design disentangles the role played by demand effects from that of impure altruism. Demand effects are usually investigated using a Give vs. Take framework. However, shifting money away from the endowment of the subjects has an additional effect via impure altruism, as demonstrated by the imperfect crowding-out phenomenon that is commonly observed (see Section 5.2 and Section 5.3 below). We find that contributions in the Patron Game are high (about 22% of the endowment), though significantly lower than in a classic VCM (31.1%). Among the determinants of the individual provision of the public good, demand effects (as induced by the allowed action space) and the warm glow of giving together explain contributions almost entirely, with the former playing the most prominent role.

The Patron Game differs from a classic Dictator Game because of several features such as ex-ante equal payoffs and the presence of an efficiency multiplier. Efficiency concerns do not have a sizable impact, however. When the efficiency multiplier is removed contributions aimed at the individual provision of a public good are much higher than that found in the literature when contributions simply represent a transfer of money. Our interpretation is that even when pursued at the individual level the provision of a public good retains its social nature, which solicits higher contributions. Finally, results in our experiment are not driven by errors and confusion.

The outline of the paper is as follows. In Section 2 we describe the Patron Game. Section 3 explains the design of the experiment and the way in which we test the individual determinants of voluntary contributions and how we disentangle demand effects from impure altruism. Section 4 summarizes the procedures. Results are presented in Section 5, while Section 6 concludes.

2. The Patron Game

In the Patron Game subjects play in groups of N players, with each subject i receiving the same endowment at the beginning of each round. The feature that distinguishes this game from the traditional VCM is that only one player, the patron, can decide how to allocate his endowment. The allocation alternatives are the same available in a classic VCM. The first is an individual account with a 1:1 return. The second is a public account characterized by a production function F = mc_p, where c_p is the contribution of the patron, which is multiplied by the efficiency factor m ≥ 1, with the additional amount being provided by the experimenters. The amount F is then divided in equal parts among all the N participants.

The N − 1 subjects who are not given the opportunity to allocate their endowment play a passive role, as their contribution is equal to zero by construction. They simply receive their share of the public account on top of their initial endowment. The individual payoff of the patron (π_p) in every period is therefore a linear function of his individual contribution (c_p) to the fund:

$${\pi }_p=e_p-c_p+(F/N).$$

The condition that makes free riding a dominant strategy is the same as in a VCM, i.e., m/N < 1. However, the patron is aware that the co-players do not have the possibility to contribute, and therefore his choice intrinsically differs from that in a classic VCM in which the opponents choose to free ride. In [5] subjects indicate how much they would be willing to contribute to the public good for each of 21 average contribution levels of the other group members. The authors report extremely low contributions (less than 5% of the endowment) when the opponents contribute zero. Despite the same monetary incentives, in [5] not contributing stems from a deliberate choice, thereby signaling intentions that cannot play any role in the Patron Game.

Some features of the Patron Game are similar to those of a Dictator Game. In fact, considerations about the behavior of the opponents are eliminated and there is only one active player who dictates the final distribution of payoffs. However, the characteristics that differentiate the two games are more relevant in our view. First, in the Patron Game there are multiple recipients. Second, the technology that transforms the patron’s contribution into group payoffs is the same as a traditional VCM. Third and foremost, the Patron Game is not framed as a simple transfer of money, but as the individual provision of a public good that benefits all the group members alike.

The Patron Game is not the first attempt to remove strategic interaction from a VCM. Reference [9] introduce a treatment in which, after a Regular Condition à la [10], every player is matched with a group of computers making predetermined and known choices. In this framework, subjects have no chance of benefitting themselves or other players by cooperating. Nevertheless, the average contribution in the Computer Condition (28.6%), although significantly lower than in the Regular Condition (52.8%), is surprisingly high. Both conditions show a decreasing pattern of contributions. Although the authors acknowledge that demand effects could confound the results, they attribute the observed behavior entirely to confusion, thereby implying that confusion can account for about half of the contributions. Using a similar design, Ferraro et al. [11,12] report lower contributions: 18% and 24% with human opponents and 9.6% and 12% with virtual players, respectively. These results confirm that approximately half of the contributions in a VCM are due to confusion and demand effects.4

The Patron Game differs from the framework of [9,11] along several dimensions. First, by involving only human opponents the Patron Game preserves the importance of other-regarding preferences. Second, by preventing the opponents from contributing, it lowers the complexity of the task reducing the role played by confusion.

The Patron Game provides a flexible framework that can be exploited for several additional purposes that are not investigated in this paper. For instance, the role played by strategic interaction can be analyzed increasing the number of active players.5 Other factors that can be easily manipulated include the strength of the efficiency multiplier and the heterogeneity of the endowments.6

3. Design

The first goal of our paper is to assess the difference in the level of contributions when the public good is provided individually rather than collectively. Therefore, we also run a standard VCM to compare the results with the outcomes of a baseline Patron Game. In both conditions we use groups of 4 subjects in a partner matching, imposing an efficiency multiplier equal to 1.5. For the sake of comparability, and in particular to allow possible learning processes to take place, we implement a repeated version of both games paying the sum of the payoffs in the 10 periods.

We then manipulate the Patron Game in several ways to identify the individual determinants to contribute, borrowing from the literature on VCM. In particular, we test the role of three determinants: (a) the expectation the patron feels about having to contribute as replicated by demand effects in the laboratory, (b) the mere act of giving (the so-called warm glow or impure altruism), and (c) efficiency concerns. At the end of this section we also describe our strategy to check that results are not driven by confusion and errors.

While the role played by efficiency concerns can be analyzed through a straightforward manipulation of the efficiency factor in the Patron Game, the empirical strategy necessary to identify the other two determinants, (a) and (b), needs to be carefully explained.

Voluntary contributions can be influenced by the perceived expectation about their fair level hold by third parties, something that can counterbalance the self-interested decision to keep the whole endowment. The experimental instructions as well as the signals the subjects receive from their peers play an active role in shaping such expectations. While usually considered as an unwanted companion of the experimental activity, this type of demand effect may instead be an interesting variable to analyze, in that it mimics the fact that agents contribute because they are expected to do so.

Following the classification proposed by [19], horizontal demand effects require strategic interaction and therefore they cannot play any role in the Patron Game. In our experiment, a cognitive demand effect can instead be induced by the information provided to the participants by the experimenter. Social demand effects, i.e., what the patron perceives as expectations of the experimenters and of the other players about the appropriate decision to make, are also present.

We exploit the particular demand effect represented by the shape of the opportunity set. Subjects may decide to contribute a positive amount to the public good because the choice they face (i.e., how much to contribute) implicitly conveys the expectation of a positive contribution. This expectation may cause the selfish option of keeping the whole endowment to be perceived as too extreme to be selected, even if allowed in principle. An observationally equivalent motivation could be that the shape of the opportunity set induces the subjects to focus on the act of giving, since it is the only decision they can make [20].

This type of demand effect can be eliminated, or at least greatly attenuated, by using an experimental design that includes both giving and taking as options, thereby reducing the salience of the choice set as a semantic cue. The use of this manipulation in the literature has systematically shown sizable effects. References [21,22] find a significant shift toward more selfish decisions when the donor also has the possibility of taking from the recipient in a Dictator Game. In the public good framework, this demand effect has been analyzed in a similar manner. Reference [23] compares a classic VCM with a payoff-equivalent Take condition assigning all the initial endowments to the public account and asking subjects to decide how much they wish to withdraw and allocate to their private accounts. He finds higher contributions in the Give condition.7 Reference [27] report that these demand effects causally affect second-order beliefs about contributions, i.e., how much subjects believe that others (the opponents as well as the experimenters) expect them to contribute. Reference [27] also show that second order beliefs significantly correlate with actual decisions, although no causal inference can be derived. In any case, this result supports the perspective of beliefs as a medium between frames and decisions, i.e., that subjects contribute also because expected to do so.8 Reference [28] extend the Give vs. Take framework implementing a convex combination of the two conditions by splitting the endowment between the private and the public account. By doing so, they make available at the same time to the subjects both the option to give and the option to take. In what follows we will refer to this framework as Give and Take (GITA).

Both the Take and the GITA conditions can be easily implemented within the Patron Game. To accomplish this task, we define the initial size of the public account (PA) as the amount of money (out of 100 cents) not assigned to the patron at the beginning of every trial:

PA = (100 − e_p),

where e_p is his actual endowment. The set of decisions of the patron, c_p, is defined in the negative domain as well, allowing him to either add to (c_p > 0) or withdraw from (c_p ≤ 0) the public account:

c_p ∈ [−PA, e_p].

In this case, the payoff of the patron can be rewritten as:

π_p = e_p − c_p + 0.375 × [PA + c_p].

The baseline Patron Game is the limit case in which e_p = 100, PA = 0, and therefore contributions are restricted to be non-negative. A payoff irrelevant Take condition could be implemented as the opposite situation in which e_p = 0 and PA = 100, which imply that c_p ≤ 0. However, any value of e_p between 0 and 100 can be chosen without changing the material payoffs and giving rise to a continuum of GITA treatments in which the domain of contributions contains both positive and negative values.9 A GITA treatment that includes taking as an option exogenously weakens the expectations to contribute, thereby reducing the salience of this demand effect.

Unfortunately, a comparison between the Patron Game and a GITA treatment does not allow us to identify the causal impact of demand effects, because the shift in money from the endowment of the patron to the public account creates a confounding factor via impure altruism, another determinant that we want to identify.

Impure altruism, also called the warm glow of giving [29], sates that subjects enjoy passing money to others. It differs from pure altruism because the utility function contains not only the payoff of the other members of the group but also an additional argument (c_p) representing the value of the contribution as an act of giving: u_p (π_p, π_-p, c_p).

Pure altruism predicts that subjects should care about final payoffs only. For instance, when comparing two different distributions of the same amount of money, e.g., 18-2 and 15-5 in a Dictator Game, subjects should give 3 units less in the 15-5 condition than in the 18-2 treatment (or zero if they passed less than 3). An implication of impure altruism is instead the imperfect crowding out of contributions when (part of) the endowment is shifted from the donor to the recipient, or in our case from the private endowment of the patron to the public account. There is convincing evidence in dictator games showing that, when part of the endowment is shifted from the donor to the recipient, contributions decrease but less than proportionally.10

Impure altruism and demand effects are therefore confounded when manipulating the choice set of the Patron Game into a GITA condition. In what follows we describe in detail the treatments that we implement, stressing whenever necessary how they help to circumvent the problem just described. Our experimental design allows us to identify the two determinants in a clean way, something that improves upon the existing literature. The summary of all treatments is reported in

Table 1. List of Treatments.

Treatment	K	m	ep	Choice Set
Patron Game	1	1.5	100	[0,100]
VCM	4	1.5	100	[0,100]
NOEFF	1	1	100	[0,100]
GITA20	1	1.5	80	[−20,80]
GITA40	1	1.5	60	[−40,60]
PG20	1	1.5	80	[0,80]

Note: The table emphasizes the changes in the parameters with respect to the baseline Patron Game, as presented in Section 2 and implemented with an efficiency factor m = 1.5 and the same endowments (e = 100) for all the N = 4 players. Independent observations correspond to each patron when K = 1 and to the average contribution of the group in the VCM.

.

3.1. Demand Effects

A clean test of demand effects requires to hold constant the distribution of the 100 cents between the endowment of the patron and the public account, to avoid the confounding factor constituted by imperfect crowding-out. At the same time, it is necessary to reduce the salience of demand effects by the possibility of taking. Hence, the following two treatments are implemented to isolate the role played by demand effects:

• GITA20:e_p = 80, e_-p = 100, PA = 20, c_p = [−20, 80]
• PG20:e_p = 80, e_-p = 100, PA = 20, c_p = [0, 80].

GITA20 is a Give and Take condition with an endowment of 20 in the public account and is payoff equivalent with respect to the baseline Patron Game. PG20 is a Patron Game with the same endowment (20) in the public account but without the option of taking. Please note that the PG20 and the baseline Patron Game are not payoff equivalent, because those who contribute zero in PG20 could indeed make this choice because their opportunity set is left-censored by the impossibility of taking.11 Nevertheless, the comparison between PG20 and GITA20 provides a clean test of demand effects because those who contribute more than zero in PG20 should be unaffected by this experimental manipulation. In contrast, if demand effects matter, also those who contribute a positive amount in PG20 will decrease their contribution when the possibility of taking is made available in the counterfactual situation represented by the GITA20. Given our between-subject design we will use a Fisher Exact Test to assess whether the fraction of subjects making strictly positive contributions significantly differs across the two treatments.

3.2. Warm Glow of Giving (Impure Altruism)

Another way to explain that impure altruism can be confounded with demand effects is to say that the utility of passing money is higher in the “only Give” condition because subjects feel stronger expectations to contribute.12 A clean test of the warm glow hypothesis requires therefore a comparison between treatments in which demand effects play a similar role. Hence, we select two conditions in which taking is always allowed:

• GITA20:e_p = 80, e_-p = 100, PA = 20, c_p= [−20, 80]
• GITA40:e_p = 60, e_-p = 100, PA = 40, c_p = [−40, 60].

We cannot claim that demand effects are eliminated in these two treatments because subjects may still be reluctant to select elements from the extreme ends of their choice set. However, what we need is simply that demand effects stay constant across the two conditions, something that can be reasonably assumed given that the possibility of taking is maintained. In contrast, the comparison of the choices in the GITA20 and in the baseline Patron Game would entail the same shift in the endowments but the impossibility of taking in the baseline Patron Game would confound the results.

3.3. Efficiency Concerns

The choice to contribute in the Patron Game may also be driven by efficiency concerns. In other words, subjects may contribute because the group gains 1.5 € for every euro of private contribution.13 Note; however, that positive contributions in the Patron Game increase the payoff of the other group members at the expenses of the patron, whose earnings decrease by construction. In other words, efficiency considerations do not allow the players to reach a Pareto superior outcome.

The NOEFF treatment implements the Patron Game with the efficiency multiplier equal to one ceteris paribus, allowing us to test the impact of efficiency concerns. This experimental manipulation renders the return of the contribution lower than in the baseline Patron Game. The NOEFF treatment is payoff-equivalent to a Dictator Game played with equally endowed multiple recipients.

3.4. Confusion

Confusion and decision errors result from an imperfect understanding of either the rules of the game or of the incentive structure and have been shown to play an important role in VCM settings [34,35]. The Patron game is simpler than the classic Public Good game, and understanding that the dominant strategy is to contribute zero should also be easier.

Nevertheless, we want to make sure that results are not driven by positive contributions made by mistake and therefore in Section 5.5 we run two types of robustness check. On the one hand we comment on the replication of the analysis based only on the last 5 periods of each treatment, when a learning process, if there, should have converged. On the other hand, we exploit the answers to two questions designed to detect a self-aware luck of understanding. The first question asks active players to indicate their level of comprehension of the game by choosing between four different levels ranging from “no comprehension” to “perfect comprehension”. The second question asks the patrons to select their level of agreement with the statement “I have contributed randomly” with answers that may range from 0 (strongly disagree) to 4 (strongly agree).

4. Procedures

The experiment is composed by 22 sessions that took place at the University of Parma between January 2011 and May 2012. A total of 440 undergraduate students were recruited from different degree programs. They had neither been exposed to coursework in Economics nor participated in other experiments involving social preferences. Every subject took part in only one treatment. Although inefficient in terms of number of observations, we chose a pure between-subject because we wanted to avoid that in a within-subject design differences in the opportunity set across repeated choices might trigger additional demand effects that could confound the results.

In all treatments, the game was played by groups of four subjects who were randomly and anonymously matched at the beginning of the experiment and then followed a partner design over the course of the 10 repetitions. Each subject’s role (active vs. passive) was also fixed during the experiment. A total of 140 subjects played an active role (20 in each condition of the Patron Game, and 40 in the VCM). We chose not to increase the number of observations by the strategy method because role uncertainty would imply acting behind a veil of ignorance and would likely alter subjects’ decisions (see for instance [36]).

At the end of each period, all subjects received information about the contribution of the active subject(s) in their group. The average payoff, including a 2.5 € show-up fee, was 12.84 €. All sessions were run using z-Tree [37] and lasted between 35 and 45 min.

5. Results

In this section, we first compare the results of the Patron Game with a classic VCM, then we show how demand effects and the warm glow of giving affect the contributions, disentangling the two effects. We then analyze efficiency concerns and we finally check the robustness of results to confusion and errors. Throughout the paper we refer to average contributions meaning the average choice of each independent observation (each patron, or the average of the group in the VCM) across the 10 periods. Differences across conditions are assessed non-parametrically (Mann-Whitney test when not specified otherwise) comparing the distribution of average contributions.

5.1. Patron Game vs. VCM

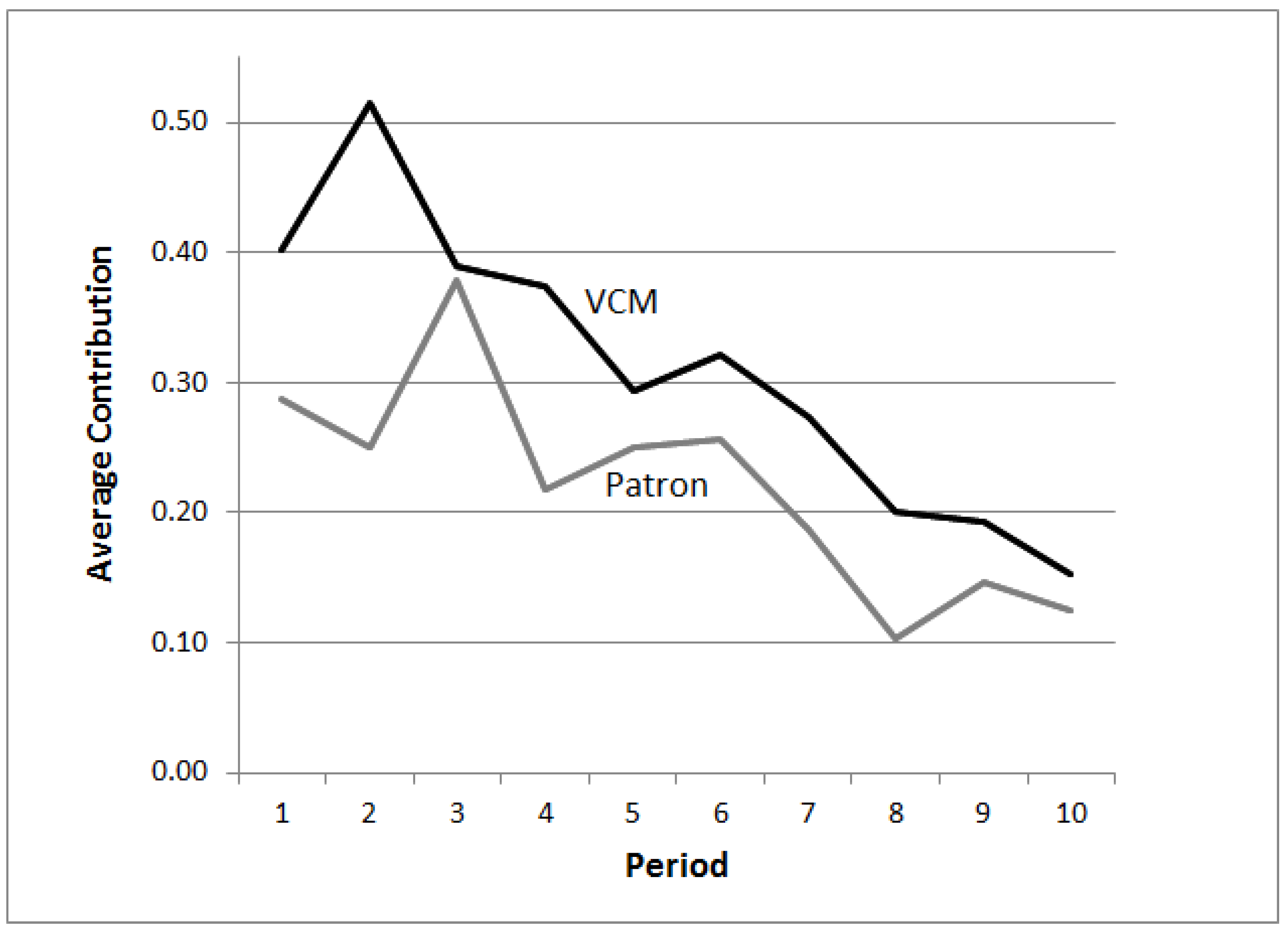
In the Patron Game, there is only one active player who chooses how much to contribute to the public good. Strategic interaction has been removed so that conditional cooperation and reciprocity do not matter. Full contribution cannot Pareto dominate the selfish option, and any positive contribution results in unfavorable inequality. Contributions must be driven by unconditional other-regarding preferences, demand effects, efficiency concerns, or confusion. We find that the average contribution is high (22% of the endowment), although significantly lower than in the VCM (31.1%) as reported in

Table 2. Average contributions: VCM vs. Patron Game.

Treatment	N. Indep. Observ.	Average Contribution				Mann-Whitney
		Mean	St. Dev.	Min	Max
VCM	10	0.311	0.077	0.195	0.457	p = 0.006
Patron	20	0.220	0.179	0	0.555

Note: Average contribution in the 10 periods across independent observations as a fraction of the endowment.

.

The effect of removing strategic interaction is significant but small because it accounts for less than one-third of the contributions in the VCM. The fact that contributions remain high when most of the determinants have been removed is not a new result in the literature (see, for instance, [9,11]). The difference is that in our experiment the active player benefits human subjects, and not automata, and therefore contributions should also reflect other-regarding preferences.

Another result worth mentioning is the decreasing pattern of contributions, similar to that typically observed in Public Good Games (see Figure 1). The decline of contributions is usually related to strategic interaction or to learning from opponents’ choices, a possibility that the Patron Game rules out by construction. Moreover, if a subject intends to contribute a certain amount over the course of the Patron Game, the pattern chosen to do so is completely irrelevant (a constant fraction in every period vs. concentrating the contribution in one period, at the beginning or at the end, etc.).

Although similar at first glance, the decreasing patterns in the two treatments are indeed different in nature. An analysis at the individual level shows that in the Patron Game subjects undertake a much more erratic behavior, as shown by the higher variance of individual decisions in Table 1. Moreover, about half of the subjects display a significant downward trend in the VCM, while this happens to only 25% of the patrons. At the aggregate level, a downward trend explains half of the variance of the contributions in the Patron Game as compared to the VCM. The decreasing pattern in the Patron Game emerges as a composition effect of distinct and uncorrelated behaviors, rather than a systematic pattern at the individual level as in the VCM. Besides the few subjects displaying a significant downward trend, also those who concentrate their contributions in one or few periods usually choose to do so in the first half of the game. As explained in Section 5.5 below, however, the higher contributions in the first periods cannot rationalize the following results as an effect of confusion. Therefore, in what follows we will base our analysis on the average contributions in all the 10 periods without further analyzing the time pattern.

5.2. Demand Effects

As explained in Section 3.1, a clean test of demand effects requires a comparison between two treatments in which the initial distribution of money between the patron’s endowment and the public account is the same, to avoid that impure altruism may confound the results. In both the GITA20 and the PG20, the value of the public account is equal to 20, while the endowment of the patron is equal to 80. The difference is that in the PG20, the patron does not have the opportunity to take from the public account. The obvious consequence is that, almost by construction, the average final value of the public account turns out to be significantly higher in the PG20 (31.1 vs. 15.6, Mann Whitney p < 0.001).

To test for the role played by demand effects; however, we need to focus on the choices that are not restricted by the opportunity set. Subjects with a contribution equal to zero in the PG20 might have preferred to take something from the public account had they been given the opportunity to do so. In contrast, subjects who opted for a strictly positive average contribution in the PG20 should not be affected by the possibility of taking because they did not exploit the opportunity of contributing a lower amount even when such a decision was possible.

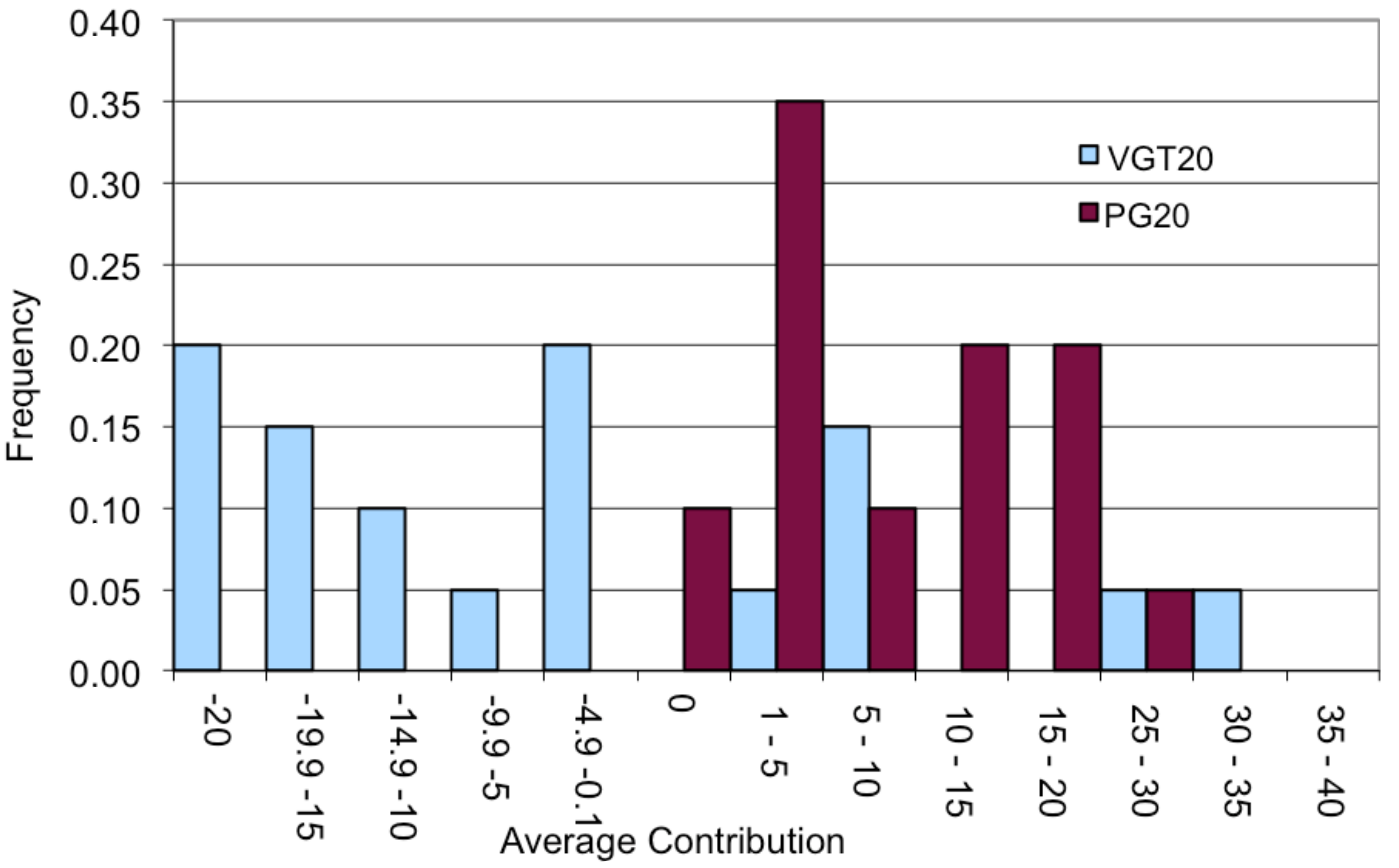
The same argument in our between-subject design predicts that the fraction of subjects contributing a strictly positive amount should be the same in the two treatments if demand effects play no role. Conservatively, we regard as positive the contributions higher than 5 cents on average to exclude positive contributions possibly made by mistake. Figure 2 clearly shows that the distribution of choices differs across conditions. 55% of subjects in the PG20 contributed more than 5 cents while only 25% contributed more than 5 cents in the GITA20. A one-sided Fisher Exact Test shows that this difference is significant at 5.3% level. The difference across treatments would be even stronger (p < 0.001) had we used the contributions higher than zero.

What happens is that the possibility of taking decreases the contributions across the board, not only those truncated by the opportunity set. In other words, when the possibility of taking reduces the perceived expectation of having to contribute a positive amount, we see a shift of the entire distribution of choices to the left.

One could argue that the structure of the Patron Game magnifies the role of demand effects because expectations about contributions are concentrated on one subject instead of being shared among all the group members as in the VCM. Indirect evidence that this is not the case may be derived from [16], who analyze a Patron Game with heterogeneous endowments, where social demand effects should be strengthened by ex-ante inequality. When starting with an endowment threefold greater than that of their groupmates the patrons do not contribute significantly more than in the baseline Patron Game (23.7%, Mann-Whitney test p = 0.871). In other words, subjects seem to react in a dichotomous way to the presence of demand effects without reacting so much to their intensity.

Our results confirm that demand effects are important in shaping voluntary contributions. This conclusion is well aligned with prior results reported in the literature about VCM [23,27,28,38]. The original contribution of our paper is to show that this effect it is not confounded with that of the warm glow of giving. To stress this point let us analyze what would emerge comparing the GITA20 with the Patron Game instead of with the PG20. Considering any amount of money not taken as contributed, we see that the average contribution in the two treatments does not significantly differ (see

Table 3. Average value of the public account: Patron Game vs. GITA20.

Treatment	N. Indep. Observ.	Value of the Public Account				Mann-Whitney
		Mean	St. Dev.	Min	Max
Patron Game	20	0.220	0.179	0	0.555	p = 0.240
GITA20	20	0.156	0.158	0	0.544

Note: Average across the 10 periods of the value of the public account after the patron’s contribution.

).

Our comparison could easily represent a false negative due to the small number of observations, but our findings are similar also in terms of point estimates to the results of [28]. In any case, no causal inference can be derived from the direct comparison of these two treatments, because there are two opposite effects at work. On the one hand, moving from the Patron Game to the GITA20 eliminates (or at least substantially decreases) demand effects, possibly causing a reduction in the average contribution. On the other hand, transferring money from the endowment of the patron to the public account should have an opposite effect due to the imperfect crowding out phenomenon, as confirmed by the results in the next section. Therefore, it is a composition effect given by the sum of these two opposite effects that is actually measured by the comparison between the Patron Game and the GITA20.

5.3. Warm Glow

We propose a clean test of impure altruism by manipulating the distribution of the same amount of money between the patron and the public account while maintaining the opportunity of taking, thereby neutralizing possible differences in demand effects. If impure altruism does not play a role, subjects should pass on average 20 cents less in the GITA40 than in the GITA20. In the GITA40 the average decision of the patrons is to take on average 14.6 cents out of the 40 in the Public Account; in the GITA20, the active players take on average of 4.4 cents out of 20 (see

Table 4. Average contributions: GITA20 vs. GITA40.

Treatment	N. Indep. Observ.	Average Contribution				Mann-Whitney
		Mean	St. Dev.	Min	Max
GITA20	20	−0.044	0.158	−0.2	0.344	p = 0.088
GITA40	20	−0.146	0.179	−0.4	0.310

Note: Average contributions in the 10 periods as a percentage of the sum of the public account and the patron’s endowment.

). Subjects take significantly more when they can do so, but the difference is much smaller than 20.

This evidence supports the imperfect crowding out hypothesis, because in case of perfect crowding out we should have seen a decrease in contributions equal to 20 cents in the GITA40. The reason is that in the GITA40 the endowment of the patron is 20 cents lower than in the GITA20, while the value of the account at the beginning is 20 cents higher. Therefore, a contribution 20 cents lower would lead to the same final value of the public account. In contrast, we see a reduction in the average contribution of only 10.2 cents, about 50% of the amount transferred from the endowment of the patron to the public account. Consequently, we find that the value of the public account is significantly higher in GITA40 than in GITA20 (25.4 vs. 15.6 cents).

This result also allows us to provide a rough quantitative estimate of the importance of demand effects. Assuming a constant warm glow of giving across treatments allows us to transpose the imperfect crowding out observed between GITA20 and GITA40 into an equivalent effect between the GITA20 and the baseline Patron Game. This exercise predicts that the average contribution in the Patron Game should be only 10.2 cents (instead of 20 cents) higher than in the GITA20 and should therefore be equal to −0.044 + 10.2 = 5.8 cents. Furthermore, if the determinants of contributions are additive allows us to estimate the magnitude of demand effects in the order of 16.2 cents, i.e., the difference between the predicted contribution of 5.8 cents in the Patron Game and the observed decision to contribute 22 cents on average.

5.4. Efficiency Concerns

Setting the multiplier of the public account equal to one decreases the average contribution to 18.4 percent as compared to 22 percent in the baseline Patron Game, with the difference that is not statistically significant possibly because of the small number of observations (see

Table 5. Average contributions: Patron Game vs. NOEFF.

Treatment	N. Indep. Observ.	Average Contribution				Mann-Whitney
		Mean	St. Dev.	Min	Max
Patron Game	20	0.220	0.179	0	0.555	p = 0.417
NOEFF	20	0.184	0.191	0	0.800

Note: Average contribution in the 10 periods as a percentage of the endowment.

).14

It is worth noting first that contributions in the NOEFF treatment are surprisingly high if compared to a very similar Dictator Game in the literature. Reference [39] report that in a Dictator Game characterized by an equally endowed recipient only 25% of the donors passes a positive amount ranging from 7% to 12% of their endowment.15 We find very different results, as 75% of the patrons contribute a positive amount corresponding on average to 24.4% of their endowment.16 We interpret this striking difference as the additional role played by the public good framing as compared to that of a payoff-equivalent transfer of money.

The small difference in contributions between the NOEFF condition and the baseline Patron Game also suggests that a larger efficiency factor is necessary to substantially increase contributions when the public good is individually provided. The reason could be that in a classic VCM joint contributions can sizably inflate the group payoffs through the efficiency factor (e.g., in our VCM from 400 to 600 under full contribution), at the same time allowing to reach Pareto superior outcomes. In the Patron Game group payoffs are instead bounded between 400 and 450, and Pareto improvements are impossible. Not surprisingly, efficiency factors in the order of magnitude usually implemented in lab experiments may therefore have a larger effect in a VCM than in the Patron Game.

5.5. Confusion

Confusion and decision errors stem from an imperfect understanding of the rules of the game and/or the incentive structure. The subjects may contribute because they do not understand that the dominant strategy is to keep their endowment and to withdraw from the public account when possible. We believe that removing strategic interaction makes the incentives of the only active player much simpler to understand in the Patron Game. Nevertheless, we check that our results are not driven by confusion following two approaches.

First, we rely upon self-reported information about subjects’ lack of understanding. We build two proxies for confusion: one dummy variable for patrons who indicate “no comprehension” of the rules of the game and another for players who agree or strongly agree with the statement “I have contributed randomly.” The evidence from an OLS regression confirms that the first dummy does a good job in capturing the effect of confusion, since a bad comprehension of the game is positively and significantly correlated with the level of the contributions (see

Table 6. Poor comprehension of the game and average contributions.

	Avg. Contribution (All Rounds)	Avg. Contribution (First 3 Rounds)	Avg. Contribution (Last 3 Rounds)
Poor Compr.	0.180 *** (0.063)	0.274 *** (0.083)	0.111 (0.068)
Constant	0.173 *** (0.016)	0.206 *** (0.022)	0.122 *** (0.018)
Adj. R-squared	0.0665	0.0901	0.0162
N	100	100	100

Note: Standard Errors in brackets. Significance levels: *** = 1%.

).17

The dummy captures an increase in the average contributions by as much as 18 cents in the pooled sample of all the Patron Game treatments. Moreover, the effect of confusion is much stronger (27.4 cents) at the beginning of the game, while it is lower and not significantly different from zero in the last three rounds as players become more familiar with the game.

The fraction of “confused” players in the different treatments is always low, ranging from zero to 15%, with an average value of 6.5%. Not surprisingly, our data consistently show that confusion affects the average contributions but not the results across conditions. For instance, the set of interaction terms between the poor comprehension variable and the treatment dummies turns out to be not significant (except for GITA20) when included in a regression explaining the average contributions (see

Table A1. Poor comprehension, treatment dummies and average contribution.

	Avg. Contribution (All Rounds)
NOEFF	−0.0386 (0.053)
GITA40	0.0406 (0.0532)
PG20	−0.0918 (0.0526)
GITA20	−0.0672 (0.2057)
Poor Compr. * Patron	0.0959 (0.0998)
Poor Compr. * NOEFF	0.1724 (0.1188)
Poor Compr. * GITA40	0.1436 (0.1636)
Poor Compr. * GITA20	0.3565 ** (0.1636)
Constant	0.2057 *** (0.0386)
Adj. R-squared	0.0904
N	100

Note: Standard Errors in brackets. Significance levels: *** = 1%, ** = 5% and * = 10%. Omitted dummy: Patron Game. The interaction term with the PG20 treatment is missing because there are no subjects reporting a bad comprehension in this condition.

in Appendix B). Furthermore, all the results displayed in the earlier sections are robust to the exclusion of the subjects reporting a poor comprehension of the game (see

Table A2. Average value of the public account: Patron Game vs. GITA20 with the exclusion of the subjects reporting a poor comprehension of the game.

Treatment	N. Indep. Observ.	Value of the Public Account				Mann-Whitney
		Mean	St. Dev.	Min	Max
Patron	17	0.205	0.179	0	0.555	p = 0.259
GITA20	19	0.113	0.140	0	0.544

,

Table A3. Average contributions: GITA20 vs. GITA40 with the exclusion of the subjects reporting a poor comprehension of the game.

Treatment	N. Indep. Observ.	Average Contribution				Mann-Whitney
		Mean	St. Dev.	Min	Max
GITA20	19	−0.087	0.140	−0.2	0.344	p = 0.042
GITA40	19	−0.154	0.181	−0.4	0.31

and

Table A4. Average contributions: Patron Game vs. NOEFF with the exclusion of the subjects reporting a poor comprehension of the game.

Treatment	N. Indep. Observ.	Average Contribution				Mann-Whitney
		Mean	St. Dev.	Min	Max
Patron	17	0.205	0.179	0	0.555	p = 0.427
NOEFF	18	0.167	0.194	0	0.800

in Appendix B).

Restricting our attention to the baseline Patron Game, poor comprehension characterizes 15% of the subjects, whose average contribution is 9.5 cents higher. Differently from the literature about VCM, we find that in the Patron Game the effect of confusion is minimal, accounting for about 1.4 out of the 22 cents of the average contribution.

Although it significantly correlates with the actual contributions, a self-reported measure of bad comprehension is not fully reliable because there may be subjects who think they understood the game but actually did not, or who felt confused but are reluctant to admit it. The second and complementary approach relies upon subjects’ choices only and consists in replicating the analysis of the earlier sections using last 5 periods only.

Figure 1 shows that average contributions in the baseline Patron Game drop substantially over time even though subjects are making the same decision without any relevant information being revealed along the way. One could then reasonably argue that if the downward trend is due to a learning process of the dominant strategy, then the average contributions may be significantly affected by initial confusion (with or without being self-reported). Extending a similar argument to the other treatments would potentially leave space for confusion to drive the results presented before.

Replicating the analysis using only the contributions in the last 5 periods shows that this is indeed not the case (see

Table A5. Average value of the public account in the last 5 periods: Patron Game vs. GITA20.

Treatment	N. Indep. Observ.	Value of the Public Account				Mann-Whitney
		Mean	St. Dev.	Min	Max
Patron	20	0.163	0.147	0	0.44	p = 0.385
GITA20	20	0.121	0.122	0	0.4

,

Table A6. Average contributions in the last 5 periods: GITA20 vs. GITA40.

Treatment	N. Indep. Observ.	Average Contribution				Mann-Whitney
		Mean	St. Dev.	Min	Max
GITA20	20	−0.079	0.122	−0.2	0.2	p = 0.152
GITA40	20	−0.190	0.213	−0.4	0.284

and

Table A7. Average contributions in the last 5 periods: Patron Game vs. NOEFF.

Treatment	N. Indep. Observ.	Average Contribution				Mann-Whitney
		Mean	St. Dev.	Min	Max
Patron	20	0.163	0.147	0	0.44	p = 0.741
NOEFF	20	0.181	0.244	0	1

in Appendix B). All the results presented in Section 5.2, Section 5.3 and Section 5.4 hold qualitatively intact in terms of both sign and significance. Results are similar also from a quantitative perspective, with the only appreciable difference being a slightly weaker role played by impure altruism.

These robustness checks confirm our conjecture that the absence of strategic interaction makes it easier to learn the dominant strategy in the Patron Game, thereby genuinely reducing confusion as compared to a VCM in which the relationship between contributions and realized earnings is mediated by the decision of the opponents.

6. Conclusions

This paper investigates the individual provision of a public good and the underlying motivations. We do so using the Patron Game, a framework that eliminates strategic interaction considerations and in which the individual return to the contribution is negative. A comparison with a classic linear VCM shows that average contributions are significantly lower in the Patron Game (22% vs. 31% of the endowment). The average contribution in the Patron Game is high, however, considering that it can only be explained by individual determinants such as unconditional other-regarding preferences, demand effects, the warm glow of giving, and efficiency concerns.

Our experimental design assesses the importance of such individual determinants of the individual provision of the public good, also providing an innovative methodological contribution towards disentangling demand effects from the warm glow of giving. Our results show that these two factors together explain contributions almost entirely, with demand effects playing the most prominent role. Our interpretation is that subjects contribute mainly because they perceive that they are expected to do so.

Another interesting result is that when the public good is individually provided without an efficiency factor, contributions are much higher than in a comparable Dictator Game in which there is a simple transfer of money to an equally endowed recipient as in [39]. Efficiency concerns induce a minor change in the average contributions, suggesting that large efficiency factors are needed to substantially increase contributions in this framework.

Results in our experiment are not driven by errors and confusion. A self-reported bad comprehension of the game is associated with significantly higher contributions but the magnitude of the effect is negligible and similar across treatments. Moreover, our results are confirmed restricting the analysis to the last periods of the game, when learning already took place.

The Patron Game is a stylized framework that is suitable to analyze forms of contributions to a public good restricted to a single provider. Volunteering activities and Open Collaboration projects are the most representative examples. Although not straightforwardly exportable in the field, our results suggest why these activities are so widespread despite entailing a negative individual return. The prominent reasons behind such contributions seems to be the willingness to give something to others and a form of social demand effect about the individual contribution. In other words, individual contributions might respond to the expectations of a community about contributing one’s fair share towards building a better society.