How to Analyze Models of Nonlinear Public Goods

Abstract

Public goods games often assume that the effect of the public good is a linear function of the number of contributions. In many cases, however, especially in biology, public goods have nonlinear effects, and nonlinear games are known to have dynamics and equilibria that can differ dramatically from linear games. Here I explain how to analyze nonlinear public goods games using the properties of Bernstein polynomials, and how to approximate the equilibria. I use mainly examples from the evolutionary game theory of cancer, but the approach can be used for a wide range of nonlinear public goods games.

1. Introduction

1.1. Public Goods

Fifty years after Garret Hardin’s “Tragedy of the Commons” [1], the problem of collective action remains one of the most influential concepts in science: free-riding on the contributions of others enables free-riders to thrive at the expense of cooperators. Examples can be found in almost all areas of human knowledge, from biology to economics, from selfish genetic elements [2], microbes secreting diffusible molecules [3] and cancer cells secreting growth factors [4,5] to cooperative hunting in mammals [6] and, indeed, the exploitation of shared natural resources described by Hardin [1]. The major transitions in evolution are considered solutions to social dilemmas of this kind [7].

The problem of cooperation can be modelled by games with at least one Pareto inefficient equilibrium: an alternative outcome exists in which at least one player could have a higher payoff without reducing any other player’s payoff (a Pareto improvement is possible; hence the inefficiency); no one, however, has an incentive to change their behavior (hence the equilibrium). The Prisoner’s Dilemma (PD) [8] is the most famous among such games, and it has been used extensively to describe the problem. The game of Chicken [9] (also known as the Hawk–Dove game [10] or the Snowdrift game [11]) has also been used to study cooperation.

1.2. Multiplayer Games and Nonlinear Benefits

The social dilemma described by Hardin [1] is essentially a multiplayer version of the PD (NPD [12,13]): individuals can be cooperators or defectors; only cooperators pay a contribution; all contributions are summed, the sum is multiplied by a reward factor and redistributed to all individuals. It is well-known and easy to prove that in this game, if group size is large enough, pure defection is the only stable outcome. The n-person prisoner’s dilemma (NPD) has become a synonym for social dilemma and the tragedy of the commons, at least in biology [14] (while in economics it is understood [15] that this is not necessarily the case). This is unfortunate, because very few cases of public goods in biology can actually be described as an NPD. The reason is that the NPD assumes linear benefits: the effect of each contribution is additive. In other words, the public good is a linear function of the number of cooperators.

In biology, however, almost everything is nonlinear. The effect of biological molecules is generally a sigmoid function of their concentration (usually described by the Hill equation [16,17,18]). A case in point is the production of growth factors by cancer cells: since they are diffusible in the extracellular matrix, growth factors are public goods that can be exploited by producer and non-producer cells. In cancer research, game theory was introduced [19,20] using a version of the game of Chicken. Subsequent papers using game theory in cancer research [21,22,23,24,25,26,27,28] were extensions (with up to four strategies) of this game, and games with pairwise interactions continue to be used in cancer research [29,30]. The production of diffusible factors by cells, however, is a clear example of collective interactions rather than pairwise, because the effect of secreted molecules is not limited to one other cell. The dynamics of growth factor production therefore should be modelled using games with collective interactions [31,32]. It is also well known that the effect of growth factors on cell growth is generally a sigmoid function of its concentration. In order to describe cooperation for the production of growth factors in cancer biology, therefore, we must use multiplayer games with collective interactions for the production of nonlinear public goods—in short, nonlinear public goods games.

1.3. Rationale of the Paper

The problem with nonlinear public goods games is that they are hard to analyze. While games with concave and convex benefits can be studied analytically, and approximate results can be derived for games with threshold benefits, games with sigmoid benefits have been considered impossible to study analytically until recently [32]. Recent work on nonlinear public goods [33,34,35,36] has been applied to the production of diffusible molecules in cancer [37,38,39,40,41,42,43,44]. Some other recent models have used linear benefits [45,46].

Here I show how to characterize analytically the dynamics of nonlinear games and how to find the equilibria analytically for well-mixed populations. I will also show how the results differ from linear and pairwise games and why glossing over nonlinearities can lead to crucial errors.

2. How to Analyze Nonlinear Public Goods Games

2.1. The Replicator Dynamics with Two Strategies

In a game with two pure strategies, an individual can be a producer (cooperator) or a non-producer (defector) of a public good. The diffusion range of the public good defines a number n of individuals that benefit from its effect (group size is n). We assume a large population and random group formation at each generation. Thus, one’s probability of having a number i of producers among the other group members, given that the frequency of producers in the population is x, is given by the probability mass function of a binomially distributed random variable i with parameters (n − 1, x):

$$p_{i,n-1}\left(x\right) = \left(\begin{array}{c}n-1\\ i\end{array}\right)x^i{\left(1-x\right)}^{n-1-i}$$

(1)

The fitnesses of producers and non-producers are given therefore by

$$W_C = {\displaystyle \sum }_{i = 0}^{n-1}{p}_{i,n-1}\left(x\right)·b\left(i+1\right)-c$$

(2)

$$W_D = {\displaystyle \sum }_{i = 0}^{n-1}{p}_{i,n-1}\left(x\right)·b\left(i\right)$$

(3)

where b(i) is the benefit (payoff) for being in a group with i other cooperators; a producer has one producer (itself) more in a group, compared to a non-producer in the same group, but it pays a cost c (0 < c < 1); if we assume that the maximum benefit is 1 and c is the cost/benefit ratio of cooperation. The average fitness of a mixed population is

$$\overline{W} = x·W_C+\left(1-x\right)·W_D$$

(4)

The replicator dynamics [47] of this system is

$$\dot{x} = x \left(1-x\right) \beta \left(x\right)$$

(5)

where the fitness difference W_C − W_D is written in the form $\beta$(x), and

$$\beta \left(x\right)={\sum }_{i = 0}^{n-1}{p}_{i,n-1}\left(x\right)·\mathsf{\Delta }{b}_i$$

(6)

is the gradient of selection, with

$$\mathsf{\Delta }{b}_i = b\left(i+1\right)-c-b\left(i\right)$$

(7)

Beyond the two trivial rest points x = 0 and x = 1, further interior rest points are given by

$$\beta \left(x\right)=0$$

(8)

When b(i) is a linear function, (8) can be easily solved analytically [25]. With non-linear benefits, however, this is generally not possible.

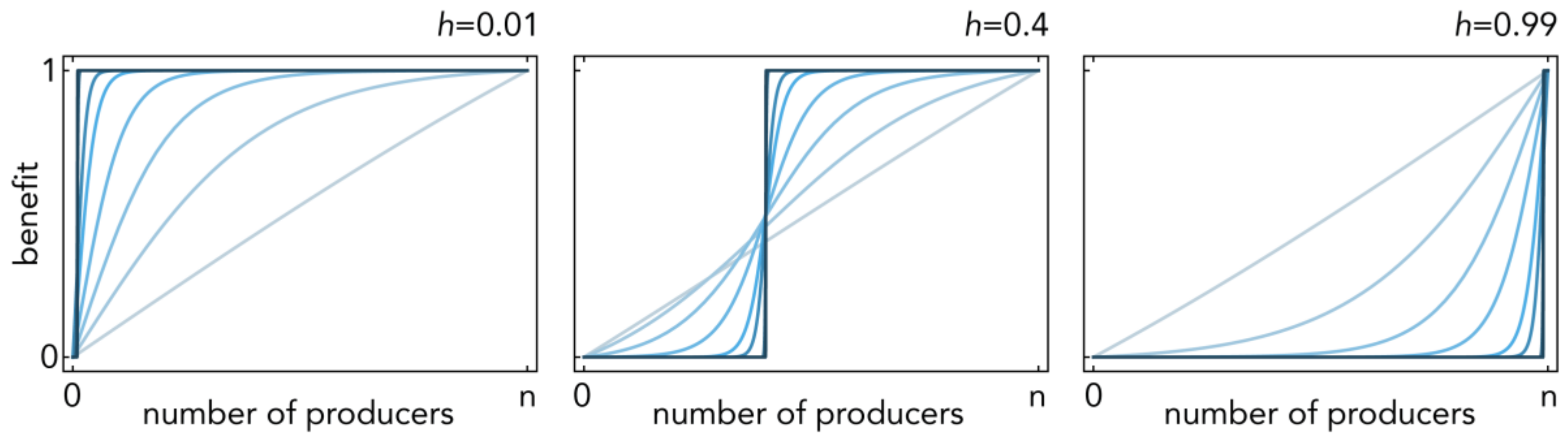
2.2. Nonlinear Benefits

Many cases of nonlinear benefits can be modelled using the following function. The benefit b(i) for an individual in a group with a number i of producers and a number (n − i) of non-producers is described by

$$b\left(i\right) = \frac{\left[l\left(i\right)-l\left(0\right)\right]}{\left[l\left(n\right)-l\left(0\right)\right]}$$

(9)

the normalized version of a logistic function l(i) with inflection h and steepness s:

$$l\left(i\right) = \frac{1}{1+e^{s\left(h-i/n\right)}}$$

(10)

The parameter h defines the position of the inflection point: h→1 gives increasing returns and h→0 diminishing returns; s defines the steepness of the function at the inflection point (s→∞ models a threshold public goods game; s→0 models an NPD; the normalization in (9) in prevents the logistic function (10) from becoming constant for s→0) (Figure 1).

When the benefit b(i) is a nonlinear function such as the one in (9) the roots of $\beta$ in (6) cannot be found analytically. We can, however, characterize the dynamics exactly, and approximate the equilibria, by resorting to the properties of Bernstein polynomials.

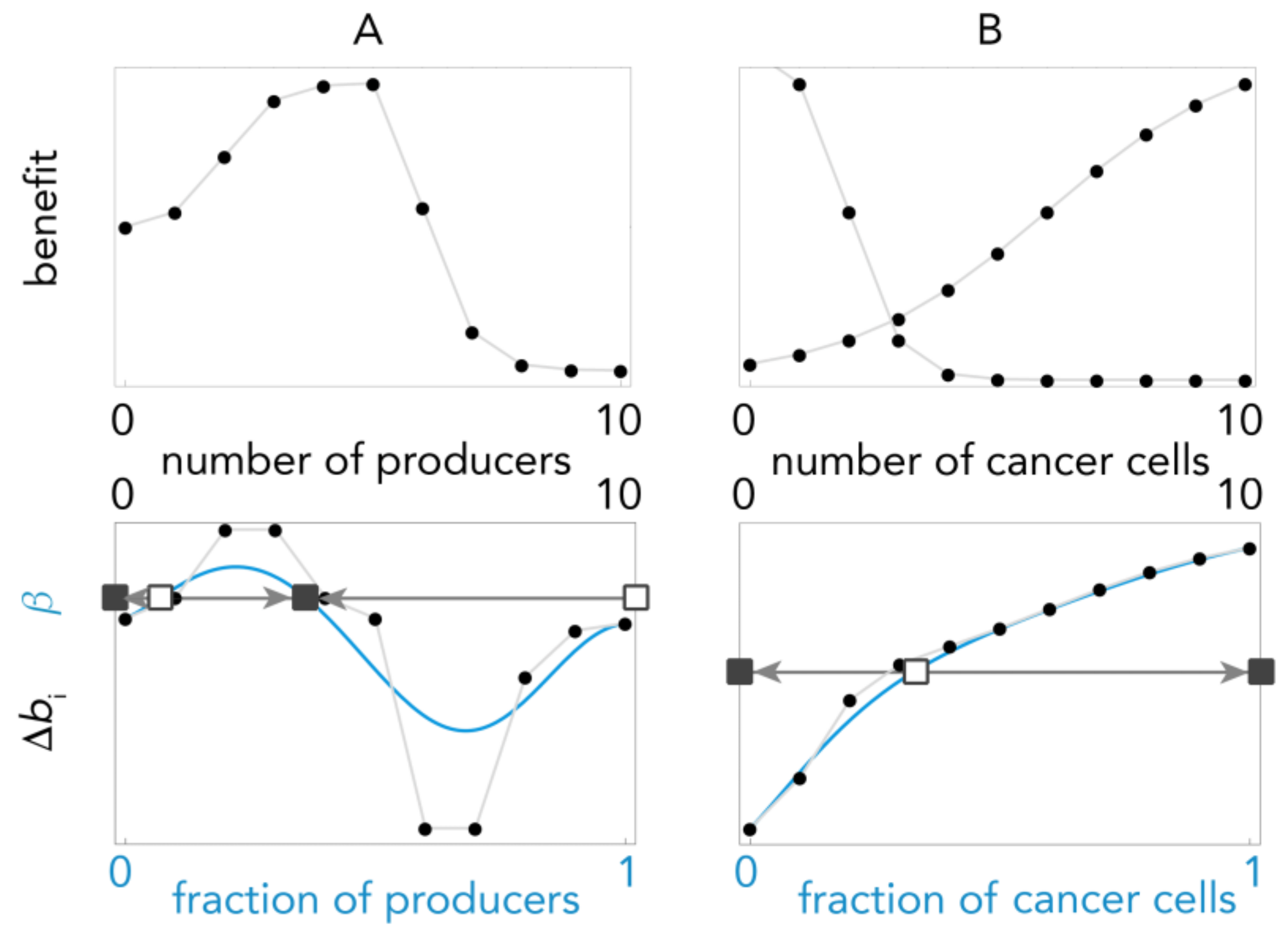
2.3. Bernstein Polynomials

Bernstein polynomials were introduced 100 years ago by Sergei Natanovich Bernstein [48] in order to constructively (employing only basic algebra) prove the Weierstrass approximation theorem: given any continuous function f(x) on an interval [a,b] and a tolerance ε > 0, a polynomial P(x) of sufficiently high degree exists, such that |f(x)−P(x)|<ε for all x in [a,b]; in other words, polynomials can uniformly approximate any continuous function over a closed interval. Bernstein polynomials are a significant advance over Taylor polynomials, as they are applicable to any continuous function, whereas the Taylor approximation requires the function to be differentiable. Probably because of their slow convergence, however, Bernstein polynomials were for a long time (and still are) a relatively unknown tool in mathematics. A review of the history of Bernstein polynomials [49] and a full treatment are available [50,51,52]. For our purposes, the following definitions are enough to set the problem.

• The Bernstein polynomial basis of degree n on x in [0, 1] is defined, for i = 0, …, n, by

  $$p_{i,n}\left(x\right) = \left(\begin{array}{c}n\\ i\end{array}\right)x^i{\left(1-x\right)}^{n-i}$$

  (11)
• A polynomial in Bernstein form of degree n associated with any continuous function f_i on [0, 1] is defined for each positive integer n as

  $$F\left(x\right){{\displaystyle \sum }}_{i = 0}^n{p}_{i,n}\left(x\right)f_i$$

  (12)
• f_i is called the Bernstein coefficient

The following properties of Bernstein polynomials are sufficient to characterize the dynamics of our system (see [49] for a complete list of properties, and [50,51,52] for further discussion):

• End-point values: The initial and final values of f and F are the same: F(0) = f₀; F(1) = f_n.
• Shape preservation: F and f have the same shape (monotonicity, convexity, concavity).
• Variation-diminishing property: The number Z of real roots of F in (0,1)is less than the number S of sign changes of f by an even amount: Z = S − 2j for some integer j greater or equal to 0 and lower than the integer part of n/2 [53] (each root contributes according to its multiplicity).

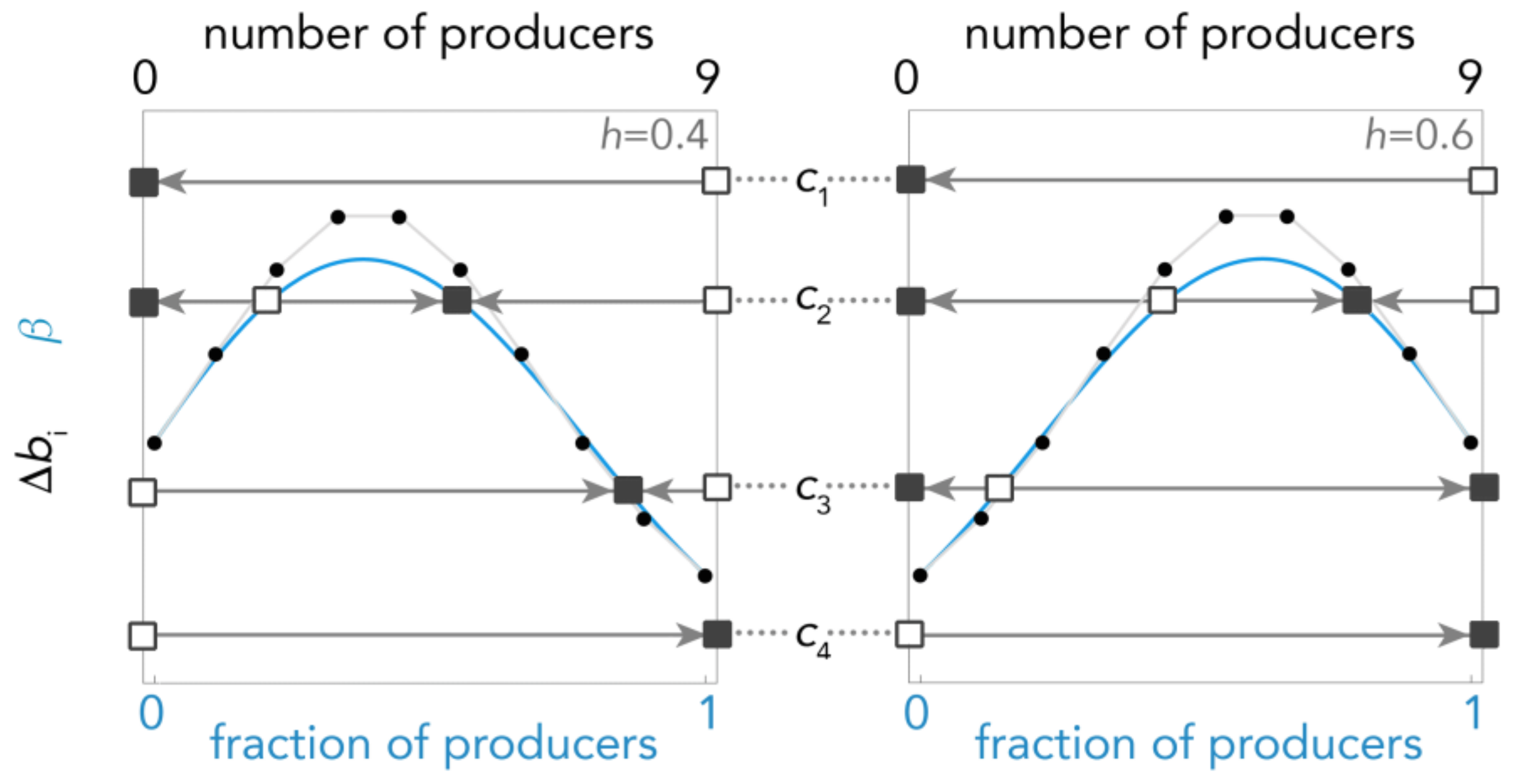
2.4. Characterizing the Dynamics

Compare (11) with (1) and (12) with (6); $\beta$ in (6) is, by definition, a polynomial in Bernstein form and Δb_i is its Bernstein coefficient. Hence, based on the properties defined above, it is straightforward to characterize the dynamics of a nonlinear public goods game based on the number of sign changes of the Bernstein coefficient Δb_i instead of inspecting the gradient of selection of the Bernstein polynomial $\beta$. This Bernstein approach was introduced to study public goods games with sigmoid benefits in the context of cancer biology [39,40]. Games with concave or convex benefits can be analyzed [54] without resorting to the properties of Bernstein polynomials, although in that case the proof is unnecessarily long—the proof is trivial using the Bernstein approach (the results of this exercise have been published in [55], which also replicated the sigmoid case analyzed in [39]).

For games in which the Bernstein coefficient never changes sign, obviously, there is no interior equilibrium. An example of this case is the NPD.

Games with concave or convex benefits are cases in which there can be at most one sign change (Figure 2). If the Bernstein coefficient has one sign change, then there is a unique interior equilibrium x* in (0,1): if the initial sign is +, then x* is stable and x = 0 and x = 1 are unstable: an example of this occurs in games with concave benefits when Δb_n−1 < c < Δb₀; if the initial sign is -, then x* is unstable and x = 0 and x = 1 are stable: an example of this occurs in games with convex benefits when Δb₀ < c < Δb_n−1. Games with concave or convex benefits can also have no sign change. Hence, with concave benefits, if c ≥ Δb₀ then x = 0 is the unique stable equilibrium and x = 1 is the unique unstable equilibrium; if Δb_n−1 < c < Δb₀ then there is a unique interior stable equilibrium and x = 0, x = 1 are unstable equilibria; if c ≤ Δb_n−1 then x = 1 is the unique stable equilibrium and x = 0 is the unique unstable equilibrium. With convex benefits, if c ≥ Δb_n−1 then x = 0 is the unique stable equilibrium and x = 1 is the unique unstable equilibrium; if Δb₀ < c < Δb_n−1 then there is a unique interior unstable equilibrium and x = 0, x = 1 are stable equilibria; if c ≤ Δb₀ then x = 1 is the unique stable equilibrium and x = 0 is the unique unstable equilibrium. In summary, games with concave or convex benefits can have at most one interior equilibrium, either stable or unstable (Figure 2).

The Bernstein approach is however essential to characterize the dynamics of games with sigmoid benefits [39,40]. If b is sigmoid, that is an h (the inflection point) exists such that Δb_i is increasing for i < h, decreasing for i > h, and satisfies Δb_i ≠ 0 ∀i, then Δb_i is single-peaked and can have at most two sign changes (Figure 3); thus, there are either two interior rest points, or one (if they coincide) or zero, and the dynamics can be characterized as follows:

• If c ≥ ${\beta }_{MAX}$ (the maximum value of $\beta$) there is a unique stable equilibrium x = 0 (producers go extinct) (c₁ in Figure 3)
• If Max[Δb₀, Δb_n−1] ≤ c < ${\beta }_{MAX}$ there are two stable equilibria: a pure equilibrium x = 0 made of all non-producers and a mixed equilibrium x*; the basins of attraction of these two equilibria are separated by a mixed unstable equilibrium x^; if the initial frequency of producers x < x^ the population will evolve to x = 0; if x > x^ it will evolve to x* (c₂ in Figure 3).
• If Δb₀ ≤ c < Δb_n−1 (this case can exist only for h > 0.5) there is a unique interior unstable equilibrium x^ separating the basins of attraction of two pure stable equilibria: x = 0 and x = 1; if x < x^ the population will evolve to x = 0; if x > x^ it will evolve to x = 1 (c₃ in Figure 3).
• If Δb_n−1 ≤ c < Δb₀ (this case can exist only for h < 0.5) there is a unique interior stable equilibrium x*, to which the population will converge irrespective of the initial frequencies of the two types (c₃ in Figure 3).
• If c < Min[Δb₀, Δb_n−1] there is a unique stable equilibrium x = 1 (non-producers will go extinct) (c₄ in Figure 3).

In summary, nonlinear games with collective interactions in which the benefit is a sigmoid function of the frequency of cooperators can have at most two internal equilibria, one of which can be stable (Figure 3).

The dynamics is the same for any benefit function in which Δb_i increases for i < h and decreases for i > h. Figure 4 shows two examples of a more complex benefit function, and a case in which the benefits of the two strategies are different functions.

Figure 4A shows the dynamics for the upregulation of glycolysis in cancer cells (the “Warburg effect”)—another example of cooperation for the production of a public good [40] (as it is energetically inefficient under adequate oxygen supply, glycolysis is costly; the products of glycolysis, however, induce the acidification of the microenvironment, which is beneficial to all cancer cells, irrespective of their metabolism). To take into account the possibility that high levels of glycolysis are detrimental to tumor cells (self-poisoning) we must use a double sigmoid function, monotonically increasing for i < d and monotonically decreasing for i > d:

$$b\left(i\right) = \{\begin{array}{c} b_1\left(i\right)=\frac{\left[l_1\left(i\right)-l_1\left(0\right)\right]}{\left[l_1\left(d·n\right)-l_1\left(0\right)\right]} for i<d·n\\ b_2\left(i\right)=1-\frac{\left[l_2\left(i,y\right)-l_2\left(d·n,y\right)\right]}{\left[l_2\left(n,1\right)-l_2\left(d·n,1\right)\right]} for i\ge d·n\end{array}$$

(13)

where

$$l_1\left(i\right) = \frac{1}{1+e^{s_1\left(h_1-i/nd\right)}}$$

(14)

$$l_2\left(i,y\right) = \frac{y}{1+e^{s_2\left[h_2-\left(\frac{i/n-d}{1-d}\right)\right]}}$$

(15)

The parameter d describes the value of i at which the benefits of acidity are overcome by the deleterious effects of self-poisoning; for i < dn, the function is monotonically increasing and has an inflection point at h₁ and steepness s₁; for i > dn, the function is monotonically decreasing and has an inflection point at h₂ and steepness s₂ (with 0 < h₁, h₂ ≤ 1 and s₁,s₂ > 0); the additional parameter y measures the maximum damage of self-poisoning. While analyzing the gradient of selection with benefits given by (13) appears hopeless, the Bernstein approach enables us to characterize the dynamics simply by looking at the number and type of sign changes of the Bernstein coefficient, as shown in Figure 4A.

Figure 4B shows another class of games that appear analytically unsolvable but that are easily characterized using the Bernstein approach. In tumor-stroma interactions, the fitness of cancer cells is an increasing function of the fraction of stromal cells, while the fitness of stromal cells is an increasing function of the fraction of cancer cells (because of stroma and tumor exchange growth factors that are mutually beneficial). Figure 4B shows the simplest model of this scenario with benefit functions for the tumor and stroma increasing in opposite directions, that is, given by:

$$g_1\left(i\right) = \frac{1}{1+e^{s_1\left(h_1-i/n\right)}}$$

(16)

$$g_2\left(i\right) = 1-\frac{1}{1+e^{s_2\left(h_2-i/n\right)}}$$

(17)

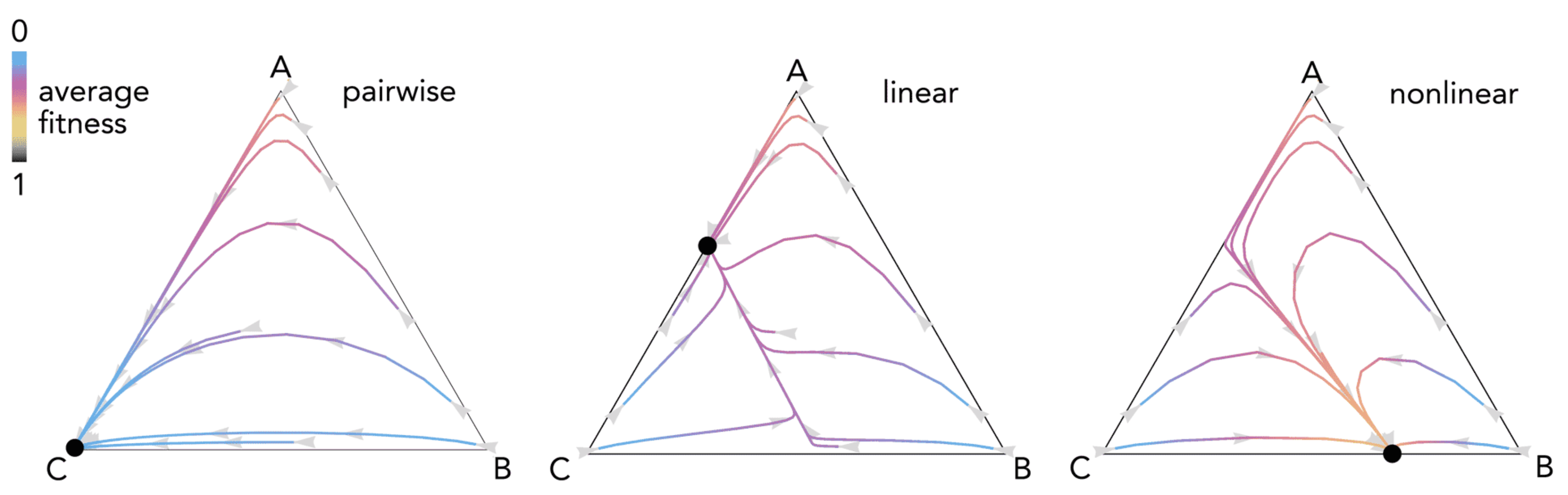
2.5. Comparison with Pairwise and Linear Games

Let us consider again the case of sigmoid benefits. Note how the steepness of the benefit function affects the dynamics (Figure 5): as we have seen, games with linear benefits (s→0) have no interior equilibria; as steepness increases interior equilibria, stable and (or) unstable, arise; also note that the approximation of the gradient of selection to its Bernstein coefficient is less accurate as s increases, and becomes inaccurate when the sigmoid function approaches a step function (s→∞).

Figure 5 also shows an example of the difference between games with pairwise interactions and collective interactions. Two-player games are a special case of collective games with n = 2 and thus there are only one or zero sign changes; not surprisingly, therefore, there are only four possible types of sign change (always +; always −; from + to −; from − to +) and therefore four possible types of dynamics and four types of equilibria in games with two strategies with pairwise interactions (the same types we saw for concave and convex benefits).

2.6. Finding the Equilibria

We can find the internal equilibria analytically by setting to zero, instead of the gradient of selection, its Bernstein coefficient Δb_i, resorting to an additional property of Bernstein polynomials–Bernstein theorem: A Bernstein polynomial F(x) converges uniformly to its coefficient f(x) in [0, 1], that is, $\underset{n\to \infty }{\lim }F\left(x\right) = f\left(x\right)$. The approximation is rather slow. By Voronovskaya’s theorem [56], for functions that are twice differentiable:

$$\underset{n\to \infty }{\lim }n\left[f\left(x\right)-F\left(x\right)\right] = x\left(1-x\right)f″\left(x\right)/2$$

(18)

In our case, let us call the benefit for having a fraction x of producers b(x) = 1/[1 + es(h−x)], the extension of b(i) in (9) to all x [0, 1], with x = i/n. Let us first consider the non-normalized version in (10), that is, let us assume that b(i) = l(i);

$${\beta }^{*}\left(x\right)= {{\displaystyle \sum }}_{i = 0}^{n-1}{p}_{i,n-1}\left(x\right)·\mathsf{\Delta }b$$

(19)

is a Bernstein polynomial of the coefficient Δb = b((i + 1)/n) − b(i/n), and by Bernstein theorem we know that it converges uniformly to Δb in [0, 1]. Furthermore, because Δb is the forward difference of the benefit function with spacing 1/n, for large enough n we can approximate Δb using the derivative of the benefit function, that is Δb ≅ (1/n)b’(i/n). For any given x, i/n converges in probability to x as n→∞, therefore by Bernstein theorem ${\beta }^{*}\left(x\right)$ converges to (1/n)b’(x), and we can find the equilibria by setting ${\beta }^{*}\left(x\right) = c$, which yields:

b’(x) = cn

(20)

Using this approach [39], the equilibrium frequencies can be found by

$$x_{stable } = h-\frac{1}{s}Log\left[-1+\frac{s-\sqrt{s\left(s-4c·n\right)}}{2c·n}\right]$$

(21)

$$x_{unstable} = h-\frac{1}{s}Log\left[-1+\frac{s+\sqrt{s(s-4c·n})}{2c·n}\right]$$

(22)

provided that c > Min[Δb₀, Δb_n−1] (otherwise x = 1 is the only stable equilibrium) and c < s/4n (otherwise x = 0 is the only stable equilibrium). A qualitatively equivalent result holds for the normalized version in (9), because b(i) differs from l(i) only by the inclusion of the normalizing term. For the normalized version, the equilibria are given by

$$x_{stable } = h-\frac{1}{s}Log\left[-1+\frac{s-\sqrt{s\left(s-4c·n·B\right)}}{2c·n·B}\right]$$

(23)

$$x_{unstable} = h-\frac{1}{s}Log\left[-1+\frac{s+\sqrt{s\left(s-4c·n·B\right)}}{2c·n·B}\right]$$

(24)

where B = b(1) − b(0).

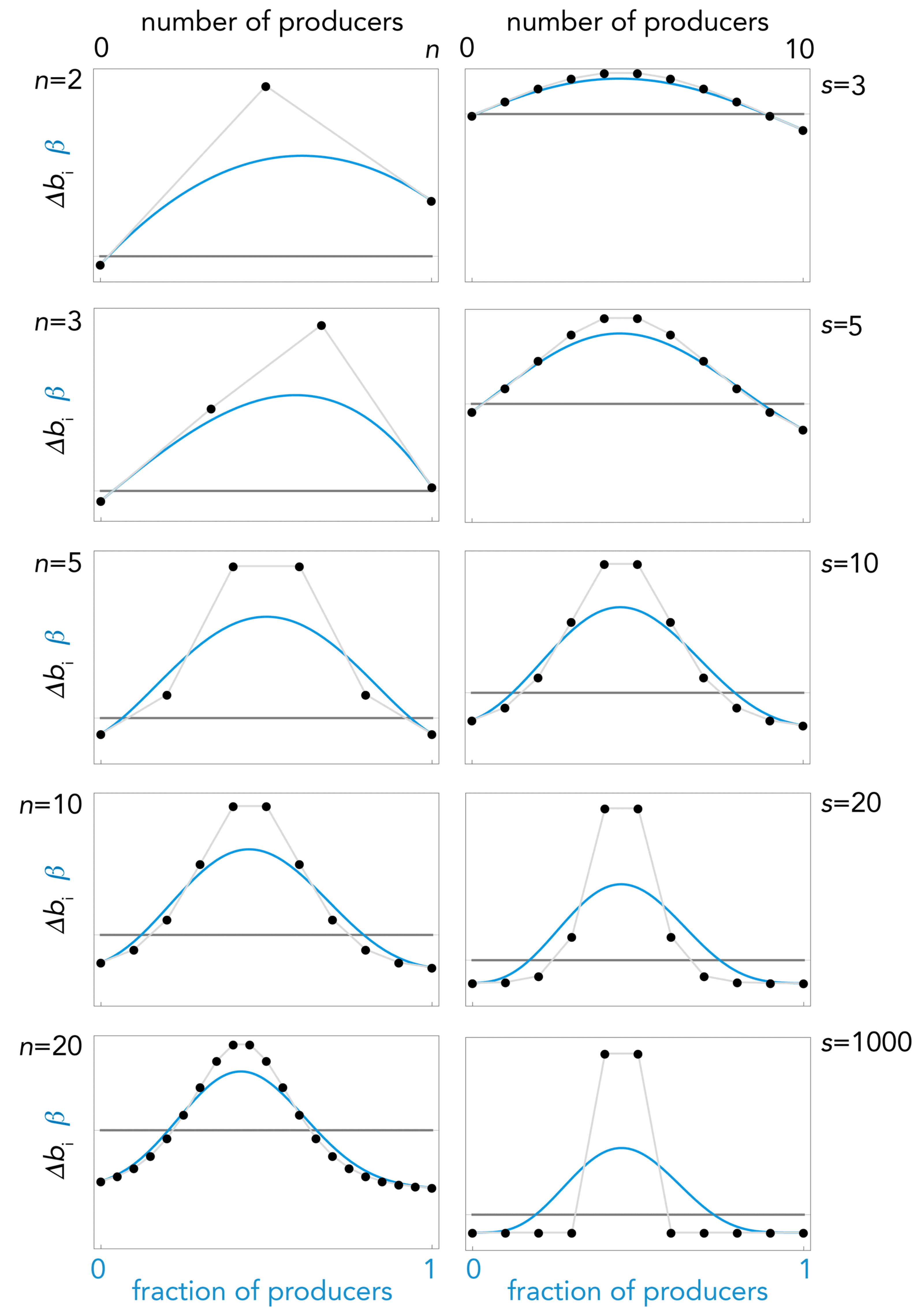
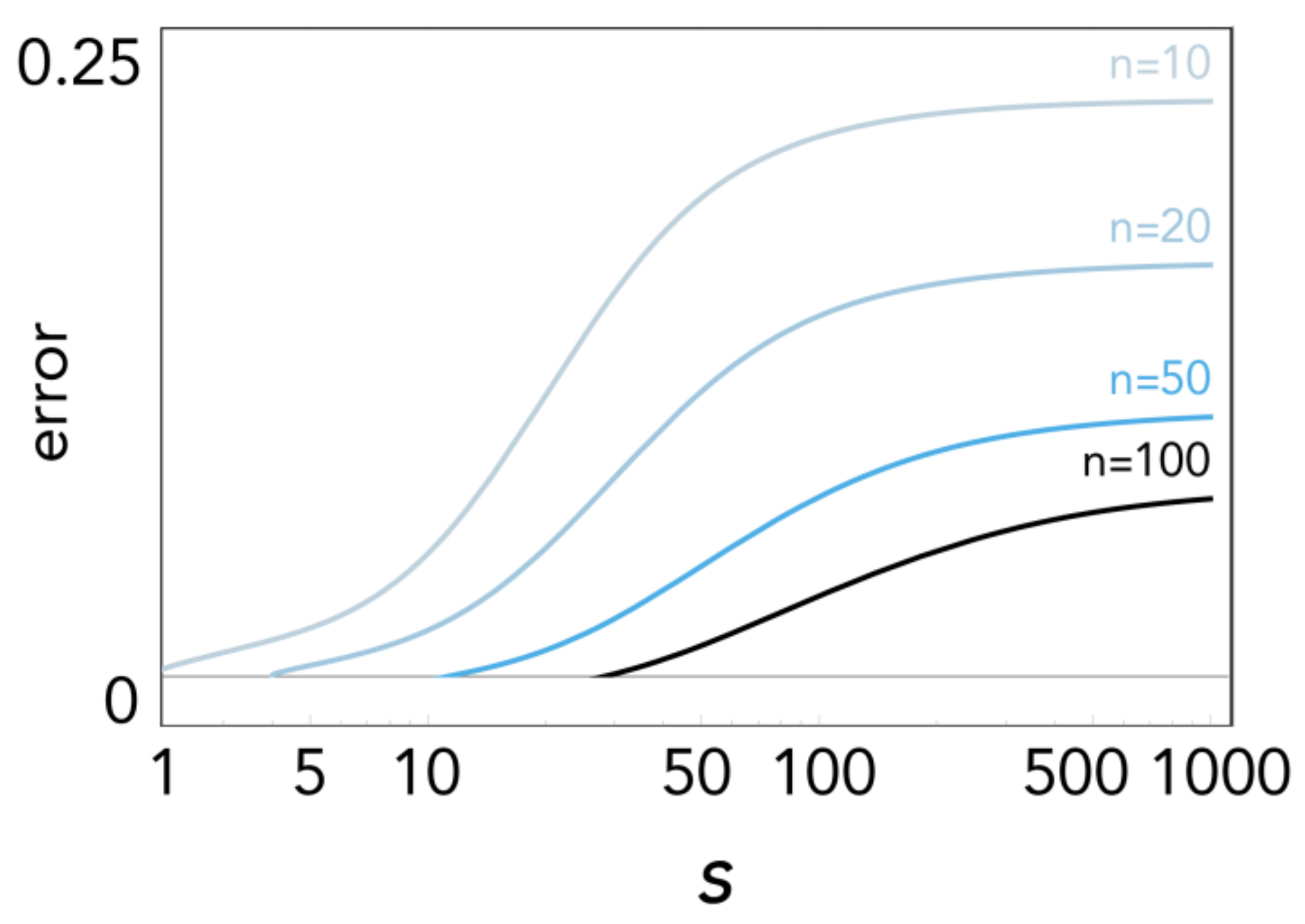
2.7. Goodness of the Approximation

The error of the approximation Δb − ${\beta }^{*}\left(x\right)$ is shown in Figure 6: convergence is slower as nonlinearity (s) increases (as we know from Voronovskaya’s theorem); it improves with n (an obvious consequence of Bernstein theorem) and as the equilibrium gets close to 1 or 0 (from the end-point values property of the Bernstein polynomials).

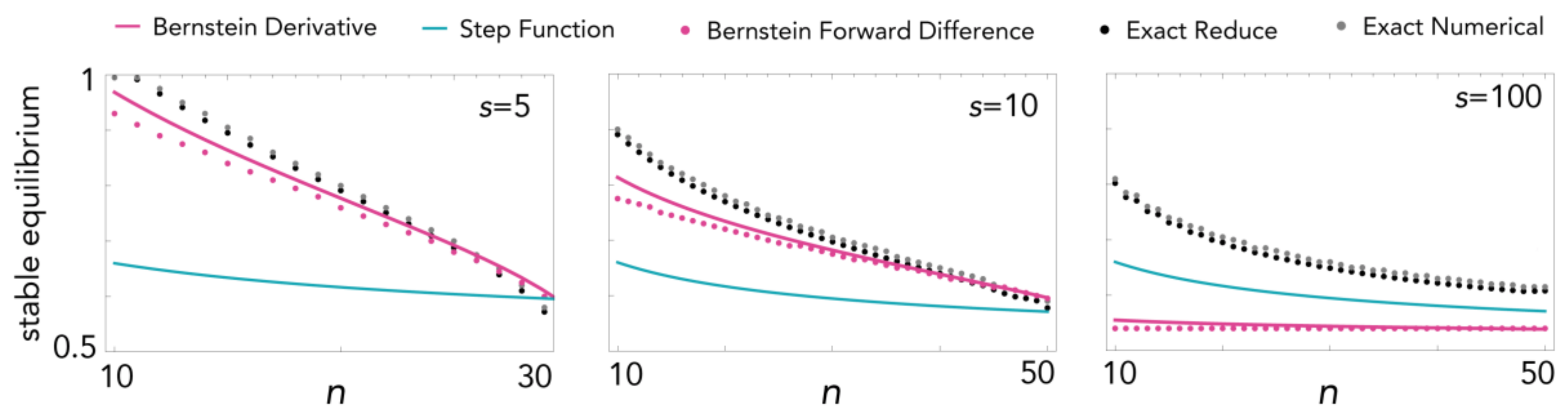
2.8. Approaches to Calculate the Equilibria

In practice the best approach to calculate the equilibria depends mainly on n and s:

• Using the exact formula from (8), by setting $\beta$(x) = 0. This is a reasonable approach for n not too large (the “Reduce” command in Mathematica 11, on a laptop with a 2.9 GHz processor and 16 GB of memory, enables this for n up to about 50) but the results become inaccurate as n grows and it is hopeless for very large n, when numerical methods become necessary.
• The equilibrium can also be approximated by setting Δb = 0, but similar computational problems arise.
• Using the Bernstein approximation outlined above, the equilibrium can be easily calculated for any n from Equations (21)–(24). The accuracy of this approach, as we have seen (Figure 6), improves with n and declines with s.
• For large n and large s, an alternative method is to find the equilibria of a Heaviside step function with the same inflection h using the following equation (25) (where k = hn):

  $$\left(\begin{array}{c}n-1\\ k-1\end{array}\right)x^{k-1}{\left(1-x\right)}^{n-k} = c$$

  (25)

For large n the equilibria can be found approximately from [35]:

$$x_{stable } = \frac{k-1}{n-1}+\sqrt{\frac{2\frac{k-1}{n-1}\left(1-\frac{k-1}{n-1}\right)}{n-1}\left[1-\frac{c}{\sqrt{\frac{1}{2\pi }·\frac{n-1}{\left(n-k\right)\left(k-1\right)}}}\right]}$$

(26)

$$x_{unstable } = \frac{k-1}{n-1}-\sqrt{\frac{2\frac{k-1}{n-1}\left(1-\frac{k-1}{n-1}\right)}{n-1}\left[1-\frac{c}{\sqrt{\frac{1}{2\pi }·\frac{n-1}{\left(n-k\right)\left(k-1\right)}}}\right]}$$

(27)

For steep sigmoid functions, the approximation to a step function is more precise than the Bernstein approximation (Figure 7) (It is perhaps of some mathematical interest to note that the envelope of the Bernstein polynomial basis of degree n is $\sqrt{2\pi nx\left(1-x\right)}$ [57], which coincides with the Stirling approximation of the ith Bernstein polynomial basis of degree n on i/n at equilibrium for threshold public goods games [35]).

2.9. More Than Two Strategies

The analysis remains problematic for games with more than two strategies. Nonlinearities, however, are clearly still important. Let us examine a game with three strategies with the following payoffs (another case of tumor-stroma interactions, similar to the example described above, but with an additional type with constant fitness γ):

ω_A = γ

(28)

ω_B(j) = r[L_B(j) − L_B(0)]/[L_B(n) − L_B(0)]

(29)

ω_C(j) = 1 − [L_C(j) − L_C(0)]/[L_C(n) − L_C(0)]

(30)

where j is the number of players of type C in the group (of size n) and

$$L_B\left(j\right) = \frac{1}{1+e^{s1\left(h1-j/n\right)}}$$

(31)

$$L_C\left(j\right) = \frac{1}{1+e^{s2\left(h2-j/n\right)}}$$

(32)

where the parameters h₁ and h₂ are analogous to h and the parameters s₁ and s₂ are analogous to s, thus (32) and (33) are sigmoid functions that can range from linear to step functions. In an infinite well-mixed population, if x_C is the frequency of cells of type C, the fitness of the three types are:

$$W_A = \gamma$$

(33)

$$W_B = {\displaystyle \sum }_{i = 0}^N{p}_{i,n-1}\left(x_C\right){\omega }_B\left(i\right)$$

(34)

$$W_C = {\displaystyle \sum }_{i = 0}^N{p}_{i,n-1}\left(x_C\right){\omega }_C\left(i\right)$$

(35)

that is, type A has constant fitness; the fitness of type B increases with the number of players of type C; the fitness of type C increases with the number of players of type B. Figure 8 shows an example of the differences between pairwise, linear, and nonlinear models.

3. Conclusions

Pairwise games and games with collective interactions can have different dynamics and equilibria [31,32]. As we have seen here, nonlinearities also have profound effects; the main difference is that pairwise and linear games usually lack the internal equilibria that are often observed in nonlinear games. This means that if benefits are nonlinear, a stable coexistence of cooperators and free-riders is often possible without positive assortment or incentives. This is in direct contradiction with most of the theoretical models that have been developed in biology—which are based on the assumption of linear benefits or pairwise games, and therefore require positive assortment between cooperators (brought about by genetic relatedness [58,59], spatial structure [60] or repeated interactions [61]) to maintain cooperation. As we have seen, with nonlinear benefits cooperation can persist as a mixture of producers and non-producers because of the nonlinear effects of the interactions.

In models of game theory of cancer with two strategies, nonlinear effects help explain seemingly puzzling empirical observations such as the persistence of intra-tumor heterogeneity and the Warburg effect [37,38,39,40,41,42,43,44]. Three-strategy games have been used to model tumor-stroma interactions in multiple myeloma and have also shown that assuming pairwise interactions [27] leads to results that differ significantly from a model with collective interactions [46], with implications for disease progression and treatment. Extending the same model to a game with nonlinear benefits reveals further differences [Sartakhti, et al., this issue].

Neglecting collective interactions and nonlinearities can also lead to other more subtle but equally misleading errors. For instance, invertase production in yeast, a clear example of diffusible public good, has been modelled as a game with pairwise interactions, initially as a PD [62] and eventually as a game of Chicken [63] leading to an incorrect prediction that still persist in microbiology: maximum growth in experimental populations of microbes is often observed at intermediate frequencies of cooperators—a fact that is often highlighted as puzzling [64] because it is based on predictions for pairwise game or linear benefits, which predicts maximum cooperation when the cooperators go to fixation; in multiplayer nonlinear games, however, it is not surprising that maximum fitness occurs for intermediate frequencies of cooperators [32].

Neglecting nonlinearities in public goods games can lead to crucial mistakes in the basic results and fundamental misunderstanding. The approach described here offers a relatively simple way to study games with payoffs that are seemingly impossible to analyze. Even for more complex cases in which the Bernstein approach fails, we should nonetheless insist on using nonlinear public goods games.