Abstract
While conformity pressures people to assimilate in a community, an individual occasionally migrates among communities when the individual feels discomfort. These two factors cause segregation and cultural diversity within communities in the society. By embedding a migration dynamic into Kuran and Sandholm’s model (2008) of preference evolution, we build an agent-based model to see how the variance of preferences in the entire society quantitatively changes over time. We find from the Monte-Carlo simulations that, while preferences assimilate within a community, self-selected migrations enlarge the diversity of preferences over communities in the society. We further study how the arrival rate of migration opportunities and the degree of conformity pressures affect the variance of preferences.
Keywords:
segregation; assimilation; polarization; cultural discontents; evolutionary dynamics; conformity; simulation JEL Classification:
C73; R23; Z13
1. Introduction
With rapid technological progress in transportation in the early twentieth century and in telecommunications in the late twentieth century through the present decade, people over the world are connected to each other beyond geometric boundaries. An enormous mass of migrants travel over continents every single day and a massive volume of information and ideas are exchanged over cultures every single second. Cosmopolitans have been dreaming of integration of the global community politically, economically and culturally.1
However, especially in the recent decade, we are instead witnessing extremism and polarization of people even within economically integrated and culturally inclusive societies such as the United States and the European Union. People with different backgrounds interact with each other economically in such an integrated society; however, these interactions seem to reinforce cultural discontents and extremism for an undeniably large portion of people, though there is certainly another large (possibly greater) portion of people who participate in cosmopolitan culture and build a more inclusive society. Such cultural polarization within the integrated society creates concerns for national security such as the growing worry about “homegrown/domestic terrorists.”2
This paper proposes a parsimoniously simple agent-based dynamic model to explain the enhanced interrelationship between cultural polarization and social integration by focusing on the self-selection of community which each person chooses to affiliate with and conformity pressures through personal interactions within the recognized community.
There has been a growing amount of literature in quantitative empirical studies on immigrants’ assimilation and segregation: see [6] for a survey as well as [7,8,9,10,11]. These studies report assimilation on average over generations in the whole society but also persistent diversity across ethnicity and communities. Generally, they find that the degree of assimilation hugely depends on communities and their surrounding neighbors.
Theoretically speaking, the choice of an affiliating community essentially involves a strategic decision because it is about who to mingle with and others’ choices are crucial in determining the value or payoff gained from joining a community. Thus, it is best formulated as a game theoretic model. On the other hand, while we consider the value system or preference as affected by the belonging community and thus as an endogenous variable determined by community choice, the influence of community on preference takes a rather unconscious and gradual psychological process: see (Brehm et al. [12], Chapter 7). Evolutionary game dynamics offer a clear framework to formalize such a dynamic interplay of the intentional rational choice of community and the unconscious process in individuals’ preferences.
In economics, Bisin and Verdier [13] (henceforth, BV) is the seminal paper on applications of evolutionary game dynamics to intertemporal cultural transmission, followed by a variation of the models by Bisin and his coauthors.3 The BV model is an overlapping generation model. Cultural traits are characterized as a binary or discrete variable, such as cultures A (say American) and J (say Japanese), etc. Each generation is inherited with either cultural identity and then decides on the effort level to succeed it to the next generation. The probability of succession depends on the effort level. There is externality in the choice—more people in one culture may yield positive or negative utility, which generates interesting and theoretically clear results in the model.
In the anthropology literature on the evolution of social norms, Boyd and Richerson [15] (henceforth, BR) consider a stag hunt game (a symmetric binary coordination game), separately played in two communities.4 In their model, an agent switches the action in the stag hunt game based on imitation, and also switches the community based on the comparison of average payoffs. If we interpret the action (social norm) as a preference or value system, the coordination game structure would represent assimilation pressures. From a comparison of a simulation in two different scenarios of parameter values, they claim that, when the migration process is relatively slower than the action imitation process, it may converge to a polymorphic equilibrium where the majority (not all the agents) of each community takes a different action from the majority of the other community and the two communities coexist.5
Qualitative characterization of cultural traits as discrete choices would be best applicable to language choices and interracial marriage, as Bisin and his coauthors indeed explore both theoretically and empirically in other papers. However, it cannot capture polarization or assimilation in the value system and social norm, as these claims need quantitative measures. While it is a clearly distinguishable, discrete choice whether to speak English or Japanese, there is gradation between American cuisine and Japanese cuisine, like California rolls. The above-mentioned empirical studies refer to qualitative measures to see cultural differences in attitudes toward risk, work ethics, and political stance, for example. Furthermore, while cultural assimilation may be driven by a coordination game structure like BR’s model, a binary coordination game structure implies multiplicity of distinct equilibria and thus the limit state may largely change by small perturbation to the initial state, as BR also noticed. For quantitative comparative static with a gradual change in parameters, this discontinuity may exaggerate the effects of parameter changes.
For a quantitative study of cultural assimilation, Kuran and Sandholm [17] (henceforth, KS) propose an evolutionary dynamic model on the continuous space of cultural traits; we build our model upon their formulation.6 The KS model consists of a large population (a continuum of a unit mass) of agents. Each agent’s preference is represented by a point on the interval ; cultural traits range over this continuous interval.7 When the gap between an agent’s own preference and the average preference of the society exists, the agent experiences cultural discontent with the norm of the society and feels disutility.8 Conformity pressure pushes each agent’s preference to the average preference at each moment in time. In their base model, KS found that all agents’ preferences converge to the average of initial preferences and thus preferences are completely assimilated in the limit state. They split the society into two subpopulations of different ethnicities and allow each to have different weights on the two ethnic groups in their calculation of the average preference; this biased interaction does not prevent people from complete assimilation, assuming that all the weights are positive—that is, the society is not separated completely. In other words, the society in the KS model is united despite biased interactions across ethnic groups.
However, reflecting on the recent phenomena of cultural crashes, we would speculate that perfect assimilation is quite an optimistic prediction on cultural evolution in contemporary global society; we are witnessing escalating polarization. Looking into the KS model’s structure, we could find that the assumption of social unity is crucial for the assimilation result but may not suit observations of the current presence of social segregation; segregation exists geographically, economically and socially.9 Each individual person interacts only with a more or less restricted part of society. Conformity pressure works among people who meet and communicate casually and regularly, but not significantly with people who belong to different communities.10 Thus, conformity pressure drives one’s preference to the belonging community’s norm. However, there are flows of people across communities and, most importantly for an economic model, people are able to freely choose which community to belong to. If one feels cultural discontents with the current community, the person could voluntarily switch to another community before getting his preference assimilated with the current community’s norm: if you do not like your neighbor, why don’t you move out to see people like you? While conformity pressure still homogenizes preferences of members in each community, the self-selection mechanism behind these flows rather reinforces the difference and results in polarization of different communities’ norms.
Division of the society and voluntary choice between communities are indeed what we add to the KS model. We found polarization across communities from Monte Carlo simulations of the model. With two ethnic groups in the society, we divide the society into three communities: the hometown of each ethnic group and the cosmopolitan city. For simplicity of analysis, we assume that the city is open to all the ethnicities, while the hometown of each ethnic group is closed to the other ethnicity. An individual agent occasionally switches communities, given the current preference of the agent itself and the current average preference of each community. Conformity pressure drives an agent’s preference toward the average preference of the community that the agent currently belongs to at that moment in time. The switch of community discontinuously changes the direction of the agent’s preference evolution. This makes our model difficult to solve analytically, unlike the KS model. In addition, the outcome of our model hugely depends on the initial values of the model—the initial distribution of the preferences, the initial choices of communities, etc. Thus, for this paper, we rely on agent-based simulation with finitely many agents over a discrete time horizon.
This paper goes as follows. In the next section, we describe the base model and summarize the fundamental properties of the model casually. It is followed by a section on simulation results. The first subsection shows transition dynamics and quick convergence to an equilibrium state in a one-shot simulation of the base model, where all the parameters are fixed. In particular, we find that agents stop migration in finite periods and preferences in each community monotonically converge to the average preference at the time when migration stops. Thus, we can identify the limit state of community choices and preference evolution from the outcome after a sufficiently long but finite period. With this convergence result in hand, we show comparative statics in the next subsection by varying parameter values in a fixed range and then comparing the initial state and the limit state identified in such a way. This includes an extension of the base model to give a (positive or negative) exogenous utility to city residence. Finally, we discusses the implications of these results. The MATLAB simulation code is available online at Github: https://github.com/zusaiEGT/Coevol_Conform_Migrat.
2. The Base Model
In our model, the society initially consists of two populations or ethnic groups of agents, . While the number of agents in the society is denoted by M, the proportion of ethnic groups in the society is denoted by . There are three communities in the society, .11 Each agent chooses a community that the agent belongs to.
Agent ’s preference is represented by point . Cultural discontent is perceived by an agent as the difference between its own preference and the average preference (social norm) of members of the community that the agent currently belongs to. Let be the average preference of agents who belong to community . Then, the agent’s payoff from choosing community c is
This represents the discontent between the agent’s own ideal and the belonging community’s social norm. Note that agent of ethnicity is indifferent between city and its hometown if the agent’s preference is exactly at the midpoint between the city’s social norm and the hometown’s social norm , i.e., if
We call this midpoint preference a preference threshold between and .
In our dynamic process, an agent occasionally makes the choice whether to stay in the current community or to switch to another, depending on the discrepancy between his own preference and the community’s average preference. In addition, conformity pressure drives each individual preference to assimilate with the belonging community’s average preference.
As for an agent’s process of switching between communities, we adopt the standard best response dynamic [32,33]. Each agent receives an opportunity to switch the community with probability at the beginning of each period due to inertia. We call the arrival rate of such an opportunity the switching possibility frequency. Upon receipt of a switching opportunity, the agent observes the average preference of each community at the end of the last period and his own current preference , and calculates the payoff to be obtained from his current community and other communities. Then, he switches to the best among them. For simplicity of analysis, we prohibit agents in ethnicity ⊕ from choosing community − and agents in ethnicity ⊖ from choosing community +; community + is meant to be a hometown of ethnicity ⊕ and similarly for −, while community 0 represents a city that could integrate people of different ethnicities. Whether an agent received a switching opportunity or not, the agent’s preference is assimilated toward the current average in the belonging community at the end of the period; if agent belongs to community c at the end of period t and , his preference is adjusted to
Here, is the speed of preference evolution, representing the strength of conformity pressure. Apart from the simplifying restriction on feasible switches of community to city and their hometown, an agent’s ethnicity only determines its own initial preferences and initial affiliation to a community, and . That is, if agent belongs to ethnicity , its initial preference is chosen from interval and the initial community is set to either or ; similarly, if agent is from ethnicity ⊖, the initial preference and the initial community are chosen from and , respectively.
From the discreteness of community choices and conformity pressure on the continuous preference space , it is readily predicted that agents would stop switches within some finitely long time, say at period T; after that, agents in each community monotonically converge to the average preference at T. Thus, in the long run, agents should settle down to a Nash equilibrium: each agent belongs to the best community and the agent’s preference is completely assimilated to the average preference of the belonging community given other agents’ community choices and preferences. Actually, coupled with the optimal choices of communities given the preference profile, any such preference profile in which agents’ preferences are completely homogenized (to a community-dependent preference) in each community constitutes a Nash equilibrium.
Given this within-community homogenization of equilibria and convergence to the average preference, we use the term polarization to mean a long-run outcome in which the average preference of each hometown’s residents is not neutralized, i.e., it converges to somewhere strictly positive or negative, not 0 like city residents. By looking at the long-run average preference of hometown residents, we can make quantitative statements such as whether and how much polarization is reinforced (the hometown preference goes farther from zero) or weakened (it goes closer to zero) by each factor in this model.
This multiplicity suggests that equilibrium analysis cannot pin down how preference should evolve in the long run. It would depend on the initial values of preferences and communities, as well as the parameters of the dynamic and , and thus it should be found by tracking the dynamic process. For this, we rely on agent-based simulation to induce a quantitative implication of the model. In a standard game setting without preference evolution, Roth and Sandholm [34] rigorously verify that, as the number of agents increases infinitely, optimization-based evolutionary dynamics with finitely many agents’ approaches to deterministic outcomes under a differential equation defined for a continuous population. In a strict sense, our model involves endogenous dynamic changes in agents’ preferences and thus it is out of the scope of their theory. However, we can expect such a justification in a rough sense.
3. Results
3.1. One-Shot Simulation
At the beginning of each run of the simulation, we fix parameters and , allocate agents to each community, and then determine the initial preferences and communities of agents by drawing them from a certain distribution. For each ethnicity, we assign 500 agents to city and another 500 agents to their hometowns, i.e., for and for . We draw initial preferences for agents of ethnicity ⊕ from a uniform distribution over and those of ethnicity ⊖ from a uniform distribution over . Then, we run the dynamic process as stated in the previous section.
First, we closely examine the transition of preferences and migration over communities within a single-shot simulation. Here, we set and . As expected, Figure 1a,b show the convergence of agents’ preferences to the average in each community and a persistence of difference in the average preference over communities as in KS model. Conformity pressure in the preference dynamic accounts for the convergence, while separation by divided communities contributes to persistent diversity, unlike in the KS model. Furthermore, Figure 1c shows that the average preference in each hometown moves farther from the social average, i.e., 0. That is, the polarization of preferences over communities is reinforced through the dynamic process.
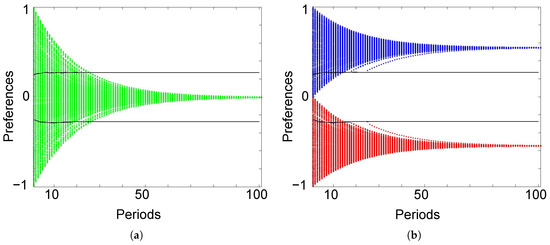
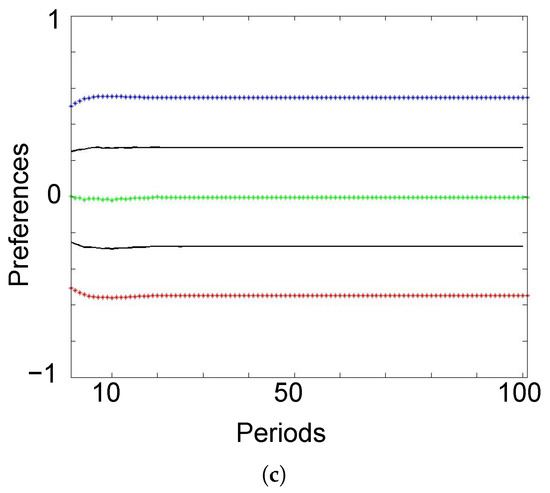
Figure 1.
Evolution of individual preferences by communities in each period: (a) city residents; (b) hometown residents; (c) average preference of residents in each community. Each dot represents the preference of an agent at each period. Green is associated with the city, blue with town + and red with town −. In (c), black lines indicate preference thresholds, as defined in Equation (2).
To closely investigate the evolution of polarized preferences, we categorize agents by the combination of their belonging community at the beginning of the simulation and at period 100. Each panel of Figure 2 shows individual preferences of agents in each category at each period: a single dot represents an agent’s preference at a certain period. As the initial community was chosen randomly, some hometown residents had a relatively neutral preference (close to 0), so they would be better off moving to the city. However, as a switching opportunity arrives only occasionally and randomly, some of them eventually stay in their hometowns. Initially, these agents contribute to neutralizing the average preference of a hometown. However, this neutralizing effect diminishes over time, as their own preference becomes assimilated with the polar preference of the hometown due to conformity pressure. Moreover, there is an inflow of agents from the city to a hometown; agents in this inflow to a hometown have relatively extreme preferences and were discontent with the city’s neutral social norm. When getting a switching opportunity, they choose to move to the hometowns and their preferences push the average preference of hometown residents to an extreme. Thus, their self-selective migrations reinforce the polarization of the hometowns’ social norms.
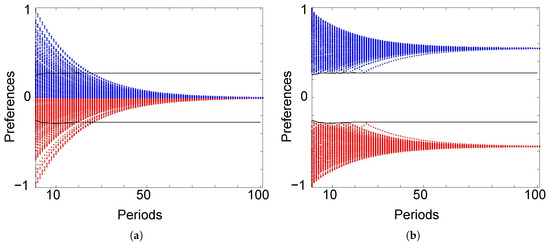
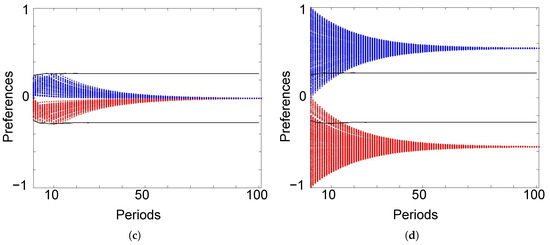
Figure 2.
Evolution of individual preferences by the initial community and the ending community: (a) staying in city, (b) city to towns; (c) towns to city; (d) staying in towns. Here, blue is associated with ethnicity ⊕ and red with ethnicity ⊖.
3.2. Monte Carlo Comparative Statics
We confirmed that the structure of our dynamics, especially the interplay of self-selective community choice and conformity pressure, results in persistent polarization. Here, we further investigate impacts of exogenous parameters on the degree of polarization. To conduct such comparative statics, we use the idea of the Monte Carlo method. For each parameter that we are interested in, we set a range on the parameter value. We repeat simulations, in each of which we first draw the parameter value from the uniform distribution on the designated range; then, with this parameter value, we run a simulation as in the last section for 200 periods. We confirm that no agent can be better off by switching communities at the end of this simulation, so the composition of agents in each community has reached the limit state; the average preference of each community will not change from there and agents’ limit preferences are supposed to match with this average preference. We keep the record of the initial values and the ending values of key endogenous variables. For each of the following comparative static analyses, we run 200 simulations and then compare the parameter values and the outcomes in the key endogenous variables.
3.2.1. Frequency of Switching Opportunity
First, we evaluate the impact of the frequency of switching opportunities on polarization. For this, we focus on ethnicity ⊕ because ethnicity ⊖ should experience the same pattern thanks to symmetry. Figure 3a shows that the average preference of the hometown residents moves farther away from the neutral preference as the switching opportunity frequency increases. That is, as it becomes easier for agents to switch communities, the self-selection process reinforces polarization in a greater degree. To see this at the individual agent’s level, we again sort agents by their initial communities and ending communities at period 200. Figure 3b shows that the number of agents who switch from city to hometown increases with . Thus, less inertia in the switch of community indeed increases the inflow of agents to hometowns. This is also the case for the inflow to the city: when a switching opportunity does not arrive frequently, agents who are born with relatively neutral preferences might stay in the hometown as they do not get a chance to get out of there. It weakens the polarization of the hometown. With more switching opportunities, they are more likely to fly out to the city and thus there is less deterrence against polarization.
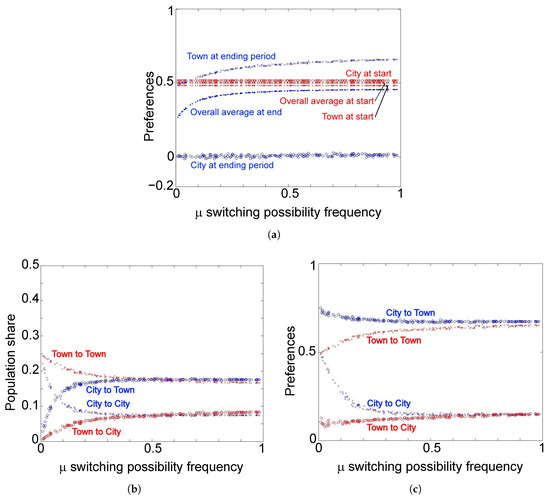
Figure 3.
The Monte Carlo simulation with switching opportunity frequency . (a) average preferences of ethnicity ⊕; (b) sizes of flows of ethnicity ⊕; (c) initial average preferences of ethnicity ⊕ by the initial community and the ending community. In (a), × represents the town, · overall average and ∘ the city, while blue markers show average preferences at the ending period and red markers show those at the beginning period. In (b,c), red markers show agents who start initially from the town and blue markers those initially from the city, while × represents ending at the town and ∘ ending at the city.
From Figure 3c, one may notice that the average preference of agents who switch from the city to a hometown becomes more neutralized (closer to 0) as increases. This is coupled with an increase in the number of such switching agents; as more switching opportunities are given, more agents choose to migrate at early periods. When a switching opportunity arrives less frequently, these agents might wait longer and then their preferences could be neutralized by conformity pressure before getting such an opportunity. However, their preferences are farther from the neutral preference than the average of the whole population with the same ethnicity p. Thus, we can conclude that, while agents in this flow from the city to a hometown have less extreme preferences, the increase in the number of agents in the flow itself contributes to the polarization of preferences.
3.2.2. Asymmetry in Population Distributions
We assumed that the population distribution over the city and a hometown is the same between the two ethnicities. Here, we relax this assumption to see the effects of population distributions on polarization.
For this, we change the initial proportion of hometown residents among agents of ethnicity ⊕ while keeping the proportion of hometown residents among ethnicity ⊖ as in the benchmark. A greater proportion of hometown residents among ethnicity ⊕ implies that the city becomes more dominated by ethnicity ⊖ at the beginning and the social norm becomes less in favor of ethnicity ⊕. Thus, more ethnicity-⊕ agents move further out of the city, as confirmed from Figure 4b; domination of the city by ethnicity ⊖ is reinforced.
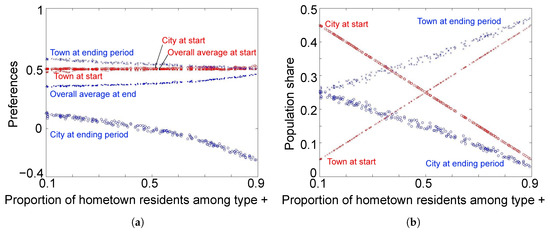
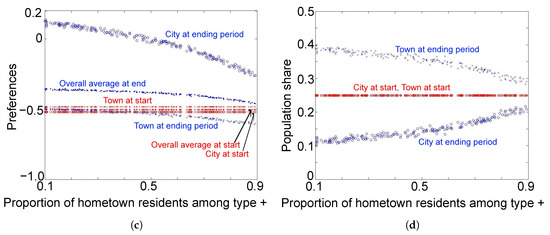
Figure 4.
The Monte Carlo simulation with varying initial share of hometown among ethnicity ⊕. Notation follows that of Figure 3a. (a) average preferences of ethnicity ⊕; (b) population shares of city and town +; (c) average preferences of ethnicity ⊖; (d) population shares of city and town −.
Those agents of ethnicity ⊕ who remain in the city are eventually assimilated with agents of ethnicity ⊖ in the city; the average preference of ethnicity-⊕ city residents eventually becomes farther away from the average preference of the entire ethnicity ⊕, as shown in Figure 4a.
On the other hand, as the city’s social norm changes from ethnicity ⊕’s average preference, the threshold for ethnicity-⊕ agents to choose the hometown over the city becomes closer to the neural preference . As a result, the hometown attracts more of those agents with less extreme preferences. Thus, the social norm of the hometown is more neutralized, though the change is not as large as the change in the social norm at the city. Since more of ethnicity ⊕ gathers at the hometown, the overall average preference of ethnicity ⊕ puts more weight on the hometown preferences and thus it appears to shift toward the extreme.
The opposite direction of change occurs in the social norm at hometown −, as agents of ethnicity ⊖ find it easier to choose the city over the hometown and those who dare to choose the hometown should have more extreme preferences; however, the change of the social norm in the hometown is not as drastic as in the city. As visually shown in Figure 4c, the social norms both in the city and in the hometown − move toward the negative extreme. However, the population share of city residents among ethnicity ⊖ becomes greater, as confirmed by Figure 4b. This shift in the population distribution mitigates the change in the average preferences of ethnicity ⊖ from going to the negative extreme.
In summary, we can say that, as either one type’s population is initially more assigned to their hometown and less to the city, the average preferences of the two types become more separated. However, the magnitude of the change is not quite as large: the change in the average preferences results from the mere shift of population shares between the city and hometowns. The social norms in hometowns do not change as drastically as in the city.
3.2.3. Extension: Exogenous Utility of City
As a virtue of simulation-based analysis, we can readily make structural changes to the model to see the consequences of the structural assumptions on the outcomes. In our base model, agents’ choice of community is solely based on cultural discontents—how much the agent’s own preference differs from the average preference or the social norm of the community. However, in reality, people often need to bear such cultural discontents with the community’s social norm for some exogenous reasons such as better job opportunities. Here, we study the impact of such exogenous factors on polarization by adding exogenous utility.
Constant exogenous utility is added to the utility of choosing the city: the utility for agent of ethnicity p is now in city and in its hometown . Over simulations, we change the value of from negative—disutility of the city—to positive.
As expected, the final population share of the city among each ethnicity correlates positively with : see Figure 5b. Symmetry of the two ethnicities’ populations keeps the city’s social norm just around zero, the neutral preference. Figure 5a shows that the social norm of each hometown moves to its extreme as the city pulls more agents with a greater exogenous incentive . Self-selection is indeed the force behind this polarization, since those who dare to choose their hometowns over the city despite must have experienced greater discontents with the neutral social norm in the city; their preferences must be on the extreme among the overall population of the same type. As increases, the power of this self-selection process becomes stronger and conformity pressure further reinforces polarization.
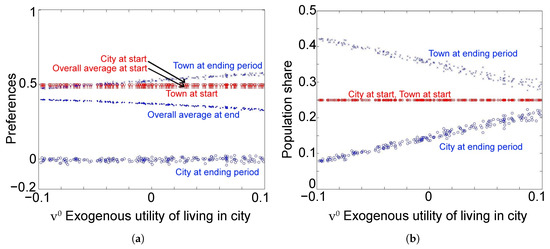
Figure 5.
The Monte Carlo simulation with varying exogenous utility of city . Notation follows that of Figure 3a. (a) average preferences of ethnicity ⊕; (b) population shares of city and town +.
If we look at the average preference of the overall population, it appears to be more neutralized. In addition, it is just dilution due to the shift of the population share in the city. This hides the trend of stronger polarization in the hometowns.
4. Conclusions
In this paper, we propose an evolutionary dynamic model of preference evolution and community choice. The model naturally explains diversification of preference across different communities and, simultaneously, assimilation within a community. From an agent-based simulation, we confirmed that the self-selecting community choice is the driving force of polarization of preferences. Actually, polarization is reinforced when agents are more likely to get migration opportunities; that is, when there are less obstacles for each agent to select its own community. From simulation experiments of adding exogenous utility to the utility of living in the cosmopolitan city, we find that people who dare to leave the city should have more extreme polarized preferences and their extremism is reinforced.
It could be criticized that complete separation between communities may be a strong assumption. Kuran and Sandholm [17] show that any mild penetration over ethnicities eventually leads to complete assimilation over different ethnicities unless there is an ever-lasting continuous inflow of new comers to hometowns (in our terminology).12 However, to explain the current actual situations of growing extremism, their result may be too optimistic. Our results suggest that the division of the society into closed communities and self-selection between communities are crucial to understanding polarization. It is reported that “homegrown terrorists” build up their beliefs in extremism when they are sent to prisons [37] or they rely on cyber social networks for personal communications [38]; they are isolated in these places from a larger civil society and lack regular contacts with diverse people.13 Multi-racial countries like Belgium divide prison cells by races and ethnicities [40]. Online social networks allow users to freely connect or disconnect with other users.14 These institutional and technological factors let those people form their own separate and closed communities. Our findings warn about the danger of worsening polarization by building physical and psychological walls between communities. Complete separation is not a result of polarization but a strong cause of it. Although human psychology drives people apart to different divisions of society, an inclusive and open society must more or less keep them connected and needs intervention to prevent self-selective isolation despite individual discontents with others. Even though the convergence to assimilation takes time even in such an open society, our result suggests that it would worsen the situation if we just let different people freely separate from each other.
Our analysis in this paper is based on simulations, while the prediction of long-run results from finite-period simulations are justified by the casual observation of finite-time convergence in agents’ community choices. While the simulation results give interesting quantitative outcomes and the mechanism behind these results can be intuitively understood, some may be hoping for general analytical results. Due to the essential dependency of the limit state on the initial state, it may not be straightforward to analytically obtain concrete quantitative results as shown from simulations in this paper. Hence, we leave it to the next agenda of this research project, while here we propose the model to answer many practically important questions in the middle of upheaval in migration and polarization across the globe.
Acknowledgments
The authors would like to thank Amelie Constant, two anonymous referees and participants of presentations at Tohoku University and SABE Annual meeting for their comments. We also thank Olena Berchuk for careful reading and editing suggestions.
Author Contributions
D.Z. initiated the project, formulated the model, drafted the simulation code, and wrote the paper. F.L. conducted simulations and improved the simulation code. Both authors equally contributed analysis of results.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Appiah, K.A. Cosmopolitanism: Ethics in a World of Strangers (Issues of Our Time); WW Norton & Company: New York, NY, USA, 2010. [Google Scholar]
- National Terrorism Advisory System Bulletin (NTAS); U.S. Department of Homeland Security: Washington, DC, USA, 2017. Available online: https://www.dhs.gov/ntas/advisory/ntas_17_0515_0001 (accessed on 21 November 2017).
- Sandler, T. Terrorism and counterterrorism: An overview. Oxf. Econ. Pap. 2015, 67, 1. [Google Scholar] [CrossRef]
- Hafez, M.; Mullins, C. The radicalization puzzle: A theoretical synthesis of empirical approaches to homegrown extremism. Stud. Confl. Terror. 2015, 38, 958–975. [Google Scholar] [CrossRef]
- Klausen, J.; Campion, S.; Needle, N.; Nguyen, G.; Libretti, R. Toward a behavioral model of “Homegrown” radicalization trajectories. Stud. Confl. Terror. 2016, 39, 67–83. [Google Scholar] [CrossRef]
- Constant, A.F.; Zimmermann, K.F. International Handbook on the Economics of Migration; Edward Elgar Publishing: Cheltenham, UK, 2013. [Google Scholar]
- Luttmer, E.F.; Singhal, M. Culture, context, and the taste for redistribution. Am. Econ. J. Econ. Policy 2011, 3, 157–179. [Google Scholar] [CrossRef]
- Aleksynska, M. Civic participation of immigrants in Europe: Assimilation, origin, and destination country effects. Eur. J. Political Econ. 2011, 27, 566–585. [Google Scholar] [CrossRef]
- Fernandez, R.; Fogli, A. Culture: An empirical investigation of beliefs, work, and fertility. Am. Econ. J. Macroecon. 2009, 1, 146–177. [Google Scholar] [CrossRef]
- Algan, Y.; Cahuc, P. Inherited trust and growth. Am. Econ. Rev. 2010, 100, 2060–2092. [Google Scholar] [CrossRef]
- Manz, C.C.; Sapienza, P.; Zingales, L. Does culture affect economic outcomes? J. Econ. Perspect. 2006, 20, 23–48. [Google Scholar]
- Brehm, S.S.; Kassin, S.M.; Fein, S. Social Psychology, 5th ed.; Houghton Mifflin: Boston, MA, USA, 2002. [Google Scholar]
- Bisin, A.; Verdier, T. The economics of cultural transmission and the dynamics of preferences. J. Econ. Theory 2001, 97, 298–319. [Google Scholar] [CrossRef]
- Bisin, A.; Verdier, T. The economics of cultural transmission and socialization. In Handbook of Social Economics; Benhabib, J., Bisin, A., Jackson, M.O., Eds.; Elsevier BV: Amsterdam, The Netherlands, 2011; Volume 1A, pp. 339–416. [Google Scholar]
- Boyd, R.; Richerson, P.J. Voting with your feet: Payoff biased migration and the evolution of group beneficial behavior. J. Theor. Biol. 2009, 257, 331–339. [Google Scholar] [CrossRef] [PubMed]
- McElreath, R.; Boyd, R.; Richerson, P.J. Shared norms and the evolution of ethnic markers. Curr. Anthropol. 2003, 44, 122–130. [Google Scholar] [CrossRef]
- Kuran, T.; Sandholm, W.H. Cultural integration and its discontents. Rev. Econ. Stud. 2008, 75, 201–228. [Google Scholar] [CrossRef]
- Buechel, B.; Hellmann, T.; Pichler, M.M. The dynamics of continuous cultural traits in social networks. J. Econ. Theory 2014, 154, 274–309. [Google Scholar] [CrossRef]
- Cheung, M.W.; Wu, J. On the Probabilistic Transmission of Continuous Cultural Traits; Working paper; University of Oregon: Eugene, OR, USA, 2017. [Google Scholar]
- Dressler, W.W.; Borges, C.D.; Balieiro, M.C.; dos Santos, J.E. Measuring cultural consonance: Examples with special reference to measurement theory in anthropology. Field Methods 2005, 17, 331–355. [Google Scholar] [CrossRef]
- Dressler, W.W.; Balieiro, M.C.; Ribeiro, R.P.; Santos, J.E.D. Cultural consonance and psychological distress: Examining the associations in multiple cultural domains. Cult. Med. Psychiatry 2007, 31, 195–224. [Google Scholar] [CrossRef] [PubMed]
- Dressler, W.W.; Bindon, J.R. The health consequences of cultural consonance: Cultural dimensions of lifestyle, social support, and arterial blood pressure in an African American Community. Am. Anthropol. 2000, 102, 244–260. [Google Scholar] [CrossRef]
- Dressler, W.W.; Oths, K.S.; Gravlee, C.C. Race and ethnicity in public health research: Models to explain health disparities. Annu. Rev. Anthropol. 2005, 34, 231–252. [Google Scholar] [CrossRef]
- Schelling, T.C. Dynamic models of segregation. J. Math. Sociol. 1971, 1, 143–186. [Google Scholar] [CrossRef]
- Clark, W.A.V. Residential preferences and neighborhood racial segregation: A test of the schelling segregation model. Demography 1991, 28, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Schuman, H.; Steeh, C.; Bobo, L.; Krysan, M. Racial Attitudes in America, rev. ed.; Harvard University Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Bruch, E.E.; Mare, R.D. Neighborhood choice and neighborhood change. Am. J. Sociol. 2006, 112, 667–709. [Google Scholar] [CrossRef]
- Pancs, R.; Vriend, N.J. Schelling’s spatial proximity model of segregation revisited. J. Public Econ. 2007, 91, 1–24. [Google Scholar] [CrossRef]
- Dokumacı, E.; Sandholm, W.H. Schelling Redux: An eVolutionary Dynamic Model of Residential Segregation; Working paper; University of Wisconsin-Madison: Madison, WI, USA, 2007. [Google Scholar]
- Zhang, J. Tipping and residential segregation: A unified schelling model. J. Reg. Sci. 2011, 51, 167–193. [Google Scholar] [CrossRef]
- Willis, P.E. Learning to Labor: How Working Class Kids Get Working Class Jobs; Columbia University Press: New York, NY, USA, 1977. [Google Scholar]
- Gilboa, I.; Matsui, A. Social stability and equilibrium. Econometrica 1991, 59, 859–867. [Google Scholar] [CrossRef]
- Hofbauer, J. Stability for the Best Response Dynamics; Working paper; University of Vienna: Vienna, Austria, 1995. [Google Scholar]
- Roth, G.; Sandholm, W.H. Stochastic approximations with constant step size and differential inclusions. SIAM J. Control Optim. 2013, 51, 525–555. [Google Scholar] [CrossRef]
- De, S.; Gelfand, M.J.; Nau, D.; Roos, P. The inevitability of ethnocentrism revisited: Ethnocentrism diminishes as mobility increases. Sci. Rep. 2015, 5, 17963. [Google Scholar] [CrossRef] [PubMed]
- Hammond, R.A.; Axelrod, R. The evolution of ethnocentrism. J. Confl. Resolut. 2006, 50, 926–936. [Google Scholar] [CrossRef]
- Johnson, T. Threat of Homegrown Islamist Terrorism; Council on Foreign Relations: New York, NY, USA, 2011. [Google Scholar]
- Sageman, M. Leaderless Jihad: Terror Networks in the Twenty-First Century; University of Pennsylvania Press: Philadelphia, PA, USA, 2011. [Google Scholar]
- Springer, N.R. Patterns of Radicalization Indentifying the Markers and Warning Signs of Domestic Lone Wolf Terrorists in Our Midst. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2009. [Google Scholar]
- Mufson, S. How Belgian prisons became a breeding ground for Islamic extremism. The Washington Post, 27 March 2016. [Google Scholar]
| 1 | For example, see the discussion by moral philosophers and social advocates for global citizenship, such as Appiah [1]. |
| 2 | For example, the U.S. Department of Homeland Security [2] issued a concern on homegrown terrorists and states that the nation is facing “one of the most serious terror threat environments since the 9/11 attacks.” The survey by [3] compares domestic and transnational terrorism in empirical data. Hafez and Mullins [4] summarize socio-psychological causes of homegrown radicalism. The research note by international political scientists Klausen et al. [5] provides a behavioral framework to assess the risk of homegrown terrorists and analyzes 68 cases. |
| 3 | See Bisin and Verdier [14] for survey and summary of their papers. |
| 4 | McElreath et al. [16] also consider the evolution of social norms in a stag hunt game, while they introduce a kind of asymmetric assortative matching between different types of agents into the model. Our model also exhibits such an asymmetric matching structure, since city residents are matched with those of different ethnicities while hometown residents are matched only with those of the same ethnicity. |
| 5 | Notice that in their choice of parameters, migration even occurs from a payoff-disadvantageous community to a payoff-advantageous community. This assumption of migration may lie somewhere between ours and Kuran and Sandholm [17], as we will see. |
| 6 | Buechel et al. [18] and Cheung and Wu [19] extend the BV model to continuous cultural traits. |
| 7 | Precisely, this is a reduced form of the KS model. Originally, each agent in the KS model chooses action from . The agents’ preference represents an individually ideal action, though there is a conformity pressure to not differ from the average action of the society. Thus, the agent’s utility from taking action is formulated as , where w denotes the strength of conformity pressure; the optimal action is just the weighted average of the agent’s individualistic ideal and the average action: . Then, unconscious psychological assimilation drives the preference to fill the gap from the current action: . This reduces to a continuous-time version of our reduced-form preference dynamic (3). |
| 8 | In medical anthropology, William Dresser and his coauthors study the health consequences of cultural discontents/consonances. They develop a measurement of cultural consonance [20] and find that it correlates with the health conditions of minorities [21,22]. See also the literature review [23]. |
| 9 | As we all know, Schelling [24] is the seminal work on theoretical framework of segregation. See Clark [25], Schuman et al. [26], Bruch and Mare [27] for classical and recent empirical studies of racial segregation in U.S. From simulations and theoretical analysis of best response dynamics, Pancs and Vriend [28] strengthen Schelling’s results on the checkerboard model by allowing agents to have a discontinuous strict preference for perfect integration (exact equal proportion of each race in the agent’s neighborhood) and finding that this still leads to segregation. Dokumacı and Sandholm [29] provide a rigorous foundation of evolutionary dynamics in the Schelling’s tipping model and remove its underlying assumption of out-of-equilibrium sorting. Zhang [30] integrates the idea of tipping in the checkerboard model. |
| 10 | To show off its identity, there may even be hostile attitudes toward the social norm of different groups, especially if the opposite group is considered as an establishment: [31] for classical socioeconomic ethnology. |
| 11 | Although we add a circle to + and − to distinguish ethnic groups from their hometowns, we ignore this notational difference when relating them: for example, “hometown of ethnicity p” means hometown + of ethnicity ⊕ and hometown − of ethnicity ⊖. |
| 12 | The theoretical result of Kuran and Sandholm [17] may be parallel to the simulation result of De et al. [35]. They modified the local interaction model of a repeated Prisoner’s Dilemma as in [36] to add an observable group identity to each agent and also force agents to move their positions occasionally. From a simulation of replicator dynamics, they found that high mobility results in less discrimination against agents from a different group. |
| 13 | Springer [39] argues that many lone wolf terrorists once sought acceptance for themselves in the majority of society, but refusals and failures turned them to extremism. |
| 14 | Sageman [38] argues that online social networks contribute to the current emergence of domestic terrorism. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).