Cyclic Competition and Percolation in Grouping Predator-Prey Populations
Abstract
:1. Introduction
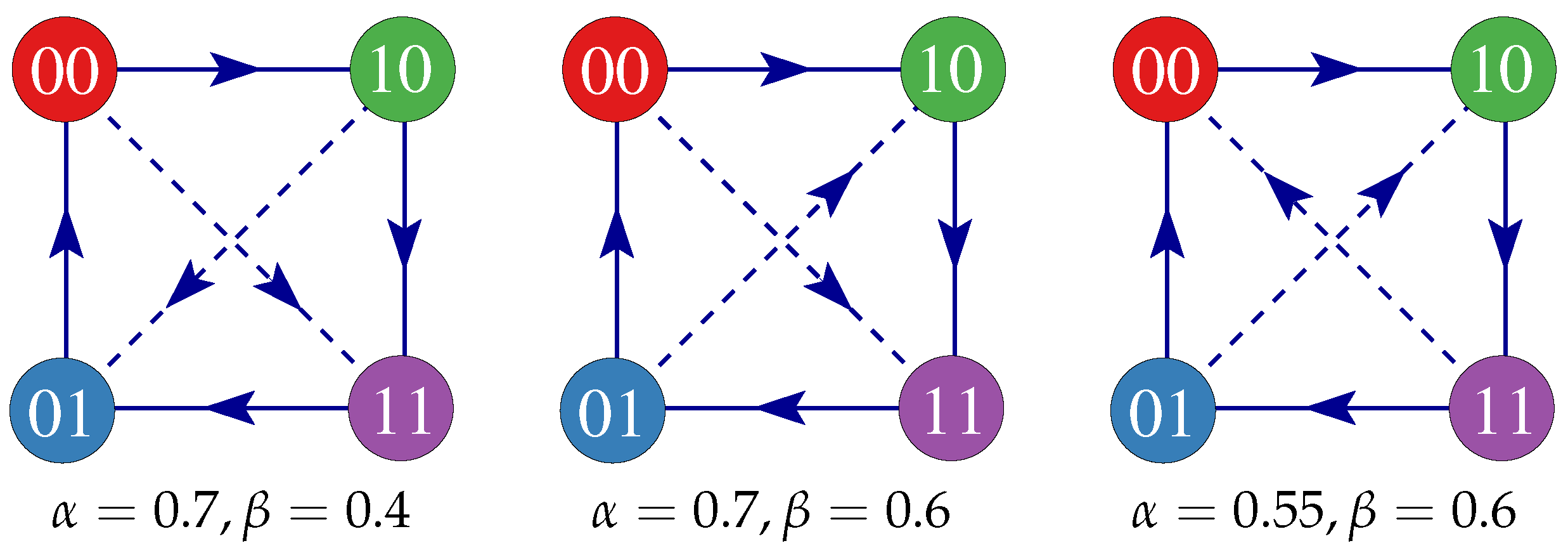
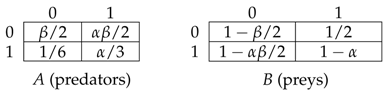
2. The Model
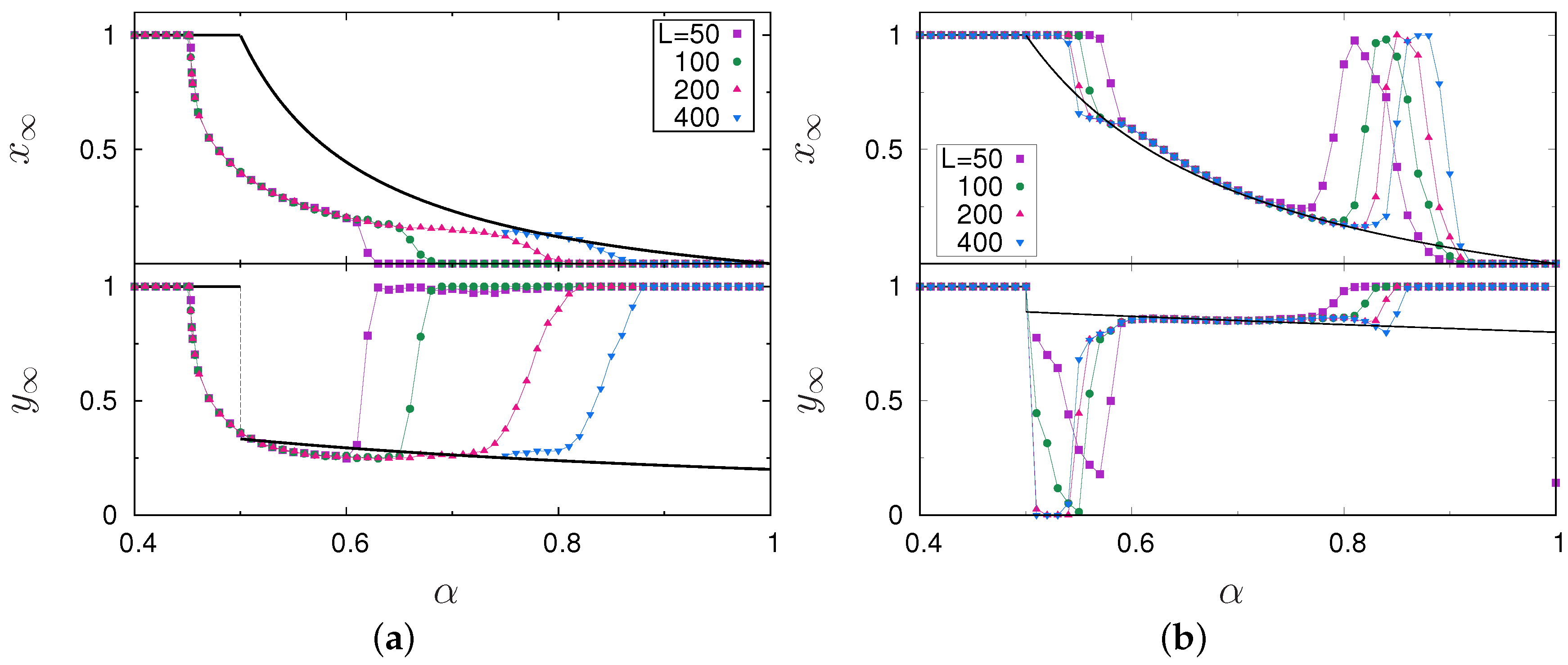
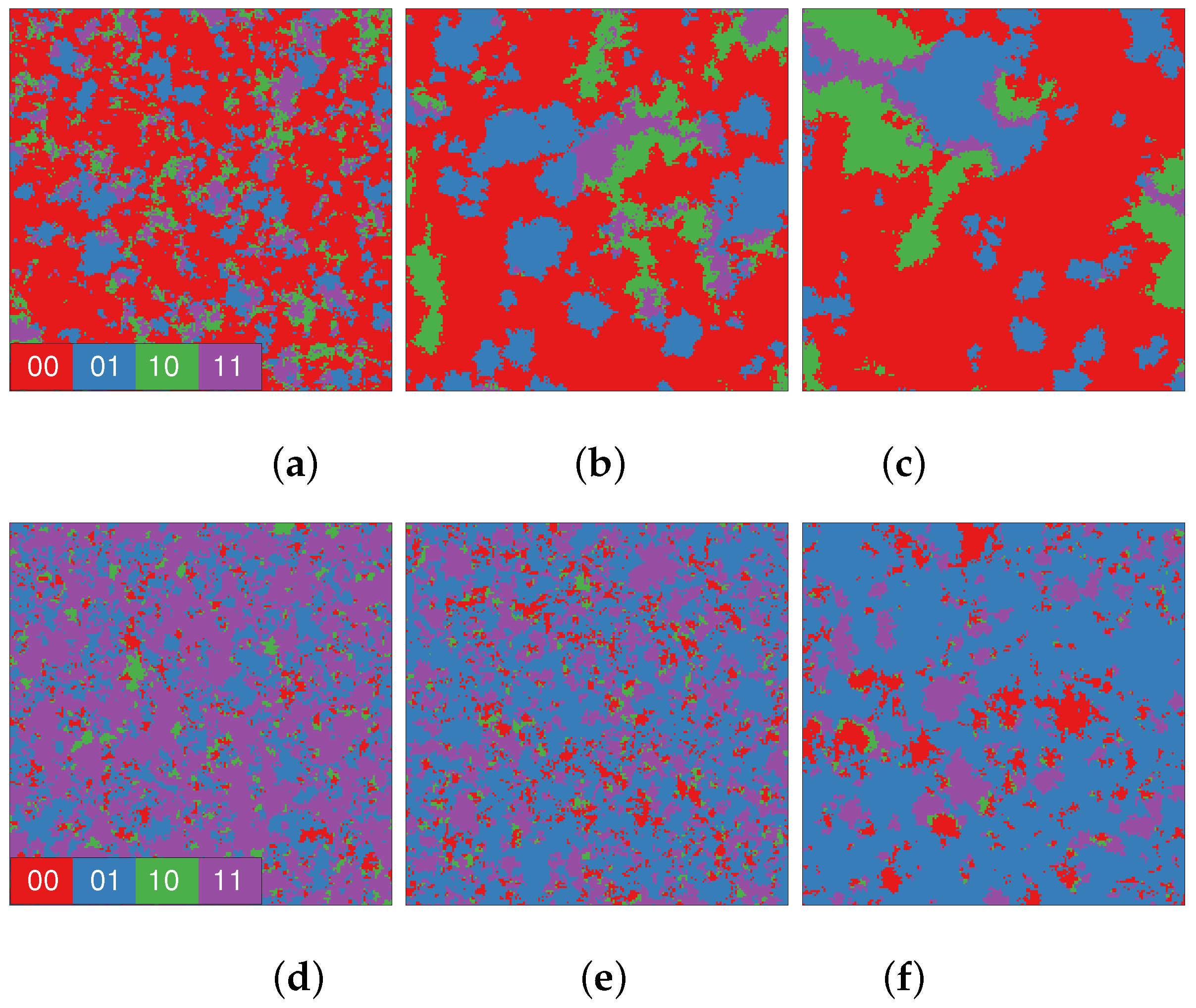
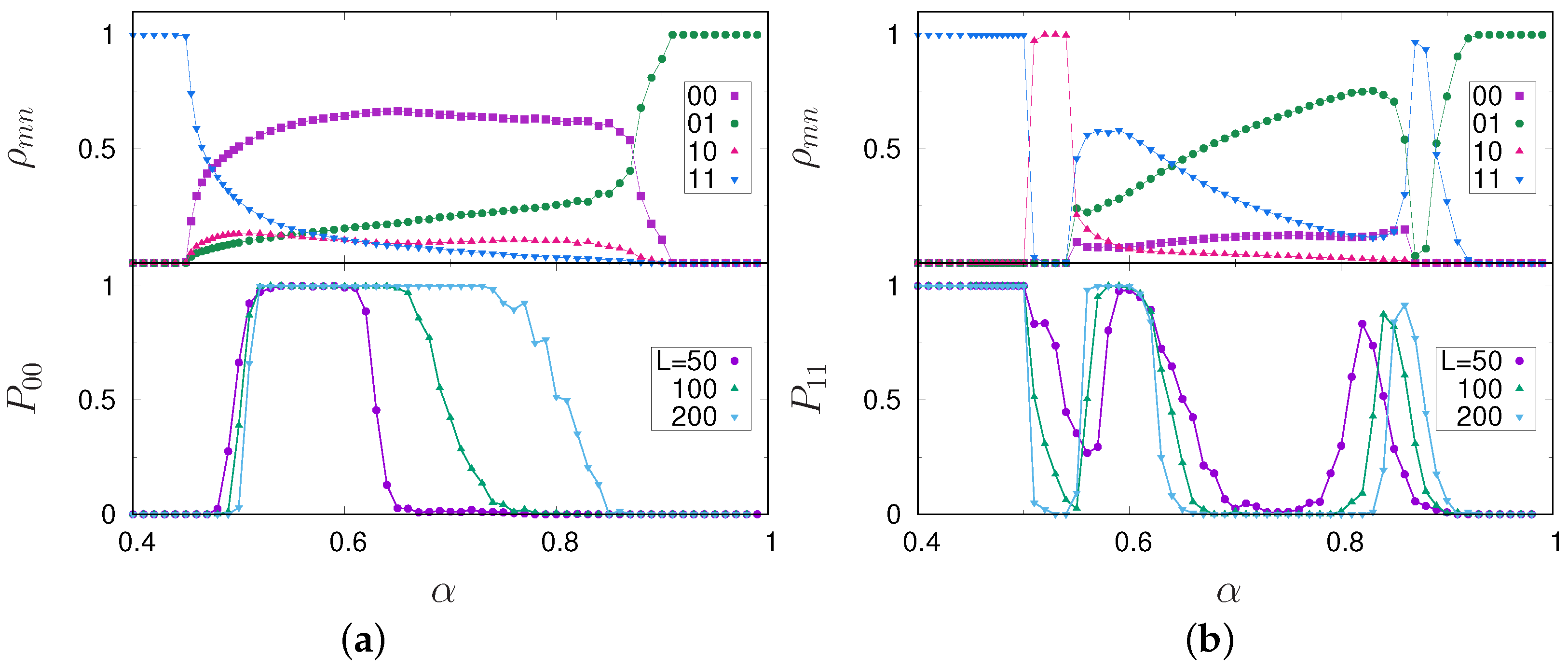
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Szabó, G.; Fáth, G. Evolutionary games on graphs. Phys. Rep. 2007, 446, 97–216. [Google Scholar] [CrossRef]
- Szolnoki, A.; Mobilia, M.; Jiang, L.L.; Szczesny, B.; Rucklidge, A.M.; Perc, M. Cyclic dominance in evolutionary games: A review. J. Royal Soc. Int. 2014, 11, 20140735. [Google Scholar] [CrossRef] [PubMed]
- Semmann, D.; Krambeck, H.J.; Milinski, M. Volunteering leads to rock-paper-scissors dynamics in a public goods game. Nature 2003, 425, 390. [Google Scholar] [CrossRef] [PubMed]
- Cazaubiel, A.; Lütz, A.F.; Arenzon, J.J. Spatial organization, grouping strategies and cyclic dominance in asymmetric predator-prey games. Available online: https://arxiv.org/abs/1611.09624 (accessed on 24 January 2017).
- Bailey, I.; Myatt, J.P.; Wilson, A.M. Group hunting within the Carnivora: Physiological, cognitive and environmental influences on strategy and cooperation. Behav. Ecol. Sociobiol. 2013, 67, 1–17. [Google Scholar] [CrossRef]
- Stander, P.E. Cooperative hunting in lions: The role of the individual. Behav. Ecol. Sociobiol. 1992, 29, 445–454. [Google Scholar] [CrossRef]
- Heinsohn, R.G.; Packer, C. Complex cooperative strategies in group-territorial Africa lions. Science 1995, 269, 1260–1262. [Google Scholar] [CrossRef] [PubMed]
- Legge, S. Cooperative lions escape the Prisoner’s Dilemma. Tree 1996, 11, 2–3. [Google Scholar] [CrossRef]
- Yeakel, J.D.; Patterson, B.D.; Fox-Dobbs, K.; Okumura, M.M.; Cerling, T.E.; Moore, J.W.; Koch, P.L.; Dominy, N.J. Cooperation and individuality among man-eating lions. Proc. Nat. Acad. Sci. 2009, 106, 19040–19043. [Google Scholar] [CrossRef] [PubMed]
- Bednarz, J.C. Cooperative Hunting in Harris’ Hawks. Science 1988, 239, 1525–1527. [Google Scholar] [CrossRef] [PubMed]
- Dinets, V. Apparent coordination and collaboration in cooperatively hunting crocodilians. Eth. Ecol. Evol. 2015, 27, 244. [Google Scholar] [CrossRef]
- Nentwig, W. Social spiders catch larger prey: A study of Anelosimus eximius (Araneae: Theridiidae). Behav. Ecol. Sociobiol. 1985, 17, 79–85. [Google Scholar] [CrossRef]
- Vakanas, G.; Krafft, B. Coordination of Behavioral Sequences Between Individuals During Prey Capture in a Social Spider, Anelosimus eximius. J. Insect Behav. 2001, 14, 777–798. [Google Scholar] [CrossRef]
- Pryor, K.; Lindbergh, J.; Lindbergh, S.; Milano, R. A Dolphin-Human Fishing Cooperative in Brazil. Mar. Mammal Sci. 1990, 6, 77–82. [Google Scholar] [CrossRef]
- Daura-Jorge, F.G.; Cantor, M.; Ingram, S.N.; Lusseau, D.; Simões-Lopes, P.C. The structure of a bottlenose dolphin society is coupled to a unique foraging cooperation with artisanal fishermen. Biol. Lett. 2012, 8, 702–705. [Google Scholar] [CrossRef] [PubMed]
- Spottiswoode, C.N.; Begg, K.S.; Begg, C.M. Reciprocal signaling in honeyguide-human mutualism. Science 2016, 353, 387. [Google Scholar] [CrossRef] [PubMed]
- Bshary, R.; Hohner, A.; Ait-el Djoudi, K.; Fricke, H. Interspecific Communicative and Coordinated Hunting between Groupers and Giant Moray Eels in the Red Sea. PLoS Biol. 2006, 4, e431. [Google Scholar] [CrossRef] [PubMed]
- Malan, G. Solitary and social hunting in pale chanting goshawk (Melierax canorus) families: Why use both strategies? J. Raptor Res. 1998, 32, 195–201. [Google Scholar]
- Brockmann, H.J.; Barnard, C.J. Kleptoparasitism in birds. Anim. Behav. 1979, 27, 487–514. [Google Scholar] [CrossRef]
- Pitcher, T.; Magurran, A.; Winfield, I. Fish in larger shoals find food faster. Behav. Ecol. Sociobiol. 1982, 10, 149–151. [Google Scholar] [CrossRef]
- Garay, J. Cooperation in defence against a predator. J. Theor. Biol. 2009, 257, 45–51. [Google Scholar] [CrossRef] [PubMed]
- Pulliam, H.R. On the advantages of flocking. J. Theor. Biol. 1973, 38, 419–422. [Google Scholar] [CrossRef]
- Beauchamp, G. What is the magnitude of the group-size effect on vigilance? Behav. Ecol. 2008, 19, 1361–1368. [Google Scholar] [CrossRef]
- Pays, O.; Renaud, P.C.; Loisel, P.; Petit, M.; Gerard, J.F.; Jarman, P.J. Prey synchronize their vigilant behaviour with other group members. Proc. R. Soc. Lond. B 2007, 274, 1287–1291. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, W. Geometry for the selfish herd. J. Theor. Biol. 1971, 31, 295–311. [Google Scholar] [CrossRef]
- Ioannou, C.C.; Guttal, V.; Couzin, I.D. Predatory Fish Select for Coordinated Collective Motion in Virtual Prey. Science 2012, 337, 1212–1215. [Google Scholar] [CrossRef] [PubMed]
- Cresswell, W.; Quinn, J.L. Attack frequency, attack success and choice of prey group size for two predators with contrasting hunting strategies. Anim. Behav. 2010, 80, 643–648. [Google Scholar] [CrossRef]
- Giraldeau, L.A. The stable group and the determinants of foraging group size. In The Ecology of Social Behavior; Slobodchikoff, C.N., Ed.; Academic Press: San Diego, USA, 1988; pp. 33–53. [Google Scholar]
- Ritz, D.A. Costs and benefits as a function of group size: Experiments on a swarming mysid, Paramesopodopsis rufa Fenton. In Animal Groups in Three Dimensions; Parrish, J.K., Hamner, W.M., Eds.; Cambridge University Press: Cambridge, UK, 1997; pp. 194–206. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Roca, C.P.; Cuesta, J.A.; Sánchez, A. Evolutionary game theory: Temporal and spatial effects beyond replicator dynamics. Phys. Life Rev. 2009, 6, 208–249. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Kokubo, S.; Jusup, M.; Tanimoto, J. Universal scaling for the dilemma strength in evolutionary games. Phys. Life Rev. 2015, 14, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Lett, C.; Auger, P.; Gaillard, J.M. Continuous cycling of grouped vs. solitary strategy frequency in a predator-prey model. Theor. Pop. Biol. 2004, 65, 263–270. [Google Scholar] [CrossRef] [PubMed]
- Packer, C.; Ruttan, L. The evolution of cooperative hunting. Am. Nat. 1988, 132, 159–198. [Google Scholar] [CrossRef]
- Mchich, R.; Auger, P.; Lett, C. Effects of aggregative and solitary individual behaviors on the dynamics of predator-prey game models. Ecol. Model. 2006, 197, 281. [Google Scholar] [CrossRef]
- Frean, M.; Abraham, E.R. Rock-scissors-paper and the survival of the weakest. Proc. R. Soc. Lond. B 2001, 268, 1323–1327. [Google Scholar] [CrossRef] [PubMed]
- Lütz, A.F.; Risau-Gusman, S.; Arenzon, J.J. Intransitivity and coexistence in four species cyclic games. J. Theor. Biol. 2013, 317, 286–292. [Google Scholar] [CrossRef] [PubMed]
- Rulquin, C.; Arenzon, J.J. Globally synchronized oscillations in complex cyclic games. Phys. Rev. E 2014, 89, 6. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, T.; Mobilia, M.; Frey, E. Coexistence versus extinction in the stochastic cyclic Lotka-Volterra model. Phys. Rev. E 2006, 74, 051907. [Google Scholar] [CrossRef] [PubMed]
- Cremer, J.; Reichenbach, T.; Frey, E. Anomalous finite-size effects in the Battle of the Sexes. Eur. Phys. J. B 2008, 63, 373–380. [Google Scholar] [CrossRef]
- van Veelen, M.; García, J.; Avilés, L. It takes grouping and cooperation to get sociality. J. Theor. Biol. 2010, 264, 1240–1253. [Google Scholar] [CrossRef] [PubMed]
- Potts, J.R.; Lewis, M.A. How do animal territories form and change? Lessons from 20 years of mechanistic modelling. Proc. R. Soc. Lond. B 2014, 281, 20140231. [Google Scholar] [CrossRef] [PubMed]
- Herbert-Read, J.E.; Romanczuk, P.; Krause, S.; Strömbom, D.; Couillaud, P.; Domenici, P.; Kurvers, R.H.J.M.; Marras, S.; Steffensen, J.F.; Wilson, A.D.M.; et al. Proto-cooperation: Group hunting sailfish improve hunting success by alternating attacks on grouping prey. Proc. R. Soc. B 2016, 283, 20161671. [Google Scholar] [CrossRef] [PubMed]
- Cortez, M.H.; Weitz, J.S. Coevolution can reverse predator-prey cycles. PNAS 2014, 111, 7486–7491. [Google Scholar] [CrossRef] [PubMed]
- Ziff, R.M.; Gulari, E.; Barshad, Y. Kinetic Phase Transitions in an Irreversible Surface-Reaction Model. Phys. Rev. Lett. 1986, 56, 2553. [Google Scholar] [CrossRef] [PubMed]
- Marro, J.; Dickman, R. Nonequilibrium phase transitions in lattice models; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lütz, A.F.; Cazaubiel, A.; Arenzon, J.J. Cyclic Competition and Percolation in Grouping Predator-Prey Populations. Games 2017, 8, 10. https://doi.org/10.3390/g8010010
Lütz AF, Cazaubiel A, Arenzon JJ. Cyclic Competition and Percolation in Grouping Predator-Prey Populations. Games. 2017; 8(1):10. https://doi.org/10.3390/g8010010
Chicago/Turabian StyleLütz, Alessandra F., Annette Cazaubiel, and Jeferson J. Arenzon. 2017. "Cyclic Competition and Percolation in Grouping Predator-Prey Populations" Games 8, no. 1: 10. https://doi.org/10.3390/g8010010
APA StyleLütz, A. F., Cazaubiel, A., & Arenzon, J. J. (2017). Cyclic Competition and Percolation in Grouping Predator-Prey Populations. Games, 8(1), 10. https://doi.org/10.3390/g8010010





