Assessing Others’ Risk‐Taking Behavior from Their Affective States: Experimental Evidence Using a Stag Hunt Game

Abstract

Researchers are increasingly exploring the role of emotions in interactive decision-making. Recent theories have focused on the interpersonal effects of emotions—the influence of the decision-maker’s expressed emotions on observers’ decisions and judgments. In this paper, we examine whether people assess others’ risk preferences on the basis of their emotional states, whether this affects their own behavior, and how this assessment matches others’ actual behavior. To test these ideas, we used an experimental Stag Hunt game (n = 98), and included non-trivial financial consequences. Participants were told (truthfully) that their counterparts’ previous task had left them happy, fearful, or emotionally neutral. People who were told their counterparts were fearful reported that they expected less risky decisions from these counterparts than people told their counterparts were neutral or happy. As a result, given that the Stag Hunt is a coordination game, these participants were themselves less risky. Interestingly, these participants’ expectations were not accurate; thus, coordination failed, and payoffs were low. This raises the possibility of a “curse of knowledge” whereby one player’s erroneous beliefs about the effects of the counterpart’s emotional state leads the first player to make poor action choices.

1. Introduction

After a century in which behavioral decision research was dominated by the power of reason, the past fifteen years has seen a renewed interest in the decisional consequences of affect [1]. Emotions have been found to be indispensable in making decisions, by providing a “somatic marker” that accompanies response options, thereby dictating choice [2]. Indeed, models of individual decision-making including affect increase their explanatory power to a large degree [3].

The bulk of what has been investigated in this area has focused on how emotions impact individual decisions. For example, researchers have found that people anticipate the emotional consequences of decision outcomes, such as rejoicing when receiving a large lottery prize or regret when making counterfactual comparisons [4,5]. Emotional states experienced by the individual at the moment of making the decision can also affect the decision at hand: they can be used as an input into the decision people face [6]; they may overwhelm thoughtful decision-making [7]; and they may change the depth of information processing [8].

Other researchers have explored the consequences of emotions in interactive decisions. Some scholars have studied how emotions affect economic decisions when the counterpart is a human being, as opposed to “Nature” [9,10]. For example, Kugler and colleagues [11] found that fearful individuals are more risk-averse than angry or happy individuals when risk is based on nature, but are less risk-averse when risk is based on the decisions of another individual (see also Schlösser et al. [12]).

In this paper, we take a different perspective on how affect influences decisions, particularly risk-related decisions. We examine whether people assess others’ risk preferences on the basis of their emotional states; and whether this affects their own behavior as well. Consider a young musician—Rick—who has a rock band and needs to borrow $1500 to take the band on a trip. His uncle Paul—a very nice guy—might loan him the money, but there is obviously a risk that Rick will not be able to pay back if the road trip goes badly. Moreover, uncle Paul generally does not like taking big risks. Imagine further that Rick, before going to talk to him, asks his cousin Janet how Paul is feeling today. She tells Rick he recently got some bad news and is quite anxious about it. Do you think that this information will change whether Rick goes ahead and asks the loan today (or whether he waits and asks Paul the question on a different day)?

An important perspective in this regard is people’s theory of mind. Human beings are said to have a theory of mind; in other words, they ascribe mental states to themselves and others [13]. A theory of mind enables people to make attributions of motivations and intentions to others. People generate hypotheses and develop theories—right or wrong—about these mental states, in order to understand and manage their environment. This allows them to make predictions, on the basis of some assumed mental states, about others’ behaviors.

Scholars examining the emotional and cognitive components of theory of mind in people have pointed out its crucial role in social relationships [14]. Understanding others’ emotions, as well as their consequences, helps individuals in shaping their interpretation of events. For example, George Lakoff [15], a cognitive linguistic, underscored how lay theories and metaphors are useful in interpreting the way people think about emotions. His focus, in particular, was on anger. Lakoff argued that people think that anger impairs normal reasoning, which is reflected in statements such as “she was blind with rage” or “I was so mad I couldn't see straight.” Anger is also likened to fire and thus is seen as a danger to others. This is echoed in expressions such as “breathing fire.” Lakoff claimed that these metaphors show that anger is not just an amorphous feeling, but rather that it has an elaborate cognitive structure.

An important distinction emotion researchers have made is between integral and incidental emotions [16]. Integral emotions are those in which the decision is directly connected to the decision at hand (e.g., disappointment if you make a decision and do not receive what you expected). However, in a number of occasions, emotions and moods arise because of factors unrelated to the focal situation, such as those emotions brought by listening to music, experiencing bad weather, or reliving stressful events [17]. These emotions, which have been labeled incidental, can also have important consequences on decision-making [18].

The present paper examines whether people have certain beliefs about how others’ incidental emotions affect decision-making, and whether in interactive settings these beliefs may guide their own behavior. We examine issues in interactive decisions involving two individuals, Player A and Player B. Thus, the main research questions are, first, how does A’s knowledge of B’s emotional state affect her expectations of B’s risk preference? Second, how do these expectations affect A’s own risk preference? Finally, how do possible inaccuracies in A’s expectations and behavioral adjustments to them affect the outcomes of the players’ interactive decisions?

1.1. The Stag Hunt Game

We specifically focus on the Stag Hunt game [19] (also known as Wolf’s Dilemma [20]) to test these predictions. An instructive way to understand the Stag Hunt is to describe it as did French philosopher Jean Jacques Rousseau [21]. Two hunters each choose, simultaneously and without communication, whether to hunt a stag or a rabbit. Both hunters are needed to successfully hunt a stag, which leads to a big payoff for each party. However, if hunter A decides to hunt a stag, and hunter B decides to hunt a rabbit, A receives nothing because this endeavor is too difficult for a solo hunter. Coordination is unnecessary when rabbit-hunting: choosing to hunt a rabbit leads to the same modest payoff regardless of what the other hunter does. That is, rabbit-hunting is riskless, but the payoff is small. Stag-hunting can lead to a big pay-off, but it is risky, with risk stemming from the uncertainty of the other hunter’s decision [22].

Kugler et al. [11] refer to this risk as being interactive or person-based, as opposed to the risk stemming from nature as in lottery gambles. In the version of the game used in the present study, we discarded the hunting cover-story and presented the game in purely financial terms: a choice between a safe and a risky option, with payoffs determined jointly by the choices made by each player and his or her counterpart.

Another important factor in this game is the players’ expectations. Indeed, this game is also known as the assurance game because “players will play stag only if they are assured others are likely to choose stag as well” [23] (p. 376). In other words, if Player B is more willing to take risks (i.e., more willing to choose the stag), Player A’s expected payoff of choosing the stag increases. Thus, any information—perhaps including others’ emotional state—that leads Player A to think that B is willing to take risks should cause an increase in the likelihood of A choosing the stag.

1.2. Player A’s Expectations

We examined the effects of two incidental emotions, fear and happiness, on expectations of others’ risk-taking. Smith and Ellsworth [24] found that people describe the experience of fear as unpleasant (i.e., negative in valence) and related to perceptions of low control and certainty. Fear involves uncertainty about whether one will be able to avoid an unpleasant outcome [25,26]. Saffrey et al. [27] showed that people associate distinct emotions with different levels of approach (e.g., studying hard) and avoidance (e.g., staying away from parties the night before an exam) behaviors. In their study, participants were asked to state their agreement with statements regarding both types of behaviors. The two items that people answered under avoidance behaviors were “Stops me from making the same mistakes again” and “Stops me from doing dangerous or harmful things” (p. 53). These statements seem to capture some dimension of caution, which is how people tend to understand risk avoidance [28]. Saffrey et al. [27] found that, among 12 negative emotions, participants reported thinking that fear were most likely to facilitate avoidance behaviors. In contrast, people describe the feeling of happiness as pleasant and related to perceptions of high control and certainty [24,29]. People think that others experiencing positive affect are more optimistic about their future [30].

Based on the above, we hypothesized that As expect that fearful Bs will be less likely to take risks (i.e., choose the Stag option less frequently) than neutral Bs (Hypothesis 1.1), and that As expect that happy Bs will be more likely to take risks (i.e., choose the Stag option more frequently) than neutral Bs (Hypothesis 1.2).

1.3. Player A’s Risk Preference

In the Stag Hunt game, Player A’s expectations of what Player B decides are strongly related to A’s actions [22]. The more likely individuals think their counterpart is to choose Stag, the more likely they are to choose Stag themselves. For example, Büyükboyacı [31] found that informing a player about her opponent’s risk aversion affected the player’s action. Thus, paralleling the predictions in the previous section, we hypothesize that As interacting with fearful Bs will be less likely risk-taking (i.e., choose the Stag option less frequently) than those interacting with neutral Bs (Hypothesis 2.1), and that As interacting with happy Bs will be more likely take risks (i.e., choose the Stag option more frequently) than those interacting with neutral Bs (Hypothesis 2.2).

1.4. Player B’s Actual Risk Preference

The final predictions concern how Bs’ emotional states affect their actual risk preferences, and how they compare to Player A’s expectations. Lerner and Keltner [29] conducted a set of studies involving both naturally occurring and experimentally induced fear and happiness. They found that fearful people made pessimistic risk estimates and risk-averse choices, whereas happy people made optimistic risk estimates and risk-seeking choices. Kugler et al. [11] extended these findings to the differential effects of lottery risk and person-based risk. They found that fearful people were less risk-seeking than angry people in a lottery task—replicating Lerner and Keltner's [29] results. However, in the Stag Hunt game, fearful people were more risk-seeking than angry people. (As they did not include a neutral condition, it is unclear whether this finding was due to the effect of incidental fear or anger or both.)

Given the somewhat equivocal nature of earlier studies regarding fear and risk, we offer no formal hypothesis, but simply pose the questions: Are fearful Bs more likely to take risks (i.e., choose the Stag option more frequently) than neutral Bs (Research Question 1.1)? Are As interacting with fearful Bs less accurate than those interacting with neutral Bs (Research Question 1.2)?

In sum, we hypothesize the following:

Hypothesis 1.1.

As expect that fearful Bs will be less likely to take risks than neutral Bs.

Hypothesis 1.2.

As expect that happy Bs will be more likely than neutral Bs.

Hypothesis 2.1.

As interacting with fearful Bs will be less likely to take risk than those interacting with neutral Bs.

Hypothesis 2.2.

As interacting with happy Bs will be more likely take risks than those interacting with neutral Bs.

Research Question 1.1.

Are fearful Bs more likely to take risks than neutral Bs?

Research Question 1.2.

Are As interacting with fearful Bs less accurate than those interacting with neutral Bs?

2. Materials and Methods

In the experiment, we investigated how participants made risk-taking decisions in light of emotional information about their opponents, and how their beliefs fared with actual behaviors. Participants made these decisions, which entailed non-trivial financial outcomes. They were asked to make their decisions after learning that their counterpart was experiencing a specific emotion.

2.1. Participants

Ninety-eight (49 As and 49 Bs) undergraduate business students participated in exchange for class credit and their earnings from the experiment. The participants’ mean age was 21.3 years (SD = 3.8) and 59 (60.2%) were male. Most (76.5%) were White, 10.2% were Hispanic, 6.1% Asian, 1.0% African-American, and 6.1% of other races. The majority (80.6%) were in their third year at the university; the rest were in their fourth year or more.

2.2. Procedure and Design

Participants were recruited via an internet-based system and the study was conducted in the University’s Decision Behavior Laboratory. They received course credit for their participation, in addition to the payoffs from the experiment. Upon arrival to the laboratory, participants were randomly assigned to the role of Player A or Player B, and then led to individual rooms, where they completed the tasks. They were informed that they would take part in two unrelated experiments. The ostensibly first experiment (“Episodic Memory Study”) attempted to induce fear and happiness among Bs by using a writing task validated in several studies [11,32,33]. As participated in a neutral writing task in all conditions (they wrote about a recent classroom session), as did Bs in the neutral condition.

In the second task—the main task—we conducted the Stag Hunt game. The study had a one-factor between-subjects design. The main manipulation was that, before they made their decision, As were informed that the Player B they were paired with completed a task that likely triggered a particular emotion (a factor we label “Knowledge of B’s emotion”).

There were 3 levels of the main manipulation: “Happy B,” “Fearful B,” and “Neutral B.” For example, participants in the Fearful B condition were told that their counterparts wrote about a scary situation (for example, being followed by potentially dangerous men at night in a third-world country) and that they were experiencing fear. As in the Neutral B condition were told that Bs participated in a task similar to the one in which they participated. Seventeen As were assigned to the Happy B condition, 16 were assigned to the Neutral B condition, and 16 were assigned to the Fearful B condition. Equal numbers of Bs were assigned to each condition (17, 16, and 16, respectively).

After the manipulation, participants made their decisions in the Stag Hunt game. This is a simultaneous game: both players make their decisions at the same time, without knowing the other’s decision.

Table 1. Payoff matrix of the Stag Hunt game in the present study.

	Player B
Player A	Option 1	Option 2
Option 1	10, 10	10, 0
Option 2	0, 10	20, 20

Note. In each cell, the first value represents Player A’s payoff; the second value represents Player B’s payoff.

shows the payoff matrix participants confronted. Option 1 (the Rabbit) is the safe option; Option 2 (the Stag) is the risky option. In a given condition, the more people tend to choose Option 2 (the Stag), the more their behaviors are considered risk-seeking (i.e., person-based risk-seeking). As response forms included reminders about the writing task that Bs completed.

Following their decision, and before they were informed about Player B’s decision, participants in the role of Player A completed a post-decision questionnaire. They were first asked what their counterparts wrote about in the memory task: an experience that made them fearful, an experience that made them happy, or a classroom session. This constituted Player A’s manipulation check.

As were also asked about their expectations that B would choose Option 2. This was presented as a one-item scale, ranging from 0% (I’m certain s/he will choose Option 1—the safe option) to 100% (I’m certain s/he will choose Option 2—the risky option), in increments of 10%. After completing the post-decision questionnaire, participants were informed about their counterpart’s decisions, paid, and dismissed. Participants took around 35 minutes in completing both tasks and were paid on average $12.80.

3. Results

3.1. Player A

3.1.1. Manipulation Checks

As were asked which emotion Bs wrote about: happiness, neutral, or fear. Of the 49 As, 47 (96%) indicated the correct emotion 1.

3.1.2. Test of Hypotheses

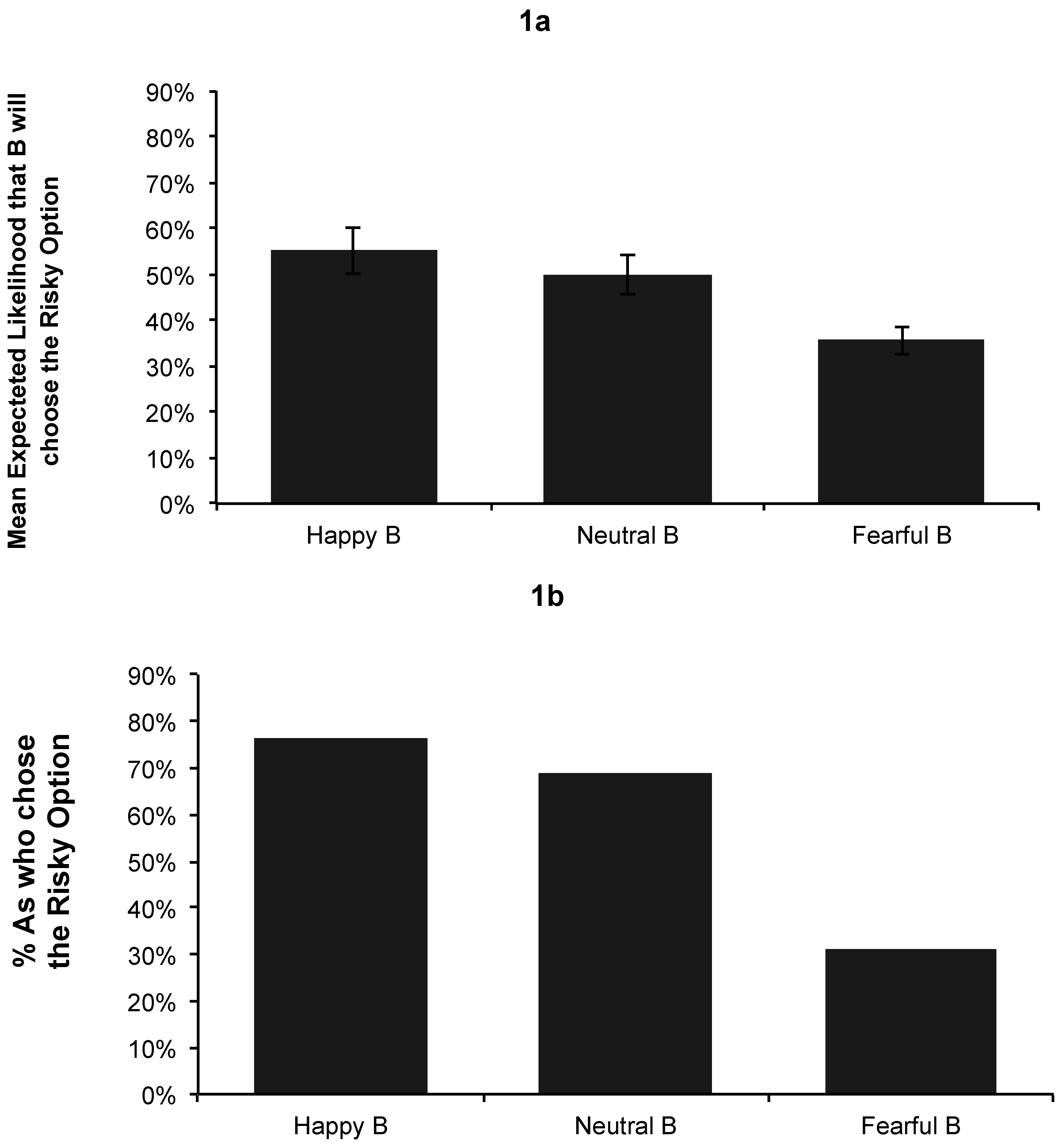
We first focused on Hypotheses 1.1–1.2, dealing with A’s expectations of B’s decisions (see Figure 1a). Hypothesis 1.1 stated that As believe that fearful Bs are less likely to take risks than neutral Bs. As in the Fearful B condition assigned a lower percentage likelihood to Bs choosing the risky option (M = 35.6%) than As in the Neutral B condition (M = 50.0%), t (30) = −2.70, p < 0.05, d = −1.14, which supports Hypothesis 1.1. Hypothesis 1.2 stated that As believe that happy Bs are more likely to take risks than neutral Bs. Contrary to this hypothesis, there were no significant differences in the expectations of As in the Happy B condition (M = 55.3%) and those in the Neutral B condition (M = 50.0%), t (31) = 0.79, p = 0.592.

We found similar results when testing Hypotheses 2.1–2.2, dealing with As’ decisions. The proportion of risky choices in each condition is shown in Figure 1b. To test the hypotheses, we used Howell’s method for categorical data. We first conducted an omnibus chi-square, which was significant, χ² (2, n = 49) = 7.88, p < 0.05, φ² = 0.41. We then compared the conditions we were interested in. Hypothesis 2.1 stated that As interacting with fearful Bs would take less risks (i.e., choose the Stag option less frequently) than those interacting with neutral Bs. Supporting this hypothesis, we found that fewer As in the Fearful B condition chose the risky option (31.3%) than did those As in the Neutral B condition (68.8%), χ² (1, n = 32) = 4.50, p < 0.05, φ² = 0.38. Hypothesis 2.2 proposed that As interacting with happy Bs would take more risks (i.e., choose the Stag option more frequently) than those interacting with neutral Bs. This hypothesis was not supported. The proportion of As in the Happy B condition who chose the risky option (76.5%) was not significantly different from that of Player As in the Neutral B condition (68.8%), χ² (1, n = 33) = 0.62, p = 0.619. As’ decisions and expectations were significantly correlated, r (49) = 0.62, p < 0.01.

3.1.3. Additional Analyses

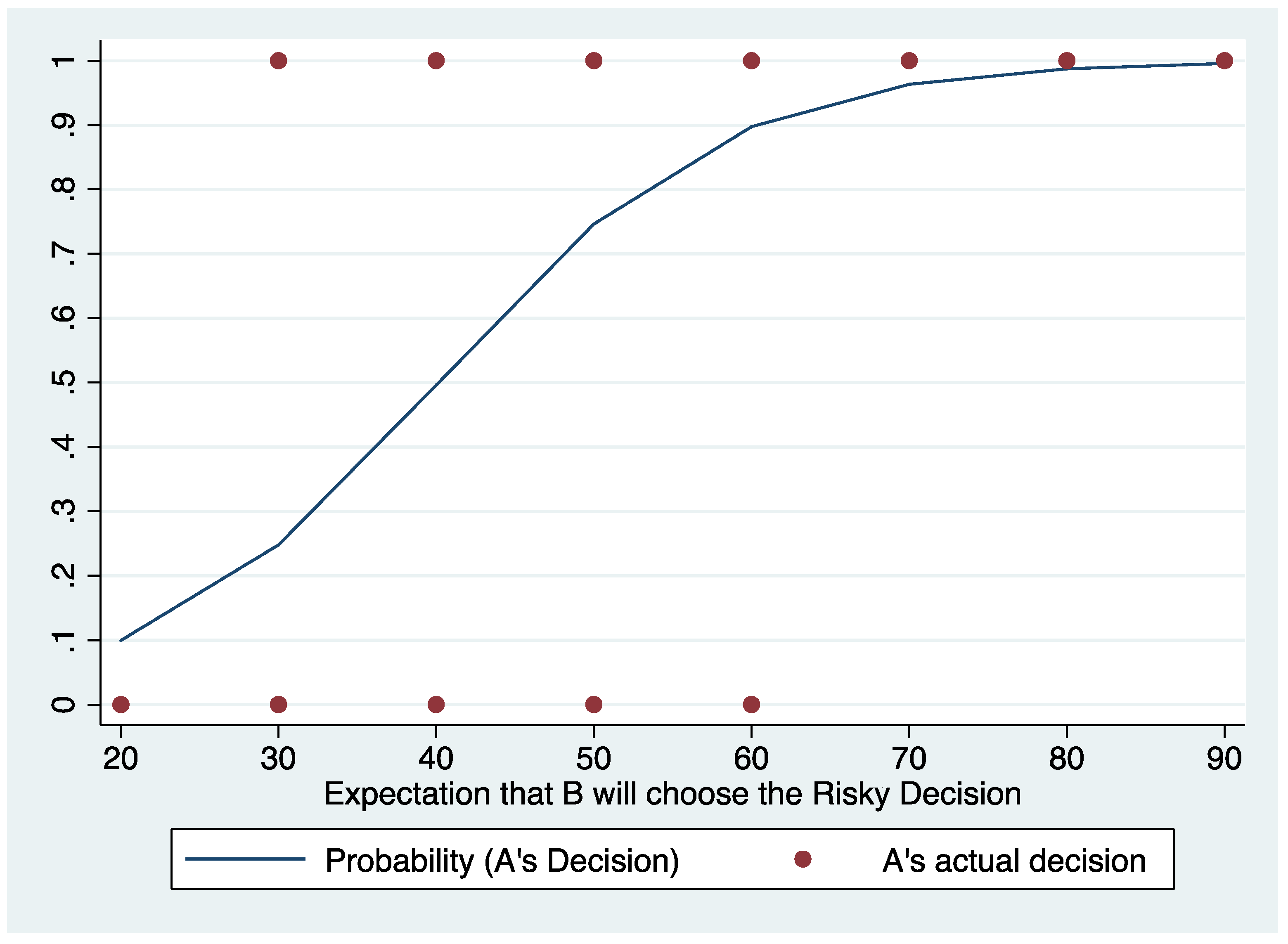
When comparing the Figure 1a,b, there seems to be a mismatch between Player A’s expectations about Player B and the actual risky choice of A2. In particular, in the Happy B and Neutral B conditions, there are substantial differences between these variables; whereas in the Fearful B condition, the differences are smaller. To further examine this issue, we conducted a logistic regression, using A’s decision as the outcome and the expectations as the predictor. Then, we plotted the predicted probabilities against the observed values (see Figure 2). A key issue seems to be the nature of the relationship between Player A’s expectations about Player B choosing the risky option and the actual risky choice of A. Whereas the mean excepted likelihood in the fear condition was around 55%, it was around 35% in the happy condition. The graph shows that, when the expectation is 35%, the predicted probability is around 35%; however, when the expectation is 55%, the predicted probability jumps to around 80%.

We also computed the expected monetary value of making a risky choice for each participant based on their expectations of B’s behavior. Then, we examined how many participants made a decision different from what the expected value would suggest. For each condition, there were only two (in the Happy B condition) and three (in the Neutral B and Fearful B conditions) cases in which participants deviated from this normative rule. Thus, we conclude that Player A’s behavior across conditions was consistent, based on their expectations of B’s behavior.

3.2. Player B

Research Question 1.1 asked whether fearful Bs would engage in more risk taking than those in the neutral condition. Although there was some trend toward the direction of the question, the answer is no. We found no significant differences between the proportion of fearful Bs who chose the Risky option (87.5%) and the proportion of neutral Bs who chose this same option (62.5%), χ² (1, n = 32) = 2.67, p = 0.102.

3.3. Joint Payoff and As’ Accuracy

Research Question 1.2 asked whether As interacting with fearful Bs are more accurate than those interacting with neutral Bs. We tested differences in accuracy using the Probability Score (PS) [34], which has been defined as “a measure of the overall accuracy of [a] probability estimate” [35] (p. 79) and has been widely used in studies of weather forecasting and medical judgment [36]. The PS is operationalized as the squared difference between the estimate of the likelihood of an event (f) and the outcome (d):

PS (f, d) = (f − d)²

(1)

In our study, f is the likelihood that the other person will choose the risky option (ranging from 0% to 100%), and d is whether the other person actually chose the risky option or not (1 or 0, respectively). Thus, the lower the score, the greater the accuracy of a given prediction.

The omnibus F-test revealed significant differences in PS scores across conditions, F (2, 46) = 3.47, p < 0.05, η² = 0.13. Then, pairwise contrasts revealed that the expectations of As in the Fearful B condition were significantly less accurate (M = 0.38) than those of As in the Neutral B condition (M = 0.24), t (30) = −2.09, p < 0.05, d = 0.80 and those in the Happy B condition (M = 0.22), t (31) = −2.27, p < 0.05, d = 0.85. The answer to Research Question 1.2 is thus positive. No differences were found between the Neutral B and Happy B conditions, t (31) = −0.32, p = 0.75.

This difference in accuracy had implications in the pairs’ joint payoff across conditions. The omnibus F-test revealed significant differences across conditions in joint payoff F (2, 46) = 4.08, p < 0.05, η² = 0.15. The joint payoff of pairs in the Fearful B condition (M = $18.13) was significantly lower than that of pairs in the Neutral B (M = $26.88) condition, t (30) = 2.89, p < 0.01, d = −1.00, and marginally significantly lower than that of the pairs in the Happy B condition (M = $31.18), t (31) = 2.89, p = 0.070, d = −0.64.

4. Discussion

The aim of the present study was to examine whether people assess others’ risk preferences on the basis of their emotional states, whether this affects their own behavior, and how this assessment match others’ actual behavior. What stands out most from the results is that people do use emotions, or at least some emotions, to make assessments of others’ risk preferences. In particular, telling As that B is fearful affects their expectations of B’s risk taking. In addition, this information also affects As’ own behavior—their own risk taking. Further, interestingly, we found that As told that B was fearful were less accurate in their expectations than As told that B was neutral or happy. As a result, pairs in the Fearful B condition ended up with significantly lower joint payoffs than those in the Happy B and Neutral B conditions. In other words, As told that B was either happy or in a neutral state correctly expected B to choose the risky option. As, however, expected fearful Bs to be risk-avoidant, while fearful Bs were equally risk seeking than happy Bs or neutral Bs.

This study has theoretical implications. Recent models of the interpersonal effects of emotions, such as the Emotions as Social Information (EASI) model, have underlined the importance of emotion expression as triggering inferential processes in others [37]. The EASI model identifies an important process by which observers’ behaviors can be influenced: inferential processes. As a result, studies testing this model have focused on integral rather than incidental emotions, because of the importance of the environment. For example, if a subordinate performs a task at some level and the supervisor reacts by displaying anger, the subordinate can infer that the supervisor thinks the performance was poor, and given their roles in the organization, the subordinate should improve her performance. However, if the supervisor’s anger is incidental—that is, disconnected from the decision at hand—such inferences are unreliable. In the present experiment, we examined only incidental emotions, separating the individual’s emotional state from prior interactions or future retribution. The decision-makers were unable to make inferences from their counterparts’ emotions concerning their environment. The interpersonal effects of emotions can thus emerge even when no decision-related information is exchanged. The mere fact that a counterpart is experiencing a specific emotion, even when it was exogenously induced, made decision-makers adopt different strategies, drawing on their specific beliefs about how discrete emotions affect behavior. Our study, therefore, extends the EASI model in an interesting way.

5. Limitations and Conclusions

A major drawback of the study is that the sample size is small. Indeed, we conducted a post-hoc power analysis, including the effect size we found across Bs’ behavior (not statistically significant) and the sample size. The resulting power was 0.38, which is low. However, we should also point out that the main focus of the paper was on As3; in other words, the main focus was on participants who received the information about the counterpart’s emotional state. From this perspective, the sample size was sufficient to detect the effects of this information on these participants’ expectations, decisions, accuracy, and outcomes. That said, the small sample in this study results in low confidence in the size and reliability of these effects.

In conclusion, we should point out that the study of “risk as feelings” started less than two decades ago [37]. However, our study shows that people have lay beliefs that emotions such as fear are linked to risk taking. More broadly, our study contributes to a growing body of research showing that people expect that affect and behavior are naturally linked [14].

In a classic article, Humphrey [38] proposed that, by the very nature of human beings’ social dynamic, those individuals who have more accurate expectations of what others would do enjoy a competitive advantage in their chance of survival. He compared the social dynamic to a game of chess because outcomes depend on the strategies that each individual chooses and how they respond to each other. In the game of social chess, knowing about others’ emotions—even if these are incidental—can change decision-makers’ expectations and strategic behaviors. These expectations, however, are not always accurate, and can have detrimental consequences on decisions makers’ outcomes. [37].