Cognitive Hierarchy Theory and Two-Person Games

Abstract

The outcome of many social and economic interactions, such as stock-market transactions, is strongly determined by the predictions that agents make about the behavior of other individuals. Cognitive hierarchy theory provides a framework to model the consequences of forecasting accuracy that has proven to fit data from certain types of game theory experiments, such as Keynesian beauty contests and entry games. Here, we focus on symmetric two-player-two-action games and establish an algorithm to find the players’ strategies according to the cognitive hierarchy approach. We show that the snowdrift game exhibits a pattern of behavior whose complexity grows as the cognitive levels of players increases. In addition to finding the solutions up to the third cognitive level, we demonstrate, in this theoretical frame, two new properties of snowdrift games: (i) any snowdrift game can be characterized by only a parameter, its class; (ii) they are anti-symmetric with respect to the diagonal of the pay-off’s space. Finally, we propose a model based on an evolutionary dynamics that captures the main features of the cognitive hierarchy theory.

1. Introduction

Many real-life situations in human societies imply interactions in which the results of one person’s choices depend not only on his/her own behavior, but also on the choices of the other individuals involved. In these situations, it is usually assumed that people behave strategically, taking into account the likely responses of the other participants who might have an impact on their own benefit. Most theories of behavior assume rationality; perfect rationality is based on two assumptions, namely that agents form correct beliefs about other agents’ behavior and that they choose those actions that maximize their own utility functions. Otherwise, when the rationality of agents is limited by practical elements, such as cognitive and time limitations or the tractability of the decision problem, it is said that there is bounded rationality. Bounded rationality does not involve a maximization of the outcome, since agents can make wrong assumptions about the behavior of others. Indeed, the level of accuracy in the predictions on the other agents’ actions plays a key role in some situations, such as stock-market transactions. These kinds of situations in which the agents’ outcome is strongly determined by their predictions are captured in the Keynesian beauty contests [1] and entry games. In the p-beauty contest game [2], participants have to simultaneously pick a number between zero and 100. The winner of the game is the person(s) whose chosen number is closest to p-times the average of all selections, where $0<p<1$, typically p = 2/3, 1/2. Entry games are anti-coordination games in which agents have to decide whether or not to incur a cost to enter a market [3,4,5,6,7]. The entrants’ profits will be positive if the other agents do not enter, but otherwise can turn out to be negative. In these games, when players act over-confidently, that is assuming that the other players do not act with such refined reasoning as they do, the players are not in equilibrium. Cognitive hierarchy theories capture this behavior by classifying the players according to their degree of reasoning in forming expectations of others [8,9,10,11,12,13,14]. These theories are characterized by a distribution of the number of iterated reasoning steps that players can do, i.e., the distribution of players’ levels. While zero-step (Level-0) players just play at random, higher level players assume they are playing against players who do fewer reasoning steps than they do. The game can be solved by knowing the distribution of players’ levels and the assumptions of players about the distribution of their opponents’ levels. Camerer et al. found that a Poisson distribution fits experimental data from many different games [10]. A Poisson distribution is fully characterized by its mean, in this case the average number of reasoning steps, and they found that an average of $1.5$ steps fits many experimental data. This value implies a fast decay: while 81% of players do, at most, two reasoning steps, only 1% of them do more than four steps , which reflects the limitations of memory and reasoning ability.

Secondly, socially-relevant situations usually involve social dilemmas where individuals profit from selfishness at the expense of collective welfare [15,16,17], as well as coordination and anti-coordination quandaries where all parties can maximize their benefits by making mutually consistent decisions [18,19,20,21,22]. These situations have been widely studied in different disciplines ranging from economics, sociology, political science to psychology, by using the framework of game theory to understand how people approach conflict and cooperation under modeling conditions [23,24,25,26]. In this sense, experimental research has shown that, when people face these situations in game theory experiments, they do not always exhibit rational behavior, either because they do not try to optimize their benefit exclusively or because of individual or practical limitations [27,28].

Here, we focus on a set of two-player-two-action games that capture two important features of social interaction, namely the dilemma between self-interest and the common good and coordination issues [29]. In line with previous literature, we refer to these two actions as cooperation, when the choice transcends self-interest and concentrates on the welfare of collective, or defection, when it is focused on promoting self-interest. This set of games includes the Stag Hunt (SH) [20], the Snowdrift Game (SG) [18,21], and the Prisoner’s Dilemma (PD) [29,30]. SH is a coordination game that describes a conflict between safety and social cooperation; the greatest benefit for both players is obtained when both choose to cooperate, but against a defector, the best action is to defect, so that cooperation is the most advantageous and risky choice. SG is an anti-coordination game where the greater individual benefit is obtained by defecting against a cooperator, but players are penalized when both choose to defect, so that it is always more advantageous to choose the opposite action of your opponent. In PD, a player always gets the highest individual benefit by defecting, while the greater collective benefit is obtained when both cooperate. For completeness, we also study the Harmony Game (HG), where the best choice is always to cooperate, regardless of the opponent’s behavior; therefore, there are no tensions between individual and collective benefits. An arrangement of these four games has been experimentally studied, finding that players can be classified into four basic personality types: optimistic, pessimistic, trusting and envious, with only a small fraction of undefined subjects [31]. Although some of these four games, particularly SH, have being solved according to the cognitive hierarchy approach [10] and the solutions for PD and HG are straightforward, SG presents an intricate pattern of behavior as the cognitive level of the players grows. In this study, we establish an algorithm to solve the SD case: in addition to analytically solving it up to the third cognitive level, we show some symmetries valid for all levels.

We round off this study by exploring the situation in which players can change their guesses about how cognitive levels are distributed in the population. Evolutionary game theory is concerned with entire populations of agents that can choose actions according to some strategies in their interactions with other agents [32,33,34]. We propose a model based on an evolutionary dynamics, in which the agents of a population interact among themselves through the above-described games. In this iterated model, the agents do not have any information of the other players, neither regarding their payments, nor their actions, but only the one-step memory of their own payment. According to this dynamics, the players make attempts to modify their assumptions about the distribution of the cognitive levels of the other players, allowing them to change their assumptions in case their payment decreases. We numerically solve the model using Monte Carlo simulations, finding patterns of behavior compatible with our theoretical predictions.

2. Results

2.1. Preliminary Concepts

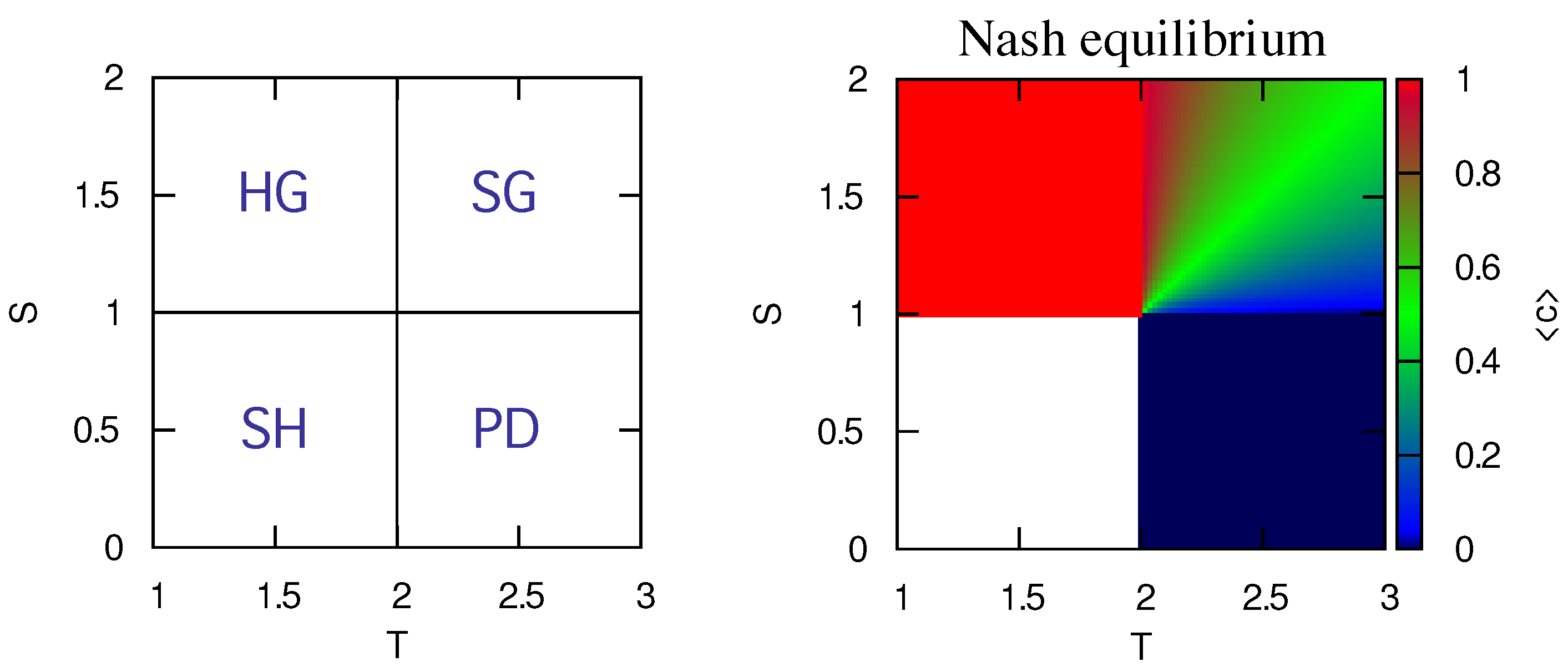
2.1.1. Two-Person Games

Symmetric two-player-two-action games can be expressed by means of the payoff matrix, where rows represent focal player’s actions, columns represent opponent’s actions and the corresponding matrix element is the payoff received by the focal player:

$$\begin{array}{cc}& \begin{array}{cc}C& D\end{array}\\ \begin{array}{c}C\\ D\end{array}& \left(\begin{array}{cc}R& S\\ T& P\end{array}\right)\end{array}.$$

(1)

Actions C and D are usually referred to as cooperation and defection, respectively. Each player chooses one of the two available actions, cooperation or defection. A cooperator receives R when playing with a cooperator and S when playing with a defector, while a defector earns P when playing with a defector and T (temptation) against a cooperator. When $T>R>P>S$, the game is a Prisoner’s Dilemma (PD), while if $T>R>S>P$ it is called a Snowdrift Game (SG), also chicken or hawks and doves. Otherwise, if $S>P$ and $R>T$, the game is referred to as a Harmony Game (HG), while if $R>T>P>S$, it is called a Stag Hunt Game (SH).

We consider a well-mixed population of N agents. According to the payoff matrix (1), a cooperator will receive a payoff $N_{c}R+(N-N_c)S$, where $N_c$ is the number of cooperators, while a defector will receive $N_{c}T+(N-1-N_c)P$. A given player will obtain a higher payoff by cooperating than defecting whenever $cR+(1-c)S>cT+(1-c)P$, where c is the fraction of cooperators in the population, excluding himself/herself. That is, there is a threshold $S_{th}$ for the parameter S:

$$S_{th}(T,P,R;c)=\frac{P+c(T-P-R)}{1-c},$$

(2)

above which a player will obtain a higher payoff by cooperating than by defecting.

In order to have a two-dimensional representation of the parameter space of the four types of games described above, let us fix the values of the payoff parameters $P=1$, $R=2$. By varying the values of T and S over the ranges $T\in [1,3]$ and $S\in [0,2]$, the plane $(T,S)$ can be divided into four quadrants, each one corresponding to a different type of game: HG ($T<2,S>1$), SG ($T>2,S>1$), SH ($T<2,S<1$) and PD ($T>2,S<1$). According to these values, Equation (2) becomes:

$$S_{th}(T;c)=\frac{1+c(T-3)}{1-c}.$$

(3)

Note that, for fixed $T>2$, $S_{th}$ is an increasing function of c, while it is decreasing for $T<2$. This observation will be crucial in some of the arguments below in the next subsections (Figure 1).

2.1.2. Cognitive Hierarchy Theory

According to the cognitive hierarchy theory, each agent i ($i=1,2,\dots ,N)$ is characterized by her/his cognitive level $l_i$ ($l_i=0,1,2\dots$) and her/his assumed distribution of other players’ levels. Level-0 players ($l_i=0$) choose their actions randomly, which means that a Level-0 player should cooperate with probability $p_c=$ 1/2, regardless of the values of the payoff matrix. A Level-1 player ($l_i=1$) assumes that the other players will act non-strategically (i.e., as Level-0 players). In the same way, a level-h player ($h>1$) assumes a heterogeneous population consisting of players of lower levels $0,1,2,\dots ,h-1$. A strategic agent i ($l_i>0$) assumes that the cognitive levels of her/his $N-1$ opponents are distributed according to a given distribution (Camerer et al. [10] considered this to be Poisson). In particular, a level-h player ($h>1$) assumes respective ratios $g_h\left(k\right)$ of level-k players, $k=0,1,\dots ,h-1$, with:

$$\sum _{k=0}^{h-1}{g}_h\left(k\right)=1.$$

(4)

Then, each agent chooses the action that would provide a higher payoff if the cognitive levels of the rest of the agents were distributed according to her/his assumption. The next subsection is devoted to the analysis of the actions taken by the agents in the four types of games under the assumptions of cognitive hierarchy theory.

2.2. Analysis

2.2.1. Harmony Game

Provided $S>P,R>T$, the expected payoff is higher for cooperation regardless of other players’ actions. As a consequence, all strategic players (a level higher than zero) will choose cooperation. In the HG, cooperation is the only strict best response to itself and to defection.

2.2.2. Prisoner’s Dilemma

Given the payoff’s ordering $T>R>P>S$, whatever the value of the cooperation level c is, the expected payoff is higher for defection, and that is what a strategic player i ($l_i>0$) should choose. In the PD game, only the defective action is a strict best response to itself and to cooperation.

2.2.3. Stag Hunt

A player of Level-1 assumes a population consisting of $N-1$ opponents of Level-0, that is she/he assumes a fraction of cooperators $c=1/2$. According to Equation (3), a Level-1 strategist playing a SH should cooperate if and only if:

$$S>S_{th}(T;c=1/2)=\frac{1+(1/2)(T-3)}{1-(1/2)}=T-1.$$

(5)

Now, a Level-2 player has to consider two situations:

(i)

For $S>T-1$, we have $S>S_{th}(T;1/2)$, and Level-1 players will cooperate. Thus, the average cooperation c assumed by a Level-2 player will be $c=g_2\left(0\right)/2+g_2\left(1\right)=g_2\left(0\right)/2+g_2\left(0\right)=1-g_2\left(0\right)/2$. Provided $g_2\left(0\right)<g_1\left(0\right)=1$, i.e., Level-2 players assume at least one Level-1 player, we have $c>1/2$, and therefore (using that, for $T<2$, $S_{th}$ is a decreasing function of c), $S_{th}(T;c)<S_{th}(T;1/2)$, which implies that a player of Level-2 playing an SH will choose to cooperate if $S>T-1$.

(ii)

For $S<T-1$, we have $S<S_{th}(T;1/2)$, and Level-1 players will defect. The assumed cooperation level c is $c=g_2\left(0\right)/2$. Provided $g_2\left(0\right)<g_1\left(0\right)=1$, we have $c<1/2$; hence (as $T<2$) $S_{th}(T;c)>S_{th}(T;1/2)$, and thus, a player of Level-2 playing an SH will chose to defect if $S<T-1$.

Consequently, a Level-2 player takes the same action as a Level-1 player does: to cooperate if and only if $S>T-1$. Let us assume that level-k players ($k=1,2,\cdots ,h-1$) cooperate if and only if $S>T-1$. Then, a level-h player will assume:

$$c=\frac{g_h\left(0\right)}{2}+\sum _{k=1}^{h-1}{g}_h\left(k\right)=1-\frac{g_h\left(0\right)}{2}>\frac{1}{2},$$

(6)

so that she/he cooperates if and only if $S>T-1$, and thus, the induction argument allows one to conclude that all strategic players cooperate if and only if $S>T-1$ in the SH game.

Summarizing, the line $S=T-1$ divides the quadrant SH into two octants: In the upper octant ($S>T-1$), all players of a level higher than zero cooperate, while in the lower one ($S<T-1$), such players defect. This result is general, for any kind of normalized distributions $g_l\left(k\right)$ ($k=0,\cdots ,l-1$; and $l\ge 1$) assumed by the agents and was already pointed out in [10].

2.2.4. Snowdrift Game

A player of Level-1 considers that the rest of the players play at random, so that she/he assumes $c=1/2$. As a consequence, a Level-1 strategist playing an SG should cooperate if and only if:

$$S>S_{th}(T;c=1/2)=\frac{1+(1/2)(T-3)}{1-(1/2)}=T-1.$$

(7)

Note that this condition coincides with the cooperation condition (5) for Level-1 players playing an SH game. However, things are different for higher level players in the SG, as we now will see. From a technical point of view, the reason is that for the SG, where $T>2$, $S_{th}$ is an increasing function of c, reflecting a well-known feature of the hawk-dove formulation of the SG, namely that in a population of hawks (doves), it is advantageous to play dove (resp. hawk).

Again, a Level-2 player has to consider two situations:

(i)

For $S>T-1$, we have $S>S_{th}(T;1/2)$, and Level-1 players cooperate. Thus, the average cooperation c assumed by a Level-2 player will be $c=g_2\left(0\right)/2+g_2\left(1\right)=g_2\left(0\right)/2+g_2\left(0\right)=1-g_2\left(0\right)/2$. Provided $g_2\left(0\right)<g_1\left(0\right)=1$, i.e., Level-2 players assume at least one Level-1 player, we have $c>1/2$, and therefore, $S_{th}(T;c)>S_{th}(T;1/2)$, which implies that a player of Level 2 playing an SG will choose to cooperate if $S>S_{th}(T;c)$, while she/he will choose to defect if $T-1<S<S_{th}(T;c)$, with $c=1-g_2\left(0\right)/2$.

(ii)

For $S<T-1$, Level-1 players defect. Then, the assumed cooperation level c is $c=g_2\left(0\right)/2$. Provided $g_2\left(0\right)<g_1\left(0\right)=1$, we have $c<1/2$; hence, (as $T>2$) $S_{th}(T;c)<S_{th}(T;1/2)$. Thus, a player of Level 2 will choose to cooperate if $S_{th}(T;c)<S<T-1$, while she/he will choose to defect if $S<S_{th}(T;c)$, with $c=g_2\left(0\right)/2$.

Consequently, regarding the action a Level-2 player takes, there are four sectors in the SG quadrant ($T\in [2,3],S\in [1,2]$):

(a)

$1<S<S_{th}(T;g_2\left(0\right)/2)$, defection.

(b)

$S_{th}(T;g_2\left(0\right)/2)<S<T-1$, cooperation.

(c)

$T-1<S<S_{th}(T;1-g_2\left(0\right)/2)$, defection.

(d)

$S_{th}(T;1-g_2\left(0\right)/2)<S<2$, cooperation.

Note that two of the borderlines separating these regions are dependent on the distribution assumed by the Level-2 player, i.e., these regions are non-universal.

At this point, one realizes that regarding the action a level-l takes, there may appear more and more regions in the SG quadrant, depending on the specific assumption on the distributions $g_h\left(k\right)$ ($k=0,\cdots ,h-1$; and $l>h\ge 1$). As an illustrative example, see Appendix A for the possibilities that arise for the actions taken by a Level-3 player.

Despite this non-universality and increasing complexity with cognitive levels that characterize the actions taken by players of the SG, we show in the next subsection two general symmetries that universally hold, under the assumptions of the cognitive hierarchy theory.

2.2.5. Symmetries in the Snowdrift Game

As before, to simplify notation, we will assume the values $P=1$ and $R=2$, though the arguments below remain valid for other values compatible with SG.

Given a particular SG game, corresponding to a pair of values $(T,S)$, with $T>2$ and $S>1$, we will say that it is a game of class m whenever:

$$m=\frac{S-1}{T-2}.$$

(8)

In other words, m is simply the slope of the straight line connecting the points $(T=2,S=1)$ and $(T,S)$.

The first statement that we will prove is the following:

S1

Any two SG games of the same class m are equivalent, in the sense that any player takes the same action in both games.

To prove this statement, note that Equation (3) can be rewritten as:

$$S_{th}(T;c)=\frac{c}{1-c}T+\left(1-\frac{2c}{1-c}\right),$$

(9)

so that a rational player playing a game of class m cooperates if $m>c/(1-c)$, and defects if $m<c/(1-c)$. Here, c is the value of the average cooperation in the population estimated by the rational player under the assumption of a particular distribution of cognitive levels.

Now, the value of c that a Level-1 player estimates is $c=1/2$, irrespective of any consideration, so the action she/he takes is the same for all games in the same class. Consequently, the estimation of c by a Level-2 player is the same in all games of the same class, so that she/he takes the same action in all of them, and so on for all cognitive levels, which ends the proof of Statement S1.

To avoid possible misunderstandings, let us emphasize that the payoffs received by a player in two equivalent games can be very different. The notion of equivalence between games means here equality of the actions taken by an agent in both games, but it does not mean equality of payoffs received.

In what follows, a game m is a game of class m. A second symmetry is the following:

S2

The action that a player takes in the game m is the opposite to the action she/he takes in the game $m^{-1}$.

Level-1 players satisfy trivially Statement S2, for if $m>1$, then $m^{-1}<1$. Now, let us assume that for levels $1,\cdots ,l-1$ the statement holds. Let us call $C_l$ the subset of these levels whose actions in the game m are cooperation and $D_l$ its complementary. Then, level-l players estimate:

$$c=\frac{g_l\left(0\right)}{2}+\sum _{i\in C_l}{g}_l\left(i\right),$$

(10)

for the game m, while they estimate:

$$c^{\prime }=\frac{g_l\left(0\right)}{2}+\sum _{i\in D_l}{g}_l\left(i\right)=1-c$$

(11)

for the game $m^{-1}$, where the last equality follows from the normalization condition on the distribution of cognitive levels. Consequently, level-l players satisfy Statement S2, for if $m>c/(1-c)$, then $m^{-1}<c^{\prime }/(1-c^{\prime })$. Thus, Statement S2 is proven by the induction argument.

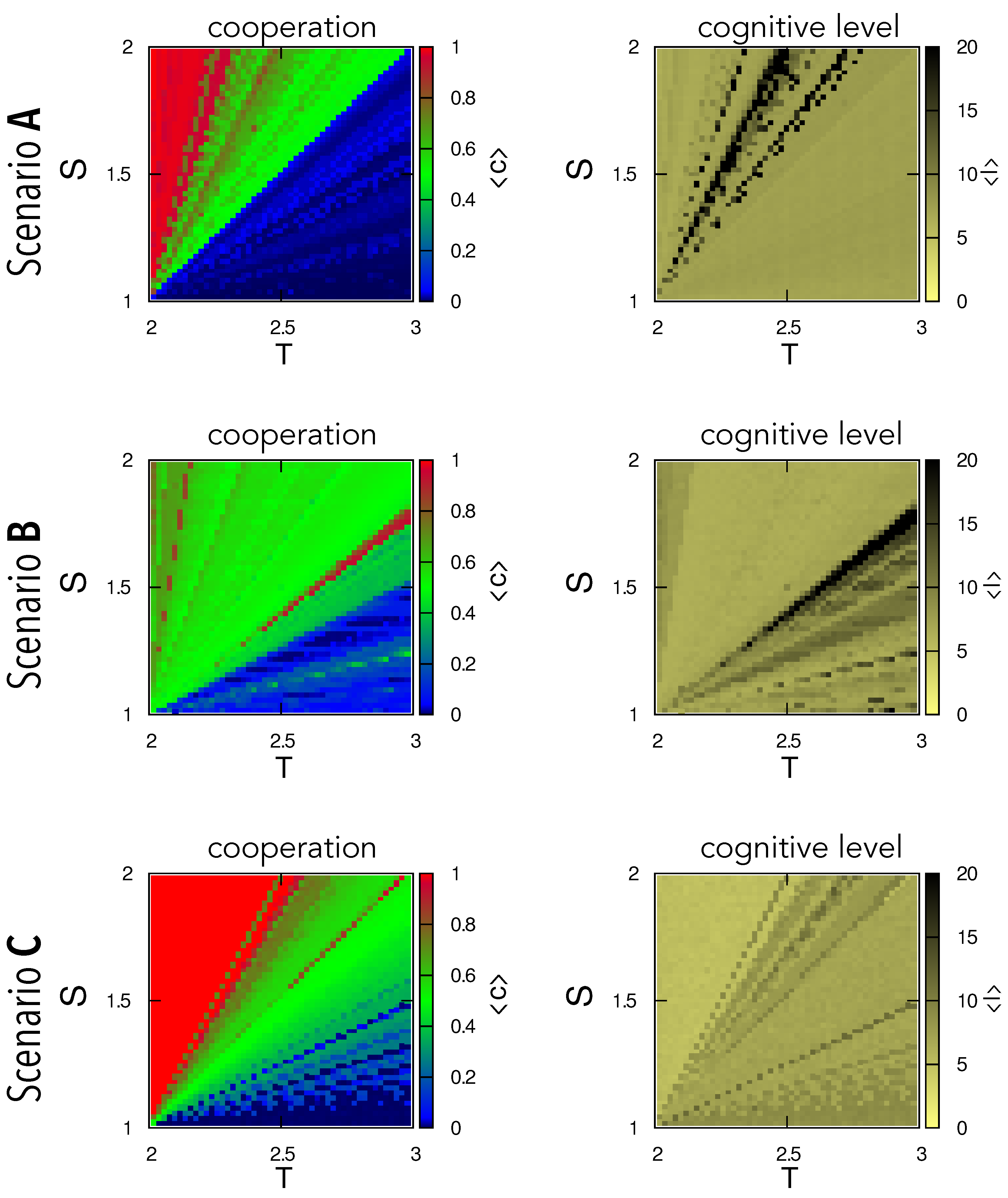
2.3. Dynamics

In this subsection, we introduce a very simple dynamics for the temporal evolution of the distribution that each agent assumes on the cognitive levels of the population and show results for this dynamics. The assumption is that the only information available to each agent i at a given instant of time $t>1$ is her/his current payoff, ${\Pi }_i^t$, and her/his previous payoff, ${\Pi }_i^{t-1}$. Before the presentation of the dynamics, we briefly discuss the types of distributions of cognitive levels considered in the simulations performed.

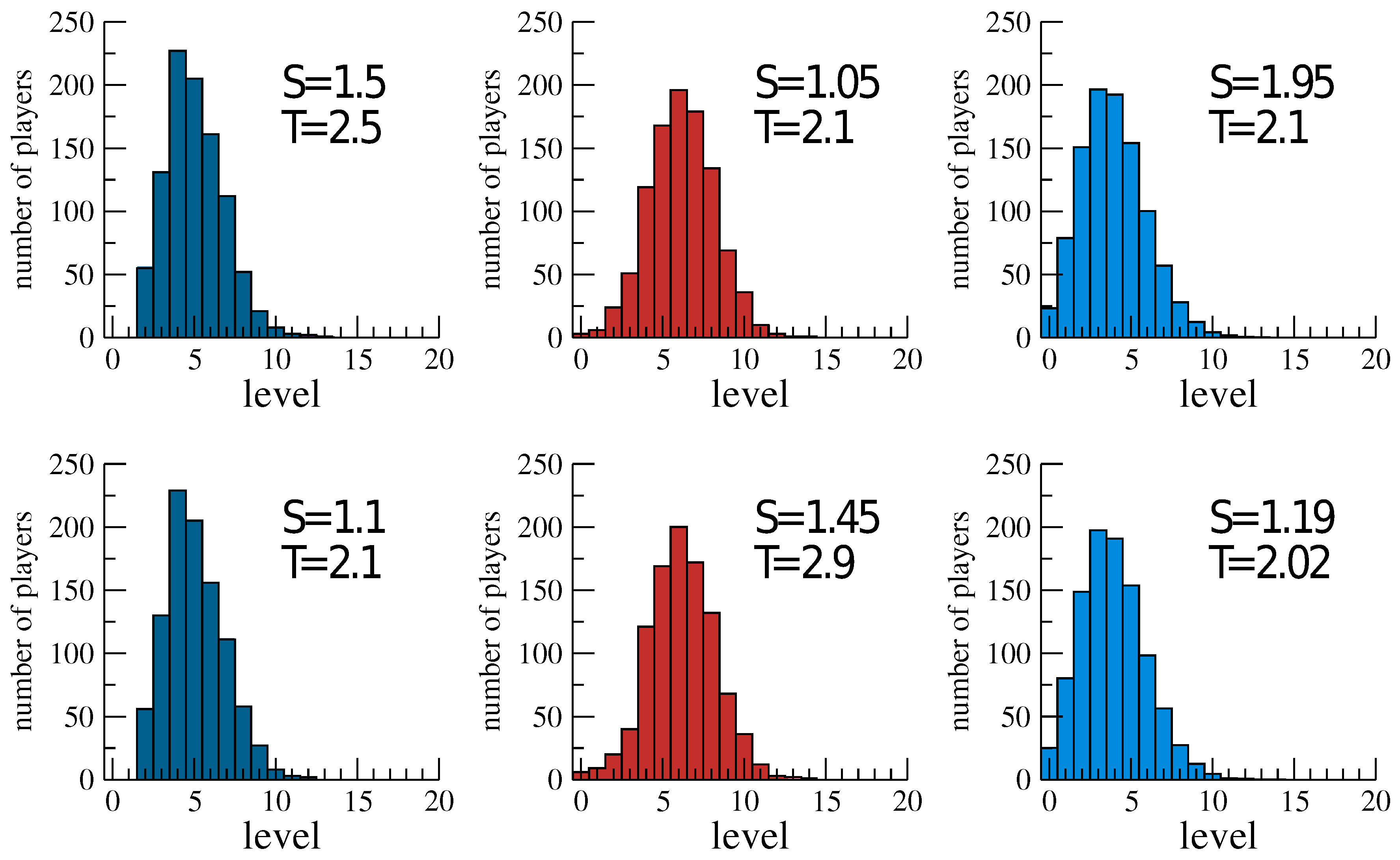
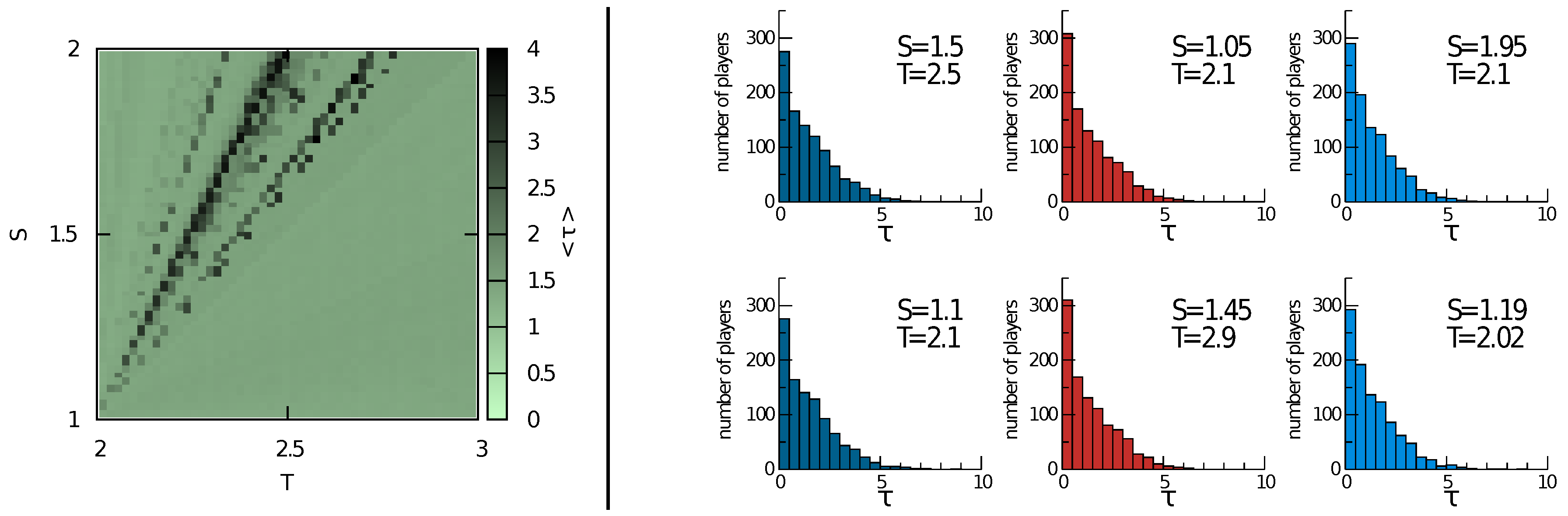
2.3.1. Distributions of Cognitive Levels

The first type of distribution that we have considered (below referred to as Scenario A) is the “normalized” (truncated) Poisson distribution employed in [10], defined as follows. A Poisson distribution is described by a single parameter τ, which is the mean and the variance:

$$f_{\tau }\left(n\right)=\frac{{\tau }^n{e}^{-\tau }}{n!}.$$

(12)

A strategic agent i whose cognitive level is $l_i$ ($>0$) assumes a value of $\tau ={\tau }_i$ and that the cognitive levels $l_j$ ($=0,\cdots ,l_i-1$) of her/his opponents are distributed according to:

$$g_{l_i,{\tau }_i}^A\left(l_j\right)=\frac{f_{{\tau }_i}\left(l_j\right)}{C_i},$$

(13)

where $f_{\tau }$ is the Poisson distribution (12) and $C_i$ is an appropriate normalization constant, i.e.,

$$C_i=\sum _{k=0}^{l_i-1}{f}_{{\tau }_i}\left(k\right).$$

(14)

Writing Equation (13) explicitly, one has:

$$g_{l_i,{\tau }_i}^A\left(l_j\right)=\frac{{\tau }_i^{l_j}}{l_j!{\sum }_{k=0}^{l_i-1}\frac{{\tau }_i^k}{k!}}.$$

(15)

A second type of cognitive level distribution (Scenario B) uses, instead of a Poisson distribution, the following exponential law:

$$f\left(n\right)=\frac{1}{2^{n+1}}.$$

(16)

Now, a strategic agent i whose cognitive level is $l_i$ ($>0$) assumes that the cognitive levels $l_j$ ($=0,\cdots ,l_i-1$) of her/his opponents are distributed according to:

$$g_{l_i}^B\left(l_j\right)=\frac{f(l_i-l_j-1))}{Z_i},Z_i=\sum _{k=0}^{l_i-1}f(l_i-k-1),$$

(17)

that is, explicitly:

$$g_{l_i}^B\left(l_j\right)=\frac{2^{l_j-l_i}}{{\sum }_{k=1}^{l_i}{2}^{-k}}.$$

(18)

The third type of distribution (Scenario C) that we consider here is just a normalized uniform distribution:

$$g_{l_i}^C\left(l_j\right)=\frac{1}{l_i}$$

(19)

2.3.2. Dynamics Algorithm

One must first specify the initial condition ($t=0$) for the dynamics. In the simulations that we show below, our choice is a population with cognitive levels $l_i$ ($0\le l_i\le l_{\max }$) distributed according to a truncated Poisson distribution $g_{l_{\max },\tau }^A\left(l_i\right)$ given by Equation (15) where $\tau =1.5$ and $l_{\max }=20$. For the cases in which the distribution of cognitive levels assumed by the agents is also “truncated Poisson”, the initial rate parameter ${\tau }_i$ of an agent i is taken to be ${\tau }_i=0$ if $l_i\le 1$, and ${\tau }_i=\frac{l_i-1}{2}$ otherwise. Then, the agents play simultaneously a one-shot game where the action taken by each strategic agent is the best response for her/his assumed distribution (either $g_{l_i,{\tau }_i}^A\left(l_j\right)$, or $g_{l_i}^B\left(l_j\right)$, or $g_{l_i}^C\left(l_j\right)$) for the cognitive levels of her/his opponents, each one receiving an initial payoff ${\Pi }_i\left(0\right)$.

Thereafter, the dynamics proceeds according to the following rules: at each time step $t>0$

Step 1

The agents play simultaneously with the action that is the best response according to their current beliefs (random for Level-0 players), each one receiving a payoff ${\Pi }_i\left(t\right)$.

Step 2

Each agent i compares her/his current and previous payoff. If ${\Pi }_i\left(t\right)\ge {\Pi }_i(t-1)$, the agent i keeps her/his current belief on the population distribution, while if ${\Pi }_i\left(t\right)<{\Pi }_i(t-1)$, the agent makes an attempt to change her/his belief.

The attempt to change the currently assumed distribution, for the cases in which this is $g_{l_i}^B$ or $g_{l_i}^C$ (say Scenario B or C), consists of two mutually exclusive possible events:

• With probability u, agent i varies her/his level $l_i$ according to $l_i(t+1)=l_i\left(t\right)\pm 1$, that is, in an equiprobable way, she/he increases or decreases its level $l_i$ at a point.
• Otherwise (i.e., with probability $1-u$), she/he keeps her/his cognitive level.

For the cases in which the agents assume a truncated Poisson distribution, $g_{l_i,{\tau }_i}^A$ (Scenario A), the trial to change the current beliefs consists of three mutually exclusive possible events:

• With probability u, agent i varies her/his level $l_i$ according to $l_i(t+1)=l_i\left(t\right)\pm 1$, that is, in an equiprobable way, she/he increases or decreases its level $l_i$ at a point.
• With probability v (where $u+v\le 1$), agent i varies her/his assumed rate parameter ${\tau }_i$ according to ${\tau }_i(t+1)={\tau }_i\left(t\right)+ϵ$, where $ϵ\in [-\delta ,\delta ]$, preserving ${\tau }_i\ge 0$.
• Otherwise (i.e., with probability $1-u-v$), nothing changes.

Let us note that the presence of non-strategic (Level-0) agents in the initial population is, within this dynamics, a necessary condition for a proper time evolution. A non-strategic agent chooses her/his action at random, and thus, with probability $1/2$, her/his action at $t=1$ is different from that at $t=0$, then making it possible that ${\Pi }_i\left(1\right)<{\Pi }_i\left(0\right)$ for some i.

2.3.3. Simulations Results

We have performed Monte Carlo simulations of the dynamics defined above for the cognitive hierarchy theory of the SG game, for the three scenarios A, B and C that correspond, respectively, to the agents’ assumption for the cognitive levels distribution given by $g^A$ (Equation (15)), $g^B$ (Equation (18)) and $g^C$ (Equation (19)). In all of the cases, the initial conditions were as described in the previous subsection, i.e., cognitive levels were initially distributed in the population according to a truncated Poisson distribution with $\tau =1.5$ and $l_{\max }=20$. The population size is $N={10}^3$; the probability of changing the current cognitive level (provided payoff decreases) is $u=0.45$; and for the Scenario A, $\delta =1$, and $v=0.45$.

In Figure 2 we show, for the three scenarios, the averaged value over one hundred simulations (for each ($T,S$) point) of the fraction of cooperators and the average cooperative level in the stationary state reached by the dynamics in the whole SG quadrant ($T\in [2,3],S\in [1,2]$).

From the inspection of Figure 2, a visible result is that the symmetry S1 (equivalence of games in the same class m) is near preserved by the dynamics. The result is indeed remarkable, in the extent that the preservation of this symmetry requires that some specific conditions hold, so that the symmetry conservation is non-generic. This is discussed in detail in Appendix B, where those specific conditions are derived. On the contrary, Figure 2 clearly shows the breaking of the symmetry S2 (mirror anti-symmetry with respect to the main diagonal of the SG quadrant), in full agreement with the analysis of this symmetry in Appendix B, which shows that no specific conditions are needed for the breaking of this symmetry.

Regarding the cooperation level reached for the different scenarios, the differences are also remarkable. In Scenario A, near full defection largely dominates below the main diagonal, with a sharp change above it to cooperation values larger than 1/2, which show an overall tendency to increase with the value m of the equivalence class slope, and near full cooperation as $m\to \infty$. In contrast, in Scenario B, neither full defection, nor full cooperation are almost present (except for a few tiny sectors), with intermediate values of cooperation being largely predominant. For Scenario C, a state of full cooperation ($c=1$) is reached for $m>2$, while almost fully-defective states are only seen for $m<1/2$, becoming dominant only as $m\to 0$.

In Figure 3, we represent the histograms, for a few selected points of the SG quadrant (T ∈ [2, 3], S ∈ [1, 2]), of the cognitive levels in the stationary state for Scenario A. Each point ($T,S$) of a lower panel belongs to the equivalence class of the correlative upper panel, to show the near preservation of the symmetry S1.

Figure 4 and Figure 5 are as Figure 3, but for Scenarios B and C, respectively. The differences between the three figures are merely of a quantitative nature, as indeed, they exhibit the same main qualitative features. This observation points to the conclusion that the qualitative aspects of the distribution of cognitive levels in the stationary state of this dynamics is, to a large extent, rather insensitive with respect to the agents’ beliefs. This should undoubtedly be ascribed to the very scarce information (own current and previous payoff) available to agents in this dynamics. On the other hand, this insensitivity is in contrast with the large differences in the average cooperation reached for the three scenarios, as observed in Figure 2. However, this is in no way contradictory: even for an identical distribution of agents’ cognitive levels in the population, as far as the agents conform their actions to their beliefs (and not to the real distribution, which they ignore), different scenarios (i.e., different beliefs) produce different cooperation patterns.

The Poisson-like aspect of the histograms in Figure 3, Figure 4 and Figure 5 may suggest that, given that our initial condition for the cognitive level distribution is truncated Poisson, the dynamics preserves the type of initial distribution, with perhaps some shift and small deformation. However, this conjecture is invalidated by simulations (not shown) performed with other non-Poisson initial distributions of cognitive levels: even for an initial uniform distribution, unimodal histograms are quickly observed to emerge from the dynamics.

In Scenario A, where the agents believe that the cognitive levels in the population are distributed following a truncated Poisson distribution, not only the cognitive levels evolve, but also the Poisson parameters ${\tau }_i$ do. Therefore, how do they evolve? Figure 6 shows, in the leftmost panel, the average $\langle \tau \rangle$ of the Poisson parameter of the population in the stationary state. A clear correlation of this quantity with the averaged cooperation level shown in the upper rightmost panel of Figure 2 is observed. In the right part of Figure 6 we show, for the same points ($T,S$) used in previous figures, the histograms of the Poisson parameter values in the stationary states.

3. Conclusions

We have analyzed here the cognitive hierarchy theory for agents playing two-person two-action games in a well-mixed population. While for the HG, PD and SH games, the results are straightforward and universal, i.e., independent of the specific distribution of cognitive levels assumed by the agents, for the SG game, the analysis shows an increasing complexity with cognitive levels, with results that are non-universal, in the sense that the actions taken by the high cognitive level agents depend on the specificities of the assumed distribution. Despite this non-universality, we find two exact symmetries: for a given assumed distribution of cognitive levels, agents of a fixed cognitive level take the same action (symmetry S1) in all of the games ($T,S$) sharing the value of $m=(S-1)/(T-2)$, while they take the opposite action (symmetry S2) in all of the games ($T^{\prime },S^{\prime }$) with $(S^{\prime }-1)/(T^{\prime }-2)=m^{-1}$.

We introduce a stochastic dynamics where agents can update their current beliefs on the distribution of cognitive levels in the population, with no available information other than their current and previous payoffs. The simulations of the SG game for this dynamics converge to stationary states of the population characterized by an average fraction of cooperators, which depend largely on the agents’ beliefs, but where in contrast, the distribution of cognitive levels reached is rather insensitive to their beliefs.

We provide arguments showing that for synchronous updating, the previous dynamics breaks forcefully the symmetry S2, while the breaking of the symmetry S1 requires some specific conditions, so that though its preservation is non-generic, nonetheless it is not forbidden. Our simulations for different scenarios show the breaking of the symmetry S2 and an apparent conservation of the symmetry S1.