Network Formation with Endogenous Link Strength and Decreasing Returns to Investment
Abstract
:1. Introduction
2. The Model
3. Results
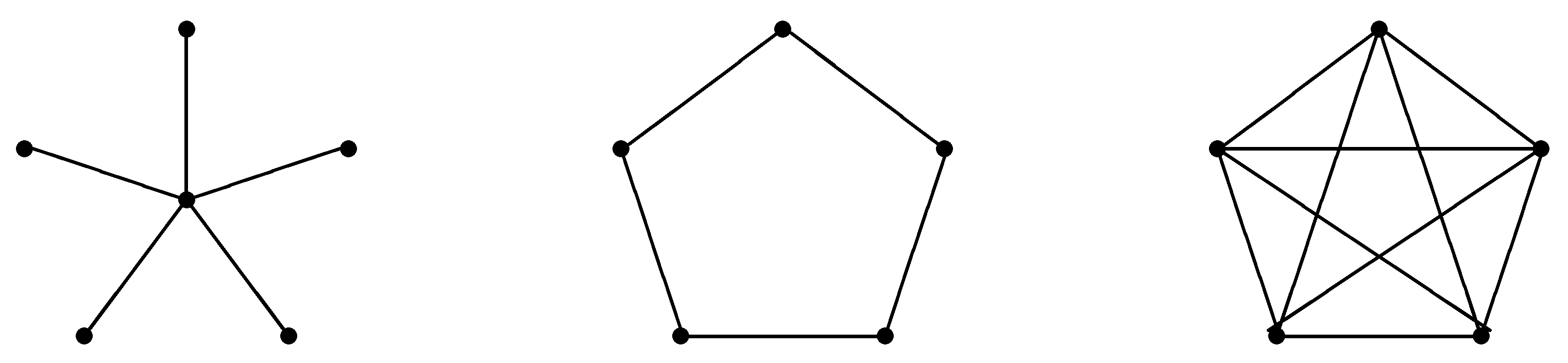
- (a)
- the symmetric complete network is Nash stable if ;
- (b)
- the symmetric star network is Nash stable if .
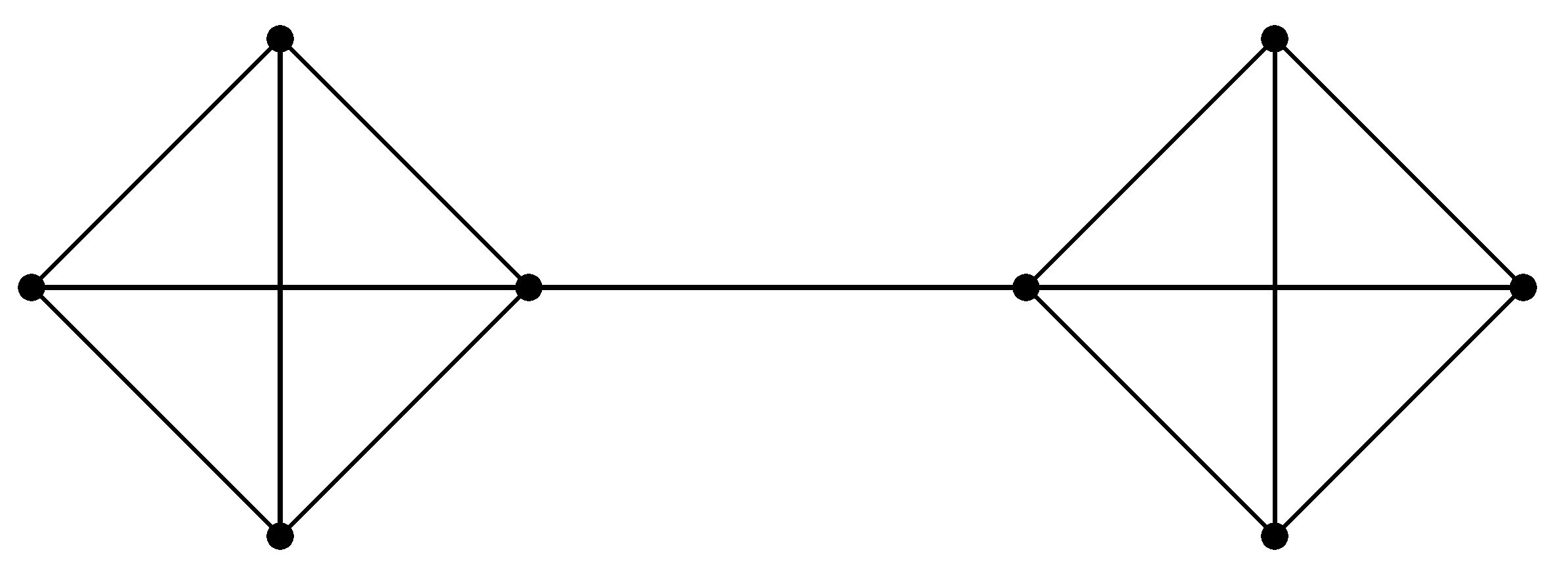
4. Discussion
Acknowledgments
Conflicts of Interest
Appendix A
References
- Granovetter, M. The strength of weak ties. Am. J. Sociol. 1973, 78, 1360–1380. [Google Scholar] [CrossRef]
- Coleman, J.; Katz, E.; Menzel, H. Medical Innovation: A Diffusion Study; Bobbs-Merrill Company: New York, NY, USA, 1966. [Google Scholar]
- Bailey, N. The Mathematical Theory of Infectious Diseases and Its Applications; Charles Griffin: London, UK, 1975. [Google Scholar]
- Enemark, D.; McCubbins, M.; Weller, N. Knowledge and networks: An experimental test of how network knowledge affects coordination. Soc. Netw. 2012, 36, 122–133. [Google Scholar] [CrossRef]
- Goyal, S. Connections: An Introduction of the Economics of Networks; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Jackson, M. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Jackson, M.; Wolinsky, A. A strategic model of social and economic networks. J. Econ. Theory 1996, 71, 44–74. [Google Scholar] [CrossRef]
- Bala, V.; Goyal, S. A noncooperative model of network formation. Econometrica 2000, 68, 1181–1229. [Google Scholar] [CrossRef]
- Dutta, B.; Mutuswami, S. Stable networks. J. Econ. Theory 1997, 76, 322–344. [Google Scholar] [CrossRef]
- Dutta, B.; Jackson, M. The stability and efficiency of directed communication networks. Rev. Econ. Des. 2000, 5, 251–272. [Google Scholar] [CrossRef]
- Jackson, M.; van den Nouweland, A. Strongly stable networks. Games Econ. Behav. 2005, 51, 420–444. [Google Scholar] [CrossRef]
- Bloch, F.; Dutta, B. Communication networks with endogenous link strength. Games Econ. Behav. 2009, 66, 39–56. [Google Scholar] [CrossRef]
- Deroïan, F. Endogenous link strength in directed communication networks. Math. Soc. Sci. 2009, 57, 110–116. [Google Scholar] [CrossRef]
- Feri, F.; Meléndez-Jiménez, M. Coordination in evolving networks with endogenous decay. J. Evol. Econ. 2013, 23, 955–1000. [Google Scholar] [CrossRef]
- Harmsen-an Hout, M.; Herings, P.; Dellaert, B. Communication network formation with link specificity and value transferability. Eur. J. Oper. Res. 2013, 229, 199–211. [Google Scholar] [CrossRef]
- Jackson, M.; Rogers, B. The economics of small worlds. J. Eur. Econ. Assoc. 2005, 3, 617–627. [Google Scholar] [CrossRef]
- Baumann, L. Time allocation in friendship networks. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2533533 (accessed on 8 December 2016).
- Salonen, H. Reciprocal equilibria in link formation games. Czech Econ. Rev. 2014, 9, 169–183. [Google Scholar]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Watts, D.; Strogatz, S. Collective dynamics of ’small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- 1.Differences arise because the two papers assume different flows of benefits. In Bloch and Dutta [12], the strength of link is the sum of the resources invested by the pair of agents. Stars arise because they can maintain a short distance between agents while each agent invests only in a single link. On the other hand, Deroïan [13] assumes the strength of link with respect to an agent is the resources invested by the same agent over that link. A wheel arises because it is the only architecture which allows each agent to be able to derive benefits from all other agents given that each agent invests only in a single link.
- 2.The assumption of additively separability is not critical for the result of efficiency in our model. However, it is critical for the result of stability. For instance, a star is always Nash stable if mutual consent is required because a peripheral cannot benefit by deviating without another peripheral deviating simultaneously. Accommodating the idea of mutual consent requires an equilibrium concept which allows for a certain degree of cooperative behavior (e.g., pairwise stability). Readers who are interested in this line of research can consult Baumann [17] and Salonen [18]. Both papers are variations of Jackson and Wolinsky [7]’s symmetric connections model in their relaxation of the assumption of exogenous link strength.
- 3.Path length is the number of intermediate agents needed in order to reach from one agent to another agents. Clustering roughly measures the likelihood of the presence of a link between a pair of agents who already have a common direct connection.
- 4.Given a wheel network, if a new direct link is being formed between a pair of agents who are far away from each other, then the average path length of the resulting network will reduce considerably [20]. A sufficiently concave strength technology is likely to lead to such outcome due to the underlying gains from diversification.
- 5.Similar structures are also studied by [16] based on a network formation model with exogenous link strength.
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
So, C.K. Network Formation with Endogenous Link Strength and Decreasing Returns to Investment. Games 2016, 7, 40. https://doi.org/10.3390/g7040040
So CK. Network Formation with Endogenous Link Strength and Decreasing Returns to Investment. Games. 2016; 7(4):40. https://doi.org/10.3390/g7040040
Chicago/Turabian StyleSo, Chiu Ki. 2016. "Network Formation with Endogenous Link Strength and Decreasing Returns to Investment" Games 7, no. 4: 40. https://doi.org/10.3390/g7040040
APA StyleSo, C. K. (2016). Network Formation with Endogenous Link Strength and Decreasing Returns to Investment. Games, 7(4), 40. https://doi.org/10.3390/g7040040




