Community-Based Reasoning in Games: Salience, Rule-Following, and Counterfactuals

Abstract

This paper develops a game-theoretic and epistemic account of a peculiar mode of practical reasoning that sustains focal points but also more general forms of rule-following behavior which I call community-based reasoning (CBR). It emphasizes the importance of counterfactuals in strategic interactions. In particular, the existence of rules does not reduce to observable behavioral patterns but also encompasses a range of counterfactual beliefs and behaviors. This feature was already at the core of Wittgenstein’s philosophical account of rule-following. On this basis, I consider the possibility that CBR may provide a rational basis for cooperation in the prisoner’s dilemma.

1. Introduction

The study of strategic interactions is traditionally based on the mathematical specification of a game which includes the set of players, the set of (pure) strategies, the payoff functions and possibly an information structure. The latter specifies what each player knows and believes about the characteristics of the game and also about the other players’ rationality. As Thomas Schelling [1] has argued long ago, such a mathematical specification of a game however is most of the time insufficient to predict and to explain the players’ actual behavior. Schelling’s point is that the mathematical specification fails to acknowledge the fact that the players’ practical reasoning is actually building on (aesthetic, cultural, psychological…) features that help them to make choices and to coordinate. He particularly emphasizes the role played by salience and focal points in the players’ reasoning process.

Following a recent literature reflecting on social conventions and the role of reasoning and common belief (e.g., [2,3,4,5]), this paper develops a game-theoretic and epistemic account of a peculiar mode of practical reasoning that sustains focal points but also more general forms of rule-following behavior which I call community-based reasoning (henceforth, CBR). The CBR notion emphasizes the fact that the working of focal points and rules depends on the ability for each player to infer correctly others’ behavior on the basis of a mutually believed state of affairs. Since each other player’s behavior also depends in principle on his own inference, this leads to an iterative and nested chains of inferences about how each player reasons from a given state of affairs. A player’s practical reasoning is community-based when it uses the belief that all the players are members of the same community as a basis for this iterative and nested chains of inferences. Formally, CBR can be modeled through an epistemic game where the players share a theory of the game they are playing. The contribution of this paper is twofold: first, I suggest that CBR provides a useful and insightful perspective to formalize Schelling’s account of focal points but also Saul Kripke’s [6] “collectivist solution” to Wittgenstein’s so-called rule-following paradox. The latter strengthens a claim already made by Giacomo Sillari [7]. Second, I argue that a formalization of CBR brings interesting insights over the issue of epistemic and causal (in)dependence in normal form games. In particular, I consider the possibility that CBR may provide a rational basis for cooperation in the prisoner’s dilemma.

The paper is organized as follows. Section 2 characterizes CBR as a mode of practical reasoning that individuals may rationally use in specific circumstances. Section 3 provides a formal account of CBR on the basis of a game-theoretic and epistemic framework. Section 4 argues that CBR offers interesting insights into characterizing the nature of rule-following behavior and more generally the working of institutions. Section 5 claims that CBR is an instance where epistemic dependence holds between the players’ beliefs in spite of causal independence between their actions. On this basis, Section 6 contemplates whether CBR provides a rational justification for cooperation in the prisoner’s dilemma. Section 7 briefly concludes.

2. CBR as a Mode of Practical Reasoning

In this paper, I will be exclusively concerned with normal form games, which correspond to interactions where the players choose simultaneously (or cannot observe each other’s choice). Game theory is the tool par excellence used in virtually all the behavioral sciences to study strategic interactions, i.e., decision problems where the consequences of each agent’s behavior are a function of the behavior of other agents. This tool can be used with different aims in mind, such as for instance characterizing the necessary or sufficient conditions for a specific solution concept to be implemented. Here, my purpose is different: the goal is to use a game-theoretic framework in order to reflect over the way more or less rational individuals reason in some kind of strategic interactions to achieve coordination or to cooperate. This purpose was already at the core of Thomas Schelling’s [1] early use of game theory to study strategic behavior. As it is well-known, Schelling emphasizes the fact that the sole mathematical description of the game (i.e., the matrix with the utility numbers embedded in) is insufficient to explain and to predict the players’ behavior. The reason is that obviously, the players’ practical reasoning in a strategic interaction does not merely rely on what corresponds to the mathematical features used by the game theorist to define a game. Aesthetic, cultural, psychological and imaginative features also enter as inputs in the players’ reasoning process. Moreover, the latter does not necessarily proceed along a logical and deductive path; various forms of inductive reasoning may be used to infer practical conclusions about what one should do from a set of premises corresponding to one’s information. The point is thus that a proper explanation of the way people behave in many strategic interactions requires to enriching the game-theoretic models with additional features. The latter must particularly capture the players’ beliefs and/or knowledge and account for the reasoning process used to ultimately make a strategic choice.

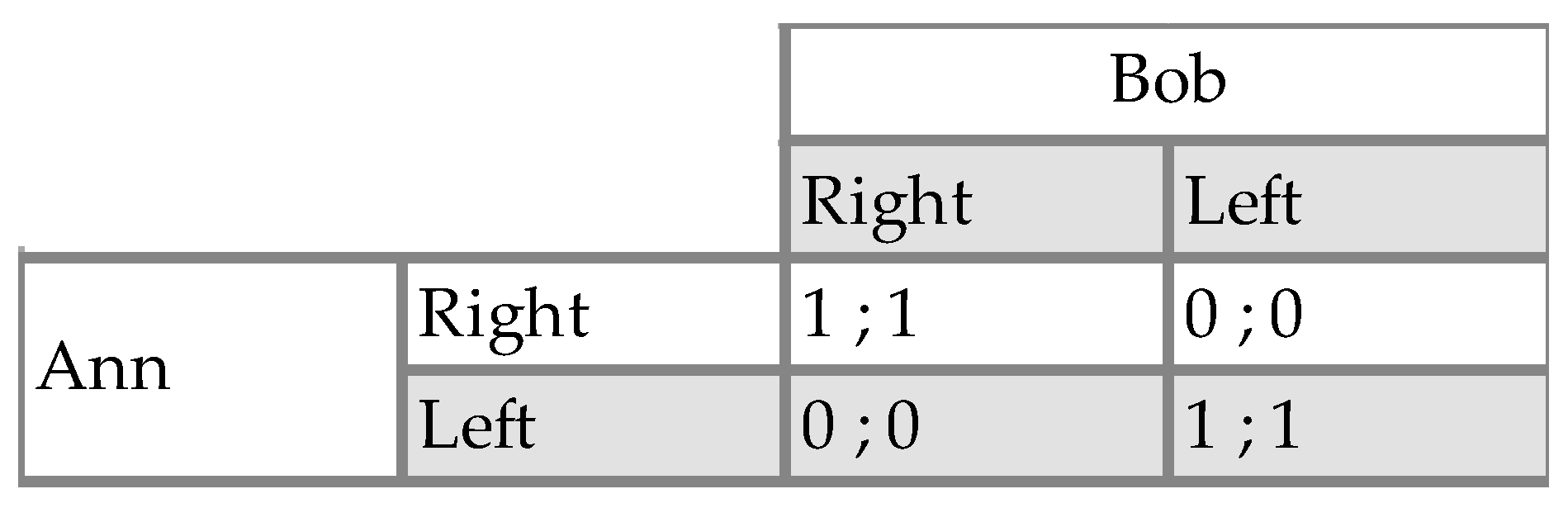
Consider Figure 1 and Figure 2 which depict two basic games. Figure 1 depicts the familiar coordination game with two Nash equilibria in pure strategies (Right, Right) and (Left, Left), and a third one in mixed strategies where each player plays each strategy with probability one-half. Assuming that the players know each other’s preferences, are rational and that these facts are commonly known,1 it is nevertheless impossible for the game theorist to predict what each player will do as a fundamental indeterminacy remains. Moreover, this indeterminacy extends to the player themselves, at least if we take for granted that their only information corresponds to the matrix and that they use the best-reply reasoning constitutive of the Nash equilibrium solution concept.

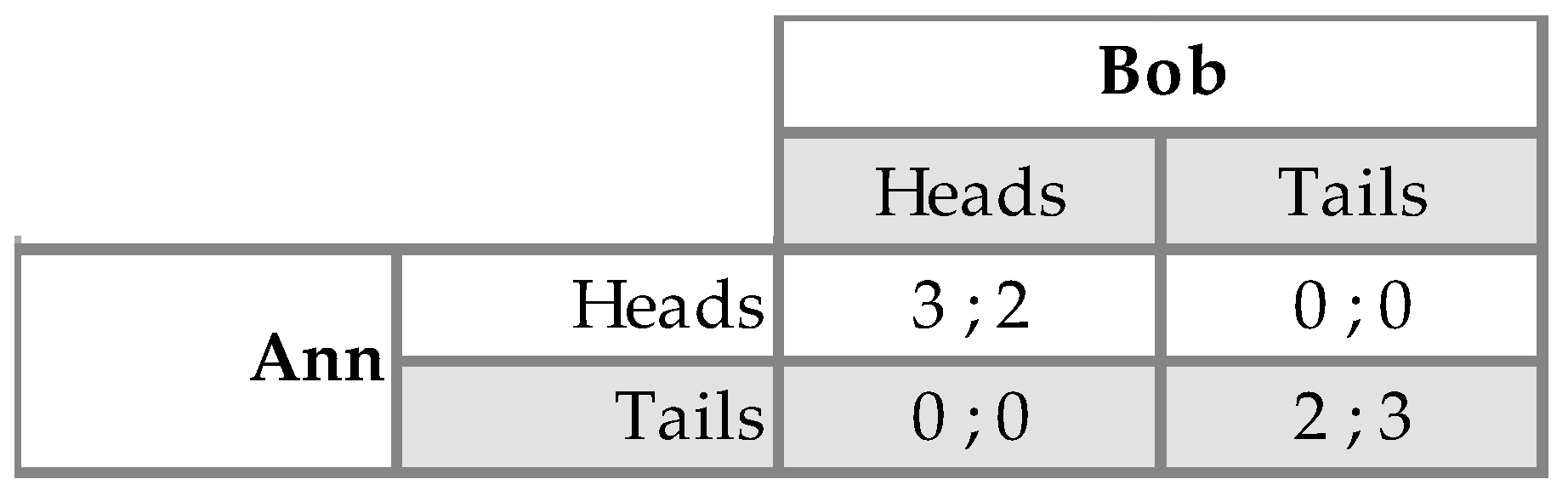
Schelling’s solution to this difficulty is now well-known to most economists and game theorists: in practice, coordination may be achieved thanks to the existence of focal points toward which the players’ expectations are converging. The precise nature of focal points is mostly left undefined by Schelling but their function is pretty clear: as everyone recognizes that a particular outcome (i.e., strategy profile) is salient for all, each player expects that everyone expects all the other players to play along this outcome. Since in a coordination game the players’ interests are perfectly aligned, this gives one a decisive reason to also play along this outcome. However, focal points may also foster coordination in cases where the players have partially conflicting interests, i.e., in so-called “mixed-motive games.” The heads-tails game (Figure 2) is an instance of this kind of games discussed by Schelling. In spite of the symmetry of the game and the fact that the players have conflicting preferences over the Nash equilibrium to be implemented (here Ann prefers (Heads, Heads) while Bob prefers (Tails, Tails)), Schelling’s informal experiments indicate that almost three-quarters of the players choose “Heads”. Interestingly, the proportion is almost the same among the players in the role of Bob than among the players in the role of Ann. A plausible explanation of this fact is that “Heads” sounds as more salient than “Tails” for almost all players in such a way that everyone expects others to play “Heads.” Of course, under such an expectation, it is clearly rational to play “Heads” even for Bob.

Some years later, the philosopher David Lewis [8] used a similar idea to account for the emergence and the nature of conventions. In particular, Lewis suggested that conventions originate through the “force of the precedent”, i.e., a particular form of salience of the history of plays in a given strategic interaction. As for Schelling, there is no clear expression of the nature of this salience in Lewis’s account. However, the most natural reading of both Schelling’s and Lewis’s writings is that salience and focal points have mostly psychological groundings. Plainly, salience is essentially natural as far as it derives from cognitive mechanisms which are themselves the ultimate product of our evolutionary history [9]. This reading is not undisputable however and a plausible (and complementary) alternative is that focal points depend on cultural factors.2 More precisely, the meaning of environmental cues for a given person arguably depends on the context in which she is embedded and, for strategic interactions, on the identity of the other persons with whom she is interacting. 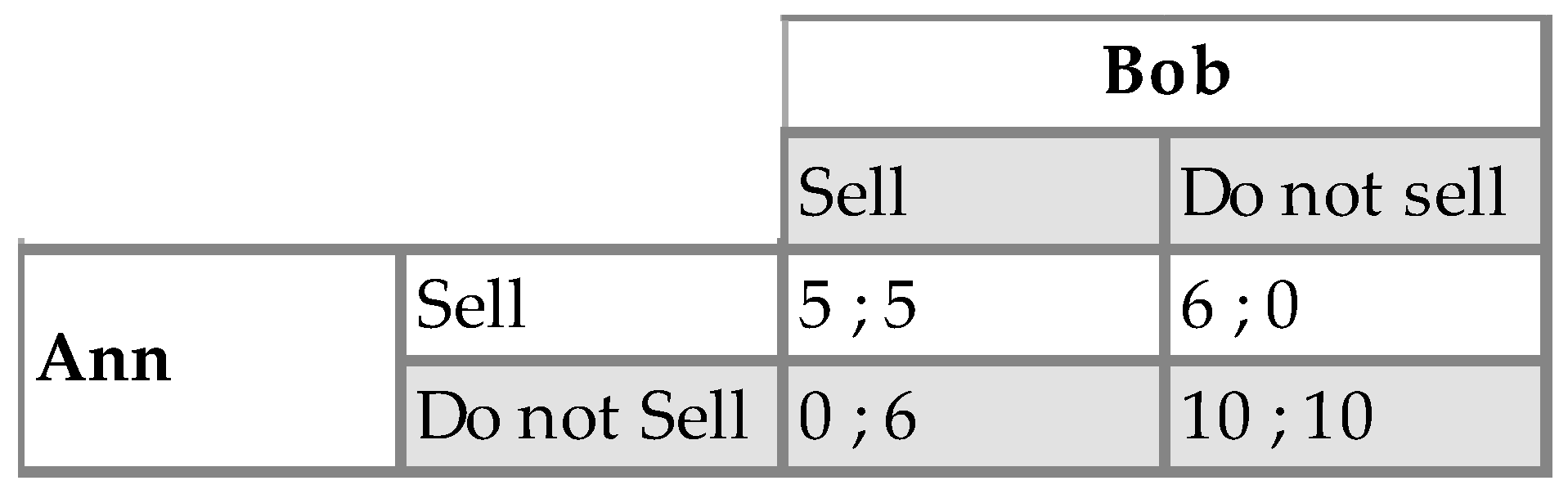In this sense, salience can be said to be community-based [4]: the degree of salience of a strategy, an outcome or more generally of an event3 is a function of the community in which the interaction is taking place. Consider for instance the market panic game depicted by Figure 3 ([4,10]):

The matrix corresponds to the classical assurance game which has once again two Nash equilibria in pure strategies, i.e., (Sell, Sell) and (Do not sell, Do not sell). Suppose now that as Ann is watching her TV she notices a speech by the Chairman of the Federal Reserve Board stating that we are close to a financial meltdown. A plausible reasoning for Ann is then the following: “it is highly probable that Bob and other agents on the financial markets have also noticed the Chairman’s speech; moreover, it is also highly probable that Bob and others will infer that everyone has noticed the Chairman’s speech. Finally, on this basis, I think it is highly probable that Bob and others will believe that everyone will choose ‘Sell’. Therefore, given my preferences, I should also choose ‘Sell’”. Note that there are two steps in Ann’s reasoning based on her listening to the Chairman’s speech. First, she infers from her listening to the Chairman’s speech that others have also probably listened to the speech. Second, she infers from the first two conclusions that others will sell and therefore that she should also sell.4 Now, acknowledging the fact that Ann may have heard of several other speeches by many different persons claiming that a financial meltdown will occur, what is that makes the Chairman’s speech salient in such a way that she noticed it and made the inferences stated above?

An obvious answer to the question above is of course that the salience of the Chairman’s speech comes from the privileged institutional status of the Chairman and from the fact that Ann, Bob and others are members of a community that acknowledges this status. It is important then to note that this salience based on community-membership not only explains why the Chairman’s speech is noticed in the very first place but also the inferences that lead to Ann’s practical conclusion. Actually, I would argue that this is the fact that Ann, Bob and others are members of the same community that allows them to make these inferences and therefore makes the Chairman’s speech salient in the very first place. In other words, the Chairman’s speech is salient because, contrary to most other potentially observable events, it allows people to reach a firm practical conclusion about what they should do.

Community-based salience is thus grounded on what I will call in the rest of the paper community-based reasoning. CBR is a special kind of practical reasoning which operates on the basis of inferences which are grounded on a belief that I and others are members of the same community. It can be stated in the following generic way:

Community-Based Reasoning—Person P’s practical reasoning is community-based if, in some strategic interaction S, her action A follows from the following reasoning steps:

(a)

P believes that her and all other persons P’ in S are members of some community C.

(b)

P believes that some state of affairs x holds.

(c)

Given (b), (a) grounds P’s belief that all other persons P’ in S believe that x holds.

(d)

From x, P inductively infers that some state of affairs y also holds.

(e)

Given (c) and (d), (a) grounds P’s belief that all other persons P’ in S believe that y also holds.

(f)

From (e) and given P’s preferences, P concludes that A is best in S.

Community-membership sustains two key steps in CBR: in step (c), community-membership serves as a basis for P to infer that the fact that x holds is mutual belief; in step (e), it serves as a basis for P for inferring that everyone infers y from x. The term “grounds” that appears in both (c) and (e) singles out that P is making an assumption about the fact that she and other members of C are sharing both an epistemic accessibility to some states of affairs and some form of inductive inference.5 Any person P that endorses CBR takes this practical reasoning as valid from her point of view, i.e., not from a logical point of view but in such a way that P considers that she is justified in endorsing it.6 Clearly, this implies that community-based reasoners may reach wrong conclusions. The point of course is that nothing per se establishes that the members of the same community actually make the same kinds of inductive inferences or that the fact that x holds is mutual belief. Moreover, CBR is partially self-referential in the sense that if P is the only person to use CBR, she will probably reach conclusions that do not match conclusions reached by others using a different kind of practical reasoning.

Finally, if steps (a) to (e) hold for all the members of the community, it can be shown that y is common belief among the members of the community. Therefore, if everyone’s preferences and practical rationality are commonly known (or believed), then everyone’s action A will also be commonly known (or believed). The next section provides a game-theoretic and epistemic framework that establishes these results and fully characterizes the nature of CBR.

3. A Game-Theoretic and Epistemic Framework

This section characterizes CBR in a game-theoretic framework. To this end, I use semantic epistemic models (s.e.m.) of games. The notion of s.e.m. comes from modal and epistemic logic and is a tool used to represent all the relevant facts about how a given game is played. More specifically, an s.e.m. formalizes the players’ knowledge, beliefs and how they reason on their basis. As a consequence, it seems that CBR can be captured within an s.e.m., as I show below.

As usual, a game G is defined as a triple < N, {S_i, u_i}_i∈N > where N is the set of n ≥ 2 players, S_i is the set of pure strategies for player i = 1, …, n and u_i is i’s utility function representing i’s preferences over the possible outcomes. The set of possible outcomes simply correspond to the set of strategy profiles S = П_i∈NS_i; therefore, for all i we have u_i: S ➔ ℜ. In the following, we only need to assume that the players’ utility functions are ordinal, i.e., they are unique up to any increasing transformation. Cardinal utility functions would be required if we used probabilistic belief operators as it is common in the literature but entering into these complications is not required here. Players are assumed to be rational in the sense that they play their best-response given their belief by choosing the strategy leading to their most preferred outcomes. Defined as such, a game is only a partial formalization of a strategic interaction as it does not state how the game is actually or would be played. This is done by adding to G an s.e.m. I: < W, w*, {C_i, B_i}_i∈N > where W is the (finite) set of states of the world (or possible worlds) w with w* the actual state. A state of the world is a complete specification of everything that is relevant from the point of view of the modeler. It can be seen as a list of true propositions about the strategies chosen by the players, what they know and believe, and so on.7 Therefore, the actual state w* specifies how the game is actually played while all the other states w’ indicate how the game would have been played or could have been played. C_i: W ➔ S_i is player i’s decision function; it indicates what strategy i is playing in each possible world. Finally, B_i is a binary relation called an accessibility relation which specifies for any given state w which are the states w’ that player i considers as possible. Therefore, wB_iw’ means that at w player i considers w’ to be possible. I denote B_i(w) = {w’∈W: wB_iw’} the set of states w’ that are accessible from w.8 The tuple I: <W, w*, {C_i, B_i}_i∈N > corresponds to what can be called the (semantic) model of game G.

The binary relations B_i may satisfy different sets of properties which will determine their substantive meaning. A standard approach in economics consists in using the knowledge-belief semantic structures pioneered by Robert Aumann ([13,14,15]). This approach relies however on strong assumptions about the players’ epistemic abilities as it assumes that the players have introspective access to their knowledge.9 Moreover, the representation of beliefs requires the definition of a probability measure over the state space that has been regarded by some authors as problematic [19]. A less demanding approach is to define the accessibility relations in purely doxastic terms, i.e., as representing the players’ beliefs. This is obtained by assuming that the accessibility relations are serial, transitive, and Euclidean [20]:

• Seriality: for all w ∈ W, ∃w’: wB_iw’.
• Transitivity: for all w, w’, w’’ ∈ W, if wB_iw’ and w’B_iw’’, then wB_iw’’.
• Euclideaness: for all w, w’, w’’ ∈ W, if wB_iw’ and wB_iw’’, then w’B_iw’’.

Seriality defines a consistency requirement over the players’ beliefs as it guarantees that in each state, the players consider at least one state as possible. Transitivity and Euclideaness guarantee that the players have introspective access to their beliefs, i.e., when they believe something, they believe this and when they do not believe something, they also believe this.10 On this basis, we can define two important notions of doxastic necessity and doxastic possibility [21]. Consider any proposition p: according to player i, p is doxastically necessary at state w if and only if p is true in all w’ ∈ B_i(w). Correspondingly, p is doxastically possible at state w if and only if p is true in at least one w’ ∈ B_i(w). I denote [p] the set of states w in which p is true and call [p] an event. An event is thus any subset of W and therefore 2^W is the set of events. Now, we can define a set of non-probabilistic operators B_i with respect to any event [p] in the following way:

B_i[p] = {w|B_i(w) ⊆ [p]}.

(1)

Expression (1) indicates that player i believes event [p] at w (i.e., believes that proposition p is true) if and only p is doxastically necessary at w. Note that this definition implies

B_i[¬p] = {w|B_i(w) ∩ [p] = ∅}.

(2)

Expression (2) states that i believes the event [¬p] at w (i.e., believes that proposition p is false) if and only if p is doxastically impossible at w. It should be noted that both B_i[p] and B_i[¬p] are themselves well-defined events as they correspond to set of states where the proposition “i believes that p is true (false)” is true.11

Throughout the paper, I make the natural assumption that the players have a doxastic access to what they are doing, i.e., they have the (right) belief that they play any strategy s_i that they are actually playing: i.e., for all w’ ∈ B_i(w), C_i(w) = C_i(w’). If we denote [s_i] the event that i plays strategy s_i, then this corresponds to the following condition:

For all w ∈ W and all players i, B_i[s_i].

(3)

A last piece in our basic framework is needed. We can derive a communal accessibility relation B* defined as the transitive closure of the set of individual accessibility relations {B_i }_i∈N. Therefore, we have wB*w’ if and only if we can design a finite sequence of worlds w₁, …, w_m with w₁ = w and w_m = w’ such that for each k from 1 to m − 1, we have at least one player j for which w_kB_jw_k+1. Correspondingly, we have B*(w) = {w’: wB*w’}. The common belief operator B* is then defined in the standard way:

B*[p] = {w|B*(w) ⊆ [p]}.

(4)

Expression (4) means that the event [p] is common belief among the n players: each player believes that each player believes that… p is true. In the following, I will assume that all the features of any game G are common belief among the players, which implies that the discussion is restricted to games of complete information.

The resulting model I: < W, w*, {C_i, B_i}_i∈N > provides a complete description of how the game G is played and what the player believes at each possible world. Therefore, it is not only an account of what actually happens but also of what could have happened. As I explain below, this makes s.e.m. a particularly useful tool to discuss the role of counterfactuals in the players’ reasoning process. It is worth noting that I is the theorist’s model of the game, not necessarily the players’ own model which, in this sense, would have to be “commonly known” as pointed out by Aumann and Brandenburger [22] (p. 132). Arguably, this can be regarded as problematic in light of Schelling’s claim emphasized above that we should not conflate the mathematical description of the game with the way the players are actually framing the strategic interaction. The point is however that the model of the game is a tool to represent the players’ reasoning process through which they reach the practical conclusion regarding their strategy choice. What this representation implies about how individuals are “really” reasoning depends on one’s philosophical commitments over the nature of the relationship between a model and the real world but also over the nature of the intentional states (beliefs, preferences) that are accounted for in the game’s model. This issue is well beyond the scope of the paper. However, it is important to acknowledge that in the current framework, we will be able to account for the players’ reasoning process through several elements. First, the assumption that the players are rational at all states w, i.e., they choose their best strategy given their preferences and their beliefs. Second, the characterization of the players’ (common) beliefs at each state w. Third, the players’ actual and counterfactual choices at each state w. As I argue in the next section, we can account for CBR in such a framework. I also argue that such an account helps to foster a better understanding of the nature of salience and more generally of the phenomenon of rule-following behavior.

4. CBR and Rule-Following Behavior

On the basis of the above framework, I will develop in this section an account of community-based salience and rule-following behavior. In particular, I shall suggest that the salience of an event may arise from the fact that the members of a population are following a rule. In turn, this rule-following behavior is grounded on CBR.

First, I add to the framework of the previous section a rationality assumption according to which a player i is rational at ω if and only if:

(R)

For every w’ ∈ B_i(w), there is no strategy s_i’ ≠ C_i(ω) such that

u_i(s_i’, C_-i(w’)) ≥ u_i(C_i(w), C_-i(w’)), with C_-i(w) = s_-i = (s₁, …, s_i-1, s_i+1, …, s_n).

Expression (R) is a statement about the players’ epistemic rationality as it indicates that player i chooses her best strategy given her belief about what others are doing. Another way to state this characterization of rationality is that a rational player never plays a strategy that he believes is strictly dominated by another one. As I will point out below, (R) does not imply that a rational player actually makes her best choice as her belief about others’ choices may be mistaken. In particular, no restriction is placed on the fact that a player may believe that others’ choices are somehow (causally) dependent on her choice. On this basis, we denote [r_i] the event that i is rational, i.e., [r_i] = {w|(R) is true}.

Before being able to characterize CBR in model semantic terms, we need to introduce an additional proposition according to which all the players in the game are members of some community. As pointed out in Section 2, this feature is an essential component of CBR as it grounds two key inferences in steps (c) and (e). We simply denote c the proposition that “everyone in population N is a member of the same community C” and [c] the corresponding event. Steps (a)–(e) of CBR can now be semantically expressed by the following conditions:

(CBR1)

For all i ∈ N, B_i[e] ∩ B_i[c] ⊆ B_i[B_-i[e]].

(CBR2)

For all i, j ∈ N, B_i[B_-i[e]] ∩ B_i[c] ⊆ B_i[r_-i] ∩ B_i[B_j[s_−j]] ⊆ B_i[s_−i] with [s_−i] the event that strategy profile s_-i = (s₁, …, s_i−1, s_i+1, …, s_n) is played.

(CBR3)

For all i ∈ N, B_i[s_-i] ∩ [r_i] ⊆ [s_i].

(CBR4)

For all i, j ∈ N and any event [f], ({B_i[e] ∩ B_i[c]} ⊆ B_i[f]) ⊆ B_i[B_j[e] ⊆ B_j[f]].

Consider each condition in turn. (CBR1) corresponds to steps (a)–(c) of CBR: i’s beliefs that event [e] holds and that everyone is a member of the same community (event [c]) allow her to infer that everyone else believes that [e] holds. (CBR2) is a complex condition that captures steps (d) and (e). It is easier to understand if we divide it into two parts:

(CBR2.1)

B_i[B_-i[e]] ∩ B_i[c] ⊆ B_i[B_j[s_-j]].

(CBR2.2)

B_i[r_-i] ∩ B_iB_j[s_-j] ⊆ B_i[s_-i].

The first inclusion relation corresponding to (CBR2.1) captures the fact that community-membership grounds i’s inference from her belief that others believe that event [e] holds to the event that each j has specific belief about what everyone else will do. The second inclusion relation corresponding to (CBR2.2) indicates that, in the context of strategic interactions, player i needs to believe that the other players are rational to infer what they will be doing given that they believe that [e] holds. In other words, this is the combination of the beliefs in community-membership and rationality that ground the inference from event B_−i[e] to event [s_−i] for any player i. It is important because it makes explicit the fact that CBR must rely on a belief that others are rational in some well-defined sense. Indeed, without rationality, CBR is only an instance of theoretical (or doxastic) reasoning, i.e., a reasoning scheme that operates only at the level of beliefs. A rationality principle is needed to make this reasoning scheme a practical one, i.e., one also concerned with action. Moreover, we need to add the fourth condition (CBR4) that was implicit in the scheme of CBR stated in Section 2: each player must be implicitly assuming that others are also community-based reasoners. Condition (CBR4) corresponds to the assumption of symmetric reasoning that underlies Lewis’ account of conventions ([2,23,24]). It expresses the idea that each player believes that others are community-based reasoners and that on this basis they make the same (inductive) inferences from event [e].12 The combination (CBR1)–(CBR3) clearly entails B_i[e] ∩ B_i[c] ⊆ [s_i] and the addition of (CBR4) implies that the event [s] that the strategy profile s = (s₁, …, s_n) is played is common belief:

(CB)

B_N[e] ∩ B_N[c] ⊆ B*[s] with [s] the event that strategy profile s = (s₁, …, s_n) is played and B_N = ∩_iB_i the mutual belief operator.13

Expression (CB) states that under the required conditions, the event that the strategy profile s played is common belief in the population. CBR, as formalized through conditions (CBR1)–(CBR4), thus indicates a specific way through which a given proposition (event) can become commonly believed. It is also worth to emphasize two additional points. First, as CBR includes condition (R), it may seem that it leads to (Nash) equilibrium play. This is not true in general as a further condition regarding the causal independence of strategy choices (and the players’ beliefs in this independence) is required. Without such requirement, CBR may justify cooperation in the prisoner’s dilemma, as I discuss in Section 6. Second, given the definition of the common belief operator B* according to Expression (4), common belief is here characterized in fixed point terms rather than in iterative terms. This does not make any difference at the substantive level though.14

Consider again the market panic game depicted by Figure 3 above played by n players on the basis of the framework of the preceding section, and take a first-person point of view (Ann’s point of view). To replicate Ann’s reasoning process stated in Section 2, we need to characterize a small set of events. Denote a the proposition that “the Chairman’s speech predicts a financial meltdown” and [a] the corresponding event. Denote (s_−Ann = Sell) and (s_Ann = Sell) the events that everyone except Ann plays “Sell” and that Ann plays “Sell” respectively. Then, what happens in the market panic game following the Chairman’s speech from Ann’s point of view can be represented through an s.e.m. with the following relationships between these different events.

B_Ann[a] ⊆ B_Ann[B_−Ann[a]].

(5a)

B_Ann[B_−Ann/[a]] ⊆ B_Ann[s_−Ann = Sell].

(5b)

B_Ann[s_−Ann = Sell] ⊆ [s_Ann = Sell].

(5c)

Expression (5a) indicates that the fact that Ann believes that the Chairman has delivered a speech implies that she believes that everyone else also listened to the Chairman’s speech. Expression (5b) states a second implication: Ann’s belief that everyone else also listened to the Chairman’s speech entails that she believes that everyone else will decide to sell. Finally, Expression (5c) indicates that this latter belief implies that Ann will also sell. However, stated in this way, Expressions (5a)–(5c) are misguided. Indeed, they seem to imply that the relationships between these different events are purely logical and therefore that Ann’s practical reasoning is a deductive one. Of course this is wrong: there is nothing logical in the fact that the Chairman’s speech leads everyone except Ann to sell their assets and therefore the relationship between Ann’s beliefs indicated by (5b) cannot be grounded on a logical reasoning.15 The same is obviously true for (5a) and (5c): this is not because of logic that Ann can infer from her listening to the Chairman’s speech that others have also listened nor that she should sell from the fact that others are selling. The point is that Ann’s practical reasoning relies on other premises that do not make the relationships between the different events logical ones. In Section 2, I suggested that Ann’s practical reasoning is community-based. Taking this claim for granted, we can expand the s.e.m. to account for this fact:

B_Ann[a] ∩ B_Ann[c] ⊆ B_Ann[B_−Ann[a]].

(6a)

B_Ann[B_−Ann[a]] ∩ B_Ann[c] ⊆ B_Ann[r_−Ann] ∩ B_Ann[B_−Ann[s_-i = Sell]] ⊆ B_Ann [s_−Ann = Sell] for all i ≠ Ann.

(6b)

B_Ann [s_−Ann = Sell] ∩ [r_Ann] ⊆ [s_Ann = Sell].

(6c)

Combined with (CBR4), (6a)–(6c) entail the event [s = Sell] is common belief, i.e., B_Ann[B*[s]]. Now, we can see that what makes the event [a] salient for Ann in the very first place in such a framework is the fact that it is the starting point of the whole reasoning scheme. This is captured by the following principle:

Community-Based Salience—The set φ_i of subjectively community-based salient events in the model I of a game G for a player i corresponds to all events [e] that implies an event B_i[B*[s]] through conditions (CBR1)–(CBR4) . The set φ of objectively community-based salient events in the model I of a game G is the set of events that are community-based salient for all i. Formally:

• Subjectively salient events: φ_i = {[e]: B_i[e] ∩ B_i[c] ⊆ B_i[B*[s]] through (CBR1)–(CBR4)}.
• Objectively salient events: φ = ∩_iφ_i.

Consider now any event [e] ⊆ φ. By assumption, (CB) obtains and therefore [e] ⊆ B*[s] with [s] the event that strategy profile s = (s₁, …, s_n) is played. This is a pretty interesting result: assuming that the players are indeed all community-based reasoners and that as a consequence they share some inductive inferences mode, an objectively salient event will generate a commonly believed strategy profile in the population. Note that this result does not depend on an assumption of common belief in rationality (only mutual belief in rationality is needed) but that community-based reasoning is common knowledge in an “informal” sense.16

To close this section, I now want to suggest that the scope of CBR actually goes beyond the phenomenon of salience but also captures an aspect of rule-following behavior that has been emphasized by some readers of the late writings of Ludwig Wittgenstein, especially his masterpiece Philosophical Investigations ([26,27]). As Wittgenstein’s writings make it clear, there is no easy way to account for the nature of rule-following behavior: there is simply no answer to questions like ‘what is it to follow a rule?’ or ‘how can I be sure that I follow this rule and not another one?’. The main difficulty lies in the kind of indeterminacy that no inductive reasoning can resolve: whatever the number of times I or others follow some specific pattern of behavior, there is no way to decide which the underlying rule that sustains the behavior is. Saul Kripke’s [6] famous “quaddition” example provides a great illustration: the rule of quaddition functions like the rule of addition for any two numbers that do not sum up to more than 57, and otherwise gives the result of 5. Now, no matter how many times I have added two numbers, as long as they do not have summed up to more than 57 I can never be sure that the rule I was following was the rule of addition rather than the rule of quaddition. Wittgenstein’s more general point is that (behavioral) patterns do not have any intrinsic meaning. In terms of practical reasoning, whatever others’ past behavior or the various other features that may indicate to me what I should do, there is no way to overcome this kind of indeterminacy regarding the underlying rule that should be followed.

There are of course many numbers of conflicting interpretations of Wittgenstein’s account. I believe however that there are at least two key ideas that are related to the notion of CBR in this game-theoretic framework. The first idea is the importance of counterfactual reasoning and makes a direct link with the next section. The second idea is the importance of the community in fostering the normative force of rules in a given population.17 Consider the latter first. Acknowledging that rule-following behavior always takes place inside some specific community whose very identity corresponds to the rules that its members are following, it is not farfetched to claim that rule-following is essentially community-based in the sense developed above. In some way, this is nothing but a generalization of Lewis’s account of the role of salience in the working of conventions to all kinds of institutional objects: social and moral norms, legal rules, customs, and so on. I would therefore argue for the following characterization of rule-following in an s.e.m.:

Rule-following behavior—The players in a game G are following a rule according to some s.e.m. I if and only if, for the behavioral pattern defined by the strategy profile s = (s₁, …, s_n) corresponding to the event [s], there is at least one objectively salient event [e] such that w* ∈ [e] ∩ B_N[c] ⊆ B*[s].

Three points are worth emphasizing regarding this characterization. First, the very salience of the event [e] is constitutively (rather than causally) explained by the fact that the member of the community are actually following a rule. On this account, the fact that an event is salient is an indication that some rule holds in the population. This is interesting because most discussions of salience in philosophy and in economics have tended to make salience either the cause of the emergence of some rules (e.g., Schelling and Lewis, at least under some interpretation) or simply the product of some relatively “blind” evolutionary process (e.g., [29]). The latter approach indeed provides an interesting account of the origins of salience in a context of cultural evolution. Game-theoretic models of cultural evolution have been argued however to rely on excessively simplistic and abstract assumptions regarding the underlying learning mechanisms [30,31,32]. Moreover, even if we grant their relevance, such evolutionary explanations of salience do not account for the reasoning process that individuals may use in cases that require an explicit deliberation. Second, the nature of the inclusion relation in the statement B_N[e] ∩ B_N[c] ⊆ B*[s] remains largely undefined. In some way, this reflects the difficulty to give a full characterization of the nature of rule-following behavior. My account points out however that this inclusion relation depends on CBR and on the fact that this practical reasoning is shared in the population, i.e., the assumption of symmetric reasoning expressed by (CBR4). Much work remains to be done to understand the latent cognitive functions and processes that underlie CBR and the more general abilities of humans to account for others’ behavior. On this issue, I conjecture that interesting contributions can be made by combining the resources of game theory with the recent advancements in the so-called “Theory of Mind” literature [33]. In particular, some scholars have argued that the reasoning process of rational individuals in a strategic interaction relies on a simulation mechanism where one assumes that the others are reasoning like her [34,35]. This could indeed provide a justification for assuming that the players are symmetric reasoners as stated by (CBR4).18 The third and last point concerns the importance of counterfactual reasoning: to follow a rule does not reduce to the actual and observable pattern of behavior. A rule also specifies what would have happened in other circumstances than those that have actually happened. A major interest of s.e.m. is that they are perfectly fitted to deal with this important feature: indeed, in the model of a game, with the exception of the actual state w*, all states describe what would have happened in other circumstances. Of course, to meaningfully state that a rule is followed, we have to be in an actual world which indeed belongs to the salient event leading to condition (CB). Hence, we should impose w* ∈ [e] ⊆ φ as a condition for an s.e.m. to formalize rule-following behavior. However, for all other worlds w ∈ [e], the model indeed expresses aspects of practical reasoning that do not materialize at the behavioral level. This distinguishes my approach with respect to some recent game-theoretic accounts of institutions in social ontology and economics [36,37]. This also naturally leads to consider a related issue that arises from my account of CBR: the kind of epistemic and causal dependence that is implied.

5. CBR and Counterfactuals in Games

The last section has pointed out that a key feature of CBR that sustains salience and rule-following behavior is the condition that players are symmetric reasoners with respect to some salient event [e] (condition (CBR4)). This can be seen as a requirement that the players have a common understanding of the situation they are embedded in and which shares some similarities with Wittgenstein’s notion of lebensform (forms of life) [7,26]. The precise nature of this condition has been left undefined as we do not have a full understanding of the cognitive mechanisms through which individuals are able to replicate others’ reasoning. As I suggested above, studies belonging to the Theory of Mind literature may bring insights on this issue in a near future. However, from a game-theoretic and philosophical perspective, the symmetric reasoning condition has interesting connections with two deeply related issues: the role of counterfactuals in strategic interactions and the distinction between causal and epistemic dependence in games.19 Indeed, I shall argue in this section that the symmetric reasoning condition may be interpreted in different ways. Either it refers to a mere epistemic dependence between the players’ beliefs and practical reasoning but with a causal independence, or it underlies some kind of causal dependence, at least from the point of view of the players themselves. Which of these two interpretations is the most convincing matters in prisoner’s dilemma type of interactions as the latter may make cooperation rational.

Consider again the first person view of any player, say Ann, in any game G like the market panic game of Figure 3. The reasoning scheme through which Ann reaches the conclusion that it is common belief that everyone will sell depends on (i) Ann’s rationality; (ii) Ann’s belief in others’ rationality; (iii) Ann’s belief that everyone is a member of some community and (iv) Ann’s belief in the symmetric reasoning that the latter entails. It is not contentious that the latter two beliefs entail, from Ann’s point of view, a form of epistemic dependence: Ann’s believes that her and others’ beliefs are somehow correlated. This is the essence of condition (CBR4). If we generalize to all players, then there is a mutual belief in the population that beliefs are correlated. For each player i, believing something implies that others have the same belief; moreover, for any two other players j and k, correlation also holds as j’s and k’s beliefs are both correlated to i’s. Ann’s rationality is expressed by (R) and the fact that [r_Ann] = W in the corresponding s.e.m. and Ann’s belief in other rationality is the event B_Ann[r_−Ann] = W. As this is also the case for all other players, there is indeed mutual belief in rationality in the population.20 This assumption sets however very few constraints on the players’ practical reasoning. What it says is that each player maximizes her utility (i.e., chooses the strategy that leads to her most preferred outcome) given her beliefs. Nothing is said however regarding the content of these beliefs and the way they are derived. The latter indeed depends on the properties of CBR. At this point, it might be argued that condition (R) should be strengthened in such a way that the formation of beliefs satisfies a condition of causal independency. The intuition is the following: in normal form games, players choose without knowing what others are doing. More specifically, a foundational assumption is that the players’ choices are causally independent: Ann’s choice cannot have any causal influence on Bob’s choice as well as the converse, as both are choosing independently. While we cannot exclude the possibility that Ann’s belief about what Bob is doing can be correlated to Bob’s corresponding belief (or someone else’s belief for that matter), this cannot be due to a causal relationship. This leads to the notion of causal rationality developed by causal decision theorists [40].

Dealing with this issue necessitates to consider the role played by counterfactuals in CBR. Counterfactuals are generally defined as false subjunctive conditionals. Subjunctive conditionals are conditionals of the form “If I were to do x, then y would result”. Counterfactuals are then of the form “If I had done x, then y would have resulted”. There are several ways to capture counterfactuals in an s.e.m.21 The simplest is to add to the structure < W, w*, {C_i, B_i}_i∈N > a selection function f: W × 2^W ➔ 2^W [43]. A selection function maps each pair of state w and event [e] into a subset f(w, [e]) ∈ [e]. The latter corresponds to the state w’ that is the closest to w, where closeness is understood in the standard sense of Stalnaker-Lewis theory of counterfactuals [38]: we assume that all states in W can be ordered with respect to any state w by a binary relation ${\preccurlyeq }_w$ which is complete, transitive, asymmetric and, centered.22 Then, x${\preccurlyeq }_w$y reads as the statement that x is closer to w than y. This provides a straightforward way to state the truth value of counterfactuals in an s.e.m. Take any two propositions p and q and denote the counterfactual “had p been the case, then q would have been the case” by p $\rightrightarrows$ q. The latter is true at w if and only if q is true at the closest world with respect to w where p is true. Denote min_w[p] = {w’|w’${\preccurlyeq }_w$w″ for all w’, w″ ∈ W} the set of the w-closest worlds where p is true, i.e., the subset of [p] that is the closest to w.23 The selection function f(w, [e]) is thus simply defined in terms of the closeness relation:

f(w, [e]) = min_w[e].

(7)

Now, the event [p $\rightrightarrows$ q] obviously holds at w if and only if min_w[p] ∈ [q]. Correspondingly, the counterfactual event [e$\rightrightarrows$ f] can be characterized through the selection function: [e$\rightrightarrows$ f] = {w | f(w, [e]) ∈ [f]}. In this perspective, two further restrictions can be naturally imposed on the selection function f [44]:

If w ∈ [e], then f(w, [e]) = {w}.

(8a)

If f(w, [e]) ∈ [f] and f(w, [f]) ∈ [e], then f(w, [e]) = f(w, [f]).

(8b)

Condition (8a) simply states that the closest (and indeed identical) world to w is w itself. This is a direct implication of the assumption that ${\preccurlyeq }_w$ is centred. (8b) says that if the w-closest state in [e] is in [f] and the w-closest state in [f] is in [e], then the two states must coincide. In the context of causal decision theory, f(w, [e]) is thus the state that would be causally true (in an objective sense) at state w if [e] were the case. The combination of the selection function f with the accessibility relations B_i allows to define the set of states that player i believes could be causally true at w. It corresponds to the union ${{\displaystyle \cup }}_{w\prime \in Bi\left(w\right)}$f(w’, [e]). Therefore, the belief that the counterfactual e$\rightrightarrows$ f is true corresponds to the event

$$B_i[e\rightrightarrows f]=\left\{w\right|{{\displaystyle \cup }}_{w\prime \in Bi\left(w\right)}f(w\prime ,[e\left]\right)\subseteq \left[f\right]\}$$

(9)

In a game-theoretic context, the set of states that i believes could be causally true at w is determined by the following counterfactual reasoning: “If I were to play s_i’ instead of s_i, then I believe that others would play some strategy profile s_−i”. Then, we have [e] = [s_i’] and therefore ${{\displaystyle \cup }}_{w\prime \in Bi\left(w\right)}$f(w, [s_i’]), i.e., the set of states that could causally happen according to i if he were to play s_-i. It is now possible to provide a formal condition of causal independence imposed to the decision functions {C_i}_i∈n:

(CI)

For every strategy s_i and for all players i, if w’$\in$ f(w, [s_i]), then C_−i(w) = C_−i(w’).

Condition (CI) states that the players’ decision functions are such that each player’s strategy choice is causally independent from other players’ choices. On this basis, we can strengthen the rationality condition (R) by requiring that the players maximize given condition (CI):

(CR)

Player i is causally rational at w if, for every w’ ∈ B_i(w), there is no strategy s_i’ ≠ C_i(ω) such that

u_i(s_i’, C_−i(f(w’, [s_i’]))) ≥ u_i(C_i(w)_, C_−i(w’)), and C_−i(f(w’, [s_i’])) = C_−i(w’) for all s_i’.

Condition (CR) states that a player i is causally rational at w if and only if she plays her best response given the fact that others’ choices are causally independent to her choice, i.e., if i were to play any other strategy s_i’, others would still play s_-i. This definition emphasizes an important point: the fact that the model satisfies (CI) is not sufficient to guarantee that the players are causally rational at w, even if they play their best response given their beliefs. Indeed, the players themselves must believe that (CI) holds at w. If we denote [ci] the event that (CI) holds, then this condition is straightforward to define [43]:

(BCI)

Player i believes that players’ choices are causally independent at w if and only if:

B_i(w) ⊆ [ci].

This implies that for every strategy s_i and every w’$\in$B_i(w), if

w″ $\in$ f(w’, [s_i]), then C_−i(w’’) = C_−i(w’).

I have assumed so far that the rationality condition (R) is constitutive of CBR. Moreover, in the context of normal form games, the causal independence condition (CI) should probably be regarded as an undisputable structural constraint as there is absolutely no reason to assume that it could not hold. The central issue concerns the status of condition (BCI) with respect to CBR and thus whether or not CBR implies the stronger condition of causal rationality (CR). The next section will discuss this issue in the context of the famous prisoner’s dilemma game.

6. CBR in the Prisoner’s Dilemma

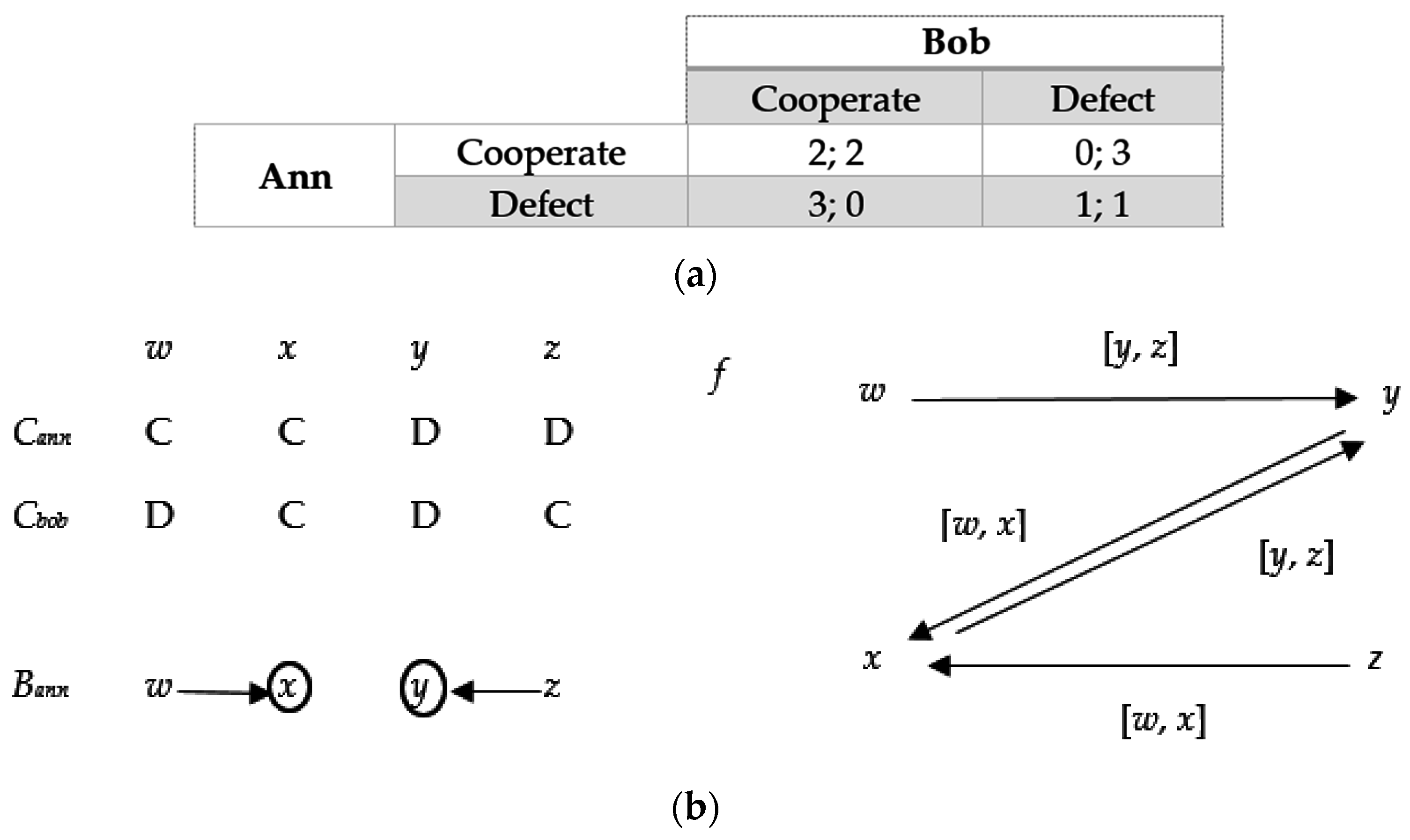
The prisoner’s dilemma (see Figure 4a below) is by far the most studied game by game theorists in all disciplinary contexts: economics, biology, philosophy… The reason is that it points out the contradiction between what can be called “collective rationality” and “individual rationality”. On the former, the players should cooperate as mutual cooperation leads to the Pareto-optimal outcome that (by assumption) maximizes social welfare. On the latter however, mutual defection is unavoidable as defection is the players’ dominant strategy. Crucially, in the prisoner’s dilemma, it is not even required that the players have a mutual belief in other’s rationality because whatever the other is doing or is expecting one to do, playing the dominant strategy appears to be the sole rational choice.

There have been many attempts (mostly by philosophers) to show that cooperation in the prisoner’s dilemma may be rational.24 Economists and game theorists have generally dismissed them as being based on a misunderstanding of both of the rationality principle and of the general purpose of game theory (e.g., [45]). However, once we take counterfactual reasoning into account, things are not so straightforward. Consider for instance the case where condition (R) holds but not (BCI). As a consequence, the players are not causally rational: they maximize their utility but we do not put any constraint on the way they form their beliefs. Suppose for instance that Ann holds the beliefs formalized by the following partial model of the prisoner’s dilemma [43] (see Figure 4b for a partial graphical representation): W = {w, x, y, z}, C_Ann(w) = C_Ann(x) = C, C_Ann(y) = C_Ann(z) = D; C_Bob(x) = C_Bob(z) = C, C_Bob(w) = C_Bob(y) = D; B_Ann(w) =B_Ann(x) = {x}, B_Ann(y) = B_Ann(z) = {y}; f(w, [w]) = f(w, [W]) ={w}, f(x, [x]) = f(x, [W]) ={x}, f(y, [y]) = f(y, [W]) = {y}, f(z, [z]) = f(z, [W]) ={z}, f(w, [y, z]) = f(x, [y, z]) = {y}, f(y, [w, x]) = f(z, [w, x]) = {x}. Suppose that the “true” state is w. In such a model, Ann believes that her and Bob’s choices are correlated since she believes that Bob is playing C (B_Ann(w) = {x}) but that if she were to play D (event {y, z}), then Bob would play D (f(x, [y, z]) = {y}). As u_Ann(C, C) > u_Ann(D, D), Ann is indeed rational at w by choosing to cooperate. Clearly however, Ann’s beliefs do not satisfy (BCI) since at w, we have B_Ann(w) = {x} and f(x, [y, z]) = {y}, but C_Bob(x) ≠ C_Bob(y). In other words, at w Ann believes that the counterfactual event [s_Ann = D $\rightrightarrows$ s_Bob = D] holds while at the same time she believes that Bob will actually cooperate. The problem is thus whether such beliefs can be justified under some kind of practical reasoning. More specifically, does CBR license the conjunction of two beliefs of the kind B_i[s_−i] but B_i[s_i’ $\rightrightarrows$ s_−i’] for any s_i’ ≠ C_i(w)?

At first sight, the assumption of symmetric reasoning seems to make beliefs in the correlation of strategy choices plausible: if my (community-based) reasoning leads me to the conclusion that I should cooperate because I believe that if I cooperate you will also cooperate but if I defect you will defect, then the fact that you and I are symmetric reasoners leads me to believe that you have the same belief. However, this is superficial because symmetric reasoning only entails epistemic dependence of the players’ beliefs: if I believe that event [e] entails event [f] and that [e] is mutual belief, then I believe that [f] is also mutual belief. Now, suppose that in the prisoner’s dilemma the players mutually believe some event [e] (for instance the instructions of the experimenter in an experimentally designed game) indicating that all should cooperate. On this basis, I may perfectly believe that, on the basis of some kind of reasoning that may be community-based, others will reach the conclusion that we all choose to cooperate. Actually, they are wrong because as far as I am concerned and because I am rational, I will choose to defect! If I believe that others are rational, then it will also occur to me that they cannot cooperate and therefore the only commonly believed outcome compatible with the mutual belief in rationality is mutual defection. The point is that community-based reasoning (and thus the underlying symmetric reasoning assumption) does not work in isolation from the rationality principle, as conditions (CBR2.2) and (CBR3) make it clear. Indeed, I have no reason to cooperate unless I have an independent belief that causal independence does not hold.

This is not to say that CBR entails condition (BCI) and thus causal rationality. CBR is simply silent regarding the combination of the selection function f and the accessibility relations B_i. The point is rather that CBR provides no support against (BCI) and that, as far as condition (CI) seems unobjectionable, there is no reason to reject the use of causal rationality per se. In this case, cooperation in the prisoner’s dilemma is not supported by CBR alone. A possibility however is discussed by Bicchieri and Green [21] and is based on the distinction between causal independence and causal necessity. While the players may be causally rational in the sense of (CR), they may hold the belief that it is causally necessary that they play the same strategy because of some “identicality” assumption. Bicchieri and Green add to the s.e.m. a “nomic accessibility” binary relation C where wCw’ reads as “w’ is causally possible relative to w”. Then, an event [e] is causally necessary at state w if and only if {w’: wCw’} ⊆ [e]. Denote [C] and [D] the event that everyone cooperates and everyone defects respectively and suppose that all the players in the prisoner’s dilemma take the following nomic relation as true: for all w, w’ ∈ W, {w’: wCw’} ⊆ [C] ∪ [D]. In words, the players consider as a causal necessity that they play identically. Then obviously, the sole fact of causal rationality entails that the players will cooperate. Clearly, it is controversial that the belief in this kind of causal necessity can be defended on the basis of any scheme of practical reasoning. I do not think that community-membership, however we expand and refine CBR, can foster and justify such a belief. I must thus conclude that CBR is unhelpful to commend cooperation as the rational choice in the prisoner’s dilemma.25

7. Conclusions

This paper has presented CBR as a specific scheme of practical reasoning in strategic interactions. Community-based reasoners use the fact that they are the members of the same community as an epistemic resource to generate common belief about everyone’s behavior. My main claim in this paper has been twofold: first, CBR plausibly grounds focal points and salience phenomena and more generally may underlie most rule-following behaviors. This first point may be worth testing experimentally. Second, I have argued that CBR emphasizes the importance of counterfactuals in strategic interactions. In particular, the existence of rules does not reduce to observable behavioral patterns but also encompasses a range of counterfactual beliefs and behaviors. On this basis, I have explored the possibility that CBR might rationalize cooperation in the prisoner’s dilemma but in the end I remain highly skeptical.