Abstract
We extend a standard two-person, non-cooperative, non-zero sum, imperfect inspection game, considering a large population of interacting inspectees and a single inspector. Each inspectee adopts one strategy, within a finite/infinite bounded set of strategies returning increasingly illegal profits, including compliance. The inspectees may periodically update their strategies after randomly inter-comparing the obtained payoffs, setting their collective behaviour subject to evolutionary pressure. The inspector decides, at each update period, the optimum fraction of his/her renewable budget to invest on his/her interference with the inspectees’ collective effect. To deter the inspectees from violating, he/she assigns a fine to each illegal strategy. We formulate the game mathematically, study its dynamics and predict its evolution subject to two key controls, the inspection budget and the punishment fine. Introducing a simple linguistic twist, we also capture the corresponding version of a corruption game.
1. Introduction
An inspection game consists of a game-theoretic framework, modelling the non-cooperative interaction between two strategic parties, called inspector and inspectee; see, e.g., [1,2] for a general survey. The inspector aims to verify that certain regulations, imposed by the benevolent principal he/she is acting for, are not violated by the inspectee. On the contrary, the inspectee has an incentive to disobey the established regulations, risking the enforcement of a punishment fine in the case of detection. The introduced punishment mechanism is a key element of inspection games, since deterrence is generally the inspector’s highest priority. Typically, the inspector has limited means of inspection at his/her disposal, so that his/her detection efficiency can only be partial.
The central objective of inspection games is to develop an effective inspection policy for the inspector to adopt, given that the inspectee acts according to a strategic plan. Within the last five decades, inspection games have been applied in the game-theoretic analysis of a wide range of issues, mainly in arms control and nuclear non-proliferation, but also in accounting and auditing of accounts, tax inspections, environmental protection, crime control, passenger ticket control, stock-keeping and others; see, e.g., [1,3,4,5,6] and the references therein. Though when initially introduced, inspection games appeared almost exclusively as two-person, zero-sum games, gradually, the need to depict more realistic scenarios shifted attention towards n-person and non-zero-sum games.
Dresher’s [7] two-person, zero-sum, perfect recall, recursive inspection game is widely recognised as the first formal approach in the field. In his model, Dresher considered n periods of time available for an inspectee to commit, or not, a unique violation, and one-period lasting inspections available for the inspector to investigate the inspectee’s abidance by the rules, assuming that a violator can be detected only if he/she is caught (inspected) in the act. This work initiated the application of inspection games to arms control and disarmament; see, e.g., [8] and the references therein. Maschler [9] generalised this archetypal model, introduced the equivalent non-zero-sum game and, most importantly, adopted from economics the notion of inspector leadership, showing (among others) that the inspector’s option to pre-announce and commit to a mixed inspection strategy actually increases his/her payoff.
Thomas and Nisgav [10] used a similar framework to investigate the problem of a patroller aiming to inhibit a smuggler’s illegal activity. In their so-called customs-smuggler game, customs patrol, using a speedboat, in order to detect a smuggler’s motorboat attempting to ship contraband through a strait. They introduced the possibility of more than one patrolling boats, namely the possibility of two or more inspectors, potentially not identical, and suggested the use of linear programming methods for the solution of those scenario. Baston and Bostock [11] provided a closed-form solution for the case of two patrolling boats and discussed the withdrawal of the perfect-capture assumption, stating that detection is ensured whenever violation and inspection take place at the same period. Garnaev [12] provided a closed-form solution for the case of three patrolling boats.
Von Stengel [13] introduced a third parameter in Dresher’s game, allowing multiple violations, but proving that the inspector’s optimal strategy is independent of the maximum number of the inspectee’s intended violations. He studied another variation, optimising the detection time of a unique violation that is detected at the following inspection, given that inspection does not currently take place. On a later version, von Stengel [14] additionally considered different rewards for the inspectee’s successfully committed violations, extending as well Maschler’s inspector leadership version under the multiple intended violations assumption. Ferguson and Melolidakis [15], motivated by Sakaguchi [16], treated a similar three-parameter, perfect-capture, sequential game, where: (i) the inspectee has the option to ‘legally’ violate at an additional cost; (ii) a detected violation does not terminate the game; (iii) every non-inspected violation is disclosed to the inspector at the following stage.
Non-zero-sum inspection games were already discussed at an early stage by Maschler [9,17], but were mainly developed after the 1980s, in the context of the nuclear non-proliferation treaty (NPT). The prefect-capture assumption was partly abandoned, and errors of Type 1 (false alarm) and Type 2 (undetected violation given that inspection takes place) were introduced to formulate the so-called imperfect inspection games. Avenhaus and von Stengel [18] solved Dresher’s perfect-capture, sequential game, assuming non-zero-sum payoffs. Canty et al. [19] solved an imperfect, non-sequential game, assuming that players ignore any information they collect during their interaction, where an illegal action must be detected within a critical timespan before its effect is irreversible. They discussed the sequential equivalent, as well. Rothenstein and Zamir [20] included the elements of imperfect inspection and timely detection in the context of environmental control.
Avenhaus and Kilgour [21] introduced a non-zero-sum, imperfect (Type 2 error) inspection game, where a single inspector can continuously distribute his/her effort-resources between two non-interacting inspectees, exempted from the simplistic dilemma whether to inspect or not. They related the inspector’s detection efficiency with the inspection effort through a non-linear detection function and derived results for the inspector’s optimum strategy subject to its convexity. Hohzaki [22] moved two steps forward, considering a similar players inspection game, where the single inspection authority not only intends to optimally distribute his/her effort among n inspectee countries, but also among facilities within each inspectee country k. Hohzaki presents a method of identifying a Nash equilibrium for the game and discusses several properties of the players’ optimal strategies.
In the special case when the inspector becomes himself the individual under investigation, namely when the question ‘who will guard the guardians?’ eventually arises [23], the same framework is used for modelling corruption. In the so-called corruption game, a benevolent principal aims to ensure that his/her non-benevolent employee does not intentionally fail his/her duty; see, e.g., [24,25,26,27] and the references therein for a general survey. For example, in the tax inspections regime, the tax inspector employed by the respective competent authority can be open to bribery from the tax payers in order not to report detected tax evasions. Generally speaking, when we switch from inspection to corruption games, the competing pair of an inspector versus an inspectee is replaced by the pair of a benevolent principal versus a non-benevolent employee, but the framework of analysis that is used for the first one can almost identically be used for the second one, as well.
Lambert et al. [28] developed a dynamic game where various private investors anticipate the processing of their applications by an ordered number of low level bureaucrats in order to ensure specific privileges; such an application is approved only if every bureaucrat is bribed. Nikolaev [29] introduced a game-theoretic study of corruption with a hierarchical structure, where inspectors of different levels audit the inspectors of the lower level and report (potentially false reports) to the inspectors of the higher level; the inspector of the highest level is assumed to be honest. In the context of ecosystem management, Lee et al. [30] studied an evolutionary game, where they analyse illegal logging with respect to the corruption of forest rule enforcers, while in the context of politics and governance, Giovannoni and Seidmann [31] investigated how power may affect the government dynamics of simple models of a dynamic democracy, assuming that ‘power corrupts and absolute power corrupts absolutely’ (Lord Acton’s famous quote).
The objective of this paper is to focus on the study of inspection games from an evolutionary perspective, aimed at the analysis of the class of games with a large number of inspectees. However, we highlight that our setting should be distinctly separated from the general setting of the standard evolutionary game theory. We emphasize the networking aspects of these games by allowing the inspectees to communicate with each other and update their strategies purely on account of their interactions. This way, we depict the real-life scenario of partially-informed optimising inspectees. For the same purpose, we set the inspectees to choose from different levels of illegal behaviour. Additionally, we introduce the inspector’s budget as a distinct parameter of the game, and we measure his/her interference with the interacting inspectees with respect to this. We also examine carefully the critical effect of the punishment fine on the process of the game. In fact, we attempt to get quantitative insights into the interplay of these key game parameters and analyse respectively the dynamics of the game.
For a real-world implementation of our game, one can think of tax inspections. Tax payers are ordinary citizens who interact on a daily basis exchanging information on various issues. Arguably, in their vast majority, if not universally, tax payers have an incentive towards tax evasion. Depending on the degree of confidence they have in their fellow citizens, on a pairwise level, they discuss their methods, the extent to which they evade taxes and their outcomes. As experience suggests, tax payers imitate the more profitable strategies. The tax inspector (e.g., the chief of the tax department) is in charge of fighting tax evasion. Having to deal with many tax payers, primarily he/she aims to confront their collective effect rather than each one individually. He/she is provided with a bounded budget from his/her superior (e.g., the finance ministry), and he/she aims to manage this, along with his/her punishment policy, so that he/she maximizes his/her utility (namely the payoff of the tax department).
Though we restrict ourselves to the use of inspection game terminology, our model also intends to capture the relevant class of corruption games. Indicatively, we aim to investigate the dynamics of the interaction between a large group of corrupted bureaucrats and their incorruptible superior, again from an evolutionary perspective. In accordance with our approach, the bureaucrats discuss in pairs their bribes and copy the more efficient strategies, while their incorruptible superior aims to choose attractive wages to discourage bribery, to invest in means of detecting fraudulent behaviour and to adopt a suitable punishment policy. Evidently, the two game settings are fully analogous, and despite the linguistic twist of inspection to corruption, they can be formulated in an identical way.
We organize the paper in the following way. In Section 2, we discuss the standard setting of a two-player, non-cooperative, non-zero-sum inspection game, and we introduce what we call the conventional inspection game. In Section 3 and Section 4, we present our generalization; we extend the two-player inspection game considering a large population of indistinguishable, interacting inspectees against a single inspector, we formulate our model for a discrete/continuous strategy setting respectively, and we demonstrate our analysis. In Section 5, we include a game-theoretic interpretation of our analysis. In Section 6, we summarize our approach and our results, and we propose potential improvements. Finally, Appendix A contains our proofs.
2. Standard Inspection Game
A standard inspection game describes the competitive interaction between an inspectee and an inspector, whose interests in principle contradict. The inspectee, having to obey certain rules imposed by the inspector, either chooses indeed to comply, obtaining a legal profit, , or to violate, aiming at an additional illegal profit, , but undertaking additionally the risk of being detected and, thus, having to pay the corresponding punishment fine, . Likewise, the inspector chooses either to inspect at some given inspection cost, , in order to detect any occurring violation, ward off the loss from the violator’s illegal profit and receive the fine, or not to inspect, avoiding the cost of inspection, but risking the occurrence of a non-detected violation.
In this two-player setting, both players are considered to be rational optimisers who decide their strategies independently, without observing their competitor’s behaviour. Thus, the game discussed is a non-cooperative one. The following normal-form table illustrates the framework described above, where the inspectee is the row player and the inspector is the column player. Left and right cells’ entries correspond to the inspectee’s and the inspector’s payoffs accordingly.
Table 1 illustrates the so-called perfect inspection game, in the sense that inspection always coincides with detection (given that a violator is inspected, the inspector will detect his/her violation with probability one). However, this is an obviously naive approach, since in practice, numerous factors deteriorate the inspector’s efficiency and potentially obstruct detection. Consequently, the need to introduce a game parameter determining the inspection’s efficiency naturally arises.

Table 1.
Two-player perfect inspection game.
In this more general setting, the parameter is introduced to measure the probability with which a violation is detected given that the inspector inspects. We can also think of λ as a measure of the inspector’s efficiency. Obviously, for , the ideal situation mentioned above is captured. The following normal-form Table 2 illustrates the so-called imperfect inspection game.

Table 2.
Two-player imperfect inspection game.
The key feature of the discussed game setting is that under specific conditions, it describes a two-player competitive interaction without any pure strategy Nash equilibria. Starting from the natural assumption that the inspector, in principle, would like the inspectee to comply with his/her rules and that ideally, he/she would prefer to ensure compliance without having to inspect, the game obtains no pure strategy Nash equilibria when both of the following conditions apply
Indicatively, one can verify that the pure strategy profile is the unique Nash equilibrium of the inspection game when only Condition (1) applies. Accordingly, profile is the unique pure strategy Nash equilibrium when only Condition (2) applies. When neither of the two conditions apply, profile is again the unique pure strategy Nash equilibrium. Hence, given that at least one of the above Conditions (1) and (2) does not apply, a pure strategy equilibrium solution always exists.
Back to the no pure strategy Nash equilibria environment, the first condition assumes that when the inspectee is violating, the inspector’s expected payoff is higher when he/she chooses to inspect. Accordingly, the second one assumes that when the inspector is inspecting, the inspectee’s expected payoff is higher when he/she chooses to comply (this is always true for a perfect inspection game).
Under these assumptions, regardless of the game’s outcome and given the competitor’s choice, both players would in turn switch their chosen strategies to the alternative ones, in an endlessly repeated switching cycle (see Figure 1). This lack of no-regrets pure strategies states that the game contains no pure strategy Nash equilibria. We name it the conventional inspection game.

Figure 1.
No pure strategy Nash equilibria conventional inspection game.
Typically, a two-player game without any pure strategy Nash equilibria is resolved by having at least one player randomising over his/her available pure strategies. In this specific scenario, it can be proven that both players resort to mixed strategies, implying that both inspection and violation take place with non-zero probabilities. In particular, the following theorem proven in [32] gives the unique mixed strategy Nash equilibrium of the conventional inspection game described above.
Theorem 1.
Proof.
See [32].
☐
3. Evolutionary Inspection Game: Discrete Strategy Setting
Let us now proceed with our extension of the two-player game we introduced in Section 2 to the real-life scenario of a multi-player problem. We consider a large population of N indistinguishable, pairwise interacting inspectees against a single inspector. Equivalently in the context of corruption games, one can think of N indistinguishable, pairwise interacting bureaucrats against their incorruptible superior. The game mechanism can be summarised into the following dynamic process.
Initially, the N inspectees decide their strategies individually. They retain their group’s initial strategy profile for a certain timespan, but beyond this point, on account of the inspector’s response to their collective effect, some of the inspectees are eager to update and switch to evidently more profitable strategies. In principle, an inspectee is an updater with a non-zero probability ω that is characteristic of the inspectees’ population.
Indicatively, assume on a periodic basis, and in particular at the beginning of each update period, that an updater discusses his/her payoff with another randomly-chosen inspectee, who is not necessarily an updater himself/herself. If the two interacting inspectees have equal payoffs, then the updater retains his/her strategy. If, however, they have a payoff gap, then the updater is likely to revise his/her strategy, subject to how significant their payoffs’ variance is.
Clearly, we do not treat the inspectees as strictly rational optimizers. Instead, we assume that they periodically compare their obtained payoffs in pairs, and they mechanically copy more efficient strategies purely in view of their pairwise interaction and without necessarily being aware of the prevailing crime rate or the inspector’s response. This assumption is described as the myopic hypothesis, and we introduce it to illustrate the lack of perfect information and the frequently adopted imitating behaviour in various multi-agent social systems. However, as we will see in Section 5, ignoring the myopic hypothesis in a strictly game-theoretic context, we can still interpret our results.
Regarding the inspector’s response, we no longer consider his/her strategy to be the choice of the inspection frequency (recall the inspector’s dilemma in the standard game setting whether to inspect or not). Instead, we take into account the overall effort the inspector devotes to his/her inspection activity. In particular, we identify this generic term as the fraction of the available budget that he/she invests on his/her objective, assuming that the inspection budget controls every factor of his/her effectiveness (e.g., the inspection frequency, the no-detection probability, the false alarms, etc.).
At each update event, we assume that the inspector is limited to the same finite, renewable available budget B. Without experiencing any policy-adjusting costs, he/she aims at maximising his/her payoff against each different distribution of the inspectees’ strategies at the least possible cost. Additionally, we assume that at each time point, he/she is perfectly informed about the inspectees’ collective behaviour. Therefore, we treat the inspector as a rational, straightforward, payoff maximising player. This suggestion is described as the best response principle.
Under this framework, the crime distribution in the population of the inspectees is subject to evolutionary pressure over time. Thus, the term evolutionary is introduced to describe the inspection game. It turns out that more efficient strategies gradually become dominant.
3.1. Analysis
We begin our analysis by assuming that the inspectees choose their strategies within a finite bounded set of strategies , generating increasingly illegal profits. Their group’s state space is then the set of sequences of non-negative integers , denoting the occupation frequency of strategy . Equivalently, it is the set of sequences of the corresponding relative occupation frequencies , where .
We consider a constant number of inspectees, namely we have for each group’s state n. Provided that the population size N is sufficiently large (formally valid for through the law of large numbers), we approximate the relative frequencies with , denoting the probabilities with which the strategies are adopted. To each strategy i we assign an illegal profit , characterizing compliers, and a strictly increasing punishment fine , with . We assume that is constant, namely that ’s form a one-dimensional regular lattice.
As explained, the inspector has to deal with an evolving crime distribution in the population of the inspectees, . We define the set of probability vectors , such that:
We introduce the inner product notation to define the group’s expected (average) illegal profit by . Respectively, we define the group’s expected (average) punishment fine by . We also define the inspector’s invested budget against crime distribution by and the inspector’s efficiency by . The last function measures the probability with which a violator is detected given that the inspector invests budget b. To depict a plausible scenario, we assume that perfect efficiency cannot be achieved within the inspector’s finite available inspection budget B (namely, the detection probability is strictly smaller than one, ).
Assumption 1.
The inspector’s efficiency, , is a twice continuously differentiable, strictly increasing, strictly concave function, satisfying:
An inspectee who plays strategy either escapes undetected with probability and obtains an illegal profit or gets detected with probability and is charged with a fine . Additionally, every inspectee receives a legal income r, regardless of his/her strategy being legal or illegal.
Therefore, to an inspectee playing strategy i, against the inspector investing budget b, we assign the following inspectee’s payoff function:
Accordingly, we need to introduce a payoff function for the inspector investing budget b against crime distribution . Recall that the inspector is playing against a large group of inspectees and intends to fight their collective illegal behaviour. For his/her macroscopic standards, the larger the group is, the less considerable absolute values corresponding to a single agent (i.e., ) are.
To depict this inspector’s subjective evaluation, we introduce the inspector’s payoff function as follows:
where κ is a positive scaling constant and , respectively , denotes the expected (average) illegal profit, respectively the expected (average) punishment fine, at time t. Without loss of generality, we set . Note that the inspector’s payoff always obtains a finite value, including the limit .
As already mentioned, an updater revises his/her strategy with a switching probability depending on his/her payoff’s difference with the randomly-chosen individual’s payoff, with whom he/she exchanges information. Then, for an updater playing strategy i and exchanging information with an inspectee playing strategy j, we define this switching probability by , for a timespan , where:
and is an appropriately-scaled normalization parameter.
This transition process dictates that in every period following an update event, the number of inspectees playing strategy i is equal to the corresponding sub-population in the previous period, plus the number of inspectees having played strategies and switching into strategy i, minus the number of inspectees having played strategy i and switching into strategies .
Hence, we derive the following iteration formula:
which can be suitably reformulated, taking the limit as , into an equation resembling the well-known replicator equation (see, e.g., [33]):
Remark 1.
We have used here a heuristic technique to derive Equation (9), bearing in mind that we consider a significantly large group of interacting individuals (formally valid for the limiting case of an infinitely large population). A rigorous derivation can be found in [34].
In agreement with our game setting (i.e., the myopic hypothesis), (9) is not a best-response dynamic. However, it turns out that successful strategies, yielding payoffs higher than the group’s average payoff, are subject to evolutionary pressure. This interesting finding of our setting, which is put forward in the above replicator equation, simply states that although the inspectees are not considered to be strictly rational maximizers (but instead myopic optimizers), successful strategies propagate into their population through the imitation procedure. This characteristic classifies (9) into the class of the payoff monotonic game dynamics [35]. Before proceeding further, it is important to state that our setting is quite different from the general setting of standard evolutionary game theory. Unlike standard evolutionary games, in our approach there are no small games of a fixed number of players through which successful strategies evolve. On the contrary, at each step and throughout the whole procedure, there is only one players game taking place (see also the game in Section 5).
Regarding the inspector’s interference, the best response principle states that at each time step, against the crime distribution he/she confronts, the inspector aims to maximise his/her payoff with respect to his/her available budget:
On the one hand, the inspector chooses his/her fine policy strategically in order to manipulate the evolution of the future crime distribution. On the other hand, at each period, he/she has at his/her disposal the same renewable budget B, while he/she is not charged with any policy adjusting costs. In other words, the inspector has a period-long planning horizon regarding his/her financial policy. Therefore, he/she instantaneously chooses at each step his/her response b that maximises his/her payoff (6) against the prevailing crime distribution.
Let us define the inspector’s best response (optimum budget), maximising his/her payoff (6) against the prevailing crime distribution, by:
Having analytically discussed the inspectees’ and the inspector’s individual dynamic characteristics, we can now combine them and obtain a clear view of the system’s dynamic behaviour as a whole.
In particular, we substitute the inspector’s best response (optimum budget) into the system of ordinary differential equations (ODEs) (9), and we obtain the corresponding system governing the evolution of the non-cooperative game described above:
Recall that through (12) we aim to investigate the evolution of illegal behaviour within a large group of interacting, myopically-maximising inspectees (bureaucrats) under the pressure of a rationally-maximising inspector (incorruptible superior).
Without loss of generality, we set . Let us also introduce the following auxiliary notation:
Proposition 1.
A probability vector is a singular point of (12), namely it satisfies the system of equations:
if and only if there exists a subset , such that for , and for .
Proof.
For any such that , , System (12) reduces to the same one, but only with coordinates (notice that I must be a proper subset of S). Then, for the fixed point condition to be satisfied, we must have for every .
☐
The determination of the fixed points defined in Proposition 1 and their stability analysis, namely the deterministic evolution of the game, clearly depend on the form of . One can identify two control elements that appear in and thus govern the game dynamics; the functional control and the control parameter B. We have set the fine to be a strictly increasing function, and we consider three eventualities regarding its convexity; (i) linear; (ii) convex; (iii) concave. To each version we assign a different inspector’s punishment profile. Indicatively, we claim that a convex fine function reveals an inspector who is lenient against relatively low collective violation, but rapidly jumps to stricter policies for increasing collective violation. Contrarily, we claim that a concave fine function reveals an inspector who is already punishing aggressively even for a relatively low collective violation. Finally, we assume that a linear fine function represents the ‘average’ inspector. We also vary in each case the constant (linear)/increasing (convex)/decreasing (concave) gradient of function . Accordingly, we vary the size of the finite available budget B. The different settings we establish with these control parameter variations and, therefore, the corresponding dynamics we obtain in each case have clear practical interpretation providing useful insight into applications. For example, the fine function can be, and usually is, defined by the inspector himself (think of different fine policies when dealing with tax evasion), while the level of budget B is decided from the benevolent principal by whom the inspector is employed. The detection efficiency is not regarded as an additional control since it characterizes the inspector’s behaviour endogenously. However, say the inspector has an excess of budget, then he/she could invest it in improving his/her expertise (e.g., his/her technical know-how) that is related with his/her efficiency indirectly. Then, he/she could improve . We do not engage with this case.
3.2. Linear Fine
Equivalently to (11), for a linear fine , the inspector’s best response (optimum budget) can be written as:
We check from (15) that we cannot have for every , since at least for , it is . However, depending on the size of B, we may have for every .
Then, it is reasonable to introduce the following notation:
where is not necessarily deliverable, i.e., may not belong to . One should think of this critical value as a measure of the adequacy of the inspector’s available budget B, namely as the ‘strength’ of his/her available budget. Obviously, if , the inspector benefits from exhausting all his/her available budget when dealing with , while, if , the inspector never needs to exhaust B in order to achieve an optimum response.
Theorem 2.
Let Assumption 1 hold. The unit vectors , , lying on the vertices of the d-simplex, are fixed points of (12). Moreover:
- (i)
- If , there is additionally a unique hyperplane of fixed points,
- (ii)
- If and , there are additionally infinitely many hyperplanes of fixed points,
Proof.
In any case, the unit probability vectors satisfy (14), since by definition of , it is , , whilst it is .
The setting we introduce with Assumption 1 ensures that is a continuous, non-decreasing, surjective function. In particular, we have that is strictly increasing in and is strictly increasing in . Hence:
- (i)
- When , there is a unique satisfying . This unique is generated by infinitely many probability vectors, , forming a hyperplane of points satisfying (14).
- (ii)
- When and , every satisfies . Each one of these infinitely many is generated by infinitely many probability vectors, , forming infinitely many hyperplanes of points satisfying (14).
☐
We refer to the points as pure strategy fixed points, to emphasize that they correspond to the group’s strategy profiles such that every inspectee plays the same strategy i. Accordingly, we refer to the points , , as mixed strategy fixed points, to emphasize that they correspond to the group’s strategy profiles such that the inspectees are distributed among two or more available strategies.
Before proceeding with the general stability results, we present the detailed picture in the simplest case of three available strategies generating increasingly illegal profits including compliance.
Figure 2 implies a budget B such that the inspector never exhausts it. For a relatively low B or for an overly lenient (see Figure 2a and Figure 3a), the pure strategy fixed point is asymptotically stable. Increasing though B or, accordingly, toughening up (see Figure 2b), a hyperplane of asymptotically-stable mixed strategy fixed points appears. Depending on the critical parameter , we may have infinitely many hyperplanes of asymptotically stable mixed strategy fixed points (see Figure 3b,d). Finally, keeping B constant, the more we increase the slope of , the closer this(ese) hyperplane(s) moves towards compliance (see Figure 2c and Figure 3c,e). We generalize these results into the following theorem.
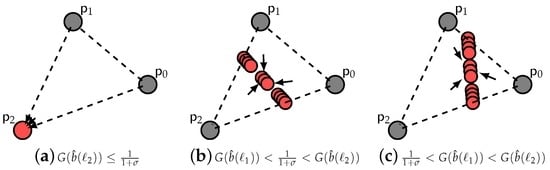
Figure 2.
Dynamics for a linear , where . Set of strategies .
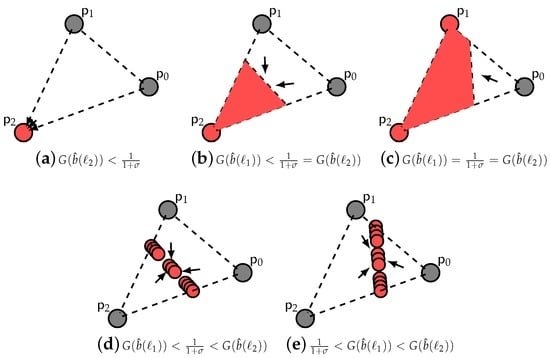
Figure 3.
Dynamics for a linear , where . Set of strategies .
Theorem 3.
Let Assumption 1 hold. Consider the fixed points given by Theorem 2. Then:
(i) the pure strategy fixed point is a source, thus unstable; (ii) the pure strategy fixed points , , are saddles, thus unstable; (iii) the pure strategy fixed point is asymptotically stable when ; otherwise, it is a source, thus unstable; (iv) the mixed strategy fixed points , are asymptotically stable.
Proof.
See Appendix A.
☐
3.3. Convex/Concave Fine
Let us introduce the auxiliary variable . As usual, using the inner product notation, we define the corresponding group’s expected/average value by , where . Then, equivalently to (11) and (15), the inspector’s best response/optimum budget can be written as:
For every , let us introduce as well the parameter:
Lemma 1.
For a convex fine, is strictly decreasing in i for constant j (or vice versa), while for a concave fine, is strictly increasing in i for constant j (or vice versa). Furthermore, for a convex fine, is strictly decreasing in for constant , while for a concave fine, is strictly increasing in for constant .
Theorem 4.
Let Assumption 1 hold. The unit vectors , , lying on the vertices of the d-simplex are fixed points of (12). Moreover, there may be additionally up to internal fixed points , living on the support of two strategies , uniquely defined for each pair of strategies; they exist given that the following condition applies respectively:
Proof.
In any case, the unit probability vectors satisfy (14), since by the definition of , it is , , whilst it is , .
Consider a probability vector satisfying (14), such that , , and . Then, from Proposition 1, should satisfy , , namely the fraction should be constant , and equal to .
To satisfy this, according to Lemma 1, the complement set may not contain more than two elements, namely the distributions may live on the support of only two strategies.
For such a distribution , such that and , , where , we get:
The setting we introduce with Assumption 1 ensures that is a continuous, non-decreasing, surjective function. In particular, we have that is strictly increasing in and is strictly increasing in . Then, for any to exist, namely for (20) to hold in each instance, the following condition must hold respectively:
☐
We refer to the points as double strategy fixed points, to emphasize that they correspond to the group’s strategy profiles, such that the inspectees are distributed between two available strategies.
Again, we present the detailed picture in the simplest case of three available strategies generating increasingly illegal profits including compliance. Like above, in Figure 4 and Figure 5, we observe how the interplay of the key parameters B and affect the game dynamics.
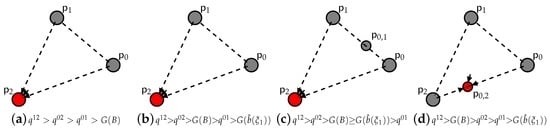
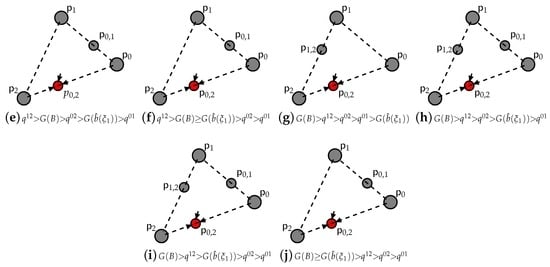
Figure 4.
Dynamics for the case of concave and three available strategies/.
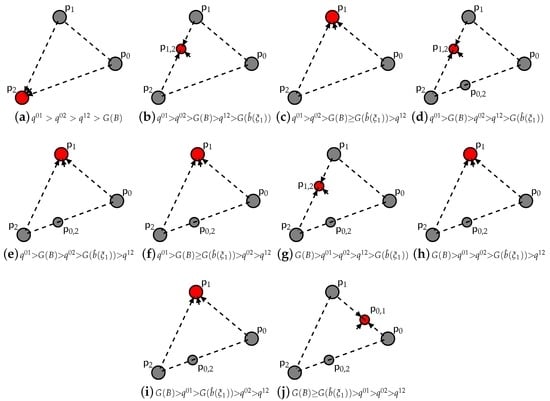
Figure 5.
Dynamics for the case of convex and three available strategies/.
The general pattern is similar to Figure 2 and Figure 3. Initially, the pure strategy fixed point appears to be asymptotically stable (see Figure 4a–c and Figure 5a), while gradually, either increasing B or toughening up , this unique asymptotically stable fixed point shifts towards compliance. However, the shift here takes place only through double strategy fixed points and not through hyperplanes of fixed points. In particular, for a concave , it occurs only through the fixed point living on the support of the two border strategies (see Figure 4d–j), while for a convex , it occurs through the fixed points , , namely only through the fixed points living on the support of two consecutive strategies (see Figure 5b–j).
Proposition 2.
For a convex fine: (i) the set of double strategy fixed points contains at most one fixed point living on the support of two consecutive strategies; (ii) there is at most one pure strategy fixed point satisfying:
Proof.
(i) Assume there are two double strategy fixed points , both living on the support of two consecutive strategies. According to Theorem 4, both of them should satisfy (19). However, since it is , then from Assumption 1, it is also , and since the fine is convex, then from Lemma 1, it is also . Overall, we have that:
which contradicts the initial assumption.
(ii) Assume there are two pure strategy fixed points , , both satisfying (22). However, since it is , then from Assumption 1, it is also , and since the fine is convex, then from Lemma 1, it is also . Overall, we have that:
which contradicts the initial assumption.
☐
We generalize the results that we discussed above on the occasion of Figure 4 and Figure 5, into the following theorem.
Theorem 5.
Let Assumption 1 hold. Consider the fixed points given by Theorem 4. Then:
- For a concave fine: (i) the pure strategy fixed point is a source, thus unstable; (ii) the pure strategy fixed points , are saddles, thus unstable; (iii) the double strategy fixed points are saddles, thus unstable; (iv) the double strategy fixed point is asymptotically stable; (v) the pure strategy fixed point is asymptotically stable when does not exist; otherwise, it is a source, thus unstable.
- For a convex fine: (i) the pure strategy fixed point is a source, thus unstable; (ii) the double strategy fixed points , are saddles, thus unstable; the double strategy fixed points are asymptotically stable; the pure strategy fixed points , are saddles, thus unstable; the pure strategy fixed point is a source, thus unstable. * When no exists, the pure strategy fixed point satisfying (22) is asymptotically stable.
Proof.
See Appendix A.
☐
4. Evolutionary Inspection Game: Continuous Strategy Setting
The discrete strategy setting is our first approach towards introducing multiple levels of violation available for the inspectees. It is an easier framework to work with for our analytic purposes, and it is more appropriate to depict certain applications. For example, in the tax inspections regime, the tax payers can be thought of as evading taxes only in discrete amounts (this is the case in real life). However, in the general crime control regime, the intensity of criminal activity should be treated as a continuous variable. Therefore, the continuous strategy setting is regarded as the natural extension of the discrete setting that captures the general picture.
We consider the scenario where the inspectees choose their strategies within an infinite bounded set of strategies, , generating increasingly illegal profits. Here, we identify the inspectees’ available strategies with the corresponding illegal profits that they generate. We retain the introduced framework (i.e., the myopic hypothesis, the best response principle, etc.), adjusting our assumptions and our analysis to the continuous local strategy space when needed. Our aim is to extend the findings of Section 3.
The group’s state space is the set of sequences , where is the n-th inspectee’s strategy. This can be naturally identified with the set consisting of the normalized sums of N Dirac measures . Let the set of probability measures on Λ be .
We rewrite the inspectee’s payoff function (5), playing for illegal profit against invested budget b in the form:
Let us introduce the notation for the sum . We rewrite the inspector’s payoff function (6) in the form:
where for the positive scaling constant, we set again . Recall the argument we introduced in Section 3.2 regarding the inspector’s subjective evaluation, which leads to Expressions (6) and (24).
It is rigorously proven in [34] that, given that initial distribution converges to a certain measure as , the group’s strategy profile evolution under the inspector’s optimum pressure corresponds to the deterministic evolution on solving the kinetic equation :
or equivalently in the weak form:
Recall that Assumption 1 ensures that is well defined. Furthermore, notice that notation introduced in Section 3.2 stands here for the expected values , , respectively, where and .
Using this inner product notation and substituting (22) into (25), the kinetic equation can be written in a symbolic form:
One can think of (25) and (27) as the continuous local strategy space equivalent of Equations (9) and (12).
Proposition 3.
Proof.
☐
4.1. Linear Fine
We consider a linear fine , and we extend the definitions (11), (15) and (16) to the continuous strategy setting.
Theorem 6.
Let Assumption 1 hold. Every Dirac measure is a fixed point of (25). Moreover:
- (i)
- If , there is additionally a unique hyperplane of fixed points:
- (ii)
- If and , there are additionally infinitely many hyperplanes of fixed points:
Proof.
Every Dirac measure satisfies (28), since by definition, it is .
In addition, Assumption 1 ensures that is a continuous, non-decreasing, surjective function. Particularly, is strictly increasing in , and is strictly increasing in . Therefore:
- (i)
- When , there is a unique satisfying . This unique is generated by infinitely many probability measures, , forming a hyperplane of points in satisfying (25).
- (ii)
- When and , every satisfies . Each one of these infinitely many is generated by infinitely many probability measures, , forming infinitely many hyperplanes of points satisfying (25).
☐
We refer to the points as pure strategy fixed points, to emphasize that they correspond to the group’s strategy profiles, such that every inspectee plays the same strategy z. Accordingly, we refer to the points as mixed strategy fixed points.
Theorem 7.
Let Assumption 1 hold. Consider the fixed points given by Theorem 6. Then:
For a linear fine: (i) the pure strategy fixed points , , are unstable; (ii) the pure strategy fixed point is asymptotically stable on the topology of the total variation norm, when ; otherwise, it is unstable; (iii) the mixed strategy fixed points , are stable.
Proof.
See Appendix A.
☐
4.2. Convex/Concave Fine
We extend the definitions (11) and (17) to the continuous strategy setting. Additionally, for every , let us introduce the parameter:
Lemma 2.
For a convex fine, is strictly decreasing in x for constant y (or vice versa), while for a concave fine, is strictly increasing in x for constant y (or vice versa). In addition, for a convex fine, is strictly decreasing in for constant , while for a concave fine, is strictly increasing in for constant .
Theorem 8.
Proof.
Every Dirac measure satisfies (28), since by definition, it is .
Consider a probability measure satisfying (28), such that , , , . Then, from Proposition 3, should satisfy for every pair of , namely the fraction should be constant and equal to .
According to Lemma 2, this is possible only when the support of contains no more than two elements, namely when it is equivalent to the normalised sum of two Dirac measures, such that . Such a probability measure satisfies:
where .
In addition, Assumption 1 ensures that is a continuous, surjective, non-decreasing function. Particularly, is strictly increasing in , and is strictly increasing in . Therefore, for any to exist, namely for (32) to hold in each instance, the following condition must hold respectively:
☐
We refer to the points as double strategy fixed points, since they correspond to the group’s strategy profiles such that the inspectees are distributed between two available strategies.
Theorem 9.
Let Assumption 1 hold. Consider the fixed points given by Theorem 8. Then:
For a concave fine: (i) the pure strategy fixed points are unstable; (ii) the double strategy fixed points are unstable; (iii) the double strategy fixed point is asymptotically stable; (iv) the pure strategy fixed point is asymptotically stable on the topology of the total variation norm, when does not exist; otherwise, it is unstable.
Proof.
See Appendix A.
☐
5. Fixed Points and Nash Equilibria
So far, we have deduced and analysed the dynamics governing the deterministic evolution of the multi-player system we have introduced (assuming the myopic hypothesis for an infinitely large population). Our aim now is to provide a game-theoretic interpretation of the fixed points we have identified. We work in the context of the discrete strategy setting. The extension to the continuous strategy setting is straightforward.
Let us consider the game of a finite number of players (N inspectees, one inspector). When the inspector chooses the strategy and each of the N inspectees chooses the same strategy , then the inspector receives the payoff , and each inspectee receives the payoff . Note that the inspectees’ collective strategy profile can be thought of as the collection of relative occupation frequencies, .
One then defines an Nash equilibrium of as a profile of strategies , such that:
and for any pair of strategies :
hold up to an additive correction term not exceeding ϵ, where denote the standard basis in .
It occurs that all of the fixed points identified in Section 3 (and by extension in Section 4) describe approximate Nash equilibria of . We state here the relevant result without a proof. A rigorous discussion can be found in [34]. Recall that for a sufficiently large population N (formally for ), we can approximate the relative frequencies with the probabilities obeying (12).
Proposition 4.
Under suitable continuity assumptions on and : (i) any limit point of any sequence , such that is a Nash equilibrium of , is a fixed point of the deterministic evolution (12); (ii) for any fixed point x of (12), there exists a Nash equilibrium of , such that the difference of any pair of coordinates of does not exceed in magnitude.
The above result provides a game-theoretic interpretation of the fixed points that were identified by Theorems 2, 4, 6 and 8, independent of the myopic hypothesis. Moreover, it naturally raises the question of which equilibria can be chosen in the long run. The fixed points stability analysis performed in Section 3 and Section 4 aims to investigate this issue. Furthermore, Proposition 4 states, in simple words, that our analysis and our results are also valid for a finite population of inspectees (recall our initial assumption for an infinitely large N), with precision that is inversely proportional to the size of N.
6. Discussion
In this paper, we study the spread of illegal activity in a population of myopic inspectees (e.g., tax payers) interacting under the pressure of a short-sighted inspector (e.g., tax inspector). Equivalently, we investigate the spread of corruption in a population of myopic bureaucrats (e.g., ministerial employees) interacting under the pressure of an incorruptible supervisor (e.g., governmental fraud investigator). We consider two game settings with regards to the inspectees’ available strategies, where the continuous strategy setting is a natural extension of the discrete strategy setting. We introduce (and vary qualitatively/quantitatively) two key control elements that govern the deterministic evolution of the illegal activity, the punishment fine and the inspection budget.
We derive the ODEs (12) and (27) that characterize the dynamics of our system; we identify explicitly the fixed points that occur under our different scenarios; and we carry out respectively their stability analysis. We show that although the indistinguishable ‘agents’ (e.g., inspectees, corrupted bureaucrats) are treated as myopic maximizers, profitable strategies eventually prevail in their population through imitation. We verify that an adequately financed inspector achieves an increasingly law-abiding environment when there is a stricter fine policy. More importantly, we show that although the inspector is able to establish any desirable average violation by suitably manipulating budget and fine, he/she is not able to combine this with any desirable group’s strategy profile. Finally, we provide a game-theoretic interpretation of our fixed points stability analysis.
There are many directions towards which one can extend our approach. To begin with, one can consider an inspector experiencing policy-adjusting costs. Equivalently, one can withdraw the assumption of a renewable budget. Moreover, the case of two or more inspectors, possibly collaborating with each other or even with some of the inspectees, could be examined. Regarding the inspectees, an additional source of interaction based on the social norms formed within their population could be introduced. Another interesting variation would be to add a spatial distribution of the population, assuming indicatively that the inspectees interact on a specific network. Some of these alternatives have been studied for more general or similar game settings; see, e.g., [26,34].
Acknowledgments
Stamatios Katsikas would like to acknowledge support from the Engineering and Physical Sciences Research Council (EPSRC), Swindon, UK.
Author Contributions
Stamatios Katsikas and Vassili Kolokoltsov conceived and designed the model, and performed the analysis. Wei Yang contributed in the initial stages of the analysis. Stamatios Katsikas wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We make use of the Hartman–Grobman theorem, stating that the local phase portrait near a hyperbolic fixed point is topologically equivalent to the phase portrait of the linearisation [36], namely that the stability of a hyperbolic fixed point is preserved under the transition from the linear to the non-linear system. For the non-hyperbolic fixed points, we resort to Lyapunov’s method [37]. Recall that a fixed point is hyperbolic if all of the eigenvalues of the linearisation evaluated at this point have non-zero real parts. Such a point is asymptotically stable if and only if all of the eigenvalues have a strictly negative real part, while it is unstable (source or saddle) if at least one has a strictly positive real part.
Appendix A.1. Proof of Theorem 3
We rewrite (12) in the equivalent form, , for arbitrary ,
The linearisation of (A1) around a pure strategy fixed point can be written in the matrix form:
where A is a diagonal matrix, with main diagonal entries, namely with eigenvalues:
- (i)
- For the pure strategy fixed point , we get:which is strictly positive . Then, is a source.
- (ii)
- For the pure strategy fixed point , we get:which is strictly negative when . Then, is asymptotically stable. Otherwise, (A5) is strictly positive, and is a source.
- (iii)
- For the pure strategy fixed points , , (A3) changes sign between and , when . Then, are saddles.
- (iv)
- For the non-isolated, non-hyperbolic mixed strategy fixed points , we resort to Lyapunov’s method. Consider the real valued Lyapunov function :
Differentiating with respect to time, we get:
From Assumption 1, is strictly increasing in , and is strictly increasing in . Additionally, from (A1), we get:
Hence, overall, we have that , if and for all (respectively for and ). Then, according to Lyapunov’s theorem, are stable.
Appendix A.2. Proof of Theorem 5
We rewrite (12) in the equivalent form, ,
Around an arbitrary fixed point , the nonlinear system (A9) is approximated by:
which is a linear system with coefficient matrix , , with:
where . This is the Jacobian matrix of (A9) at an arbitrary fixed point . We use the characteristic equation to find the eigenvalues of A for every fixed point.
Let us introduce the notation for the elementary matrix corresponding to the row/column operation of swapping rows/columns . The inverse of is itself; namely, it is .
For a pure strategy fixed point , , first swapping rows of A and then swapping columns of the resulting matrix, we obtain the upper triangular matrix:
For , the Jacobian A is already an upper triangular matrix. Matrices A and B are similar, namely they have the same characteristic polynomial and, thus, the same eigenvalues. The eigenvalues of an upper triangular matrix are precisely its diagonal elements.
Consequently, the eigenvalues of A at a pure strategy fixed point , , are given by:
For a double strategy fixed point , , swapping rows of A and then swapping in order rows , columns and columns , we obtain the matrix:
where we have used the inverse matrix product identity. For , the Jacobian A has already the form of C. For , we need to swap only the n row, n column. Respectively for . Matrices A and C are similar. The characteristic polynomial of C, and thus of A, is:
where and are upper triangular matrices.
Thus, the eigenvalues of A at a double strategy fixed point , are given by:
Concave fine:
- (i)
- For the pure strategy fixed point , we get the form (A13):which is strictly positive . Then, is a source.
- (ii)
- (iii)
- For the double strategy fixed points , (A16) changes sign, indicatively between and (since is strictly increasing in i). Then, are saddles.
- (iv)
- For the double strategy fixed point , we get from (A16):which is strictly negative (since , is strictly increasing in i). Then, is asymptotically stable.
- (v)
- For the pure strategy fixed point , we get from (A13):which is strictly negative when does not exist, namely when . Then, is asymptotically stable. Otherwise, it is strictly positive , and is a source.
- (i)
- For the pure strategy fixed point , we get from (A13):which is strictly positive . Then, is a source.
- (ii)
- For the double strategy fixed points , (A16) changes sign, indicatively between and (since is strictly decreasing in i). Then, are saddles.
- (iii)
- For the double strategy fixed points , (A16) is strictly negative (since , is strictly decreasing in i). Then, is asymptotically stable.
- (iv)
- (v)
Appendix A.3. Proof of Theorem 7
- (i)
- From the proof of Theorem (3), we have seen that the pure strategy fixed points , , have at least one unstable trajectory.
- (ii)
- For the pure strategy fixed point , consider the real valued function , where E is an open subset of , with radius and centre :The total variation distance between any two is given by:thus, E does not contain any other Dirac measures. Using variational derivatives, we get:When , we have that , if and for all . Then, according to Lyapunov’s Theorem, is asymptotically stable.
- (iii)
- For the mixed strategy fixed points , take the real valued function :Using variational derivatives, we get:
From Assumption 1, is strictly increasing in , and is strictly increasing in . Hence, we have that , if and for all (respectively for ). Then, according to Lyapunov’s theorem, are stable.
Appendix A.4. Proof of Theorem 9
- (i),(ii)
- From the proof of Theorem (5), we have seen that the pure strategy fixed points and the double strategy fixed points have at least one unstable trajectory.
- (iii)
- For the mixed strategy fixed point , consider the real valued function where E is an open subset of , with radius and centre :Using variational derivatives, we get:Consider a small deviation from :where ϵ is small, and . In first order approximation, one can show that:holds, when:where:For a concave fine, it is:and from Assumption 1, is strictly increasing in and strictly increasing in . Then, overall, we have that , if and , for any small deviation from . Thus, according to Lyapunov’s theorem, is asymptotically stable.
- (iv)
- For the pure strategy fixed point , consider the real valued function , where E is an open subset of , with radius and centre (so that E does not contain any other Dirac measures):
Using variational derivatives, we get:
When does not exist, namely when , take a small deviation from :
where ϵ is small, and . In first order approximation, one can show that:
holds, since for a concave fine, it is:
and, for any , it is:
Then, overall, we have that , if and for any small deviation from within E. Thus, according to Lyapunov’s theorem, is asymptotically stable.
References
- Avenhaus, R.; von Stengel, B.; Zamir, S. Inspection games. Hand. Game Theory Econ. Appl. 2002, 3, 1947–1987. [Google Scholar]
- Avenhaus, R.; Canty, M.J. Inspection Games; Springer: New York, NY, USA, 2012; pp. 1605–1618. [Google Scholar]
- Alferov, G.V.; Malafeyev, O.A.; Maltseva, A.S. Programming the robot in tasks of inspection and interception. In Proceedings of the IEEE 2015 International Conference on Mechanics-Seventh Polyakhov’s Reading, Saint Petersburg, Russia, 2–6 February 2015; pp. 1–3.
- Avenhaus, R. Applications of inspection games. Math. Model. Anal. 2004, 9, 179–192. [Google Scholar]
- Deutsch, Y.; Golany, B.; Goldberg, N.; Rothblum, U.G. Inspection games with local and global allocation bounds. Naval Res. Logist. 2013, 60, 125–140. [Google Scholar] [CrossRef]
- Kolokoltsov, V.; Passi, H.; Yang, W. Inspection and crime prevention: An evolutionary perspective. Available online: https://arxiv.org/abs/1306.4219 (accessed on 18 June 2013).
- Dresher, M. A Sampling Inspection Problem in Arms Control Agreements: A Game-Theoretic Analysis (No. RM-2972-ARPA); Rand Corp: Santa Monica, CA, USA, 1962. [Google Scholar]
- Avenhaus, R.; Canty, M.; Kilgour, D.M.; von Stengel, B.; Zamir, S. Inspection games in arms control. Eur. J. Oper. Res. 1996, 90, 383–394. [Google Scholar] [CrossRef]
- Maschler, M. A price leadership method for solving the inspector’s non-constant-sum game. Naval Res. Logist. Q. 1966, 13, 11–33. [Google Scholar] [CrossRef]
- Thomas, M.U.; Nisgav, Y. An infiltration game with time dependent payoff. Naval Res. Logist. Q. 1976, 23, 297–302. [Google Scholar] [CrossRef]
- Baston, V.J.; Bostock, F.A. A generalized inspection game. Naval Res. Logist. 1991, 38, 171–182. [Google Scholar] [CrossRef]
- Garnaev, A.Y. A remark on the customs and smuggler game. Naval Res. Logist. 1994, 41, 287–293. [Google Scholar] [CrossRef]
- Von Stengel, B. Recursive Inspection Games; Report No. S 9106; Computer Science Faculty, Armed Forces University: Munich, Germany, 1991. [Google Scholar]
- Von Stengel, B. Recursive inspection games. Available online: https://arxiv.org/abs/1412.0129 (accessed on 29 November 2014).
- Ferguson, T.S.; Melolidakis, C. On the inspection game. Naval Res. Logist. 1998, 45, 327–334. [Google Scholar] [CrossRef]
- Sakaguchi, M. A sequential allocation game for targets with varying values. J. Oper. Res. Soc. Jpn. 1977, 20, 182–193. [Google Scholar]
- Maschler, M. The inspector’s non-constant-sum game: Its dependence on a system of detectors. Naval Res. Logist. Q. 1967, 14, 275–290. [Google Scholar] [CrossRef]
- Avenhaus, R.; von Stengel, B. Non-zero-sum Dresher inspection games. In Operations Research’91; Physica-Verlag HD: Heidelberg, Gernamy, 1992; pp. 376–379. [Google Scholar]
- Canty, M.J.; Rothenstein, D.; Avenhaus, R. Timely inspection and deterrence. Eur. J. Oper. Res. 2001, 131, 208–223. [Google Scholar] [CrossRef]
- Rothenstein, D.; Zamir, S. Imperfect inspection games over time. Ann. Oper. Res. 2002, 109, 175–192. [Google Scholar] [CrossRef]
- Avenhaus, R.; Kilgour, D.M. Efficient distributions of arms-control inspection effort. Naval Res. Logist. 2004, 51, 1–27. [Google Scholar] [CrossRef]
- Hohzaki, R. An inspection game with multiple inspectees. Eur. J. Oper. Res. 2007, 178, 894–906. [Google Scholar] [CrossRef]
- Hurwicz, L. But Who Will Quard the Quardians? Prize Lecture 2007. Available online: https://www.nobelprize.org (accessed on 8 December 2007).
- Aidt, T.S. Economic analysis of corruption: A survey. Econ. J. 2003, 113, F632–F652. [Google Scholar] [CrossRef]
- Jain, A.K. Corruption: A review. J. Econ. Surv. 2001, 15, 71–121. [Google Scholar] [CrossRef]
- Kolokoltsov, V.N.; Malafeyev, O.A. Mean-field-game model of corruption. Dyn. Games Appl. 2015. [Google Scholar] [CrossRef]
- Malafeyev, O.A.; Redinskikh, N.D.; Alferov, G.V. Electric circuits analogies in economics modeling: Corruption networks. In Proceedings of the 2014 2nd International Conference on Emission Electronics (ICEE), Saint-Petersburg, Russia, 30 June–4 July 2014.
- Lambert-Mogiliansky, A.; Majumdar, M.; Radner, R. Petty corruption: A game-theoretic approach. Int. J. Econ. Theory 2008, 4, 273–297. [Google Scholar] [CrossRef]
- Nikolaev, P.V. Corruption suppression models: The role of inspectors’ moral level. Comput. Math. Model. 2014, 25, 87–102. [Google Scholar] [CrossRef]
- Lee, J.H.; Sigmund, K.; Dieckmann, U.; Iwasa, Y. Games of corruption: How to suppress illegal logging. J. Theor. Biol. 2015, 367, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Giovannoni, F.; Seidmann, D.J. Corruption and power in democracies. Soc. Choice Welf. 2014, 42, 707–734. [Google Scholar] [CrossRef]
- Kolokoltsov, V.N.; Malafeev, O.A. Understanding Game Theory: Introduction to the Analysis of Many Agent Systems with Competition and Cooperation; World Scientific: Singapore, 2010. [Google Scholar]
- Zeeman, E.C. Population dynamics from game theory. In Global Theory of Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 1980; pp. 471–497. [Google Scholar]
- Kolokoltsov, V. The evolutionary game of pressure (or interference), resistance and collaboration. Available online: https://arxiv.org/abs/1412.1269 (accessed on 3 December 2014).
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 2014. [Google Scholar]
- Jordan, D.W.; Smith, P. Nonlinear Ordinary Differential Equations: An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).