Abstract
The increasing number of patients affected by chronic kidney disease makes it necessary to rely on living donors. However, a patient often cannot exploit her potential donor, due to blood or tissue incompatibility. Therefore, crossover transplantation programs have been developed in several countriesin order to increase the number of people receiving a kidney from a living donor. After reviewing the essential medical facts needed for the subsequent results, we quickly introduce two known algorithms for crossover transplantation. Next, we consider a dataset provided by the Nord Italia Transplant program, and we apply the above algorithms in order to highlight the benefits of these efficient procedures.
1. Introduction
Although dialysis represents an efficient therapy for the management of end-stage kidney disease, kidney transplantation is the treatment of choice for most patients, due to a strong improvement in quality of life and increased survival advantages.
The shortage of kidneys from deceased donors and longer waiting times make it necessary to look for alternatives. One possibility is living kidney donation: in this case, the patient with end-stage renal disease receives a kidney from a living genetically or emotionally related person. However, a willing donor is often unable to give a kidney to the intended patient because of incompatibilities that would lead to transplant rejection [1]. To overcome immunological barriers and expand the donor pool, new strategies have been introduced, including crossover transplantation (kidney exchange).
So far, despite encouraging results, this procedure has not been systematically applied in Italy. For this reason, we implemented two well-known algorithms for kidney exchange and performed simulations considering a dataset of Italian patients. The aim of this work is to increase the interest in such methods and to provide mathematical arguments that could lead to the extension and the improvement of the kidney exchange program in Italy.
This note is organized as follows. The next two subsections present a concise medical background suited to understanding the main issues related to kidney transplantation. The first one deals with general aspects of transplantation, while the second one focuses on specific characteristics of the kidney transplantation. In a subsequent subsection, we provide the mathematical background to treat the problem, and we briefly illustrate the two methods we shall consider in our simulations. The second section deals with the description of how we use the dataset to implement the algorithms. The next section provides the results, which are discussed in the final section.
1.1. Medical Background
The main obstacle to successful transplantation is usually the rejection of foreign tissue by the host’s immune system.
ABO blood group incompatibility between donor and recipient represents one of the most common causes of rejection. There are four blood types: A, B, AB, and O, representing different kinds or the absence of carbohydrate chains on red blood cells and vascular endothelium. People are sensitized to non-self chains, and therefore develop special antibodies against them. For instance, blood type O individuals do not express any chain and develop antibodies to both A and B chains: they are called universal donors, but can receive only from the same blood type. Type A or type B kidneys can be transplanted into the same type or type AB patients, while type AB kidneys can only be transplanted into type AB patients [2,3].
Another genetic characteristic that plays a key role in the success of a kidney transplant is HLA (human leukocyte antigen) type. HLAs are proteins located on the surface of the white blood cells and other tissues in the body that are different from one person to another. Although there are many HLAs, the A, B, and DR antigens have been identified as having a greater influence on the immune response. Since each person inherits one A, B, and DR antigen from each parent, HLA matching between donor and recipient ranges from 0 to 6: the closer the match, the lower the likelihood of rejection of the graft [2].
The sensitization of the recipient also represents a contraindication for kidney transplantation. Indeed, if the recipient has developed preformed antibodies against certain HLA antigens of the donor, due (among several other reasons) to pregnancy, previous transplants, or blood transfusions, the transplant cannot be carried out [4]. An immunological test called PRA (panel reactive antibody) is usually performed on patients waiting for a transplant to assess their degree of sensitization. Individuals with a high PRA usually have difficulty in finding a suitable donor [2,4]. Based upon the distribution of blood groups and recipients’ sensitization, it is estimated that more than 30% of living donors are incompatible with their intended recipient, and cannot proceed to living donor transplantation [5,6,7].
1.2. Kidney Exchange
The concept of kidney exchange was first proposed by Rapaport in 1986 [8]. After a few successful attempts around the world, in 2004, the Netherlands launched the first national exchange program [9]. Since then, kidney exchange has increased in popularity, and many other countries have developed national programs, including the United States, Australia, Canada, Romania, South Korea, India, the UK, and Italy in 2006 [10,11].
In the simplest case (pairwise exchange), kidney exchange offers an incompatible donor–recipient pair the opportunity to match with another incompatible pair and swap donors, allowing each recipient to receive a compatible kidney (Figure 1). However, cycles involving more than two pairs are also feasible: the donor of the first pair gives a kidney to the recipient of the next pair, whose donor gives to the recipient of the next pair, and so on, until the donor of the last pair in the cycle gives to the recipient of the first pair. Exchanges involving three or more incompatible pairs usually increase the likelihood that any pair will find a match, but they turn out to be logistically harder to organize, since transplants in a kidney exchange are usually carried out simultaneously in order to prevent a donor from withdrawing after the intended recipient is given a kidney [6].
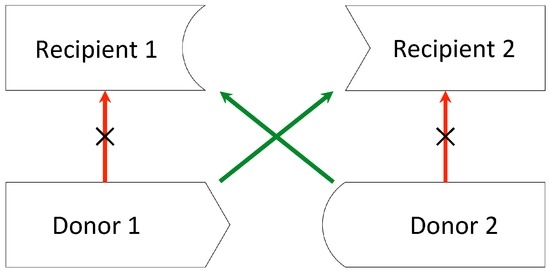
Figure 1.
Pairwise exchange. Donor 1 and donor 2 are both incompatible with their intended recipients. By exchanging donors, recipient 1 receives a kidney from donor 2, while recipient 2 receives a kidney from donor 1.
If a suitable match cannot be found, an incompatible pair can take part in a list exchange, which allows the recipient to receive priority on the deceased donor waiting list by giving one of the donor’s kidneys to a recipient on the list (Figure 2), but several concerns with regard to the equity of such exchanges have been raised. One of the major concerns is that O blood-type patients whose ABO-incompatible donors donate to the cadaveric pool would get priority over those O blood-type patients who do not have a living donor, regardless of the time spent in the waiting list. Since blood-type O patients usually have the longest mean waiting time for a deceased donor kidney, an already vulnerable group would further be harmed. Even though a few solutions have been proposed, the matter is not completely settled, and this option is so far not available in Italy or in other countries [12,13].
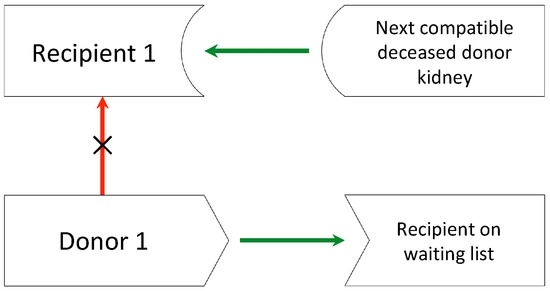
Figure 2.
List exchange. Donor 1 donates a kidney to a patient on the waiting list for a deceased donor kidney, and her intended incompatible recipient (recipient 1) receives priority for the next appropriate deceased donor kidney.
More recent strategies include non-simultaneous chains of transplants, starting with a non-directed altruistic donor; i.e., a person who wants to donate a kidney to a stranger with nothing in return [5].
Either way, the fundamental problem is to find the best combination of matches that maximizes the number of transplants, trying to accommodate those patients who are difficult to match.
1.3. Mathematical Aspects
From a mathematical point of view, a kidney exchange problem consists of a set of incompatible donor–recipient pairs, a set of compatible kidneys for each patient, and a preference relation over kidneys for each patient. Many algorithms have been developed in the last few years, providing different approaches and solutions. In this section, we outline two of the best-known models for kidney exchange, the priority mechanism and the Top Trading Cycles and Chains mechanism (TTCC).
The priority mechanism, proposed by Roth et al. in 2005 [14], is based on two main assumptions:
- An exchange can involve only two pairs (pairwise exchange);
- Each patient is indifferent between all compatible donors and between all incompatible donors. The own donor is strictly preferred to any other incompatible donor, and any compatible donor is considered to be strictly better than the own donor (0–1 preferences).
In this case, the kidney exchange problem can be modeled through an undirected graph, where each node indicates an incompatible donor–recipient pair of the pool and connecting two nodes indicates a possible exchange. A matching is a subset of the edges of the graph such that no two edges share an endpoint. Since the goal is to arrange as many transplants as possible, finding an efficient matching reduces to finding a maximum-cardinality matching. Easy examples show that for the same problem there can be several maximum-cardinality matchings that settle different subsets of vertices. Thus, the problem is to select one of them: this can be done through a priority mechanism. In a priority mechanism, the vertices are ranked before the mechanism begins, producing a priority matching which matches as many patients as possible, starting with the one with the highest priority and following the priority ordering, never excluding a higher priority patient in favor of a lower priority one. A priority mechanism produces a matching as follows:
- It considers the set of all maximum-cardinality matchings;
- It selects those matchings that assign a kidney to the patient with the highest priority in the priority ordering. Among this subgroup of matchings, it selects those that also match the patient who is ranked second in the priority ordering, and so on.
Taking into account that every patient prefers to get a kidney rather than remain with the incompatible donor, it can be shown that a priority matching is maximal; i.e., it cannot be expanded by adding any other edge, and hence is also Pareto-efficient. Moreover, it makes it a dominant strategy to reveal both the full sets of acceptable kidneys and of available donors [14], a very important aspect from a game theoretical point of view.
The TTCC mechanism proposed by Roth et al. in 2004, extends some results of the mechanism design literature for indivisible goods [15]. It is characterized as follows:
- There are no constraints on the size of exchanges, and list exchanges are allowed;
- Recipients have heterogenous preferences over compatible kidneys, which are supposed to be strict and based on different factors, such as HLA match, donor’s age, and so on.
The TTCC mechanism relies on an algorithm consisting of several rounds:
- Initially, all kidneys are available;
- In each round, each couple points towards its patient’s favourite option (a donor of the pool or a high priority on the waiting list).
- –
- There can be either a cycle, a w-chain (i.e., chains in which the last patient points towards the waiting list option), or both. Whenever a cycle is formed, the corresponding transplants are carried out until there are no cycles left, but only w-chains.
- –
- The algorithm selects one chain following a preselected rule and carrying out transplantations on that chain and so on. Some selection rules and their implications are discussed in [15].
- At the end of the procedure, the TTCC mechanism assigns each patient a kidney or a high priority in the waiting list for a kidney from a deceased donor.
Once again, the goal is to maximize the number of patients receiving a transplant, but different assumptions obviously lead to different allocations. To point out the major differences between the two methods, we can observe that the assumption of non-dichotomous preferences in the TTCC mechanism allows in principle for increasing the medical quality of the transplants. For instance, a young patient naturally prefers (unless some different criterion is more stringent) a kidney from a relatively young person rather than a compatible kidney from an old person. On the other side, the pairwise kidney exchange is more easily implementable and has the advantage of implementing dominant strategies. Furthermore, it avoids appealing to the waiting list.
Even though in real life, the pool of incompatible donor–recipient pairs evolves over time, both of these algorithms consider a static situation. Dynamic matching mechanisms have recently been studied [16], but the static approach is more common in the literature and is easier to implement. Moreover, the fact that many national programs perform match runs once per month or once every three months [17], makes it possible as a first approximation to consider each run as a static problem.
2. Materials and Methods
A computer model was developed in Python to simulate the impact of the two different options for crossover transplantation summarized above and discussed in [14,15]. We identified a solution that maximizes the number of patients receiving a transplant when:
- Only pairwise exchanges are allowed (priority mechanism);
- There are no constraints on the size of exchanges, and list exchanges are also allowed (TTCC).
2.1. Dataset
We conducted simulations based on data from the Nord Italia Transplant program (NITp), considering 38 patients who had been evaluated for a living kidney transplantation but were found to be incompatible with their potential donor in the period 2001–2013. Our data included age, ABO blood type, and HLA type (HLA-A, -B, -DR) of donors and recipients, %PRA and antibody profile of recipients, the reason of incompatibility between donor and recipient, and the transplant center. Patients’ and donors’ characteristics are summarized in Table 1.

Table 1.
Sex, blood type, and panel reactive antibody (PRA) distribution of recipients and donors.
2.2. Implementation
To implement the priority mechanism, we first determined the compatibility graph by considering the blood type, antibodies, and HLA information of each pair. Donors were considered to be compatible if they were ABO compatible and did not have any of the antigens that the potential recipient had preformed antibodies against. Weights were assigned to the edges of the compatibility graph, according to a priority ordering that gives higher priority to patients with a high PRA level. We then determined the maximum-cardinality matching with maximum weight using the max_weight_matching function of the library NetworkX, which is based on two algorithms created by Jack Edmonds [18,19].
As far as the TTCC is concerned, the first step is to determine patients’ preferences over the set of donors: we considered not only the blood group compatibility and the presence of preformed antibodies against a donor’s antigen, but also the HLA matching and the donor–recipient age difference. A bonus is considered if the donor belongs to the same transplant center as the recipient, or if they have the same blood group or a perfect HLA matching. The scoring system, inspired by the one of Alliance for Paired Donation [10], is summarized in Table 2. To select chains, we used a selection rule that chooses the w-chain, starting with the highest priority pair according to a priority ordering based on time spent on the waiting list. Transplants are not carried out until the end of the procedure, giving other pairs the possibility to extend the w-chain. The TTCC mechanism implemented with this chain selection rule is efficient. Moreover, a patient cannot receive a more preferred kidney by misrepresenting their preferences; i.e., the mechanism is strategy-proof [15].

Table 2.
Scoring system for the Top Trading Cycles and Chains mechanism. HLA: human leukocyte antigen.
3. Results
The results obtained by using the priority mechanism can be summarized as follows (Figure 3):
- Twenty patients are mutually incompatible with any donor, for them there is no way to receive a transplant;
- Of the 18 patients left, 16 will be matched, and two will not.
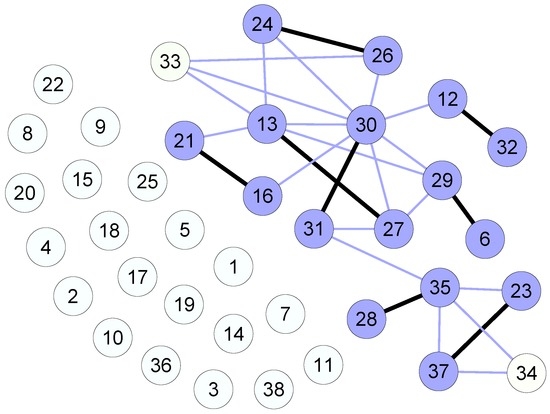
Figure 3.
Graph model for the priority mechanism, with links indicating mutually compatible pairs and bold link indicating an efficient matching. The priority ordering is based on the PRA level.
On the contrary, with the TTCC algorithm, the results are as follows (Figure 4):
- Two cycles of three patients each will form;
- Seven patients point directly to the waiting list and are not involved in any cycle or chain;
- Seven chains will form: three of length two, one of length three, one of length four two of length six;
- As a result, 24 patients will receive a kidney from a living donor, and seven will get high priority on the waiting list.
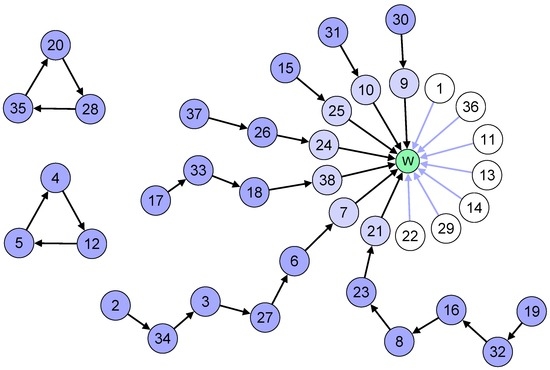
Figure 4.
Graph model for the Top Trading Cycles and Chains algorithm. The node W represents the waiting list option. The priority ordering is based on time spent on the waiting list.
4. Discussion
As all data show, there is a dramatic and always increasing number of people needing a kidney transplant. Even if the donation from cadaver could be profitably enhanced, the demand will always be higher than the supply. On the other hand, donation from a living person is possible. Many patients have a potential donor—often a relative—but incompatibility reasons allow only for approximately two thirds of these donations. Thus, an efficient crossover program should be taken into serious consideration. In this paper, we considered the situation of the Nord Italia Transplant program, which provided us with the data of 38 patients and their donors. In our dataset, a significant percentage of patients cannot be matched with any donor. Since incompatibility is not a completely dichotomic issue, it could be interesting to consider the possibility of weakening the constraints. In other words, a cost–benefit analysis could be performed to choose a compromise between the quality of the transplant and the number of people benefiting from a donation. Secondly, in this experiment, we see that the TTCC system looks better than the priority mechanism, as it involves more people. Certainly, this result does not apply to every dataset, and further studies are required. Our simulation is based on real data; thus, it is interesting from a medical point of view. However, the solutions reported in the results section would have been unfeasible, because patients in our dataset were on the waiting list at different times. Moreover, at the moment, a chain pointing to the waiting list is not allowed in Italy for ethical reasons. One motivation at the basis of this decision is the fact that giving a high priority to some people for being the terminals of the chain will harm those patients not having a related donor [12], especially those with blood type O, as previously mentioned. The argument is very serious; however, once more a trade-off between individual rights and social efficiency should be considered, because significantly more people will get a kidney when chains are allowed.
To conclude, let us remark that in our analysis, we did not consider the new feature introduced in this context by the idea of good samaritan (i.e., a person donating a kidney to the community expecting nothing in return). Of course, this is a very delicate issue; however, for several reasons, this possibility has been considered, since it has incredible advantages—the most obvious being that starting a procedure with a Good Samaritan does not force contemporary surgeries to be made [6,7]. Furthermore, this allows for very long chains, usually ended by a person not having a related donor. Successful chains were performed, for example, in the United States in 2012 and in Italy as well in 2015, when six patients received a new kidney taking part in the first italian chain [20,21].
Finally, we want to mention some other very recent approaches to the kidney exchange problem, mainly focused on the mathematics dealing with the case when a samaritan donation is present, see [22,23].
Acknowledgments
We want to acknowledge Massimo Cardillo, Nicola De Fazio, and Giuseppe Piccolo from the Nord Italia Transplant program for the kindness in assisting us in this work, for the many explanations they provided about the medical aspects and for providing us with the dataset. We are also indebted to the referees for several suggestions that allowed us to improve the paper.
Author Contributions
Roberto Lucchetti and Monica Salvioli equally contributed to the mathematical aspects of the paper, the simulations were performed by Monica Salvioli, collecting data and managing the dataset was done by Rosanna Torelli.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HLA | Human Leukocyte Antigen |
| PRA | Panel Reactive Antibody |
| TTCC | Top Trading Cycles and Chains |
References
- Garibotto, G.; Pontremoli, R. Manuale di Nefrologia, 1st ed.; Minerva Medica: Torino, Italy, 2012. [Google Scholar]
- Abbas, A.K.; Lichtman, A.H.; Pillai, S. Transplantation Immunology. In Cellular and Molecular Immunology, 6th ed.; Elsevier/Saunders: Philadelphia, PA, USA, 2007. [Google Scholar]
- Wongsaroj, P.; Kahwaji, J.; Vo, A.; Jordan, S.C. Modern approaches to incompatible kidney transplantation. World J. Nephrol. 2015, 4, 354–362. [Google Scholar] [CrossRef] [PubMed]
- Heeger, P.S.; Dinavahi, R. Transplant immunology for non-immunologist. Mt. Sinai J. Med. 2012, 79, 376–387. [Google Scholar] [CrossRef] [PubMed]
- Aull, M.J.; Kapur, S. Kidney paired donation and its potential impact on transplantation. Surg. Clin. N. Am. 2013, 93, 1407–1421. [Google Scholar] [CrossRef] [PubMed]
- Glorie, K.; Haase-Kromwijk, B.; van de Klundert, J.; Wagelmans, A.; Weimar, W. Allocation and matching in kidney exchange programs. Transpl. Int. 2014, 27, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Chkhotua, A. Paired kidney donation: Outcomes, limitations, and future perspectives. Transplant. Proc. 2012, 44, 1790–1792. [Google Scholar] [CrossRef] [PubMed]
- Rapaport, F.T. The case for a living emotionally related international kidney donor exchange registry. Transplant. Proc. 1986, 18, 5–9. [Google Scholar] [PubMed]
- De Klerk, M.; Keizer, K.M.; Claas, F.H.J.; Witvliet, M.; Haase-Kromwijk, B.J.; Weimar, W. The Dutch national living donor kidney exchange program. Am. J. Transplant. 2005, 5, 2302–2305. [Google Scholar] [CrossRef] [PubMed]
- Mierzejewska, B.; Durlik, M.; Lisik, W.; Baum, C.; Schroder, P.; Kopke, J.; Rees, M.; Stepkowski, S. Current approaches in national kidney paired donation programs. Ann. Transplant. 2013, 18, 112–124. [Google Scholar] [CrossRef] [PubMed]
- Barsotti, M.; Boggi, U.; Tregnaghi, C.; Paleologo, G.; Nerucci, B.; Bianchi, A.; Vistoli, F.; Croce, C.; Amorese, G.; Mariotti, M.L.; et al. Living donor kidney transplant: The crossover modality. G. Ital. Nefrol. 2009, 26, 488–498. [Google Scholar] [PubMed]
- Den Hartogh, G. Trading with the waiting-list: The justice of living donor list exchange. Bioethics 2010, 24, 190–198. [Google Scholar] [CrossRef] [PubMed]
- Zenios, S.A.; Woodle, E.S.; Ross, L.F. Primum non nocere: Avoiding harm to vulnerable wait list candidates in an indirect kidney exchange. Transplantation 2001, 72, 648–654. [Google Scholar] [CrossRef] [PubMed]
- Roth, A.E.; Sönmez, T.; Ünver, M.U. Pairwise kidney exchange. J. Econ. Theor. 2005, 125, 151–188. [Google Scholar] [CrossRef]
- Roth, A.E.; Sönmez, T.; Ünver, M.U. Kidney exchange. Q. J. Econ. 2004, 119, 457–488. [Google Scholar] [CrossRef]
- Ünver, M.U. Dynamic kidney exchange. Rev. Econ. Stud. 2010, 77, 372–414. [Google Scholar] [CrossRef]
- Ferrari, P.; Weimar, W.; Johnson, R.J.; Lim, W.H.; Tinckam, K.J. Kidney paired donation: Principles, protocols and programs. Nephrol. Dial. Transplant. 2015, 30, 1276–1285. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, J. Maximum matching and a polyhedron with 0,1 vertices. J. Res. Nat. Bur. Stand. 1965, 69, 125–130. [Google Scholar] [CrossRef]
- Edmonds, J. Path, trees and flowers. Can. J. Math. 1965, 17, 449–467. [Google Scholar] [CrossRef]
- 60 Lives, 30 Kidneys, All Linked. Available online: http://www.webcitation.org/6gRckXL3y (accessed on 1 April 2016).
- Centro Nazionale Trapianti—Comunicato Stampa del 10 Aprile 2015. Available online: http://www.webcitation.org/6gRcwxUmi (accessed on 1 April 2016).
- Anderson, R.; Ashlagi, I.; Gamarnik, D.; Roth, A.E. Finding long chains in kidney exchange using the traveling salesman problem. Proc. Natl. Acad. Sci. USA 2015, 112, 663–668. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.; Ashlagi, I.; Gamarnik, D.; Rees, M.; Roth, A.E.; Sönmez, T.; Ünver, M.U. Kidney Exchange and the Alliance for Paired Donation: Operations Research Changes the Way Kidneys Are Transplanted. Interfaces 2015, 45, 26–42. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).