Abstract
In strategic situations, humans infer the state of mind of others, e.g., emotions or intentions, adapting their behavior appropriately. Nonetheless, evolutionary studies of cooperation typically focus only on reaction norms, e.g., tit for tat, whereby individuals make their next decisions by only considering the observed outcome rather than focusing on their opponent’s state of mind. In this paper, we analyze repeated two-player games in which players explicitly infer their opponent’s unobservable state of mind. Using Markov decision processes, we investigate optimal decision rules and their performance in cooperation. The state-of-mind inference requires Bayesian belief calculations, which is computationally intensive. We therefore study two models in which players simplify these belief calculations. In Model 1, players adopt a heuristic to approximately infer their opponent’s state of mind, whereas in Model 2, players use information regarding their opponent’s previous state of mind, obtained from external evidence, e.g., emotional signals. We show that players in both models reach almost optimal behavior through commitment-like decision rules by which players are committed to selecting the same action regardless of their opponent’s behavior. These commitment-like decision rules can enhance or reduce cooperation depending on the opponent’s strategy.
1. Introduction
Although evolution and rationality apparently favor selfishness, animals, including humans, often form cooperative relationships, each participant paying a cost to help one another. It is therefore a universal concern in biological and social sciences to understand what mechanism promotes cooperation. If individuals are in a kinship, kin selection fosters their cooperation via inclusive fitness benefits [1,2]. If individuals are non-kin, establishing cooperation between them is a more difficult problem. Studies of the Prisoner’s Dilemma (PD) game and its variants have revealed that repeated interactions between a fixed pair of individuals facilitates cooperation via direct reciprocity [3,4,5]. A well-known example of this reciprocal strategy is Tit For Tat (TFT), whereby a player cooperates with the player’s opponent only if the opponent has cooperated in a previous stage. If one’s opponent obeys TFT, it is better to cooperate because in the next stage, the opponent will cooperate, and the cooperative interaction continues; otherwise, the opponent will not cooperate, and one’s total future payoff will decrease. Numerous experimental studies have shown that humans cooperate in repeated PD games if the likelihood of future stages is sufficiently large [6].
In evolutionary dynamics, TFT is a catalyst for increasing the frequency of cooperative players, though it is not evolutionarily stable [7]. Some variants of TFT, however, are evolutionarily stable; Win Stay Lose Shift (WSLS) is one such example in which a player cooperates with the player’s opponent only if the outcome of the previous stage of the game has been mutual cooperation or mutual defection [8]. TFT and WSLS are instances of so-called reaction norms in which a player selects an action as a reaction to the outcome of the previous stage, i.e., the previous pair of actions selected by the player and the opponent [9]. In two-player games, a reaction norm is specified by conditional probability by which a player selects next action a depending on the previous actions of the player and the opponent, i.e., and , respectively.
Studies of cooperation in repeated games typically assume reaction norms as the subject of evolution. A problem with this assumption is that it describes behavior as a black box in which an action is merely a mechanical response to the previous outcome; however, humans and, controversially, non-human primates have a theory of mind in which they infer the state of mind (i.e., emotions or intentions) of others and use these inferences as pivotal pieces of information in their own decision-making processes [10,11]. As an example, people tend to cooperate more when they are cognizant of another’s good intentions [6,12]. Moreover, neurological bases of intention or emotion recognition have been found [13,14,15,16,17]. Despite the behavioral and neurological evidence, there is still a need for a theoretical understanding of the role of such state-of-mind recognition in cooperation; to the best of our knowledge, only a few studies have focused on examining the interplay between state-of-mind recognition and cooperation [18,19].
From the viewpoint of state-of-mind recognition, the above reaction norm can be decomposed as:
where s represents the opponent’s state of mind. Equation (1) contains two modules. The first module, , handles the state-of-mind recognition; given observed previous actions and , a player infers that the player’s opponent is in state s with probability , i.e., a belief, and thinks that the opponent will select some action depending on this state s. The second module, , controls the player’s decision-making; the player selects action a with probability , which is a reaction to the inferred state of mind of opponent s. In our present study, we are motivated to clarify what decision rule, i.e., the second module, is plausible and how it behaves in cooperation when a player infers an opponent’s state of mind via the first module. To do so, we use Markov Decision Processes (MDPs) that provide a powerful framework for predicting optimal behavior in repeated games when players are forward-looking [20,21]. MDPs even predict (pure) evolutionarily stable states in evolutionary game theory [22].
The core of MDPs is the Bellman Optimality Equation (BOE); by solving the BOE, a player obtains the optimal decision rule, which is called the optimal policy, that maximizes the player’s total future payoff. Solving a BOE with beliefs, however, requires complex calculations and is therefore computationally expensive. Rather than solving the BOE naively, we instead introduce approximations of the belief calculation that we believe to be more biologically realistic. We introduce two models to do so and examine the possibility of achieving cooperation as compared to a null model (introduced in Section 2.2.1) in which a player directly observes an opponent’s state of mind. In the first model, we assume that a player believes that an opponent’s behavior is deterministic such that the opponent’s actions are directly (i.e., one-to-one) related to the opponent’s states. A rationale for this approximation is that in many complex problems, people use simple heuristics to make a fast decision, for example a rough estimation of an uncertain quantity [23,24]. In the second model, we assume that a player correctly senses an opponent’s previous state of mind, although the player does not know the present state of mind. This assumption could be based on some external clue provided by emotional signaling, such as facial expressions [25]. We provide the details of both models in Section 2.2.2.
2. Analysis Methods
We analyze an MDP of an infinitely repeated two-player game in which an agent selects optimal actions in response to an opponent, who behaves according to a reaction norm and has an unobservable state of mind. For the opponent’s behavior, we focus on four major reaction norms, i.e., Contrite TFT (CTFT), TFT, WSLS and Grim Trigger (GRIM), all of which are stable and/or cooperative strategies [4,8,26,27,28,29]. These reaction norms can be modeled using Probabilistic Finite-State Machines (PFSMs).
2.1. Model
For each stage game, the agent and opponent select actions, these actions being either cooperation (C) or defection (D). We denote the set of possible actions of both players by . When the agent selects action and the opponent selects action , the agent gains stage-game payoff . The payoff matrix of the stage game is given by:
where the four outcomes, i.e., mutual cooperation ((the agent’s action, the opponent’s action) = ), one-sided cooperation (), one-sided defection () and mutual defection (), result in , , and , respectively. Depending on S and T, the payoff matrix (2) yields different classes of the stage game. If and , it yields the Harmony Game (HG), which has a unique Nash equilibrium of mutual cooperation. If and , it yields the PD game, which has a unique Nash equilibrium of mutual defection. If and , it yields the Stag Hunt (SH) game, which has two pure Nash equilibria, one being mutual cooperation, the other mutual defection. If and , it yields the Snowdrift Game (SG), which has a mixed strategy Nash equilibrium with both mutual cooperation and defection being unstable. Given the payoff matrix, the agent’s purpose at each stage t is to maximize the agent’s expected discounted total payoff , where and are the actions selected by the agent and opponent at stage , respectively, and is a discount rate.
The opponent’s behavior is represented by a PFSM, which is specified via probability distributions φ and w. At each stage t, the opponent is in some state and selects action with probability . Next, the opponent’s state changes to next state with probability . We study four types of two-state PFSMs as the opponent’s model, these being Contrite Tit for Tat (CTFT), Tit for Tat (TFT), Win Stay Lose Shift (WSLS) and Grim Trigger (GRIM). We illustrate the four types of PFSMs in Figure 1 and list all probabilities φ and w in Table 1. Here, the opponent’s state is either Happy (H) or Unhappy (U), i.e., . Note that H and U are merely labels for these states. An opponent obeying the PSFMs selects action C in state H and selects action D in state U with a stochastic error, i.e., (hence, ) and (hence, ), where is a small probability with which the opponent fails to select an intended action. For all four of the PFSMs, the opponent in state H stays in state H if the agent selects action C and moves to state U if the agent selects action D. The state transition from state U is different between the four PFSMs. A CTFT opponent moves to state H irrespective of the agent’s action. A TFT opponent moves to state H or U if the agent selects action C or D, respectively. Conversely, a WSLS opponent moves to state H or U if the agent selects action D or C, respectively. A GRIM opponent stays in state U irrespective of the agent’s action. The state transitions are again affected by errors that occur with probability .
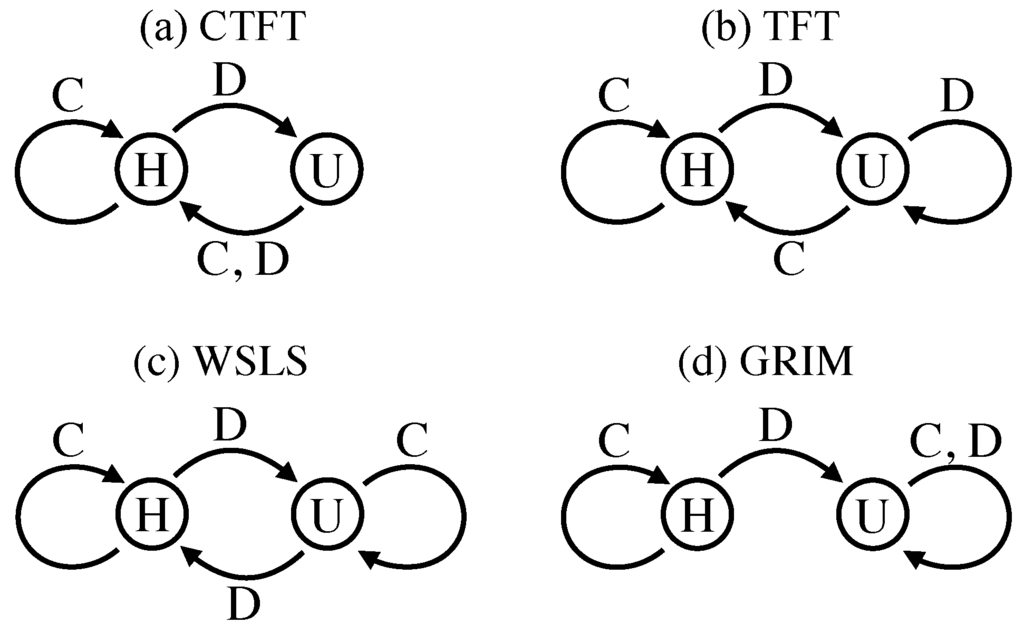
Figure 1.
Probabilistic Finite-State Machines (PFSMs). Open circles represent the opponent’s states (i.e., Happy (H) or Unhappy (U) inside the circles); arrows represent the most likely state transitions, which occur with probability , depending on the opponent’s present state (i.e., the roots of the arrows) and the agent’s action (i.e., C or D aside the arrows).

Table 1.
Parameters of the PFSMs. Note that and for any and . CTFT, Contrite Tit for Tat; WSLS, Win Stay Lose Shift; GRIM, Grim Trigger.
2.2. Bellman Optimality Equations
Because the repeated game we consider is Markovian, the optimal decision rules or policies are obtained by solving the appropriate BOEs. Here, we introduce three different BOEs for the repeated two-player games assuming complete (see Section 2.2.1) and incomplete (see Section 2.2.2) information about the opponent’s state. Table 2 summarizes available information about the opponent in these three models.

Table 2.
Available information about the opponent.
2.2.1. Complete Information Case: Null Model (Model 0)
In our first scenario, which we call Model 0, we assume that the agent knows the opponent’s present state, as well as which PFSM the opponent obeys, i.e., φ and w. At stage t, the agent selects sequence of actions to maximize expected discounted total payoff , where is the expectation conditioned on the opponent’s present state . Let the value of state s, , be the maximum expected discounted total payoff the agent expects to obtain when the opponent’s present state is s, given that the agent obeys the optimal policy and, thus, selects optimal actions in the following stage games. Here, is represented by:
which has recursive relationship:
The BOE when the opponent’s present state is known is therefore represented as:
where we rewrite V as for later convenience. Equation (5) reads that if the agent obeys the optimal policy, the value of having the opponent in state (i.e., the left-hand side) is the sum of the expected immediate reward when the opponent is in state and the expected value, discounted by β, of having the opponent in the next state (i.e., the right-hand side). Note that the time subscripts in the BOEs being derived hereafter (i.e., Equations (5), (10) and (12)) can be omitted because they hold true for any game stages, i.e., for any t.
2.2.2. Incomplete Information Cases (Models 1 and 2)
For the next two models, we assume that the agent does not know the opponent’s state of mind, even though the agent knows which PFSM the opponent obeys, i.e., the agent knows the opponent’s φ and w. The agent believes that the opponent’s state at stage t is with probability , which is called a belief. Mathematically, a belief is a probability distribution over the state space. At stage , is updated to in a Markovian manner depending on information available at the previous stage. The agent maximizes expected discounted total payoff , where is the expectation based on present belief . Using the same approach as that of Section 2.2.1 above, the value function, denoted by , when the agent has belief regarding opponent’s state has recursive relationship:
The BOE when the opponent’s present state is unknown is then:
where is the belief at the next stage. Equation (7) reads that if the agent obeys the optimal policy, the value of having belief regarding the opponent’s present state (i.e., the left-hand side) is the expected (by belief ) sum of the immediate reward and the value, discounted by β, of having next belief regarding the opponent’s next state (i.e., the right-hand side).
We can consider various approaches to updating the belief in Equation (7). One approach is to use Bayes’ rule, which then is called the belief MDP [30]. After observing actions and in the present stage, the belief is updated from to as:
Equation (8) is simply derived from Bayes’ rule as follows: (i) the numerator (i.e., ) is the joint probability that the opponent’s present action and next state are observed, given the agent’s present belief and action ; and (ii) the denominator (i.e., ) is the probability that is observed, given the agent’s present belief . Finding an optimal policy via the belief MDP is unfortunately difficult, because there are infinitely many beliefs, and the agent must simultaneously solve an infinite number of Equation (7). To overcome this problem, a number of computational approximation methods have been proposed, including grid-based discretization and particle filtering [31,32]. When one views the belief MDP as a biological model for decision-making processes, these computational approximations might likely be inapplicable, because animals, including humans, tend to employ more simplified practices rather than complex statistical learning methods [24,33,34]. We explore such possibilities in the two models below.
A Simplification Heuristic (Model 1)
In Model 1, we assume that the agent simplifies the opponent’s behavioral model in the agent’s mind by believing that the opponent’s state-dependent action selection is deterministic; we replace in Equation (8) with , where δ is Kronecker’s delta (i.e., it is one if and zero otherwise). Here, σ is a bijection that determines the opponent’s action r depending on the opponent’s present state s, which we define as and . Using this simplification heuristic, Equation (8) is greatly reduced to:
where is an inverse map of σ from actions to states. In Equation (9), the agent infers that the opponent’s state changes to , because the agent previously selected action and the opponent was definitely in state . Applying a time-shifted Equation (9) to Equation (7), we obtain the BOE that the value of previous outcome should satisfy, i.e.,
where we rewrite as and as . Here, represents the belief regarding the opponent’s present action , which is approximated by the agent given previous outcome . Equation (10) reads that if the agent obeys the optimal policy, the value of having observed previous outcome (i.e., the left-hand side) is the expected (by approximate belief ) sum of the immediate reward and the value, discounted by β, of observing present outcome (i.e., the right-hand side).
Use of External Information (Model 2)
In Model 2, we assume that after the two players decide actions and in a game stage (now at time ), the agent comes to know or correctly infers the opponent’s previous state by using external information. More specifically, in Equation (8) is replaced by . In this case, Equation (8) is reduced to:
Applying a time-shifted Equation (11) to Equation (7), we obtain the BOE that the value of the previous pair comprised of the agent’s action and the opponent’s (inferred) state should satisfy, i.e.,
where we rewrite as . Because we assume that the previous state inference is correct, and in Equation (12) can be replaced by and , respectively. Equation (12) then reads that if the agent obeys the optimal policy, the value of having observed the agent’s previous action and knowing the opponent’s previous state (i.e., the left-hand side) is the expected (by state transition distribution w) sum of the immediate reward and the value, discounted by β, of observing the agent’s present action and getting to know the opponent’s present state (i.e., the right-hand side).
2.3. Conditions for Optimality and Cooperation Frequencies
Overall, we are interested in the optimal policy against a given opponent, but identifying such a policy depends on the payoff structure, i.e., Equation (2). We follow the procedure below to search for a payoff structure that yields an optimal policy.
- Fix an opponent type (i.e., CTFT, TFT, WSLS or GRIM) and a would-be optimal policy (i.e., , or for Model 0, 1 or 2, respectively).
- Calculate the value function (i.e., , or for Model 0, 1 or 2, respectively) from the BOE by assuming that the focal policy is optimal.
- Using the obtained value function, determine the payoff conditions under which the policy is consistent with the value function, i.e., the policy is actually optimal.
Figure 2 illustrates how each model’s policy uses available pieces of information. In Appendix A, we describe in detail how to calculate the value functions and payoff conditions for each model.

Figure 2.
Different policies of the models. Depending on the given model, the agent’s decision depends on different information as indicated by orange arrows. At the present stage in which the two players are deciding actions a and r, (a) policy depends on the opponent’s present state s, (b) policy depends on the agent’s previous action and the opponent’s previous action and (c) policy depends on the agent’s previous action and the opponent’s previous state . The open solid circles represent the opponent’s known states, whereas dotted circles represent the opponent’s unknown states. Black arrows represent probabilistic dependencies of the opponent’s decisions and state transitions.
Next, using the obtained optimal policies, we study to what extent an agent obeying the selected optimal policy cooperates in the repeated game when we assume a model comprising incomplete information (i.e., Models 1 and 2) versus when we assume a model comprising complete information (i.e., Model 0). To do so, we consider an agent and an opponent playing an infinitely repeated game. In the game, both the agent and opponent fail in selecting the optimal action with probabilities ν and ϵ, respectively. After a sufficiently large number of stages, the distribution of the states and actions of the two players converges to a stationary distribution. As described in Appendix B, we measure the frequency of the agent’s cooperation in the stationary distribution.
Following the above procedure, all combinations of models, opponent types and optimal policies can be solved straightforwardly, but such proofs are too lengthy to show here; thus, in Appendix C, we demonstrate just one case in which policy CDDD (see Section 3) is optimal against a GRIM opponent in Model 2.
3. Results
Before presenting our results, we introduce a short hand notation to represent policies for each model. In Model 0, a policy is represented by character sequence , where is the optimal action if the opponent is in state . Model 0 has at most four possible policies, namely CC, CD, DC and DD. Policies CC and DD are unconditional cooperation and unconditional defection, respectively. With policy CD, an agent behaves in a reciprocal manner in response to an opponent’s present state; more specifically, the agent cooperates with an opponent in state H, hence the opponent cooperating at the present stage, and defects against an opponent in state U, hence the opponent defecting at the present stage. Policy DC is an asocial variant of policy CD: an agent obeying policy DC defects against an opponent in state H and cooperates with an opponent in state U. We call policy CD anticipation and policy DC asocial-anticipation. In Model 1, a policy is represented by four-letter sequence , where is the optimal action, with the agent’s and opponent’s selected actions and at the previous stage. In Model 2, a policy is represented by four-letter sequence , where is the optimal action, with the agent’s selected action and the opponent’s state at the previous stage. Models 1 and 2 each have at most sixteen possible policies, ranging from unconditional cooperation (CCCC) to unconditional defection (DDDD).
For each model, we identify four classes of optimal policy, i.e., unconditional cooperation, anticipation, asocial-anticipation and unconditional defection. Figure 3 shows under which payoff conditions each of these policies are optimal, with a comprehensive description for each panel given in Appendix D. An agent obeying unconditional cooperation (i.e., CC in Model 0 or CCCC in Models 1 and 2, colored blue in the figure) or unconditional defection (i.e., DD in Model 0 or DDDD in Models 1 and 2, colored red in the figure) always cooperates or defects, respectively, regardless of an opponent’s state of mind. An agent obeying anticipation (i.e., CD in Model 0, CCDC against CTFT, CCDD against TFT, CDDC against WSLS or CDDD against GRIM in Models 1 and 2, colored green in the figure) conditionally cooperates with an opponent only if the agent knows or guesses that the opponent has a will to cooperate, i.e., the opponent is in state H. As an example, in Model 0, an agent obeying policy CD knows an opponent’s current state, cooperating when the opponent is in state H and defecting when in state U. In Models 1 and 2, an agent obeying policy CDDC guesses that an opponent is in state H only if the previous outcome is (C, C) or (D, D), because the opponent obeys WSLS. Since the agent cooperates only if the agent guesses that the opponent is in state H, it is clear that anticipation against WSLS is CDDC. Finally, an agent obeying asocial-anticipation (i.e., DC in Model 0, DDCD against CTFT, DDCC against TFT, DCCD against WSLS or DCCC against GRIM in Models 1 and 2, colored yellow in the figure) behaves in the opposite way to anticipation; more specifically, the agent conditionally cooperates with an opponent only if the agent guesses that the opponent is in state U. This behavior increases the number of outcomes of (C, D) or (D, C), which induces the agent’s payoff in SG.
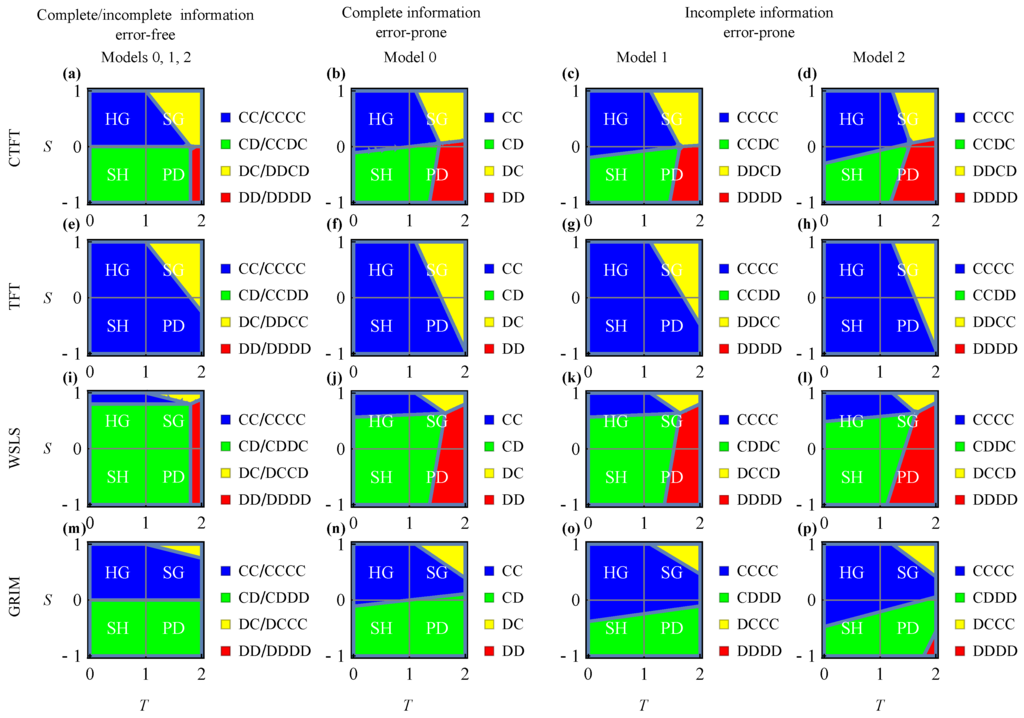
Figure 3.
Optimal policies with an intermediate future discount. Here, the opponent obeys (a–d) CTFT, (e–h) TFT, (i–l) WSLS and (m–p) GRIM. (a,e,i,m) Error-free cases () of complete and incomplete information (common to Models 0, 1 and 2). (b,f,j,n) Error-prone cases () of complete information (i.e., Model 0). (c,g,k,o) Error-prone cases () of incomplete information (i.e., Model 1). (c,g,k,o) Error-prone cases () of incomplete information (i.e., Model 2). Horizontal and vertical axes represent payoffs for one-sided defection, T, and one-sided cooperation, S, respectively. In each panel, Harmony Game (HG), Snowdrift Game (SG), Stag Hunt (SH) and Prisoner’s Dilemma (PD) indicate the regions of these specific games. We set parameter .
The boundaries that separate the four optimal policy classes are qualitatively the same for Models 0, 1 and 2, which is evident by comparing them column by column in Figure 3, although they are slightly affected by the opponent’s errors, i.e., ϵ and μ, in different ways. These boundaries become identical for the three models in the error-free limit (see Table D1 and Appendix E). This similarity between models indicates that an agent using a heuristic or an external clue to guess an opponent’s state (i.e., Models 1 and 2) succeeds in selecting appropriate policies, as well as an agent that knows an opponent’s exact state of mind (i.e., Model 0). To better understand the effects of the errors here, we show the analytical expressions of the boundaries in a one-parameter PD in Appendix F.
Although the payoff conditions for the optimal policies are rather similar across the three models, the frequency of cooperation varies. Figure 4 shows the frequencies of cooperation in infinitely repeated games, with analytical results summarized in Table 3 and a comprehensive description of each panel presented in Appendix G. Hereafter, we focus on the cases of anticipation since it is the most interesting policy class we wish to understand. In Model 0, an agent obeying anticipation cooperates with probability when playing against a CTFT or WSLS opponent, with probability when playing against a TFT opponent and with probability when playing against a GRIM opponent, where μ and ν are probabilities of error in the opponent’s state transition and the agent’s action selection, respectively. To better understand the effects of errors, these cooperation frequencies are expanded by the errors except for in the GRIM case. In all Model 0 cases, the error in the opponent’s action selection, ϵ, is irrelevant, because in Model 0, the agent does not need to infer the opponent’s present state through the opponent’s action.
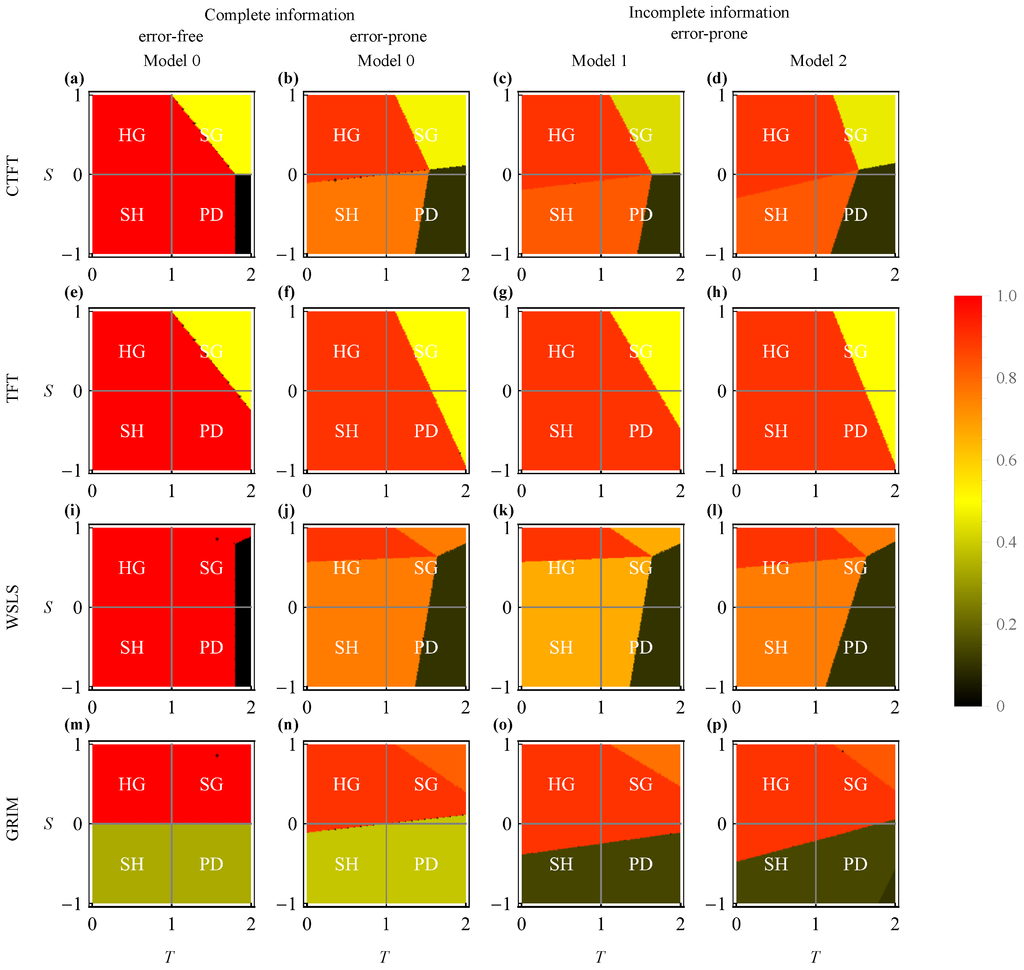
Figure 4.
Frequency of cooperation with an intermediate future discount. Here, the opponent obeys (a–d) CTFT, (e–h) TFT, (i–l) WSLS and (m–p) GRIM. (a,e,i,m) Error-free cases (; in the cases of GRIM, this is achieved by setting and taking the limit ) of complete information (i.e., Model 0). (b,f,j,n) Error-prone cases () of complete information (i.e., Model 0). (c,g,k,o) Error-prone cases () of incomplete information (i.e., Model 1). (c,g,k,o) Error-prone cases () of incomplete information (i.e., Model 2). Horizontal and vertical axes represent payoffs for one-sided defection, T, and one-sided cooperation, S, respectively. In each panel, HG, SG, SH and PD indicate the regions of these specific games. We set parameter .

Table 3.
Frequencies of cooperation in infinitely repeated games. Here, , , and .
Interestingly, in Models 1 and 2, an agent obeying anticipation cooperates with a CTFT opponent with probability , regardless of the opponent’s error μ. This phenomenon occurs because of the agent’s interesting policy CCDC, which prescribes selecting action C if the agent self-selected action C in the previous stage; once the agent selects action C, the agent continues to try to select C until the agent fails to do so with a small probability ν. This can be interpreted as a commitment strategy to bind oneself to cooperation. In this case, the commitment strategy leads to better cooperation than that of the agent knowing the opponent’s true state of mind; the former yields frequency of cooperation and the latter . A similar commitment strategy (i.e., CCDD) appears when the opponent obeys TFT; here, an agent obeying CCDD continues to try to select C or D once action C or D, respectively, is self-selected. In this case, however, partial cooperation is achieved in all models; here, the frequency of cooperation by the agent is . When the opponent obeys WSLS, the frequency of cooperation by the anticipating agent in Model 2 is the same as in Model 0, i.e., . In contrast, in Model 1, the frequency of cooperation is reduced by to . In Model 1, because the opponent can mistakenly select an action opposite to what the opponent’s state dictates, the agent’s guess regarding the opponent’s previous state could fail. This misunderstanding reduces the agent’s cooperation if the opponent obeys WSLS; if the opponent obeys CTFT, the opponent’s conditional cooperation after the opponent’s own defection recovers mutual cooperation. When the opponent obeys GRIM, the agent’s cooperation fails dramatically. This phenomenon again occurs due to a commitment-like aspect of the agent’s policy, i.e., CDDD; once the agent selects action D, the agent continues to try to defect for a long time.
4. Discussion and Conclusions
In this paper, we analyzed two models of repeated games in which an agent uses a heuristic or additional information to infer an opponent’s state of mind, i.e., the opponent’s emotions or intentions, then adopts a decision rule that maximizes the agent’s expected long-term payoff. In Model 1, the agent believes that the opponent’s action-selection is deterministic in terms of the opponent’s present state of mind, whereas in Model 2, the agent knows or correctly recognizes the opponent’s state of mind at the previous stage. For all models, we found four classes of optimal policies. Compared to the null model (i.e., Model 0) in which the agent knows the opponent’s present state of mind, the two models establish cooperation almost equivalently except when playing against a GRIM opponent (see Table 3). In contrast to the reciprocator in the classical framework of the reaction norm, which reciprocates an opponent’s previous action, we found the anticipator that infers an opponent’s present state and selects an action appropriately. Some of these anticipators show commitment-like behaviors; more specifically, once an anticipator selects an action, the anticipator repeatedly selects that action regardless of an opponent’s behavior. Compared to Model 0, these commitment-like behaviors enhance cooperation with a CTFT opponent in Model 2 and diminish cooperation with a GRIM opponent in Models 1 and 2.
Why can the commitment-like behaviors be optimal? For example, after selecting action C against a CTFT opponent, regardless of whether the opponent was in state H or U at the previous stage, the opponent will very likely move to state H and select action C. Therefore, it is worthwhile to believe that after selecting action C, the opponent is in state H, and thus, it is good to select action C again. Next, it is again worthwhile to believe that the opponent is in state H and good to select action C, and so forth. In this way, if selecting an action always yields a belief in which selecting the same action is optimal, it is commitment-like behavior. In our present study, particular opponent types (i.e., CTFT, TFT and GRIM) allow such self-sustaining action-belief chains, and this is why commitment-like behaviors emerge as optimal decision rules.
In general, our models depict repeated games in which the state changes stochastically. Repeated games with an observable state have been studied for decades in economics (see, e.g., [35,36]); however, if the state is unobservable, the problem becomes a belief MDP. In this case, Yamamoto showed that with some constraints, some combination of decision rules and beliefs can form a sequential equilibrium in the limit of a fully long-sighted future discount, i.e., a folk theorem [21]. In our present work, we have not investigated equilibria, instead studying what decision rules are optimal against some representative finite-state machines and to what extent they cooperate. Even so, we can speculate on what decision rules form equilibria as follows.
In the error-free limit, the opponent’s states and actions have a one-to-one relationship, i.e., H to C and U to D. Thus, the state transitions of a PFSM can be denoted as , where is the opponent’s next state when the agent’s previous action was and the opponent’s previous state was . Using this notation, the state transitions of GRIM and WSLS can be denoted by HUUU and HUUH, respectively. Given this, in , we can rewrite the opponent’s present state s with present action r and previous state with previous action by using the one-to-one correspondence between states and actions in the error-free limit. Moreover, from the opponent’s viewpoint, in can be rewritten as , which is the agent’s pseudo state; here, because of the one-to-one relationship, the agent appears as if the agent had a state in the eyes of the opponent. In short, we can rewrite as in Model 1 and as in Model 2, where we flip the order of the subscripts. This rewriting leads HUUU and HUUH to CDDD and CDDC, respectively, which are part of the optimal decision rules when playing against GRIM and WSLS; GRIM and WSLS can be optimal when playing against themselves depending on the payoff structure. The above interpretation suggests that some finite-state machines, including GRIM and WSLS, would form equilibria in which a machine and a corresponding decision rule, which infers the machine’s state of mind and maximizes the payoff when playing against the machine, behave in the same manner.
Our models assume an approximate heuristic or ability to use external information to analytically solve the belief MDP problem, which can also be numerically solved using the Partially-Observable Markov Decision Process (POMDP) [32]. Kandori and Obara introduced a general framework to apply the POMDP to repeated games of private monitoring [20]. They assumed that the actions of players are not observable, but rather players observe a stochastic signal that informs them about their actions. In contrast, we assumed that the actions of players are perfectly observable, but the states of players are not observable. Kandori and Obara showed that in an example of PD with a fixed payoff structure, grim trigger and unconditional defection are equilibrium decision rules depending on initial beliefs. We showed that in PD, CDDD and DDDD decision rules in Models 1 and 2 are optimal against a GRIM opponent in a broad region of the payoff space, suggesting that their POMDP approach and our approach yield similar results if the opponent is sufficiently close to some representative finite-state machines.
Nowak, Sigmund and El-Sedy performed an exhaustive analysis of evolutionary dynamics in which two-state automata play -strategy repeated games [37]. The two-state automata used in their study are the same as the PFSMs used in our present study if we set in the PFSMs, i.e., if we consider that actions selected by a PFSM completely correspond with its states. Thus, their automata do not consider unobservable states. They comprehensively studied average payoffs for all combinations of plays between the two-state automata in the noise-free limit. Conversely, we studied optimal policies when playing against several major two-state PFSMs that have unobservable states by using simplified belief calculations.
In the context of the evolution of cooperation, there have been a few studies that examined the role of state-of-mind recognition. Anh, Pereira and Santos studied a finite population model of evolutionary game dynamics in which they added a strategy of Intention Recognition (IR) to the classical repeated PD framework [18]. In their model, the IR player exclusively cooperates with an opponent that has an intention to cooperate, inferred by calculating its posterior probability using information from previous interactions. They showed that the IR strategy, as well as TFT and WSLS, can prevail in the finite population and promote cooperation. There are two major differences between their model and ours. First, their IR strategists assume that an individual has a fixed intention either to cooperate or to defect, meaning that their IR strategy only handles one-state machines that always intend to do the same thing (e.g., unconditional cooperators and unconditional defectors). In contrast, our model can potentially handle any multiple-state machines that intend to do different things depending on the context (e.g., TFT and WSLS). Second, they examined the evolutionary dynamics of their IR strategy, whereas we examined the state-of-mind recognizer’s static performance of cooperation when using the optimal decision rule against an opponent.
Our present work is just a first step to understanding the role of state-of-mind recognition in game theoretic situations, thus further studies are needed. For example, as stated above, an equilibrium established between a machine that has a state and a decision rule that cares about the machine’s state could be called ‘theory of mind’ equilibrium. A thorough search for equilibria here is necessary. Moreover, although we assume it in our present work, it is unlikely that a player knows an opponent’s parameters, i.e., φ and w. An analysis of models in which a player must infer an opponent’s parameters and state would be more realistic and practical. Further, our present study is restricted to a static analysis. The co-evolution of the decision rule and state-of-mind recognition in evolutionary game dynamics has yet to be investigated.
multiple
Acknowledgments
M.N. acknowledges support by JSPS KAKENHI Grant Number JP 13J05595. H.O. acknowledges support by JSPS KAKENHI Grant Number JP 25118006. The authors thank three anonymous reviewers for their thoughtful comments and criticisms.
Author Contributions
M.N. and H.O. conceived of and designed the model. M.N. performed the analysis. M.N. and H.O. wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Method for Obtaining Optimal Policies
In this Appendix, we describe our method for obtaining the optimal policies in each model. Table A1 summarizes the definitions of symbols used in this Appendix.

Table A1.
Meaning of symbols.
| Symbol | Meaning |
|---|---|
| Available actions (Cooperation or Defection) | |
| Opponent’s states (Happy or Unhappy) | |
| Agent’s payoff when the agent and opponent select actions a and r, respectively | |
| S | Payoff to one-sided cooperation |
| T | Payoff to one-sided defection |
| β | Discount rate |
| Probability that the opponent in state s selects action r | |
| Probability that the opponent’s state changes from s to when the agent selects action a | |
| ϵ | Probability that the opponent selects an unintended action |
| μ | Probability that the opponent changes the state to an unexpected state |
| ν | Probability that the agent selects an unintended action in actual games |
| Expectation based on the opponent’s present state s | |
| Expectation based on the agent’s present belief b regarding the opponent’s present state | |
| Value when the opponent is in state s | |
| Value when the agent has belief b regarding the opponent’s state | |
| Agent’s action at stage t | |
| Opponent’s state at stage t | |
| Opponent’s action at stage t | |
| Agent’s belief regarding the opponent’s state at stage t, where s is the opponent’s state at stage t | |
| Value function in Model i ( or 2) | |
| Agent’s optimal policy in Model i ( or 2) | |
| Stationary joint distribution of the agent’s action a and the opponent’s state s in Model i ( or 2) | |
| Frequency of cooperation by the agent in Model i ( or 2) |
Appendix A.1. Model 0
We first describe the case of Model 0 from Section 2.2.1. In Model 0, a policy is a map that determines an action in response to the opponent’s present state, as illustrated in Figure 2a. Suppose that a policy is strictly optimal, i.e., that an agent obeying policy gains the largest payoff when playing against a given opponent. Then, from Equation (5),
holds true for all , where . By solving Equation (A1), we obtain value function . Because policy is strictly optimal, the agent has no incentive to obey a policy other than ; i.e., for any , the right-hand side of Equation (A1) is larger than:
which is the value that the agent would obtain if the agent deviated from . Thus,
holds true for all and .
Appendix A.2. Model 1
In the case of Model 1 from Section 2.2.2, a policy is a map that determines an action in response to the previous outcome, as illustrated in Figure 2b. Suppose that a policy is strictly optimal. Then, the corresponding value function satisfies:
for all , where . By solving Equation (A4), we obtain value function . Because policy is strictly optimal,
holds true for all and .
Appendix A.3. Model 2
In the case of Model 2 from Section 2.2.2, a policy is a map that determines an action in response to the agent’s previous action and the opponent’s previous state, as illustrated in Figure 2c. Suppose that a policy is strictly optimal. Then, the corresponding value function satisfies:
for all , where . By solving Equation (A6), we obtain value function . Because policy is strictly optimal,
holds true for all and .
Appendix B. Method for Calculating Cooperation Frequencies
In this Appendix, we describe how to calculate the cooperation frequency in the stationary distribution of states and actions of players in each model.
In general, the frequency of cooperation by the agent, for Model i, is given by:
where is the stationary joint distribution of the agent’s action a and the opponent’s state s at the same given time. In Equation (B1), the stationary joint distribution satisfies:
where the action–state transition from to occurs with probability:
in Model 0,
in Model 1 and:
in Model 2. In Equations (B3)–(B5), the agent selects action a with probability , and , respectively, and the opponent’s state changes to s with probability , where if and if . For each model, Equation (B2) can be solved by obtaining the left eigenvector of the corresponding transition matrix.
Appendix C. An Example Solution for the Case in which Policy CDDD Is Optimal against a GRIM Opponent in Model 2
Appendix C.1. The Condition under which Policy CDDD Is Optimal
In Model 2, if policy CDDD is optimal against a GRIM opponent, from Equation (12),
and:
hold true, where . Using the payoff matrix (2) and Table 1, we observe that is satisfied for all . Therefore, Equation (C6) reduces to:
and:
where , , , and . By solving Equation (C7), we obtain:
and:
To satisfy Equation (C6), which is equivalent to Equation (A7),
and:
must be satisfied using Equation (C8). This yields:
and:
In the error-free limit (i.e., ), Equation (C10) reduces to:
and:
as shown in Table D1.
Appendix C.2. The Long-term Frequency of Cooperation by the CDDD Agent
Applying Table 1 to Equations (B2) and (B5), we observe:
where transition probability matrix is given by:
in which row labels represent the action-state pairs in the previous stage, and column labels represent the action-state pairs in the present stage, , in Equation (B2). Thus, the stationary distribution of the action-state pairs, , is a left eigenvector of matrix that corresponds to a unit eigenvalue. Normalizing the obtained left eigenvector, we obtain:
and:
Therefore,
Appendix D. Comprehensive Description of the Optimal Policies
Table D1 summarizes the optimal policies and conditions in which they are optimal against various opponent types (i.e., CTFT, TFT, WSLS and GRIM) under various information assumptions (i.e., Models 0, 1 and 2) and the error-free limit (i.e., ). Although the obtained policies differ across models, the corresponding conditions in which they are optimal are common among them; as an example, CD and CCDC have the same condition when playing against a CTFT opponent. This phenomenon occurs because in the error-free limit, the BOEs (i.e., Equations (5), (10) and (12)) become identical; to confirm this, see Appendix E.

Table D1.
Optimal policies and their conditions for optimality (error-free limit).
| Opponent | Policy | Condition for Optimality | ||||
|---|---|---|---|---|---|---|
| CTFT | CC | CCCC | CCCC | |||
| CD | CCDC | CCDC | ||||
| DC | DDCD | DDCD | ||||
| DD | DDDD | DDDD | ||||
| TFT | CC | CCCC | CCCC | |||
| CD | CCDD | CCDD | ||||
| DC | DDCC | DDCC | ||||
| DD | DDDD | DDDD | ||||
| WSLS | CC | CCCC | CCCC | |||
| CD | CDDC | CDDC | ||||
| DC | DCCD | DCCD | ||||
| DD | DDDD | DDDD | ||||
| GRIM | CC | CCCC | CCCC | |||
| CD | CDDD | CDDD | ||||
| DC | DCCC | DCCC | ||||
| DD | DDDD | DDDD | ||||
Appendix D.1. Myopic Future Discount
In Model 0 with a fully-myopic future discount (i.e., ), policies CC, CD, DC and DD are optimal in HG (i.e., and ), SH (i.e., and ), SG (i.e., and ) and PD (i.e., and ), respectively, regardless of opponent type because knowing the opponent’s state, to obey CC, CD, DC or DD, is optimal in a one-shot HG, SH, SG or PD, respectively. In Models 1 and 2 with a fully-myopic future discount, optimal policies corresponding to those of Model 0 depend on the opponent type in SH and SG, but not in HG and PD.
Those corresponding with anticipation (i.e., CD) in Model 0 are CCDC, CCDD, CDDC and CDDD when playing against an opponent obeying CTFT, TFT, WSLS and GRIM, respectively. In SH, according to its payoff structure, i.e., and , the agent wants to realize mutual cooperation (i.e., (the agent’s action, the opponent’s action) = (C, C)) or mutual defection (i.e., (D, D)). In Model 1, if the opponent obeys CTFT, the agent infers that the opponent is in state H when the opponent previously defected or the agent previously cooperated, i.e., when the outcome in the previous stage was (C, C), (C, D) or (D, D); see Equation (9). Therefore, policy CCDC is optimal against a CTFT opponent in SH. If the opponent obeys TFT, policy CCDD is optimal because the agent infers that the opponent is in state H when the agent previously cooperated, i.e., when the outcome in the previous stage was (C, C) or (C, D). If the opponent obeys WSLS, policy CDDC is optimal because the agent infers that the opponent is in state H when the previous actions of the two were in agreement, i.e., when the outcome in the previous stage was (C, C) or (D, D). If the opponent obeys GRIM, policy CDDD is optimal because the agent infers that the opponent is in state H when both the agent and opponent previously cooperated, i.e., when the outcome in the previous stage was (C, C). For Model 2, similar interpretations to those of Model 1 justify each optimal policy; see Equation (11).
In SG, because its payoff structure, i.e., and , is opposite of that of SH, the agent wants to realize one-sided cooperation (i.e., C and D) or one-sided defection (i.e., D and C). Thus, the optimal policies are opposite of those of SH, i.e., DDCD, DDCC, DCCD and DCCC when playing against an opponent obeying CTFT, TFT, WSLS and GRIM, respectively.
Appendix D.2. Long-Sighted Future Discounts
If the future discount is long-sighted (i.e., ), the conditions in which the above policies become optimal are different from the case of . Conditions in the error-free limit (i.e., ) are listed in the and columns of Table D1 and shown in Figure 3a,e,i,m when . In the myopic limit (), unconditional cooperation (CC or CCCC) and anticipation (CD and its variants, depending on opponent type) are optimal in HG and SH, respectively. With long-sighted future discounts, the regions in which either of them is optimal (i.e., the blue or green regions) broaden and can be optimal in SG or PD.
If the opponent obeys CTFT (see the CTFT row of Table D1 and Figure 3a for the error-free limit), unconditional cooperation (CC or CCCC) can be optimal in HG and some SG; further, anticipation (CD or CCDC) can be optimal in SH and some PD. Numerically-obtained optimal policies in the error-prone case are shown in Figure 3b–d (). With a small error, the regions in which the policies are optimal slightly change from the error-free case. With a fully-long-sighted future discount (i.e., ), the four policies that can be optimal when can be optimal (see the CTFT row, column of Table D1).
If the opponent obeys TFT (see the TFT row of Table D1 and Figure 3e for the error-free limit), unconditional cooperation (CC or CCCC) can be optimal in all four games (i.e., HG, some SG, SH and some PD), while asocial-anticipation (DC or DDCC) can be optimal in some SH and some PD, but the region in which anticipation is optimal falls outside of the drawing area (i.e., and ) in Figure 3e. Numerically-obtained optimal policies in the error-prone case are shown in Figure 3f–h (). With a fully-long-sighted future discount (i.e., ), among the four policies that can be optimal when , only unconditional cooperation (CC or CCCC) and asocial-anticipation (DC or DDCC) can be optimal (see the TFT row, column of Table D1).
If the opponent obeys WSLS (see the WSLS row of Table D1 and Figure 3i for the error-free limit), unconditional cooperation (CC or CCCC) can be optimal in some HG and some SG, and anticipation (CD or CDDC) can be optimal in all four games (some HG, some SG, SH and some PD). Numerically-obtained optimal policies in the error-prone case are shown in Figure 3j–l (). With a fully-long-sighted future discount (i.e., ), among the four policies that are optimal when , only anticipation (CD or CDDC) and unconditional defection (DD or DDDD) can be optimal (see the WSLS row, column of Table D1).
If the opponent obeys GRIM (see the GRIM row of Table D1 and Figure 3m for the error-free limit), unconditional cooperation (CC or CCCC) can be optimal in some HG and some SG and anticipation (CD or CDDD) can be optimal in SH and PD. Numerically-obtained optimal policies in the error-prone case are shown in Figure 3n–p (). With a fully-long-sighted future discount (i.e., ), among the four policies that are optimal when , only unconditional cooperation (CC or CCCC) and anticipation (CD or CDDD) can be optimal (see the GRIM row, column of Table D1).
Appendix E. Isomorphism of the BOEs in the Error-Free Limit
In the error-free limit, an opponent’s action selection and state transition are deterministic; i.e., using maps σ and ψ, we can write and for any stage t. Thus, Equation (5) becomes:
Similarly, Equations (10) and (12) become:
and:
respectively, where . Each right-hand side of Equations (E2) and (E3) depends only on s, thus using some v, we can rewrite and as . This means that the optimal policies obtained from Equations (E2) and (E3) are isomorphic to those obtained from Equation (E1) in the sense that corresponding optimal policies have an identical condition for optimality. As an example, policy CC in Model 0 and policy CCCC in Models 1 and 2 are optimal against a CTFT opponent under identical conditions, (see Table D1).
Appendix F. Optimal Policies in the Additive PD
In this Appendix, we focus on PD (i.e., and ) and assume that the payoff matrix is additive (i.e., ). These constraints fulfill the classical donation game in which cooperation decreases an agent’s payoff by and increases an opponent’s payoff by ; to confirm this, set and and multiply the payoff matrix by .
Table F1 summarizes the conditions in which anticipation (CD in Model 0, CCDC, CCDD or CDDD in Models 1 and 2) is optimal in the additive PD. For clarity, lower and upper bounds are expanded by errors (i.e., ϵ and μ, represented by ). If T is below the given lower bounds, unconditional cooperation (CC or CCCC) is optimal. If T is above the given upper bounds, unconditional defection (DD or DDDD) is optimal. Against a TFT opponent, unconditional cooperation (CC or CCCC) is always optimal. In contrast to Model 0, Models 1 and 2 equally allow small regions in which unconditional cooperation is optimal against CTFT and GRIM opponents. In Models 0 and 2, regions in which anticipation is optimal are narrowed by the effects of errors, i.e., ϵ and μ, as a comparison with the error-free case. For all opponent types, regions in which anticipation is optimal in Model 2 are narrower than those in Model 0 by the effect of the opponent’s state transition error, μ; compared to Model 0, the agent in Model 2 has less information regarding the opponent’s state; thus, the agent tends to select unconditional defection in broader parameter regions. In Model 1, the regions in which anticipation is optimal are narrowed only by the effect of μ. This is because the agent in Model 1 believes that the opponent is deterministic in selecting an action, i.e., . For all opponent types, regions in which anticipation is optimal in Model 2 are narrower than those in Model 1 by the effect of the opponent’s action-selection error, ϵ. When comparing Models 0 and 2, we cannot determine which one has broader optimal regions of anticipation, because this depends on ϵ and μ.

Table F1.
Conditions in which anticipation is optimal in the additive PD. Here, we assume , and . Note that .
| Opponent | Model | Condition for Optimality of Anticipation |
|---|---|---|
| CTFT | Model 0 | |
| Model 1 | ||
| Model 2 | ||
| TFT | Model 0 | |
| Model 1 | ||
| Model 2 | ||
| WSLS | Model 0 | |
| Model 1 | ||
| Model 2 | ||
| GRIM | Model 0 | |
| Model 1 | ||
| Model 2 |
Appendix G. Comprehensive Description of Cooperation Frequencies
Table 3 shows the frequencies of cooperation by an agent in infinitely repeated games with various opponent types (i.e., CTFT, TFT, WSLS and GRIM) under various information assumptions (i.e., Models 0, 1 and 2); those numerically obtained when are shown in Figure 4. As a matter of course, if the optimal policy is unconditional cooperation (CC or CCCC) or unconditional defection (DD or DDDD), the frequency of cooperation is or ν, respectively. If the optimal policy is anticipation (i.e., CD or its variants) or asocial-anticipation (i.e., DC or its variants), the frequency of cooperation depends on what PFSM the opponent obeys.
If the opponent obeys CTFT (see the CTFT row of Table 3), an agent obeying anticipation (CD or CCDC) is mostly cooperative, while one obeying asocial-anticipation (DC or DDCD) is partially cooperative. Let us first describe the case of anticipation. In Model 0, the frequency of cooperation, , is less than that of Models 1 and 2, , by μ (i.e., the probability that the opponent fails in a state transition). In Model 0, because the agent knows the opponent’s state, which is affected by error rate μ, the agent’s frequency of cooperation is reduced by μ. While in Models 1 and 2, because the agent obeying policy CCDC tries to select action C when the previous outcome is (C, C) or (C, D), the agent continues to try to cooperate regardless of the opponent’s state transition; thus, the frequency of cooperation is not affected by μ. In the case of asocial-anticipation, a DC or DDCD agent selects an action opposite of what the agent believes the opponent intends to do, i.e., the agent selects action D when the agent believes that the opponent is in state H and selects action C when the agent believes that the opponent is in state U. Conversely, the CTFT opponent changes the state from H to U when the agent selects action D and recovers state H after that stage. Therefore, the agent alternately selects C and D in a repeated game, and the frequency of cooperation becomes approximately in all models.
If the opponent obeys TFT (see the TFT row of Table 3), an agent obeying anticipation (CD or CCDD) is partially cooperative in all of the models. In Model 0, the opponent’s stochastic error leads to confusion in which the two players alternately select actions C and D [7,8]. In contrast, in Models 1 and 2 (CCDD), because an agent obeying this policy continues to try to select the same action and mistakenly selects an unintended action with fixed probability ν, the frequency of cooperation over the long term becomes . Policy CCDD can be optimal against a TFT opponent, because the opponent’s state transition depends only on the agent’s action, i.e., the agent can determine an action using only information regarding the agent’s previously self-selected action. An agent obeying asocial-anticipation (DC or DDCC) is partially cooperative in any model, because of a similar reason to that of CTFT.
If the opponent obeys WSLS (see the WSLS row of Table 3), an agent obeying either anticipation (CD or CDDC) or asocial-anticipation (DC or DCCD) is mostly cooperative, but the opponent’s behavior differs. For anticipation, the opponent stays in state H most of the time because the CD or CDDC agent tries to select action C when the opponent would be in state H and action D when the opponent would be in state U. As a result, the CD or CDDC agent and the WSLS opponent establish mutual cooperation. In the case of asocial-anticipation, the opponent stays in state U most of the time because the DC or DCCD agent does the opposite to what anticipators do. As a result, the WSLS opponent continues to defect unilaterally.
If the opponent obeys GRIM (see the GRIM row of Table 3), an agent obeying anticipation is partially cooperative in Model 0 (CD) and mostly defective in Models 1 and 2. An agent obeying asocial-anticipation (DC or DCCC) is mostly cooperative in all models. For anticipation in Model 0 (CD), because of the agent’s reciprocal action, i.e., C to H and D to U, the transition probabilities from H to U and from U to H are and μ, respectively. Therefore, the GRIM opponent stays in state H with probability , resulting in the CD agent’s partial cooperation, i.e.,
as shown in Table 3. Here, ’s asymptotic behavior about ν and μ depends on how we assume the order of errors ν and μ. If the error in the agent’s action is far less than the error in the opponent’s state transition (i.e., ), then we obtain . If the error in the opponent’s state transition is far less than the error in the agent’s action (i.e., ), then we obtain . If the two errors have the same order (i.e., for some constant c and ), then we obtain . For anticipation in Models 1 and 2, once the CDDD agent selects action D, the agent continues to try to select D, which is why the CDDD agent’s cooperation is incurable, i.e.,
and:
Whatever the fraction terms in and are, and are if ϵ, μ and ν are finite. For asocial-anticipation (DC or DCCC), a mechanism opposite of the above works, and the agent is mostly cooperative.
References
- Hamilton, W.D. The genetical evolution of social behaviour I. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef]
- West, S.A.; Griffin, A.S.; Gardner, A. Evolutionary explanations for cooperation. Curr. Biol. 2007, 17, R661–R672. [Google Scholar] [CrossRef] [PubMed]
- Trivers, R.L. The evolution of reciprocal altruism. Q. Rev. Biol. 1971, 46, 35–37. [Google Scholar] [CrossRef]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Rand, D.G.; Nowak, M.A. Human cooperation. Trends Cogn. Sci. 2013, 17, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game. Nature 1993, 364, 56–58. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Tomasello, M. Origins of Human Communication; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Heyes, C.M. Theory of mind in nonhuman primates. Behav. Brain Sci. 1998, 21, 101–114. [Google Scholar] [CrossRef] [PubMed]
- Rand, D.G.; Fudenberg, D.; Dreber, A. It’s the thought that counts: The role of intentions in noisy repeated games. J. Econ. Behav. Organ. 2015, 116, 481–499. [Google Scholar] [CrossRef]
- Fogassi, L.; Ferrari, P.F.; Gesierich, B.; Rozzi, S.; Chersi, F.; Rizzolatti, G. Parietal lobe: From action organization to intention understanding. Science 2005, 308, 662–667. [Google Scholar] [CrossRef] [PubMed]
- Andersen, R.A.; Cui, H. Intention, action planning, and decision making in parietal-frontal circuits. Neuron 2009, 63, 568–583. [Google Scholar] [CrossRef] [PubMed]
- Bonini, L.; Ferrari, P.F.; Fogassi, L. Neurophysiological bases underlying the organization of intentional actions and the understanding of others’ intention. Conscious. Cogn. 2013, 22, 1095–1104. [Google Scholar] [CrossRef] [PubMed]
- Adolphs, R. Neural systems for recognizing emotion. Curr. Opin. Neurobiol. 2002, 12, 169–177. [Google Scholar] [CrossRef]
- Phillips, M.L.; Drevets, W.C.; Rauch, S.L.; Lane, R. Neurobiology of emotion perception I: The neural basis of normal emotion perception. Biol. Psych. 2003, 54, 504–514. [Google Scholar] [CrossRef]
- Anh, H.T.; Pereira, L.M.; Santos, F.C. Intention recognition promotes the emergence of cooperation. Adapt. Behav. 2011, 19, 264–279. [Google Scholar]
- Han, T.A.; Santos, F.C.; Lenaerts, T.; Pereira, L.M. Synergy between intention recognition and commitments in cooperation dilemmas. Sci. Rep. 2015, 5, 9312. [Google Scholar] [CrossRef] [PubMed]
- Kandori, M.; Obara, I. Towards a Belief-based Theory of Repeated Games with Private Monitoring: An Application of POMDP; Department of Economics, UCLA: Los Angeles, CA, USA, 2010. [Google Scholar]
- Yamamoto, Y. Stochastic Games with Hidden States, Second Version (June 1, 2015); SSRN: Rochester, NY, USA, 2015; PIER Working Paper No. 15-019. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Iwasa, Y.; Nowak, M.A. Indirect reciprocity provides only a narrow margin of efficiency for costly punishment. Nature 2009, 457, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Schwenk, C.R. Cognitive simplification processes in strategic decision-making. Strat. Manag. J. 1984, 5, 111–128. [Google Scholar] [CrossRef]
- Goldstein, D.G.; Gigerenzer, G. Models of ecological rationality: The recognition heuristic. Psychol. Rev. 2002, 109, 75–90. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, K.L.; Cohn, J.F. Human facial expressions as adaptations: Evolutionary questions in facial expression research. Am. J. Phys. Anthropol. 2001, 116, 3–24. [Google Scholar] [CrossRef] [PubMed]
- Kraines, D.; Kraines, V. Pavlov and the prisoner’s dilemma. Theor. Decis. 1989, 26, 47–79. [Google Scholar] [CrossRef]
- Fudenberg, D.; Maskin, E. Evolution and cooperation in noisy repeated games. Am. Econ. Rev. 1990, 80, 274–279. [Google Scholar]
- Sugden, R. The Economics of Rights, Co-operation and Welfare; Blackwell: Oxford, UK, 1986. [Google Scholar]
- Friedman, J.W. A non-cooperative equilibrium for supergames. Rev. Econ. Stud. 1971, 38, 1–12. [Google Scholar] [CrossRef]
- Kaelbling, L.P.; Littman, M.L.; Cassandra, A.R. Planning and acting in partially observable stochastic domains. Artif. Intell. 1998, 101, 99–134. [Google Scholar] [CrossRef]
- Hauskrecht, M. Value-function approximations for partially observable Markov decision processes. J. Artif. Intell. Res. 2000, 13, 33–94. [Google Scholar]
- Murphy, K.P. A survey of POMDP solution techniques. Technical report. 2000. [Google Scholar]
- Delton, A.W.; Krasnow, M.M.; Cosmides, L.; Tooby, J. Evolution of direct reciprocity under uncertainty can explain human generosity in one-shot encounters. Proc. Natl. Acad. Sci. USA 2011, 108, 13335–13340. [Google Scholar] [CrossRef] [PubMed]
- Castellano, S. Bayes’ rule and bias roles in the evolution of decision making. Behav. Ecol. 2015, 26, 282–292. [Google Scholar] [CrossRef]
- Dutta, P.K. A folk theorem for stochastic games. J. Econ. Theor. 1995, 66, 1–32. [Google Scholar] [CrossRef]
- Hörner, J.; Sugaya, T.; Takahashi, S.; Vieille, N. Recursive methods in discounted stochastic games: An algorithm for δ → 1 and a folk theorem. Econometrica 2011, 79, 1277–1318. [Google Scholar]
- Nowak, M.A.; Sigmund, K.; El-Sedy, E. Automata, repeated games and noise. J. Math. Biol. 1995, 33, 703–722. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).