1. Introduction
In various instances, the mere act of considering one’s strategic options and gathering information about the possible costs and benefits of an action will be met with distrust (see also [
1]). For example, in most romantic relationships, it will be taken as suspicious if one of the partners starts to flirt with another potential mate. Similarly, societies often have a set of taboo topics (like eating beef in India) whose mere consideration is socially sanctioned. In these examples, people are prevented from seeking for detailed information to ensure that they withstand situations in which there would be a high temptation to defect. Herein, we propose a simple model that formalizes this mechanism.
Our model is a modified version of the envelope game proposed by Hoffman
et al. [
1], and we refer to it as the non-repeated envelope game (in contrast with the original model, which requires repeated interactions). The non-repeated envelope game describes a strategic interaction with four stages, involving two players, Player 1 and Player 2 (as illustrated in
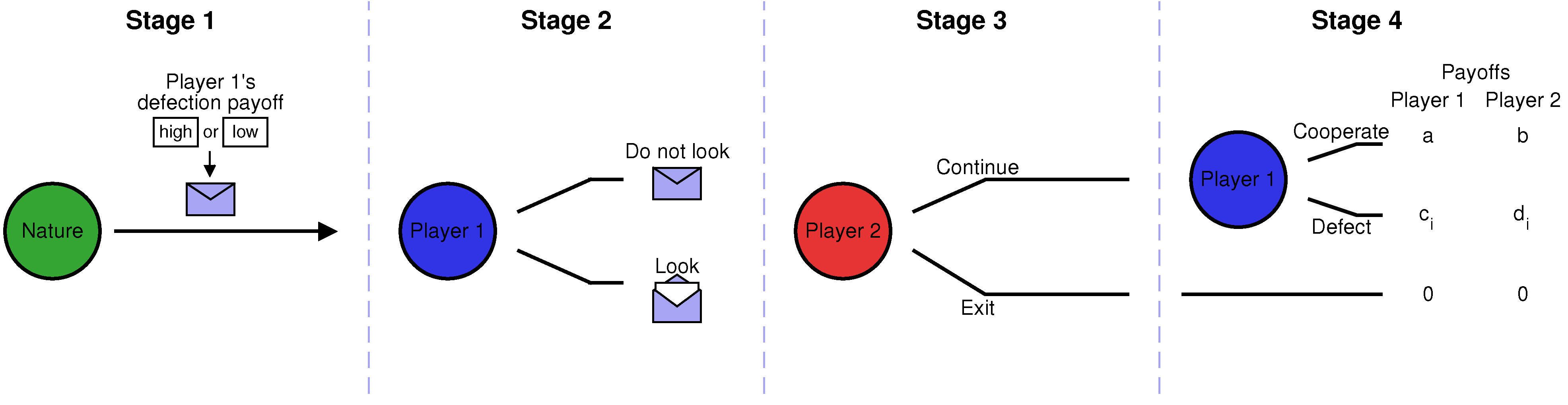
Figure 1; a more detailed explanation is given in the next section). In the first stage, nature randomly determines the possible payoffs of the game. In the second stage, Player 1 can decide whether she wants to learn the realized payoffs. However, Player 1’s decision is observed by Player 2, who can then decide in the third stage whether to exit the interaction or whether to continue. Only if Player 2 continues, there is a fourth stage in which Player 1 decides whether to cooperate or to defect. We will show that if nature only occasionally chooses a game in which Player 1 is tempted to defect (but these instances of defection are extremely damaging to the co-player), then there is an equilibrium in which Player 1 cooperates without looking.
Figure 1.
Schematic representation of the non-repeated envelope game. We consider a game with four stages, involving two players. In the first stage of the game, nature randomly determines Player 1’s payoff from defection, which can be either high (h) or low (l). Nature puts the respective information into an envelope. In the second stage, Player 1 is given the chance to learn the realized payoff by opening the envelope. In the third stage, Player 2 decides whether to exit the interaction, depending on whether Player 1 knows the realized payoffs. If Player 2 continues, there is a fourth stage in which Player 1 decides whether or not to cooperate. We assume that if Player 1 defects, the payoffs of both players, and , depend on the state of nature : when the state is h, then Player 1 has a higher incentive to defect (i.e., ).
Figure 1.
Schematic representation of the non-repeated envelope game. We consider a game with four stages, involving two players. In the first stage of the game, nature randomly determines Player 1’s payoff from defection, which can be either high (h) or low (l). Nature puts the respective information into an envelope. In the second stage, Player 1 is given the chance to learn the realized payoff by opening the envelope. In the third stage, Player 2 decides whether to exit the interaction, depending on whether Player 1 knows the realized payoffs. If Player 2 continues, there is a fourth stage in which Player 1 decides whether or not to cooperate. We assume that if Player 1 defects, the payoffs of both players, and , depend on the state of nature : when the state is h, then Player 1 has a higher incentive to defect (i.e., ).
In such an equilibrium, Player 1 may sometimes cooperate, although cooperation happens to be against her own material interests. In this way, our model suggests an alternative explanation for altruistic acts in anonymous one-shot social dilemmas (as documented, for example, in [
2,
3,
4,
5]). Previous explanations have suggested that such seemingly irrational behaviors have evolved because there is uncertainty about the possibility of future encounters [
6] or that they are a consequence of group selection [
7].
1 Others have emphasized the role of heuristics [
13,
14,
15]. According to that latter explanation, people develop simple heuristics in order to help them deal with recurring situations without having to employ the more costly mental process of conscious deliberation [
16,
17,
18]. In contrast, our model does not require intuitive cooperation to be inherently more efficient than a conscious calculation of payoffs. Instead, our model suggests an endogenous incentive to ignore payoff-relevant information: when people cooperate without looking, they can hope to gain their co-player’s trust.
2. Model: The Non-Repeated Envelope Game
In the following, let us describe the four stages of the non-repeated envelope game in more detail. In the first stage, nature chooses between two different states
, with the two letters
l and
h referring to the defection payoff of Player 1 (which can be either low or high). Let
p denote the probability that nature chooses the low defection payoff. We assume that
p is common knowledge, but the players do not observe directly which state nature has chosen. That is, both players know how often on average there will be a low defection payoff for Player 1, but they do not know whether defection is particularly beneficial for Player 1 in the current situation. In
Figure 1, this scenario is represented by a closed envelope, which contains the information about the realized state of nature.
In the second stage, Player 1 decides whether or not to learn the state of nature (i.e., whether or not to open the envelope). We suppose that learning the state of nature does not entail any direct costs. However, it may affect the players’ actions in the subsequent course of the game. Specifically, we assume that in the third stage, Player 2 can decide whether or not to continue the interaction, based on whether or not Player 1 has looked at the state of nature in the previous stage. If Player 2 decides to exit the interaction, the game ends, and both players’ payoffs are zero.
Only if Player 2 continues, we assume that there is a fourth stage in which Player 1 decides whether to cooperate (C) or to defect (D). Player 1’s cooperation decision may depend on the information she has up to that point (
i.e., on what she has learned about the realized payoffs during the second stage of the game). The players’ payoffs are:
The first variable (
a or
) refers to the payoff of Player 1, whereas the second variable (
b or
) corresponds to the payoff of Player 2. The values of
and
depend on the state of nature
. Without loss of generality, we can assume that payoffs satisfy:
The first inequality formalizes our interpretation that the state l corresponds to a situation in which Player 1 gets a low payoff from defection. The second inequality , incorporates the assumption that Player 1’s move in the fourth stage can be interpreted as an act of cooperation: Player 2 would always prefer his co-player to choose C. After these four stages, the game is over.
For this non-repeated envelope game to be interesting, we impose five further inequalities on the payoff parameters. The first two inequalities,
ensure that Player 1 has no dominant action in Stage 4; in some situations cooperation is in her best interest, whereas in other situations, she is tempted to defect. The next two inequalities,
prevent Player 2’s exiting decision in the third stage from being trivial. If
, Player 2 would continue even if Player 1 always chose D, whereas for
, Player 2 would always exit.
Although the final stage of the envelope game involves a decision between cooperation and defection, the primary aim of the model is not merely to explore when people will cooperate. Rather, we will be interested in situations in which Player 1 cooperates without looking, without even paying attention to whether cooperation is in her own interest. In order to allow for such acts of cooperation, we will furthermore make the final assumption that:
With this assumption, we ensure that Player 1 prefers a game that ends with cooperation to a game that ends by Player 2 exiting the interaction.
3. Static Analysis
The non-repeated envelope game in
Figure 1 describes a simple sequential interaction, which we can solve by backward induction. The result is summarized in the following theorem; to allow for a convenient treatment of degenerate cases, the proof uses the tie-breaking rule that Player 1 cooperates when she is indifferent between C and D and that Player 2 continues when he is indifferent between continue and exit.
Theorem 1. Depending on the probability p, backward induction implies the following behaviors along the unique equilibrium path:- (ONLYL)
If , Player 1 looks in the second stage, Player 2 continues in the third stage, and in the fourth stage, Player 1 cooperates if and only if her payoff from defection is low.
- (CWOL)
If , Player 1 does not look in the second stage, Player 2 continues in the third stage, and Player 1 always cooperates in the fourth stage.
- (EXIT)
If , Player 2 exits the interaction in the third stage, independent of Player 1’s decision in the second stage.
Proof. The proof is by backward induction. Optimal behavior in Stage 4: Suppose the interaction has reached Stage 4. Then, there are two cases, depending on whether or not Player 1 knows the state of nature: (a) if Player 1 has not looked at the state of nature in the second stage, she should cooperate if and only if
holds, such that cooperation yields at least the expected payoff from defection; (b) if Player 1 knows the state of nature, it follows from Equation (
3) that she should cooperate when there is a low defection payoff, whereas she should defect when there is a high defection payoff.
Optimal behavior in Stage 3: Again, we distinguish the previous two cases based on Player 1’s information: (a) without knowledge about the state of nature, Player 1 will cooperate in the fourth stage if and only if condition Equation (
6) holds; in that case, it pays for Player 2 to continue in the third stage; (b) when Player 1 knows her own state, she will cooperate if and only if her defection payoff happens to be low. That implies that Player 2 continues if and only if
that is, if the expected continuation payoff is above the exit payoff.
Optimal behavior in Stage 2: Since there is no direct cost for acquiring information, Player 1 would always prefer to have as much information as possible (subject to the restriction that this does not lead Player 2 to exit the interaction). That is, if possible, Player 1 looks at the state of nature, which will be accepted by Player 2 if and only if Equation (
7) holds (or, equivalently, when
). If looking at the payoffs is not feasible, Player 1 will either cooperate without looking (if Equation (
6) holds, or, equivalently,
), or Player 2 will exit the interaction irrespective of Player 1’s choice in the second stage (if
).□
Remark. In the following, let us make a few simple observations that follow immediately from Theorem 1.
The two equilibrium scenarios ONLYL and CWOL both allow for some cooperation along the equilibrium path. However, Player 2’s interpretation of an observed cooperative act of Player 1 will be different between these two scenarios. In an ONLYL equilibrium, Player 2 knows that Player 1 only cooperated because cooperation happened to be in Player 1’s own interest. Only in the CWOL equilibrium, Player 2 can be certain that Player 1 cooperates in any case; since Player 1 does not even care to learn the possible gains from defection.
In a CWOL equilibrium, there may be instances in which Player 1 cooperates although realized payoffs do not make it profitable for Player 1 to do so. In such instances, an outsider who only observes the fourth stage of the game may interpret Player 1’s behavior as altruistic. Our model suggests that such seemingly altruistic acts occur because Player 1’s cooperation decision is only the final stage of a larger game. When the whole game is considered, Player 1’s cooperation behavior is part of an equilibrium. In fact, Player 1 cooperates in such instances because: (i) Player 2 would not accept a purely opportunistic co-player as an interaction partner (i.e., the general parameters of the game do not allow for an ONLYL equilibrium); and (ii) on average, it pays for Player 1 to engage in such interactions and to occasionally cooperate, even if cooperation may happen to be not in Player 1’s self-interest.
There is a strong analogy between the equilibrium conditions in Theorem 1 and the equilibrium conditions for the repeated-game setup considered in Hoffman
et al. [
1]. For the repeated game model, Hoffman
et al. [
1] find that Player 2 will exit in the first round of the game if payoffs satisfy
, with
being the expected payoff from cooperating in every round (
w is the constant probability of having another round). If
, they observe the occurrence of an additional equilibrium, in which Player 1 cooperates without looking. The condition
, with
, is incorporated as a basic assumption, which is introduced exactly to exclude the opportunistic ONLYL equilibria.
The equilibrium condition for CWOL, , suggests that CWOL can only be sustained if there is sufficient variability in Player 1’s temptation to defect. If it happens too often that Player 1’s payoff of defection is low (i.e., if ), then Player 2 would also accept a Player 1 who defects in the few cases in which she is tempted to defect, resulting in an ONLYL equilibrium. On the other hand, if it only happens occasionally that Player 1 has a low defection payoff (i.e., if ), then Player 1 who does not look at the state of nature would prefer to defect by default, forcing Player 2 to exit the interaction. In particular, the equilibrium conditions for CWOL are easier to satisfy when decreases and when Player 1’s cooperation payoff a approaches her maximum defection payoff . This observation suggests that CWOL is more likely to occur if occasional events of defection can be very harmful to Player 2, while only giving a negligible advantage to Player 1.
Whether CWOL can be obtained as an equilibrium also depends on the correlation between Player 1’s defection payoff
and the resulting payoff
to Player 2. To see this in more detail, let us assume that
and
take the following form,
with
and
being payoff parameters, such that
. The parameter
is a measure for the correlation between the payoffs of the two players when Player 1 defects. When
, then
and
, and thus, our assumptions imply
and
. In this case, Player 1 gets a comparably low payoff from defection if and only if Player 2’s payoff after defection is comparably low (
i.e., if the payoffs of the two players have a positive correlation). On the other hand, if
, then
while still
. This implies that when Player 1 is tempted to defect, defection is particularly harmful to Player 2 (
i.e., there is a negative correlation between the players’ payoffs). Because
is monotonically increasing in
λ and because
is monotonically decreasing in
, it follows from Theorem 1 that CWOL is most likely to be an equilibrium when
,
i.e., when there is a negative correlation between payoffs. Intuitively, if there is a negative correlation, instances in which Player 1 would be tempted to defect are more harmful to Player 2, and thus, Player 2 has a stronger interest to prevent his co-player from looking.
Finally, let us note that our previous conclusions are independent of the assumption that nature chooses among two states only. To see this, suppose there are
n states of nature,
, and let
be the corresponding probability distribution (such that
). If Player 1 cooperates, the payoffs are
a (for Player 1) and
b (for Player 2), respectively. If Player 1 defects, the players’ payoffs again depend on the state of nature; they are given by
(for Player 1) and
(for Player 2), with
. For simplicity, let us assume that the states are ordered such that
and such that there is a
j with
with
. That is, in the first
j states, Player 1 has an incentive to cooperate, whereas in the remaining
states, Player 1 would like to defect. Then, we can define
p as the probability that nature chooses one of the first
j states,
and
denote the expected payoffs in that case, whereas
and
denote the expected payoffs given that nature has chosen one of the remaining
states. Assuming that this extended model again satisfies Inequalities (
2) and (
4), one can take the same proof as in Theorem 1 to show that CWOL is an equilibrium if
.
4. Evolutionary Simulations
In the previous section, we have used backward induction to analyze when people will cooperate without looking. However, backward induction imposes certain assumptions on the players’ rationality and on the players’ trust in their co-players’ rationality [
19]. For some applications, such a rationality-based view may appear inappropriate. In the following, we will thus argue that our previous conclusions remain valid even if we consider a simple evolutionary setup, in which individuals do not perform the calculations necessary for backward induction. Instead, they simply imitate others based on the relative success of their strategies [
20,
21,
22,
23].
2To this end, let us consider two populations of players, a population of individuals who play the non-repeated envelope game in the role of Player 1 and a population of individuals who play the game in the role of Player 2. We will refer to these populations as Population 1 and Population 2, with population sizes
and
, respectively. Members of the two populations are randomly matched to play the game, and they derive a payoff depending on their respective strategies. A strategy for Player 1 is a four-tuple (
) with
. The first entry
is the player’s probability to look in the second stage; the other entries
,
and
correspond to Player 1’s cooperation probability in the fourth stage (given that she does not know the state of the world, she knows the state is
l or she knows the state is
h, respectively). Overall, players in Population 1 can thus choose among 16 strategies.
3 Similarly, a strategy for Player 2 is a two-tuple (
), where
is the probability to exit the interaction in the third stage depending on whether or not Player 1 has looked in the second stage, respectively.
4 Players in Population 2 can thus choose among four possible strategies.
The current composition of a population can be described by a vector,
and
, where
denotes the number of players in population
i that employ strategy
j. In particular, it follows that
and
. Initially, we suppose that individuals in Population 1 are non-looking defectors, whereas individuals in Population 2 always exit the interaction. However, the composition of the two populations is allowed to change over time, depending on the relative success of each strategy. Specifically, we consider a simple pairwise comparison process (see also [
30,
31,
32,
33]). In each time step, some individual
i from one of the two populations is chosen at random and given the chance to update the strategy. To this end, another individual
j is chosen from the same population to act as a potential role model. If expected payoffs of the two players are given by
and
(which depend on the current composition of the other population), then we assume that the focal individual
i adopts
j’s strategy with probability:
The parameter is called the strength of selection. It measures how strongly i’s updating decision is affected by relative payoff differences. In the extreme case , the imitation probability becomes (irrespective of the payoffs of the players), and imitation essentially occurs at random. In the other extreme case , the focal player i only imitates co-players that have at least the payoff of player i (because implies ).
In addition to these imitation events, we also allow for random strategy exploration (corresponding to spontaneous mutation events in evolutionary biology). Specifically, we assume that in each time step, there is a probability μ that one of the individuals (in one of the two populations) is chosen at random. This individual then randomly switches to a different strategy (with all alternative strategies for the respective individual having the same probability to be picked). Overall, these assumptions on the evolutionary dynamics result in an ergodic process. In particular, the time average of the population compositions will converge towards a unique invariant distribution over time. In the following, we estimate this invariant distribution by simulating the evolutionary process for a large number of time steps.
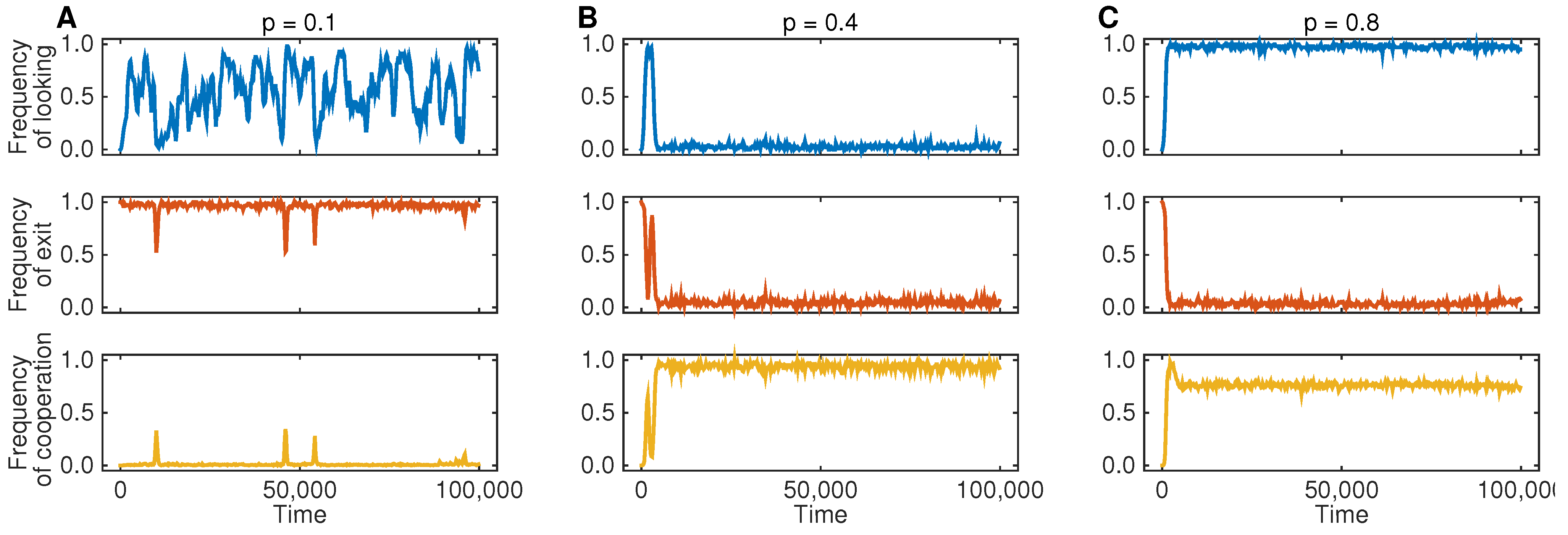
Figure 2 shows the resulting dynamics for three different parameter regimes. In
Figure 2A, we assume that the probability
p is comparably small; in that case, Player 1 will be often tempted to defect, such that Theorem 1 predicts the occurrence of an EXIT equilibrium. Indeed, the simulations show that players in Population 2 predominantly exit any interaction. As a consequence, there is no selection on Player 1’s looking behavior, which is governed by neutral drift. Because most interactions end after the third stage, we only see very few cases in which the game reaches the fourth stage and in which Player 1 decides to cooperate. In
Figure 2B, we show the results for a simulation that uses an intermediate probability of low temptations, such that Theorem 1 predicts a CWOL equilibrium. The simulation result is in line with this prediction: individuals in Population 1 quickly learn not to look at payoffs and to cooperate unconditionally, while individuals in Population 2 learn not to exit. Finally, in the last simulation run (
Figure 2C), low temptations are now even more likely, for which case Theorem 1 predicts an ONLYL equilibrium. The simulation indeed leads to a state in which individuals in Population 2 allow their co-players to observe the realized payoffs of the game and to act opportunistically (resulting in an overall cooperation rate of 80%). In particular, all three simulation runs are in line with the predictions based on Theorem 1.
Figure 2.
Three representative simulation runs for different combinations of p (the probability that Player 1 has a low defection payoff). The populations’ evolution depends on the game parameters: (A) for the dynamics lead to an EXIT equilibrium: individuals in Population 2 exit the interaction, irrespective of Player 1’s looking decision in the second stage; (B) for , individuals in Population 1 quickly learn not to look and to cooperate, whereas individuals in Population 2 learn not to exit; (C) for , the evolutionary simulations lead to an ONLYL equilibrium, as predicted by backward induction. For the simulations, we have used the game parameters , , , , and . The population parameters are as follows: population size , mutation rate and strong selection .
Figure 2.
Three representative simulation runs for different combinations of p (the probability that Player 1 has a low defection payoff). The populations’ evolution depends on the game parameters: (A) for the dynamics lead to an EXIT equilibrium: individuals in Population 2 exit the interaction, irrespective of Player 1’s looking decision in the second stage; (B) for , individuals in Population 1 quickly learn not to look and to cooperate, whereas individuals in Population 2 learn not to exit; (C) for , the evolutionary simulations lead to an ONLYL equilibrium, as predicted by backward induction. For the simulations, we have used the game parameters , , , , and . The population parameters are as follows: population size , mutation rate and strong selection .
To explore the predictive value of backward induction more generally, we have run additional simulations for various other parameter combinations, as shown in
Figure 3. Again, the emerging looking frequencies (in Stage 2), exit frequencies (in Stage 3) and cooperation frequencies (in Stage 4) compare nicely to the results expected from Theorem 1. In particular, it is worth noting that the resulting cooperation frequencies do not depend monotonically on the game parameters. Instead, cooperation rates are highest when CWOL is an equilibrium, requiring an intermediate chance for high defection payoffs and a negative correlation between the players’ payoffs.
Figure 3.
Results of the evolutionary simulations for various combinations of
p and
λ (the probability that Player 1 has a low defection payoff and the correlation parameter, respectively). The three graphs show the percentage of games in which Player 1 decides to look, in which Player 2 decides to exit and in which the interaction ends with Player 1 cooperating. To generate the contour plot, we have simulated the evolutionary process for
strategy updating events for
different combinations of
p and
λ. The depicted colors show the time average over the whole course of such a simulation. As indicated, the numerical results are in agreement with the predictions based on backward induction (the inequalities in Theorem 1 are depicted by the thick black lines). The parameters are the same as in
Figure 2.
Figure 3.
Results of the evolutionary simulations for various combinations of
p and
λ (the probability that Player 1 has a low defection payoff and the correlation parameter, respectively). The three graphs show the percentage of games in which Player 1 decides to look, in which Player 2 decides to exit and in which the interaction ends with Player 1 cooperating. To generate the contour plot, we have simulated the evolutionary process for
strategy updating events for
different combinations of
p and
λ. The depicted colors show the time average over the whole course of such a simulation. As indicated, the numerical results are in agreement with the predictions based on backward induction (the inequalities in Theorem 1 are depicted by the thick black lines). The parameters are the same as in
Figure 2.
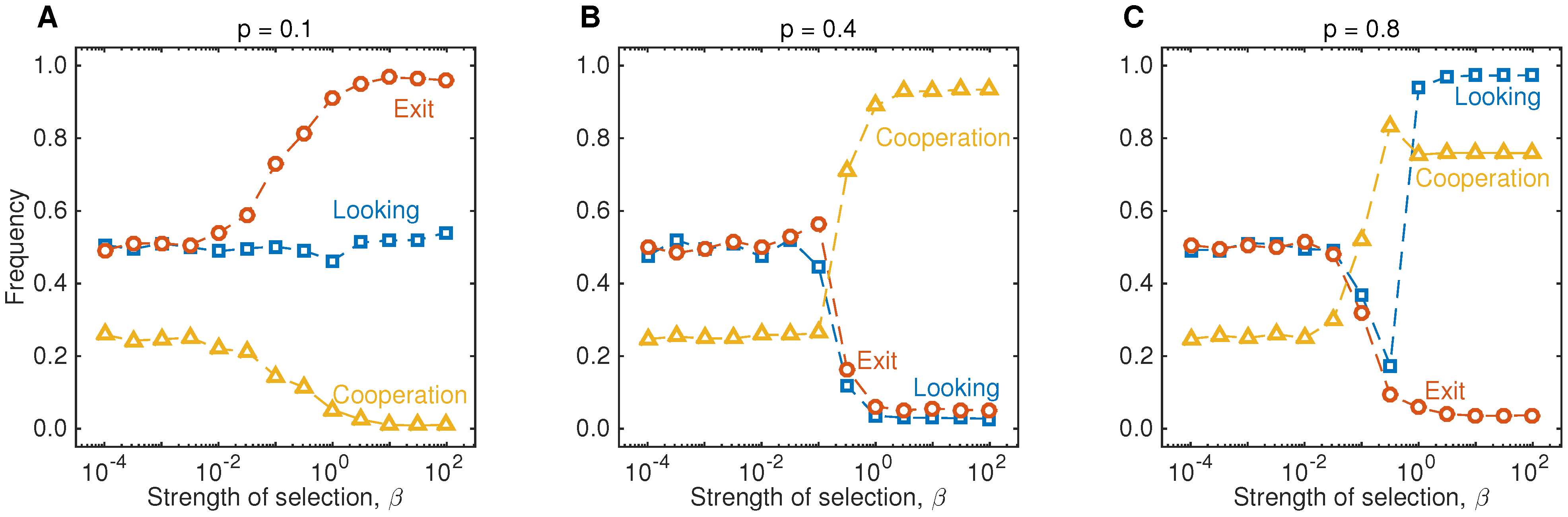
In addition, we have also run simulations to illustrate the impact of selection strength on the evolutionary outcome. As shown in
Figure 4, populations converge to the backward induction outcome provided that the selection parameter is sufficiently large compared to the mutation rate. Overall, the simulations shown in
Figure 2,
Figure 3 and
Figure 4 underline that people do not need to engage in explicit strategic considerations to adopt behaviors that resemble cooperate without looking. In contrast, cooperate without looking can be considered as an emergent heuristics, which helps people to deal with recurring situations in which cooperation is a profitable default strategy.
Figure 4.
Results of the evolutionary simulations for different strengths of selection. The three graphs show the long-run outcome of the simulations shown in
Figure 2, for various values of
β. In particular, this graph shows that the backward induction outcome gives a reasonable prediction when selection is sufficiently strong,
. When
β is small, all strategies tend to be present in the population in equal proportions. In particular, the fourth stage of the game is only reached in roughly 50% of the interactions, and as a result, only 25% of the games end with Player 1 cooperating. The parameters are the same as in
Figure 2.
Figure 4.
Results of the evolutionary simulations for different strengths of selection. The three graphs show the long-run outcome of the simulations shown in
Figure 2, for various values of
β. In particular, this graph shows that the backward induction outcome gives a reasonable prediction when selection is sufficiently strong,
. When
β is small, all strategies tend to be present in the population in equal proportions. In particular, the fourth stage of the game is only reached in roughly 50% of the interactions, and as a result, only 25% of the games end with Player 1 cooperating. The parameters are the same as in
Figure 2.
5. Discussion and Conclusions
Herein, we have proposed a simple model to explain intuitive cooperation in one-shot games. Our model is based on the assumption that individuals may find themselves in different strategic situations during their lives (as determined by the move of nature); in some of these situations, cooperation is in a player’s own interest (for example, due to direct benefits from mutualistic interactions or due to indirect benefits because of reputation effects); in other situations, cooperation is a dominated action. If subjects were free to choose, they would act opportunistically: they would try to learn the payoffs in each particular situation, and then they would act accordingly (i.e., they would cooperate when it is beneficial for themselves and would defect otherwise). However, as we have shown here, people may refrain from such opportunistic behavior in order to gain their co-players’ trust.
Our model is closely related to Hoffman
et al. [
1], which also attempts to model why people cooperate without looking. The model in Hoffman
et al. [
1] requires repeated interactions between the same two individuals. Their stage game is similar to the setup of the non-repeated envelope game displayed in
Figure 1: Player 1 has to choose whether to look at the payoffs and whether to cooperate, whereas Player 2 decides whether to exit the interaction or not (in their model, exit means that the repeated game ends after the current round). According to Hoffman
et al. [
1], cooperate without looking may be an equilibrium although ‘cooperate with looking’ is not (that is, there is no equilibrium in which Player 1 would always cooperate after looking at the realized payoffs). In general, as is typical for repeated game models [
34], the game considered in Hoffman
et al. [
1] allows for a multitude of possible equilibria, which makes it difficult to predict when one equilibrium will be favored over another. Moreover, their model requires sufficiently many interactions between the same two individuals for cooperate without looking to be an equilibrium. In contrast, our model does not require repeated interactions and always yields a unique equilibrium.
Our results in some ways demonstrate the robustness of the key predictions of Hoffman
et al. [
1], but also yield slightly different and novel insights. In agreement with the results in Hoffman
et al. [
1], we show that cooperate without looking is an important way to establish cooperation when high temptations to defect are rare, but defection is very damaging to the co-player. A result unique to our paper is that cooperate without looking is particularly likely to emerge when there is a negative correlation between the players’ payoffs in case Player 1 defects (because under those circumstances, Player 2 has a strong incentive to reject opportunistic co-players). It is also worth noting that one criticism of the original model Hoffman
et al. [
1] does not apply to this model. In the original model, the strategy profile that yields cooperate without looking along the equilibrium path requires that if Player 1 has deviated and looked, she defects ever after, regardless of the realized temptation. However, in reality, someone who looks is likely to cooperate when the temptation to defect happens to be low. Our current model is not subject to this concern. In the current model, someone who looks would still cooperate if given the opportunity, and the defection payoff is low.
In our model, people learn to cooperate without looking in order to make themselves more attractive as interaction partners. Thus, our model seems to be related to the literature on competitive altruism, which posits that cooperative individuals are more likely to be selected as mating partners [
35,
36,
37,
38]; or similarly, that defecting individuals are more likely to be excluded from an interaction or from a community [
39,
40,
41]. However, models of competitive altruism focus on the players’ actions, whereas the model presented herein rather focuses on the information to which the players attend. Our primary interest is not to explore when people cooperate; rather, we want to explore when people cooperate without considering the potential consequences.
When people cooperate without looking, this can be thought of as a particular type of commitment: when we deliberately ignore any cues as to whether defection would be worthwhile in a given situation, we forgo any possibility to act opportunistically. However, it is important to note that this is a very different type of commitment than that described in Frank [
42]. According to Frank [
42], people have evolved emotions to commit to take an action even if the action would never be beneficial to take. Instead, in our model, players are only committed not to condition their behavior on the exact payoff realizations. The two models will yield the same outcome only if the expected gain of the respective action is positive. Our notion of commitment does not negate subgame perfection and is not subject to the same evolutionary criticism that Frank’s model is; Frank must assume that agents can never evolve to mimic the commitment type, but then deviate in subgames where it is advantageous. Our model only requires that we cannot evolve to pretend not to have looked when we in fact have looked.
Our model certainly neglects several aspects that may have an additional effect on the evolution of intuitive cooperation, such as population structure (see, for example, [
43]) or diversity among individuals (as considered in [
44]). Our model is simple, to make the underlying intuition most transparent: there is an individual benefit to cooperate without looking, as it helps to gain the co-player’s trust.