Indirect Reciprocity with Optional Interactions and Private Information
Abstract
:1. Introduction
2. Model
3. Results
3.1. Single Defector

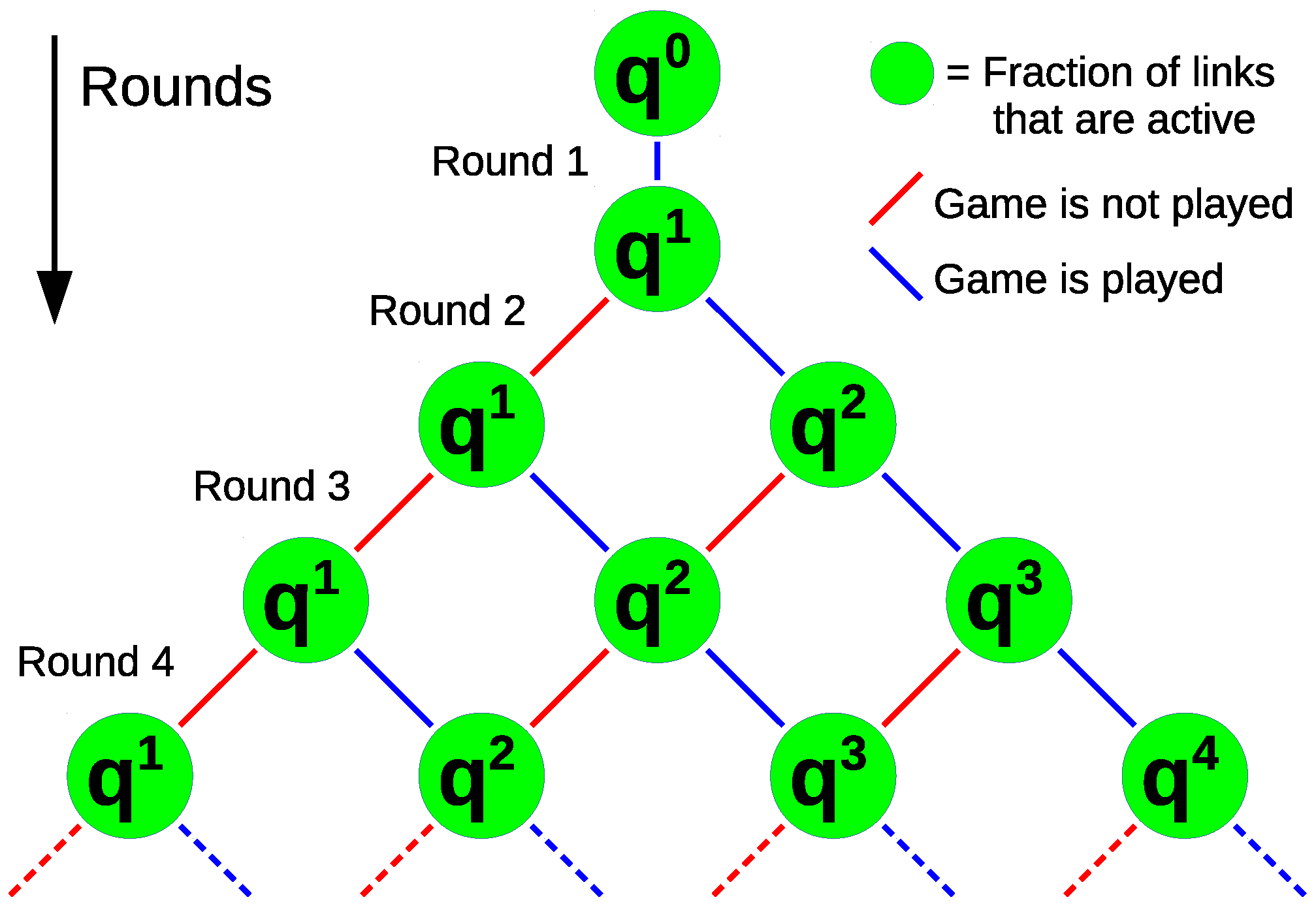
3.1.1. Probability of i Games in m Rounds
3.1.2. Average Number of Games
3.2. Fixed Number of Rounds per Generation
3.2.1. Average Number of Games

3.2.2. Critical Benefit-to-Cost Ratio
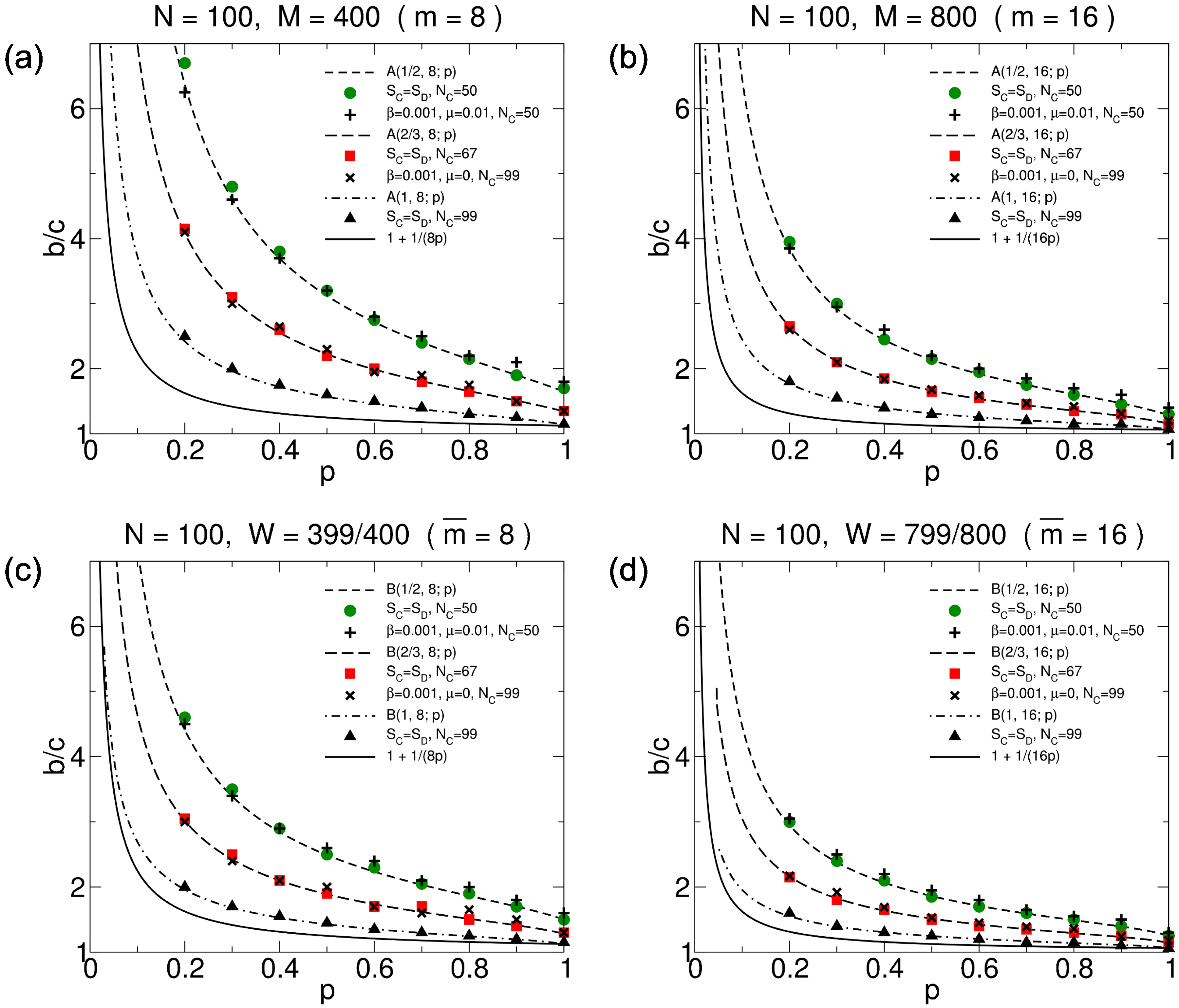
3.2.3. Simulation Results
3.3. Variable Number of Rounds per Generation
3.3.1. Average Number of Games
3.3.2. Critical Benefit-to-Cost Ratio
3.3.3. Simulation Results
3.4. Simple Lower Bound on
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
A. Alternative Proof of the Formula for
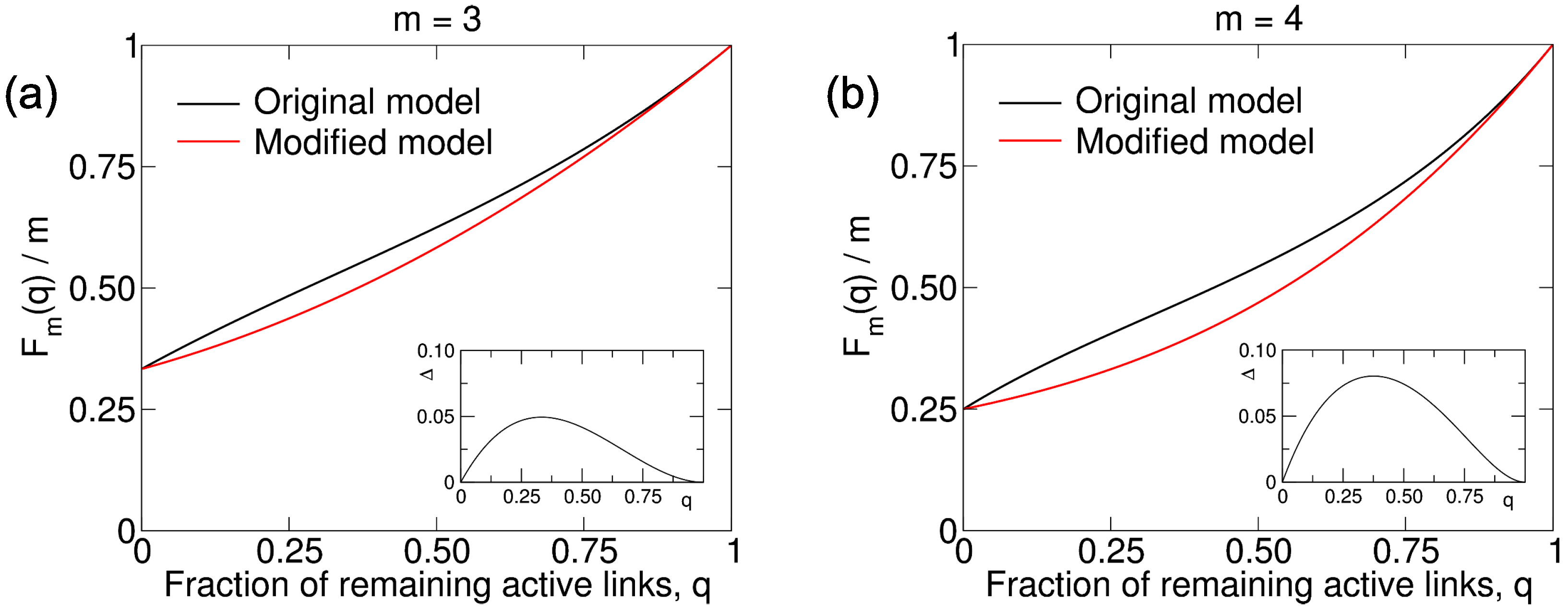
B. Modification to the Model: Loss of Links on Every Round
References
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Evolutionary Dynamics; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Bergstrom, T.C. Evolution of social behavior: Individual and group selection. J. Econ. Perspect. 2002, 16, 67–88. [Google Scholar] [CrossRef]
- Sasaki, T.; Uchida, S. The evolution of cooperation by social exclusion. Proc. R. Soc. Lond. B 2013, 280, 20122498. [Google Scholar] [CrossRef] [PubMed]
- Sugden, R. The Economics of Rights, Cooperation and Welfare; Basil Blackwell: Oxford, UK, 1986. [Google Scholar]
- Alexander, R.D. The Biology of Moral Systems; Aldine de Gruyter: New York, NY, USA, 1987. [Google Scholar]
- Kandori, M. Social norms and community enforcement. Rev. Econ. Stud. 1992, 59, 63–80. [Google Scholar] [CrossRef]
- Milinski, M.; Semmann, D.; Krambeck, H.-J. Reputation helps solve the “tragedy of the commons”. Nature 2002, 415, 424–426. [Google Scholar] [CrossRef] [PubMed]
- Rand, D.G.; Nowak, M.A. Human cooperation. Trends Cogn. Sci. 2013, 17, 413–425. [Google Scholar] [CrossRef] [PubMed]
- Yoeli, E.; Hoffman, M.; Rand, D.G.; Nowak, M.A. Powering up with indirect reciprocity in a large-scale field experiment. Proc. Natl. Acad. Sci. USA 2013, 110, 10424–10429. [Google Scholar] [CrossRef] [PubMed]
- Roberts, G. Evolution of direct and indirect reciprocity. Proc. R. Soc. Lond. B 2008, 275, 173–179. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Berger, U. Learning to cooperate via indirect reciprocity. Games Econ. Behav. 2011, 72, 30–37. [Google Scholar] [CrossRef]
- Wedekind, C.; Milinski, M. Cooperation through image scoring in humans. Science 2000, 288, 850–852. [Google Scholar] [CrossRef] [PubMed]
- Bolton, G.E.; Katok, E.; Ockenfels, A. Cooperation among strangers with limited information about reputation. J. Public Econ. 2005, 89, 1457–1468. [Google Scholar] [CrossRef]
- Semmann, D.; Krambeck, H.-J.; Milinski, M. Reputation is valuable within and outside one’s own social group. Behav. Ecol. Sociobiol. 2005, 57, 611–616. [Google Scholar] [CrossRef]
- Rockenbach, B.; Milinski, M. The efficient interaction of indirect reciprocity and costly punishment. Nature 2006, 444, 718–723. [Google Scholar] [CrossRef] [PubMed]
- Seinen, I.; Schram, A. Social status and group norms: indirect reciprocity in a repeated helping experiment. Eur. Econ. Rev. 2006, 50, 581–602. [Google Scholar] [CrossRef]
- Sommerfeld, R.D.; Krambeck, H.-J.; Semmann, D.; Milinski, M. Gossip as an alternative for direct observation in games of indirect reciprocity. Proc. Natl. Acad. Sci. USA 2007, 104, 17435–17440. [Google Scholar] [CrossRef] [PubMed]
- Ule, A.; Schram, A.; Riedl, A.; Cason, T.N. Indirect punishment and generosity toward strangers. Science 2009, 326, 1701–1704. [Google Scholar] [CrossRef] [PubMed]
- Jacquet, J.; Hauert, C.; Traulsen, A.; Milinski, M. Shame and honour drive cooperation. Biol. Lett. 2011, 7, 899–901. [Google Scholar] [CrossRef] [PubMed]
- Pfeiffer, T.; Tran, L.; Krumme, C.; Rand, D.G. The value of reputation. J. R. Soc. Interface 2012, 9, 2791–2797. [Google Scholar] [CrossRef] [PubMed]
- Leimar, O.; Hammerstein, P. Evolution of cooperation through indirect reciprocation. Proc. R. Soc. Lond. B 2001, 268, 745–753. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Iwasa, Y. How should we define goodness? Reputation dynamics in indirect reciprocity. J. Theor. Biol. 2004, 231, 107–120. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Iwasa, Y. The leading eight: Social norms that can maintain cooperation by indirect reciprocity. J. Theor. Biol. 2006, 239, 435–444. [Google Scholar] [CrossRef] [PubMed]
- Fishman, M.A. Indirect reciprocity among imperfect individuals. J. Theor. Biol. 2003, 225, 285–292. [Google Scholar] [CrossRef]
- Suzuki, S.; Akiyama, E. Evolution of indirect reciprocity in groups of various sizes and comparison with direct reciprocity. J. Theor. Biol. 2007, 245, 539–552. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, S.; Akiyama, E. Three-person game facilitates indirect reciprocity under image scoring. J. Theor. Biol. 2007, 249, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Vaquero, L.A.; Cuesta, J.A. Evolutionary stability and resistance to cheating in an indirect reciprocity model based on reputation. Phys. Rev. E 2013, 87, 052810. [Google Scholar] [CrossRef]
- Suzuki, S.; Kimura, H. Indirect reciprocity is sensitive to costs of information transfer. Sci. Rep. 2013, 3. [Google Scholar] [CrossRef] [PubMed]
- Tanabe, S.; Suzuki, H.; Masuda, N. Indirect Reciprocity with Trinary Reputations. J. Theor. Biol. 2013, 317, 338–347. [Google Scholar] [CrossRef] [PubMed]
- Matsuo, T.; Jusup, M.; Iwasa, Y. The conflict of social norms may cause the collapse of cooperation: Indirect reciprocity with opposing attitudes towards in-group favoritism. J. Theor. Biol. 2014, 7, 34–46. [Google Scholar] [CrossRef] [PubMed]
- Brandt, H.; Sigmund, K. The logic of reprobation: Assessment and action rules for indirect reciprocation. J. Theor. Biol. 2004, 231, 475–486. [Google Scholar] [CrossRef] [PubMed]
- Brandt, H.; Sigmund, K. Indirect reciprocity, image scoring, and moral hazard. Proc. Natl. Acad. Sci. USA 2005, 102, 2666–2670. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. Evolution of indirect reciprocity. Nature 2005, 427, 1291–1298. [Google Scholar] [CrossRef] [PubMed]
- Ohtsuki, H.; Iwasa, Y.; Nowak, M.A. Indirect reciprocity provides only a narrow margin of efficiency for costly punishment. Nature 2009, 457, 79–82. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. Moral assessment in indirect reciprocity. J. Theor. Biol. 2012, 299, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Evolution of indirect reciprocity by image scoring. Nature 1998, 393, 573–577. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sigmund, K. The dynamics of indrect reciprocity. J. Theor. Biol. 1998, 194, 561–574. [Google Scholar] [CrossRef] [PubMed]
- Uchida, S. Effect of private information on indirect reciprocity. Phys. Rev. E 2010, 82, 036111. [Google Scholar] [CrossRef]
- Uchida, S.; Sigmund, K. The competition of assessment rules for indirect reciprocity. J. Theor. Biol. 2010, 263, 13–19. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, M.; Masuda, N. Indirect Reciprocity under Incomplete Observation. PLoS. Comput. Biol. 2011, 7, e1002113. [Google Scholar] [CrossRef] [PubMed]
- Uchida, S.; Sasaki, T. Effect of assessment error and private information on stern-judging in indirect reciprocity. Chaos Solitons Fractals 2013, 56, 175–180. [Google Scholar] [CrossRef]
- Ghang, W.; Nowak, M.A. Indirect reciprocity with optional interactions. J. Theor. Biol. 2015, 365, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Van Lint, J.H.; Wilson, R.M. A Course in Combinatorics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Koekoek, R.; Swarttouw, R.F. The Askey-Scheme of Hypergeometric Orthogonal Polynomials and Its Q-Analogue; Faculty of Technical Mathematics and Informatics Report 98-17; Technische Universiteit Delft: Delft, The Netherlands, 1998; p. 7. [Google Scholar]
- Ohtsuki, H.; Bordalo, P.; Nowak, M.A. The one-third law of evolutionary dynamics. J. Theor. Biol. 2007, 249, 289–295. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; Sasaki, A.; Taylor, C.; Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004, 428, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Imhof, L.A.; Nowak, M.A. Evolutionary game dynamics in a Wright-Fisher process. J. Math. Biol. 2006, 52, 667–681. [Google Scholar] [CrossRef]
- Lessard, S.; Ladret, V. The probability of fixation of a single mutant in an exchangeable selection model. J. Math. Biol. 2007, 54, 721–744. [Google Scholar] [CrossRef] [PubMed]
- Ladret, V.; Lessard, S. Evolutionary game dynamics in a finite asymmetric two-deme population and emergence of cooperation. J. Theor. Biol. 2008, 255, 137–151. [Google Scholar] [CrossRef] [PubMed]
- Brandt, H.; Sigmund, K. The good, the bad and the discriminator—Errors in direct and indirect reciprocity. J. Theor. Biol. 2006, 239, 183–194. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olejarz, J.; Ghang, W.; Nowak, M.A. Indirect Reciprocity with Optional Interactions and Private Information. Games 2015, 6, 438-457. https://doi.org/10.3390/g6040438
Olejarz J, Ghang W, Nowak MA. Indirect Reciprocity with Optional Interactions and Private Information. Games. 2015; 6(4):438-457. https://doi.org/10.3390/g6040438
Chicago/Turabian StyleOlejarz, Jason, Whan Ghang, and Martin A. Nowak. 2015. "Indirect Reciprocity with Optional Interactions and Private Information" Games 6, no. 4: 438-457. https://doi.org/10.3390/g6040438
APA StyleOlejarz, J., Ghang, W., & Nowak, M. A. (2015). Indirect Reciprocity with Optional Interactions and Private Information. Games, 6(4), 438-457. https://doi.org/10.3390/g6040438




