On the Three-Person Game Baccara Banque

Abstract

Baccara banque is a three-person zero-sum game parameterized by $\theta \in (0,1)$. A study of the game by Downton and Lockwood claimed that the Nash equilibrium is of only academic interest. Their preferred alternative is what we call the independent cooperative equilibrium. However, this solution exists only for certain θ. A third solution, which we call the correlated cooperative equilibrium, always exists. Under a “with replacement” assumption as well as a simplifying assumption concerning the information available to one of the players, we derive each of the three solutions for all θ.

1. Introduction

The three-person game baccara banque (or baccara à deux tableaux) is closely related to the two-person game baccara chemin de fer. In fact, baccara banque has been described as “a game in which a banker plays chemin-de-fer simultaneously against two players” (Downton and Lockwood [1]). Game-theoretic analyses of baccara chemin de fer have been provided by Kemeny and Snell [2], Foster [3], Downton and Lockwood [4], Deloche and Oguer [5], and Ethier and Gámez [6]. The more complicated game baccara banque has received less attention. Foster [7] was the first to approach the game from the perspective of game theory, though the details of his research were not published. Kendall and Murchland [8] used simulation to study the game. Downton and Holder [9] discussed the special case of highly unbalanced stakes. Judah and Ziemba [10] analyzed a variant of the game in which two of the three players have mandated strategies. Downton and Lockwood [1] provided the most detailed study of baccara banque, although it is partially incorrect.

To explain the purpose of this paper, we must first describe the rules of baccara banque. There are three players, Player 1, Player 2, and Banker. Two bets are available to participants, a bet on the hand of Player 1 and a bet on the hand of Player 2. Six 52-card decks are mixed together and dealt from a sabot or shoe. Denominations A, 2–9, 10, J, Q, K have values 1, 2–9, 0, 0, 0, 0, respectively, and suits are irrelevant. The total of a hand, comprising two or three cards, is the sum of the values of the cards, modulo 10. In other words, only the final digit of the sum is used to evaluate a hand. Two cards are dealt face down to each of Player 1, Player 2, and Banker. A two-card total of 8 or 9 is a natural. First, if either Banker or both Players have naturals, play ends. If only one Player has a natural and Banker does not, that Player wins the amount bet from Banker, while play continues between the other Player and Banker. Next, if neither Player 1 nor Banker has a natural, Player 1 has the option of drawing a third card. Then, if neither Player 2 nor Banker has a natural, Player 2 has the option of drawing a third card. In either case, the Player must draw on a two-card total of 4 or less and stand on a two-card total of 6 or 7. When his two-card total is 5, he is free to draw or stand as he chooses. Any third card is dealt face up. Finally, if at least one Player and Banker fail to have naturals, Banker has the option of drawing a third card, and his strategy is unconstrained. Bets are then settled, both Player 1 vs. Banker and Player 2 vs. Banker. In both competitions, the higher total wins. Winning bets are paid by Banker at even odds. Losing bets are collected by Banker. Equal totals result in a push (no money changes hands).

There is a subtle point in the rules that is left ambiguous in most descriptions of the game, concerning the information available to Player 2 when he makes his decision. In what Downton and Lockwood [1] called the traditional form of the game, Player 2 sees Player 1’s third card, if any, or that he has a natural. The traditional rule is unambiguously stated in Morehead and Mott-Smith ([11] pp. 522–523), for example. In a more recent variation, Player 2 would know only Player 1’s intention to draw or stand, or that he has a natural. This rule has been used in Great Britain (Downton and Lockwood [1]) and in Monte Carlo (Barnhart ([12] pp. 42–43)).

Thus, we have a three-person zero-sum game. Let us assume, as did Kemeny and Snell [2], that cards are dealt with replacement and that only two-card totals (not compositions) are seen. Player 1 has two pure strategies, draw or stand on two-card totals of 5. Assuming the traditional form of the game, Player 2 also has a draw-or-stand decision on two-card totals of 5 in each of 12 possible situations (Player 1 third-card value 0–9; or stand or natural). Banker then has a draw-or-stand decision in each of $(12\times 12-1)\times 8=1144$ possible situations (12 possibilities for Player 1, 12 for Player 2, and 8 for Banker, except when both Players have naturals). Therefore, the game is a $2\times 2^{12}\times 2^{1144}$ trimatrix game, which is zero-sum. Under the rules of the more recent variation, the game would be $2\times 2^3\times 2^{1144}$.

A simplified model assumes that Player 2 ignores his information about Player 1’s third card (or stand or natural). We then have a $2\times 2\times 2^{1144}$ trimatrix game, which is again zero-sum.

In any case, the payoffs depend on $\theta \in (0,1)$, where the amounts bet on Player 1’s and Player 2’s hands are in the proportions $\theta :1-\theta$. To see intuitively why θ plays an important role, suppose Player 1’s third card is 7 and Player 2’s third card is 8. If Banker were playing baccara chemin de fer against Player 1, he would draw on 0–6 and stand on 7. If he were playing baccara chemin de fer against Player 2, he would draw on 0–2 and stand on 3–7. Notice that Banker would act differently against the two Players if his two-card total were 3–6. In baccarat banque, however, he must make the same move (draw or stand) against both Players. Le Myre ([13] p. 114) called this a “cruel embarrassment” for Banker. The parameter θ determines his correct choice in these conflicting situations.

Downton and Lockwood [1] claimed that the Nash equilibrium is of only academic interest because “it implies an attitude to the game by all three participants, which is unlikely to be realized in practice.” Presumably, they meant that the two Players regard themselves as competing against Banker but not against each other. Downton and Lockwood’s preferred alternative is what we call the independent cooperative equilibrium, that is, the solution of the two-person zero-sum game in which Players 1 and 2, acting independently, form a coalition against Banker. Actually, the idea goes back to Foster [7]. The independence is a requirement of rules not previously stated, which do not permit collaboration between Players 1 and 2. We emphasize that baccara banque is a noncooperative game, so any cooperation between Players 1 and 2 must be limited to their agreement, prior to the game, that they use, independently, the strategies of the independent cooperative equilibrium. But, as we will show, this solution does not necessarily exist, in the sense that the lower and upper values of the game may differ. Nevertheless, the lower value and the Players’ maximin strategy are of relevance to the Players. A third solution, which we call the correlated cooperative equilibrium, always exists. Its value and Banker’s minimax strategy are of relevance to Banker. Here there is no independence constraint, so the implementation of these strategies requires collaboration between Players 1 and 2 during the course of play. Despite the fact that these strategies are technically illegal, this concept will turn out to be a useful one.

Downton and Lockwood [1] assumed the full model (in which Player 2 has $2^{12}$ pure strategies). They evaluated the Players’ behavioral strategies in the independent cooperative equilibrium at $\theta =0.1,0.2,\dots ,0.9$, reporting Banker’s behavioral strategy at $\theta =0.3,0.5,0.7$. They rounded the Players’ mixing probabilities to two decimal places, and rounded Banker’s mixing probabilities to 0 or 1. These results are, with minor exceptions, correct. They also derived the Nash equilibrium at the same level of detail, but these results are incorrect because their algorithm for finding the Nash equilibrium is flawed, as we explain later.

In this paper we focus our attention on the simplified model (in which Player 2 has two pure strategies). In particular, by symmetry we may assume, without loss of generality, that $\theta \in (0,1/2]$. In effect, we interpret Player 1 as the Player on whose hand the smaller amount is bet. We have found, for every $\theta \in (0,1/2]$, the correlated cooperative equilibrium, which is typically unique in behavioral strategies, and the Nash equilibrium, which is often nonunique in behavioral strategies. As for the independent cooperative equilibrium, we have found the maximin strategy of the Players, which is again typically unique in behavioral strategies; the minimax strategy of Banker coincides with the corresponding strategy in the correlated cooperative equilibrium. As Downton and Lockwood [1] put it, the latter Banker strategy “provides a safety-first strategy which guarantees a return to the bank, whatever strategy the players actually adopt.” It is for this reason that we regard the correlated cooperative equilibrium as more useful, from Banker’s perspective, than the Nash equilibrium. On the other hand, from the Players’ perspective, it is arguable whether the independent cooperative equilibrium is more useful than the Nash equilibrium. (The Players’ strategy in the correlated cooperative equilibrium typically requires collaboration and is therefore illegal.)

To mention a few of our findings, the two cooperative equilibria coincide when $\theta \in (9588/37663,55716/128711)\approx (0.254573,0.432877)$, and the Nash equilibrium is nearly the same. Elsewhere, with two exceptions, they differ. The correlated cooperative equilibrium is piecewise continuous in θ but with 109 discontinuities in $(0,1/2)$. The Nash equilibrium is piecewise continuous in θ but with 102 discontinuities in $(0,1/2)$. In both cases, the discontinuities come from Banker’s strategy. The Players’ strategies are continuous in θ in the Nash equilibrium except for one point of discontinuity. In the independent cooperative equilibrium, there are as many as 13 points of discontinuity in the Players’ strategies. The game’s lower value (to the Players) is continuous on $(0,1/2]$ and increasing on $[0,0.496000]$, approximately, and it is maximized at about $0.496000$. The maximum value is about $-0.008679984$. The game’s upper value (to the Players) is continuous on $(0,1/2]$ andincreasing on $(0,0.496088]$, approximately, and it is maximized at about $0.496088$. The maximum value is about $-0.008677388$.

The correlated cooperative equilibrium, the independent cooperative equilibrium, and the Nash equilibrium are not easy to describe precisely. Complete, albeit necessarily lengthy, descriptions are provided in Appendixes A, B, and C of the arXiv version of this paper [14]. Examples of the Mathematica notebook files we used can be downloaded [15,16,17].

As we have already noticed, several British statisticians [1,7,8,9] studied baccara banque in the 1960s and 1970s. Their primary concern was in the fairness of the game and in particular whether it met the standards of the British Gaming Acts of 1960 and 1968. In fact, Foster was hired by a London gambling club specifically to investigate the legality of baccara banque. Our motivation for this paper was different. We wanted to know whether technology not available in the 1970s (specifically, computer algebra software) would allow a more complete analysis of a complex game such as baccara banque than was possible at that time. Baccara banque is a three-player game complicated not just by the large number of strategy profiles but also by the fact that it depends on a continuous parameter θ. It is not a contrived game—it is a relative of baccara chemin de fer, which attracted the interest of game theorists in the 1950s [2]. As we have seen, the work of Downton and Lockwood [1] is the most complete study of the game in the scientific literature. They considered two solution concepts and computed approximate solutions for several values of θ. In this paper we introduce a third solution concept and we compute exact solutions for all θ. How does one even describe a Nash equilibrium, for example, of such a game as a function of θ? Our goal in this paper is to answer questions like this, to clarify the distinctions between the three solution concepts, and in doing so to better understand the game baccara banque.

There have been a number of attempts to quantify Banker’s advantage at baccara banque in the case of equal amounts bet on Players 1 and 2 (i.e., $\theta =1/2$). Le Myre ([13] p. 166) and Boll ([18] pp. 43, 70) made the first estimates (1.11% and 0.87%, resp.), assuming that the Players independently draw on 5 with probability 1/2, and Banker makes a best response. The same assumption was made by Barnhart ([12] p. 81), who obtained 0.84%. None of these authors was familiar with game theory (or with computers). Foster [7] and Downton and Lockwood [1] gave the first game-theoretic estimates (0.87% and 0.85%, resp.), which are in fact accurate to two significant digits under their respective assumptions. Kendall and Murchland [8] gave a simulated estimate (0.819%), which is inaccurate owing to small sample size. Judah and Ziemba [10] determined Banker’s best response when the Players always draw on 5, and obtained 0.81685% (the correct figure is about 0.922104%). Under the simplified model that we are assuming and with $\theta =1/2$, Banker’s advantage is about 0.8677394%, as we will see below.

We conclude this introduction with a historical note. Baccara banque was made famous by the Prince of Wales (later Edward VII) in the Royal Baccarat Scandal of 1891 (Shore [19]). It became the game of choice for wealthy gamblers in 1922 when Nicolas Zographos, a founding member of the Greek Syndicate, announced “Tout va” or unlimited stakes. As he put it (Graves ([20] pp. 27–28)),

My idea is so sensational that practically nobody will play chemin-de-fer. If I guarantee to take any stake of any size, all the millionaires will want to take part in this fantastic party. The biggest gamblers in the world will come to ruin me. I suggest we start at Deauville.

In recent years, both baccara banque and baccara chemin de fer have been largely superseded by a nonstrategic form of the game. Nevertheless, baccara banque is still offered at the Salons Privés of the Casino de Monte-Carlo, Thurs.–Sun. from 5 p.m.

2. Evaluation of the Payoffs

We consider the simplified game, a $2\times 2\times 2^{1144}$ trimatrix game parameterized by $\theta \in (0,1/2]$. Here θ can be interpreted as the proportion of the total amount bet that is bet on Player 1. Both Players and Banker are assumed to know θ. The distribution of the total of a two-card hand is

$$q\left(i\right):=\frac{16+9{\delta }_{i,0}}{{\left(13\right)}^2},i=0,1,\dots ,9,$$

where ${\delta }_{i,j}$ is the Kronecker delta, and the distribution of the value of a card is

$$q^{\prime }\left(k\right):=\frac{1+3{\delta }_{k,0}}{13},k=0,1,\dots ,9.$$

Let $M:\{0,1,\dots \}\mapsto \{0,1,\dots ,9\}$ be the function $M\left(i\right):=\text{Mod}(i,10)$, the remainder when i is divided by 10. We denote Player 1’s pure strategies by 0 (stand on 5) and 1 (draw on 5), and similarly for Player 2’s pure strategies. Banker’s pure strategies are identified with subsets $T\subset \left[\right\{0,1,\dots ,11\}\times \{0,1,\dots ,11\}-\{(11,11)\left\}\right]\times \{0,1,\dots ,7\}$, with T indicating the set of triples $(k_1,k_2,j)$ on which Banker draws. Here $k_1$ is Player 1’s third-card value, $k_2$ is Player 2’s third-card value, and j is Banker’s two-card total. We let $T^c$ denote the complement of T with respect to this product set containing $(12\times 12-1)\times 8=1144$ triples. Here Player third-card values 10 and 11 are code for “stand” and “natural”, respectively.

We define the $2\times 2\times 2^{1144}$ three-dimensional array $\mathit{>a}\left(\theta \right)$ to have $(u_1,u_2,T)$ entry, for $u_1\in \{0,1\}$, $u_2\in \{0,1\}$, and $T\subset \left[\right\{0,1,\dots ,11\}\times \{0,1,\dots ,11\}-\{(11,11)\left\}\right]\times \{0,1,\dots ,7\}$, equal to

$$\begin{array}{cc}& a_{u_1,u_2,T}\left(\theta \right)\hfill \\ & =\left(\sum _{i_1=0}^9\sum _{i_2=0}^9\sum _{j=8}^9+\sum _{i_1=8}^9\sum _{i_2=8}^9\sum _{j=0}^7\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)[\theta \text{sgn}(i_1-j)+(1-\theta )\text{sgn}(i_2-j)]\hfill \end{array}$$

(1)

$$\begin{array}{cc}& +\sum _{i_1=8}^9\sum _{i_2=0}^{4+u_2}\sum _{j=0}^7\sum _{k_2=0}^9\sum _{l=0}^9{1}_T\left((11,k_2,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_2\right)q^{\prime }\left(l\right)\hfill \\ & [\theta +(1-\theta )\text{sgn}(M(i_2+k_2)-M(j+l))]\hfill \end{array}$$

(2)

$$\begin{array}{cc}& +\sum _{i_1=8}^9\sum _{i_2=0}^{4+u_2}\sum _{j=0}^7\sum _{k_2=0}^9{1}_{T^c}\left((11,k_2,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_2\right)[\theta +(1-\theta )\text{sgn}(M(i_2+k_2)-j)]\hfill \end{array}$$

(3)

$$\begin{array}{cc}& +\sum _{i_1=8}^9\sum _{i_2=5+u_2}^7\sum _{j=0}^7\sum _{l=0}^9{1}_T\left((11,10,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(l\right)[\theta +(1-\theta )\text{sgn}(i_2-M(j+l))]\hfill \end{array}$$

(4)

$$\begin{array}{cc}& +\sum _{i_1=8}^9\sum _{i_2=5+u_2}^7\sum _{j=0}^7{1}_{T^c}\left((11,10,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)[\theta +(1-\theta )\text{sgn}(i_2-j)]\hfill \end{array}$$

(5)

$$\begin{array}{cc}& +\sum _{i_1=0}^{4+u_1}\sum _{i_2=8}^9\sum _{j=0}^7\sum _{k_1=0}^9\sum _{l=0}^9{1}_T\left((k_1,11,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_1\right)q^{\prime }\left(l\right)\hfill \\ & [\theta \text{sgn}(M(i_1+k_1)-M(j+l))+(1-\theta )]\hfill \end{array}$$

(6)

$$\begin{array}{cc}& +\sum _{i_1=0}^{4+u_1}\sum _{i_2=8}^9\sum _{j=0}^7\sum _{k_1=0}^9{1}_{T^c}\left((k_1,11,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_1\right)[\theta \text{sgn}(M(i_1+k_1)-j)+(1-\theta )]\hfill \end{array}$$

(7)

$$\begin{array}{cc}& +\sum _{i_1=5+u_1}^7\sum _{i_2=8}^9\sum _{j=0}^7\sum _{l=0}^9{1}_T\left((10,11,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(l\right)[\theta \text{sgn}(i_1-M(j+l))+(1-\theta )]\hfill \end{array}$$

(8)

$$\begin{array}{cc}& +\sum _{i_1=5+u_1}^7\sum _{i_2=8}^9\sum _{j=0}^7{1}_{T^c}\left((10,11,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)[\theta \text{sgn}(i_1-j)+(1-\theta )]\hfill \end{array}$$

(9)

$$\begin{array}{cc}& +\sum _{i_1=0}^{4+u_1}\sum _{i_2=0}^{4+u_2}\sum _{j=0}^7\sum _{k_1=0}^9\sum _{k_2=0}^9\sum _{l=0}^9{1}_T\left((k_1,k_2,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_1\right)q^{\prime }\left(k_2\right)q^{\prime }\left(l\right)\hfill \\ & [\theta \text{sgn}(M(i_1+k_1)-M(j+l))+(1-\theta )\text{sgn}(M(i_2+k_2)-M(j+l))]\hfill \end{array}$$

(10)

$$\begin{array}{cc}& +\sum _{i_1=0}^{4+u_1}\sum _{i_2=0}^{4+u_2}\sum _{j=0}^7\sum _{k_1=0}^9\sum _{k_2=0}^9{1}_{T^c}\left((k_1,k_2,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_1\right)q^{\prime }\left(k_2\right)\hfill \\ & [\theta \text{sgn}(M(i_1+k_1)-j)+(1-\theta )\text{sgn}(M(i_2+k_2)-j)]\hfill \end{array}$$

(11)

$$\begin{array}{cc}& +\sum _{i_1=0}^{4+u_1}\sum _{i_2=5+u_2}^7\sum _{j=0}^7\sum _{k_1=0}^9\sum _{l=0}^9{1}_T\left((k_1,10,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_1\right)q^{\prime }\left(l\right)\hfill \\ & [\theta \text{sgn}(M(i_1+k_1)-M(j+l))+(1-\theta )\text{sgn}(i_2-M(j+l))]\hfill \end{array}$$

(12)

$$\begin{array}{cc}& +\sum _{i_1=0}^{4+u_1}\sum _{i_2=5+u_2}^7\sum _{j=0}^7\sum _{k_1=0}^9{1}_{T^c}\left((k_1,10,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_1\right)\hfill \\ & [\theta \text{sgn}(M(i_1+k_1)-j)+(1-\theta )\text{sgn}(i_2-j)]\hfill \end{array}$$

(13)

$$\begin{array}{cc}& +\sum _{i_1=5+u_1}^7\sum _{i_2=0}^{4+u_2}\sum _{j=0}^7\sum _{k_2=0}^9\sum _{l=0}^9{1}_T\left((10,k_2,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_2\right)q^{\prime }\left(l\right)\hfill \\ & [\theta \text{sgn}(i_1-M(j+l))+(1-\theta )\text{sgn}(M(i_2+k_2)-M(j+l))]\hfill \end{array}$$

(14)

$$\begin{array}{cc}& +\sum _{i_1=5+u_1}^7\sum _{i_2=0}^{4+u_2}\sum _{j=0}^7\sum _{k_2=0}^9{1}_{T^c}\left((10,k_2,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(k_2\right)\hfill \\ & [\theta \text{sgn}(i_1-j)+(1-\theta )\text{sgn}(M(i_2+k_2)-j)]\hfill \end{array}$$

(15)

$$\begin{array}{cc}& +\sum _{i_1=5+u_1}^7\sum _{i_2=5+u_2}^7\sum _{j=0}^7\sum _{l=0}^9{1}_T\left((10,10,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)q^{\prime }\left(l\right)\hfill \\ & [\theta \text{sgn}(i_1-M(j+l))+(1-\theta )\text{sgn}(i_2-M(j+l))]\hfill \end{array}$$

(16)

$$\begin{array}{cc}& +\sum _{i_1=5+u_1}^7\sum _{i_2=5+u_2}^7\sum _{j=0}^7{1}_{T^c}\left((10,10,j)\right)q\left(i_1\right)q\left(i_2\right)q\left(j\right)[\theta \text{sgn}(i_1-j)+(1-\theta )\text{sgn}(i_2-j)].\hfill \end{array}$$

(17)

Term 1 corresponds to the case in which Banker and/or both Players have naturals. Terms 2–5 (resp., 6–9) correspond to the case in which only Player 1 (resp., only Player 2) has a natural. Terms 10–17 correspond to the case in which there are no naturals.

Notice that, in the three-person zero-sum game, $\theta a_{u_1,u_2,T}\left(1\right)$ is the payoff to Player 1, $(1-\theta )a_{u_1,u_2,T}\left(0\right)$ is the payoff to Player 2, and

$$-[\theta a_{u_1,u_2,T}\left(1\right)+(1-\theta )a_{u_1,u_2,T}\left(0\right)]=-a_{u_1,u_2,T}\left(\theta \right)$$

is the payoff to Banker, all measured in units of total amount bet.

3. Correlated Cooperative Equilibrium

We first find the correlated cooperative equilibrium, that is, the solution of the two-person zero-sum game in which the two Players form a coalition against Banker and are not constrained to act independently. This is a $2^2\times 2^{1144}$ matrix game with payoff matrix having entries $a_{u_1,u_2,T}\left(\theta \right)$ as defined in Section 2. For fixed $\theta \in (0,1/2]$, we can obtain a solution as follows: Given an arbitrary mixture $\mathit{p}=(p_{00},p_{01},p_{10},p_{11})$ of the four pure strategies of the Players, minimize

$$p_{00}{a}_{0,0,T}\left(\theta \right)+p_{01}{a}_{0,1,T}\left(\theta \right)+p_{10}{a}_{1,0,T}\left(\theta \right)+p_{11}{a}_{1,1,T}\left(\theta \right)$$

as a function of T (this is Banker’s best response $T=T_{\theta }\left(\mathit{p}\right)$; for information sets where Banker is indifferent, Banker can either draw or stand; for specificity we let Banker stand in such cases), and then maximize

$$E_{\theta }\left(\mathit{p}\right):=p_{00}{a}_{0,0,T_{\theta }\left(\mathit{p}\right)}\left(\theta \right)+p_{01}{a}_{0,1,T_{\theta }\left(\mathit{p}\right)}\left(\theta \right)+p_{10}{a}_{1,0,T_{\theta }\left(\mathit{p}\right)}\left(\theta \right)+p_{11}{a}_{1,1,T_{\theta }\left(\mathit{p}\right)}\left(\theta \right)$$

as a function of p. The maximizing p is the Players’ maximin strategy, and the maximal value of $E_{\theta }\left(\mathit{p}\right)$ is the value of the game, assuming θ is fixed.

For a given Banker information set $(k_1,k_2,j)$ ($k_1=$ Player 1’s third-card value, $k_2=$ Player 2’s third-card value, $j=$ Banker’s two-card total), Banker’s optimal move (draw or stand) may or may not depend on the Players’ mixed strategy p. In fact, for only m of the 1144 information sets, where $52\le m\le 69$, is there dependence on p.

Let us elaborate on this point. First, assume that $\theta =1/2$. Suppose Player 1’s third card is 7 and Player 2’s third card is 8 (as in the example mentioned in Section 1). We can compute, for each Banker total $j\in \{0,1,\dots ,7\}$, the difference between the Players’ expectation when Banker draws and when Banker stands. We find that Banker draws with totals $0,1,2$, regardless of p, and stands with total 7, regardless of p, but may draw or stand with totals $3,4,5,6$, depending on p, accounting for four undetermined cases. Doing the same analysis for the 142 other possible pairs of Player 1 and 2 third cards, we find that there are an additional 64 undetermined cases. Thus, $m=68$ when $\theta =1/2$. On the other hand, it is easy to see that $m=52$ when θ is near 0 but positive. In that case Banker plays baccara chemin de fer against Player 2 and ignores Player 1. In baccara chemin de fer it is well known that $m=4$. This must be multiplied by 12 (possible Player 1 third cards), and there are an additional four cases when Player 2 has a natural, in which Banker plays baccara chemin de fer against Player 1. Thus, $m=52$ for θ positive and small enough. In general, we have found that $52\le m\le 69$.

Writing $p_{11}=1-p_{00}-p_{01}-p_{10}$, it follows that

$$\begin{array}{cc}\hfill E_{\theta }\left(\mathit{p}\right)& =a_0+b_0{p}_{00}+c_0{p}_{01}+d_0{p}_{10}\hfill \\ & +\sum _{i=1}^{m}min(a_i+b_i{p}_{00}+c_i{p}_{01}+d_i{p}_{10},a_i^{\prime }+b_i^{\prime }{p}_{00}+c_i^{\prime }{p}_{01}+d_i^{\prime }{p}_{10}),\hfill \end{array}$$

where the constants $a_i,b_i,c_i,d_i,a_i^{\prime },b_i^{\prime },c_i^{\prime },d_i^{\prime }$ are computable rational numbers (if θ is rational) depending on θ.

For fixed θ, the function $E_{\theta }\left(\mathit{p}\right)$ is concave in p and its maximum occurs at an intersection of three of the $m+4$ planes

$$a_i+b_i{p}_{00}+c_i{p}_{01}+d_i{p}_{10}=a_i^{\prime }+b_i^{\prime }{p}_{00}+c_i^{\prime }{p}_{01}+d_i^{\prime }{p}_{10},1\le i\le m,$$

(18)

and $p_{00}=0$, $p_{01}=0$, $p_{10}=0$, and $1-p_{00}-p_{01}-p_{10}=0$. The m planes in Equation (18) might be called “indifference planes”. This leads to a simple algorithm to find the optimal p. For each of the $\left(\genfrac{}{}{0pt}{}{m+4}{3}\right)$ potential points p just mentioned, check whether $p_{00}\ge 0$, $p_{01}\ge 0$, $p_{10}\ge 0$, and $1-p_{00}-p_{01}-p_{10}\ge 0$, and if so, evaluate $E_{\theta }\left(\mathit{p}\right)$. Then determine at which such p the value $E_{\theta }\left(\mathit{p}\right)$ is largest and if it isuniquely so.

In the case $\theta =1/2$, the number of summands is $m=68$, hence there are $\left(\genfrac{}{}{0pt}{}{72}{3}\right)=59640$ potential points of intersection p. Of these only 2364 belong to the three-dimensional simplex and there is a unique maximum at

$$\mathit{p}=(p_{00},p_{01},p_{10},p_{11})=\left(0,\frac{110}{543},\frac{110}{543},\frac{323}{543}\right);$$

in addition, $E_{1/2}\left(\mathit{p}\right)=-16655514960/\left[181{\left(13\right)}^9\right]\approx -0.008677394$ there. The point p is the intersection of three planes, the two indifference planes for $(6,10,6)$ (Player 1’s third card is 6, Player 2 stands, Banker’s two-card total is 6) and $(10,6,6)$ and the plane $p_{00}=0$. Banker’s best response is displayed in Table 1.

Table 1. Banker’s strategy in the correlated cooperative equilibrium when $\theta =1/2$. Specifically the table displays Banker’s maximum drawing total as a function of Player 1’s and Player 2’s third-card values. For example, if Player 1’s third card is 7 and Player 2’s third card is 8, the entry 3 signifies that Banker draws on 0–3 and stands on 4–7. 5+ signifies that Banker draws on 0–5, mixes on 6, and stands on 7. The table is symmetric in Player 1 and Player 2. Similar entries are shaded similarly for readability.

Player 1’s Third-Card Value	Player 2’s Third-Card Value (10 = Stand, 11 = Natural)
	0	1	2	3	4	5	6	7	8	9	10	11
0	3	3	3	4	4	4	4	3	3	3	5	3
1	3	3	4	4	4	4	4	4	3	3	5	3
2	3	4	4	4	4	4	5	4	3	3	5	4
3	4	4	4	4	4	5	5	4	4	3	5	4
4	4	4	4	4	5	5	5	5	4	4	5	5
5	4	4	4	5	5	5	5	5	5	4	5	5
6	4	4	5	5	5	5	6	6	5	4	5+	6
7	3	4	4	4	5	5	6	6	3	3	6	6
8	3	3	3	4	4	5	5	3	2	3	5	2
9	3	3	3	3	4	4	4	3	3	3	5	3
10	5	5	5	5	5	5	5+	6	5	5	5	5
11	3	3	4	4	5	5	6	6	2	3	5

Table 1. Banker’s strategy in the correlated cooperative equilibrium when $\theta =1/2$. Specifically the table displays Banker’s maximum drawing total as a function of Player 1’s and Player 2’s third-card values. For example, if Player 1’s third card is 7 and Player 2’s third card is 8, the entry 3 signifies that Banker draws on 0–3 and stands on 4–7. 5+ signifies that Banker draws on 0–5, mixes on 6, and stands on 7. The table is symmetric in Player 1 and Player 2. Similar entries are shaded similarly for readability.

Player 1’s Third-Card Value	Player 2’s Third-Card Value (10 = Stand, 11 = Natural)
	0	1	2	3	4	5	6	7	8	9	10	11
0	3	3	3	4	4	4	4	3	3	3	5	3
1	3	3	4	4	4	4	4	4	3	3	5	3
2	3	4	4	4	4	4	5	4	3	3	5	4
3	4	4	4	4	4	5	5	4	4	3	5	4
4	4	4	4	4	5	5	5	5	4	4	5	5
5	4	4	4	5	5	5	5	5	5	4	5	5
6	4	4	5	5	5	5	6	6	5	4	5+	6
7	3	4	4	4	5	5	6	6	3	3	6	6
8	3	3	3	4	4	5	5	3	2	3	5	2
9	3	3	3	3	4	4	4	3	3	3	5	3
10	5	5	5	5	5	5	5+	6	5	5	5	5
11	3	3	4	4	5	5	6	6	2	3	5

There are two information sets, $(6,10,6)$ and $(10,6,6)$, at which Banker is indifferent. This leads to a $4\times 4$ matrix game with payoff matrix

$$\mathit{A}:=-\frac{8}{{\left(13\right)}^9}\left(\begin{array}{cccc}11815316& 11681780& 11681780& 11548244\\ 11621229& 11427789& 11680301& 11486861\\ 11621229& 11680301& 11427789& 11486861\\ 11421510& 11467270& 11467270& 11513030\end{array}\right).$$

(19)

Rows correspond to pure strategies of the Players, SS, SD, DS, and DD on 5 by Player 1 and Player 2. Columns correspond to pure strategies of Banker, which follow Table 1 except for SS, SD, DS, DD on $(6,10,6)$ and $(10,6,6)$. This game has two extreme equilibria $(\mathit{p},\mathit{q})$, where p is as above, and

$$\mathit{q}=(q_{00},q_{01},q_{10},q_{11})=\left(0,\frac{671}{5792},\frac{671}{5792},\frac{2225}{2896}\right)$$

or

$$\mathit{q}=(q_{00},q_{01},q_{10},q_{11})=\left(\frac{671}{5792},0,0,\frac{5121}{5792}\right).$$

The corresponding Banker behavioral strategies are the same for both equilibria,

$$\begin{array}{cc}\hfill P\left(\text{Banker}\text{draws}\text{on}\right(6,10,6\left)\right)& =q_{10}+q_{11}=5121/5792,\hfill \\ \hfill P\left(\text{Banker}\text{draws}\text{on}\right(10,6,6\left)\right)& =q_{01}+q_{11}=5121/5792.\hfill \end{array}$$

This completes the derivation in the case $\theta =1/2$.

Next, we extend this solution to the largest θ-interval in $(0,1/2]$ for which the best response coincides with Table 1. The maximum of $E_{1/2}\left(\mathit{p}\right)$ found above occurred at the intersection of three planes, the two indifference planes for $(6,10,6)$ and $(10,6,6)$ and the plane $p_{00}=0$. The intersection of the three corresponding θ-dependent planes occurs at

$$\begin{array}{cc}\mathit{p}\left(\theta \right)& :=(0,\frac{10(-3171-17332\theta +20640{\theta }^2)}{3[901-443072\theta (1-\theta \left)\right]},\frac{10(137-23948\theta +20640{\theta }^2)}{3[901-443072\theta (1-\theta \left)\right]},\hfill \\ & \frac{33043-916416\theta (1-\theta )}{3[901-443072\theta (1-\theta \left)\right]}).\hfill \end{array}$$

With this choice of $\mathit{p}\left(\theta \right)$ we can ask, what is the smallest θ for which Banker’s best response coincides with Table 1? Checking each of the 1144 Banker information sets, we find that the first change occurs at $(2,5,5)$. The contribution to the difference between the Players’ expectation when Banker draws and the Players’ expectation when Banker stands (due to $(2,5,5)$) vanishes at ${\theta }_{*}\approx 0.496088$; more precisely, ${\theta }_{*}$ is a root of the cubic polynomial $6896169-1190915420\theta +3549548480{\theta }^2-2372477184{\theta }^3$.

On the interval $({\theta }_{*},1/2]$ Banker mixes at $(6,10,6)$ and $(10,6,6)$, and it remains to determine the mixing probabilities. With $\mathit{A}\left(\theta \right)$ denoting the θ-dependent version of Equation (19), the value $v\left(\theta \right)$ of the game satisfies

$$\mathit{p}\left(\theta \right)\mathit{A}\left(\theta \right)=\left(v\right(\theta ),v(\theta ),v(\theta ),v(\theta \left)\right).$$

We find that

$$v\left(\theta \right)=-\frac{80[2421541645-515181045616\theta (1-\theta \left)\right]}{{\left(13\right)}^9[901-443072\theta (1-\theta )]}.$$

(20)

Since the Players have three strategies active, we seek a $3\times 3$ kernel, and two of the four possibilities give nonnegative Banker mixing probabilities, the ones corresponding to $q_{00}\left(\theta \right)=0$ and to $q_{01}\left(\theta \right)=0$. The resulting two solutions of

$$\mathit{A}\left(\theta \right)\mathit{q}{\left(\theta \right)}^{\text{T}}=\left(x\left(\theta \right),v\left(\theta \right),v\left(\theta \right),{v\left(\theta \right)}^{\text{T}}\right),$$

where x(θ) ≤ v(θ), give the same Banker behavioral strategies, namely,

$$\begin{array}{cc}\hfill P\left(\text{Banker}\text{draws}\text{on}\right(6,10,6\left)\right)& =q_{10}\left(\theta \right)+q_{11}\left(\theta \right)=\frac{21311777-393439433\theta +620812136{\theta }^2}{208[901-443072\theta (1-\theta \left)\right]},\hfill \\ \hfill P\left(\text{Banker}\text{draws}\text{on}\right(10,6,6\left)\right)& =q_{01}\left(\theta \right)+q_{11}\left(\theta \right)=\frac{248684480-848184839\theta +620812136{\theta }^2}{208[901-443072\theta (1-\theta \left)\right]}.\hfill \end{array}$$

This completes the derivation for the interval (θ_*, 1/2].

Repeating this process (from right to left, or from left to right), we find that there are 110 such intervals in (0, 1/2]. That is, there exist 0 = θ₀ < θ₁ < θ₂ < … θ₁₀₉ = θ₈ < θ₁₁₀ = 1/2 such that the correlated cooperative equilibrium is a rational function of θ on interval i, namely (θ_i−1, θ_i), for i = 1, 2, …, 110. Each θ_i is a root of a polynomial of degree 4 or less. At the boundary points, discontinuities occur in Banker’s strategy.

There are two types of intervals, those in which the number of Banker information sets at which Banker mixes is two and those in which it is three. When it is two, the resulting 4 × 4 game has a 3 × 3 kernel. This is a consequence of the fact that the payoff matrix has the form

$$\left(\begin{array}{cccc}{a}_1& a_1+b_1& a_1+c_1& a_1+b_1+c_1\\ a_2& a_2+b_2& a_2+c_2& a_2+b_2+c_2\\ a_3& a_3+b_3& a_3+c_3& a_3+b_3+c_3\\ a_4& a_4+b_4& a_4+c_4& a_4+b_4+c_4\end{array}\right)$$

When it is three, the resulting 4 × 8 game has a 4 × 4 kernel. For intervals 1–41, p₁₁(θ) = 0; for intervals 42–46, 102–103, and 107–110, p₀₀(θ) = 0; for internals 61-66, p₁₀(θ) = 0; and for all remaining intervals the Players have all strategies active. In all cases, despite the correlated cooperative equilibrium being nonunique in mixed strategies, it is unique in behavioral strategies. (This can be proved algebraically.) However, there are exceptions. At each boundary point, the solutions from both adjacent intervals apply, so there is nonuniqueness of Banker behavioral strategies at the 109 such θ.

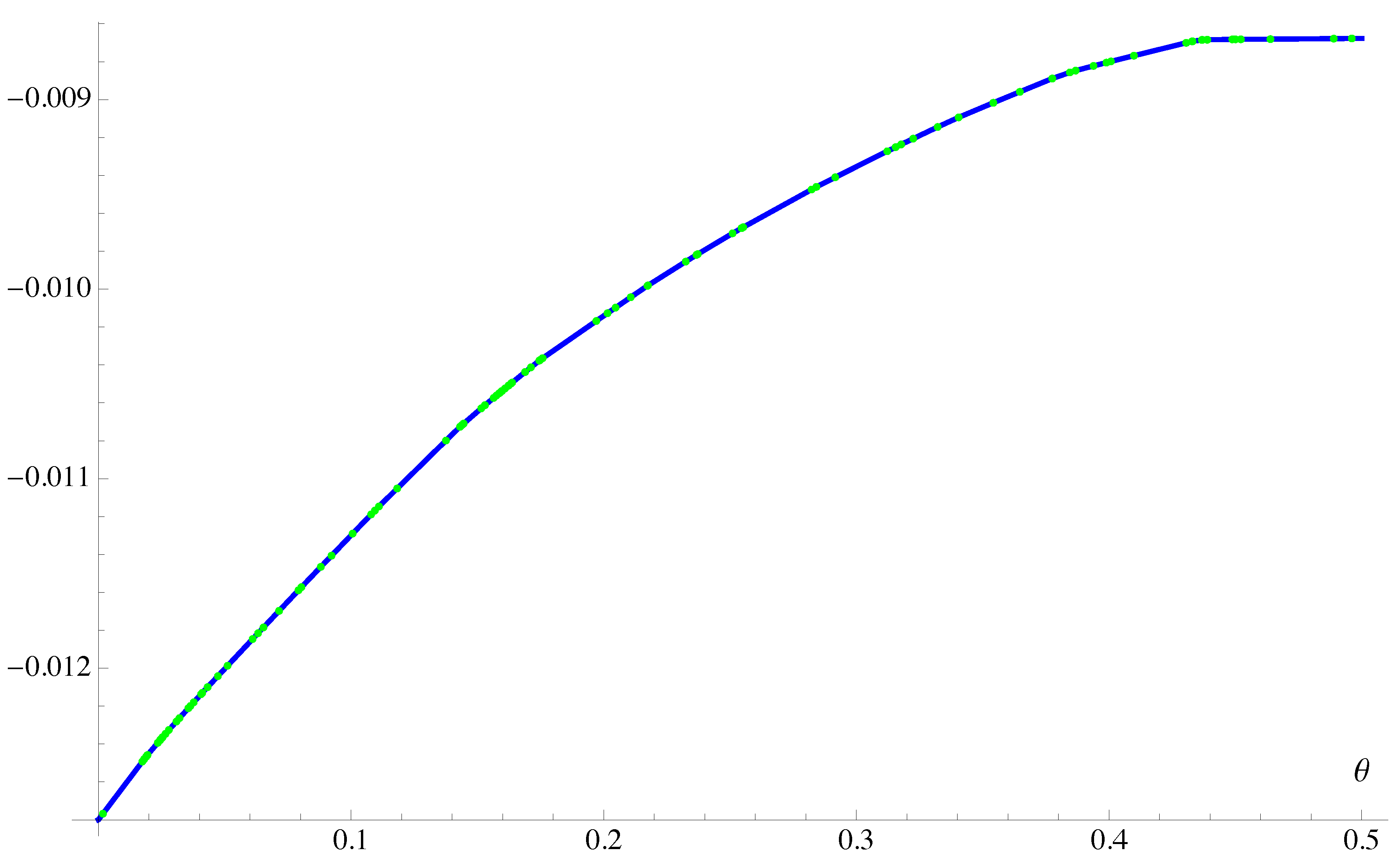
The value function is continuous on $(0,1/2]$, increasing on $(0,{\theta }_{*}]$ and decreasing on $[{\theta }_{*},1/2]$ (see Equation (20)). Its maximum value is $v\left({\theta }_{*}\right)\approx -0.008677388$. See Figure 1 for a sketch of the graph.

Figure 1. The graph of the value of the game to the Players (or minus the value to Banker), assuming the correlated cooperative equilibrium.

Figure 1. The graph of the value of the game to the Players (or minus the value to Banker), assuming the correlated cooperative equilibrium.

Of particular interest are intervals 75–97, in which the Players’ strategy at equilibrium is$p_{00}\left(\theta \right)=4/121$, $p_{01}\left(\theta \right)=p_{10}\left(\theta \right)=18/121$, and $p_{11}\left(\theta \right)=81/121$, that is, Players 1 and 2 play independently, drawing on 5 with probabilities $p_1\left(\theta \right)=p_2\left(\theta \right)=9/11$. In this case, the correlated and independent cooperative equilibria coincide, as we demonstrate in Proposition 1 below.

4. Independent Cooperative Equilibrium

Let $X_1$ and $X_2$ be Player 1’s and Player 2’s two-card totals, and let $X_1^{\prime }$ and $X_2^{\prime }$ be their third-card values. Let Y be Banker’s two-card total, and let $Y^{\prime }$ be Banker’s third-card value. Let $p_1$ be the probability that Player 1 draws on 5, and let $p_2$ be the probability that Player 2 draws on 5. Let $U_1$ and $U_2$ be the mixed strategies of Players 1 and 2, that is, random variables with distributions $P(U_1=1)=p_1=1-P(U_1=0)$ and $P(U_2=1)=p_2=1-P(U_2=0)$. Assume they are independent of $X_1,X_2,Y,X_1^{\prime },X_2^{\prime },Y^{\prime }$ but not necessarily of each other.

Then Equation (2.1b) of Downton and Lockwood [1], which represents the conditional expected gain to Banker when he draws (measured in units of total amount bet), given that Player 1’s third-card value is $k_1\in \{0,1,\dots ,9\}$, Player 2’s third-card value is $k_2\in \{0,1,\dots ,9\}$, and Banker’s two-card total is $j\in \{0,1,\dots ,7\}$, can be writte

$$\begin{array}{cc}\hfill e(k_1,k_2,j;p_1,p_2)& =\theta E[\mathrm{sgn}(M(Y+Y^{\prime })-M(X_1+X_1^{\prime }))\mid X_1\le 4+U_1,X_1^{\prime }=k_1,Y=j]\hfill \\ & +(1-\theta )E[\mathrm{sgn}(M(Y+Y^{\prime })-M(X_2+X_2^{\prime }))\mid X_2\le 4+U_2,X_2^{\prime }=k_2,Y=j].\hfill \end{array}$$

Generally, one does not add two conditional expectations when they are conditioned on different events. However, if $U_1$ and $U_2$ are independent, then

$$\begin{array}{cc}& e(k_1,k_2,j;p_1,p_2)\hfill \\ & =\theta E[\mathrm{sgn}(M(Y+Y^{\prime })-M(X_1+X_1^{\prime }))\mid X_1\le 4+U_1,X_1^{\prime }=k_1,Y=j,\hfill \\ & X_2\le 4+U_2,X_2^{\prime }=k_2]\hfill \\ & +(1-\theta )E[\mathrm{sgn}(M(Y+Y^{\prime })-M(X_2+X_2^{\prime }))\mid X_2\le 4+U_2,X_2^{\prime }=k_2,Y=j,\hfill \\ & X_1\le 4+U_1,X_1^{\prime }=k_1]\hfill \\ & =E[\theta \mathrm{sgn}(M(Y+Y^{\prime })-M(X_1+X_1^{\prime }))+(1-\theta )\mathrm{sgn}(M(Y+Y^{\prime })-M(X_2+X_2^{\prime }))\mid \hfill \\ & X_1\le 4+U_1,X_2\le 4+U_2,X_1^{\prime }=k_1,X_2^{\prime }=k_2,Y=j],\hfill \end{array}$$

which is evidently what was intended. Here we have used the simple fact that

$$E[X\mid A]=E[X\mid A\cap B]\text{if}{1}_B\text{is}\text{independent}\text{of}{1}_A\text{and}X.$$

The point is that Downton and Lockwood [1] effectively assumed that Player 1 and Player 2 act independently, even though they make no such assumption explicitly. Thus, their “co-operative optimum strategy” is what we call the independent cooperative equilibrium.

Let us find the independent cooperative equilibrium, that is, the solution of the two-person zero-sum game in which the two Players form a coalition against Banker but are constrained to act independently. This is a $2^2\times 2^{1144}$ matrix game with payoff matrix having entries $a_{u_1,u_2,T}\left(\theta \right)$ as defined in Section 2, but mixtures of the four pure strategies of the Players must have the form $((1-p_1)(1-p_2),(1-p_1)p_2,p_1(1-p_2),p_1{p}_2)$ for some $p_1,p_2\in [0,1]$. The following proposition shows that the solution need not exist, in the sense that the lower and upper values of the game may differ. (For a closely related result, see Maschler et al. ([21] p. 179).) Let ${\Delta }_n:=\{\mathit{p}=(p_1,\dots ,p_n)\in {[0,1]}^n:p_1+\cdots +p_n=1\}$.

Proposition 1 Given $n\ge 2$, let A be the payoff matrix for a $4\times n$ matrix game, with the additional constraint that the row player is required to use a mixed strategy of the form

$$\mathit{p}=((1-p_1)(1-p_2),(1-p_1)p_2,p_1(1-p_2),p_1{p}_2)$$

for some $p_1,p_2\in [0,1]$. Let us describe such elements of ${\Delta }_4$ as belonging to ${\Delta }_2\times {\Delta }_2$. Then the lower value of the game is

$$\underline{v}=\underset{\mathit{p}\in {\Delta }_2\times {\Delta }_2}{max}\underset{\mathit{q}\in {\Delta }_n}{min}\mathit{p}\mathit{A}{\mathit{q}}^{⊺}=\underset{\mathit{p}\in {\Delta }_2\times {\Delta }_2}{max}\underset{1\le j\le n}{min}{\left(\mathit{p}\mathit{A}\right)}_j,$$

(21)

while the upper value of the game is

$$\overline{v}=\underset{\mathit{p}\in {\Delta }_4}{max}\underset{\mathit{q}\in {\Delta }_n}{min}\mathit{p}\mathit{A}{\mathit{q}}^{⊺}=\underset{\mathit{p}\in {\Delta }_4}{max}\underset{1\le j\le n}{min}{\left(\mathit{p}\mathit{A}\right)}_j,$$

(22)

which is equal to the value of the unconstrained game. In particular, $\underline{v}=\overline{v}$ if and only if the maximum in Equation (22) occurs at a point in ${\Delta }_2\times {\Delta }_2$.

Proof. Equation (21) is by definition. The value of the unconstrained game is, by the minimax theorem,

$$\underset{\mathit{p}\in {\Delta }_4}{max}\underset{\mathit{q}\in {\Delta }_n}{min}\mathit{p}\mathit{A}{\mathit{q}}^{⊺}=\underset{\mathit{q}\in {\Delta }_n}{min}\underset{\mathit{p}\in {\Delta }_4}{max}\mathit{p}\mathit{A}{\mathit{q}}^{⊺}=\underset{\mathit{q}\in {\Delta }_n}{min}\underset{\mathit{p}\in {\Delta }_2\times {\Delta }_2}{max}\mathit{p}\mathit{A}{\mathit{q}}^{⊺}$$

(23)

the right side of which is, by definition, the upper value of the constrained game. The last equality uses the fact that a linear function has the same maximum over Δ₄ as over Δ₂ × Δ₂ because the latter contains the extreme points of the former (namely (0, 0, 0, 1), (0, 0, 1, 0), (0, 1, 0, 0), (1, 0, 0, 0).

Remark 1. A mixed strategy p for the row player that achieves the maximum in Equation (21) is called a maximin strategy, and it assures the row player of an expected gain of at least v. A mixed strategy q for the column player that achieves the minimum in the center or on the right side of Equation (23) is called a minimax strategy, and it assures the column player of an expected loss of at most $\stackrel{\_}{v}$.

For fixed $\theta \in (0,1/2]$, we can obtain the Players’ maximin strategy and the lower value of the game as follows: Given an arbitrary probabilities $p_1$ and $p_2$ (of drawing on 5 for Player 1 and Player 2), minimize

$$(1-p_1)(1-p_2)a_{0,0,T}\left(\theta \right)+(1-p_1)p_2{a}_{0,1,T}\left(\theta \right)+p_1(1-p_2)a_{1,0,T}\left(\theta \right)+p_1{p}_2{a}_{1,1,T}\left(\theta \right)$$

as a function of T (this is Banker’s best response $T=T_{\theta }(p_1,p_2)$), and then maximize

$$\begin{array}{cc}\hfill E_{\theta }^0(p_1,p_2)& :=(1-p_1)(1-p_2)a_{0,0,T_{\theta }(p_1,p_2)}\left(\theta \right)+(1-p_1)p_2{a}_{0,1,T_{\theta }(p_1,p_2)}\left(\theta \right)\hfill \\ & +p_1(1-p_2)a_{1,0,T_{\theta }(p_1,p_2)}\left(\theta \right)+p_1{p}_2{a}_{1,1,T_{\theta }(p_1,p_2)}\left(\theta \right)\hfill \end{array}$$

(24)

as a function of $(p_1,p_2)$. The maximizing $(p_1,p_2)$ is the Players’ maximin strategy, and the maximal value of $E_{\theta }^0(p_1,p_2)$ is the lower value of the game, assuming θ is fixed. (Cf. Equation (21).)

For a given Banker information set $(k_1,k_2,j)$, Banker’s optimal move (draw or stand) may or may not depend on the Players’ strategy $(p_1,p_2)$. In fact, for only m of the 1144 information sets, where $52\le m\le 69$, is there dependence on $(p_1,p_2)$. It follows that $E_{\theta }^0(p_1,p_2)$ has the form

$$\begin{array}{cc}\hfill E_{\theta }^0(p_1,p_2)& =E_{\theta }((1-p_1)(1-p_2),(1-p_1)p_2,p_1(1-p_2),p_1{p}_2)\hfill \\ & =a_0+b_0{p}_1+c_0{p}_2+d_0{p}_1{p}_2\hfill \\ & +\sum _{i=1}^{m}min(a_i+b_i{p}_1+c_i{p}_2+d_i{p}_1{p}_2,a_i^{\prime }+b_i^{\prime }{p}_1+c_i^{\prime }{p}_2+d_i^{\prime }{p}_1{p}_2),\hfill \end{array}$$

where the constants $a_i,b_i,c_i,d_i,a_i^{\prime },b_i^{\prime },c_i^{\prime },d_i^{\prime }$ are computable rational numbers (if θ is rational) depending on θ—but they are not the same as the ones in Section 3.

For fixed θ, the function $E_{\theta }^0(p_1,p_2)$, although it depends on only two variables instead of three, is more complicated than $E_{\theta }\left(\mathit{p}\right)$. It is not concave, and its maximum does not necessarily occur at an intersection of two of the $m+4$ curves

$$a_i+b_i{p}_1+c_i{p}_2+d_i{p}_1{p}_2=a_i^{\prime }+b_i^{\prime }{p}_1+c_i^{\prime }{p}_2+d_i^{\prime }{p}_1{p}_2,1\le i\le m,$$

(25)

and $p_1=0$, $p_1=1$, $p_2=0$, and $p_2=1$. Its maximum could occur at a point on a single curve but typically occurs at a point of intersection. The m curves in Equation (25) might be called “indifference curves”. This leads to an algorithm to find the optimal $(p_1,p_2)$. For each of the $2\left(\genfrac{}{}{0pt}{}{m+4}{2}\right)$ potential points $(p_1,p_2)$ just mentioned, check whether $0\le p_1\le 1$ and $0\le p_2\le 1$, and if so, evaluate $E_{\theta }^0(p_1,p_2)$. Then determine at which such $(p_1,p_2)$ the value $E_{\theta }^0(p_1,p_2)$ is largest and if it is uniquely so. Finally, confirm that this gives a global maximum. (If it does not, look for a global maximum along one of the $m+4$ curves. The global maximum cannot occur at a point that avoids all of these curves because 1, $p_1$, $p_2$, and $p_1{p}_2$ are harmonic in $(p_1,p_2)$; a smooth function $h=h(p_1,p_2)$ is harmonic if $({\partial }^2/\partial p_1^2+{\partial }^2/\partial p_2^2)h=0$ throughout its domain.)

In the case $\theta =1/2$, the number of summands is $m=68$, hence there are $2\left(\genfrac{}{}{0pt}{}{72}{2}\right)=5112$ potential points of intersection $(p_1,p_2)$. Of these, only 1003 belong to the unit square and there is a unique maximum at

$$p_1=p_2=\frac{-319+\sqrt{245569}}{224}\approx 0.788166;$$

and $E_{1/2}^0(p_1,p_2)=5(-1933207795+260493\sqrt{245569})/\left[98{\left(13\right)}^9\right]\approx -0.00867999$ there. It can then be confirmed that this determines a global maximum. Furthermore, Banker’s best response to this choice of $(p_1,p_2)$ is exactly as in Table 1. This completes the derivation in the case $\theta =1/2$.

Next, we extend this solution to the largest θ-interval in $(0,1/2]$ for which Banker’s best response coincides with Table 1. The maximum of $E_{1/2}^0(p_1,p_2)$ found above occurred at the intersection of the two indifference curves for $(6,10,6)$ and $(10,6,6)$. The θ-dependent versions of these two indifference curves intersect at the point $(p_1\left(\theta \right),p_2\left(\theta \right))$, where

$$\begin{array}{cc}\hfill p_1\left(\theta \right)& =\frac{-6191+932160\theta -1065024{\theta }^2-s\left(\theta \right)}{32(151-12928\theta +8256{\theta }^2)},\hfill \\ \hfill p_2\left(\theta \right)& =\frac{139055-1197888\theta +1065024{\theta }^2+s\left(\theta \right)}{32(4521+3584\theta -8256{\theta }^2)},\hfill \end{array}$$

(26)

and $s\left(\theta \right)=\sqrt{[20687-1065024\theta (1-\theta \left)\right][20687-1556544\theta (1-\theta \left)\right]}$. Then, with $\mathit{A}\left(\theta \right)$ as before,

$$\begin{array}{cc}& ((1-p_1\left(\theta \right))(1-p_2\left(\theta \right)),(1-p_1\left(\theta \right))p_2\left(\theta \right),p_1\left(\theta \right)(1-p_2\left(\theta \right)),p_1\left(\theta \right)p_2\left(\theta \right))\mathit{A}\left(\theta \right)\hfill \\ & =\left(v\right(\theta ),v(\theta ),v(\theta ),v(\theta \left)\right)\hfill \end{array}$$

with

$$\begin{array}{cc}\hfill v\left(\theta \right)& :=-[94430296089921-6646323952883456\theta -25262343281817856{\theta }^2\hfill \\ & +63817334469402624{\theta }^3-31908667234701312{\theta }^4\hfill \\ & -3(980324411-4975425984\theta (1-\theta \left)\right)s\left(\theta \right)]\hfill \\ & /\left[21208998746(151-12928\theta +8256{\theta }^2)(4521+3584\theta -8256{\theta }^2)\right].\hfill \end{array}$$

The first change in the matrix of Table 1 occurs at the $(9,3)$ entry, which changes from 3 to 4 as θ goes from $\theta >{\theta }_{*}$ to $\theta <{\theta }_{*}$, where ${\theta }_{*}\approx 0.4958752$ (${\theta }_{*}$ is a root of a quartic polynomial). However, for θ close to but greater than ${\theta }_{*}$, we find that Banker is indifferent at $(9,3,4)$ and $(10,6,6)$, so there must be a change in Banker’s best response in $({\theta }_{*},1/2)$. To find the θ at which the first change occurs, we determine where the lower value functions for θ near and to the left of 1/2, which is $v\left(\theta \right)$, and for θ near and to the right of ${\theta }_{*}$ are equal. This occurs at about $0.496162$. When θ is close to this value, we find that the global maximum occurs along the indifference curve for $(10,6,6)$. This leads to a third expression for the lower value function, call it $v_{*}\left(\theta \right)$, and the θ at which $v\left(\theta \right)=v_{*}\left(\theta \right)$, call it ${\theta }_{**}$, is the actual left endpoint of the first interval, $({\theta }_{**},1/2]$. We find that ${\theta }_{**}\approx 0.496212$ (${\theta }_{**}$ is a root of a polynomial of degree 8). This completes the derivation for the interval $({\theta }_{**},1/2]$.

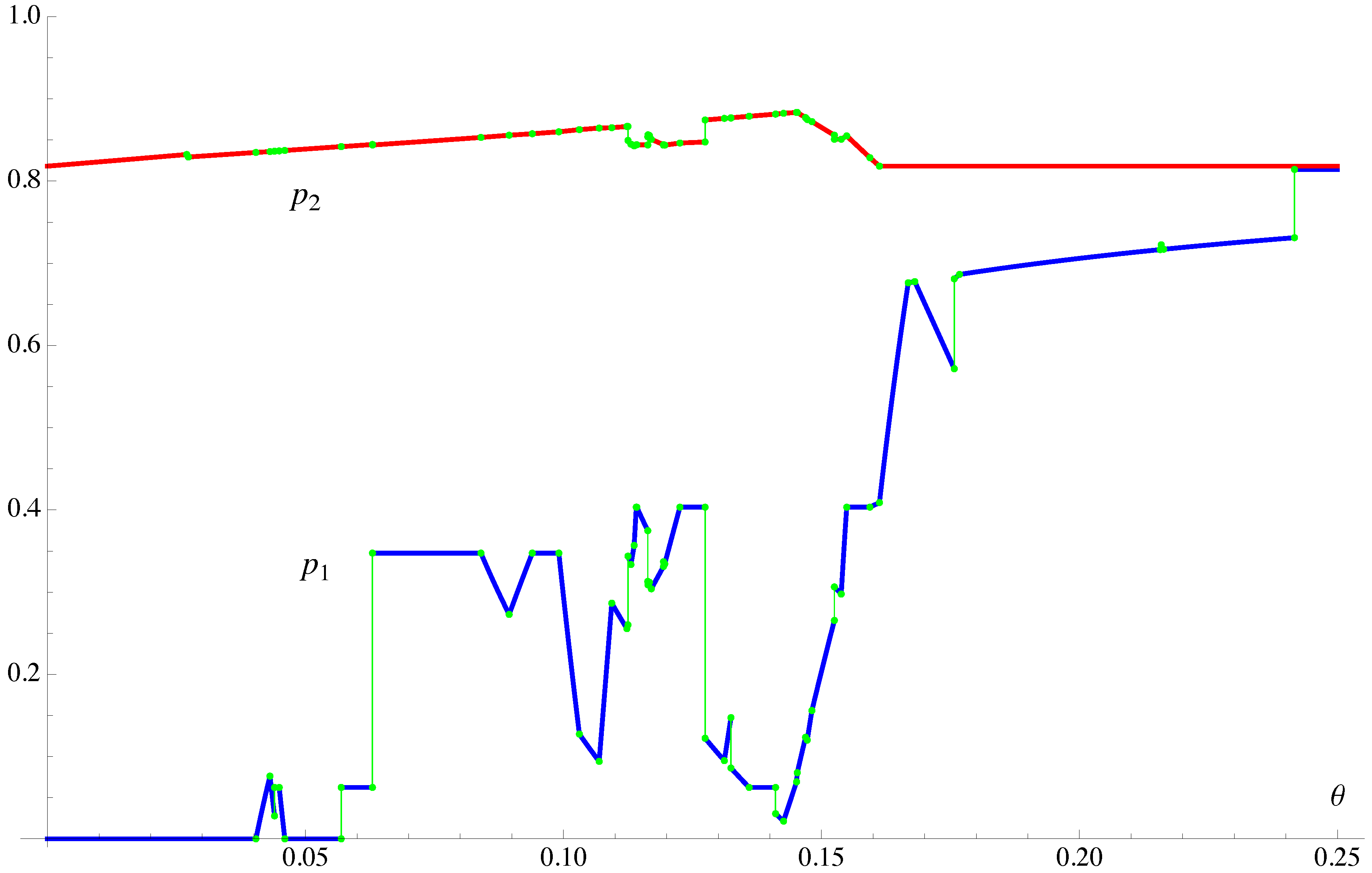
Figure 2. The graphs of the Players’ strategies $p_1$ and $p_2$ in the independent cooperative equilibrium, restricted to $\theta \in (0,1/4]$. ($p_1=9/11$ for $0.241681<\theta <0.432877$ and $p_2=9/11$ for $0.161238<\theta <0.495084$, approximately.) $p_1$ has 13 discontinuities on $(0,1/2]$, whereas $p_2$ has 11 discontinuities.

Figure 2. The graphs of the Players’ strategies $p_1$ and $p_2$ in the independent cooperative equilibrium, restricted to $\theta \in (0,1/4]$. ($p_1=9/11$ for $0.241681<\theta <0.432877$ and $p_2=9/11$ for $0.161238<\theta <0.495084$, approximately.) $p_1$ has 13 discontinuities on $(0,1/2]$, whereas $p_2$ has 11 discontinuities.

Repeating this process, we find that there are 131 such intervals in $(0,1/2]$. That is, there exist $0={\theta }_0<{\theta }_1<{\theta }_2<\cdots <{\theta }_{130}={\theta }_{**}<{\theta }_{131}=1/2$ such that the independent cooperative equilibrium (described by the Players’ maximin strategy and Banker’s best response; the latter, as we saw in Proposition 1, is not Banker’s minimax strategy so is useful primarily for determining the lower value function) is a continuous function of θ on interval i, namely $({\theta }_{i-1},{\theta }_i)$, for $i=1,2,\dots ,131$. Each ${\theta }_i$ is a root of a polynomial of degree 13 or less. In exactly nine of these intervals, the maximum occurs along a single indifference curve rather than at a point of intersection. At the boundary points there are discontinuities in Banker’s best response, whereas the Players’ strategies are typically continuous except for a number of discontinuities. Actually, at the boundary points, solutions from both adjacent intervals apply, so there is nonuniqueness of the Players’ strategies at points of discontinuity. In Figure 2 we graph $p_1$ and $p_2$ as functions of θ.

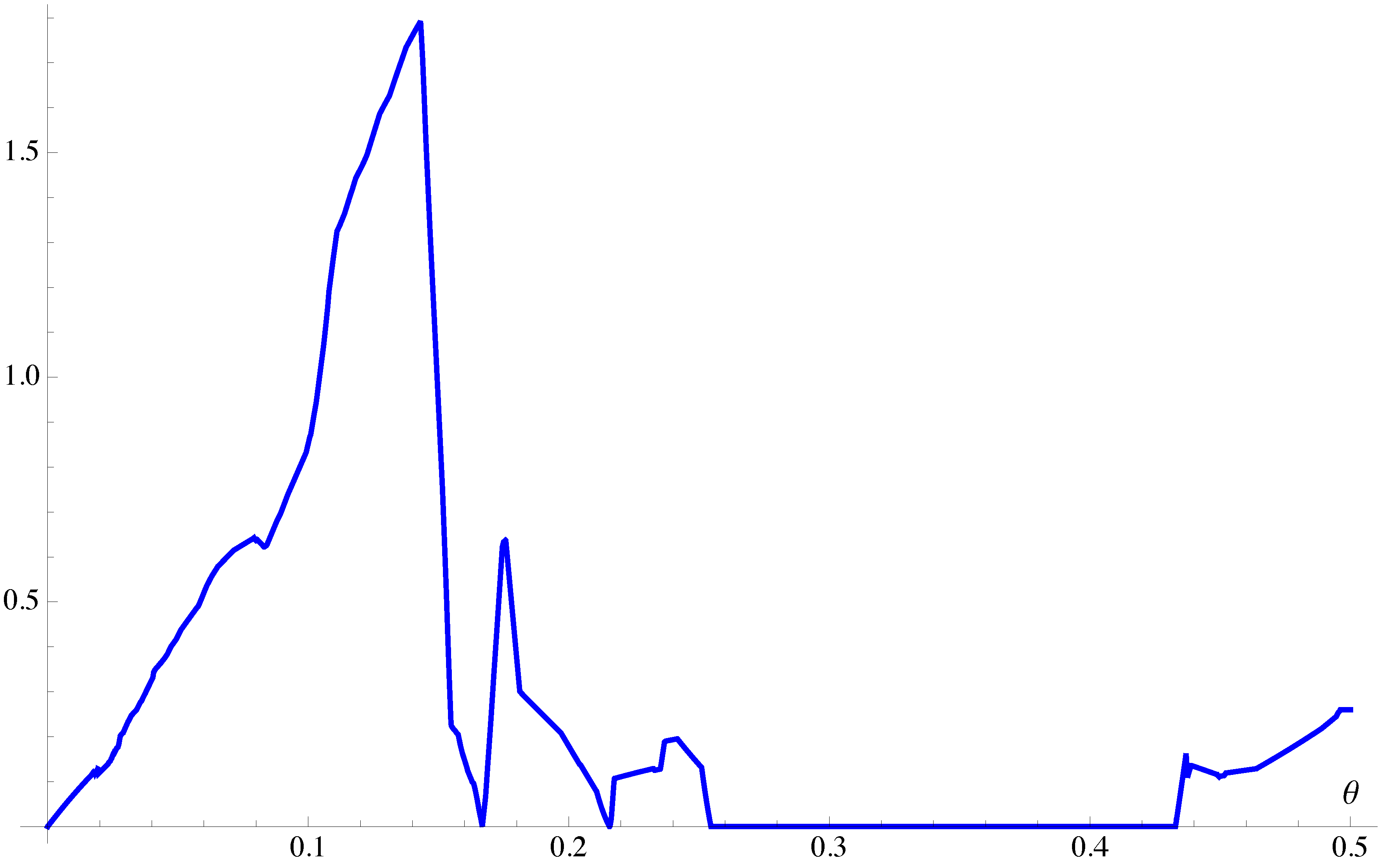
We have seen that the correlated and independent cooperative equilibria coincide when $\theta \in (9588/37663,55716/128711)\approx (0.254573,0.432877)$. With two exceptions, these are the only θ values at which the two equilibria coincide. The exceptions are ${\theta }_{79}\approx 0.166815$ and ${\theta }_{88}\approx 0.215651$, as can be seen from the plot of the difference between the upper and lower value functions in Figure 3.

Figure 3. The graph of the difference between the upper and lower value functions, multiplied by ${10}^5$, in the independent cooperative equilibrium.

Figure 3. The graph of the difference between the upper and lower value functions, multiplied by ${10}^5$, in the independent cooperative equilibrium.

5. Nash Equilibrium

Here we find the Nash equilibrium of our $2\times 2\times 2^{1144}$ trimatrix game. Our method involves finding one or more Nash equilibria explicitly, but it does not permit any uniqueness assertions. Let us begin with the case $\theta =1/2$. For now we simply claim that there exists a Nash equilibrium in this case with $p_1=p_2=9/11$. Banker’s best response is as in Table 1 but with five changes: Entry 5 at $(10,10)$, $(10,11)$, and $(11,10)$ becomes 5+. Entry 5+ at $(6,10)$ and $(10,6)$ becomes 6. Thus, there are now three information sets at which Banker is indifferent, $(10,10,6)$, $(10,11,6)$, and $(11,10,6)$.

Let A and B be the $4\times 8$ payoff matrices for Player 1 vs. Banker and for Player 2 vs. Banker, but with the rows labeled by the Players’ pure strategies: SS, SD, DS, DD on 5 by Player 1 and Player 2. The columns are labeled by Banker’s eight pure strategies: SSS, SSD, SDS, SDD, DSS, DSD, DDS, DDD on $(10,10,6)$, $(10,11,6)$, and $(11,10,6)$. Of course, Banker makes a best response except in the three cases in which he is indifferent. We find that

$$\begin{array}{c}\hfill \mathit{A}=-\frac{16}{{\left(13\right)}^9}\left(\begin{array}{cccccccc}5774122& 5774122& 4995370& 4995370& 4605994& 4605994& 3827242& 3827242\\ 6359098& 6359098& 5580346& 5580346& 5580346& 5580346& 4801594& 4801594\\ 5127763& 5127763& 5300819& 5300819& 5387347& 5387347& 5560403& 5560403\\ 5756515& 5756515& 5929571& 5929571& 5929571& 5929571& 6102627& 6102627\end{array}\right)\end{array}$$

and

$$\begin{array}{c}\hfill \mathit{>B}=-\frac{16}{{\left(13\right)}^9}\left(\begin{array}{cccccccc}5774122& 4995370& 5774122& 4995370& 4605994& 3827242& 4605994& 3827242\\ 5127763& 5300819& 5127763& 5300819& 5387347& 5560403& 5387347& 5560403\\ 6359098& 5580346& 6359098& 5580346& 5580346& 4801594& 5580346& 4801594\\ 5756515& 5929571& 5756515& 5929571& 5929571& 6102627& 5929571& 6102627\end{array}\right).\end{array}$$

Since the Players must act independently, we let

$$\begin{array}{cc}\hfill \mathit{>a}(p_1,p_2)& :=((1-p_1)(1-p_2),(1-p_1)p_2,p_1(1-p_2),p_1{p}_2)\mathit{A},\hfill \\ \hfill \mathit{>b}(p_1,p_2)& :=((1-p_1)(1-p_2),(1-p_1)p_2,p_1(1-p_2),p_1{p}_2)\mathit{>B}.\hfill \end{array}$$

We now determine whether there is a mixture $\mathit{q}=(q_1,q_2,q_3,q_4,q_5,q_6,q_7,q_8)$ of Banker’s eight pure strategies such that $\mathit{>a}(p_1,9/11){\mathit{q}}^{⊺}$ is constant in p₁ and b(9/11, p₂)q^⊺ is constant in p₂. This would ensure that p₁ = 9/11 (in fact any strategy p₁ of Player 1) is a best response to p₂ = 9/11 and q; similarly, p₂ = 9/11 (in fact any p₂) is a best response to p₁ = 9/11 and q. And of course q is automatically a best response to p₁ = p₂ 9/11. A necessary and sufficient condition on q is

$$\begin{array}{cc}\hfill q_6& =\frac{15175619}{10469888}-\frac{23q_1+23q_2+12q_3+12q_4+11q_5}{11},\hfill \\ \hfill q_7& =\frac{15175619}{10469888}-\frac{23q_1+12q_2+23q_3+12q_4+11q_5}{11},\hfill \\ \hfill q_8& =-\frac{9940675}{5234944}+\frac{35q_1+24q_2+24q_3+13q_4+11q_5}{11},\hfill \end{array}$$

and q_j ≥ 0 for j = 1, 2, …, 8. Summing the three equations gives q₆ + q₇ + q₈ = 1 − q₁ − q₂ − q₃ − q₄ − q₅, so any such q is automatically a probability vector.

By testing all possible supports of size two or three, we find that the eight Banker pure strategies are mixed in 11 extreme Nash equilibria as follows:

1.	(0, 15175619=33313280, 15175619=33313280, 0, 0, 0, 0, 1481021=16656640).
2.	(0, 1=2, 4229827=11421696, 0, 0, 0, 1481021=11421696, 0).
3.	(0, 4229827=11421696, 1=2, 0, 0, 1481021=11421696, 0, 0).
4.	(0, 4705731=12373504, 4705731=12373504, 0, 1481021=6186752, 0, 0, 0).
5.	(0, 3753923=10469888, 3753923=10469888, 1481021=5234944, 0, 0, 0, 0).
6.	(15175619=21891584, 0, 0, 0, 0, 0, 0, 6715965=21891584).
7.	(1988135=3331328, 0, 0, 0, 0, 1343193=6662656, 1343193=6662656, 0).
8.	(1568577=3807232, 0, 0, 0, 2238655=3807232, 0, 0, 0).
9.	(3753923=10469888, 0, 0, 6715965=10469888, 0, 0, 0, 0).
10.	(4229827=10945792, 0, 6715965=21891584, 0, 0, 6715965=21891584, 0, 0).
11.	(4229827=10945792, 6715965=21891584, 0, 0, 0, 0, 6715965=21891584, 0).

If Player 1, Player 2, and Banker play according to their equilibrium strategies, Banker’s expected gain per unit stake is

$$\frac{11138203216}{{\left(11\right)}^2{\left(13\right)}^9}\approx 0.00868040.$$

A list of extreme Nash equilibria is the usual way to express the solutions of a noncooperative game, but it is unnecessarily complicated in this case. A better approach is to express these equilibria in terms of behavioral strategies. Only one of the three information sets, (10; 10; 6), (10; 11; 6), and (11; 10; 6), is encountered during the play of a single game. Thus, knowing the draw probabilities in each of the three cases is sufficient. Expressed in terms of these behavioral strategies, the Banker strategies in the 11 extreme equilibria all have the form (r₁, r₂, r₂), and there are only two extreme points, namely

$$\left(0,\frac{6715965}{10469888},\frac{6715965}{10469888}\right)\text{and}\left(\frac{2238655}{3807232},0,0\right).$$

This completes the derivation in the case θ = 1/2.

In fact the same Nash equilibria apply on the interval $({\theta }_{*},1/2]$ for ${\theta }_{*}=799/1604\approx 0.498130$. (Here they are not θ-dependent.) This is the first θ (moving right to left) at which a change occurs in Table 1 (beyond the five changes already noted). As θ moves from $\theta >{\theta }_{*}$ to $\theta <{\theta }_{*}$, the $(2,5)$ entry in Table 1 changes from 4 to 5.

We can repeat this process 40 times. In each new interval the Players’ strategy is the same (independent with $p_1=p_2=9/11$), while Banker’s strategy changes from the previous interval. This determines the Nash equilibria for all $\theta >5772/33847\approx 0.170532$. At the next interval there is no mixture q satisfying the required properties.

Now let us consider what happens when $\theta <5772/33847\approx 0.170532$. Each of the remaining 62 intervals is one of two types: Banker mixes on two information sets (40 cases), or Banker mixes on one information set and $p_1=0$ (22 cases). First we consider the interval whose right endpoint is ${\theta }^{\prime \prime }:=5772/33847\approx 0.170532$. Suppose we know that Banker mixes on $(10,0,4)$ and on $(11,10,6)$ in this interval. The intersection of the two indifference curves occurs at $(p_1\left(\theta \right),p_2\left(\theta \right))$, where

$$p_1\left(\theta \right)=\frac{1443-9304\theta }{481-3850\theta },p_2\left(\theta \right)=\frac{9}{11}.$$

Evaluating the payoff matrices A and B for Players 1 and 2 (now $4\times 4$), we can argue as above, and this leads to two extreme equilibria, which have the same Banker behavioral strategies. The left endpoint of the interval is

$${\theta }^{\prime }:=(82755888+1123\sqrt{2262279009})/803081778\approx 0.169559$$

because of a change in Banker’s strategy at $(9,8,3)$. As for the information sets on which Banker mixes in the next interval, there are three candidates, namely any two of the three $(10,0,4)$, $(11,10,6)$, and $(9,8,3)$, with the first two being most likely. This approach allows us to move from one interval to the next in a systematic way. In those cases where Banker mixes on only one information set and $p_1=0$, we do not need to have $\mathit{>a}(p_1,p_2\left(\theta \right)){\mathit{q}}^{⊺}$ constant in p₁; it suffices that it be maximized at p₁ = 0.

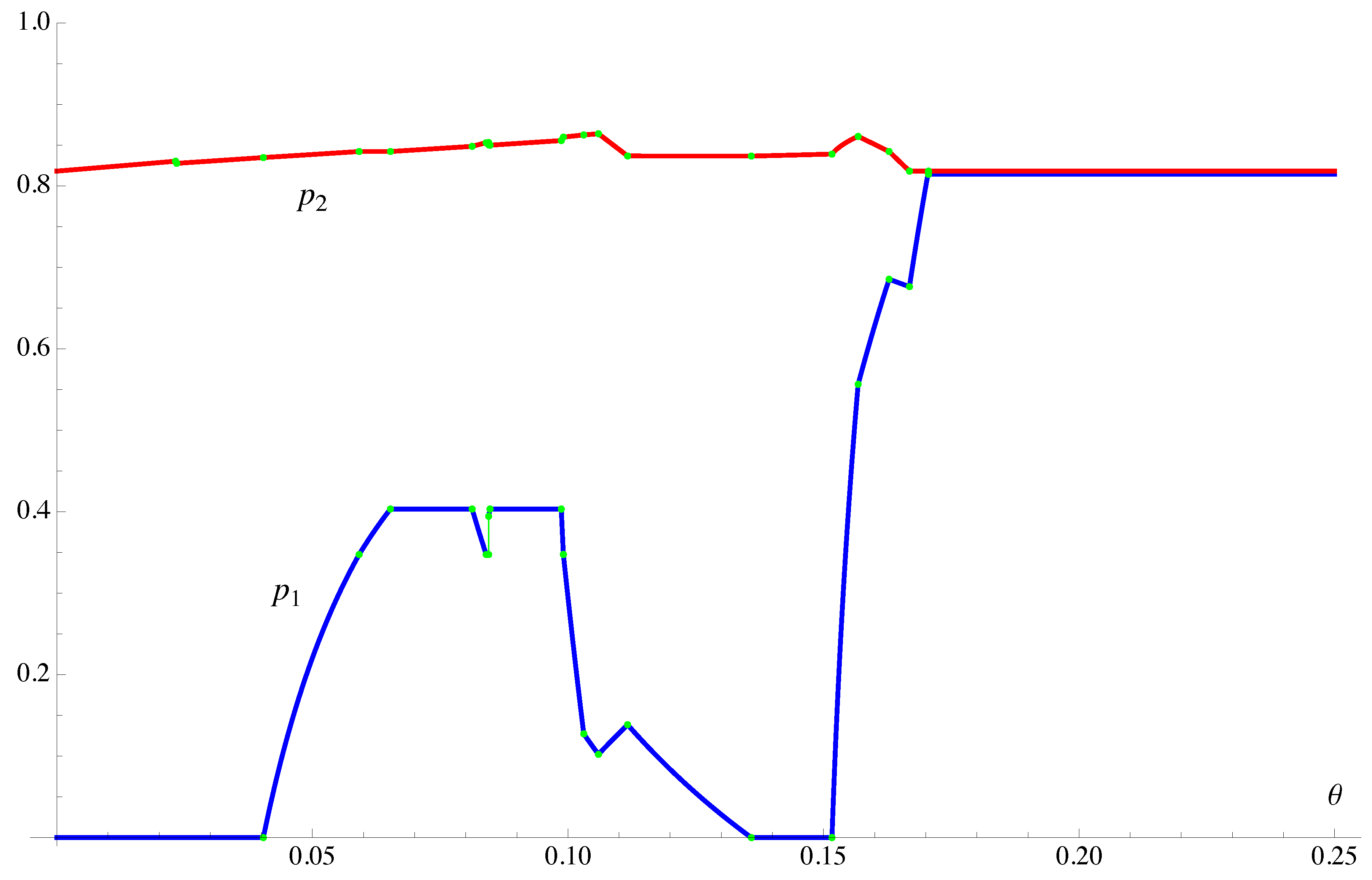
In Figure 4 we graph $p_1$ and $p_2$ as functions of θ. We restrict to $\theta \in (0,1/4]$ since $p_1=p_2=9/11$ whenever $\theta >5772/33847\approx 0.170532$.

Figure 4. The graphs of the Players’ strategies $p_1$ and $p_2$ in the Nash equilibrium, restricted to $\theta \in (0,1/4]$. ($p_1=p_2=9/11$ for $\theta >5772/33847\approx 0.170532$.) Both $p_1$ and $p_2$ have a unique discontinuity, at ${\theta }_{31}\approx 0.0844782$.

Figure 4. The graphs of the Players’ strategies $p_1$ and $p_2$ in the Nash equilibrium, restricted to $\theta \in (0,1/4]$. ($p_1=p_2=9/11$ for $\theta >5772/33847\approx 0.170532$.) Both $p_1$ and $p_2$ have a unique discontinuity, at ${\theta }_{31}\approx 0.0844782$.

Downton and Lockwood [1] observed that Player 1 has positive expectation for $\theta =1/10$. The reason is clear: Banker focusses his attention on Player 2 and therefore plays suboptimally against Player 1. How large is this expectation for small θ? Let us consider interval 1 ($0<\theta <0.0172597$), in which Player 2 bets about 56.9383 or more times as much as Player 1. Player 1’s expectation, per unit bet by Player 1, when both Players and Banker use their equilibrium strategies, is

$$\frac{928(53214419-33787088\theta )}{116649493103(89-68\theta )},$$

which is about $0.00475669$ at the left endpoint of the interval and about $0.00476743$ at the right endpoint. A 0.475% advantage is substantial but it presumably occurs rarely.

Finally, let us explain why Downton and Lockwood’s [1] Nash equilibrium algorithm is incorrect. Let $E_{\theta }^1(p_1,p_2)$ be the expectation of Player 1 per unit bet by Player 1 when Players 1 and 2 independently draw on 5 with probabilities $p_1$ and $p_2$ and Banker makes a best response to $(p_1,p_2)$ and θ. Let $E_{\theta }^2(p_1,p_2)$ be defined analogously. Then, recalling Equation (24),

$$E_{\theta }^0(p_1,p_2)=\theta E_{\theta }^1(p_1,p_2)+(1-\theta )E_{\theta }^2(p_1,p_2).$$

($E_{\theta }^0(p_1,p_2)$ is continuous in $(p_1,p_2)$ for fixed θ, but $E_{\theta }^1(p_1,p_2)$ and $E_{\theta }^2(p_1,p_2)$ are not.) Downton and Lockwood [1] proposed an algorithm for evaluating the Nash equilibrium based on the functions $E_{\theta }^1(p_1,p_2)$ and $E_{\theta }^2(p_1,p_2)$. (We consider it in the context of our simplified model rather than in terms of the more elaborate model they analyzed.) Specifically, they defined

$${\widehat{p}}_2\left(p_1\right):=\underset{p_2\in [0,1]}{arg\; max}{E}_{\theta }^2(p_1,p_2),p_1\in [0,1],$$

(27)

and

$${\widehat{p}}_1:=\underset{p_1\in [0,1]}{arg\; max}{E}_{\theta }^1(p_1,{\widehat{p}}_2\left(p_1\right)),{\widehat{p}}_2:={\widehat{p}}_2\left({\widehat{p}}_1\right).$$

(28)

It appears that the aim was to find $({\widehat{p}}_1,{\widehat{p}}_2)$ such that

$$E_{\theta }^1({\widehat{p}}_1,{\widehat{p}}_2)\ge E_{\theta }^1(p_1,{\widehat{p}}_2)\text{for}\text{all}{p}_1\in [0,1]$$

(29)

and

$$E_{\theta }^2({\widehat{p}}_1,{\widehat{p}}_2)\ge E_{\theta }^2({\widehat{p}}_1,p_2)\text{for}\text{all}{p}_2\in [0,1],$$

(30)

though only the second of these two inequalities actually follows from Equations (26) and (27). Then Banker would make a best response to $({\widehat{p}}_1,{\widehat{p}}_2)$. While inequality (28) appears to say that ${\widehat{p}}_1$ is a best response by Player 1, it does not do so because its right-hand side $E_{\theta }^1(p_1,{\widehat{p}}_2)$ is defined in terms of a Banker best response to $(p_1,{\widehat{p}}_2)$, not $({\widehat{p}}_1,{\widehat{p}}_2)$. Inequality (29) has the same problem. We observe that, when $\theta =1/2$ and ${\widehat{p}}_1={\widehat{p}}_2=9/11$, Equations (28) and (29) fail, which helps to confirm that the method is flawed.

6. Conclusions

Baccara banque is a three-person zero-sum game parameterized by $\theta \in (0,1)$. The players are called Player 1, Player 2, and Banker, and the amounts bet on the hands of Players 1 and 2 are in the proportions $\theta :1-\theta$. Assuming cards are dealt with replacement, the game is a $2\times 2^{12}\times 2^{1144}$ trimatrix game. Downton and Lockwood [1] argued that the independent cooperative equilibrium, in which Players 1 and 2 form a coalition against Banker but act independently, is more useful than the Nash equilibrium. They did not realize that the independent cooperative equilibrium need not exist, in the sense that the lower and upper values of the game may differ. They also computed the Nash equilibrium incorrectly.

We consider a simplified model, in which Player 2 ignores Player 1’s hand, and the game becomes a $2\times 2\times 2^{1144}$ trimatrix game. This allows us to assume that $\theta \in (0,1/2]$. We find what we call the correlated cooperative equilibrium, in which Players 1 and 2 are not constrained to act independently in their coalition against Banker, and the Nash equilibrium. Moreover, in the independent cooperative equilibrium, we evaluate the game’s lower value (to the Players) and its upper value, as well as the corresponding maximin strategy of the Players and minimax strategy of Banker.

Results are necessarily complicated by the fact that Banker’s strategy has more than 100 discontinuities over the interval $(0,1/2]$. The Players’ strategies are simpler, having only a single discontinuity in the Nash equilibrium and at most 13 discontinuities in the independent cooperative equilibrium. Necessary and sufficient conditions on θ are given for the independent and correlated cooperative equilibria to coincide.