Should Law Keep Pace with Society? Relative Update Rates Determine the Co-Evolution of Institutional Punishment and Citizen Contributions to Public Goods

Abstract

Until recently, theorists considering the evolution of human cooperation have paid little attention to institutional punishment, a defining feature of large-scale human societies. Compared to individually-administered punishment, institutional punishment offers a unique potential advantage: the ability to control how quickly legal rules of punishment evolve relative to social behavior that legal punishment regulates. However, at what rate should legal rules evolve relative to society to maximize compliance? We investigate this question by modeling the co-evolution of law and cooperation in a public goods game with centralized punishment. We vary the rate at which States update their legal punishment strategy relative to Citizens’ updating of their contribution strategy and observe the effect on Citizen cooperation. We find that when States have unlimited resources, slower State updating lead to more Citizen cooperation: by updating more slowly, States force Citizens to adapt to the legal punishment rules. When States depend on Citizens to finance their punishment activities, however, we find evidence of a ‘Goldilocks’ effect: optimal compliance is achieved when legal rules evolve at a critical evolutionary rate that is slow enough to force citizens to adapt, but fast enough to enable states to quickly respond to outbreaks of citizen lawlessness.

1. Introduction

Cooperation is central to the success of human societies. However, cooperation poses an evolutionary challenge: why would natural selection favor helping others at a cost to oneself? How have humans managed to construct large-scale societies that feature very high levels of inter-personal cooperation? Evolutionary theorists have proposed a range of mechanisms for the evolution of cooperation, including direct reciprocity, indirect reciprocity, spatial structure, kin selection and group selection (for a review, see [1]). This work has generated many important theoretical and empirical insights into the forces that constrain free-riding and promote cooperation.

Only recently, however, have theorists begun to pay attention to the role of institutional punishment [2,3,4,5] in human cooperation. Most modern large-scale human societies have adopted institutional rules of legal punishment administered by a centralized punisher, the state, to promote collaborative behavior by citizens [6,7,8]. Centralized punishment offers several unique advantages [9], including the ability to overcome coordination failures and free-riding problems [10] and the avoidance of anti-social punishment and retaliation [11,12,13,14,15,16] (although anti-social punishment may also be averted by other means [17,18]).

Beyond these advantages, centralized legal punishment also offers the unitary punisher a unique ability: the capacity to decide how often to revise legal punishment rules. Put differently, institutional punishers can control their own rates of evolution. Legal punishers often adopt procedural rules that make amending legal rules more or less frequent. For example, in the Unites States, the federal regulations that limit penalties on tax or environmental law violators can be amended to change the maximum sentences available via an ordinary act of Congress. In contrast, the Eighth Amendment of the U.S. Constitution, which limits government from imposing excessive fines or punishments for any violation, can only be repealed or modified via a more complicated and time-consuming amendment process, requiring either a constitutional convention or ratification by the states of a proposed amendment. Not surprisingly, the Eighth Amendment has never been modified in its 225-year history, while federal maximum sentences for environmental crimes have already been revised in the thirty years since their enactment [19].

In general, legal theorists disagree about how quickly law should evolve relative to the social behavior that law regulates. Some argue that stable law prevents an unchecked majority from abandoning rules that are effective in the long-term when expedient in the short term to do so [20,21]. Others argue that if legal rules evolve too slowly relative to the updating of social norms, large segments of society will abandon the legal rules altogether when they become outdated or obsolete [22].

We investigate this issue theoretically by simulating the co-evolution of legal punishment and social norms in an evolutionary game theoretic framework. We study a collection of States, each composed of Citizens playing a public goods game. Citizens choose how much to contribute and then face centralized punishment within each State. Periodically, Citizens (States) learn from other Citizens (States) by comparing payoffs. We use this model to investigate the relationship between Citizen cooperation and the frequency of States’ strategy updating relative to Citizen strategy updating.

In most modern states, centralized punishment is not fully unilateral and depends to a significant degree on support from citizens themselves. Given that punishment activities are costly, most modern states depend on citizen financial support. In democracies, the ability to punish depends on citizens’ political support; rules of punishment that are illegitimate are disciplined at the ballot box. In an extension to the basic model, we investigate the effect of this state dependence on its citizenry by examining the effect of a budget constraint that makes each State’s funds available for punishment proportional to the contributions of its Citizens.

2. Model

Our co-evolutionary model considers a series of public goods games, with punishment within each game determined by centralized States. We consider N separate States, $S_1,\dots ,S_N$, each containing a population of n Citizens.

In each iteration of the game, each Citizen j of each State i adopts a contribution strategy $c_{i,j}\in [0,1]$, which defines the amount of income the Citizen pays to its State in the given period. All Citizens have equal income, normalized to one unit per iteration. After Citizens have chosen how much to contribute, every State $S_i$ chooses whether to punish each Citizen based on the Citizen’s contribution $c_{i,j}$. Each State $S_i$ adopts a punishment threshold $T_i$, such that all Citizens contributing below this mandated threshold are punished a fixed amount. Punishment costs the State α per punished Citizen and inflicts a loss of γ on each punished Citizen.

To reflect the public goods that States provide, the sum of Citizen contributions in State i, ${\sum }_{j=1}^n{c}_{i,j}$, is multiplied by a factor r with $1<r<n$. This amount is then divided equally among all Citizens in the State. Thus, Citizens face a social dilemma in deciding whether to contribute to the common pool.

The payoff of Citizen j in State i is given by:

$${\pi }_{i,j}=1-c_{i,j}+\sum _{k=1}^n\frac{r{c}_{i,k}}{n}-\gamma I_{c_{i,j}<T_i}$$

(1)

where $I_{c_{i,j}<T_i}$ is an indicator function that returns one when $c_{i,j}<T_i$ and zero otherwise.

In modern democratic states, a state’s success is judged by the welfare of its citizens, but also by the coerciveness of a state’s punishment machinery: a more coercive state incurs more costs and is less successful than a less coercive state with the same level of citizen welfare. Accordingly, in this model, a State’s payoff is the aggregate payoffs of its Citizens minus the cost of administering punishment to any non-compliant Citizens. Thus, the payoff of State i is given by:

$${\Pi }_i=\sum _{j=1}^n{\pi }_{i,j}-\alpha \sum _{j=1}^n{I}_{c_{i,j}<T_i}$$

(2)

After each iteration of game play, strategy updating occurs. In any given iteration, either Citizens or States update their strategies. Both Citizens and States update their strategies by comparing their payoff to one of their peers to determine whether to switch their strategies: when a given Citizen updates, she compares her payoff to that of a randomly-selected peer Citizen from the same State and adopts the peer’s contribution strategy if the peer has a higher payoff. If both have equal payoff, the updating Citizen adopts the peer’s strategy with probability $0.5$. If the peer has a lower payoff, the Citizen does not change strategy. When a given State updates, it compares its payoff to a randomly-selected other State and adopts the other State’s punishment threshold using the same deterministic payoff comparison process.

The relative evolutionary rate (or update rate) of States is given by θ, which represents the number of State updates per Citizen update. In our simulations, $n/\theta$ Citizen updates occur, in which one randomly chosen Citizen per State compares her payoffs with a peer Citizen and decides whether to switch strategies. Every set of $n/\theta$ Citizen updates is followed by one State update, in which all States compare themselves to randomly-picked peer States and update simultaneously. The State update is followed again by $n/\theta$ Citizen updates, then a State update, and so on. In this context, higher values of θ therefore represent States that update more frequently.

In addition to copying others, modern citizens and states experiment with new innovative strategies to see if they can improve their own outcomes in the context of the others’ response. States revise their rules radically, most often via legislative changes, or incrementally, via revisions in judge-made common law, in which rules of precedent constrain radical experimentation. Citizen strategies for contribution likewise can change radically or incrementally.

Accordingly, in the model, both Citizen and State updates are susceptible to mutation. Each time a State considers changing strategy, there is a probability ${\mu }_s$ that it picks a random strategy from a uniform distribution on $[0,1]$ (representing the potential for States to radically revise their rules via legislative change). Similarly, each time a Citizen considers changing strategy, the Citizen picks a random strategy from a uniform distribution with probability ${\mu }_c$ (as with states, global mutation also gives Citizens the possibility of radical innovation).

We also analyze the case in which States engage in local mutation, to simulate more incremental common-law-driven innovation in which rules of precedent constrain radical experimentation. In the local mutation case, a State mutant selects a new threshold that equals its previous threshold T plus a value randomly sampled from a normal distribution with mean zero and standard deviation σ (resulting strategies are censored, such that negative T values are set to zero, and values greater than one are set to one).

Modern states depend on citizen financial or political support. To incorporate this important fact, in an extension of the model, our simulations introduce a “budget constraint” parameter, δ, which linearly varies the amount that the cost and effect of punishment depend proportionally on Citizen contributions.

Thus, in the presence of a constraint, the actual cost imposed on a punished Citizen contributing under the threshold changes from γ to:

$$\gamma \left(\delta \sum _{j=1}^n\frac{c_{i,j}}{n}+(1-\delta )\right)$$

(3)

and the actual cost to the State of punishing such a Citizen changes from α to:

$$\alpha \left(\delta \sum _{j=1}^n\frac{c_{i,j}}{n}+(1-\delta )\right)$$

(4)

The budget constraint models the State’s need to raise capital or rely on political support to maintain a fully-functioning enforcement mechanism. Varying levels of the constraint δ from zero to one correspond to different sensitivities of punishment ability to Citizen contributions. Setting $\delta =0$ gives the baseline model in which punishment is unconstrained by Citizen contribution.

To explore the dynamics of this system, simulations were performed using MATLAB. Simulations were initialized with all Citizens contributing $c=0$ and all States having punishment thresholds of $T=0$. Every simulation was run for ${10}^6$ generations, and results were averaged over the second half of the simulation. Results were further averaged over 10 simulation runs. The following parameters were used as a base case: a population of $N=10$ States and $n=10$ Citizens, with $r=3$, $\alpha =0.5,\gamma =1.25$ and ${\mu }_C={\mu }_S=0.05.$ We then varied the update rate θ from 0.01 to 10, with constraint δ set to zero in our consideration of unconstrained States and varied from zero to 0.8 when considering the effect of constraints.

3. Results

3.1. Nash Equilibrium Calculations

We begin with a Nash equilibrium calculation for this game. Because one State’s choice of punishment threshold does not affect the payoff of other States, we consider only the interaction between a State and a Citizen. For a State with threshold $T^{\prime }$, given a Citizen contributing $c=T^{\prime }$, it will always be costly for the State to increase to $T>T^{\prime }$ (because the State will then have to punish the Citizen), and it will always be cost-neutral for the State to decrease the punishment threshold to $T<T^{\prime }$.

As a result, numerous strategy combinations in which the State punishment threshold and Citizens’ contribution are equal may be equilibria, so long as conditions are such that the Citizens do not have an incentive to deviate. The no-punishment, no-contribution state $c=T=0$ is always an equilibrium for this reason.

Beyond this zero-based combination, the key to determining whether a given positive level of threshold and contribution is also a Nash equilibrium lies in the Citizen’s contribution decision, which can be narrowed to a choice between two options. Given that a Citizen lives in a State with threshold $T^{\prime }$, it will be payoff maximizing for the Citizen to either choose $c=T^{\prime }$ (and thus avoid punishment), in which case $c=T^{\prime }$ is an equilibrium, or to choose $c=0$ (incurring punishment, but avoiding the cost of contribution), in which case $c=T^{\prime }$ is not an equilibrium.

Beyond these two options, other Citizen choices are not relevant. Citizens who choose to contribute more than the legal punishment threshold, $c>T^{\prime }$, will earn lower payoffs than Citizens who choose to contribute the threshold amount, $c=T^{\prime }$, given that contribution is costly, yet contributing more than the threshold brings no added individual benefit; and Citizens who choose to contribute less than the threshold, $0<c<T^{\prime }$, will earn lower payoffs than Citizens who choose to contribute nothing, $c=0$, given that the higher contribution choice receives the same punishment, but incurs a greater contribution cost.

To determine which levels of matching punishment threshold and contribution beyond $c=T=0$ are Nash equilibria for a given set of parameter values, we therefore ask when the Citizen payoff for contributing at the threshold, $c=T^{\prime }$, is at least as large as the Citizen payoff of contributing nothing, $c=0$ (we assume that the $n-1$ other Citizens contribute at the threshold, $T^{\prime }$, as the Nash calculation involves a unilateral deviation by one Citizen).

Citizen payoffs from contributing the threshold will be at least as large as Citizen payoffs from contributing nothing (and therefore, that threshold and contribution level will constitute a Nash equilibrium) when:

$$1+T^{\prime }(r-1)\ge 1+T^{\prime }r(n-1)/n-\gamma (\delta \frac{T^{\prime }(n-1)}{n}+(1-\delta ))$$

(5)

Rearranging this condition in terms of punishment strength γ shows that if $\gamma \ge \frac{1-r/n}{1-\delta /n}$, then all possible matching combinations $0\le c=T\le 1$ are Nash equilibria. Conversely, if $\gamma <\frac{1-r/n}{1-\delta /n}$, then matching combinations with $0\le c=T\le T_{Max}$ are Nash equilibria, where:

$$T_{Max}=\frac{\gamma (1-\delta )}{1-\delta \gamma (n-1)/n-r/n}$$

(6)

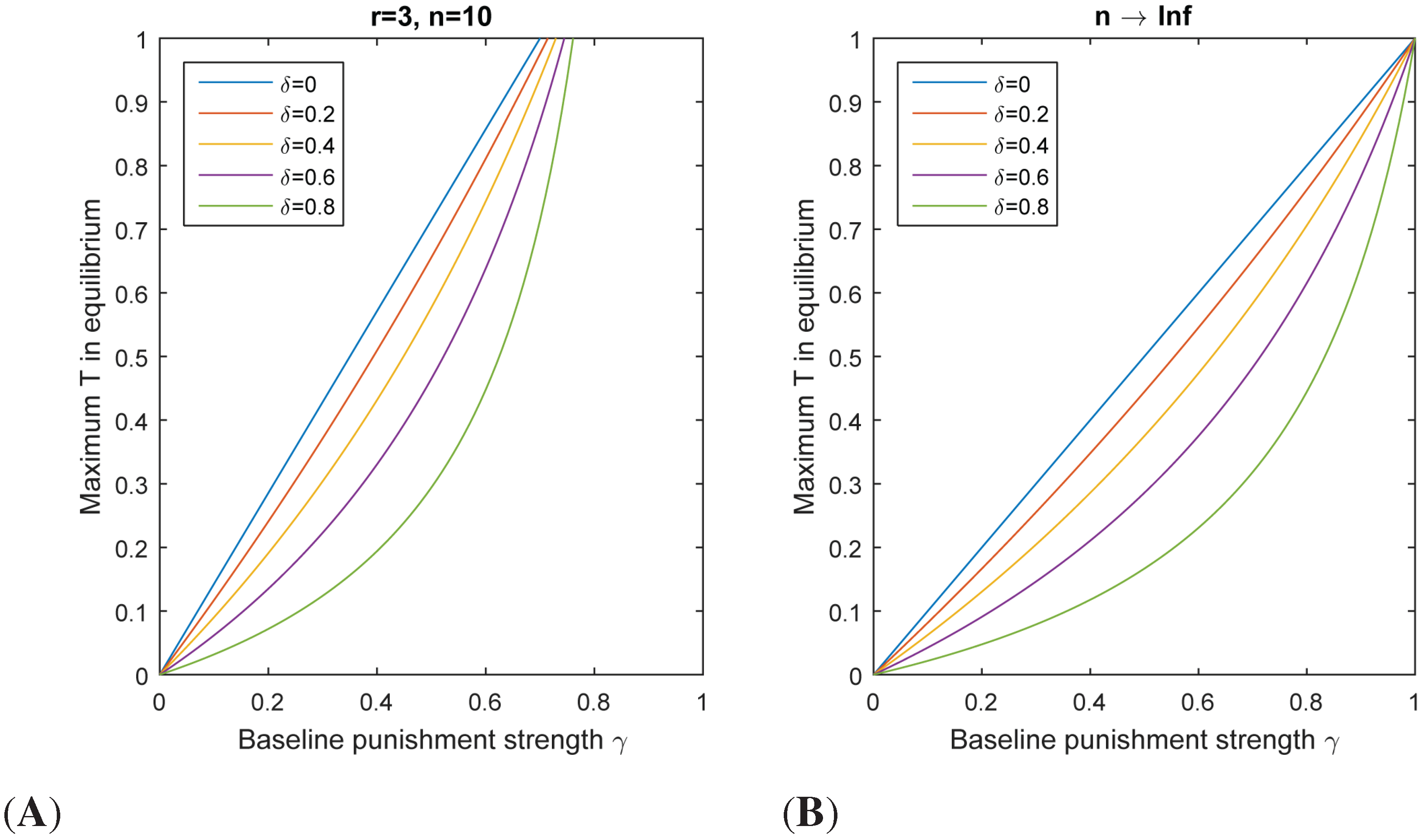
Thus, for situations in which baseline punishment strength $\gamma <\frac{1-r/n}{1-\delta /n}$, the value of $T_{Max}$ indicates the highest threshold for which Citizen payoffs will be maximized by choosing to contribute at the State threshold and avoid punishment, rather than contributing nothing and incurring punishment. Accordingly, any combinations in which the State’s threshold is at or below the maximum threshold constitute Nash equilibria. (To determine which of this infinite set of equilibria is selected, we turn to dynamics in the following section.)

To help visualize these relationships, Figure 1 shows the maximum punishment threshold T that can be sustained in equilibrium as a function of punishment strength.

This result has important implications for the effect of a budget constraint δ. When baseline punishment strength γ is sufficiently low, the maximum equilibrium punishment threshold will decrease as the budget constraint δ increases. Because we want to explore the dynamics of our system in a parameter regime where full cooperation is a possible equilibrium (and we want to ask when this equilibrium is selected), we focus on a set of baseline parameters in which this maximum threshold T is greater than one for all values of the budget constraint δ.

Finally, we consider the sub-game perfection of these equilibria. To do so, we consider the game as a two-stage one-shot game: first, the Citizen contributes c, and then the State punishes the Citizen if $c<T$. We see that no equilibrium in which the State punishes (i.e., $T>0$) is sub-game perfect: because punishment is costly, the State’s threat to punish is not credible. As is discussed in more detail below, this lack of credible threat is precisely why the relative State update rate will play a critical role in the co-evolutionary dynamics of our public goods game. By updating slowly, the State can effectively commit to punishing, even though doing so is not sub-game perfect.

Figure 1. Nash equilibrium calculations for game between a State and a Citizen. Shown is the maximum punishment threshold T that can be sustained in equilibrium, for $r=3,n=10$ (A) and in the limit as n approaches infinity (in which case, r does not affect the calculation) (B).

Figure 1. Nash equilibrium calculations for game between a State and a Citizen. Shown is the maximum punishment threshold T that can be sustained in equilibrium, for $r=3,n=10$ (A) and in the limit as n approaches infinity (in which case, r does not affect the calculation) (B).

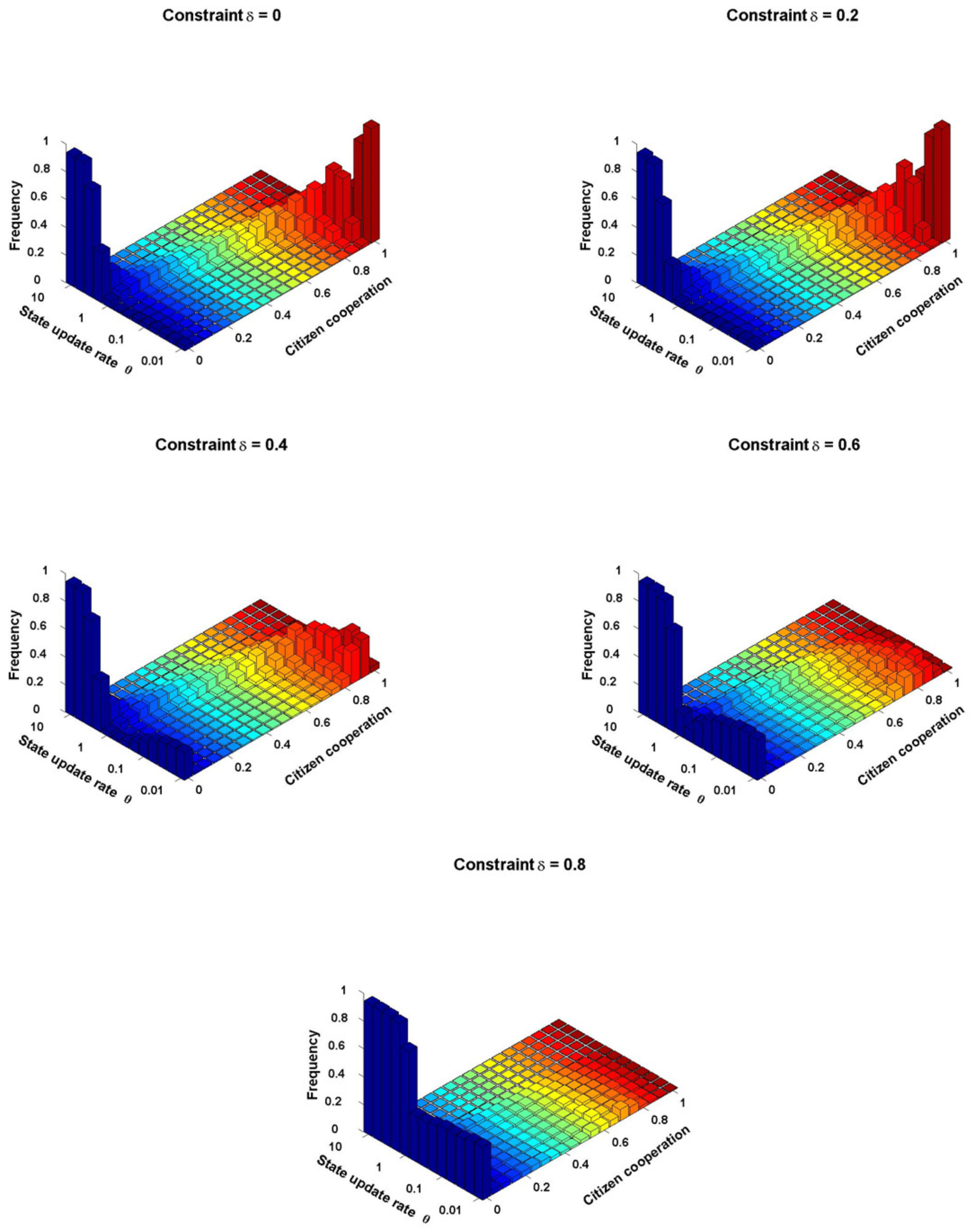
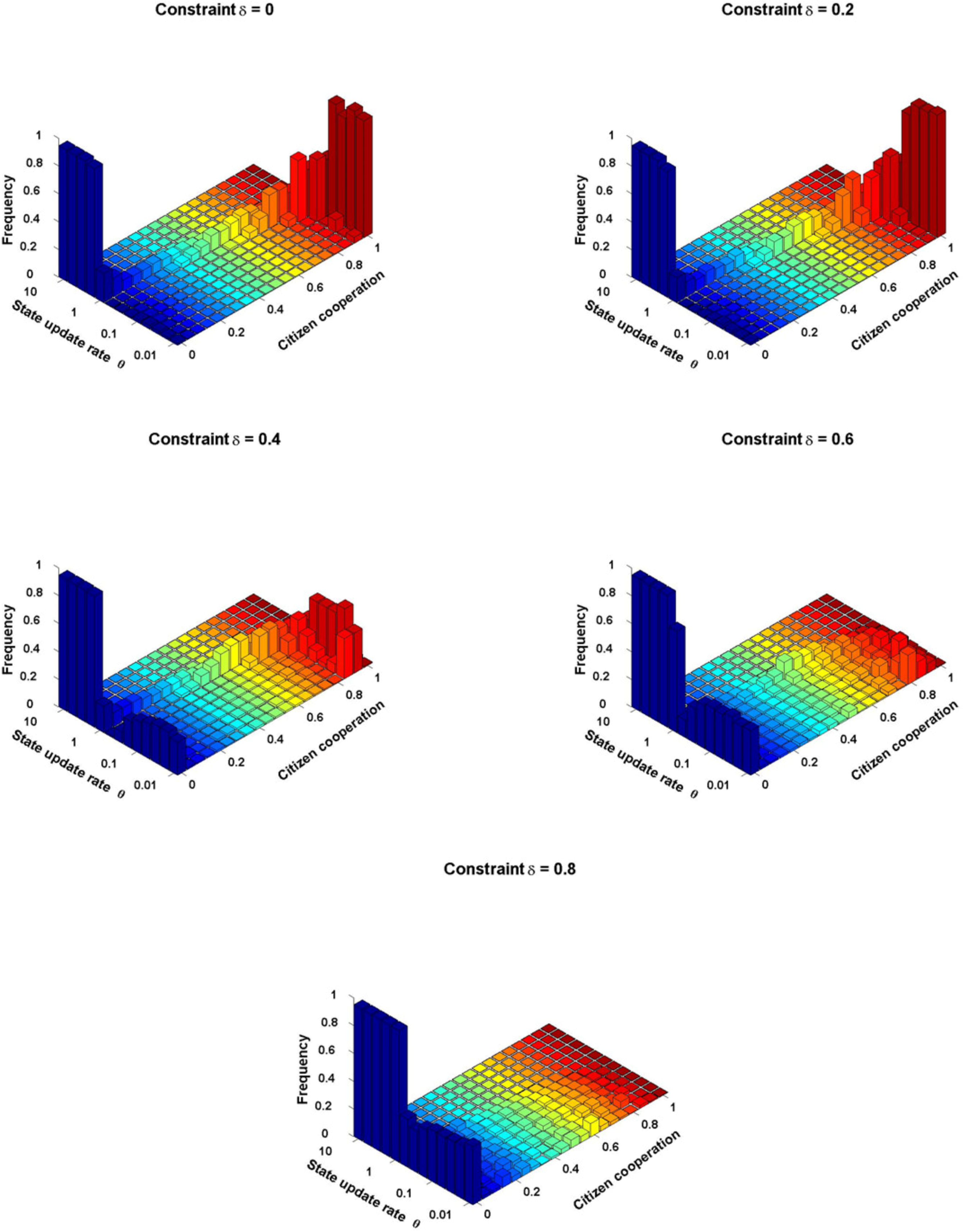
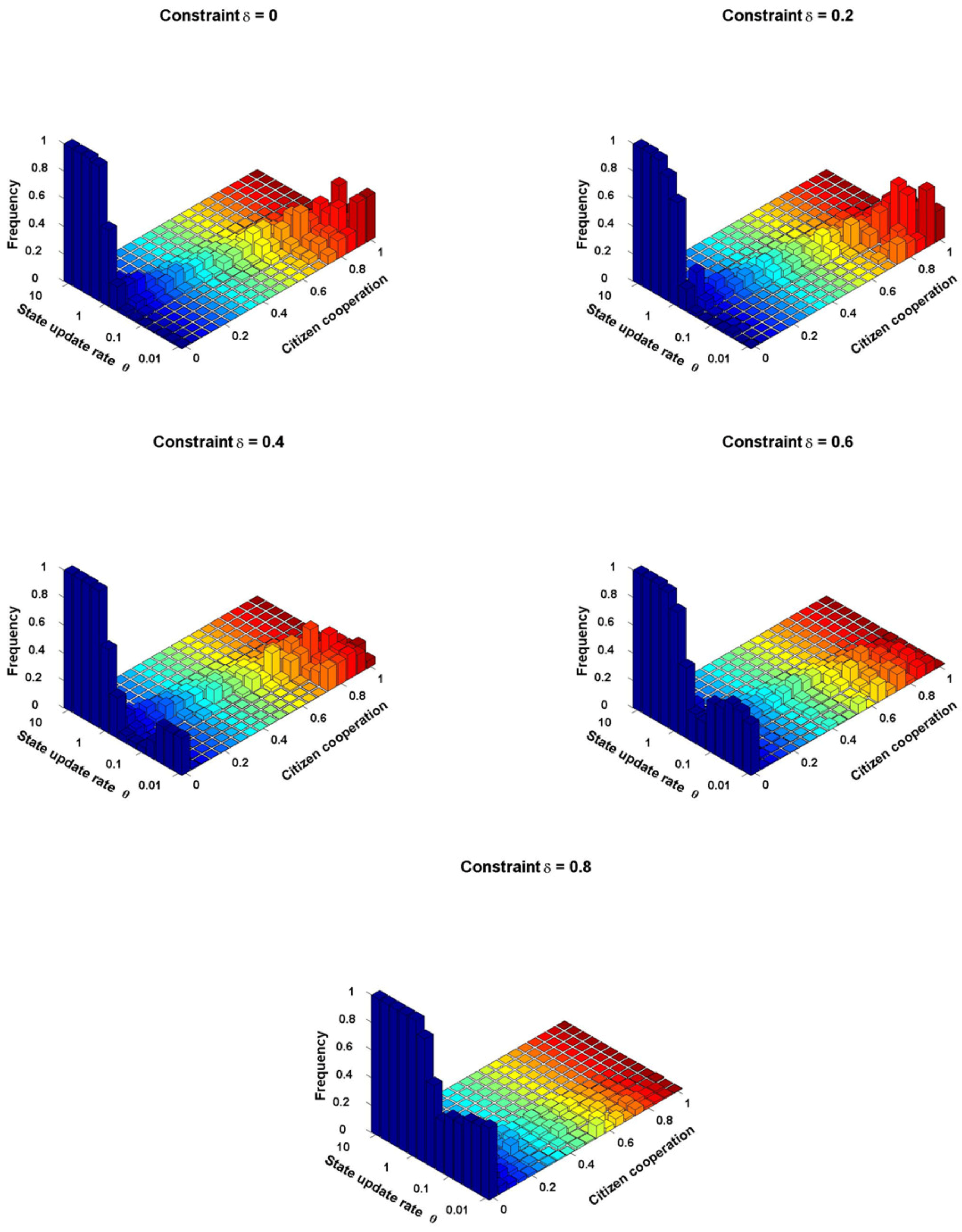
3.2. Effect of States’ Update Rate on Evolutionary Dynamics of Cooperation

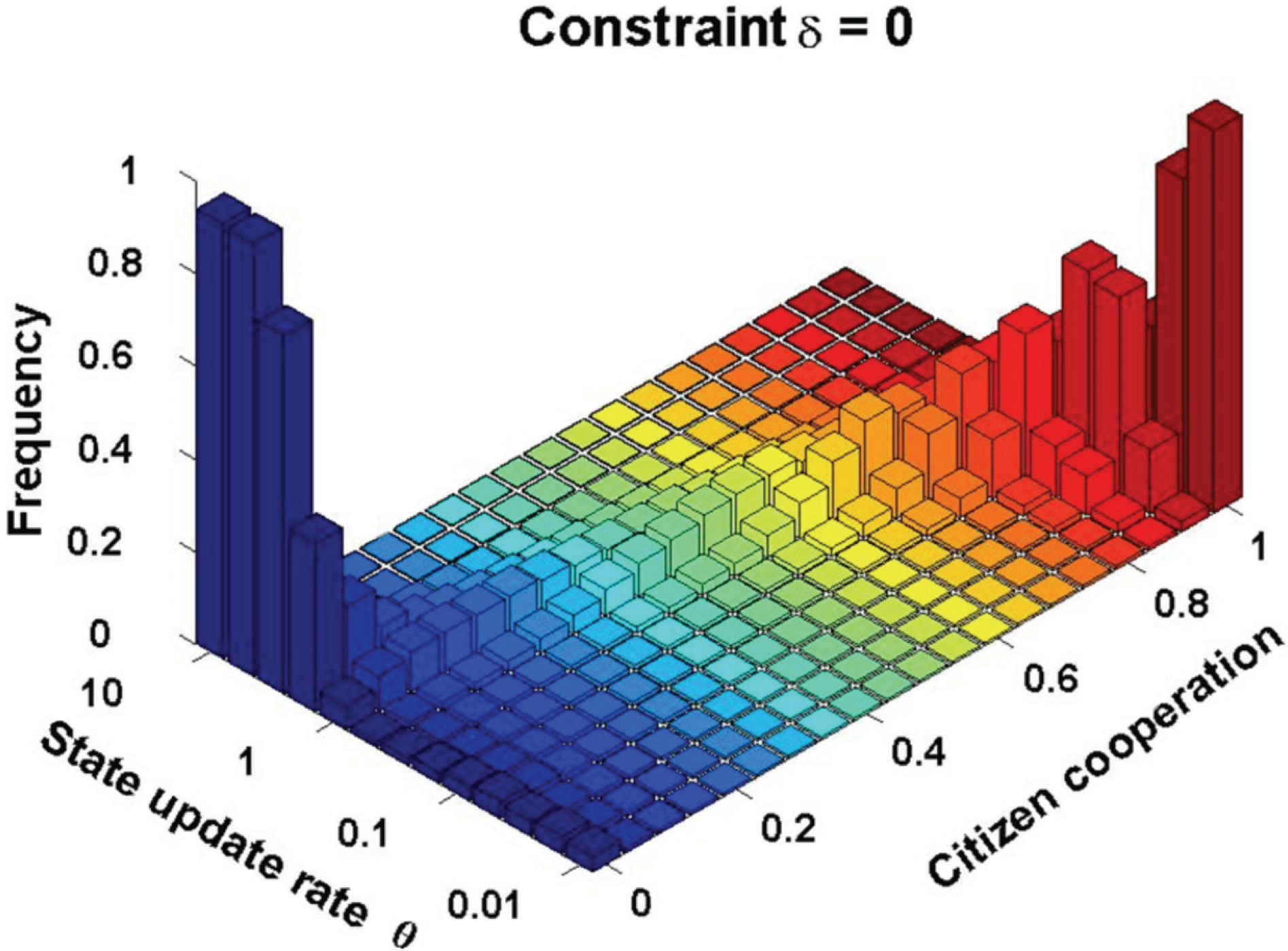
Figure 2 depicts the way in which the distribution of Citizen cooperation levels changes with State update rate θ in a setting where States have unlimited resources with which to finance punishment, $\delta =0$ (for corresponding distributions of State punishment threshold T and Citizen and State payoffs relative to θ, see Appendix Figure A1, Figure A2, Figure A3 and Figure A4). Figure 2 shows that more slowly-updating legal rules promote greater Citizen cooperation (in the absence of a budget constraint). When States update quickly, Citizens learn to contribute nothing. As θ decreases and the States’ relative update rates become slower, however, Citizen cooperation shifts dramatically and in a non-linear way from no cooperation by the Citizens to a high level of cooperation.

This shift in cooperation occurs because slowing the evolutionary rate of legal punishment prevents the States from abandoning a costly legal punishment strategy before Citizens have learned to adapt. Depriving the States of the opportunity to update effectively functions as a pre-commitment device: a relatively slower updating rate forces the States to continue punishing at significant cost where those States might otherwise have shifted to a strategy of non-punishment, to avoid the cost of punishment. A driver playing the game of chicken (in which cars drive straight at each other) can win by throwing her steering wheel out the window. Playing against an opponent who is disabled from changing strategy, players who swerve will be favored by natural selection. Likewise, by adopting a slower rate of updating, the State forces its Citizens to adapt to State punishment rules before the States update their punishment strategy. This connection between update rate and coercive power has an analog in biology: some scholars in the relevant literature have suggested that slower relative evolutionary rates produce the same results as giving the slower-evolving species the first move in a sequential game [23].

Figure 2. Effect of States’ relative update rate on cooperation in the absence of budget constraints. Counts represent the fraction of time that the system spends at the relevant contribution level, averaged over the last half in each of ten runs of $1\times {10}^6$ generations. $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05,\delta =0$.

Figure 2. Effect of States’ relative update rate on cooperation in the absence of budget constraints. Counts represent the fraction of time that the system spends at the relevant contribution level, averaged over the last half in each of ten runs of $1\times {10}^6$ generations. $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05,\delta =0$.

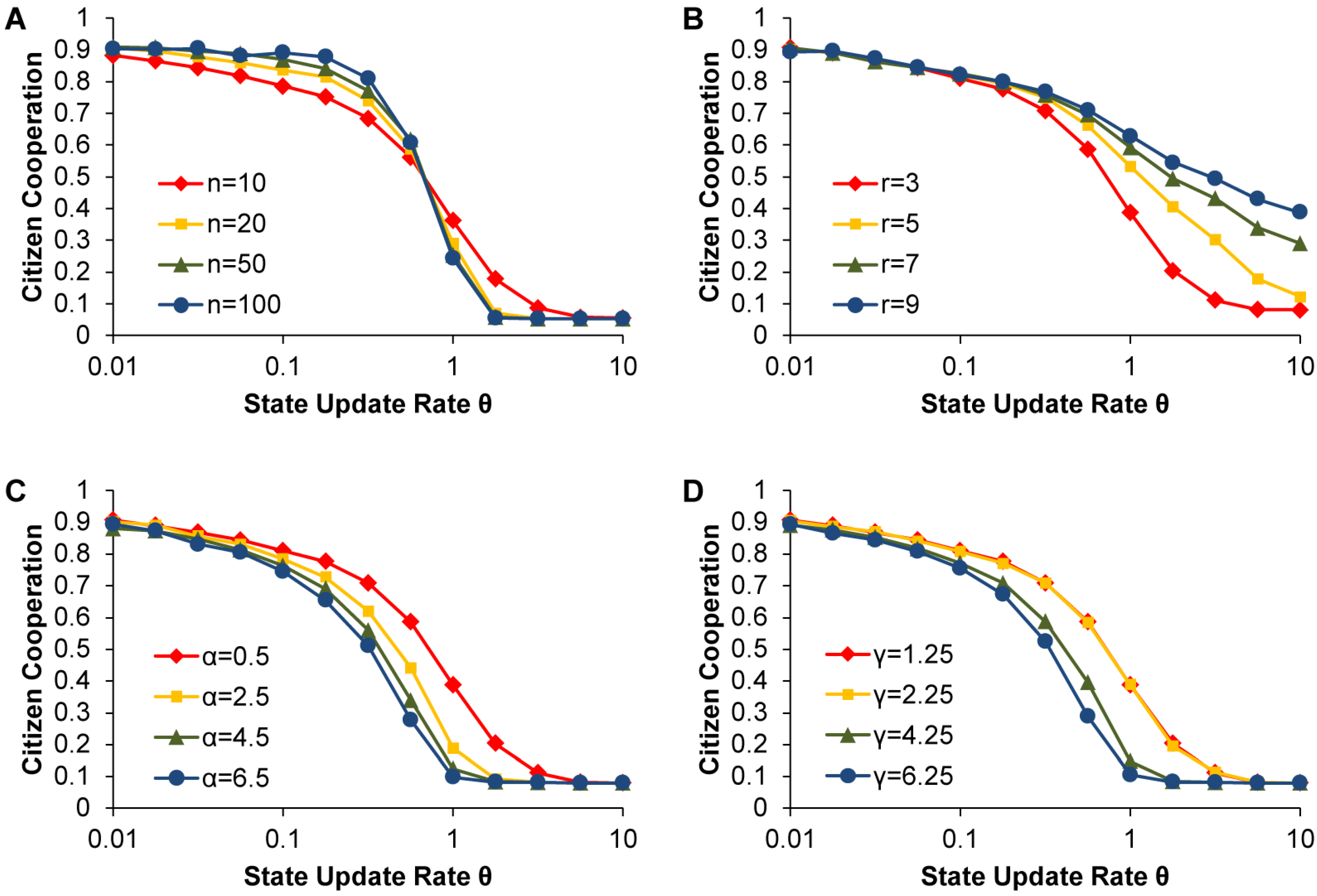
We now investigate the effect of varying the game parameters on the relationship between State update rate θ and Citizen cooperation. To do so, we take the parameter values used to generate Figure 2 as our base case and examine the effect of varying parameters one at a time. First, we consider the effect of varying n, the number of Citizens per State. We find that as States become larger, the maximum θ that can maintain cooperation does not change, but the transition from non-cooperation to cooperation becomes sharper (Figure 3A), with greater change occurring over a smaller change in relative update rate. This increased sharpness occurs because larger States are less susceptible to the stochastic effects that vary depending on which Citizens happen to get picked as the peer model and which as learner in a given update.

Next, we consider the effect of varying r, the cooperation multiplier. We observe that larger values of r allow faster updating States to achieve higher levels of cooperation (Figure 3B). Larger r values mean that fewer Citizens need to switch to cooperation before punishment starts to pay off for the State, because each cooperator increases the State’s payoff by a larger factor.

Finally, we find that increasing either the cost of punishment α (Figure 3C) or the effect of punishment γ (Figure 3D) requires the State to update more slowly to achieve the same level of cooperation. Increases in both of these parameters have the effect of increasing the cost of punishment for the State: α increases cost directly, and γ increases cost because the State payoff depends on the sum of the Citizen payoffs, which incorporate losses from being punished. Thus, increasing the cost or effect of punishment increases the number of Citizens who must switch to cooperation before punishment starts to pay off for the State, and States therefore must update more slowly to achieve the same level of cooperation.

Figure 3. Effect of game parameters n (A), r (B), α (C), and γ (D) on relationship between relative update rate and cooperation. Within each panel, parameters not indicated in the legend are set at $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05$.

Figure 3. Effect of game parameters n (A), r (B), α (C), and γ (D) on relationship between relative update rate and cooperation. Within each panel, parameters not indicated in the legend are set at $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05$.

3.3. Effect of State Update Rate on Citizen Cooperation with a Budget Constraint

We now consider the dynamics of the model in a setting where the State operates under a budget constraint. This budget constraint can represent a variety of ways in which modern states depend on their citizens for effective punishing. For example, states that deploy centralized punishment often depend on citizen revenues to finance punishment activities. Democratic states often depend on citizen political support for particular legal punishment rules, like the death penalty; in the absence of such support, government cannot continue such punishment strategies.

Thus, in our model, as described above, the States’ resources to finance legal punishment are set, at least to some extent, to be proportional to citizen contributions. For example, a constraint of $\delta =1$ indicates that States’ revenues for punishment activities in their entirety are directly proportional to Citizen contributions . In contrast, a constraint of $\delta =0.2$ indicates that 20 percent of State revenues are proportional to Citizen contributions, and the rest are exogenously supplied with no limitation.

Figure 4 illustrates the way in which Citizen cooperation varies with State update rate θ under constraints that vary from $\delta =0.2$ to $\delta =0.8$ (for corresponding distributions of State punishment threshold T and Citizen and State payoffs, see Appendix Figures A1, Figures A2, Figures A3 and Figures A4). When the budget constraint is low, $\delta =0.2$ (Figure 4a), the dynamics mirror those of unconstrained States at δ = 0. Because the baseline punishment strength is set to $\gamma =1.25$, States are still able to fully disincentivize defection even when all Citizens contribute nothing; with no Citizen support, the cost of being punished is one, which is enough to wipe out any gains from non-cooperation. Thus, when $\delta =0.2$, Citizen cooperation increases as the States’ relative update rate θ decreases.

Figure 4. Effect of relative update rate on cooperation with constraint $\delta =0.2$ (a), $\delta =0.4$ (b), $\delta =0.6$ (c), and $\delta =0.8$ (d). $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05$.

Figure 4. Effect of relative update rate on cooperation with constraint $\delta =0.2$ (a), $\delta =0.4$ (b), $\delta =0.6$ (c), and $\delta =0.8$ (d). $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05$.

When States are more heavily constrained, $\delta =0.4$ (Figure 4b), we see important differences. As States update more slowly relative to citizens, we now observe a bimodal distribution, in which Citizens spend time at both very high and very low levels of cooperation, with significant variance and little to no time at intermediate levels of contribution.

When the States are very severely constrained, $\delta =0.6$ and $\delta =0.8$, (Figure 4c,d), Citizens spend almost all of their time not contributing. Thus, unlike the unconstrained State, decreasing θ in the presence of constraints is not uniformly good. Past the θ at which cooperation first arises, slowing the State also increases the probability of Citizens contributing nothing. Additional simulations demonstrate qualitatively equivalent results using larger States with 50 Citizens each (Appendix Figure A5), as well as lower Citizen and State mutation rates (${\mu }_S={\mu }_C=0.005$; Appendix Figure A6).

What accounts for these dynamics? More particularly, why does slowing the rate at which the State updates its legal rules create significant variance in cooperation levels in the presence of a non-negative budget constraint? The answer can be traced to the fact that budget constraints, which essentially link the States’ ability to punish to Citizen cooperation, require the States to be able to respond quickly when a significant number of Citizens switch to non-cooperation.

Even in unconstrained States, from time to time, Citizens shift from high levels of contribution to very low levels of contribution, defecting en masse. This dramatic shift is particularly likely when a State mutates to a new legal rule requiring substantially higher contributions. On those occasions, the State begins to punish all of its Citizens, who are currently contributing a middling amount that is below the new threshold, but greater than zero. Thus, a Citizen mutant who contributes zero will earn higher payoffs than the middling cooperators. Because both strategies are punished, a Citizen earns higher payoffs if she avoids the cost of contribution. Accordingly, such a defector mutant can invade.

In unconstrained States, these rebellions are self-correcting. Eventually, a mutant Citizen with a compliant high contribution strategy that avoids State punishment will arise and earn higher payoffs than the punished defectors. Other Citizens will then copy the innovator mutant’s compliant cooperative strategy, to complete the recovery.

For constrained States, however, this recovery is significantly slowed. Owing to the budget constraints that tie punishment ability to Citizen contributions, an individual State’s ability to punish non-contributing Citizens is severely hindered when its Citizens stop contributing. Once Citizens stop contributing, the State is no longer able to fully enforce punishment to achieve the high level of cooperation that corresponds to its threshold. As a result, a compliant mutant that might arise would not be able to out-compete defectors, because defectors are not adequately punished to render their payoffs less than the mutant’s.

Instead, to restore recovery, a constrained State must initially lower its threshold and then ‘bootstrap’ its way back up to full cooperation. Eventually, a mutant State will arise that adopts a sufficiently low threshold that the State will be able to incentivize its Citizens. Even when Citizens have defected en masse, a constrained State $(\delta <1)$ still has the power to impose a small punishment to enforce a lower threshold, such that a mutant compliant Citizen contributing at a slightly greater level will earn higher payoffs than defectors. Once such a mutant fixates, contribution levels increase, and these contributions can then finance a larger punishment, favoring Citizens who contribute an even larger amount, and so on. States can bootstrap upwards in this way.

Figure 5 provides evidence for such bootstrapping. The key to the bootstrapping dynamic is that under a budget constraint, a State with no Citizen cooperation (and thus, a low State payoff) must lower its threshold and make initially small and then progressively larger increases in punishment threshold T. The smaller increases at the beginning of the recovery generate enough Citizen cooperation (and State revenue) to give States the financial ability to punish at a higher threshold, which, in turn, will generate even more cooperation and revenue. In this way, the State is able to bootstrap up to higher levels of punishment. Unconstrained States, on the other hand, can move directly to punish at a high T without the need for intermediate ‘stepping stone’ thresholds.

Consistent with this analysis, Figure 5A demonstrates that States with higher budget constraints are more likely to change their threshold during State update rounds, especially among States that are in the process of increasing their threshold. Figure 5B then shows that among the low threshold States ($T<0.1$) that increase their threshold, the average size of the threshold increase is larger for unconstrained and smaller for constrained States. Constrained States that are increasing their threshold change the threshold more often and in smaller increments, working their way up to the larger threshold. States without a budget constraint move in far larger increments, jumping immediately to large T, and, thus, do not change as often. Thus, as shown in Figure 5C, States under higher constraint spend a greater fraction of their time at intermediate levels of T.

Figure 5. (A) Fraction of State updates in which the State changes punishment threshold, as a function of constraint δ. The y-axis is cropped at the mutation rate of $\mu =0.05$, because this is the minimum possible value. (B) Average change in punishment threshold T for States with low thresholds ($T<0.1$) that do change strategy. (C) Cumulative distribution function of State punishment thresholds across the second half of each simulation. All simulations use $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05,\theta =1000$.

Figure 5. (A) Fraction of State updates in which the State changes punishment threshold, as a function of constraint δ. The y-axis is cropped at the mutation rate of $\mu =0.05$, because this is the minimum possible value. (B) Average change in punishment threshold T for States with low thresholds ($T<0.1$) that do change strategy. (C) Cumulative distribution function of State punishment thresholds across the second half of each simulation. All simulations use $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05,\theta =1000$.

Owing to the need for bootstrapping to address outbreaks of Citizen defection, slowing the State’s relative evolutionary rate becomes a double-edged sword. As States update slowly enough to force Citizens to respond to punishment, Citizens respond by contributing at progressively greater levels. However, less frequent updating also gives constrained States progressively fewer opportunities to bootstrap between punishment levels in order to recover cooperation after an outbreak of lawless defection.

Put differently, States whose ability to punish depends on Citizen contribution are vulnerable to Citizen rebellion. Slowly evolving States that update their rules less frequently lose the flexibility and agility to respond when Citizens have defected en masse and Citizen norms have deviated significantly from the legal rule.

Importantly, this dynamic creates an optimal update rate for legal rules that maximizes the payoff to the State at the same time that it minimizes the variance in cooperation levels. This optimal update rate is slow enough to force Citizens to respond to legal punishment by adopting and copying a compliant strategy, but is also fast enough to maximize the States’ ability to respond quickly to Citizen rebellions via bootstrapping. If the State updates at a rate faster than this critical threshold rate, it cannot force Citizens to respond to legal incentives. If the State slows its update rate past the optimal level, it will increase periods in which levels of cooperation are high, but also increase periods during which Citizens have defected en masse, generating an increasingly volatile cycling between the two.

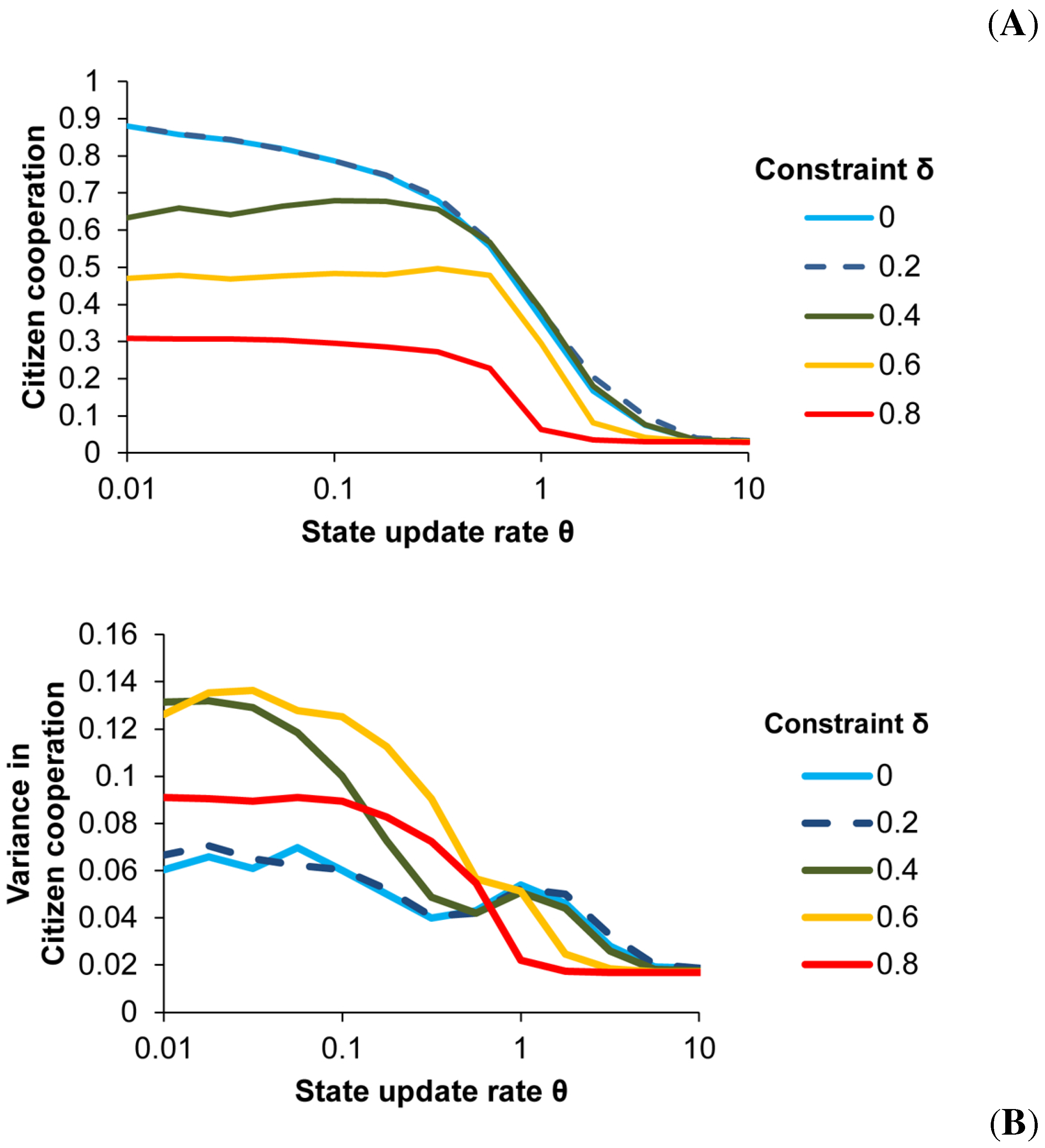
The optimal evolutionary rate can be seen in Figure 6, where average cooperation and variance in cooperation are shown as a function of θ. At the optimal update rate θ, the curves for constrained States flatten dramatically, and further slowing generates no additional increase in mean Citizen cooperation (and often a slight decrease in cooperation). This is because past the critical point, a slower update rate θ makes things simultaneously better and worse. Slower State relative updating promotes greater contribution by Citizens, but also promotes greater defection, because the States are not able to respond quickly to mass Citizen defections.

In addition, Figure 6 shows that further slowing generates a dramatic increase in the variance of cooperation rates, as Citizens cycle between periods of high cooperation and longer periods of mass defection. In the real world, increased variance creates significant problems for states’ legal systems. Unstable legal systems are unable to protect reliance-based interests or encourage long-term investments that assume a certain degree of predictability. For example, a state experiencing extreme cycling between a coercive regime (maximum punishments and contributions) and an anarchical regime (low or no punishment and contributions) would be far less likely to invest citizen contributions into a long-term construction or public works project, because the state could not guarantee a sustained availability of revenue from citizens [24].

To summarize, if the States’ relative update rate is too fast, States are unable to force Citizens to respond. If the States’ update rate is too slow, States are unable to address mass outbreaks of Citizen defection, and Citizens experience volatile cycles between social order and long periods of mass defection. The ideal or critical State update rate maximizes cooperation while simultaneously minimizing Citizen defection and volatility.

Figure 6. Citizen cooperation as a function of State relative update rate. (A) Mean; (B) variance. $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05$.

Figure 6. Citizen cooperation as a function of State relative update rate. (A) Mean; (B) variance. $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05$.

Finally, we provide additional evidence for the role of bootstrapping in our results for constrained States by examining States that undergo local, rather than global, mutation. In our main simulations, State mutants select a new punishment threshold T from the uniform distribution on [0,1], representing the possibility of more radical innovation or experimentation characteristic of legislature-driven rules. Because mutation is global, a State with a low punishment threshold can jump directly to a high punishment threshold. The main factor that potentially prevents such a jump from successfully motivating cooperation is a budget constraint. If the State cannot afford to finance its radically higher punishment threshold, reaching that higher threshold will require returning to a lower threshold and then bootstrapping up, as discussed above.

If, however, we implement local mutation, which represents more incremental innovations consistent with precedent-constrained judge-made law, even non-constrained States must now bootstrap. Recall that in our local mutation simulations, State mutants select a new T, which is their previous T plus a value randomly sampled from a normal distribution with mean zero and standard deviation σ (censored such that negative T values are set to zero and values greater than one set to one). Now, even in the absence of a budget constraint, States beginning with a low threshold will on average have to go through a series of gradually increasing T values and are far less likely to jump directly to a higher T. As a result, we expect to observe an optimal intermediate update rate using local mutation, regardless of budget constraints. This result is in fact what we observe, as shown in Figure 7.

Figure 7. Mean citizen cooperation as a function of State relative update rate, using local State mutation. $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05,\sigma =0.1$.

Figure 7. Mean citizen cooperation as a function of State relative update rate, using local State mutation. $N,n=10,r=3,\alpha =0.5,\gamma =1.25,{\mu }_s,{\mu }_c=0.05,\sigma =0.1$.

In addition to providing support for the role of bootstrapping in our previous simulations, these simulations using local mutation potentially give additional insight into the dynamics for different forms of legal institutions. Our results suggest that statutory (legislature-driven) and common law legal rules and systems potentially display different vulnerabilities connected to the States’ update rate. Legislative rules and systems are capable of more radical innovation, but are vulnerable to a loss of public political or financial support in the context of a citizen rebellion. Common law rules and systems that evolve more incrementally are less likely to lose public support, because new rules differ only marginally from existing rules. However, owing to that incrementalism, a common law system that updates more slowly than the Goldilocks point takes too long to achieve maximum coercive power by the state and is far less able to respond to sudden changes in citizen norms.

4. Discussion and Conclusions

In recent years, a large body of cross-disciplinary research has investigated the role that peer punishment plays in generating cooperation. Most existing evolutionary game theory literature exploring punishment focuses on informal punishment administered by peer individuals: vigilante punishment that depends on social norms to enforce cooperation [26,27,28,29,30,30].

Our co-evolutionary model contributes to a nascent literature that studies the punishment dynamics of centralized institutions, which offer unique advantages in the regulation of human behavior. Recent work explores the relative cost advantage of institutional punishers who spread the cost of punishment among themselves [2,3,16]. Our model extends the study of institutions beyond this simple cost-sharing function of group-based punishment, to investigate a unique advantage that legal punishment offers relative to decentralized punishment. As an institution, legal punishment differs from vigilante punishment precisely because a centralized institution can generate procedural rules that affect the evolutionary rates of primary legal punishment rules. In particular, lawmakers can deliberately adopt procedural rules to slow or accelerate the rate at which legal rules are amended in order to promote the possibility of successful long-term citizen collaboration. These procedural rules constitute the meta-rules that make law distinctive from ordinary social norms or behavior [31].

We show that the evolutionary rate of legal punishment rules can itself affect both the level and variance of cooperation that a state can incentivize. Our model demonstrates that, in the absence of budgetary constraints, a state can force its citizens to adapt to rules of punishment if the opportunity for legal punishment rules to evolve is restricted. Beyond longer time horizons and a check on impulsive decision-making, relatively slow updating provides the state with an additional benefit: a first-mover advantage that comes from the ability to pre-commit to punishing by tying its own hands.

A similar phenomenon has been observed in biological contexts, where species that evolve relatively more slowly in symbiotic or parasitic relationships can force their partners or hosts to play a more cooperative strategy. In particular, when a species evolves more slowly than its partner, the partner will adaptively respond to the species’ strategy rather than the other way around [4,23,32,33,34]. Likewise, when legal punishment rules evolve more slowly than citizen contribution strategies, citizens will adaptively respond to punishment rules.

At the same time, our model also illustrates the potential real-world limit of states’ first-mover advantage. Most democratic states rely on citizens for budget revenues or political legitimacy. Our model demonstrates that this dependence on the citizenry might make legal punishment vulnerable to sudden shifts in which citizens en masse abandon compliance with the rules. As the model demonstrates, any procedural rule that makes it more difficult to revise law simultaneously forces citizens to adapt to legal rules more responsively and lessens the law’s ability to adapt responsively to outbreaks of citizen lawlessness.

The evidence of a ‘Goldilocks’ effect, in which states maximize cooperation and minimize its variance, is a potentially important finding for policymakers looking to optimize the rate of state updating. The optimal rate avoids volatile cycling between high cooperation and mass defection; such stability likely permits economic and social actors to engage in long-term planning.

Quantitative empirical evidence suggests the existence of a real-world Goldilocks effect in the context of amendment rates for national constitutions. Elkins et al. [35] document a nonmonotonic relationship between a constitution’s amendment rate and the constitution’s life expectancy. Extremely high and low amendment rates are both associated with shorter life spans. Interestingly, India’s constitution, which has adopted different amendment procedures for different topics, possesses an amendment rate that is ‘just right’, neither too flexible nor inflexible.

The existence of an optimal relative update rate for legal rules also has significant implications for both evolutionary game theory and legal scholarship. The optimal Goldilocks rate of evolution reflects the twin sources of power available in modern states: the power of the states to coerce cooperation and the power of citizens to rebel. Our results suggest that in modern democratic states in which a state’s ability to regulate is constrained by citizen support, states must take citizen support into account in considering at what rate to revise legal rules.

Our model includes some important simplifying assumptions that should be noted. First, our States do not engage in any explicit form of strategic reasoning, future planning or introspective rationality. Instead, states update purely based on the imitation of other states that are more successful. We chose to focus on imitation in light of the significant empirical evidence that states frequently copy each others’ legal rules, both domestically in the U.S. and internationally [36,37,38,39]. However, it will be important for future work to explore how adding varying degrees of strategic planning affect the outcomes of our model.

Furthermore, as recent events in Europe and the Middle East show, when citizens rebel en masse for a sufficiently long period of time, a state will sometimes lose legitimacy and cease to function altogether. Our model does not include this loss of state functioning, nor does it consider legitimacy. More generally, there are many possible ways in which budget constraints could be implemented, only one of which we explore here. Future work should investigate the consequences of alternative forms of budget constraint.

In addition, our model includes the simplifying assumption of binary punishment, which reflects the nature of discrete criminal penalties that apply in many legal areas, like environmental law, tax law and financial regulation. The institution of graduated punishment, which is observed in various civil fines and penalties, represents an important opportunity for future work [40,41,42]. We also assume that all states are identical in terms of size, punishment cost and strength, mutation rate, degree of budget constraint and update rate. Future studies should explore the evolutionary dynamics among heterogeneous states, as well as asking what happens when the state update rate is itself allowed to evolve, rather than being exogenously fixed as it is in our model. It will also be illuminating to explore the interaction between the institutional incentives wielded by States in our model and Citizen behavior in contexts that are beyond the reach of the State’s punishment (e.g., [43]), as well as the State’s use of monetary versus social sanctions [44].

In these and other ways, we hope our work will spur further theoretical study of the co-evolutionary dynamics of institutional forms of punishment, and the relationship between the evolutionary rate of legal rules and efficient regulation of human behavior. Such work is particularly important in areas like financial regulation and tax law, where citizen behavior changes at a very rapid pace, and lawmakers often argue that law should adapt quickly in response.

Our work can also guide an emerging experimental literature that investigates how to design centralized punishment institutions to best promote cooperation [45,46,47]. Further theoretical and experimental inquiry can help us understand how best to design institutions that appropriately balance the restraining pull of stability and tradition with the adaptive push of transformation and change.