How Moral Codes Evolve in a Trust Game

Abstract

This paper analyzes the dynamic stability of moral codes in a two population trust game. Guided by a moral code, members of one population, the Trustors, are willing to punish members of the other population, the Trustees, who defect. Under replicator dynamics, adherence to the moral code has unstable oscillations around an interior Nash Equilibrium (NE), but under smoothed best response dynamics we obtain convergence to Quantal Response Equilibrium (QRE).

1. Introduction

In the lab, as in everyday life, we often observe trusting behavior even when it is unwarranted according to simple models of rational play. One possible explanation is that agents are willing and able to punish violations of trust. That explanation gains credence when the punishment is supported by a moral code and not just by arbitrary social preferences.

The purpose of the present paper is to explore that explanation by constructing and analyzing a simple evolutionary game model. In the context of a simple Trust game (aka sequential Prisoner’s Dilemma), we show how to (i) specify a moral code in an analytically tractable way, and (ii) analyze the stability of the equilibria under alternative dynamic adaption processes. The approach originates [1] but we extend it considerably by introducing and formalizing the idea of a moral code. Some of the ideas in the present paper are described (with attribution) in Chapter 13 of [2].

Loose verbal definitions of moral codes can be gleaned from writers from Aristotle down to [3] and beyond. Here we take a moral code to be an understanding of how to live and work together shared within a cohesive group of humans. The shared understanding can be summarized in a set of rules, which can be explicit or implicit [4]. Typically group members share, via gossip, information on code compliance, helping them avoid exploitation and reducing (and sharing) the cost of punishing noncompliers [5].

To build analytical structures capturing aspects of this verbal description, we focus on a very specific but revealing strategic interaction, a simple Trust game adapted from [1]. In that context, we introduce a moral code that enables Trustors to reduce interactions with, and to share the cost of punishing, untrustworthy partners. Our approach in some ways is reminiscent of the trustworthiness-detection approach of [6,7]) and in other ways is reminiscent of assortative matching protocols based on observables (e.g., see [8,9]). In our case, sorting is imperfect (gossip is not completely reliable) so some abuse of trust remains and the cost of punishing the abusers is shared within the group.

Our point of departure, [1], assumes that vengeful players derive utility from punishing trust violators. These vengeful players can be thought of as altruists, since they bear a personal material cost to punish while contributing to social efficiency: the fear of punishment leads to more trustworthy behavior. Nevertheless, the model has a long-run equilibrium in which vengeful players survive and trusting and trustworthy behaviors are quite common. Other known ways to support substantial altruistic cooperation include repeated interaction (for a helpful survey, see [10]), genetic relatedness (for nice summaries, see [11,12]) and the presence of types that favor cooperation in games of incomplete information (e.g., see [13,14]). The current paper adds moral codes to the list.

Our model of a moral code was inspired by reading accounts of hunter-gatherer cultures, but it could be reinterpreted as a model of corporate culture. The papers [15,16] argue that the Trust game is fundamental to corporate culture, and that firms exist to overcome distrust via social learning. The paper [17] finds that teamwork (captured in an assortative matching protocol) can explain trusting behavior in a Trust game with only one population.

This single population approach is quite common in the related literature. We simplify the analysis by working with a two population game assuming that roles evolve independently. We have in mind learning and adaptation dynamics, but the genetic analogue to our independence assumption would be that behavior in the Trustor role and the Trustee roles are controlled by genes on different chromosomes so that there is no linkage. Absent such independence, stability properties may differ in games with one versus two populations (e.g., see [18]).

We begin in Section 2 with an exposition of the Trust game with and without the moral code. The moral code affects the behavior of Trustors and of Trustees and creates a new mixed Nash Equilibrium (NE). We also compute the expected payoffs necessary to study the dynamics presented in the following sections. Section 3 reviews replicator dynamics ([19,20]) and then shows that the mixed NE is not evolutionarily stable under two-population replicator dynamics (see [21]). The next section reviews smoothed best response dynamics (aka logit dynamics, see [22,23]), and applies them to the current model. We obtain convergence to a quantal response equilibrium near the mixed NE. The stability of each dynamic system is then studied by analyzing the Jacobian matrix and the accompanying phase diagrams. Finally, Section 5 discusses implications of our results.

2. The Game

The basic Trust game can be thought of as a sequential, two-population version of the Prisoner’s Dilemma. Each Trustor (labelled 1 in what follows) can choose either to not to play (N), ensuring zero payoff for herself and her Trustee partner (labelled 2), or else chose to trust (T). In that case, the Trustee partner decides whether to cooperate (C) or defect (D), with respective payoffs (1, 1) or (–1, 2). Of course, the Trustees’ best response is D, implying that cooperation unravels in this basic game.

Now suppose that Trustors have the ability, at personal cost $c·h$, to inflict a chosen amount of harm $h>0$ on Trustees, where $c\in (0,1)$ can be thought of as a punishment technology parameter, and that Trustors may have a vengeful disposition. Specifically, suppose that in an angry state triggered by Trustees choosing D, Trustors get utility bonus of $vlnh$ from inflicting harm h, while in other emotional states, Trustors’ utility is just the material payoff. The motivation (vengeance) parameter $v\ge 0$ captures the individual’s temperament and evolves only according to the material payoffs.

Thus, following a choice of D by a Trustee, the Trustor maximizes $U=-1-c·h+vlnh$. The unique solution is $h^{*}=v/c$, and the Trustor’s material payoff in this case is $W^1=-1-c·h^{*}=-1-v.$ The material (and also utility) payoff for the Trustee then becomes $2-h^{*}=2-v/c$, as in Figure 1. If $v>c$, then this payoff is less than 1 and choosing D is no longer a best response. As noted in [1], the threat of vengeance thus rationalizes Trustees’ cooperation and justifies Trustors’ initial trust, and so the first-order free rider problem is solved.

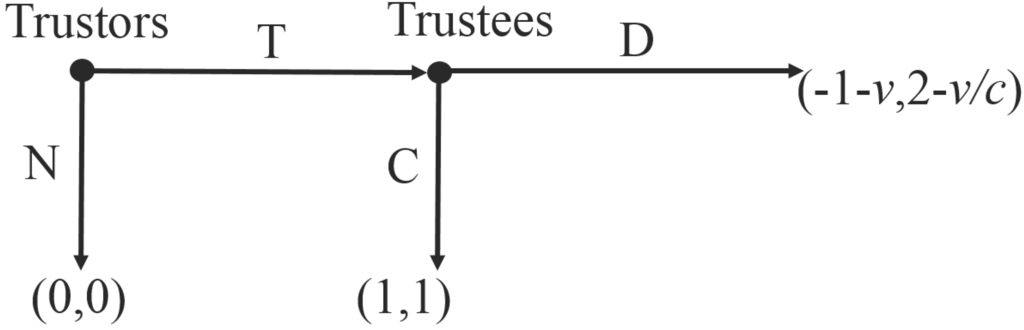
Figure 1. Trust Game in Extensive Form.

Figure 1. Trust Game in Extensive Form.

However, this happy conclusion is based on the implausible assumption that the Trustees can see that indeed $v>c$ or in other words that Trustors have a transparent and quite vengeful disposition. Further, it is in the interest of a non-vengeful (where $v=0$) Trustor to mimic the outward appearance of a vengeful type, but without incurring the cost of actually inflicting harm. Assuming opaque dispositions, we obtain the population game payoff matrix shown in Table 1.

Table 1. Trustors’ (row) and Trustees’ (column) Material Payoffs.

	Trustees:
Trustors:	C [p]	D [1−p]
$\left[q\right]:v>c$	1, 1	$-(1+v),2-\frac{v}{c}$
$[1-q]:v=0$	1, 1	–1, 2

Table 1. Trustors’ (row) and Trustees’ (column) Material Payoffs.

	Trustees:
Trustors:	C [p]	D [1−p]
$\left[q\right]:v>c$	1, 1	$-(1+v),2-\frac{v}{c}$
$[1-q]:v=0$	1, 1	–1, 2

The vengeful Trustor type receives the material payoff given in first row.1 Facing a p share of Cooperators and $(1-p)$ share of Defectors, the expected (material) payoff for a vengeful Trustor is then $W_v^1=2p-1-v(1-p)$. A non-vengeful type of Trustor, with payoffs given in the second row of Table 1, obtains an expected payoff of $W_0^1=2p-1.$ The Trustor population mean payoff therefore is $W^1=q·W_v^1+(1-q)·W_0^1=-vq(1-p)+2p-1$. The payoff to the Trustees, when cooperative, is $W_C^2=1$, and when defecting is $W_D^2=2-\frac{qv}{c}.$ The Trustee population mean payoff thus is $W^2=p+(1-p)·(2-\frac{qv}{c})$. The game has two pure strategy NE with $(p^{*},q^{*})=(0,0),(1,1)$ and a family of mixed NE such that $p^{*}=1$ and $q^{*}\ge \frac{c}{v}$.

Evolutionary forces for Trustors are driven by payoff differential $\Delta W^1=W_v^1-W_0^1=-v(1-p)$. As for Trustees, the payoff differential is $\Delta W^2=W_C^2-W_D^2=\frac{qv}{c}-1$. Figure 2 illustrates the phase diagram assuming $v=2c,c=0.5$ under replicator dynamics.2

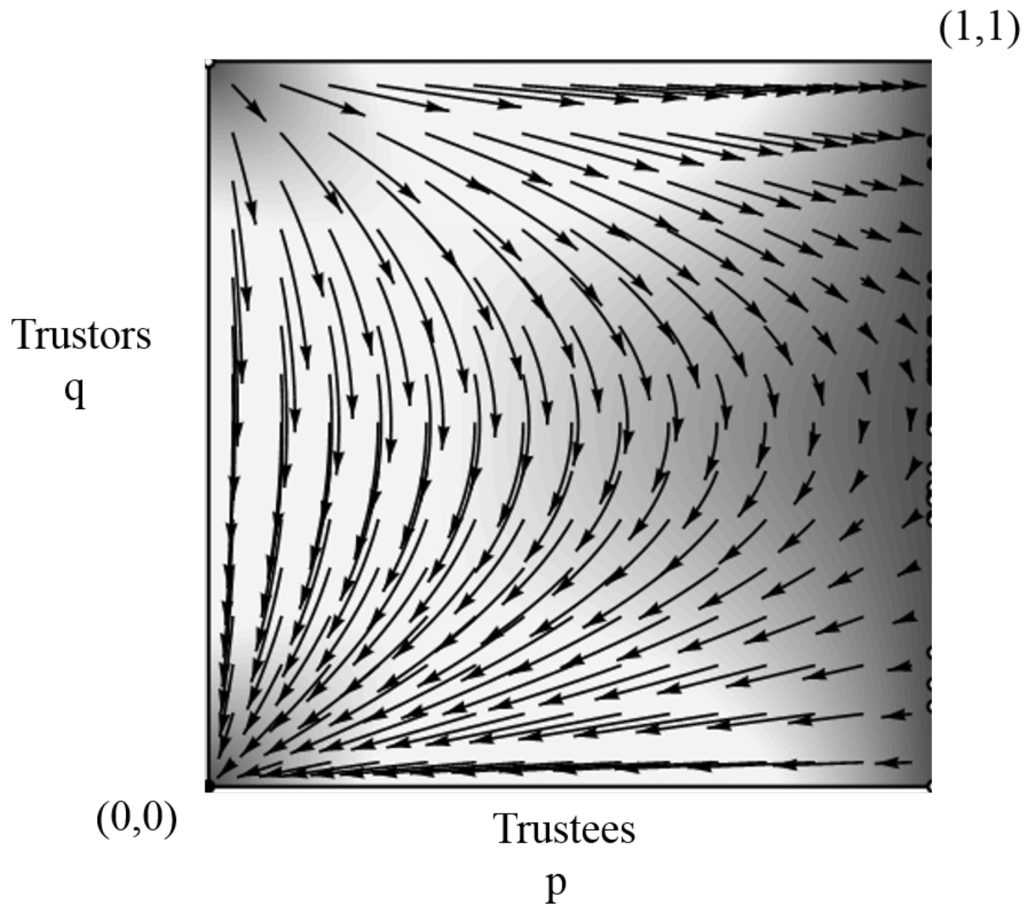
Figure 2. Replicator dynamics of the simple game ($v=2c=1$).

Figure 2. Replicator dynamics of the simple game ($v=2c=1$).

Clearly the sub game perfect pure NE $(0,0)$ has a large basin of attraction. The NE segment consists of neutrally stable points, but in a long-run sense the entire segment is unstable and the ultimate destination is $(0,0)$ from every initial condition. The idea is that small perturbations from $p=1$ converge back to the segment at smaller values of q because they entail costly punishment by vengeful trustors. Thus q tends to drift to lower values until it crosses the boundary $\frac{c}{v}$, below which the point $(1,q)$ is unstable (a source) rather than neutrally stable. Replicator dynamics then lead directly to $(0,0)$. We don’t formalize this intuitive argument here because it would clash with the very similar (but not quite identical) formulation of trembles e in the next model, and point to [26] for the formal analysis of a closely related model. The upshot is that the present model, neither vengeance nor trust is evolutionary viable.

Now suppose that vengeance in our model is backed by a moral code which calls on each Trustor (a) to share equally the cost of punishing all Trustees who defect, and (b) to share information via gossip on which Trustees defect so that they can be avoided in the future.

One scenario on cost sharing is that a random person detects the defector and is called on to bear the entire cost of punishment, e.g., by destroying some of the defector’s personal property. Another scenario is that gossip immediately makes everyone aware of the transgression and everyone bears an equal share of the punishment cost, e.g., by shunning the culprit for a month. In a large population, either extreme scenario works, as do intermediate scenarios that involve larger cost shares for individuals who happen to be nearer the scene of the crime, so to speak. It is the expected cost that matters in our matrix game, and our assumption is that the expected cost is shared equally among all individuals who comply fully with the moral code.

Clearly it is personally advantageous to free ride, i.e., to receive information as in (b) but not to share costs of punishing third parties as in (a). We have in mind a coherent group of Trustors who interact frequently, and who therefore can discipline free riders. As argued by [4,5] and numerous other authors, without such discipline a moral code will soon disappear. Thus (a) and (b) are a package adopted by some Trustors, who we refer to as code compliers (K). The other Trustors, called non-compliers (N), avoid the costs of punishing third parties but have no access to gossip.

Payoffs are derived as follows. Trustors adopting strategy K gossip among themselves, but the information is imperfect, as captured in the error rate parameter $e\in (0,1)$: K-Trustors mistakenly avoid Trustees playing C with probability e, and with the same probability they encounter Trustees playing D. The K-Trustors also share equally the cost v of punishing the Defectors they encounter to the utility-maximizing degree $h^{*}=\frac{v}{c}.$ This cost v is incurred at rate $(1-p)e$ and spread over population share q of compliers, so the pro-rata punishment cost is $\frac{ev(1-p)}{q}$ for all compliers. Compliers also get the sucker payoff $-1$ with probability e when matched with Defectors, and with the same probability, those Defectors receive the temptation payoff (2) less the total punishment ($\frac{v}{c}$). Compliers matched with Cooperators get the reward payoff (1) with probability $1-e$, as do the Cooperators. Applying the pro-rata punishment cost, we get the payoffs shown in the top row of Table 2. The bottom row, for the fraction $1-q$ of non-compliers, is the same as in Table 1.

Table 2. Payoffs Under the Moral Code.

	Trustees:
Trustors:	C [p]	D [1−p]
$\left[q\right]:K$	$1-e-\frac{ev(1-p)}{q},1-e$	$-e-\frac{ev(1-p)}{q},e(2-\frac{v}{c})$
$[1-q]:N$	1, 1	-1, 2

Table 2. Payoffs Under the Moral Code.

	Trustees:
Trustors:	C [p]	D [1−p]
$\left[q\right]:K$	$1-e-\frac{ev(1-p)}{q},1-e$	$-e-\frac{ev(1-p)}{q},e(2-\frac{v}{c})$
$[1-q]:N$	1, 1	-1, 2

The expected payoff for non-compliers (N) coincides with that of unvengeful Trustor in the previous model, $W_N^1=2p-1.$ Cost sharing boosts K’s expected payoff when D is relatively rare and K is relatively common. Further, the reduction of D encounters due to the adoption of a moral code helps increase compliers’ expected payoff. The payoff for a compliant Trustor is then $W_K^1=p-e(1+\frac{v(1-p)}{q}).$ The presence of a moral code also changes the payoff for Trustees; the cooperative expected payoff is now $W_C^2=1-qe$ and defecting expected payoff is $W_D^2=qe(2-\frac{v}{c})+2(1-q).$

Besides the trivial NE $(p,q)=(0,0)$, we also obtain an interior NE in this game at the intersection of the loci $\Delta W^2=0$ and $\Delta W^1=0$, where $\Delta W^1=W_K^1-W_N^1=1-p-e(1+\frac{v(1-p)}{q})$ and $\Delta W^2=W_C^2-W_D^2=q(2+e(\frac{v}{c}-3))-1.$ For example, let $e=0.05,v=2c=1$. Then the interior NE is $(p^{*},q^{*})=(0.945,0.513)$ with a high degree of trustworthy Trustees, and slight majority of moral code compliance.

Is this equilibrium dynamically stable with a large basin of attraction? Does the answer depend on the assumed family of dynamics? We answer these questions in the following sections.

3. Replicator Dynamics

We begin our analysis with replicator dynamics. First developed by [19] to describe biological evolution of phenotypes, these dynamics were later shown to describe certain sorts of imitation processes ([27,28]). Under replicator dynamics, the growth rate of each strategy’s share (e.g., $\dot{p}/p$) is equal to its payoff relative to population average payoff. Recall that our game has two populations (Trustees and Trustors), whose behavior determines the payoffs. The population average payoff for Trustees is ${\overline{W}}^2=p{W}_C^2+(1-p)W_D^2$, so we can write the relative payoff for cooperation as $W_C^2-{\overline{W}}^2=W_C^2-p{W}_C^2-(1-p)W_D^2=(1-p)\Delta W^2$. Similar algebra applies to Trustors. Thus, for the two population Trust game in Table 2, replicator dynamics are given by the following system of ordinary differential equations in the state variables ($p,q$).

$$\begin{array}{ccc}\hfill \dot{p}& =& p(1-p)\Delta W^2=p(1-p)[q(2+e(\frac{v}{c}-3))-1]\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \dot{q}& =& q(1-q)\Delta W^1=q(1-q)[1-p-e(1+\frac{v(1-p)}{q})]\hfill \end{array}$$

In order to determine the local stability of an interior equilibrium under replicator dynamics, we form the Jacobian matrix $J=\left(\begin{array}{cc}\frac{\partial \dot{p}}{\partial p}& \frac{\partial \dot{p}}{\partial q}\\ \frac{\partial \dot{q}}{\partial p}& \frac{\partial \dot{q}}{\partial q}\end{array}\right)$ which results in

$$\begin{array}{ccc}\hfill \frac{\partial \dot{p}}{\partial p}& =& (1-2p)\Delta W^2+p(1-p)\left[\frac{\partial \Delta W^2}{\partial p}\right]=(1-2p)0+p(1-p)0=0.\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \frac{\partial \dot{p}}{\partial q}& =& p(1-p)\left[\frac{\partial \Delta W^2}{\partial q}\right]=p(1-p)[2+e(\frac{v}{c}-3)]\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \frac{\partial \dot{q}}{\partial p}& =& q(1-q)\left[\frac{\partial \Delta W^1}{\partial p}\right]=q(1-q)[-1+\frac{ev}{q}].\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \frac{\partial \dot{q}}{\partial q}& =& 0+q(1-q)\left[\frac{\partial \Delta W^1}{\partial q}\right]=(1-q)\left[\frac{ev(1-p)}{q}\right]\hfill \end{array}$$

(5)

Evaluating these expressions at $e=0.05,v=2c=1$ and $(p^{*},q^{*})=(0.945,0.513)$, we obtain $J\approx \left(\begin{array}{cc}0& 0.102\\ -0.226& 0.003\end{array}\right).$ The characteristic equation is $0=|J-\text{λ}I|\approx {\text{λ}}^2-0.003\text{λ}+0.023$ with approximate roots (eigenvalues) $\text{λ}=0.001\pm 0.152\sqrt{-1}.$

The implication is that, under replicator dynamics, the interior equilibrium is locally unstable and trajectories (depicted in Figure 3a) near it tend to slowly spiral outwards, in a clockwise direction.3 Figure 3a also shows that the trivial corner NE is evolutionary stable, but its basin of attraction is narrow, including only initial states where Trustors’ compliance rate q is very low.

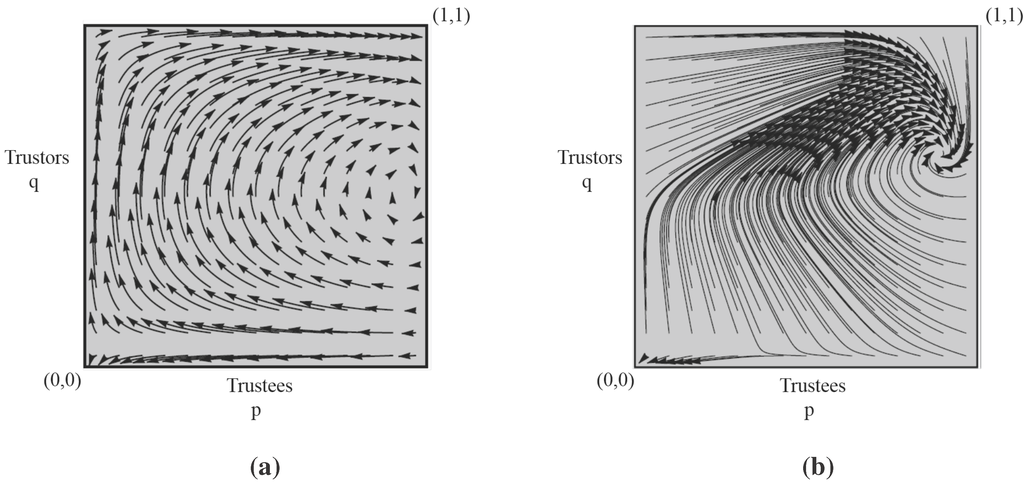
Figure 3. Evolutionary dynamics of the game under moral codes ($e=0.05$, $v=2c=1$). (a) Replicator; (b) Logit ($\eta =0.1$)

Figure 3. Evolutionary dynamics of the game under moral codes ($e=0.05$, $v=2c=1$). (a) Replicator; (b) Logit ($\eta =0.1$)

4. Logit Dynamics

An alternative to replicator dynamics, often favored by economists (e.g., see [29]), is smoothed best response dynamics, or more specifically, logit dynamics (e.g., [22,23]). Logit dynamics has elements of both belief-based learning (since it is derived from a form of perturbation of the best-reply dynamics) and reinforcement learning (since players seek to maximize instantaneous payoffs at each revision opportunity). In particular, logit dynamics predicts that players choose a best-reply to the distribution of strategies existing in the population with a probability given by the logistic distribution.

The ODE system under logit dynamics of the state variables (p, q) is defined as

$$\begin{array}{ccc}\hfill \dot{p}& =& \frac{exp[(1/\eta )·W_C^2]}{exp[(1/\eta )·W_C^2]+exp[(1/\eta )·W_D^2]}-p\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \dot{q}& =& \frac{exp[(1/\eta )·W_K^1]}{exp[(1/\eta )·W_K^1]+exp[(1/\eta )·W_N^1)]}-q\hfill \end{array}$$

(7)

where $1/\eta$ is the precision parameter. It is well known that the equilibrium $\dot{q}=\dot{p}=0$, called the quantal response equilibrium (QRE), exists but differs from the mixed NE except in the infinitely precise limit $\eta \to 0$ (e.g., [30]). For $\eta =0.1$ and the other parameters used earlier, the QRE is $(p^{**},q^{**})=(0.892,0.512)$, fairly close to the NE $(p^{*},q^{*})=(0.945,0.513)$.

In order to determine the local stability of $(p^{**},q^{**})$ under logit dynamics, we form the Jacobian matrix for (6) and evaluate it at that equilibrium point using baseline parameters. We obtain $J=\left(\begin{array}{cc}-0.165& 0.188\\ -0.216& -0.08\end{array}\right).$ The characteristic equation is $0=|J-\text{λ}I|\approx {\text{λ}}^2+0.245\text{λ}+0.043$ with approximate roots (eigenvalues) $\text{λ}=-0.009\pm 0.186\sqrt{-1}.$

Thus the interior equilibrium is locally stable under logit dynamics. As depicted in Figure 3, logit dynamics quickly take the state to a medium size neighborhood of the equilibrium, and then slowly spiral into $(p^{**},q^{**})$. The trivial NE remains evolutionary stable within its narrow basin of attraction.

Stability under logit dynamics depends on parameter values, but is rather robust. In the baseline scenario when $v=2c=1$, it includes the range $0\le e\le .24$ that a compliant Trustor meets an defecting Trustee. Indeed, when $e=0.24$, the QRE becomes $(0.536,0.576)$, which is not too far from the NE $(0.584,0.568)$.4 The eigenvalues of the corresponding Jacobian are $\text{λ}=-0.591\pm 2.5\sqrt{-1}$, which imply that the QRE remains evolutionary stable. However, as shown in Figure 4, its basin of attraction is much smaller and conversely the trivial NE has a much larger basin. This makes intuitive sense, since very unreliable gossip prevents Trustors from properly identifying Defectors, and reduces assortativity.

The impact of the other parameters, c and v, on the stability of the interior steady state and its basin of attraction is minor. For example, assuming parameters values of $e=0.05$ and $c=v=1$, the dynamics remain qualitatively unchanged (although, of course, the steady state values change). This suggests that gossip allows cooperation in populations with lower vengeance or high punishment costs.

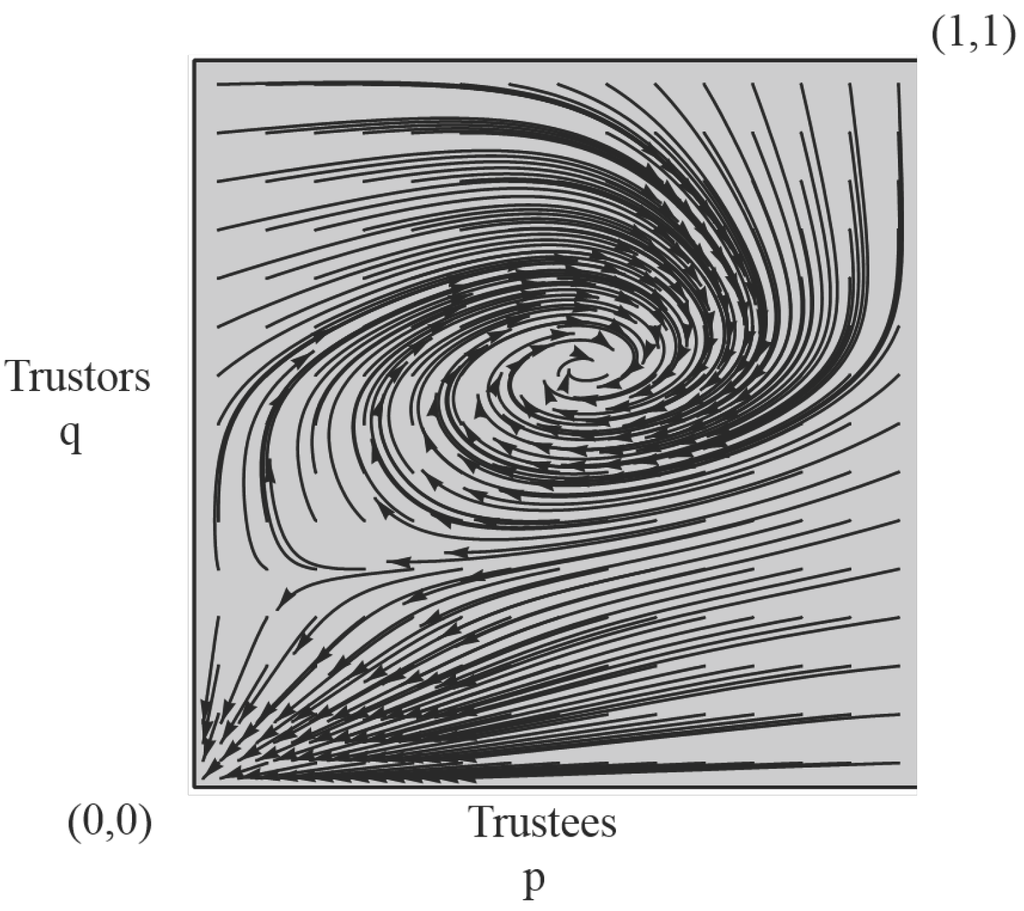
Figure 4. Logit dynamics of the game under moral codes ($\eta =0.1$, $e=0.24$, $v=2c=1$).

Figure 4. Logit dynamics of the game under moral codes ($\eta =0.1$, $e=0.24$, $v=2c=1$).

5. Conclusions

In this paper we illustrate how moral codes can help sustain trust and trustworthiness. The idea is that gossip permits the identification (with some error) of untrustworthy players, and that the cost of punishing such players is shared among norm-compliant trustors.

The model assumes two large populations, whose behavior is analyzed using two alternative forms evolutionary dynamics. Replicator dynamics lead to behavior that oscillates around the interior NE. An intuition behind replicator dynamics is that players imitate the strategy of other players in the same role only to the extent that the other’s strategy currently earns a higher payoff. Arguably, logit dynamics are more economically meaningful because they involve a smoothed best response to the current state, and thus incorporate a greater degree of rationality that is compatible with both beliefs-based and reinforcement learning.

Under reasonable parameters, we find that the steady state under logit dynamics is not far from the interior NE. The system converges to this interior equilibrium, and the size of the basin of attraction then mainly depends the effectiveness of moral codes, especially the reliability of gossip. Less reliable gossip implies a smaller basin of attraction around the interior NE. Drawing on the results presented above, Chapter 13 of [2] will note that results are rather insensitive to parameters representing the cost of punishment c, and the morally sanctioned degree of punishment v.

One can imagine more technically advanced versions of the model. For example, the exogenous inaccuracy rate e for gossip could be endogenized, depending on the share of code compliers and on how they discipline free riders. Alternatively, it would be interesting to study whether moral codes are robust to random pertubations in the spirit of [31] or [32]. The effect of allowing an individual’s play in one role to be correlated with play in another role could be investigated using a deterministic one-population model with a higher dimensional state space. One could also investigate the extent to which our model supports the ideas of [33,34], whose agents may possess virtuous disposition, i.e., may be a type of individual with an underlying desire to act as morality requires, together with a particular belief about what morality requires.

The modeling approach presented in this paper surely can be extended broad classes of games and moral codes. Which sorts of moral code will be most effective in promoting pro-social behavior? Which sorts of games are most amenable to moral policing? We hope that our simple examples will inspire other researchers to seek general answers to these questions.