The Hitchhiker’s Guide to Adaptive Dynamics
Abstract
:1. Introduction
2. Fundamental Concepts
| Term | Description |
|---|---|
| Canonical equation | Differential equation describing a deterministic approximation of evolutionary dynamics with small mutational steps. |
| Convergence stable strategy | Singular strategy that, within a neighborhoods, is approached gradually. |
| Continuously stable strategy (CSS) | Singular strategy that is both convergence stable and evolutionarily stable. |
| Dimorphic population | Population with individuals having either of two distinct trait values. |
| Evolutionarily singular strategy | Trait value at which the selection gradient vanishes. |
| Evolutionarily stable strategy (ESS) | Trait value that cannot be invaded by any nearby mutant. |
| Invasion fitness | The expected growth rate of a rare mutant. |
| Monomorphic population | Population consisting of individuals with only one distinct trait value. |
| Pairwise invasibility plot (PIP) | Graphical illustration of invasion success of potential mutants when the population is monomorphic. |
| Per capita growth rate | The expected rate at which an individual produces offspring. Can be determined by dividing the population growth rate by the number of individuals. |
| Polymorphic population | Population with individuals having either of several distinct trait values. |
| Selection gradient | Slope of the invasion fitness at the resident trait value. Gives information on the direction and speed of evolutionary change. |
| Trait evolution plot (TEP) | Graphical illustration of invasion success of potential nearby mutants when the population is dimorphic. |
3. Monomorphic Evolution
3.1. Invasion Fitness and the Selection Gradient
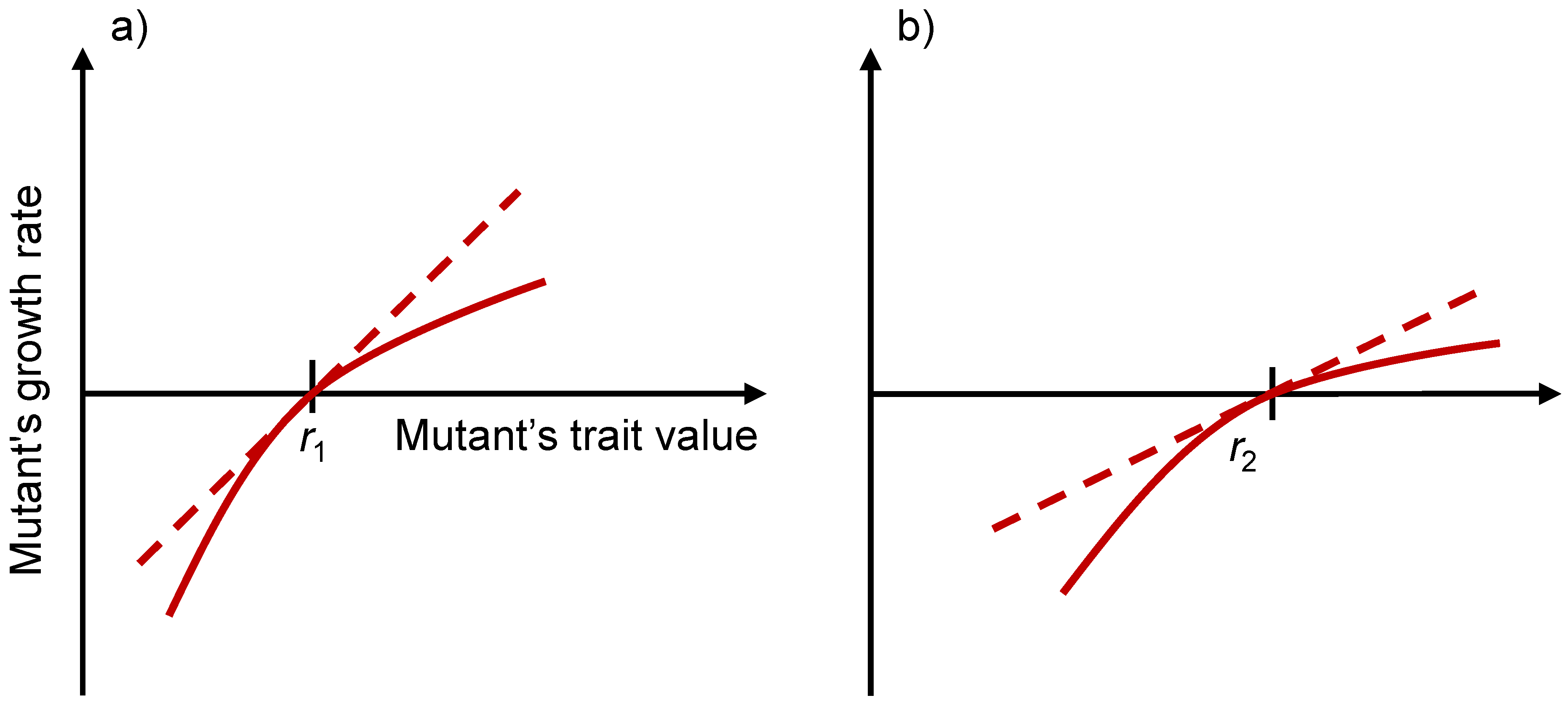
3.2. Deriving the Invasion Fitness and the Selection Gradient from a Demographic Model
3.3. Evolutionarily Singular Strategies and the Fitness Landscape
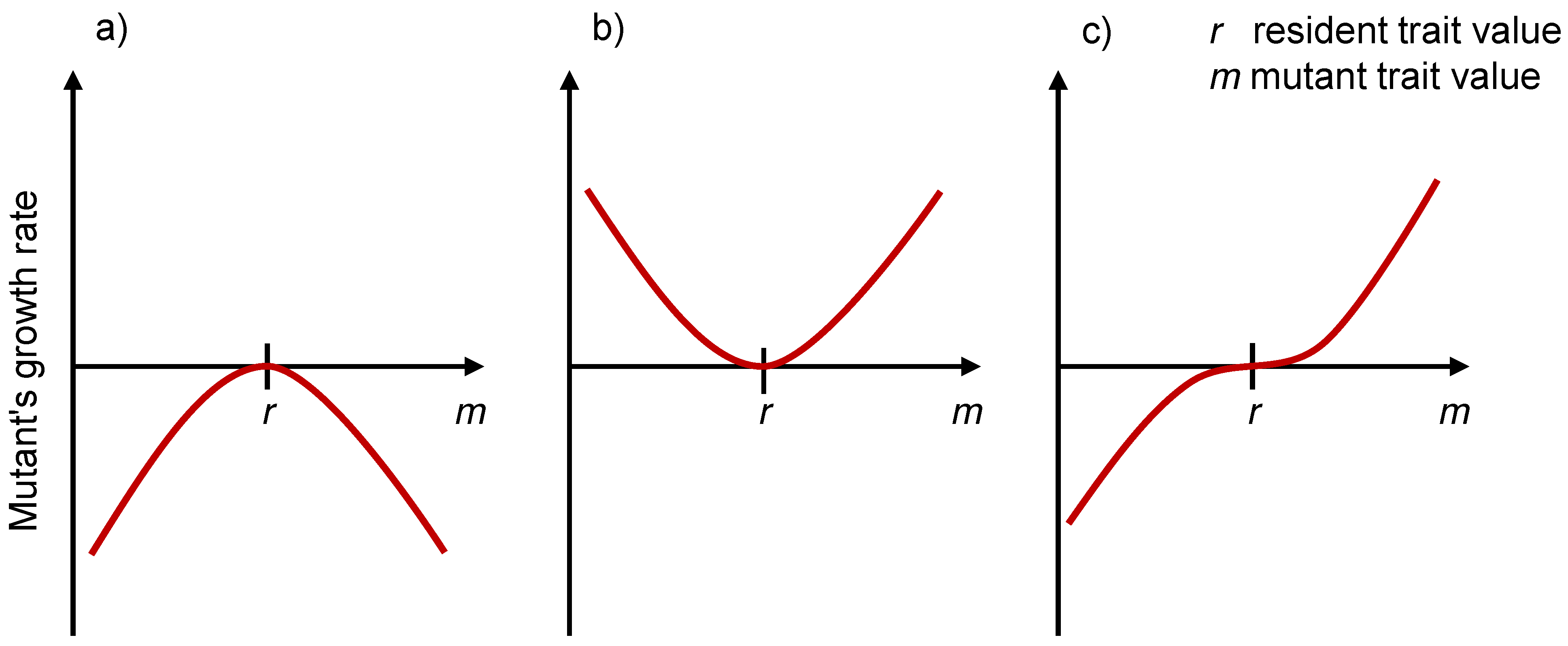
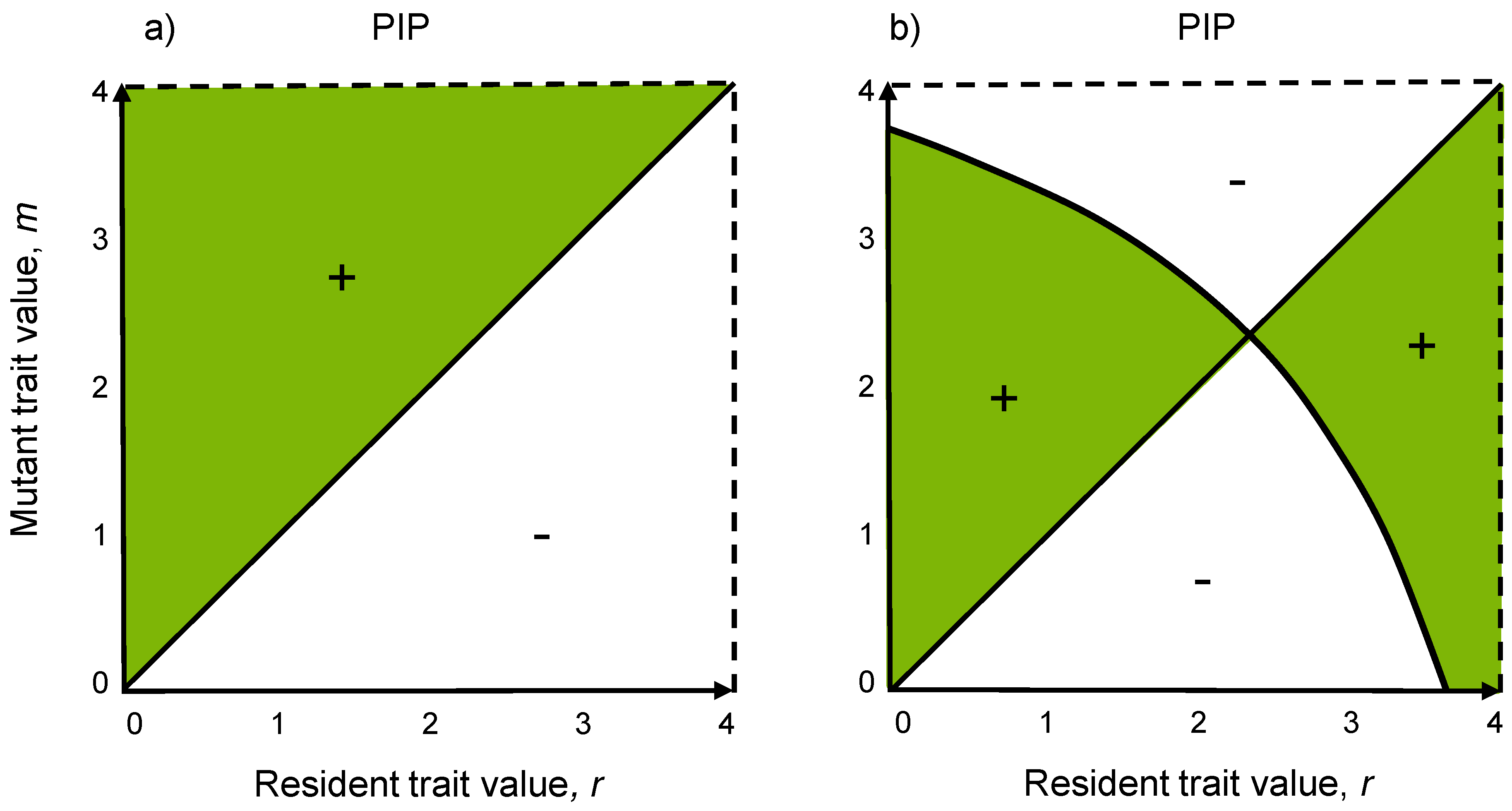
3.4. Pairwise Invasibility Plots
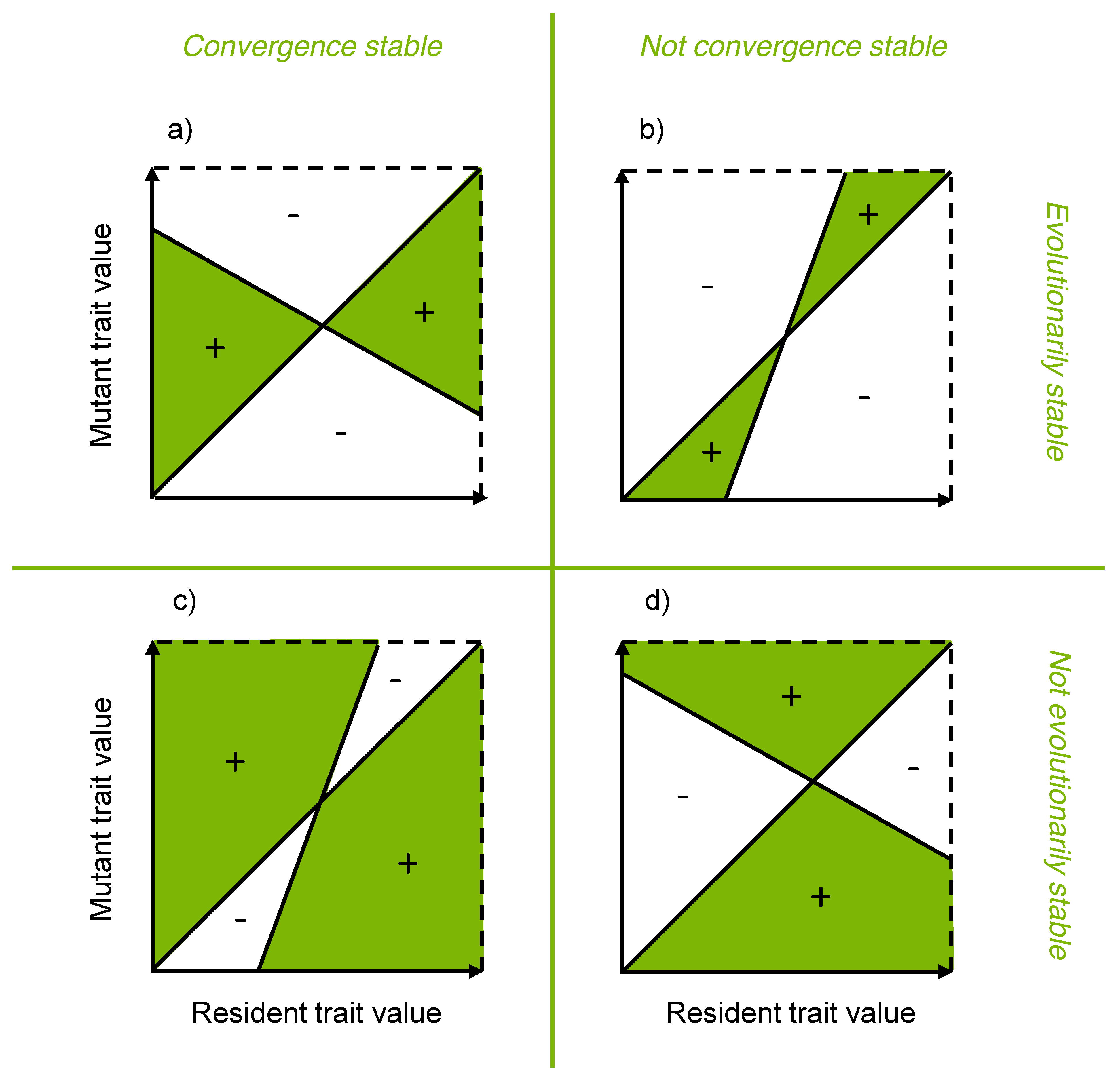
3.5. Evolutionary Stability Analysis
3.6. Modeling Gradual Evolution
4. Example: Evolution of Arrival Time of Migratory Birds
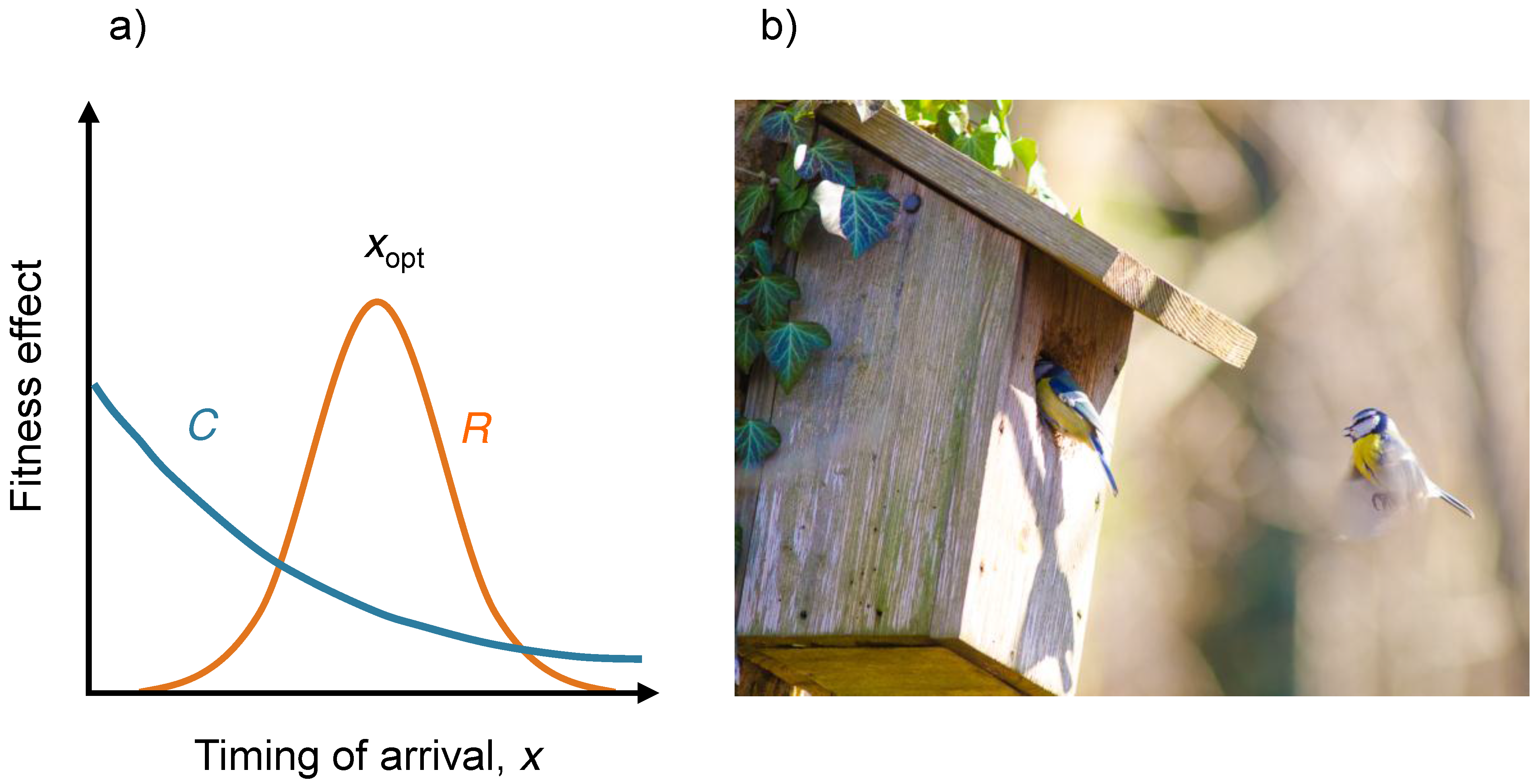
5. Polymorphic Evolution
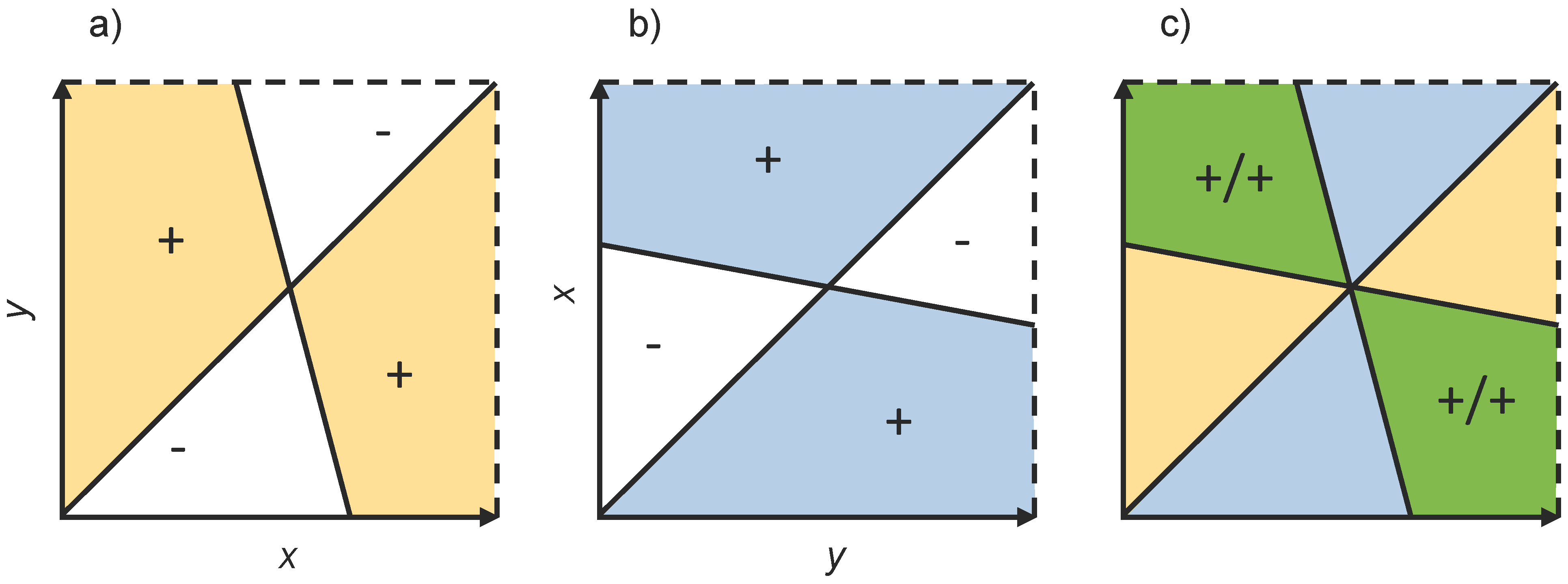
5.1. Invasion Fitness and Selection Gradients in Polymorphic Populations
5.2. Evolutionary Branching
5.3. Trait Evolution Plots
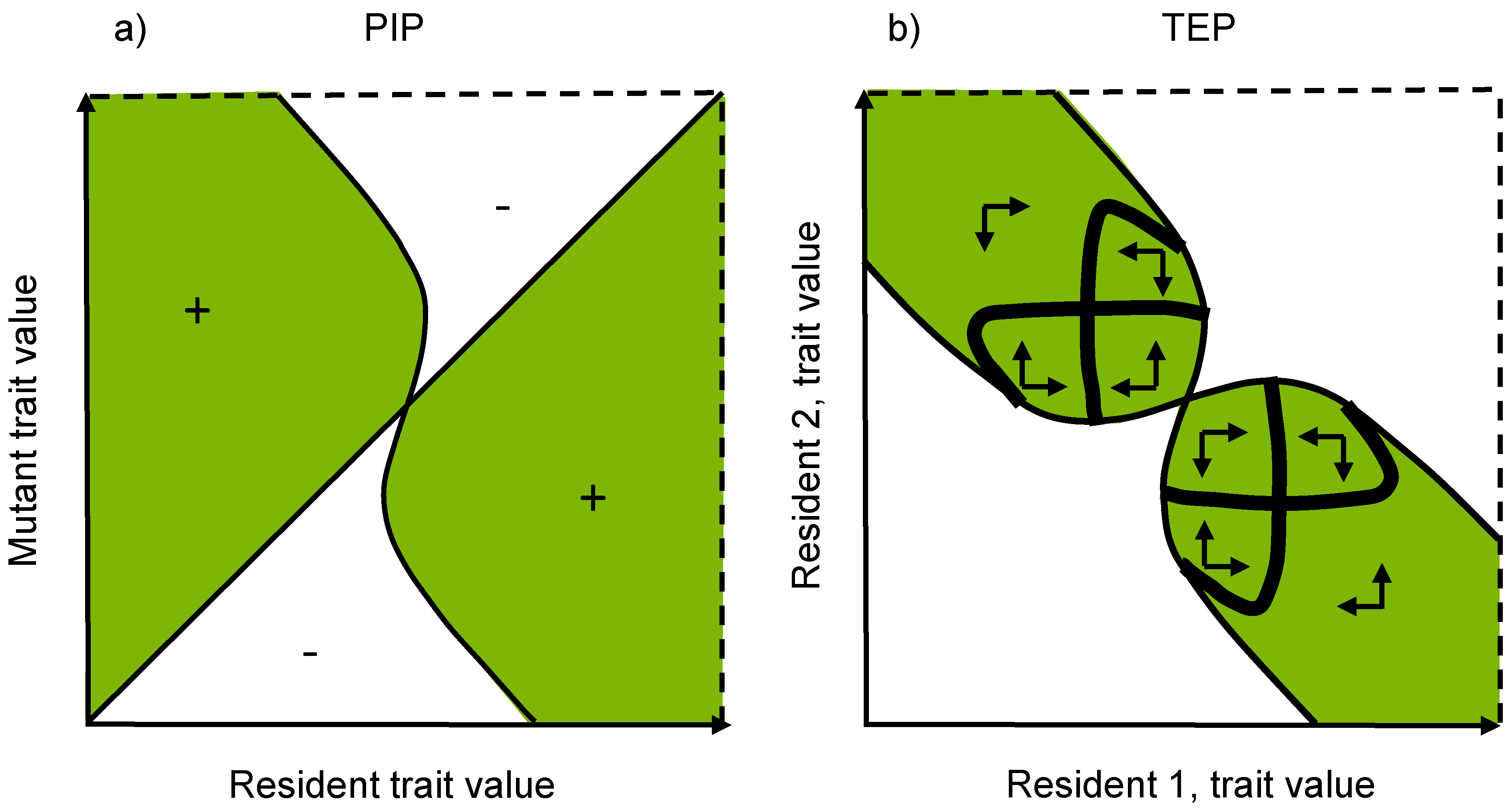
5.4. Evolutionarily Singular Coalitions
5.5. Connection of the Isoclines to the Boundary
5.6. Further Evolutionary Branching
6. Discussion
6.1. Relation to Evolutionary Game Theory
6.2. Role in Speciation Research
6.3. Recommendations for Further Reading
| Type of generalization | References |
|---|---|
| Explicit genetics and standing genetic variation | [39,58,59,60,61] |
| Mathematical underpinnings | [42,62,63,64,65] |
| Multiple species | [9,66,67,68] |
| Multiple traits and function-valued traits | [43,69,70,71] |
| Physiologically structured populations | [55,56] |
| Sexually-reproducing populations | [72] |
| Spatially-structured populations | [73,74,75] |
| Stochastic environments | [76,77,78] |
| Trade-off analysis | [79,80,81,82,83] |
Acknowledgments
A. Appendix: Local Classification of Singular Strategies
References
- Crow, J.F.; Kimura, M. An Introduction to Population Genetics Theory; Harper & Row: New York, NY, USA, 1970. [Google Scholar]
- Lande, R. Natural selection and random genetic drift in phenotypic evolution. Evolution 1976, 314–334. [Google Scholar] [CrossRef]
- Falconer, D.S.; Mackay, T.F.C. Introduction to Quantitative Genetics, 4th ed.; Prentice Hall: Harlow, UK, 1996. [Google Scholar]
- Maynard Smith, J. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Dieckmann, U.; Doebeli, M. On the origin of species by sympatric speciation. Nature 1999, 400, 354–357. [Google Scholar] [CrossRef] [PubMed]
- Doebeli, M.; Dieckmann, U. Speciation along environmental gradients. Nature 2003, 421, 259–264. [Google Scholar] [CrossRef] [PubMed]
- Dieckmann, U.; Ferrière, R. Adaptive dynamics and evolving biodiversity. In Evolutionary Conservation Biology; Ferrière, R., Dieckmann, U., Couvet, D., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 188–224. [Google Scholar]
- Brännström, Å.; Loeuille, N.; Loreau, M.; Dieckmann, U. Emergence and maintenance of biodiversity in an evolutionary food-web model. Theor. Ecol. 2011, 4, 467–478. [Google Scholar]
- Doebeli, M.; Hauert, C.; Killingback, T. The evolutionary origin of cooperators and defectors. Science 2004, 306, 859–862. [Google Scholar] [CrossRef] [PubMed]
- Brännström, Å.; Dieckmann, U. Evolutionary dynamics of altruism and cheating among social amoebas. Proc. R. Soc. Lond., B, Biol. Sci. 2005, 272, 1609–1616. [Google Scholar]
- Sumpter, D.J.T.; Brännström, Å. Synergy in social communication. In Sociobiology of Communication: An Interdisciplinary Perspective; Oxford University Press: Oxford, UK, 2008; pp. 191–208. [Google Scholar]
- Brännström, Å.; Gross, T.; Blasius, B.; Dieckmann, U. Consequences of fluctuating group size for the evolution of cooperation. J. Math. Biol. 2011, 63, 263–281. [Google Scholar]
- Cornforth, D.M.; Sumpter, D.J.T; Brown, S.P.; Brännström, Å. Synergy and group size in microbial cooperation. Am. Nat. 2012, 180, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Dieckmann, U.; Metz, J.A.; Sabelis, M.W.; Sigmund, K. Adaptive Dynamics of Infectious Diseases: In Pursuit of Virulence Management; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Boldin, B.; Diekmann, O. Superinfections can induce evolutionarily stable coexistence of pathogens. J. Math. Biol. 2008, 56, 635–672. [Google Scholar] [CrossRef] [PubMed]
- Best, A.; White, A.; Boots, M. The implications of coevolutionary dynamics to host-parasite interactions. Am. Nat. 2009, 173, 779–791. [Google Scholar] [CrossRef] [PubMed]
- Svennungsen, T.O.; Kisdi, É. Evolutionary branching of virulence in a single-infection model. J. Theor. Biol. 2009, 257, 408–418. [Google Scholar] [CrossRef] [PubMed]
- Parvinen, K. Evolutionary suicide. Acta Biotheoretica 2005, 53, 241–264. [Google Scholar] [CrossRef] [PubMed]
- Nonaka, E.; Parvinen, K.; Brännström, Å. Evolutionary suicide as a consequence of runaway selection for greater aggregation tendency. J. Theor. Biol. 2012. [Google Scholar]
- Marrow, P.; Dieckmann, U.; Law, R. Evolutionary dynamics of predator-prey systems: An ecological perspective. J. Math. Biol. 1996, 34, 556–578. [Google Scholar] [CrossRef] [PubMed]
- Kisdi, É.; Jacobs, F.; Geritz, S. Red Queen evolution by cycles of evolutionary branching and extinction. Selection 2002, 2, 161–176. [Google Scholar]
- Dercole, F.; Ferriere, R.; Gragnani, A.; Rinaldi, S. Coevolution of slow–fast populations: Evolutionary sliding, evolutionary pseudo-equilibria and complex Red Queen dynamics. Proc. R. Soc. Lond., B, Biol. Sci. 2006, 273, 983–990. [Google Scholar] [CrossRef] [Green Version]
- Metz, J.A.J.; Nisbet, R.; Geritz, S. How should we define “fitness” for general ecological scenarios? Trends Ecol. Evol. 1992, 7, 198–202. [Google Scholar] [CrossRef]
- Dieckmann, U.; Law, R. The dynamical theory of coevolution: A derivation from stochastic ecological processes. J. Math. Biol. 1996, 34, 579–612. [Google Scholar] [CrossRef] [PubMed]
- Metz, J.A.J.; Geritz, S.A.; Meszéna, G.; Jacobs, F.J.; Van Heerwaarden, J. Adaptive dynamics, a geometrical study of the consequences of nearly faithful reproduction. In Stochastic and Spatial Structures of Dynamical Systems; van Strien, S.J., Verduyn Lunel, S.M., Eds.; North-Holland Publishing Co: Amsterdam, The Netherlands, 1996; pp. 183–231. [Google Scholar]
- Geritz, S.A.; Kisdi, E.; Mesze, G.; Metz, J. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 1997, 12, 35–57. [Google Scholar] [CrossRef]
- McGill, B.J.; Brown, J.S. Evolutionary game theory and adaptive dynamics of continuous traits. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 403–435. [Google Scholar] [CrossRef]
- Waxman, D.; Gavrilets, S. 20 questions on adaptive dynamics. J. Evol. Biol. 2005, 18, 1139–1154. [Google Scholar] [CrossRef] [PubMed]
- Metz, J.A.J. Adaptive dynamics. In Encyclopedia of Theoretical Ecology; Hastings, A., Gross, L.J., Eds.; University of California Press: Berkeley, US, 2012; Vol. 4, pp. 7–17. [Google Scholar]
- Rueffler, C.; Egas, M.; Metz, J.A.J. Evolutionary predictions should be based on individual-level traits. Am. Nat. 2006, 168, 147–162. [Google Scholar] [CrossRef] [PubMed]
- Edelstein-Keshet, L. Mathematical Models in Biology; McGraw-Hill Companies: New York, NY, USA, 1988. [Google Scholar]
- Bernstein, M.A.; Friedman, W.A. Thinking About Equations; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Metz, J.A.J. Thoughts on the geometry of Meso-evolution: Collecting mathematical elements for a postmodern synthesis. In The Mathematics of Darwin’s Legacy; Chalub, F.A., Rodrigues, J.F., Eds.; Birkhäuser: Basel, Germany, 2011; pp. 193–232. [Google Scholar]
- Champagnat, N.; Ferrière, R.; Arous, G.B. The canonical equation of adaptive dynamics: A mathematical view. Selection 2001, 2, 73–83. [Google Scholar] [CrossRef]
- Iwasa, Y.; Pomiankowski, A.; Nee, S. The evolution of costly mate preferences II. The “handicap” principle. Evolution 1991, 45, 1431–1442. [Google Scholar] [CrossRef]
- Ito, H.C.; Dieckmann, U. A new mechanism for recurrent adaptive radiations. Am. Nat. 2007, 170, E96–E111. [Google Scholar] [CrossRef] [PubMed]
- Dieckmann, U.; Brännström, Å.; HilleRisLambers, R.; Ito, H.C. The adaptive dynamics of community structure. In Mathematics for Ecology and Environmental Sciences; Springer: Berlin, Germany, 2007; pp. 145–177. [Google Scholar]
- Sasaki, A.; Dieckmann, U. Oligomorphic dynamics for analyzing the quantitative genetics of adaptive speciation. J. Math. Biol. 2011, 63, 601–635. [Google Scholar] [CrossRef] [PubMed]
- Johansson, J.; Jonzén, N. Game theory sheds new light on ecological responses to current climate change when phenology is historically mismatched. Ecol. Lett. 2012, 15, 881–888. [Google Scholar] [CrossRef] [PubMed]
- Rankin, D.J.; Bargum, K.; Kokko, H. The tragedy of the commons in evolutionary biology. Trends Ecol. Evol. 2007, 22, 643–651. [Google Scholar] [CrossRef] [PubMed]
- Geritz, S.A.H.; Gyllenberg, M.; Jacobs, F.J.A.; Parvinen, K. Invasion dynamics and attractor inheritance. J. Math. Biol. 2002, 44, 548–560. [Google Scholar] [CrossRef] [PubMed]
- Leimar, O. Multidimensional convergence stability. Evol. Ecol. Res. 2009, 11, 191–208. [Google Scholar]
- Maynard Smith, J.; Price, G. The logic of animal conflict. Nature 1973, 246, 15. [Google Scholar] [CrossRef]
- Bishop, D.; Cannings, C. A generalized war of attrition. J. Theor. Biol. 1978, 70, 85–124. [Google Scholar] [CrossRef]
- Meszéna, G.; Kisdi, É.; Dieckmann, U.; Geritz, S.A.; Metz, J.A.J. Evolutionary optimisation models and matrix games in the unified perspective of adaptive dynamics. Selection 2002, 2, 193–220. [Google Scholar] [CrossRef]
- Dieckmann, U.; Metz, J.A.J. Surprising evolutionary predictions from enhanced ecological realism. Theor. Popul. Biol. 2006, 69, 263–281. [Google Scholar] [CrossRef] [PubMed]
- Gavrilets, S. ”Adaptive speciation”—It is not that easy: Reply to Doebeli et al. Evolution 2005, 59, 696–699. [Google Scholar] [CrossRef]
- Nosil, P. Speciation with gene flow could be common. Mol. Ecol. 2008, 17, 2103–2106. [Google Scholar] [CrossRef] [PubMed]
- Flaxman, S.M.; Feder, J.L.; Nosil, P. Genetic hitchhiking and the dynamic buildup of genomic divergence during speciation with gene flow. Evolution 2013. [Google Scholar] [CrossRef] [PubMed]
- Crespi, B.; Nosil, P. Conflictual speciation: Species formation via genomic conflict. Trends Ecol. Evol. 2012. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O. A beginner’s guide to Adpative Dynamics. Banach Center Publ. 2003, 63, 47–86. [Google Scholar]
- Geritz, S.A.H.; van der Meijden, E.; Metz, J.A.J. Evolutionary dynamics of seed size and seedling competitive ability. Theor. Popul. Biol. 1999, 55, 324–343. [Google Scholar] [CrossRef] [PubMed]
- Brännström, Å.; Sumpter, D.J. The role of competition and clustering in population dynamics. Proc. R. Soc. Lond., B, Biol. Sci. 2005, 272, 2065–2072. [Google Scholar]
- Durinx, M.; Metz, J.A.J. Multi-type branching processes and adaptive dynamics of structured populations. In Branching Processes: Variation, Growth and Extinction of Populations; Haccou, P., Jagers, P., Vatutin, V.A., Eds.; Cambridge University Press: Cambridge, UK, 2005; pp. 266–277. [Google Scholar]
- Durinx, M.; Metz, J.A.; Meszéna, G. Adaptive dynamics for physiologically structured population models. J. Math. Biol. 2008, 56, 673–742. [Google Scholar] [CrossRef] [PubMed]
- Champagnat, N.; Ferrière, R.; Méléard, S. Unifying evolutionary dynamics: From individual stochastic processes to macroscopic models. Theor. Popul. Biol. 2006, 69, 297–321. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kisdi, É.; Geritz, S.A. Adaptive dynamics in allele space: evolution of genetic polymorphism by small mutations in a heterogeneous environment. Evolution 1999, 993–1008. [Google Scholar]
- van Dooren, T.J.V. The evolutionary dynamics of direct phenotypic overdominance: emergence possible, loss probable. Evolution 2007, 54, 1899–1914. [Google Scholar] [CrossRef]
- van Doorn, G.S.; Dieckmann, U. The long-term evolution of multilocus traits under frequency-dependent disruptive selection. Evolution 2006, 60, 2226–2238. [Google Scholar] [CrossRef] [PubMed]
- Kopp, M.; Hermisson, J. The evolution of genetic architecture under frequency-dependent disruptive selection. Evolution 2006, 60, 1537–1550. [Google Scholar] [CrossRef] [PubMed]
- Geritz, S.A.H. Resident-invader dynamics and the coexistence of similar strategies. J. Math. Biol. 2003, 50, 67–82. [Google Scholar] [CrossRef] [PubMed]
- Gyllenberg, M.; Jacobs, F.J.A.; Metz, J.A.J. On the concept of attractor for community-dynamical processes II: the case of structured populations. J. Math. Biol. 2003, 47, 235–248. [Google Scholar] [CrossRef] [PubMed]
- Champagnat, N. A microscopic interpretation for adaptive dynamics trait substitution sequence models. Stoch. Proc. Appl. 2006, 116, 1127–1160. [Google Scholar] [CrossRef]
- Klebaner, F.C.; Sagitov, S.; Vatutin, V.A.; Haccou, P.; Jagers, P. Stochasticity in the adaptive dynamics of evolution: the bare bones. J. Biol. Dyn. 2011, 5, 147–162. [Google Scholar] [CrossRef] [PubMed]
- Jones, E.I.; Ferrière, R.; Bronstein, J.L. Eco-evolutionary dynamics of mutualists and exploiters. Am. Nat. 2009, 174, 780–794. [Google Scholar] [CrossRef] [PubMed]
- Ripa, J.; Storlind, L.; Lundberg, P.; Brown, J. Niche co-evolution in consumer-resource communities. Evol. Ecol. Res. 2009, 11, 305–323. [Google Scholar]
- Brännström, Å.; Jacobsson, J.; Loeuille, N.; Kristensen, N.; Troost, T.; Hille Ris Lambers, R.; Dieckmann, U. Modelling the ecology and evolution of communities: a review of past achievements, current efforts, and future promises. Evol. Ecol. Res. 2012, 14, 601–625. [Google Scholar]
- Claessen, D.; Dieckmann, U. Ontogenetic niche shifts and evolutionary branching in size-structured populations. Evol. Ecol. Res. 2002, 4, 189–217. [Google Scholar]
- Dieckmann, U.; Heino, M.; Parvinen, K. The adaptive dynamics of function-valued traits. J. Theor. Biol. 2006, 241, 370–389. [Google Scholar] [CrossRef] [PubMed]
- Ravigné, V.; Dieckmann, U.; Olivieri, I. Live where you thrive: joint evolution of habitat choice and local adaptation facilitates specialization and promotes diversity. Am. Nat. 2009, 174, E141–E169. [Google Scholar] [CrossRef] [PubMed]
- Geritz, S.A.; Éva, K. Adaptive dynamics in diploid, sexual populations and the evolution of reproductive isolation. Proc. R. Soc. Lond., B, Biol. Sci. 2000, 267, 1671–1678. [Google Scholar] [CrossRef] [PubMed]
- Mizera, F.; Meszéna, G. Spatial niche packing, character displacement and adaptive speciation along an environmental gradient. Evol. Ecol. Res. 2003, 5, 363–382. [Google Scholar]
- Parvinen, K. Evolution of dispersal in a structured metapopulation model in discrete time. Bull. Math. Biol. 2006, 68, 655–678. [Google Scholar] [CrossRef] [PubMed]
- Débarre, F.; Gandon, S. Evolution of specialization in a spatially continuous environment. J. Evol. Biol. 2010, 23, 1090–1099. [Google Scholar] [CrossRef] [PubMed]
- Kisdi, É. Dispersal: risk spreading versus local adaptation. Am. Nat. 2002, 159, 579–596. [Google Scholar] [CrossRef] [PubMed]
- Johansson, J.; Ripa, J. Will sympatric speciation fail due to stochastic competitive exclusion? Am. Nat. 2006, 168, 572–578. [Google Scholar] [CrossRef]
- Ripa, J.; Dieckmann, U. Mutant invasions and adaptive dynamics in variable environments. Evolution 2013. [Google Scholar] [CrossRef] [PubMed]
- de Mazancourt, C.; Dieckmann, U. Trade-off geometries and frequency-dependent selection. Am. Nat. 2004, 164, 765–778. [Google Scholar] [CrossRef]
- Rueffler, C.; Van Dooren, T.; Metz, J. Adaptive walks on changing landscapes: Levins’ approach extended. Theor. Popul. Biol. 2004, 65, 165–178. [Google Scholar] [CrossRef] [PubMed]
- Bowers, R.G.; Hoyle, A.; White, A.; Boots, M. The geometric theory of adaptive evolution: Trade-off and invasion plots. J. Theor. Biol. 2005, 233, 363–377. [Google Scholar] [CrossRef] [PubMed]
- Kisdi, E. Trade-off geometries and the adaptive dynamics of two co-evolving species. Evol. Ecol. Res. 2006, 8, 959–973. [Google Scholar]
- Geritz, S.A.; Kisdi, É.; Yan, P. Evolutionary branching and long-term coexistence of cycling predators: critical function analysis. Theor. Popul. Biol. 2007, 71, 424–435. [Google Scholar] [CrossRef] [PubMed]
- 1.To be precise, the phrase “survival of the fittest” was coined by the philosopher Herbert Spencer and adopted by Darwin from the fifth edition of On the origin of species.
- 2.In structured population models, there will be an initial transient phase during which the per capita growth rate depends on the population structure, whether the population is structured in space, size, stage, or according to another characteristic. The invasion fitness then has to be defined as the long-term per capita growth rate of the mutant population.
- 3.Metz [34] argues that the name evolutionarily stable strategy (ESS) is a partial misnomer as the strategy does not need to be evolutionarily attracting. Since the ESS concept is deeply ingrained, it has been proposed that the meaning of the acronym should be altered to evolutionarily steady strategy. An ESS that is also evolutionarily attracting is called a continuously stable strategy (CSS).
- 4.The fixed point is stable since the slope of seen as a function of at is exactly equal to p, which is positive and less than 1 in magnitude.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Brännström, Å.; Johansson, J.; Von Festenberg, N. The Hitchhiker’s Guide to Adaptive Dynamics. Games 2013, 4, 304-328. https://doi.org/10.3390/g4030304
Brännström Å, Johansson J, Von Festenberg N. The Hitchhiker’s Guide to Adaptive Dynamics. Games. 2013; 4(3):304-328. https://doi.org/10.3390/g4030304
Chicago/Turabian StyleBrännström, Åke, Jacob Johansson, and Niels Von Festenberg. 2013. "The Hitchhiker’s Guide to Adaptive Dynamics" Games 4, no. 3: 304-328. https://doi.org/10.3390/g4030304
APA StyleBrännström, Å., Johansson, J., & Von Festenberg, N. (2013). The Hitchhiker’s Guide to Adaptive Dynamics. Games, 4(3), 304-328. https://doi.org/10.3390/g4030304





