1. Introduction
Frank [
1] states that “Our utility-maximization framework has proven its usefulness for understanding and predicting human behavior. With more careful attention to the specification of the utility function, the territory to which this model applies can be greatly expanded.” This is a particularly germane observation with respect to game theory. Theorists tend simply to assume that they are given the full and correct final preferences of players in a game, and that their object is to analyze the resulting strategic interactions. Where these preferences come from, and especially what differences might arise between the payoff to an individual and his or her ultimate preference over outcomes, has generally not been considered to be within the purview of game theory. However, as Frank pointed out, this necessarily limits the scope of the theory. For instance, it is probably not an exaggeration to say that all game theorists feel that no rational player should ever knowingly play a strictly dominated strategy. And yet this is exactly what robustly occurs in the one-shot Prisoner’s Dilemma. The fault lies not with the theory, but with the inattention as to its application.
This paper attempts to provide a general, formal, theoretical link between the base payoffs in a game, and the resulting final utilities or preferences. The discrepancy is due to the fact that players care about the utilities of the other players in the game, e.g. due to altruism. The main reason to formalize this link is to provide applied and experimental economists with a model for this pervasive interaction, so they are not forced to come up with new (and ad hoc) formulations every time it is relevant. There is also a second reason, the stock-in-trade of theorists: to understand the process better. The jump from payoffs to final utilities goes on all the time in almost all games, so we should have a model (or, better yet, several competing models) of how it happens and what it implies.
We introduce a general definition of games with synergistic utility. Synergistic utility functions capture the idea that utility increases in one’s own payoff, and may increase or decrease in others’ utilities. Sufficient technical conditions are imposed for the concept to be well-defined, but otherwise the formulation is general enough to allow maximal variety in specific applications. All players are fully rational (including being expected-utility maximizers) and no new equilibrium concepts are introduced. A specific example, the linear synergistic utility function, is introduced and analyzed in greater detail. Several applications of the theory are given, including: cooperation in the Prisoner’s Dilemma, overproduction in Cournot oligopoly, extended play in the centipede game, and interior solutions in the dictator game.
The paper proceeds to
Section 2, in which some of the related literature, both applied and theoretical, is discussed and compared with the synergistic utility concept. In
Section 3, the formal model, including the central definition, is given. Next,
Section 4 illustrates the theory with examples both of different synergistic utility functions and of their application to different games of interest.
Section 5 addresses several topics from game theory, such as incomplete information, in the context of synergistic games. Finally,
Section 6 briefly concludes.
2. Literature
The literature relating to altruism and interdependent preferences is wide and diverse, with each paper seemingly taking its own course. The first broad category can be considered to be the various applications of altruistic-like tendencies in specific situations. This includes, in the macroeconomics literature using overlapping generations (OLG) models, the famous paper of Barro [
2] on Ricardian equivalence, the subsequent paper by Kotlikoff
et al. [
3] which disputes the finding, and Kimball’s [
4] extension to two-sided altruism. The models in these papers have “dynasties” in which ancestors care about their descendants’ consumption as well as their own. Bisin [
5] and Verdier [
6] study the Prisoner’s Dilemma in the context of cultural transmission, modeling altruism with the addition of a positive constant. All of these papers model altruism in one direction only,
i.e. there is no feedback effect between the players. In labor economics, Rotemberg [
7] studies relations in the workplace. He determines under what conditions cooperation can be obtained and when this benefits the employer, but defines altruism only insofar as an employee’s utility is the sum of payoffs to the group. He states, “Cooperative outcomes for
either individual in the Prisoner’s Dilemma obtain only when
both individuals feel altruistic toward each other.” As we shall see, this contradicts the conclusions of a synergistic utility model, in which an altruistic player may desire to cooperate even when facing a non-altruistic opponent.
Altruism within the family has been studied since Becker [
8] and his ‘Rotten Kid Theorem’. He models interdependent utilities using a basic additive form. Bruce and Waldman [
9] compare this line of work to the Samaritan’s Dilemma and Barro-Ricardian equivalence in a similar framework. Other work applying some degree of altruism includes Coate [
10], who studies insurance with rich and poor agents, Bernheim and Stark [
11], who address some negative consequences of altruism, and Collard [
12] in a general equilibrium framework. In the context of society rather than family, Maccheroni, Marinacci, and Rustichini [
13] give an axiomatic representation of interdependent preferences in the presence of a social value function. It is to be emphasized that this is only a small sample of the work that employs altruism or interrelated utilities in some form or other. In addition to the various subfields of economics already mentioned, these types of models have been used in areas ranging from law to philosophy to political science.
The second general class of papers are those on evolution and biology, which are also closely tied to the theoretical psychology literature. Frank [
1] is in this vein when he studies the commitment problem. He finds that if one can choose to be a guilty type (perhaps through an evolutionary process) and show it, one can commit credibly. This can be of great benefit, for instance in the provision of public goods. Bergstrom [
14] studies genetically predetermined behaviors, which is to say there is no free choice on the part of the players. He finds that cooperation in the Prisoner’s Dilemma can be a stable outcome when players have preferences taking into account the payoffs (not the utility) of others and genetic propagation occurs through imitation of successful strategies. A recent extension of the traditional “evolution-of-strategies” literature is the “evolution-of-preferences” literature, typified e.g. by Dekel, Ely, and Yilankaya [
15], which discusses optimality of utility at a meta-level. This is, once again, only a sample of the papers which consider this sort of evolutionary fitness paradigm. They are distinguished from the present work in that the latter is concerned with rational and strategic players in a non-dynamic setting, but it is interesting to note that some of the conclusions reached are similar.
A large number of experimental economics papers have looked at different games and found results that diverge from those predicted by the basic equilibrium concepts. Dawes and Thaler [
16] study experiments with public goods, ultimatum games, and the Prisoner’s Dilemma. They discuss altruism in general as an explanation but do not suggest a model. Palfrey and Rosenthal [
17] also study public goods provision, with altruism consisting of a single lump-sum addition to payoffs (from “doing the right thing”) when a player contributes. Cooper
et al. [
18] consider altruism in the setting of cheap talk and coordination games. One of the complications that arise from explaining the data in these and other games in this way is that it requires not only positive emotional interactions, such as altruism, but also negative interactions, such as spite (or at least retribution). For instance, it is otherwise impossible to rationalize rejected offers in the ultimatum game. Levine [
19] creates a relatively simple theory with utility linear in one’s own and one’s opponent’s payoffs (with a possibly negative weight on the opponent). He pins down the parameters of his model by matching data on ultimatum and centipede games. He then tests the model, with some success, on public goods games and on market games. The main distinctions between his theory and the synergistic utility theory are that his players care about the payoffs, rather than the utilities, of their opponents, and that he includes a reciprocity factor, so that how a player cares about others depends on how they care about him. It turns out that much of the observed behavior can be explained without introducing this additional slight complexity, as will be seen below, and that synergistic utilities can also rationalize some behavior (e.g. in the dictator game) that Levine’s model, as it stands, cannot. Charness and Haruvy [
20] experimentally test several models within a single framework, and Andreoni and Miller [
21] show that preferences involving altruism are rational in the sense that they satisfy GARP.
This leads naturally to the final group of related papers, those from the game theory literature. Geanakoplos, Pearce and Stacchetti [
22] introduce the concept of psychological games (and psychological equilibrium), in which utility is a function not only of actions but also of beliefs over actions. Among other things, this allows utility to depend on reactions of pleasure or anger, although only with respect to expected actions in a particular game. Players do not explicitly care about the welfare of their opponents, though as always it can in theory be incorporated into their preferences. This is an extremely powerful and all-encompassing structure, but because of this there is very little in the way of a common backbone from which to deduce or to explain results observed across a variety of different games. Rabin [
23] specializes this idea by introducing a
fairness equilibrium, a more inherent concept which begins with a
kindness function between the two players. Because of the special nature of the equilibrium concept, his results depend on the absolute level of the base payoffs and apply only to two-person games. Nevertheless, he is able to draw several fairly general conclusions. Sally [
24] has a similar but somewhat more extended approach, building on the “psychological distance” between players. He develops the
sympathetic equilibrium concept, and finds that it is sometimes possible to choose cooperation in the one-shot Prisoner’s Dilemma. As in Rabin’s paper, reciprocity is the starting point and again, essentially because of reciprocity, it is unclear how to extend the results to more than two players.
Returning to the traditional equilibrium concepts, Bergstrom [
25,
26] and Hori [
27] are perhaps closest to the present paper. Bergstrom presents a general model in which a player’s utility is an increasing transformation of his own payoff and the other players’ utilities. Instead of taking limits of this process (as will be clear in the model below), he uses a fixed-point approach, which can easily violate monotonicity. Thus, although he is able to explain cooperation in the Prisoner’s Dilemma, his approach leads to some rather counter-intuitive conclusions in other situations. For instance, lovers may prefer
less of a mutually enjoyable good to more, since otherwise their joint utility would spiral out of control. Hori is able to prove slightly stronger results than in the synergistic model, but only in the case of a linear formulation and assuming nonnegative altruism. Finally, Wolpert
et al. [
28] formalize Schelling’s insight that it may be rational to commit to being irrational, and in particular that publicly choosing an altruistic “persona” may allow self-interested players to cooperate more often. Note that we are not pursuing a specifically behavioral approach, since all players in the synergistic model are fully rational with standard preferences over final utility (and we use standard equilibrium concepts), but we are interested in some of the same questions.
3. Model
One way to introduce an altruism-like aspect in a formal game-theoretic model is to add a positive constant to payoffs following a “good” action, such as contributing in a public goods game or cooperating in the Prisoner’s Dilemma. This “warm glow” effect is plausible in some circumstances, but does not capture the positive or negative benefits that a player may receive depending on the welfare of his or her opponents
1. These can be captured most simply be adding a proportion of the opponents’ payoffs to that of the player in question. This approach, however, has an inherent inconsistency: if the benefit, for instance, arises not just from doing good, but instead from being glad that a fellow player is happy, then it should be the other player’s utility and not payoff that matters
2. That is, rational players will be farsighted and will think through more than one step of the process. In general, then, final utilities will be a function of one’s own payoff and of the [final] utilities of the other players.
It is not unreasonable to ask why utilities should not be a function of own
utility and others’ utilities. The short answer is that this too is inconsistent: preferences are utilities, they are not over utilities. As an example, consider an altruistic player with an indifferent (
i.e. entirely self-concerned) opponent. The opponent will necessarily always have final utility equal to base payoff. If the altruist has utility equal to a weighted average between own payoff and the other’s utility, her final utility will lie somewhere in between the two original payoffs. If, however, her utility is a weighted average between own
utility and the other’s utility, her final utility must equal that of her opponent no matter what her original payoff. In fact, it is not uncommon under these assumptions that the final utilities of both players will depend only on their altruism types and will be wholly independent of their original payoffs, an undesirable feature
3.
One final matter that should be clarified before proceeding to the formal model is the interpretation of the base payoffs. They are already objects in utility space, so they should not be thought of as monetary payoffs or profits. Rather, they can be considered to be the utility resulting from that outcome if it were in a one-person setting, or in a setting where the effects of that outcome on other players are unknown. Alternately, they are the utilities of thoughtless players, to whom it has not yet occurred that there are other players or what implications that might entail. We assume, as ever, that they already include any positive feelings from simply doing good or being fair, or on the flip side any negative feelings directly arising from an act of, say, betrayal. What they do not include are preference changes due to the realized utility of one’s opponents in a particular outcome of the game
4.
We are given a game
G with
I players and payoffs
vi. A
synergism type for a player
i is an element
θi drawn from a type-space Θ. In effect, this type will describe the relative weights that the player puts on his own and his opponents’ utilities; see Proposition 3 below for the prototypical formulation. Denote the vector of synergism types for the
I players by
θ. Let
f be a real-valued function taking as arguments
I real numbers (interpreted as welfare measures for oneself and one’s opponents, respectively) and as parameters the elements of Θ. Hence
f:
RI × Θ →
R. So
f is the same for all players, but each has a separate synergism type. The base payoff for player
i is
![Games 03 00041 i009]()
. Following the motivation above, we define
![Games 03 00041 i010]()
and in general
![Games 03 00041 i011]()
. At each suppositional round, players recalculate their opponents’ utility levels and then adjust their view of their own utility in response, continuing ad infinitum. Finally, let
![Games 03 00041 i012]()
. Of course this may not exist in general.
Definition: Given Θ, a function f: RI × Θ → R is a synergistic utility function if
(i) f is everywhere both continuous and strictly increasing in its first argument
(ii) f is everywhere both continuous and either strictly increasing, decreasing, or constant in each of its other real arguments
(iii) there exists θE ∈ Θ such that for all vectors v in RI, f (v;θE) = v1
(iv) for all θ ∈ Θ, f (0;θ) = 0
(v) for all θ ∈ Θ and all v in RI, u∞ (v;θ) exists (as defined above)
In words, then, requirement (i) states that utility must be increasing in one’s own payoff. Requirement (ii) asks that utility, if it is affected by someone else’s payoff, always be affected in the same direction. This could be weakened, but imposes no untoward restrictions
5. Requirement (iii) imposes that there exist a traditional game-theoretic type,
i.e. one who has utility equal to own payoff regardless of the other players in the game
6. Requirement (iv) is a moderately weak normalization that rules out adding arbitrary constants to the utility: you can’t get something for nothing. And finally, requirement (v) insures that utilities exist in all cases and are well-defined.
Definition: If
G is a game with payoffs
vi, then we say (
G,
f,
θ) is a
game with synergistic utility (a synergistic game) if it is identical to
G except that utility is given by
![Games 03 00041 i013]()
for all
i, and
f is a synergistic utility function
Proposition 1: If (G, f, θ) is a synergistic game, then ui = f (vi,u-i;θi) for all i
The proposition says that the limit utilities, which necessarily exist, satisfy a fixed-point property. The proof follows straightforwardly from the definitions and the continuity of
f. One can imagine defining synergistic utilities directly as solutions to the fixed-point equation, but this has several factors against it. First, the motivation for synergistic utilities, that players update their own welfare by taking into account the welfare of the other players, leads directly to the limit process. Secondly, the fixed-point solution may exist even if the limit does not
7. For example, suppose that we have two altruistic players of the same type; in particular we assume
f =
vi + 2
u-i for both
8. If
v1 =
v2 = 1 then the limit diverges, as would be expected (utilities go to infinity as each player gets happier and happier contemplating the situation). The fixed-point solution, on the other hand, yields
u1 =
u2 = -1, which appears unreasonable. Thus the limit is central to the definition, but Proposition 1 may provide a short-cut in explicit calculations.
Proposition 2: In a synergistic game, utilities ui are continuous in payoffs v
Proof: Let
v ∈
RI have associated synergistic utilities
u ∈
RI. Take any sequence
![Games 03 00041 i014]()
such that
![Games 03 00041 i015]()
. We wish to show that
![Games 03 00041 i016]()
. If not, there exists
ε > 0 such that
![Games 03 00041 i017]()
. From the definition of synergistic utility,
![Games 03 00041 i018]()
and hence there exists
M such that
![Games 03 00041 i019]()
for all m ≥ M. But since
f is continuous, we know that
![Games 03 00041 i020]()
, and iterating
![Games 03 00041 i021]()
, … so that in particular
![Games 03 00041 i022]()
. Thus we can choose
N with the property that
![Games 03 00041 i023]()
for all n ≥ N. But now
![Games 03 00041 i024]()
, implying
![Games 03 00041 i025]()
. This is a contradiction, and so we’re done.
Proposition 2 gives us another general property of synergistic utility functions, but this is about as much as can be said in complete generality. It may be helpful at this point, in part to clarify the definitions, to consider some examples of potential synergistic utility functions. We say potential because for the moment we ignore condition (v), and we leave Θ unspecified. The most obvious is probably the linear formulation
![Games 03 00041 i026]()
. Here
θ = (
a,
b) and Θ ⊆
RI. On the other hand,
f =
avi +
b(
u‒i)
2 is impermissible, for instance, because it violates (ii). The effect of an increase in the other player’s utility on one’s own should be independent of the absolute levels involved. Thus,
f =
avi +
b(
u‒i)
3 is once again acceptable. Cobb-Douglas formulations, more common in macroeconomics, look like
f = (
vi)
a (
u‒i)
b and require that “consumptions” be non-negative. However, upon taking logs, this is equivalent to the original linear form
9. All of the above satisfy condition (iii) by choosing
a=1 and
b=0, and satisfy condition (i) if
a>0. Examples of applications of these utility functions to particular games, along with an additional nonlinear formulation, are given in
Section 4.
To apply the theory in a specific situation, one must choose an appropriate (f,Θ) pair and show that this pair yields a synergistic utility function. We do this now for the two-player linear case, though it is easy to extend it to more players.
Proposition 3: Let Θ = (0,∞) × (-1,1) and θ = (a,b). Then f (vi,u‒i;θ) = avi + bu‒i is a synergistic utility function.
Proof: We have the recursive equations
![Games 03 00041 i027]()
and
![Games 03 00041 i028]()
, or
We may write this as un = Mun‒1, and hence un = Mnu0, where u0= [v1 v2 1]´. Then multiplying out the powers of M yields
But by assumption |b1b2| ˂ 1 so
Now
![Games 03 00041 i029]()
is simply the
ith row of the 3
rd column of the matrix above so it too exists (and in fact this gives an explicit formula for it). Naturally, this is the same solution one would find from solving the system of two fixed-point equations. It is clear that conditions (i)-(iv) also hold.
Note that the perverse example mentioned earlier, which had
b = 2, is not allowed in this scenario. Nonlinear synergistic utility functions will have their own requirements for Θ
10. Turning to another question that can be answered given a specific synergistic utility function, it is well-known that positive linear transformations of any player’s payoffs leave the strategic structure (
i.e. the preferences over final outcomes) of a game unaffected. This result carries over to synergistic games as much as possible (it is clear that multiplying only one player’s payoffs by some constant may substantively change utilities in an interdependent setting).
Proposition 4: In a linear synergistic game, preferences over outcomes are unaffected if
(a) all player’s payoffs are multiplied by the same positive constant, or
(b) any or all players have a constant added to their payoffs
Proof:
(a) Since f is linear in vi (or in fact more generally whenever f is homogeneous of degree one in vi), utilities all along the limiting sequence, and hence also final utilities, will also be multiplied by this constant. So then, by the standard result, preferences remain the same.
(b) Adding a constant to one player’s payoffs affects all players, but only to the extent of adding some constant to each of their payoffs. Although this constant may be different for each player, it is the same for a given player across his or her outcomes. This is clear from the explicit formulas found in the proof of Proposition 3. But now, once again, the standard result applies.
Although this result does not hold in general for all synergistic games, it will hold in other particular settings. We now turn our attention to illustrating the theory with a spectrum of examples.
4. Examples
The proof of the pudding lies in the taste, and the believability of synergistic utilities lies in its potential applications. For the time being, we confine ourselves to the linear synergistic utility function analyzed above,
f =
avi +
bu‒i. We first define three types of players to give some idea of the range of possibilities. Although unnecessary, it is convenient to choose them such that
a + |
b| = 1; this keeps the magnitude of the utilities directly comparable to those of the base payoffs
11. The first type is the one required by part (iii) of the definition,
θE = (1,0)
. This type always has final utility equal to base payoff regardless of the other players. The second type is an altruist, denoted by
S for socialist:
![Games 03 00041 i030]()
. This type approximately treats the two players equally. Finally, we define an unfriendly type:
![Games 03 00041 i031]()
. In the game theory literature, this general type has been called spiteful, but that is perhaps too strong a condemnation for these preferences. Rather, this player simply enjoys doing better than his or her opponent; the notation is thus Jones, for “keeping up with the Joneses”
12. Note that since we apply the theory to single games, it is possible to switch types over time or in differing situations or against different players. The model does not require them to be intrinsic. Also, it is fairly easy to see how to come up with multi-player analogues for these types.
The basic Prisoner’s Dilemma can be written as:
Here C stands for cooperate and D for defect, as usual. Of course the unique Nash Equilibrium is (D,D). If two type E’s (economists) play against one another, the payoffs remain as they started and the game is unchanged. So the unique NE is also the same. We next consider an economist player 1 opposing a Jones player 2. E’s utilities are the same as ever, while J’s may then be calculated using f (it takes only one step in this case). We arrive at the following game form:
The unique NE is again for both players to defect. What is interesting, however, is that this outcome is no longer Pareto inefficient, as it was previously. The economist is so unhappy that it makes the Jones player happy. This depends, of course, on the exact payoff structure and type of player 2, but holds over a wide class. Consider next a socialist player 1 against a Jones type:
This game now has two pure NE, in both of which type J defects (unsurprisingly it turns out that types E and J always defect). Type S is completely indifferent, and is thus willing to cooperate. Of course this is knife-edge; types near to S will be pushed in one direction or the other, some of them always cooperating. The (C,D) equilibrium is [weakly] Pareto efficient in this case. We now change player 2 to a type S as well:
Cooperation is a dominant strategy here for both players; it is also the optimal outcome in the game. This is the stereotype of altruistic cooperation in the Prisoner’s Dilemma. The final combination of players that we consider is when player 1 is a type E once more:
The unique and strict NE is (
D,
C). The surprising observation here is that it requires less inherent altruism to cooperate with a type
E than with a type
S 13. This result can be explained by noting that defection hurts a type
E opponent more than it does a type
S opponent (who is consoled by the fact that one’s own payoff has been improved). Hence a type
S will have a stronger incentive not to defect when playing against a type
E. Recall that we have tried to put aside any issues of reciprocity.
Turning next to an example of a continuous game, we consider Cournot duopoly. In the simplest case with linear unit demand and zero marginal cost, price
p = 1 -
q, where
q is the total quantity produced. Payoffs are simply net profits, so
vi =
qi(1-
q). The unique Nash Equilibrium with standard (
i.e. type
E) players is for both to produce at
![Games 03 00041 i032]()
. It is plausible, however, to model the firms as type
J. Perhaps it is a small market so that profits themselves are not important but beating the rival firm is critical for advertising. Or perhaps the managers are paid with yardstick competition incentives, so again what is important is to do better than the other firm. The symmetric equilibrium in this case is that both produce
![Games 03 00041 i033]()
. In the end of course neither firm actually does any better than the other, but each is willing to overproduce (“sacrificing” profits) in order to try to do so. Note also that this is much closer to the zero profit outcome of Bertrand competition, and in fact it converges to that outcome as the firms get more and more extreme in the Jones direction.
Experimental game theory has included extensive work not only with the Prisoner’s Dilemma but also with other games such as ultimatum, dictator, centipede, and public goods games. As in the case of the Prisoner’s Dilemma, the results are often quite disparate from those predicted by standard theories. For instance, no positive quantity should ever be rejected in an ultimatum game, yet this is often observed in experiments. This outcome can be explained using synergistic utilities: types similar to Jones will reject all offers up to some level (which will depend on the exact type chosen and on the type of the opponent). Of course altruism alone, without some sort of negative analogue, can never rationalize these rejections. Recall that it is possible to extend the theory to include reciprocity if desired, so a player’s type need not be constant. As has been documented previously (see
Section 2), altruism can explain extended play in a centipede game or contribution in a public goods game. The point is that a simple theory, such as synergistic utilities, is sufficient to do this.
In the so-called dictator game, player one simply decides how to divide an amount of money (typically around $10 in experiments) between him- or herself and an often anonymous opponent. Player two has no action other than to accept the split as dictated. Traditional equilibrium concepts predict that player one should keep the entire amount, and previous models of altruism have not altered this prediction. For instance, continuing with the types as defined above, if an altruistic type
S opposes another type
S, the optimal action is still to give nothing away. No linear model can predict an interior solution, although in practice this is what the data clearly support. We turn, then, to a nonlinear synergistic utility function. For simplicity we assume that player two is a type
E, so that as always
u2 =
v2. For player one, we assume the altruistic formulation
![Games 03 00041 i034]()
. In this case the optimal allocation is an even split,
i.e. $5 for each player. This outcome is occasionally, though rarely, observed in experiments. If we assume instead the slightly less magnanimous utility
![Games 03 00041 i035]()
, then we find
![Games 03 00041 i036]()
. In fact this agrees remarkably well with the observed average division. Naturally, this is meant only to illustrate the potential applicability of the theory, in addition to the fact that nonlinear functions do not simply provide generality but in fact may be necessary in practice.
5. Topics
Despite the fact that the game structure remains the same in synergistic games (only the payoffs have changed), there are several topics that take on new meaning in this context. For instance, cooperative games with transferable utility will be difficult to analyze since some players may actually prefer a smaller total surplus to divide (think of the type
J above). As another example, evolutionary game theory has been a popular subject of study recently. In the present setting, it is possible to discuss the evolutionary strengths not just of different strategies but also of different synergistic types. What is unclear, however, is what to use as a measure of reproductive fitness. One could argue that players with the highest welfare (final utility) will be the most productive and successful. On the other hand, it may be that the determination of success is made by physical rather than mental well-being, so that base payoffs (food or money leading to direct consumption) should enter the calculation of the dynamics. A player might be happy that his or her fellows do well, but this does not necessarily grant an increased chance of survival. The appropriate measure may depend on the particular situation. In the Prisoner’s Dilemma example of
Section 4, note that altruistic players, type
S in the notation there, fare relatively poorly under either system.
A related consideration, though more in the mode of full rationality, is the idea of segregation. Since players are of different types, they may prefer to play against one type of opponent rather than another, and thus selectively associate. Of course, they may not have the opportunity to make this choice, but if they do then it has long-term welfare (and hence possibly evolutionary) implications. Returning once again to the Prisoner’s Dilemma example of the previous Section, note that while types E and S always prefer an altruistic type S opponent, this is not necessarily true of type J players, who like to play type E’s (since the latter end up so unhappy). So a plausible scenario is that S types play against themselves, while J’s and E’s pair off against one another. This leaves the self-centered economist types quite unhappy; their only hope is to run across extremely altruistic players, who will actually like to make them happy by cooperating (in effect, happily sacrificing themselves). Recall that all players are fully utility maximizing at all times.
There is no doubt at least some element of reciprocity in almost all human interactions. Synergistic utilities, as defined, make no account for this; a player’s degree of altruism is independent of the attitudes of the other players. The work of Rabin [
23] and Sally [
24] depend explicitly on these added interactions, and similar constraints can be added to synergistic games. One method would be to require that players enter a game with their own individual synergistic type
θ, but that then all of the players play the game using the average
θ of the group (if Θ is such that this has meaning). Another possibility is to add a reciprocity player, type
R, who takes on the
θ of whomever he or she is playing. As always, this is difficult to implement with more than two players. The point is that altruism, jealousy, and so on make sense independently of any reciprocity arguments, so the simplest models of such behavioral tendencies will not include them as a building block. They may however be necessary in order to fully explain either our own introspective assessments or all empirically observed behavior.
As a first step toward examining how important reciprocity is in influencing other-regarding behavior, and as an experimental exploration of synergistic utilities, the following study could be implemented
14. In a laboratory setting, first deduce a partial utility function over outcomes at the individual level, where agents have no information about anyone else; this is basically
u0 in the model above. Then allow them to observe the outcomes (underlying payoffs) of others, but without any information about the utility functions (indirect preferences) of others; this is
u1. Finally, give them information about the deduced utility functions for others, which should feed into their own preferences synergistically; this is
u2. To the extent that their choices change when they learn about utilities rather than simply outcomes, but regardless of how others behave toward them (
i.e. reciprocity or process utility), this would support the specific model presented here.
Finally, games with incomplete information take on an added dimension if there is also the possibility of synergistic types. There is no reason in general to assume that all players know the type of each of their opponents, synergistic or otherwise. Fortunately, the entire game-theoretic apparatus developed to analyze this eventuality is still perfectly applicable. In particular, the Bayesian equilibrium concepts apply just as well here. As synergistic types are certainly payoff relevant, signaling will be an important component to playing extensive-form synergistic games. It may or may not be beneficial for a player in a given situation to reveal his or her synergistic type (consider, for instance, the discussion of segregation above). In fact, incomplete information aspects of synergistic games seem to be perhaps the most fruitful line for future theoretical research using this model.
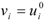 . Following the motivation above, we define
. Following the motivation above, we define 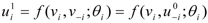 and in general
and in general  . At each suppositional round, players recalculate their opponents’ utility levels and then adjust their view of their own utility in response, continuing ad infinitum. Finally, let
. At each suppositional round, players recalculate their opponents’ utility levels and then adjust their view of their own utility in response, continuing ad infinitum. Finally, let  . Of course this may not exist in general.
. Of course this may not exist in general. for all i, and f is a synergistic utility function
for all i, and f is a synergistic utility function such that
such that  . We wish to show that
. We wish to show that  . If not, there exists ε > 0 such that
. If not, there exists ε > 0 such that 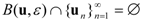 . From the definition of synergistic utility,
. From the definition of synergistic utility,  and hence there exists M such that
and hence there exists M such that 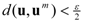 for all m ≥ M. But since f is continuous, we know that
for all m ≥ M. But since f is continuous, we know that  , and iterating
, and iterating 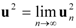 , … so that in particular
, … so that in particular 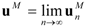 . Thus we can choose N with the property that
. Thus we can choose N with the property that 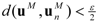 for all n ≥ N. But now
for all n ≥ N. But now 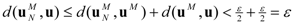 , implying
, implying  . This is a contradiction, and so we’re done.
. This is a contradiction, and so we’re done. . Here θ = (a,b) and Θ ⊆ RI. On the other hand, f = avi + b(u‒i)2 is impermissible, for instance, because it violates (ii). The effect of an increase in the other player’s utility on one’s own should be independent of the absolute levels involved. Thus, f = avi + b(u‒i)3 is once again acceptable. Cobb-Douglas formulations, more common in macroeconomics, look like f = (vi)a (u‒i)b and require that “consumptions” be non-negative. However, upon taking logs, this is equivalent to the original linear form 9. All of the above satisfy condition (iii) by choosing a=1 and b=0, and satisfy condition (i) if a>0. Examples of applications of these utility functions to particular games, along with an additional nonlinear formulation, are given in Section 4.
. Here θ = (a,b) and Θ ⊆ RI. On the other hand, f = avi + b(u‒i)2 is impermissible, for instance, because it violates (ii). The effect of an increase in the other player’s utility on one’s own should be independent of the absolute levels involved. Thus, f = avi + b(u‒i)3 is once again acceptable. Cobb-Douglas formulations, more common in macroeconomics, look like f = (vi)a (u‒i)b and require that “consumptions” be non-negative. However, upon taking logs, this is equivalent to the original linear form 9. All of the above satisfy condition (iii) by choosing a=1 and b=0, and satisfy condition (i) if a>0. Examples of applications of these utility functions to particular games, along with an additional nonlinear formulation, are given in Section 4. and
and 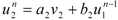 , or
, or


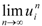 is simply the ith row of the 3rd column of the matrix above so it too exists (and in fact this gives an explicit formula for it). Naturally, this is the same solution one would find from solving the system of two fixed-point equations. It is clear that conditions (i)-(iv) also hold.
is simply the ith row of the 3rd column of the matrix above so it too exists (and in fact this gives an explicit formula for it). Naturally, this is the same solution one would find from solving the system of two fixed-point equations. It is clear that conditions (i)-(iv) also hold.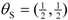 . This type approximately treats the two players equally. Finally, we define an unfriendly type:
. This type approximately treats the two players equally. Finally, we define an unfriendly type: 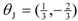 . In the game theory literature, this general type has been called spiteful, but that is perhaps too strong a condemnation for these preferences. Rather, this player simply enjoys doing better than his or her opponent; the notation is thus Jones, for “keeping up with the Joneses” 12. Note that since we apply the theory to single games, it is possible to switch types over time or in differing situations or against different players. The model does not require them to be intrinsic. Also, it is fairly easy to see how to come up with multi-player analogues for these types.
. In the game theory literature, this general type has been called spiteful, but that is perhaps too strong a condemnation for these preferences. Rather, this player simply enjoys doing better than his or her opponent; the notation is thus Jones, for “keeping up with the Joneses” 12. Note that since we apply the theory to single games, it is possible to switch types over time or in differing situations or against different players. The model does not require them to be intrinsic. Also, it is fairly easy to see how to come up with multi-player analogues for these types.




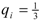 . It is plausible, however, to model the firms as type J. Perhaps it is a small market so that profits themselves are not important but beating the rival firm is critical for advertising. Or perhaps the managers are paid with yardstick competition incentives, so again what is important is to do better than the other firm. The symmetric equilibrium in this case is that both produce
. It is plausible, however, to model the firms as type J. Perhaps it is a small market so that profits themselves are not important but beating the rival firm is critical for advertising. Or perhaps the managers are paid with yardstick competition incentives, so again what is important is to do better than the other firm. The symmetric equilibrium in this case is that both produce 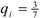 . In the end of course neither firm actually does any better than the other, but each is willing to overproduce (“sacrificing” profits) in order to try to do so. Note also that this is much closer to the zero profit outcome of Bertrand competition, and in fact it converges to that outcome as the firms get more and more extreme in the Jones direction.
. In the end of course neither firm actually does any better than the other, but each is willing to overproduce (“sacrificing” profits) in order to try to do so. Note also that this is much closer to the zero profit outcome of Bertrand competition, and in fact it converges to that outcome as the firms get more and more extreme in the Jones direction. . In this case the optimal allocation is an even split, i.e. $5 for each player. This outcome is occasionally, though rarely, observed in experiments. If we assume instead the slightly less magnanimous utility
. In this case the optimal allocation is an even split, i.e. $5 for each player. This outcome is occasionally, though rarely, observed in experiments. If we assume instead the slightly less magnanimous utility 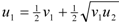 , then we find
, then we find  . In fact this agrees remarkably well with the observed average division. Naturally, this is meant only to illustrate the potential applicability of the theory, in addition to the fact that nonlinear functions do not simply provide generality but in fact may be necessary in practice.
. In fact this agrees remarkably well with the observed average division. Naturally, this is meant only to illustrate the potential applicability of the theory, in addition to the fact that nonlinear functions do not simply provide generality but in fact may be necessary in practice.


