Abstract
In a recent paper, we analyzed the self-assembly of a complex cooperation network. The network was shown to approach a state where every agent invests the same amount of resources. Nevertheless, highly-connected agents arise that extract extraordinarily high payoffs while contributing comparably little to any of their cooperations. Here, we investigate a variant of the model, in which highly-connected agents have access to additional resources. We study analytically and numerically whether these resources are invested in existing collaborations, leading to a fairer load distribution, or in establishing new collaborations, leading to an even less fair distribution of loads and payoffs.
1. Introduction
Cooperation shapes our lives on many different scales [1,2]: Humans cooperate in communities, companies, ethnicities and nations [3,4,5]. Thereby, the collaborative behavior of the individuals is strongly influenced by the embedding social structure, the partners’ social positions, and by social norms [6,7,8,9]. Conversely, social structures, social positions, and social norms evolve in response to the individuals’ collaborative behavior [10,11].
The adaptive interplay between social structure and social behavior has mostly been studied in a specific evolutionary context: Previous models of human cooperation studied the influence of external factors such as social structure [12,13,14,15,16,17], and social norms [18,19,20] on an individual’s collaborative behavior. Here, we adopt the complementary non-evolutionary perspective, asking for the implications of an individual’s behavior on the emergence of social structures, social norms, and on the rise of leaders that hold distinguished social positions.
In a recent paper, we considered a model which allows agents to maintain different levels of cooperation with different self-chosen partners and adapt them in response to their partners’ behavior [21]. This revealed that a high degree of social coordination can arise purely from the selective and adaptive interaction of self-interested agents even if no social norm is imposed externally: Although the agents possess little information, the system approaches a state in which every agent makes the same cooperative investment and every social interaction produces the same benefit. We note that this coordination was not imposed externally; different levels of investment evolved when the model was run multiple times from effectively identical initial conditions.
Despite the emergent coordination of investments, the final configuration is generally not fair. Although we start the model in an initially symmetric configuration which gave neither agent an advantage, some agents manage to secure positions of high centrality, where they interact with many other agents. In these positions, they receive significantly higher benefits than every other agent while making the same total investment. The system thus evolves into a state where payoffs are unfairly distributed.
The evolving network displays unfairness also in a second aspect. As highly connected agents spend the same amount of resources as every other agent, their contribution to any of their collaborations is necessarily small. So collaborating with a highly connected agent generally implies that one has to carry a large fraction of the investment. Thus, the existence of highly connected agents implies both unfairness in the global payoff distribution and unfairness in the interaction-specific load distribution.
In the present paper, we investigate if a fairer load distribution can be achieved if additional resources are available to agents of high centrality. We extend the model class studied in [21] by including that an agent’s success feeds back on his cooperative investments. We show that the additional feedback loop reduces the unfairness in the distribution of loads but intensifies the unfairness in the distribution of payoffs.
The paper is organized as follows: We start with a short summary of the original model and outline the basic results. This will also give us the opportunity to introduce the conventions needed. We then include the additional feedback loop, discuss its effects on the emergence of coordination and differentiation and study the implications for fairness.
2. Basic Model
Consider a population of N agents engaged in bilateral interactions. The agents can for instance be people maintaining social contacts, scientists collaborating on some project, or companies entering business relationships. Every agent can invest time/money/effort into each of the N − 1 potential interactions with another agent. Furthermore the N2 − N individual amounts eij, invested by agent i into the interaction with agent j can be adapted selectively, independently, and continuously by the agents. In other words, every agent is free to chose the amount of resources invested into the collaboration with every single other agent. Neither the total investment nor the structure of the collaboration network are imposed a priori.
One can imagine that over time the population approaches an equilibrium in which many potential interactions receive no investment, while others are reinforced, forming links in a complex network of cooperation. But, how will this network look like? How will the investments be distributed? And will the network be fair in the sense that all agents benefit in equal measure?
Let us assume rational agents trying to maximize some payoff. A generic model for a single interaction is the continuous snowdrift game [2]. In this game the payoff is P = B − C, where B and C are non-linear functions. The benefit function B depends on the sum of both investments while the cost function C depends only on the investment of the agent under consideration. While we do not restrict B and C to specific functional forms, we assume that B is sigmoidal and C is superlinear (see Figure 1). This captures basic features of real-world systems such as inefficiency of small investments, saturation of benefits, and additional costs incurred by overexertion of personal resources.
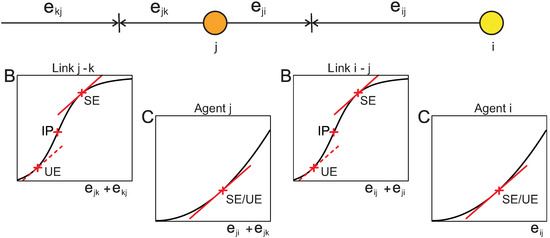
Figure 1.
(Reprinted from [21]) Adjustment of investments. Shown are the perceived cost functions C and benefit functions B (insets) for the example of an agent i of degree one interacting with an agent j of degree two (sketched). The function B depends on the sum of the agents investments into the interaction while C depends on the sum of all investments of the agent. In every equilibrium (SE or UE) stationarity demands that the slope of these functions be identical. This requires that the agents make identical total investments. In stable equilibria (SE), the operating point lies in general above the inflection point (IP) of B, whereas equilibria found below the IP are in general unstable (UE). Therefore, in a stable equilibrium both links produce the same benefit and both agents make the same total investment. Iterating this argument along a sequence of bidirectional links yields the coordination properties (i) and (ii).
In order to allow for multiple bilateral interactions per agent, let us extend the snowdrift game by assuming that the benefits received add linearly, while the cost is a function of the sum of investments made by an agent. The payoff received by agent i from the interaction with an agent j can then be written as
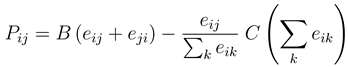 where we have allocated a proportional share of the total cost incurred by i to the interaction with j. We let the agents maximize their payoff dynamically in time by following a steepest ascent approach [22]
where we have allocated a proportional share of the total cost incurred by i to the interaction with j. We let the agents maximize their payoff dynamically in time by following a steepest ascent approach [22]
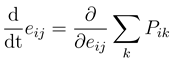
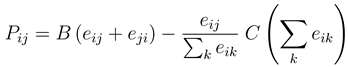
By locally adapting their investments in the direction of the steepest incline of payoff, agents may change the selection as well as number of their collaborators, the amount invested in any specific collaboration as well as the amount invested in total.
2.1. Coordination of Investments
In simulations the system shows frustrated, glass-like behavior; starting from a homogeneous initial configuration, in which all potential links are realized with identical investment plus a small stochastic fluctuation, the system approaches either one of a large number of different final configurations, which are local maxima of the total payoff. To describe these configurations, the following naming conventions are advantageous: Below, interactions which do receive no investments such that eij + eji = 0 will be denoted as vanishing interactions. Non-vanishing interactions will be denoted as links. Further, a set of agents and the links connecting them are said to form a bidirectionally-connected community (BCC) if every agent in the set can be reached from every other agent in the set by following a sequence of bidirectional (reciprocal) links.
In [21], it was shown analytically that all final configurations share certain properties. Thus, within every evolved BCC (i) every node makes the same total investment, and (ii) every link produces the same benefit. The properties (i) and (ii) are essential for a solution of the ODE system Equation (1) to be stationary and stable (Figure 1). They thus apply to all stable steady states.
2.2. Differentiation of Payoffs
The properties (i) and (ii) point to a remarkable degree of coordination inside a BCC. This coordination results from the selective and adaptive interaction of self-interested agents and is achieved although no agent has sufficient information to estimate the investment of any other agent in the network [21]. Interestingly, the emergent coordination of investments does not necessarily imply that the evolving networks are fair: Since all links in the BCC produce an identical benefit, the total benefit received by an agent is proportional to his degree, i.e., to the number of his collaborations. Agents of high degree thus receive significantly higher benefits while making the same investment as every other agent.
Figure 2 shows a representative degree distribution pk specifying the relative frequency of nodes with degree k of an evolved network in the final state. Although agents follow identical rules and the network of collaborations is initially almost homogeneous, the distribution has a finite width indicating a certain heterogeneity. However, the distribution is narrower, and therefore fairer, than that of an Erdös–Rényi random graph, which constitutes a null-model for network topology.

Figure 2.
Emergent heterogeneity in self-organized networks. In comparison to a random graph (red), the degree distribution of networks evolved in the basic model is relatively narrow (light blue), but broadens as cost reduction for successful agents is introduced (dark blue). All simulations rely on the functions  ,
,  . Parameters are chosen to obtain networks with identical mean degree (basic model: ρ = 0.1, τ = 0.124, µ = 2.731, adaptive model ρ = 0.395, τ = 0.1, µ = 2.32, ν = 0.05). Results are averaged over 1000 networks of size N = 100.
. Parameters are chosen to obtain networks with identical mean degree (basic model: ρ = 0.1, τ = 0.124, µ = 2.731, adaptive model ρ = 0.395, τ = 0.1, µ = 2.32, ν = 0.05). Results are averaged over 1000 networks of size N = 100.
 ,
, 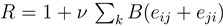 . Parameters are chosen to obtain networks with identical mean degree (basic model: ρ = 0.1, τ = 0.124, µ = 2.731, adaptive model ρ = 0.395, τ = 0.1, µ = 2.32, ν = 0.05). Results are averaged over 1000 networks of size N = 100.
. Parameters are chosen to obtain networks with identical mean degree (basic model: ρ = 0.1, τ = 0.124, µ = 2.731, adaptive model ρ = 0.395, τ = 0.1, µ = 2.32, ν = 0.05). Results are averaged over 1000 networks of size N = 100.
The emergence of the payoff disparity can be traced to the discrete nature of the links. As we reported above the local optimization carried out by the agents leads both to a coordination of investments in the links and to a local optimization of the total payoff. For a given choice of parameters, the optimal payoff will be extracted if a certain number of collaborations exist in average per agent. However, the optimal total number of links is not necessarily commensurable with the number of agents and hence the maximal total payoff can only be extracted when the collaborations are distributed unfairly.
2.3. Imbalance in Load Distributions
In order to sustain the extraction of high payoffs by agents with high degree, investments have to be redistributed across the network. While the transport of resources is not explicitly included in the model, it enters through the asymmetry of the individual interactions. Consider for instance an agent of degree one. This agent has to focus his investment on a single link. The partner participating in this link will therefore only need to make a small investment in the interaction to make it profitable. He is thus free to invest a large portion of his total investment into links to other agents of possibly even higher degree. In this way, investments flow toward regions of high connectivity where large payoffs are extracted.
The most extreme case for an unequal load distribution within a cooperation is realized in unidirectional links. These correspond to interactions, in which one partners invests without any reciprocation. While the behavior of the exploited agent seems irrational, the analysis in [21] shows that it can arise in a population of rational self-interested agents. Simulations reveal that unidirectional investments are not even rare: Depending on the mean degree of the evolving network, up to 50% of all cooperative links can be unidirectional [21].
3. Adaptive Model
As shown above, the individual selection of eligible cooperation partners promotes the coordination of cooperative investments, the differentiation of received payoffs but also the emergence of unequal workloads within a cooperation. One can now argue that in the real world successful agents have access to more resources, which could allow them to reciprocate more strongly in their collaborations, which would in turn lead to a fairer load sharing. Below, we study the effect of an agent’s success feeding back on his cooperative investments. Including a benefit-dependent reduction of C in the model yields a fully adaptive network [23].
In our adaptive model, agents enjoy benefit-dependent cost reduction
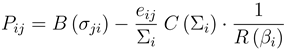 where
where 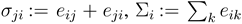 , and R is a monotonically increasing function of the total benefit of agent
, and R is a monotonically increasing function of the total benefit of agent 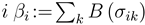 . As above, we assume the benefit function B to be sigmoidal. Moreover, we assume the cost function to be super-linear and of the general form
. As above, we assume the benefit function B to be sigmoidal. Moreover, we assume the cost function to be super-linear and of the general form 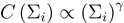 .
.
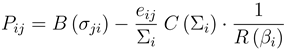
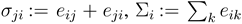 , and R is a monotonically increasing function of the total benefit of agent
, and R is a monotonically increasing function of the total benefit of agent 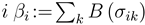 . As above, we assume the benefit function B to be sigmoidal. Moreover, we assume the cost function to be super-linear and of the general form
. As above, we assume the benefit function B to be sigmoidal. Moreover, we assume the cost function to be super-linear and of the general form 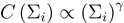 .
.Below, we show that in the adaptive model property (ii) still holds while property (i) needs to be modified: The total amount of investment differs among agents within a BCC as agents enjoy benefit-dependent cost reduction (Figure 3). However, we find that agents of the same degree approach the same investment level. Consequently distinct classes of agents arise which differ both in investment and in payoff.

Figure 3.
Self-organized network evolved in the adaptive model. Nodes represent agents, while each link represents a non-vanishing cooperative interaction. The small dash on the link is a fairness indicator: the further it is shifted toward one agent, the lower is the fraction of the total investment into the cooperation that he contributes. Nodes extracting more payoff are shown in darker color and are placed toward the center of the community. The size of a node indicates the total investment the agent makes. In the final configuration all links within a BCC receive the same total investment and all nodes of the same degree make the same total investment. Simulation parameters: ρ = 0.7, τ = 0.1, µ = 2.24, ν = 0.588.
3.1. Coordination and Differentiation
For deriving the modified coordination properties (i) and (ii) we proceed analogously to the non-adaptive case, i.e., we evaluate the conditions for a solution of the ODE system Equation (1) to be stationary and stable.
First the stationarity condition. Defining 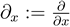 , we can rewrite the stationarity condition
, we can rewrite the stationarity condition
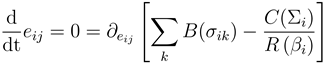 as
as
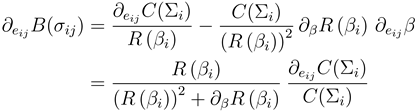 where we used ∂eij β = ∂eij B(σij ). The right hand side of Equation (4) does only depend on the node parameters Σi and βi, i.e., in a steady state ∂eijB(σij) is identical for all bilateral links ij of agent i. From ∂eij B(σij ) = ∂eji B(σij ) it then follows that all bilateral links of j, and, by iteration, that all bilateral links within one BCC are identical with respect to ∂emn B (σmn). Since the benefit function is sigmoidal, a given slope can be found in at most two points along the curve: one above and one below the inflection point (IP) (Figure 1). This implies that if a stationary level of investment is observed in one link, then the investment of all other links of the same BCC is restricted to one of two operating points.
where we used ∂eij β = ∂eij B(σij ). The right hand side of Equation (4) does only depend on the node parameters Σi and βi, i.e., in a steady state ∂eijB(σij) is identical for all bilateral links ij of agent i. From ∂eij B(σij ) = ∂eji B(σij ) it then follows that all bilateral links of j, and, by iteration, that all bilateral links within one BCC are identical with respect to ∂emn B (σmn). Since the benefit function is sigmoidal, a given slope can be found in at most two points along the curve: one above and one below the inflection point (IP) (Figure 1). This implies that if a stationary level of investment is observed in one link, then the investment of all other links of the same BCC is restricted to one of two operating points.
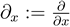 , we can rewrite the stationarity condition
, we can rewrite the stationarity condition
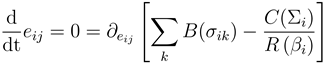
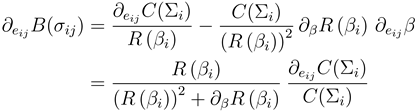
In the basic model, stability analysis revealed that the operating point below the IP is unstable and can thus be ruled out (Figure 1). Unfortunately, in the extended model, the analysis cannot be performed to the same extent. However, in extensive numerical simulations we have not observed a single equilibrium which contained a link operating below the IP. This strongly indicates that the dynamics of the extended model are governed by similar stability conditions as the dynamics of the basic model, which reproduces property (ii):
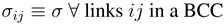
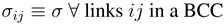
Combining Equations (4) and (5), we can now derive property (i): Let us consider a single BCC. According to Equation (5), the total benefit of an agent i in this BCC is a function of its degree di:
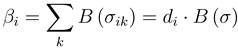
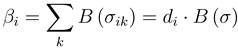
Inserting this relation in Equation (4), we find that the left hand side is constant, while the first factor on the right hand side only depends on di. The second factor on the right hand side is injective, as we assumed 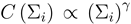 . It thus follows that nodes of the same degree have to make the same total investment Σi, even if they are only connected through a chain of nodes making different investments. However, nodes of different degree di can differ in their total investment.
. It thus follows that nodes of the same degree have to make the same total investment Σi, even if they are only connected through a chain of nodes making different investments. However, nodes of different degree di can differ in their total investment.
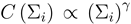 . It thus follows that nodes of the same degree have to make the same total investment Σi, even if they are only connected through a chain of nodes making different investments. However, nodes of different degree di can differ in their total investment.
. It thus follows that nodes of the same degree have to make the same total investment Σi, even if they are only connected through a chain of nodes making different investments. However, nodes of different degree di can differ in their total investment.The emergence of distinct classes of nodes, which differ in degree (and therefore in payoff) and total investment, is illustrated in Figure 3. The figure shows the final configuration of an exemplary model realization with 100 nodes. Nodes of high degree received high payoffs (coded in the node color) and run high total investments (coded in the node size).
Compared to the basic model, the adaptive model leads to considerably broadened degree distributions (Figure 2). We can thus conclude that the additional resources available to high degree agents are at least in part used to establish additional links. This leads to an increased income disparity in the evolving network.
3.2. Fairness of Load Distribution
Let us now address the fairness of individual interactions. As in the basic model, also in the adaptive model the investments of two interacting agents into a common collaboration are usually asymmetric. In Figure 3, this is apparent in the position of the fairness indicators on the links: The further it is shifted toward one agent i, the lower the fraction eij /σij that he contributes. Even in small network components, the fairness indicators reveal a flow of investments towards regions of high connectivity; as a general rule high-degree nodes contribute less to an interaction than their lower-degree partner.
In both the basic and the adaptive model, the specific load distribution in an interaction depends on the exact topological configuration of the respective network component. Hence, for comparing the fairness of load distributions in both models, it is necessary to consider components of the same structure.
The simplest degree-heterogeneous structure is a chain of three nodes i, j and k. In such a structure, the two degree-one nodes i and k necessarily concentrate all their investment in the cooperation with the middle node j, while the latter splits its investment in equal parts. The fraction exj /σxj that the middle node contributes to each of the two links can be calculated as
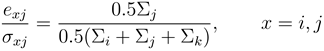
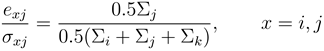
In the basic model, the total investment of all three nodes are identical. Thus, exj /σxj = 1/3. In the adaptive model, Σj > Σi = Σk. Thus, eij /σij > 1/3, i.e., the load distribution is fairer than in the basic model (cf. fairness indicators on three node chain in Figure 3).
Generalizing the reasoning sketched above, we find that for any given topological configuration, the imbalance in the load distribution is milder in the adaptive model than in the basic model. We can thus conclude that the additional resources available to high degree agents are partly reinvested in existing links enhancing the fairness of the respective interactions.
Further confirmation for fairer load distributions in the adaptive model comes from the numerical data: In extensive simulations using a wide range of parameters we have not observed a single unidirectional link. This observation stands in sharp contrast to the observations made in the basic model, where unidirectional links—the most extreme case of unequal load distribution—constitute a considerable fraction of all links in a network.
4. Summary
In this paper, we have extended a recently studied model for the formation of cooperation networks by taking into account that an agent’s success feeds back on his cooperative investments. Although agents have large freedom in their investment strategy and little information about investments of others, we find that like the basic model, the adaptive self-organizes toward configurations exhibiting a high degree of coordination: In all final configurations, bidirectionally connected communities approach a state in which the benefit produced by each link is identical and in which the total investment made by a agent is either identical (basic model) or falls into distinct classes (adaptive model).
Despite coordination, both models display unfairness in two aspects: payoffs are unequally distributed in the population and loads are unequally distributed between cooperating partners. Both aspects can be traced back to the local payoff optimization governing the dynamics of the system. The optimization of payoffs implies an optimal number of links in the system. The latter, however, is usually incommensurable with the number of agents leading to configurations, in which some agents have more links, i.e., a higher degree, than others. In both versions of the model, agents of higher degree are found to extract more payoff and contribute less to a cooperation than their lower degree partners.
In the adaptive model, cost reduction for successful agents makes additional resources available to highly-connected agents. These resources are partly invested in existing collaborations, leading to fairer load distributions, but also in establishing new collaborations, leading to broadened degree distributions. Let us emphasize that differentiation and emergence of unfairness in an initially homogeneous population has previously been discussed in the context of the adaptive networks [24,25,26]. However, to our knowledge the here proposed framework is the first, in which the phenomena can be linked to details of the dynamic self-organization process. Our analysis has greatly profited from the dual nature of the model class under consideration. The continuous nature allowed for a model description in terms of ordinary differential equations and thus for an analysis with the tools of dynamical systems theory. On the other hand, the discrete, unweighted nature of the final configurations allowed us to use the concepts of graph theory.
References
- Axelrod, R.; Hamilton, W.D. The evolution of cooperation. Science 1981, 211, 1390–1396. [Google Scholar] [CrossRef] [PubMed]
- Doebeli, M.; Hauert, C.; Killingback, T. The evolutionary origin of cooperators and defectors. Science 2004, 306, 859–862. [Google Scholar] [CrossRef] [PubMed]
- Gulati, R.; Singh, H. The architecture of cooperation: Managing coordination costs and appropriation concerns in strategic alliances. Adm. Sci. Q. 1998, 43, 781–814. [Google Scholar] [CrossRef]
- Raustiala, K. The architecture of international cooperation: Transgovernmental networks and the future of international law. Va. J. Int. Low 2002 43, 1–92. [CrossRef]
- Acharya, A. Asian regional institutions and the possibilities for socializing the behavior of states. In ADB Working Paper Series on Regional Economic Integration; Asian Development Bank: City of Mandaluyong, Metro Manila, Phillipines, 2011. [Google Scholar]
- Gould, R.V. Collective action and network structure. Am. Soc. Rev. 1993, 58, 182–196. [Google Scholar] [CrossRef]
- Willers, D. Network Exchange Theory; Praeger Publishers: Westport, CT, USA, 1999. [Google Scholar]
- Fehr, E.; Fischbacher, U. The nature of human altruism. Nature 2003, 425, 785–791. [Google Scholar] [CrossRef]
- Schmidt, M.F.H.; Sommerville, J.A. Fairness expectations and altruistic sharing in 15-month-old human infants. PLoS One 2011, 6. [Google Scholar] [CrossRef]
- Macy, M.W. Learning to cooperate: Stochastic and tacit collusion in social exchange. Am. J. Soc. 1991, 97, 808–843. [Google Scholar] [CrossRef]
- Vos, M.; van der Zee, K. Prosocial behavior in diverse workgroups: How relational identity orientation shapes cooperation and helping. Group Process. Intergroup Relat. 2011, 1–17. [Google Scholar] [CrossRef]
- Nowak, M.A.; May, R.M. Evolutionary games and spatial chaos. Nature 1992, 92, 826–829. [Google Scholar] [CrossRef]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef]
- Santos, F.C.; Pacheco, J.M. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef]
- Santos, F.C.; Santos, M.D.; Pacheco, J.M. Social diversity promotes the emergence of cooperation in public goods games. Nature 2008, 454, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Pacheco, J.M.; Pinheiro, F.L.; Santos, F.C. Population structure induces a symmetry breaking favoring the emergence of cooperation. PLoS Comput. Biol. 2009, 5, e1000596. [Google Scholar] [CrossRef] [PubMed]
- Zschaler, G.; Traulsen, A.; Gross, T. A homoclinic route to full cooperation in adaptive networks and its failure. New J. Phys. 2010, 12, 093015:1–093015:12. [Google Scholar] [CrossRef]
- Bowles, S.; Gintis, H. The moral economy of communities: Structured populations and the evolution of pro-social norms. Evol. Hum. Behav. 1998, 19, 3–25. [Google Scholar] [CrossRef]
- Ohtsuki, H.; Hauert, C.; Lieberman, E.; Nowak, M.A. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef]
- Hauert, C.; Traulsen, A.; Brandt, H.; Nowak, M.A.; Sigmund, K. Via freedom to coercion: The emergence of costly punishment. Science 2007, 316, 1905–1907. [Google Scholar] [CrossRef]
- Do, A.L.; Rudolf, L.; Gross, T. Patterns of cooperation: Fairness and coordination in networks of interacting agents. New J. Phys. 2010, 12. [Google Scholar] [CrossRef]
- Snyman, J.A. Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms; Springer: New York, NY, USA, 2005. [Google Scholar]
- Gross, T.; Blasius, B. Adaptive coevolutionary networks: A review. JRS Interface 2008, 5, 259–271. [Google Scholar] [CrossRef]
- Ito, J.; Kaneko, K. Spontaneous structure formation in a network of chaotic units with variable connection strength. Phys. Rev. Lett. 2002, 88. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, M.G.; Egu´ıluz, V.M.; San Miguel, M.; Spadaro, A. Cooperation in an adaptive network. In Application of Simulations to Social Sciences; Ballot, G., Weisbuch, G., Eds.; Hermes Science Publications: Paris, France, 2000; Volume 3, pp. 283–297. [Google Scholar]
- Eguíluz, V.M.; Zimmerman, M.G.; Cela-Conde, C.J.; San Miguel, M. Cooperation and the emergence of role differentiation in the dynamics of social Networks. Am. J. Soc. 2005, 110, 977–1008. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/). |
© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).