Provision of Public Goods via Unilateral but Mutually Conditional Commitments—Mechanism, Equilibria, and Learning
Abstract
1. Introduction
2. The Conditional Commitment Function Mechanism
3. Correspondence Between Strong Equilibria and Core Action Profiles
4. Finding Strong Equilibria via Simple Learning Rules
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCF | Conditional commitment function |
| CPEP | Costly positive externality problem |
Appendix A. The Framework of Costly Positive Externality Problems
Appendix A.1. Actions
Appendix A.2. Preferences
Appendix A.3. Unique Nash Equilibrium of the Base Game
Appendix A.4. Pareto-Efficiency and the Core
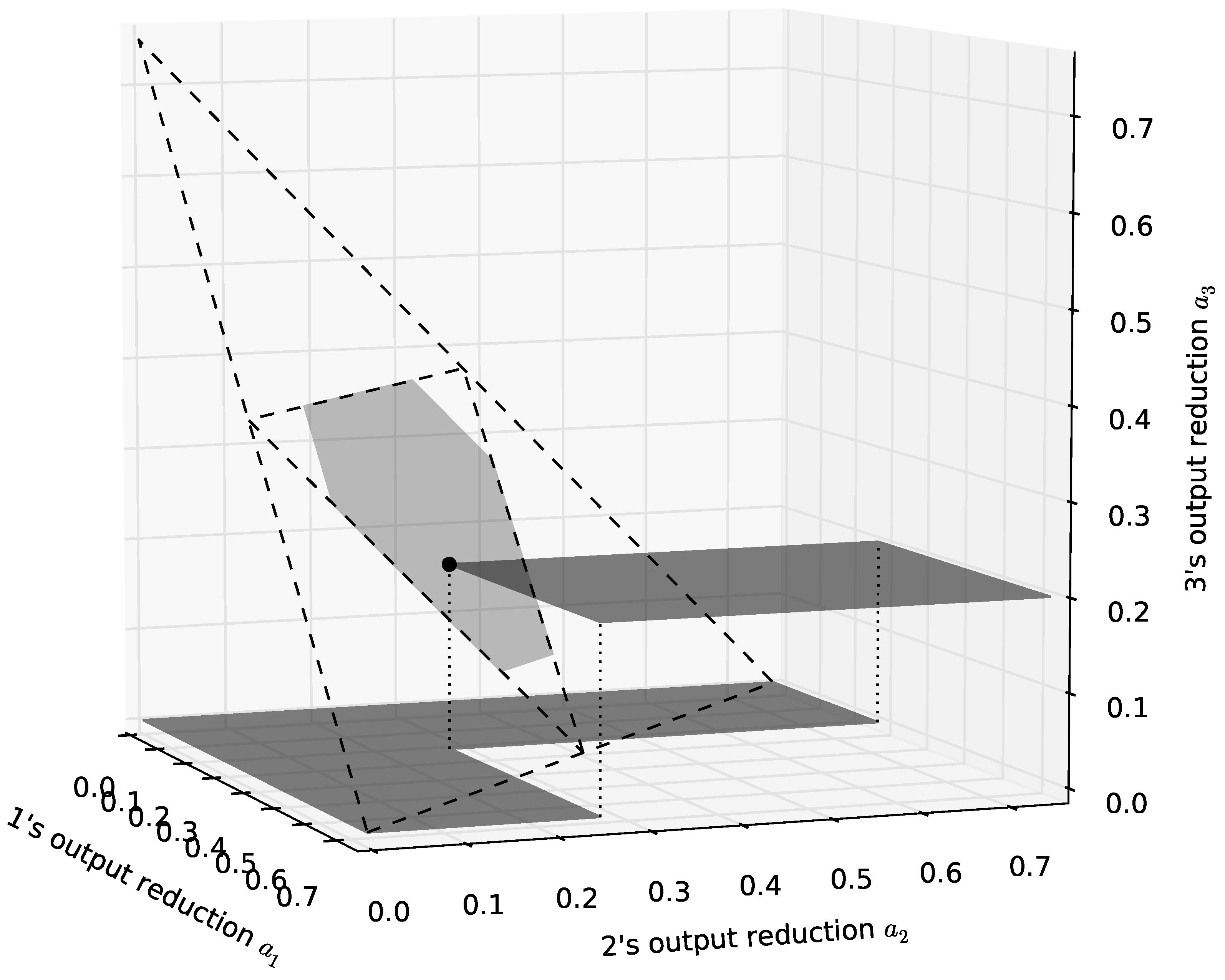
Appendix A.5. Further Examples of CPEPs
- (A1) The US would reduce oil imports and decontrol the oil price.
- (A2) The US would reduce inflation and currency fluctuations.
- (B) The UK would cut tariffs in the Tokyo GATT round.
- (C) Canada would increase economic growth.
- (F) France and the UK would cut tariffs in the Tokyo GATT round.
- (G) Germany would increase economic growth.
- (J1) Japan would increase economic growth.
- (J2) Japan would decrease their trade surplus.
Appendix B. The CCF Mechanism
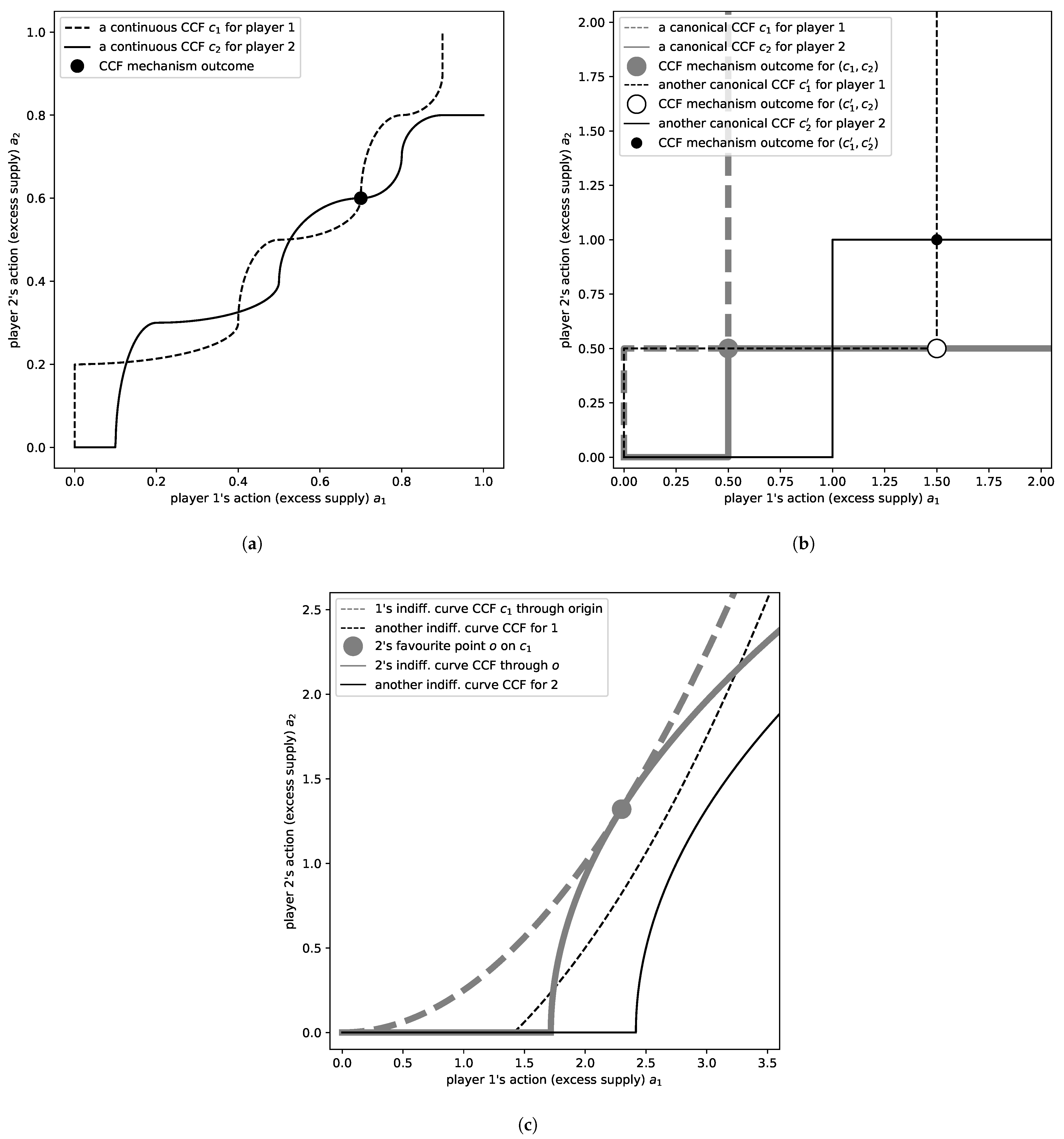
Appendix B.1. CCFs, Canonical and Indifference Curve CCFs, and Feasibility
- 1.
- has a largest element, denoted as .
- 2.
- This is a weakly increasing function of and .
- 3.
- Assume that within , society prefers larger contributions, i.e., for all with . Then, is a socially optimal and, thus, a strictly Pareto-efficient element of , and we call it the best realization of given .
- 4.
- If a subgroup switches to the canonical CCF of the best realization, the latter does not change: If , and , then .
Appendix B.2. The Mechanism and Its Equilibria
- 1.
- If c is a Nash equilibrium, then for all .
- 2.
- If for all , then is a Nash equilibrium.
- 3.
- If c is a strong Nash equilibrium, then is in the weak core.
- 4.
- If c is a strictly strong Nash equilibrium, is in the strict core.
- 5.
- If a is in the weak core and strictly Pareto-efficient, is a strong Nash equilibrium, and if preferences are continuous, , too, is a strong Nash equilibrium.
- 6.
- If a is in the strict core, is a strictly strong Nash equilibrium, and if preferences are continuous, , too, is a strictly strong Nash equilibrium.
- 7.
- Assume that for all and , the set and has a strictly G-optimal element, i.e., some with for all . Then, if c is a weakly [strictly] coalition-proof Nash equilibrium, it is already a strong [strictly strong] Nash equilibrium.
Appendix C. Convergence of Learning Rules
Appendix C.1. Indifference Curve-Based Learning
- We say that actions are dense if and only if for all and with , there is with and .
- We say that preferences are strictly monotonic if and only if for all , with , and with , we have and .
- (1)
- is an i-optimal -feasible action profile with , i.e., , for no .
- (2)
- is i’s indifference curve through , i.e., .
- (1)
- is an i-optimal -feasible action profile, i.e., , for no , where .
- (2)
- As in Theorem A2, is i’s indifference curve through , i.e., .
- (3)
- Either or .
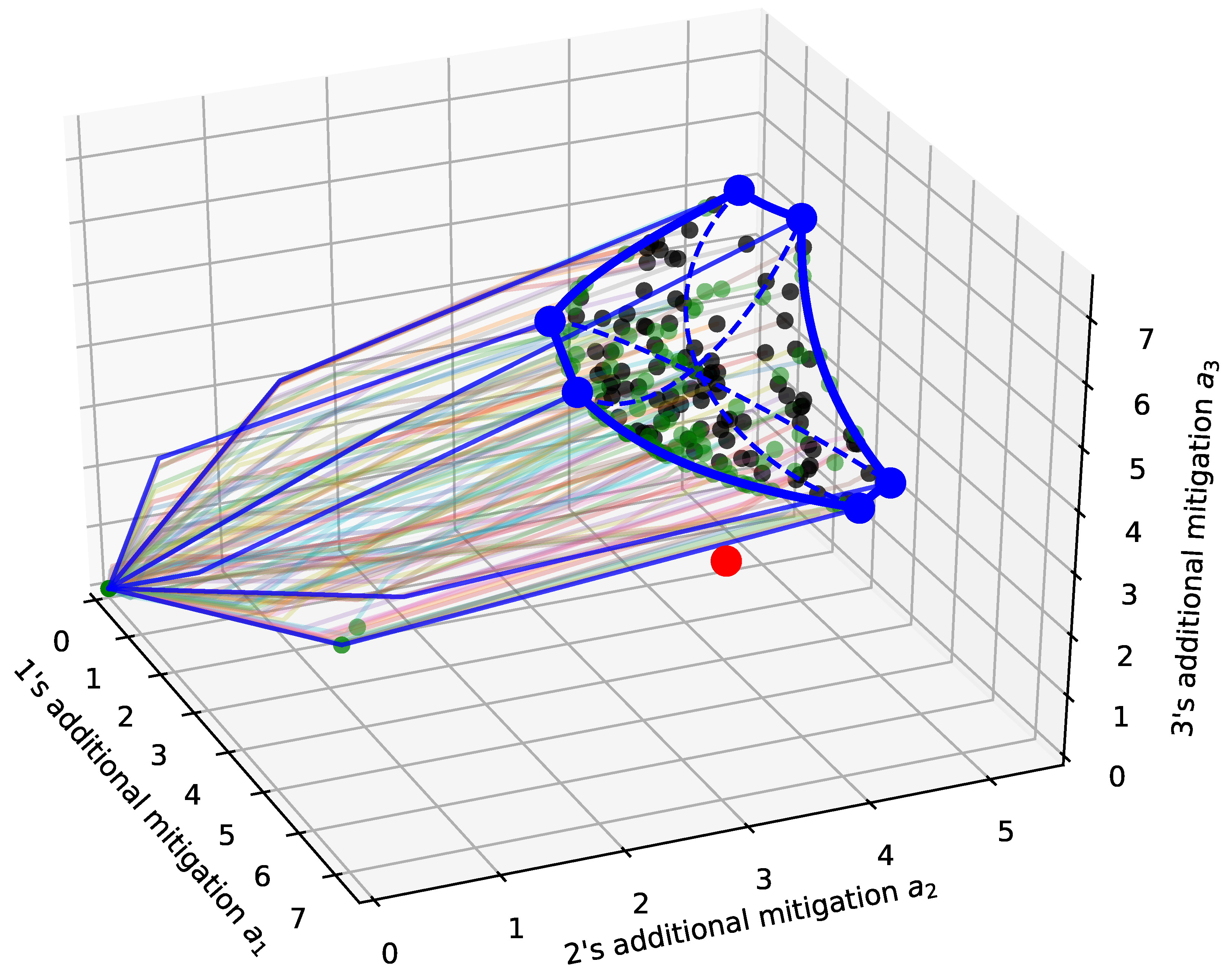
Appendix C.2. Convergence of Learning with Random Convex Combinations
- We say that actions are metric vectors if and only if each is a real vector space and d is a vector space metric on the product space .
- We say that preferences are metrically continuous and bounded if and only if all have a continuous von-Neumann–Morgenstern utility function .
- (0)
- At , all .
- (1)
- At , some is chosen independently according to some fixed positive probabilities .
- (2)
- j picks some optimal currently feasible action profile and draws some random coefficient according to some fixed positive probability density function .
- (3)
- j changes her CCF to the convex combination between her canonical and indifference CCFs through o, , while all other CCFs remain unchanged, .
Appendix D. Alternative (Dual) Mechanism
Appendix E. Relationship to Quasi-Supermodular Games
Appendix F. Conjectures
| 1 | An alternative mechanism would be to select the smallest profile with for all i, but one can show that that version would not lead to desirable equilibria with simple enough CCFs; see Appendix D. |
| 2 | There are different versions of ‘core’ in the literature, and most of them are defined for games or economies with transferable utility, so they only require . Ours is a non-transferable-utility version of the - and -core of (Zhao, 1999). Still, for some specifications of the utility functions , in particular those with separable costs and benefits and constant marginal costs, our public goods problem effectively has transferable utility, since transfers can then be realized by shifting supply between players, and in that case, our core equals the - and -cores of (Zhao, 1999). |
| 3 | This result is also interesting from a purely game-theoretic point of view, since it can be seen as a contribution to the “Nash program”, which is to justify key solution concepts from cooperative game theory, such as the core, by providing plausible non-cooperative mechanisms for their implementation. Its prime example is the implementation of the Nash bargaining solution via the Markov-perfect equilibria of the Rubinstein bargaining protocol, which is a certain repeated game form. In contrast to the latter, our mechanism is a one-shot mechanism and, to my knowledge, the only known mechanism for implementing the core established so far, at least in the subclass of games considered here. |
| 4 | A closely related result to this one is the following, which we state here without proof. Assume players choose their CCFs only once and for all, but in a fixed order that is known to all players in advance. Then, all the subgame-perfect equilibria of the resulting game give the same core outcome, and this core outcome is the same as when the learning rule of Theorem 3 was used with the reverse order of players. |
| 5 | This is probably a coincidence caused by the fact that, here, . In general, the core will be defined by ’s many inequalities and might have more or fewer than corners. |
| 6 | i.e., one may have neither nor for some pairs . Note that some authors call this “incomplete”, but we reserve the term “complete” for its lattice-theoretic or topological meaning. |
| 7 | Note that in the case where all actions can be represented by real numbers, and the orderings are just the usual ordering of real numbers; the base game is a potential game in the sense of Monderer and Shapley (1996), with ordinal potential . |
| 8 | We slightly deviate from common practice here in using the qualifiers “weak” and “strict” in a consistent way for both preferences, Pareto-efficiency and core properties, even though many authors omit the adjective “strict” for Pareto-efficiency and use “strong” instead of “strict” in case of cores. To avoid confusion, we reserve the adjective “strong” here for “strong Nash equilibria” where it relates to deviations by groups rather than strict preferences, which allows us to also introduce “strictly strong Nash equilibria” in a natural way. |
| 9 | This is similar to the notion of “very strong correlated equilibrium” used in Heitzig and Simmons (2012). |
References
- Aumann, R. J. (1959). Acceptable points in general cooperative n-person games. In Contributions to the theory of games (Vol. IV). Princeton University Press. [Google Scholar] [CrossRef]
- Barrett, S. (1994). Self-enforcing international environmental agreements. Oxford Economic Papers. Available online: http://www.jstor.org/stable/2663505 (accessed on 1 September 2025).
- Bennett, R. W. (2001). State coordination in popular election of the president without a constitutional amendment. Green Bag, 4, 241–246. [Google Scholar]
- Bernheim, B. D., Peleg, B., & Whinston, M. D. (1987). Coalition-proof nash equilibria I. Concepts. Journal of Economic Theory, 42(1), 1–12. [Google Scholar] [CrossRef]
- Buchholz, W., Cornes, R., & Rübbelke, D. (2011). Interior matching equilibria in a public good economy: An aggregative game approach. Journal of Public Economics, 95(7–8), 639–645. [Google Scholar] [CrossRef]
- Chander, P., & Tulkens, H. (1997). The core of an economy with multilateral environmental externalities. International Journal of Game Theory, 26(3), 379–401. [Google Scholar] [CrossRef]
- Delgado, J., & Moreno, D. (2004). Coalition-proof supply function equilibria in oligopoly. Journal of Economic Theory, 114(2), 231–254. [Google Scholar] [CrossRef][Green Version]
- Gerber, A., & Wichardt, P. C. (2009). Providing public goods in the absence of strong institutions. Journal of Public Economics, 93(3–4), 429–439. [Google Scholar] [CrossRef]
- Heitzig, J., & Simmons, F. W. (2012). Some chance for consensus: Voting methods for which consensus is an equilibrium. Social Choice and Welfare, 38(1), 43–57. [Google Scholar] [CrossRef]
- Klemperer, P. D., & Meyer, M. A. (1989). Supply function equilibria in oligopoly under uncertainty. Econometrica, 57(6), 1243–1277. [Google Scholar] [CrossRef]
- Milgrom, P., & Shannon, C. (1994). Monotone comparative statics. Econometrica: Journal of the Econometric Society, 62(1), 157–180. [Google Scholar] [CrossRef]
- Monderer, D., & Shapley, L. S. (1996). Potential games. Games and Economic Behavior, 14, 124–143. [Google Scholar] [CrossRef]
- Muller, D. T. (2007). The compact clause and the national popular vote interstate compact. Election Law Journal, 6(4), 372–393. [Google Scholar] [CrossRef]
- Oechssler, J., Reischmann, A., & Sofianos, A. (2022). The conditional contribution mechanism for repeated public goods—The general case. Journal of Economic Theory, 203, 105488. [Google Scholar] [CrossRef]
- Pauw, W. P., Castro, P., Pickering, J., & Bhasin, S. (2020). Conditional nationally determined contributions in the Paris Agreement: Foothold for equity or Achilles heel? Climate Policy, 20(4), 468–484. [Google Scholar] [CrossRef]
- Putnam, R. D., & Henning, C. R. (1986). The bonn summit of 1978: How does international economic policy coordination actually work? (Vol. 38; Tech. Rep.). The Brookings Institution. [Google Scholar]
- Reischmann, A., & Oechssler, J. (2018). The Binary Conditional Contribution Mechanism for public good provision in dynamic settings—Theory and experimental evidence. Journal of Public Economics, 159, 104–115. [Google Scholar] [CrossRef]
- Zhao, J. (1999). A β-core existence result and its application to oligopoly markets. Games and Economic Behavior, 27(1), 153–168. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heitzig, J. Provision of Public Goods via Unilateral but Mutually Conditional Commitments—Mechanism, Equilibria, and Learning. Games 2025, 16, 58. https://doi.org/10.3390/g16060058
Heitzig J. Provision of Public Goods via Unilateral but Mutually Conditional Commitments—Mechanism, Equilibria, and Learning. Games. 2025; 16(6):58. https://doi.org/10.3390/g16060058
Chicago/Turabian StyleHeitzig, Jobst. 2025. "Provision of Public Goods via Unilateral but Mutually Conditional Commitments—Mechanism, Equilibria, and Learning" Games 16, no. 6: 58. https://doi.org/10.3390/g16060058
APA StyleHeitzig, J. (2025). Provision of Public Goods via Unilateral but Mutually Conditional Commitments—Mechanism, Equilibria, and Learning. Games, 16(6), 58. https://doi.org/10.3390/g16060058





