Dividend Representations for Two Influence Assessments

Abstract

This paper establishes dividend-based representations for two influence assessments. First, we define a system of min-dividends derived from the minimal-influence evaluation via a unique linear decomposition using unanimity-type spanning models. Building on this, we further construct a pair of internal and external min-dividends satisfying Completeness and Balancedness conditions, through which we express the stable min-value as the net difference of internal gains and external losses. We then demonstrate that the minimal self-stable value can be represented as accumulated average min-dividends across all coalitions they have participated in. Furthermore, the proposed expression also is adopted to analyze the stability of the minimal self-stable value. These results extend the classical notion of dividends into a minimal-influence-based framework with potential applications in fair resource allocation and responsibility apportionment.

1. Introduction

In the analysis of cooperative behavior, particularly within transferable utility (TU) model frameworks, the notion of a dividend serves as a fundamental structural unit that bridges global outcomes and localized coalition dynamics. Originally formalized through the unanimity game decomposition of Shapley (1953), dividends quantify the marginal worth allocated to coalitions and their components. Dividends serve not only as algebraic primitives for value representation, but also as a conceptual mechanism to trace the internal contributions that underpin fair distributing schemes. In practical domains, such as cost sharing, voting power, influence evaluation, or coalition formation under uncertainty, dividends enable decomposability, tractability, and interpretability of cooperative structures. The recent literature has actively extended the role of dividends beyond the Shapley value. In particular, Hwang and Hsiao (2007) provided dividend-based representations for solution such as the equal allocation of non-separable costs (EANSC Ransmeier (1942)). Related works introduced dividend-loss functions, emphasizing internal versus external contribution mechanisms. The central idea is that every agent’s payoff can be interpreted as a summation of internal dividends from the coalitions they belong to, adjusted by external losses from those they are excluded from.

However, an emerging challenge in many influence-driven or responsibility-sharing contexts lies in identifying and characterizing minimal impact-based evaluating values, where the goal is not to distribute the entire worth under game-theoretical models, but to assess and generate minimal sufficient contributions. Motivated by the above considerations, Wang (2025) proposed two influence assessments, the stable min-value and the minimal self-stable value, under multi-choice TU models. Under the assessment notion of the stable min-value, each component first evaluates its marginal impact relative to wholesale minimal influence, and the rest of the influence is further assessed uniformly through whole components. The minimal self-stable value can be evaluated to be accumulated expected minimal values related to min-marginal influence from all coalitions each component has been a part of. Wang (2025) analyzed concerning expediency due to these two assessments by potential and axiomatic approaches.

Differently from the work of Wang (2025), this study would like to analyze these two assessments by utilizing the notion of dividends. In these contexts, however, traditional dividend structures tied to total value might be not directly applicable. That is,

A different form of dividend representation is thus required to characterize these influence-sensitive assessments.

This paper addresses this gap by constructing min-dividend-based representations for the stable min-value and the minimal self-stable value. The investigation structure and related outcomes are as follows.

• Section 2 introduces the basic setup and notations of the multi-choice settings, the minimal-influence evaluation, the stable min-value, and the minimal self-stable value.
• Section 3.1 presents the min-dividend structure via a unique decomposition over spanned unanimity-type models.
• Section 3.2 defines the min-(dividend & loss) function, consisting of a pair for each coalition, and establishes the axioms of Completeness and Balancedness for its interpretation. Based on this structure, this proves in this section that the stable min-value can be expressed as the internal dividend and the external loss across coalitions.
• Section 3.3 studies the minimal self-stable value, and shows that it admits a specific min-dividend representation as accumulated average min-dividends over the coalition-wise coefficients. Section 3.3 also proves that both dividend-based representations preserve reduction stability across subgames (via reduction), confirming that the evaluating values are behaviorally consistent across nested domains of analysis.

Through these developments, this work extends the structural role of dividends beyond classical TU game formulations into the domain of minimal-influence evaluations, offering both analytical tractability and operational relevance in contexts where fairness is tied to restrained or responsibility-sensitive assessments.

2. Model and Assessment

Assume that $\overline{\ddot{\mathsf{\Omega }}}$ is the universe of components. Let $k\in \overline{\ddot{\mathsf{\Omega }}}$ and ${\overrightarrow{\mu }}_k\in \mathbb{N}$; one would set ${\overline{\mathbf{U}}}_k=\{0,1,\cdots ,{\overrightarrow{\mu }}_k\}$ as the operating measure collection of component k, where 0 denotes non-action. For $\overline{\mathsf{\Omega }}\subseteq \overline{\ddot{\mathsf{\Omega }}}$, we assume that ${\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}={\prod }_{i\in \overline{\mathsf{\Omega }}}{\overline{\mathbf{U}}}_i$ as a product set of operating measures for all components of $\overline{\mathsf{\Omega }}$, and denote ${\overrightarrow{0}}_{\overline{\mathsf{\Omega }}}$ as the zero vector under ${\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}$.

Let $\overline{\mathsf{\Omega }}\subseteq \overline{\ddot{\mathsf{\Omega }}}$, $\overrightarrow{\mathbf{b}}\in {\mathbb{R}}^{\overline{\mathsf{\Omega }}}$, and $j\in \overline{\mathsf{\Omega }}$. One would utilize ${\overrightarrow{\mathbf{b}}}_{-j}$ to represent the restriction of $\overrightarrow{\mathbf{b}}$ to $\overline{\mathsf{\Omega }}\setminus \left\{j\right\}$, and consider $\overrightarrow{\beta }=({\overrightarrow{\mathbf{b}}}_{-j},m)$ by picking ${\overrightarrow{\mathbf{b}}}_{-j}={\overrightarrow{\beta }}_{-j}$ and ${\overrightarrow{\beta }}_j=m$. Let $k\in \overline{\mathsf{\Omega }}$, and define ${\overrightarrow{\mathbf{b}}}_{-jk}$ as the restriction of $\overrightarrow{\mathbf{b}}$ to $\overline{\mathsf{\Omega }}\setminus \{j,k\}$, and $({\overrightarrow{\mathbf{b}}}_{-jk},m,n)$ to represent $({({\overrightarrow{\mathbf{b}}}_{-j},m)}_{-k},n)$. For $\overline{\mathbf{M}},\overline{\mathbf{N}}\subseteq \overline{\mathsf{\Omega }}$, the set difference $\overline{\mathbf{M}}\setminus \overline{\mathbf{N}}$ is defined as $\{k\in \overline{\mathsf{\Omega }}\mid k\in \overline{\mathbf{M}}\mathrm{and}k\notin \overline{\mathbf{N}}\}$.

A multi-choice TU model is denoted by $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$, where $\overline{\mathsf{\Omega }}$ with $0<|\overline{\mathsf{\Omega }}|<\infty$ is the collection of components, $\overrightarrow{\mu }={\left({\overrightarrow{\mu }}_k\right)}_{k\in \overline{\mathsf{\Omega }}}$ means the amounts of non-zero measures of every component, and $\widehat{\kappa }:{\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}\to \mathbb{R}$ is a mapping with $\widehat{\kappa }\left({\overrightarrow{0}}_{\overline{\mathsf{\Omega }}}\right)=0$ which allots to each $\overrightarrow{\mathbf{b}}={\left({\overrightarrow{\mathbf{b}}}_k\right)}_{k\in \overline{\mathsf{\Omega }}}\in {\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}$ the value produced via joint operating measures of all components, where each component k operates measure ${\overrightarrow{\mathbf{b}}}_k$. One would denote $\widehat{\mathbb{O}}\left(\overrightarrow{\mathbf{b}}\right)=\{k\in \overline{\mathsf{\Omega }}|{\overrightarrow{\mathbf{b}}}_k\ne 0\}$ and ${\overrightarrow{\mathbf{b}}}_{\overline{\mathbf{M}}}$ as the restriction of $\overrightarrow{\mathbf{b}}$ at $\overline{\mathbf{M}}$ for every $\overline{\mathbf{M}}\subseteq \overline{\mathsf{\Omega }}$, and denote $(\overline{\mathsf{\Omega }},\overrightarrow{\gamma },\widehat{\kappa })$ as the multi-choice TU submodel of $(\overline{\mathsf{\Omega }},\overrightarrow{\mathbf{b}},\widehat{\kappa })$ given via restricting $\widehat{\kappa }$ to $\{\overrightarrow{\gamma }\in {\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}\mid {\overrightarrow{\gamma }}_k\le {\overrightarrow{\mathbf{b}}}_k\mathrm{for}\mathrm{every}k\in \overline{\mathsf{\Omega }}\}$.

The family of all multi-choice TU models is denoted as $\overline{\mathbf{MM}}$. An assessment over $\overline{\mathbf{MM}}$ is a mapping $\rho$ allotting to every $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ an evaluating vector

$$\rho \left(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }\right)={\left({\rho }_i\left(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }\right)\right)}_{i\in \overline{\mathsf{\Omega }}}\in {\mathbb{R}}^{\overline{\mathsf{\Omega }}},$$

where ${\rho }_i\left(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }\right)$ is the influence due to component i assessed by $\widehat{\kappa }$.

To evaluate the minimal influence fairly across multi-choice environments, two assessments are introduced by Wang (2025) as follows.

Definition 1.

• The stable min-value $\widehat{\chi }$ is defined as follows. For all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and for each component $k\in \overline{\mathsf{\Omega }}$,

  $${\widehat{\chi }}_k(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\chi }_k(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })+{\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}|}}[{\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\right)-\sum _{i\in \overline{\mathsf{\Omega }}}{\chi }_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })],$$

  where ${\chi }_k(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\right)-{\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\setminus \left\{k\right\}\right)$. For every $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$, ${\widehat{\kappa }}_{\#}\left(\overline{\mathbf{S}}\right)={min}_{\overrightarrow{\mathbf{b}}\in {\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}}\left\{\widehat{\kappa }\left(\overrightarrow{\mathbf{b}}\right)\right|\widehat{\mathbb{O}}\left(\overrightarrow{\mathbf{b}}\right)=\overline{\mathbf{S}}\}$ is the minimal influence achieved if whole units of $\overline{\mathbf{S}}$ take non-zero operating measures and all other units remain stand-by. Moreover, ${\chi }_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\right)-{\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\setminus \left\{i\right\}\right)$ means the relative minimal influence of unit i due to the whole coalition $\overline{\mathsf{\Omega }}$. Based upon assessment $\widehat{\chi }$, every component assesses its minimal influence firstly, and the rest of the influence is further assessed uniformly through whole components.
• The minimal self-stable value η is defined as follows. For all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and for each component $k\in \overline{\mathsf{\Omega }}$,

  $${\eta }_k(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })=\sum _{\stackrel{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}{k\in \overline{\mathbf{S}}}}{\displaystyle \frac{\left(\right|\overline{\mathbf{S}}|-1)!\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}\left|\right)!}{|\overline{\mathsf{\Omega }}|!}}·\left[{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{S}}\right)-{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{S}}\setminus \left\{k\right\}\right)\right].$$

  Based upon assessment η, every component obtains its expected values computed with respect to the minimal influences through every coalition this component has joined.

Remark 1.

An assessment ρ matches multi-attribute entire-optimality (MAEO) if ${\sum }_{i\in \overline{\mathsf{\Omega }}}{\rho }_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\right)$ for all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$. MAEO asserts that the whole assessing value aggregated by total components coincides with the minimal influence achieved via whole coalition. Wang (2025) showed that the stable min-value and the minimal self-stable value satisfy MAEO.

For quick cross-reference,

Table 1. Notation.

Symbol	Meaning/Role in Model
$\overline{\ddot{\mathsf{\Omega }}}$	universe of components
$\overline{\mathsf{\Omega }}\subseteq \overline{\ddot{\mathsf{\Omega }}}$	working set of components; let $|\overline{\mathsf{\Omega }}|=n$
${\overline{\mathbf{U}}}_k=\{0,1,\cdots ,{\overrightarrow{\mu }}_k\}$	operating measures of component k
${\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}={\prod }_{i\in \overline{\mathsf{\Omega }}}{\overline{\mathbf{U}}}_i,{\overrightarrow{0}}_{\overline{\mathsf{\Omega }}}$	joint measure set; zero vector
$\widehat{\kappa }:{\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}\to \mathbb{R}$	influence evaluation
${\widehat{\kappa }}_{\#}\left(\overline{\mathbf{S}}\right)$	minimal influence at coalition $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$
$\widehat{\chi }$	stable min-value
$\eta$	minimal self-stable value

summarizes the main symbols used in Section 2.

3. Dividend Representations

This section proposes a structured representation of the stable min-value through a specially constructed dividend–loss pair system, referred to as the min-(dividend & loss) function. This formulation is motivated by the need to capture both the internal contribution of an agent within a coalition and the external pressure exerted by coalitions from which the agent is excluded. Unlike classical dividend expressions that relate to total game worth, the framework here is developed in terms of minimal-influence values.

Before presenting the spanned model, we outline a concise analytical road-map as follows.

Analytical framework.

• Evaluate minimal influence related to ${\widehat{\kappa }}_{\#}$ over coalitions.
• Decompose ${\widehat{\kappa }}_{\#}$ through spanned models via Möbius inversion to obtain corresponding dividends.
• Specify the (dividend & loss) pair under specific conditions, which yields the unique coefficients.
• Obtain the dividend representations of the two assessments $\widehat{\chi }$ and $\eta$.
• Use the dividend view to analyze several results and applications.

3.1. Spanned Model and Min-Dividend

This section begins by proceeding to construct a dividend-based decomposition for the minimal-influence function, leading to a coefficient system, which we define as the min-dividends.

In order to generate alternative representations for the stable min-value and the minimal self-stable value, some more definitions and results related to multi-choice structure should be considered. Let $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$. The spanned model for TU games, $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },{\widehat{P}}_{\overline{\mathbf{S}}})$ with $\overline{\mathbf{S}}\ne \varnothing$, is defined by

$${\widehat{P}}_{\overline{\mathbf{S}}}\left(\overline{\mathbf{T}}\right)=\left\{\begin{array}{cc}1\hfill & \overline{\mathbf{S}}\subseteq \overline{\mathbf{T}},\hfill \\ 0\hfill & \mathrm{o}.\mathrm{w}.\hfill \end{array}\right.$$

In the following, it will be shown that each $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ can be formed by spanned models.

Lemma 1.

Let $\overline{\mathbf{S}}$ be a finite set and $\overline{\mathbf{R}}\subset \overline{\mathbf{S}}$ with $\overline{\mathbf{R}}\ne \overline{\mathbf{S}}$. Then

$$\sum _{\overline{\mathbf{R}}\subseteq \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}{(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|}=0.$$

Proof. 

Let $\overline{\mathbf{S}}$ be a finite set and $\overline{\mathbf{R}}\subset \overline{\mathbf{S}}$ with $\overline{\mathbf{R}}\ne \overline{\mathbf{S}}$.

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\overline{\mathbf{R}}\subseteq \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|}& =({\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subseteq \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\\ |\overline{\mathbf{T}}|=|\overline{\mathbf{R}}|\end{array}}}+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subseteq \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\\ |\overline{\mathbf{T}}|=|\overline{\mathbf{R}}|+1\end{array}}}+\cdots +{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subseteq \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\\ |\overline{\mathbf{T}}|=|\overline{\mathbf{S}}|\end{array}}}){(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|}\hfill \\ & ={\displaystyle \sum _{k=0}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}}{C}_k^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}{(-1)}^k\hfill & \hfill \left(\mathbf{let} |\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|=k\right)\\ & ={\displaystyle \sum _{k=0}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}}{C}_k^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}{(-1)}^k{\left(1\right)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|-k}\hfill \\ & ={(-1+1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}\hfill \\ & =0.\hfill & \hfill \left(\mathbf{since} |\overline{\mathbf{S}}|\ne |\overline{\mathbf{R}}|\right)\end{array}$$

The proof is completed. □

Lemma 2.

If for all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$, collection ${\left\{{\mathbf{b}}_{\overline{\mathbf{S}}}\right\}}_{\overline{\mathbf{S}}\in 2^{\overline{\mathsf{\Omega }}}}$ satisfies ${\widehat{\kappa }}_{\#}={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}$, then for all $\overline{\mathbf{S}}\in 2^{\overline{\mathsf{\Omega }}}$, ${\mathbf{b}}_{\overline{\mathbf{S}}}={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)$.

Proof. 

Assume that for all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$, collection ${\left\{{\mathbf{b}}_{\overline{\mathbf{S}}}\right\}}_{\overline{\mathbf{S}}\in 2^{\overline{\mathsf{\Omega }}}}$ satisfies ${\widehat{\kappa }}_{\#}={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}$. Let $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$. We shall complete this proof by induction on $|\overline{\mathbf{S}}|$. Since

$$\begin{array}{cc}\hfill {\widehat{\kappa }}_{\#}(\varnothing )& ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}(\varnothing )\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{S}}=\varnothing }}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}(\varnothing )+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{S}}\ne \varnothing \end{array}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}(\varnothing )\hfill \\ & ={\mathbf{b}}_{\varnothing }·1+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{S}}\ne \varnothing \end{array}}}{\mathbf{b}}_{\overline{\mathbf{S}}}·0\hfill \\ & ={\mathbf{b}}_{\varnothing },\hfill \end{array}$$

it is clear that ${\mathbf{b}}_{\varnothing }={\widehat{\kappa }}_{\#}(\varnothing )={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \varnothing }}{(-1)}^{|\varnothing |-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)$, which shows that it holds if $|\overline{\mathbf{S}}| =0$. Suppose that it holds for all $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$ with $|\overline{\mathbf{S}}| <t$ where $0<t\le |\overline{\mathsf{\Omega }}|$. Let $\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}$ with $|\overline{\mathbf{T}}| =t$. So

$$\begin{array}{cc}\hfill {\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)& ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{T}}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}\left(\overline{\mathbf{T}}\right)+{\displaystyle \sum _{\overline{\mathbf{S}}⊈\overline{\mathbf{T}}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{T}}}}{\mathbf{b}}_{\overline{\mathbf{S}}}·1+{\displaystyle \sum _{\overline{\mathbf{S}}⊈\overline{\mathbf{T}}}}{\mathbf{b}}_{\overline{\mathbf{S}}}·0\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{T}}}}{\mathbf{b}}_{\overline{\mathbf{S}}}.\hfill \end{array}$$

Thus,

$${\mathbf{b}}_{\overline{\mathbf{T}}}=\sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{T}}}{\mathbf{b}}_{\overline{\mathbf{S}}}-\sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}{\mathbf{b}}_{\overline{\mathbf{S}}}={\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)-\sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}{\mathbf{b}}_{\overline{\mathbf{S}}}.$$

By induction hypothesis,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{\mathbf{b}}_{\overline{\mathbf{S}}}& ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\overline{\mathbf{R}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{S}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right){\delta }_{\overline{\mathbf{R}}\overline{\mathbf{S}}},\mathbf{where} {\delta }_{\overline{\mathbf{R}}\overline{\mathbf{S}}}=\left\{\begin{array}{cc}\mathbf{1}\hfill & \mathrm{if}\overline{\mathbf{R}}\subseteq \overline{\mathbf{S}},\hfill \\ \mathbf{0}\hfill & \mathrm{if}\overline{\mathbf{R}}⊈\overline{\mathbf{S}}.\hfill \end{array}\right.\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right){\delta }_{\overline{\mathbf{R}}\overline{\mathbf{S}}}\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}}({\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}{\delta }_{\overline{\mathbf{R}}\overline{\mathbf{S}}}){\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}}({\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subseteq \overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}){\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}}(-{(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|}+{\displaystyle \sum _{\overline{\mathbf{R}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathbf{T}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{R}}|}){\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)\hfill \end{array}$$

Therefore, by applying Lemma 1, ${\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{S}}\ne \overline{\mathbf{T}}\end{array}}}{\mathbf{b}}_{\overline{\mathbf{S}}}=-{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}}{(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)$. Hence,

$${\mathbf{b}}_{\overline{\mathbf{T}}}={\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)-(-\sum _{\begin{array}{c}\overline{\mathbf{R}}\subset \overline{\mathbf{T}}\\ \overline{\mathbf{R}}\ne \overline{\mathbf{T}}\end{array}}{(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right))=\sum _{\overline{\mathbf{R}}\subseteq \overline{\mathbf{T}}}{(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right).$$

The proof is completed. □

Lemma 3.

If ${\mathbf{b}}_{\overline{\mathbf{S}}}={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)$ for all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and for all $\overline{\mathbf{S}}\in 2^{\overline{\mathsf{\Omega }}}$, then ${\widehat{\kappa }}_{\#}={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}$.

Proof. 

Assume that for all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and for all $\overline{\mathbf{S}}\in 2^{\overline{\mathsf{\Omega }}}$, ${\mathbf{b}}_{\overline{\mathbf{S}}}={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)$. We claim that ${\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}\left(\overline{\mathbf{R}}\right)$ for all $\overline{\mathbf{R}}\subseteq \overline{\mathsf{\Omega }}$. Let $\overline{\mathbf{R}}=\varnothing$. Clearly,

$${\mathbf{b}}_{\varnothing }=\sum _{\overline{\mathbf{T}}\subseteq \varnothing }{(-1)}^{|\varnothing |-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)={\widehat{\kappa }}_{\#}(\varnothing ),$$

so that

$$\sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}(\varnothing )={\widehat{\kappa }}_{\#}(\varnothing ),$$

hence it holds if $\overline{\mathbf{R}}=\varnothing$. Assume that $\overline{\mathbf{R}}\ne \varnothing$. Similarly to the previous lemma,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}\left(\overline{\mathbf{R}}\right)& ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{\mathbf{b}}_{\overline{\mathbf{S}}}\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{R}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right){\delta }_{\overline{\mathbf{T}}\overline{\mathbf{S}}}\hfill & \hfill \mathbf{\left(}\mathbf{by}\mathbf{definition}\mathbf{of}{\delta }_{\overline{\mathbf{T}}\overline{\mathbf{S}}}\mathbf{\right)}\\ & ={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{R}}}}{\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right){\delta }_{\overline{\mathbf{T}}\overline{\mathbf{S}}}\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{R}}}}\left({\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\delta }_{\overline{\mathbf{T}}\overline{\mathbf{S}}}\right){\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{R}}}}({\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}){\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\hfill \\ & =({\displaystyle \sum _{\overline{\mathbf{T}}=\overline{\mathbf{R}}}}+{\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{R}}}})({\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}){\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={(-1)}^{|\overline{\mathbf{R}}|-|\overline{\mathbf{R}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subset \overline{\mathbf{R}}\\ \overline{\mathbf{T}}\ne \overline{\mathbf{R}}\end{array}}}({\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}){\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right).\hfill & \hfill \left(\mathbf{by}\mathbf{Lemma}\mathbf{1}\right)\end{array}$$

The proof is completed. □

Remark 2.

1. 

Based on the above two lemmas, it is clear that ${\widehat{\kappa }}_{\#}={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}$ with ${\mathbf{b}}_{\overline{\mathbf{S}}}={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)$ for all $\overline{\mathbf{S}}\in 2^{\overline{\mathsf{\Omega }}}$. By adopting the proof of previous lemma, it is also clear that ${\widehat{\kappa }}_{\#}\left(\overline{\mathbf{R}}\right)={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{R}}}}{\mathbf{b}}_{\overline{\mathbf{S}}}$ for all $\overline{\mathbf{R}}\subseteq \overline{\mathsf{\Omega }}$.

2. 

It is clear from the mathematical expression for ${\mathbf{b}}_{\overline{\mathbf{S}}}$ that ${\mathbf{b}}_{\overline{\mathbf{S}}}$ represents the minimal influence if coalition $\overline{\mathbf{S}}$ is formed, which is referred to as the min-dividend.

3. 

The present analysis does not decompose total worth; it develops dividend formulas relative to the minimal influence ${\widehat{\kappa }}_{\#}$. Accordingly, the min-dividend ${\mathbf{b}}_{\overline{\mathbf{S}}}$ and the min-(dividend & loss) system (under Completeness and Balancedness) provide a net representation for $\widehat{\chi }$, while η averages ${\mathbf{b}}_{\overline{\mathbf{S}}}$ with the factor $|\overline{\mathbf{S}}{|}^{-1}$. The next section establishes these representations and their proofs under the above framework.

3.2. Dividend Representation for the Stable Min-Value

From the basis of the min-dividend, we define a pair of functions, and impose two essential properties, Completeness and Balancedness, to guide their allocation semantics. Under these two axioms, we then derive a closed-form expression for the stable min-value as the net effect of internal dividends and external losses across all coalitions.

Here, we formally define the min-(dividend & loss) function as a pair of mappings assigned to each coalition. These values are constructed from the previously defined min-dividend coefficients, and are intended to represent, respectively, the internal dividend distributed among components of a coalition, and the external loss allocated to non-components of a coalition due to the coalition’s formation. To ensure that this allocation framework is coherent and consistent with the structure of the minimal-influence function, two axioms will also be introduced in this section as follows.

• Completeness, requiring that the sum of internal min-dividends and external min-losses across all subsets of any coalition equals the influence evaluating value of this coalition.
• Balancedness, imposing a numerical equivalence between the total supply (internal min-dividends scaled by coalition size) and total demand (external min-losses scaled via the amount of excluded components).

These two properties provide the mathematical foundation that permits the dividend-based expression of the stable min-value in this section.

Definition 2.

A min-(dividend&loss) evaluation on $\overline{\mathbf{MM}}$ is a function $\widehat{\mathbb{D}}$ assigned to each $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ with a pair ${({\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }),{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }))}_{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}$ satisfying

$${\widehat{\kappa }}_{\#}\left(\overline{\mathbf{H}}\right)=\sum _{\overline{\mathbf{S}}\subseteq \overline{\mathbf{H}}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })+{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\left(Completeness\right)$$

(1)

for all $\overline{\mathbf{H}}\subseteq \overline{\mathsf{\Omega }}$, and

$${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })+{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })= |\overline{\mathbf{S}}|{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })-|\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{S}}|{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })(Balancedtreatment)$$

(2)

for all $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$, where ${\widehat{\mathbb{D}}}_{\varnothing }^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\widehat{\mathbb{D}}}_{\varnothing }^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })=0$.

Condition (1) can be treated as the multi-choice entire-optimality property. As for condition (2), we imagine that if a coalition $\overline{\mathbf{S}}$ forms, then

• $\overline{\mathbf{S}}$ possesses simultaneously the internal min-dividend “${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$” and the external min-loss “${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$”; therefore, the sum is “${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })+{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$”.
• $\overline{\mathbf{S}}$ evaluates “${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$” to its every component as internal min-dividend.
• $\overline{\mathbf{S}}$ evaluates “$-{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$” to every component of $\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{S}}$ as external min-loss.

These assert that “$|\overline{\mathbf{S}}|{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$” is the sum of internal min-dividends and “$-|\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{S}}|{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$” is the sum of external min-losses. Therefore, the left part in condition (2) can be treated to be the amount of “supply” if a coalition $\overline{\mathbf{S}}$ generates; and the right part can be regarded as the amount of “demand” if a coalition $\overline{\mathbf{S}}$ generates. The condition (2) asserts that supply coincides with demand. Note that ${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathbf{H}},\overrightarrow{\mu },\widehat{\kappa })\ne {\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$ and ${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathbf{H}},\overrightarrow{\mu },\widehat{\kappa })\ne {\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$ for $\overline{\mathbf{S}}\subseteq \overline{\mathbf{H}}\subseteq \overline{\mathsf{\Omega }}$ in general.

Interpretation. 

Completeness states that, for any coalition under consideration, aggregating internal dividends and external losses across all relevant subcoalitions reconstructs the same minimal-influence evaluation for that coalition. Balancedness complements this by requiring that the total internal supply distributed within a coalition equals the total external demand borne by those outside it. Together, these two requirements pin down a unique and transparent accounting scheme for the dividend–loss pair and prepare the ground for the representation of the stable min-value in Theorem 1.

Theorem 1.

There exists a unique min-(dividend&loss) evaluation on $\overline{\mathbf{MM}}$ such that the stable min-value can be expressed to be the sum of internal min-dividends and external min-losses simultaneously. Furthermore, for all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and for all $i\in \overline{\mathsf{\Omega }}$,

$${\widehat{\chi }}_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })=\sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })-\sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }).$$

Proof. 

Let $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$. Put ${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\displaystyle \frac{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}|+1}{|\overline{\mathsf{\Omega }}|}}{\mathbf{b}}_{\overline{\mathbf{S}}}$ and ${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\displaystyle \frac{|\overline{\mathbf{S}}|-1}{|\overline{\mathsf{\Omega }}|}}{\mathbf{b}}_{\overline{\mathbf{S}}}$ for all $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$. Clearly, there exists a unique min-(dividend&loss) function $\widehat{\mathbb{D}}$ on $\overline{\mathbf{MM}}$ satisfying conditions (1) and (2).

To verify the related expression, based on Remark 2, let $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$; by substituting ${\widehat{\kappa }}_{\#}\left(\overline{\mathbf{S}}\right)$ with ${\sum }_{\overline{\mathbf{K}}\subseteq \overline{\mathbf{S}}}{\mathbf{b}}_{\overline{\mathbf{K}}}$ into the formulation of the stable min-value of $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$, one can obtain that

$$\begin{array}{cc}\hfill {\widehat{\chi }}_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })& ={\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}|}}\{{\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\right)-\left(\right|\overline{\mathsf{\Omega }}|-1){\widehat{\kappa }}_{\#}(\overline{\mathsf{\Omega }}\setminus \left\{i\right\})+{\displaystyle \sum _{k\in \overline{\mathsf{\Omega }}\setminus \left\{i\right\}}}{\widehat{\kappa }}_{\#}(\overline{\mathsf{\Omega }}\setminus \left\{k\right\})\}\hfill \\ & ={\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}|}}\{{\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}-\left(\right|\overline{\mathsf{\Omega }}|-1){\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\setminus \left\{i\right\}}}{\mathbf{b}}_{\overline{\mathbf{S}}}+{\displaystyle \sum _{k\in \overline{\mathsf{\Omega }}\setminus \left\{i\right\}}}{\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\setminus \left\{k\right\}}}{\mathbf{b}}_{\overline{\mathbf{S}}}\}\hfill \\ & ={\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}|}}\{{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}{\mathbf{b}}_{\overline{\mathbf{S}}}+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}}{\mathbf{b}}_{\overline{\mathbf{S}}}-\left(\right|\overline{\mathsf{\Omega }}|-1){\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}}{\mathbf{b}}_{\overline{\mathbf{S}}}+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}\left|\right){\mathbf{b}}_{\overline{\mathbf{S}}}\}+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}}\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}|-1){\mathbf{b}}_{\overline{\mathbf{S}}}\}\hfill \\ & ={\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}|}}\{{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}|+1){\mathbf{b}}_{\overline{\mathbf{S}}}+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}}[1-(|\overline{\mathsf{\Omega }}|-1)+\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}|-1)]{\mathbf{b}}_{\overline{\mathbf{S}}}\}\hfill \\ & ={\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}|}}\{{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}|+1){\mathbf{b}}_{\overline{\mathbf{S}}}+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}}(1-|\overline{\mathbf{S}}\left|\right){\mathbf{b}}_{\overline{\mathbf{S}}}\}\hfill \\ & ={\displaystyle \frac{1}{|\overline{\mathsf{\Omega }}|}}\{{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}|+1){\mathbf{b}}_{\overline{\mathbf{S}}}-{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}}\left(\right|\overline{\mathbf{S}}|-1){\mathbf{b}}_{\overline{\mathbf{S}}}\}\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })-{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{S}}\end{array}}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }).\hfill \end{array}$$

The proof is completed. □

Reading Theorem 1.

The formula expresses the assessment for a component as a net balance: the sum of internal dividends contributed by coalitions that include the component, minus the sum of external losses imposed by coalitions that exclude it. Unlike classical worth–based dividends, the present representation is anchored to minimal influence, so it highlights how responsibility is allocated when only the least sufficient contributions are recognized. This perspective yields a clear audit trail from basic combinatorial building blocks to an interpretable measure that is useful for accountability, compliance budgeting, and other influence-sensitive applications.

3.3. Dividend Representation for the Minimal Self-Stable Value

Building on the structure proposed in Section 3.1, this section presents that the minimal self-stable value of each component, as expressed in Definition 1, is equivalent to its average accumulated min-dividend from all coalitions each component has been a part of. Further, the H-stability of the minimal self-stable value will be verified by applying the min-dividend.

Theorem 2.

The minimal self-stable value also can be expressed by the min-dividend. For each $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and each $i\in \overline{\mathsf{\Omega }}$, ${\eta }_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{S}}}}{|\overline{\mathbf{S}}|}}$.

Proof. 

For all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and for all $i\in \overline{\mathsf{\Omega }}$,

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{S}}}}{|\overline{\mathbf{S}}|}}& ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}\left({\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\right){\displaystyle \frac{1}{|\overline{\mathbf{S}}|}}\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}{\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right){\displaystyle \frac{1}{|\overline{\mathbf{S}}|}}{\delta }_{\overline{\mathbf{T}}\overline{\mathbf{S}}}\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right){\delta }_{\overline{\mathbf{T}}\overline{\mathbf{S}}}\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\\ i\in \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}\\ i\notin \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}{\widehat{\kappa }}_{\#}(\overline{\mathbf{T}}\setminus \left\{i\right\})\hfill \\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{T}}\end{array}}}[{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}]({\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)-{\widehat{\kappa }}_{\#}(\overline{\mathbf{T}}\setminus \left\{i\right\}))\hfill \end{array}$$

That is,

$$\sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\displaystyle \frac{1}{|\overline{\mathbf{S}}|}}=\sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathsf{\Omega }}\\ i\in \overline{\mathbf{T}}\end{array}}(\sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ \overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\end{array}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}})({\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)-{\widehat{\kappa }}_{\#}(\overline{\mathbf{T}}\setminus \left\{i\right\})).$$

(3)

For every $\overline{\mathbf{T}}\subset \overline{\mathsf{\Omega }}$, one can have that

$$\begin{array}{cc}\hfill {\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\end{array}}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}& =({\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ |\overline{\mathbf{S}}|=|\overline{\mathbf{T}}|\end{array}}}+{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ |\overline{\mathbf{S}}|=|\overline{\mathbf{T}}|+1\end{array}}}+\cdots +{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ |\overline{\mathbf{S}}|=|\overline{\mathsf{\Omega }}|\end{array}}}){\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}\hfill \\ & =C_0^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{T}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{T}}|}}+C_1^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{T}}|+1-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{T}}|+1}}+\cdots +C_{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}^{|\overline{\mathsf{\Omega }}|-|\overline{\overline{\mathbf{T}}}|}{\displaystyle \frac{{(-1)}^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}}{|\overline{\mathsf{\Omega }}|}}\hfill \\ & ={\displaystyle \sum _{k=0}^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}}{C}_k^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}{\displaystyle \frac{{(-1)}^k}{|\overline{\mathbf{T}}|+k}}\hfill \\ & ={\displaystyle \sum _{k=0}^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}}{C}_k^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}{(-1)}^k{\int }_0^1{x}^{|\overline{\mathbf{T}}|+k-1}dx\hfill \\ & ={\int }_0^1{\displaystyle \sum _{k=0}^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}}{C}_k^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}{(-1)}^k{x}^{|\overline{\mathbf{T}}|+k-1}dx\hfill \\ & ={\int }_0^1{x}^{|\overline{\mathbf{T}}|-1}{\displaystyle \sum _{k=0}^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}}{C}_k^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}{(-1)}^k{x}^{k}dx\hfill \\ & ={\int }_0^1{x}^{|\overline{\mathbf{T}}|-1}{(1-x)}^{|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}|}dx\hfill \\ & ={\displaystyle \frac{\left(\right|\overline{\mathbf{T}}|-1)!\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}\left|\right)!}{|\overline{\mathsf{\Omega }}|!}}.\hfill \\ & (\mathrm{Recall}\mathrm{that}B(\alpha ,\beta )={\int }_0^1{x}^{\alpha -1}{(1-x)}^{\beta -1}dx={\displaystyle \frac{(\alpha -1)!(\beta -1)!}{(\alpha +\beta -1)!}}\mathrm{for}\mathrm{all}\alpha ,\beta >0)\hfill \end{array}$$

That is,

$$\sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\end{array}}{\displaystyle \frac{{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}}{|\overline{\mathbf{S}}|}}={\displaystyle \frac{\left(\right|\overline{\mathbf{T}}|-1)!\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{T}}\left|\right)!}{|\overline{\mathsf{\Omega }}|!}}.$$

(4)

By Definition 1 and Equations (3) and (4), the proof is completed. □

Intuition for Theorem  2.

The minimal self-stable value can be understood as an accumulated coalition average of min-dividends over all coalitions containing the component. This average-based view complements the net internal-versus-external balance in Theorem 1 and facilitates the analysis of reduction stability, because it tracks how a component’s attributed influence persists when the evaluation is restricted to smaller systems. The result thus provides both conceptual clarity and a practical route for interpreting stability in applications.

Motivated by Hart and Mas-Colell (1989), Maschler and Owen (1989), and Hwang and Liao (2008), Wang (2025) introduced a specific reduction and related stability to axiomatize the minimal self-stable value as follows. The H-reduction $(\overline{\mathbf{N}},{\overrightarrow{\mu }}_{\overline{\mathbf{N}}},{\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\rho })$ is considered as

$${\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\rho }\left(\overrightarrow{\alpha }\right)={\widehat{\kappa }}_{\#}\left(\widehat{\mathbb{O}}(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{N}}})\right)-\sum _{k\in \overline{\mathsf{\Omega }}\setminus \overline{\mathbf{N}}}{\rho }_k\left(\widehat{\mathbb{O}}(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{N}}}),(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{N}}}),\widehat{\kappa }\right)\forall \overrightarrow{\alpha }\in {\overline{\mathbf{U}}}^{\overline{\mathbf{N}}}.$$

An assessment $\rho$ fits H-stability (HSTA) if

$${\rho }_k(\overline{\mathbf{N}},{\overrightarrow{\mu }}_{\overline{\mathbf{N}}},{\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\rho })={\rho }_k(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$$

(5)

for all $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$, for all $\overline{\mathbf{N}}\subseteq \overline{\mathsf{\Omega }}$, and for all $k\in \overline{\mathbf{N}}$.

Lemma 4.

Let $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and $(\overline{\mathbf{N}},{\overrightarrow{\mu }}_{\overline{\mathbf{N}}},{\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\eta })$ be a reduction of $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$ with respect to η and $\overline{\mathbf{N}}\subseteq \overline{\mathsf{\Omega }}$. It is shown that ${\widehat{\kappa }}_{\#}={\displaystyle \sum _{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}}{\mathbf{b}}_{\overline{\mathbf{S}}}{\widehat{P}}_{\overline{\mathbf{S}}}$ with ${\mathbf{b}}_{\overline{\mathbf{S}}}={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)$ for all $\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}$. Then

$${\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\eta }=\sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{N}}}{\mathbf{b}}_{\overline{\mathbf{T}}}^{\eta }{\widehat{P}}_{\overline{\mathbf{T}}},where{\mathbf{b}}_{\overline{\mathbf{T}}}^{\eta }=\sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{N}}}^c}{\displaystyle \frac{|\overline{\mathbf{T}}|{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \overline{\mathbf{T}}}}{|\overline{\mathbf{T}}|+|\overline{\mathbf{Q}}|}}.$$

Proof. 

Let $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and $\overline{\mathbf{N}}\subseteq \overline{\mathsf{\Omega }}$. For convenience, one can denote ${\overline{\mathbf{N}}}^c=\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{N}}$. For every $\overrightarrow{\alpha }\in {\overline{\mathbf{U}}}^{\overline{\mathbf{N}}}$,

$$\begin{array}{cc}\hfill {\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\eta }\left(\overrightarrow{\alpha }\right)& ={\widehat{\kappa }}_{\#}\left(\widehat{\mathbb{O}}(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{{\overline{\mathbf{N}}}^c})\right)-{\displaystyle \sum _{k\in {\overline{\mathbf{N}}}^c}}{\eta }_k\left(\widehat{\mathbb{O}}(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{{\overline{\mathbf{N}}}^c}),(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{{\overline{\mathbf{N}}}^c}),\widehat{\kappa }\right)\hfill \\ & ={\displaystyle \sum _{k\in \widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)}}{\eta }_k\left(\widehat{\mathbb{O}}(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{{\overline{\mathbf{N}}}^c}),(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{{\overline{\mathbf{N}}}^c}),\widehat{\kappa }\right)\hfill \\ & ={\displaystyle \sum _{k\in \widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)}}{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{K}}\subseteq \widehat{\mathbb{O}}(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{{\overline{\mathbf{N}}}^c})\\ k\in \overline{\mathbf{K}}\end{array}}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{K}}}}{|\overline{\mathbf{K}}|}}\hfill \\ & ={\displaystyle \sum _{\overline{\mathbf{K}}\subseteq \widehat{\mathbb{O}}(\overrightarrow{\alpha },{\overrightarrow{\mu }}_{{\overline{\mathbf{N}}}^c})}}|\overline{\mathbf{K}}\cap \widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)|{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{K}}}}{|\overline{\mathbf{K}}|}}\hfill \\ & ={\displaystyle \sum _{\left\{k\right\}\subseteq \widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)}}{\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{N}}}^c}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \left\{k\right\}}}{|\overline{\mathbf{Q}}|+1}}+{\displaystyle \sum _{\{k,j\}\subseteq \widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)}}{\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{N}}}^c}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \{k,j\}}}{|\overline{\mathbf{Q}}|+2}}+\cdots \hfill \\ & +{\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{H}}\subseteq \widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)\\ |\overline{\mathbf{H}}|=|\widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)|-1\end{array}}}{\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{N}}}^c}}\left(\right|\widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)|-1){\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \left\{k\right\}}}{|\overline{\mathbf{Q}}|+|\widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)|-1}}+\left|\widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)\right|{\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{N}}}^c}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \left\{k\right\}}}{|\overline{\mathbf{Q}}|+|\widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)|}}\hfill \end{array}$$

Set ${\mathbf{b}}_{\overline{\mathbf{T}}}^{\eta }={\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{N}}}^c}}{\displaystyle \frac{|\overline{\mathbf{T}}|{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \overline{\mathbf{T}}}}{|\overline{\mathbf{T}}|+|\overline{\mathbf{Q}}|}}$ for every $\overline{\mathbf{T}}\subseteq \overline{\mathbf{N}}$. Therefore,

$${\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\eta }\left(\overrightarrow{\alpha }\right)=\sum _{k\in \overline{\mathbf{T}}}{\mathbf{b}}_{\left\{k\right\}}^{\eta }+\sum _{\begin{array}{c}\{k,j\}\subseteq \overline{\mathbf{T}}\end{array}}{\mathbf{b}}_{\{k,j\}}^{\eta }+\cdots +\sum _{\begin{array}{c}\overline{\mathbf{H}}\subseteq \overline{\mathbf{T}}\\ |\overline{\mathbf{H}}|=|\overline{\mathbf{T}}|-1\end{array}}{\mathbf{b}}_{\overline{\mathbf{H}}}^{\eta }+{\mathbf{b}}_{\overline{\mathbf{T}}}^{\eta }.$$

So one can have that ${\widehat{\kappa }}_{\overline{\mathbf{N}},\overrightarrow{\mu },\eta }={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{N}}}}{\mathbf{b}}_{\overline{\mathbf{T}}}^{\eta }{\widehat{P}}_{\overline{\mathbf{T}}}$, where ${\mathbf{b}}_{\overline{\mathbf{T}}}^{\eta }={\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{N}}}^c}}{\displaystyle \frac{|\overline{\mathbf{T}}|{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \overline{\mathbf{T}}}}{|\overline{\mathbf{T}}|+|\overline{\mathbf{Q}}|}}$. □

Based on the potential approach, Wang (2025) showed that the minimal self-stable value satisfies H-stability. Differently from the work of Wang (2025), the H-stability of the minimal self-stable value will be analyzed by applying the min-dividend in this study.

Lemma 5.

The minimal self-stable value fits H-stability.

Proof. 

Let $(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\in \overline{\mathbf{MM}}$ and $\overline{\mathbf{H}}\subseteq \overline{\mathsf{\Omega }}$. For $k\in \overline{\mathbf{H}}$,

$$\begin{array}{ccc}\hfill {\eta }_k(\overline{\mathbf{H}},{\overrightarrow{\mu }}_{\overline{\mathbf{H}}},{\widehat{\kappa }}_{\overline{\mathbf{H}},\overrightarrow{\mu },\eta })& ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{H}}\\ k\in \overline{\mathbf{T}}\end{array}}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{T}}}^{\eta }}{|\overline{\mathbf{T}}|}}\hfill & \hfill \left(\mathrm{By}\mathrm{Lemma}4\mathrm{and}\mathrm{Theorem}2\right)\\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{H}}\\ k\in \overline{\mathbf{T}}\end{array}}}{\displaystyle \frac{1}{|\overline{\mathbf{T}}|}}{\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{H}}}^c}}{\displaystyle \frac{|\overline{\mathbf{T}}|{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \overline{\mathbf{T}}}}{|\overline{\mathbf{T}}|+|\overline{\mathbf{Q}}|}}\hfill & \hfill \left(\mathrm{By}\mathrm{Lemma}4\right)\\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{T}}\subseteq \overline{\mathbf{H}}\\ k\in \overline{\mathbf{T}}\end{array}}}{\displaystyle \sum _{\overline{\mathbf{Q}}\subseteq {\overline{\mathbf{H}}}^c}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{Q}}\cup \overline{\mathbf{T}}}}{|\overline{\mathbf{Q}}\cup \overline{\mathbf{T}}|}}\hfill & \hfill \left(\mathrm{Since}\overline{\mathbf{Q}}\cap \overline{\mathbf{T}}=\varnothing \right)\\ & ={\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ k\in \overline{\mathbf{S}}\end{array}}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{S}}}}{|\overline{\mathbf{S}}|}}\hfill \\ & ={\eta }_k(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\hfill & \hfill \left(\mathrm{By}\mathrm{Theorem}2\right).\end{array}$$

The proof is completed. □

3.4. Summary and Comparison of Dividend-Based Expressions

To consolidate the theoretical constructions established in this section, we provide a comparative summary of the two influence-based assessments, the stable min-value $\widehat{\chi }$ and the minimal self-stable value $\eta$, and highlight their respective representations based on the min-dividend structure. The following table juxtaposes the original forms of these two values, as introduced in Definition 1, against their dividend-based expressions established in Theorems 1 and 2.

These equivalent formulations emphasize the structural coherence and analytical clarity provided by the min-dividend framework introduced in Definition 1 and

Table 2. Dividend-based representations of the stable min-value and the minimal self-stable value.

The Stable Min-Value ${\widehat{\mathit{\chi }}}_{\mathit{k}}(\overline{\mathbf{\Omega }},\overrightarrow{\mathit{\mu }},\widehat{\mathit{\kappa }})$, $\mathit{k}\in \overline{\mathbf{\Omega }}$	The Minimal Self-Stable Value ${\mathit{\eta }}_{\mathit{k}}(\overline{\mathbf{\Omega }},\overrightarrow{\mathit{\mu }},\widehat{\mathit{\kappa }})$, $\mathit{k}\in \overline{\mathbf{\Omega }}$
${\displaystyle {\chi }_k(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })+\frac{1}{|\overline{\mathsf{\Omega }}|}\left[{\widehat{\kappa }}_{\#}\left(\overline{\mathsf{\Omega }}\right)-\sum _{i\in \overline{\mathsf{\Omega }}}{\chi }_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })\right]}$	${\displaystyle \sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ k\in \overline{\mathbf{S}}\end{array}}\frac{\left(\right|\overline{\mathbf{S}}|-1)!\left(\right|\overline{\mathsf{\Omega }}|-|\overline{\mathbf{S}}\left|\right)!}{|\overline{\mathsf{\Omega }}|!}\left[{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{S}}\right)-{\widehat{\kappa }}_{\#}(\overline{\mathbf{S}}\setminus \left\{k\right\})\right]}$
${\displaystyle =\sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ k\in \overline{\mathbf{S}}\end{array}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })-\sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ k\notin \overline{\mathbf{S}}\end{array}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })}$	${\displaystyle =\sum _{\begin{array}{c}\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}\\ k\in \overline{\mathbf{S}}\end{array}}\frac{{\mathbf{b}}_{\overline{\mathbf{S}}}}{|\overline{\mathbf{S}}|}}$

.

• In Definition 1, the stable min-value of a component integrates this component’s marginal minimal influence with a balanced redistribution of the residual influence. In Theorem 1, the stable min-value of a component can be expressed via the internal min-dividends received from all coalitions including this component and the external min-losses due to exclusion from other coalitions.
• In Definition 1, the minimal self-stable value of a component admits a direct expression as the sum of expected values related to min-marginal influence, accumulated through the coalitions this component joined. In Theorem 1, the minimal self-stable value of a component can be expressed as the sum of average min-dividends, accumulated across all coalitions containing the component.

Together, these dividend-based representations play a central role in enabling alternative and interpretable representations of both assessments. These formulations not only enhance analytical tractability, but also support applications in minimal-attribution decision systems, responsibility budgeting, and fair evaluation designs where each participant’s contribution is assessed through coalition-based influence potential.

Consolidated comparison.

For readability, the following comparison highlights how the present min-dividend framework differs from classical worth-based dividends and potential-based approaches. Classical dividend expressions are tied to the total worth of a TU game and explain payoffs by marginal contributions to that worth; in contrast, the present framework develops dividends relative to the minimal influence ${\widehat{\kappa }}_{\#}$. Through the spanned unanimity-type models and Möbius inversion, ${\widehat{\kappa }}_{\#}$ admits a unique min-dividend decomposition ${\left\{{\mathbf{b}}_{\overline{\mathbf{S}}}\right\}}_{\overline{\mathbf{S}}\subseteq \overline{\mathsf{\Omega }}}$ (Lemmas 1–3), which then feeds into the min-(dividend & loss) system under Completeness and Balancedness (Definition 2). This yields two complementary representations: Theorem 1 writes the stable min-value as an internal dividends minus external losses net expression, while Theorem 2 writes the minimal self-stable value as an average of min-dividends across coalitions including the player. These representations provide an influence-oriented counterpart to classical worth-oriented dividends and prepare for the application in Section 4.

Aspect	Classical dividends (worth)	This work: min-dividend (minimal influence)
Kernel object	total worth on TU games	${\widehat{\kappa }}_{\#}$ via spanned models
Decomposition	unanimity dividend of worth	Möbius min-dividend ${\mathbf{b}}_{\overline{\mathbf{S}}}$ of ${\widehat{\kappa }}_{\#}$
Balance principle	efficiency (sum to worth)	Completeness and Balancedness (Definition 2)
Value formulas	worth-based dividend values	${\widehat{\chi }}_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\displaystyle \sum _{\overline{\mathbf{S}}\ni i}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })-{\displaystyle \sum _{\overline{\mathbf{S}}\not\ni i}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }),{\eta }_i(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\displaystyle \sum _{\overline{\mathbf{S}}\ni i}}{\displaystyle \frac{{\mathbf{b}}_{\overline{\mathbf{S}}}}{|\overline{\mathbf{S}}|}}$
Interpretation	marginal contribution to worth	internal vs. external net; coalition average of ${\mathbf{b}}_{\overline{\mathbf{S}}}$

4. Application in Influence Evaluating Systems

This section constructs an illustrative yet policy-relevant situation to demonstrate the practical interpretability of the proposed min-dividend structure and the influence-based assessments derived from it. The situation illustration highlights the internal consistency and comparative behavior related to the stable min-value and the minimal self-stable value.

Consider three interacting components, labeled A, B, and C, i.e., $\overline{\mathsf{\Omega }}=\{A,B,C\}$. These components respectively represent the following:

• A: A national environmental authority (e.g., environmental protection agency);
• B: A metropolitan or local regulatory entity (e.g., city-level governance);
• C: A consortium of industrial actors subject to environmental constraints.

Each can exert influence through a discrete number of possible intervention measures. The total number of available measures is given by $\overrightarrow{\mu }=(1,1,2)$, reflecting one potential acting measure from each public authority and two potential acting measures from the industrial side. That is, ${\overline{\mathbf{U}}}_A=\{0,1\}$, ${\overline{\mathbf{U}}}_B=\{0,1\}$, and ${\overline{\mathbf{U}}}_C=\{0,1,2\}$. The joint measure collection is

$${\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}=\prod _{i\in \overline{\mathsf{\Omega }}}{\overline{\mathbf{U}}}_i=\{0,1\}\times \{0,1\}\times \{0,1,2\}.$$

One would define an influence evaluation $\widehat{\kappa }$ over ${\overline{\mathbf{U}}}^{\overline{\mathsf{\Omega }}}$ that reflects diminishing marginal returns and cross-component synergy in improving environmental quality (e.g., air pollution reduction or emission mitigation). The corresponding evaluating values are shown in

Table 3. Influence evaluating values $\widehat{\kappa }\left(\overrightarrow{\alpha }\right)$ for selected measure vectors.

${\overrightarrow{\mathit{\alpha }}}_{\mathit{A}}$	${\overrightarrow{\mathit{\alpha }}}_{\mathit{B}}$	${\overrightarrow{\mathit{\alpha }}}_{\mathit{C}}$	$\widehat{\mathit{\kappa }}({\overrightarrow{\mathit{\alpha }}}_{\mathit{A}},{\overrightarrow{\mathit{\alpha }}}_{\mathit{B}},{\overrightarrow{\mathit{\alpha }}}_{\mathit{C}})$
0	0	0	0.0
1	0	0	2.1
0	1	0	1.8
0	0	1	2.0
1	1	0	3.2
1	0	1	3.3
0	1	1	3.0
1	1	1	4.5
0	0	2	3.1
1	0	2	4.2
0	1	2	4.0
1	1	2	5.4

, and are interpreted as resulting environmental improvement levels under respective joint configurations of actions.

Each measure vector $\overrightarrow{\alpha }$ corresponds to a coalition $\overline{\mathbf{S}}$ of active participants, defined as $\widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)=\{i\in \{A,B,C\}\mid {\overrightarrow{\alpha }}_i>0\}$. The associated minimal influence evaluation is defined by

$${\widehat{\kappa }}_{\#}\left(\overline{\mathbf{S}}\right)=min\{\widehat{\kappa }\left(\overrightarrow{\alpha }\right)\mid \widehat{\mathbb{O}}\left(\overrightarrow{\alpha }\right)=\overline{\mathbf{S}}\}.$$

From these evaluating values, one can compute min-dividend coefficients ${\mathbf{b}}_{\overline{\mathbf{S}}}$ by using the inclusion–exclusion expression ${\mathbf{b}}_{\overline{\mathbf{S}}}={\displaystyle \sum _{\overline{\mathbf{T}}\subseteq \overline{\mathbf{S}}}}{(-1)}^{|\overline{\mathbf{S}}|-|\overline{\mathbf{T}}|}{\widehat{\kappa }}_{\#}\left(\overline{\mathbf{T}}\right)$.

These coefficients are then used to compute the stable min-value ${\widehat{\chi }}_i$ (via Theorem 1) and the minimal self-stable value ${\eta }_i$ (via Theorem 2), which respectively express fair attribution of influence responsibility under two principles: one that balances internal gain and external burden, and one that averages direct coalition-level min-dividends.

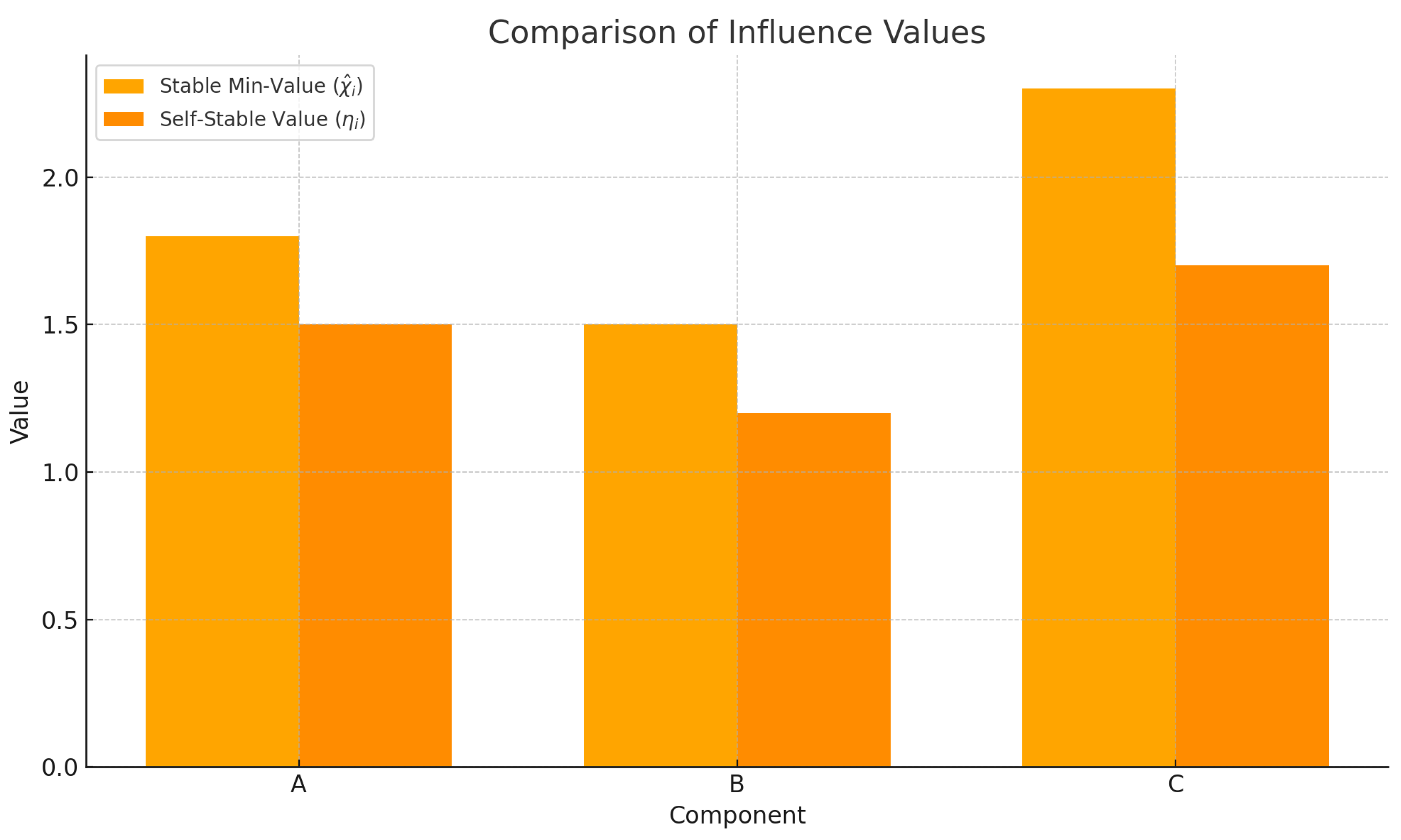
Illustration (component $\mathit{A}$).

With $|\overline{\mathsf{\Omega }}|=3$ and the min-dividends reported in

Table 4. Min-dividend coefficients ${\mathbf{b}}_{\overline{\mathbf{S}}}$.

Coalition of Active Participants in Measure Vector $\overline{\mathbf{S}}$	${\mathbf{b}}_{\overline{\mathbf{S}}}$
$\left\{A\right\}$	2.1
$\left\{B\right\}$	1.8
$\left\{C\right\}$	2.0
$\{A,C\}$	−0.8
$\{B,C\}$	−0.8
$\{A,B\}$	−0.7
$\{A,B,C\}$	0.9

, Theorem 1 gives

$${\widehat{\chi }}_A(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })=\underset{\mathrm{internal}{\displaystyle \sum _{\overline{\mathbf{S}}\ni A}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })}{\underbrace{1·{\mathbf{b}}_{\left\{A\right\}}+\frac{2}{3}\left({\mathbf{b}}_{\{A,B\}}+{\mathbf{b}}_{\{A,C\}}\right)+\frac{1}{3}{\mathbf{b}}_{\{A,B,C\}}}}-\underset{\mathrm{external}{\displaystyle \sum _{\overline{\mathbf{S}}\not\ni A}}{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })}{\underbrace{\left(0·{\mathbf{b}}_{\left\{B\right\}}+0·{\mathbf{b}}_{\left\{C\right\}}+\frac{1}{3}{\mathbf{b}}_{\{B,C\}}\right)}},$$

hence, using ${\mathbf{b}}_{\left\{A\right\}}=2.1$, ${\mathbf{b}}_{\{A,B\}}=-0.7$, ${\mathbf{b}}_{\{A,C\}}=-0.8$, ${\mathbf{b}}_{\{A,B,C\}}=0.9$, and ${\mathbf{b}}_{\{B,C\}}=-0.8$,

$${\widehat{\chi }}_A(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })=2.1+\frac{2}{3}(-0.7-0.8)+\frac{1}{3}·0.9-\frac{1}{3}·(-0.8)=1.666\dots$$

which matches

Table 5. Computed assessment values for each component.

Component	The Stable Min-Value ${\widehat{\mathit{\chi }}}_{\mathit{i}},\mathit{i}\in \overline{\mathbf{\Omega }}$	The Self-Stable Value ${\mathit{\eta }}_{\mathit{i}},\mathit{i}\in \overline{\mathbf{\Omega }}$
A	1.6660	1.6500
B	1.3670	1.3500
C	1.4670	1.5000

. By Theorem 2,

$${\eta }_A(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })={\mathbf{b}}_{\left\{A\right\}}+\frac{1}{2}\left({\mathbf{b}}_{\{A,B\}}+{\mathbf{b}}_{\{A,C\}}\right)+\frac{1}{3}{\mathbf{b}}_{\{A,B,C\}}=2.1+\frac{1}{2}(-0.7-0.8)+\frac{1}{3}·0.9=1.65.$$

The same substitutions yield ${\widehat{\chi }}_B(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }),{\widehat{\chi }}_C(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$ and ${\eta }_B(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa }),{\eta }_C(\overline{\mathsf{\Omega }},\overrightarrow{\mu },\widehat{\kappa })$ in Table 5.

Figure 1 and Figure 2 respectively display the following:

• A bar chart comparing ${\widehat{\chi }}_i$ and ${\eta }_i$, visualizing their allocation differences;
• A heatmap of pairwise min-dividend coefficients ${\mathbf{b}}_{\overline{\mathbf{S}}}$ for $\{|\overline{\mathbf{S}}|=2\}$, highlighting interactive synergy or redundancy.

Reading the signs of ${\mathbf{b}}_{\overline{\mathbf{S}}}$.

A positive min-dividend ${\mathbf{b}}_{\overline{\mathbf{S}}}>0$ indicates a net incremental minimal influence generated by coalition $\overline{\mathbf{S}}$ after deducting all proper sub-coalitions; a negative ${\mathbf{b}}_{\overline{\mathbf{S}}}<0$ reflects redundancy or conflict at the $\overline{\mathbf{S}}$-level. Under Balancedness (Definition 2), the total internal supply $|\overline{\mathbf{S}}|{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{+}$ equals the total external demand $|\overline{\mathsf{\Omega }}\setminus \overline{\mathbf{S}}|{\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}$ for each $\overline{\mathbf{S}}$, so negative pairwise dividends (e.g., ${\mathbf{b}}_{\{A,C\}},{\mathbf{b}}_{\{B,C\}}<0$) are transmitted as larger external burdens through ${\widehat{\mathbb{D}}}_{\overline{\mathbf{S}}}^{-}$. This interpretation bridges the numerical entries in Table 4 and Table 5 with the visual patterns in Figure 1 and Figure 2 and clarifies how min-dividends shape the two assessments.

This situation shows that the min-dividend structure yields interpretable, disaggregated contributions. The stable min-value reflects both cooperation and externalities, while the minimal self-stable value distributes influence attribution purely among directly involved coalitions. These results support applications in responsibility allocation, cooperative impact control, and minimal-intervention policy design in multi-actor regulatory systems.

5. Concluding Remarks

• This paper develops a structured framework for representing influence-based assessments in multi-choice TU models. The central idea is to extend dividend reasoning—traditionally tied to total-worth decompositions—to minimal-influence contexts where responsibility or influence is allocated under restrained, level-sensitive contributions.

  (a)

  First, a min-dividend decomposition of the minimal-influence evaluation is constructed on unanimity-type spanned models, yielding a unique system of coefficients.

  (b)

  Second, a min-(dividend & loss) function is introduced and justified by two balancing requirements, Completeness and Balancedness. This structure leads to a closed-form, net expression of the stable min-value as internal dividends from coalitions including a component minus external losses from coalitions excluding it (Theorem 1).

  (c)

  Third, the minimal self-stable value admits a clean dividend-based representation as an accumulated average of min-dividends across coalitions that include the component, and its reduction stability is analyzed through this expression (Theorem 2).

• This study departs from existing lines of work such as Shapley (1953), Hwang and Hsiao (2007), and Wang (2025). Prior research on dividends and potential-based allocations largely addresses total-worth settings under TU games or treats equal-allocation principles from axiomatic viewpoints. By contrast, the present approach develops a dividend-theoretic account for minimal influence within multi-choice TU environments.

  (a)

  Scope: classical dividend analyses and related results operate on total worth in traditional TU games, whereas the present work targets minimal influence under multi-choice TU settings.

  (b)

  Method: potential-based and axiomatic treatments in the literature are complemented here by an explicit min-dividend and min-(dividend & loss) construction that institutionalizes internal-versus-external accounting.

  (c)

  Focus: rather than complete value decompositions, the emphasis is on minimal-influence evaluations, enabling a more granular view of component roles under coalition formation.

  (d)

  Consistency: the dividend representation of the minimal self-stable value aligns with the established notion of reduction stability, ensuring conceptual compatibility with the cooperative-game perspective.

• From a theoretical standpoint, the results show that even non-additive, influence-oriented assessments can be captured by transparent combinatorial primitives, providing interpretable decomposition and clear coalition semantics. From a practical standpoint, the representations enable responsibility allocation when only minimal sufficient influence is to be recognized, with natural applicability to regulatory systems, sustainability governance, and minimally disruptive intervention planning.
• By establishing dividend representations in a minimal-influence setting, this work offers a foundation for addressing fairness under structural constraints or heterogeneity. Looking forward, several directions merit further research.

  (a)

  Extending the min-dividend framework to dynamic or stochastic multi-level contribution environments.

  (b)

  Designing scalable algorithms and approximations for large coalition spaces.

  (c)

  Developing axiomatic characterizations of the two assessments under alternative fairness principles.

  (d)

  Applying the min-dividend-based expressions in empirical domains such as climate attribution and responsibility assignment in decentralized systems.