Optimal Vaccination Strategies to Reduce Endemic Levels of Meningitis in Africa

Abstract

Meningococcal meningitis is a deadly acute bacterial infection caused by the Neisseria meningitidis bacterium that affects the membrane covering the brain and spinal cord. The World Health Organization launched the “Defeating bacterial meningitis by 2030” initiative in 2018, which relies on recent discoveries of cheap and effective vaccines. Here, we consider one important factor—human behavior—which is often neglected by immunization campaigns. We constructed a game-theoretic model of meningitis in the meningitis belt, where individuals make selfish rational decisions whether to vaccinate based on the assumed costs and the vaccination decisions of the entire population. We identified conditions when individuals should vaccinate, and we found the optimal (equilibrium) population vaccination rate. We conclude that voluntary compliance significantly reduces the endemic levels of meningitis if the cost of vaccination relative to the cost of the disease is sufficiently low, but it does not eliminate the disease. We also performed uncertainty and sensitivity analysis on our model.

1. Introduction

Meningitis killed almost 280,000 people in 2016 World Health Organization (2018b). Yet many of those deaths could have been prevented by vaccination. What causes humans to forgo vaccination against a dangerous infectious disease such as meningitis? Is it a lack of vaccine access or misconceptions about immunization? Can such behavior be rationally justified? Our motivation for this research is to understand how the vaccination decisions of rational selfish individuals may affect the spread and prevalence of meningitis in Africa.

Meningitis is an inflammation of the protective membranes covering the brain and spinal cord. A bacterial or viral infection of the fluid surrounding the brain and spinal cord usually causes swelling Centers for Disease Control and Prevention (n.d.-c). Bacterial meningitis is a serious—and potentially deadly—disease often resulting in permanent disabilities such as brain damage, deafness, and loss of limbs. It can be caused by several types of bacteria Centers for Disease Control and Prevention (n.d.-a). Meningococcal meningitis is of special interest due to its potential to result in large epidemics; it is caused by the bacterium Neisseria meningitidis (meningococcus) Centers for Disease Control and Prevention (n.d.-d). This bacterium is not as contagious as the germs that cause the flu, and it is not spread through casual contact. People spread meningococcal bacteria through respiratory and throat secretions (saliva), and it takes prolonged close contact, such as coughing, sneezing, kissing, or drinking, or eating right after an infected person to infect another person Centers for Disease Control and Prevention (n.d.-e).

An estimated 10% of people have Neisseria meningitidis bacteria in the back of their nose and throat with no signs or symptoms of the disease; they are called carriers Centers for Disease Control and Prevention (n.d.-e). Carriers can unknowingly transmit the bacteria to others; therefore, they are potentially more infectious than those individuals who exhibit symptoms of the disease. In less than 1% of carriers, the bacteria enters the bloodstream, causing an infection Centers for Disease Control and Prevention (n.d.-b). About 10–15% of people infected with meningococcal meningitis will die (even with antibiotic treatment). Of those who survive, about 11–19% will have long-term disabilities Centers for Disease Control and Prevention (n.d.-f). A previous infection will not offer lifelong immunity. It is possible—but rare—to contract meningococcal meningitis again from the same bacterium; this may be caused by an underlying immune deficiency Centers for Disease Control and Prevention (n.d.-h).

There are twelve serogroups of Neisseria meningitidis, six of which (A, B, C, W, X, and Y) can cause epidemics and hence induce the most cases of the disease World Health Organization (n.d.-b). Serogroups B, C, and Y account for most cases of meningococcal meningitis in the Americas, Australia, and Europe Centers for Disease Control and Prevention (n.d.-g). The largest number of cases of meningococcal meningitis occurs in the infamous “meningitis belt” of sub-Saharan Africa, with serogroup A historically being responsible for 90% of these cases Centers for Disease Control and Prevention (n.d.-g). Following the introduction of a monovalent serogroup A meningococcal conjugate vaccine MenAfriVac in 2010, epidemics due to serogroup A have been eliminated in vaccination areas World Health Organization (2018a), and recent epidemics in the meningitis belt have been mostly due to serogroups C and W Centers for Disease Control and Prevention (n.d.-g).

There are many vaccines available to prevent meningococcal meningitis World Health Organization (n.d.-c). Polysaccharide vaccines are usually used during a response to outbreaks in Africa; they offer 3-year protection but do not induce herd immunity. Conjugate vaccines are used in prevention and outbreak response; their effect lasts for 5+ years, and they do induce herd immunity. In particular, the monovalent serogroup A meningococcal conjugate vaccine is a cheap (around $0.60 per dose), safe, and effective vaccine. The introduction of this affordable vaccine in 2010 in Africa through mass vaccination campaigns resulted in significant decline in meningitis incidence and epidemic risk there World Health Organization (n.d.-c).

Because significant progress has been made in the global fight against meningitis in recent years, the World Health Organization launched the “Defeating bacterial meningitis by 2030” initiative in May 2018 World Health Organization (n.d.-a). One of its immediate goals is to develop a strategic global meningitis control roadmap. It includes addressing country priorities through evidence regarding policy and impact, detecting meningitis epidemics through strengthened surveillance, controlling meningitis epidemics, preserving human capital by preventing and treating meningitis sequelae, strong immunization programs, and increased access to care and meningitis treatment. In particular, ensuring long-term protection of the at-risk population in the meningitis belt by means of vaccination campaigns is vital for the success of this project. The majority of such campaigns, however, neglect one important factor—voluntary personal participation in these immunization programs.

Modeling how human behavior affects the spread and prevalence of infectious diseases became part of a new field called behavioral epidemiology Manfredi and D’Onofrio (2013). One of the human factors which may influence outcomes of a vaccination campaign is rationally selfish behavior. A selfish rational individual would attempt to inform their vaccination decision as a best response to the behavior of the entire population. Even the slightest risk of the vaccine-induced morbidity may outweigh the potential risk of the disease if a sufficiently large proportion of the population is already immune. Thus, optimizing individual utility may prevent the population from reaching the herd immunity coverage level, resulting in the tragedy-of-the-commons-like effect.

Models of this type can be formulated and solved within the framework of game theory, which studies strategic interactions between rational individuals, with its initial applications coming in the field of economics von Neumann and Morgenstern (1944). Since then, game theory has become a powerful tool for analyzing biological phenomena Broom and Rychtář (2013); Cressman (2003); Hofbauer and Sigmund (1998); Maynard Smith (1982); Vincent and Brown (2005). A significant application lies in understanding individual-level vaccination decisions, originating from the foundational concept of “vaccination games” Bauch and Earn (2004). This approach has been extensively employed to explore optimal vaccination strategies across a diverse range of infectious diseases, including chickenpox Liu et al. (2012), cholera Kobe et al. (2018), COVID-19 Agusto et al. (n.d.); Marquez et al. (2024), Ebola Brettin et al. (2018), hepatitis B Chouhan et al. (2020); Scheckelhoff et al. (2021), influenza Galvani et al. (2007); Shim, Chapman, et al. (2012), measles Shim, Grefenstette, et al. (2012), monkeypox Augsburger et al. (2022); Bankuru et al. (2020), poliomyelitis Cheng et al. (2020), rabies Campo et al. (2022); Hassan et al. (2024), rubella Shim et al. (2009), Schistosomiasis Lopez et al. (2024), smallpox Bauch et al. (2003), toxoplasmosis Sykes and Rychtář (2015), typhoid fever Acosta-Alonzo et al. (2020), and yellow fever Caasi et al. (2022). Furthermore, this game-theoretic framework has proven effective for analyzing decisions related to other protective health measures, such as the use of clean injecting equipment Scheckelhoff et al. (2025) or condoms Gribovskii and Erovenko (n.d.), access to clean water Kobe et al. (2018), adoption of facial cleanliness practices Barazanji et al. (2023), use of insecticide-treated bed nets Broom et al. (2016); Fortunato et al. (2021); Han et al. (2020); Onifade et al. (2024) and insecticide-treated cattle Crawford et al. (2015), application of mosquito repellent Angina et al. (2022); Dorsett et al. (2016); Klein et al. (2020); Rychtář and Taylor (2022), and support for public health measures like school/workplace closures and isolation Agusto et al. (2022). For a comprehensive overview of behavior-linked vaccination models, readers may consult the review by Wang et al. (2016).

In a vaccination game, a susceptible individual may choose to vaccinate and face the morbidity risk of the vaccine, or they may choose not to get vaccinated and risk infection. The probability that a non-vaccinating individual gets infected is computed as the transition probability from the susceptible state to the infected state using an epidemiological model of the disease. This probability depends on the prevalence of the disease, which, in turn, depends on the vaccination strategies employed by the rest of the population. The more individuals in the population are vaccinated, the less likely a susceptible individual is to get infected. As a result, if too many individuals are vaccinated, then susceptible individuals would tend to forgo vaccination, and the population vaccination coverage would drop. Conversely, if few individuals are vaccinated, then a susceptible individual would have a strong incentive to vaccinate, and the vaccination coverage would rise. A game-theoretic model finds an equilibrium vaccination rate for the entire population, which corresponds to equal payoffs of both vaccinating and non-vaccinating strategies.

In this paper, we construct a game-theoretic model of vaccination decisions by rational selfish individuals against meningococcal meningitis. Payoffs of the game-theoretic model are informed by a deterministic compartment epidemiological model of meningococcal meningitis in the meningitis belt. We concentrate on the serogroup A meningitis and consider a monovalent serogroup A meningococcal conjugate vaccine, MenAfriVac, as the individual protective measure. We found that with voluntary participation in the immunization campaign, meningitis caused by serogroup A bacteria could be reduced to very low endemic levels (given the low cost of the MenAfriVac vaccine) but not eliminated. We also performed sensitivity analysis of the model parameters.

2. Methods

We adopt a modified version of a compartment model of the transmission of meningococcal meningitis in the meningitis belt with immunity from both disease and carriage Djatcha Yaleu et al. (2017); Irving et al. (2012). The human population (N) is divided into five compartments: susceptible (S), vaccinated (V), asymptomatic carriers (C), infected (I), and recovered (R) individuals.

Individuals enter the population into the susceptible compartment at a constant rate $\Pi$, and there is a natural per capita mortality $\mu$. Both carriers and infected individuals are infectious; the force of infection is given by

$$\lambda =\beta {\displaystyle \frac{C+\epsilon I}{N}}$$

(1)

where $\beta$ is the transmission rate and $\epsilon$ is a modification parameter, which accounts for the fact that carriers are potentially more infectious than symptomatically infected individuals Djatcha Yaleu et al. (2017). The susceptible individuals vaccinate at a rate $\phi$. We assume that the vaccine is 100% effective, and an individual in the vaccinated class is immune from the disease. Protection of the vaccine wears off at a rate $\omega$, and vaccinated individuals return to the susceptible class. A susceptible individual that contracted meningococcus enters the carrier class. Carriers either develop an invasive disease at a rate $\gamma$ or lose carriage and recover at a rate $\rho$. Infected individuals (with invasive disease) either die from the disease at a rate d or recover at a rate $\alpha$. Recovered individuals enjoy temporary immunity, which wanes at a rate $\theta$. A diagram of the disease transmission is presented in Figure 1.

Table 1. Summary of the parameters of the compartmental model.

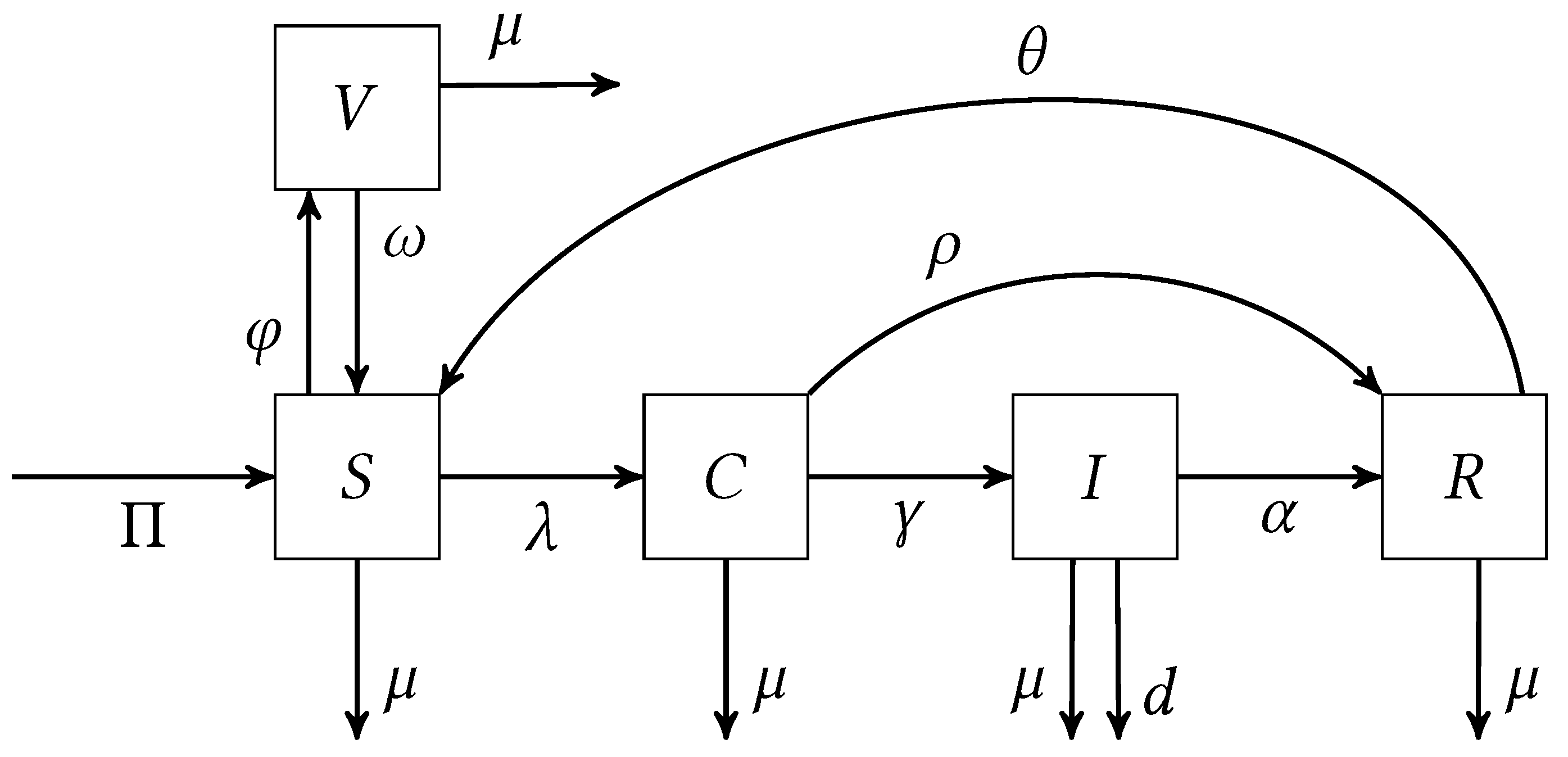
Symbol	Meaning
$\Pi$	Population recruitment rate
$\mu$	Natural death rate
$\phi$	Vaccination rate
$\omega$	Vaccine wear-off rate
$\gamma$	Rate of carriers developing invasive disease
$\rho$	Recovery rate of carriers
$\alpha$	Recovery rate of infected individuals
d	Rate of mortality due to invasive disease
$\theta$	Rate of immunity loss in recovered individuals
$\beta$	Transmission rate
$\epsilon$	Modification parameter for infectiousness of infected individuals

contains a summary of the notation of the model parameters, and

Table 2. Parameter values and ranges for sensitivity analysis.

Symbol	Baseline Value	Range of Values	Unit	Source
$\Pi$	5	none	1/day	Assumed
$\mu$	${(50·365)}^{-1}$	$[{(65·365)}^{-1},{(40·365)}^{-1}]$	1/day	Irving et al. (2012)
$\phi$	varies	$[0,0.0006]$	1/day	Inferred
$\omega$	${(5·365)}^{-1}$	$[{(10·365)}^{-1},{(1·365)}^{-1}]$	1/day	Assumed
$\gamma$	${\left(300\right)}^{-1}$	$[{900}^{-1},{60}^{-1}]$	1/day	Irving et al. (2012)
$\rho$	${30}^{-1}$	$[{180}^{-1},{14}^{-1}]$	1/day	Irving et al. (2012)
$\alpha$	$7^{-1}$	$[{10}^{-1},5^{-1}]$	1/day	Irving et al. (2012)
d	${70}^{-1}$	$[{100}^{-1},{30}^{-1}]$	1/day	Irving et al. (2012)
$\theta$	${(10·365)}^{-1}$	$[{(25·365)}^{-1},{(0.5·365)}^{-1}]$	1/day	Irving et al. (2012)
$\beta$	${14}^{-1}$	$[{21}^{-1},7^{-1}]$	1/day	Inferred
$\epsilon$	$0.75$	$[0.5,1]$	none	Djatcha Yaleu et al. (2017)

contains baseline values of the parameters, as well as the ranges of values used in the sensitivity analysis. In particular, the base value of the transmission rate parameter $\beta$ was computed to ensure that the basic reproduction number is approximately 2.

The dynamics of the meningitis transmission model are given by the following system of differential equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =\Pi +\omega V+\theta R-(\phi +\lambda +\mu )S,\hfill \\ \hfill {\displaystyle \frac{dV}{dt}}& =\phi S-(\omega +\mu )V,\hfill \\ \hfill {\displaystyle \frac{dC}{dt}}& =\lambda S-(\rho +\gamma +\mu )C,\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& =\gamma C-(\alpha +\mu +d)I,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =\alpha I+\rho C-(\theta +\mu )R.\hfill \end{array}$$

(2)

The disease-free equilibrium (DFE) of our model is then given by

$$\left(S^0,V^0,C^0,I^0,R^0,N^0\right)=\left({\displaystyle \frac{\Pi (\omega +\mu )}{\mu (\omega +\phi +\mu )}},{\displaystyle \frac{\Pi \phi }{\mu (\omega +\phi +\mu )}},0,0,0,{\displaystyle \frac{\Pi }{\mu }}\right).$$

(3)

We used the next-generation matrix method van den Driessche and Watmough (2002) to compute the basic reproduction number:

$${\mathcal{R}}_0={\displaystyle \frac{\beta (\omega +\mu )(\alpha +\epsilon \gamma +\mu +d)}{(\alpha +\mu +d)(\rho +\gamma +\mu )(\omega +\phi +\mu )}}.$$

(4)

Full details of this computation are provided in Appendix A. If ${\mathcal{R}}_0>1$, then the system converges to the endemic equilibrium (EE):

$$\begin{array}{cc}\hfill S^{*}& ={\displaystyle \frac{(\alpha +\mu +d)(\gamma +\rho +\mu )(\Pi -d{I}^{*})}{\beta \mu (\alpha +\epsilon \gamma +\mu +d)}},\hfill \\ \hfill V^{*}& ={\displaystyle \frac{\phi (\alpha +\mu +d)(\gamma +\rho +\mu )(\Pi -d{I}^{*})}{\beta \mu (\omega +\mu )(\alpha +\epsilon \gamma +\mu +d)}},\hfill \\ \hfill C^{*}& ={\displaystyle \frac{(\alpha +\mu +d)I^{*}}{\gamma }},\hfill \\ \hfill R^{*}& ={\displaystyle \frac{(\rho (\alpha +\mu +d)+\alpha \gamma )I^{*}}{\gamma (\theta +\mu )}},\hfill \\ \hfill N^{*}& ={\displaystyle \frac{\Pi -d{I}^{*}}{\mu }},\hfill \\ \hfill I^{*}& ={\displaystyle \frac{\Pi a}{b+da}},\hfill \end{array}$$

(5)

where

$$\begin{array}{cc}\hfill a& =\gamma (\mu +\theta )({\mathcal{R}}_0-1),\hfill \\ \hfill b& ={\mathcal{R}}_0\mu ((\alpha +\mu +d)(\rho +\mu +\theta )+\alpha \gamma ).\hfill \end{array}$$

(6)

These expressions make biological sense only if ${\mathcal{R}}_0-1>0$ (i.e., ${\mathcal{R}}_0>1$).

3. Results

3.1. Optimal Vaccination Strategies

We begin by finding the minimum population vaccination rate necessary to reach herd immunity ${\phi }_{\mathrm{HI}}$; this is obtained by setting ${\mathcal{R}}_0$ in Equation (4) to ensure it is equal to 1 and solving for $\phi$:

$${\phi }_{\mathrm{HI}}={\displaystyle \frac{\beta (\omega +\mu )(\alpha +\epsilon \gamma +\mu +d)}{(\alpha +\mu +d)(\rho +\gamma +\mu )}}-(\omega +\mu ).$$

(7)

The graph of ${\mathcal{R}}_0$ as a function of the population vaccination rate is shown in Figure 2a. If the population vaccinates at a rate less than ${\phi }_{\mathrm{HI}}$, then the disease remains endemic; if the population vaccinates at a rate greater than ${\phi }_{\mathrm{HI}}$, then the disease is eradicated.

Figure 3 illustrates the dynamics of system (2) for two different regimes. In Figure 3a, $\phi =0.0001<{\phi }_{\mathrm{HI}}$, and the system converges to the endemic equilibrium given by Equation (5). Waning immunity results in decaying oscillations in the number of susceptible and recovered individuals. In Figure 3b, $\phi =0.001>{\phi }_{\mathrm{HI}}$, and the system converges to the disease-free equilibrium given by Equation (3).

We next set up and solve a game-theoretic model of selfish individual vaccinating behavior. An individual has two strategies to choose from: to vaccinate or to not vaccinate. We define an expected payoff of each strategy (indexed by v and nv, respectively) following the modeling framework of Bauch and Earn (2004):

$$\begin{array}{cc}\hfill E_{\mathrm{v}}& =-C_{\mathrm{v}}-{\pi }_{\mathrm{v}}{C}_{\mathrm{i}},\hfill \\ \hfill E_{\mathrm{nv}}& =-{\pi }_{\mathrm{nv}}{C}_{\mathrm{i}},\hfill \end{array}$$

(8)

where $C_{\mathrm{v}}$ is the cost of vaccination, $C_{\mathrm{i}}$ is the cost of infection, and ${\pi }_{\mathrm{v}}$ and ${\pi }_{\mathrm{nv}}$ are the probabilities of getting infected for a vaccinated and non-vaccinating susceptible individual, respectively. Since scaling payoff functions does not affect the outcome of a game, we let $C=C_{\mathrm{v}}/C_{\mathrm{i}}$ be the cost of vaccination relative to the cost of infection; then we simplify Equation (8) to

$$\begin{array}{cc}\hfill E_{\mathrm{v}}& =-C-{\pi }_{\mathrm{v}},\hfill \\ \hfill E_{\mathrm{nv}}& =-{\pi }_{\mathrm{nv}}.\hfill \end{array}$$

(9)

We compute the probability of getting infected for a non-vaccinating individual as the transition probability from the S compartment to the I compartment in Figure 1:

$${\pi }_{\mathrm{nv}}={\displaystyle \frac{\lambda }{\lambda +\mu }}{\displaystyle \frac{\gamma }{\gamma +\rho +\mu }}.$$

(10)

A vaccinated individual may contract meningitis if the vaccine wears off. We compute the probability of getting infected for a vaccinated individual as transition probability from the V compartment to the I compartment assuming that the vaccinated individual does not revaccinate:

$${\pi }_{\mathrm{v}}={\displaystyle \frac{\omega }{\omega +\mu }}{\displaystyle \frac{\lambda }{\lambda +\mu }}{\displaystyle \frac{\gamma }{\gamma +\rho +\mu }}.$$

(11)

The assumption of a singular vaccination for a focal vaccinating individual is based on natural cognitive limitations. Conditions affecting vaccination decisions (e.g., vaccine efficacy, cost, or harmful side effects) may change over time. Moreover, individuals are more likely to estimate the immediate risk of either decision rather than a lifetime vaccinating strategy. In particular, individuals who elect not to vaccinate now may switch their strategy later. Therefore, the computations in Equations (10) and (11) correspond to short-term estimates rather than lifetime probabilities of infection.

We now find conditions when a focal individual should vaccinate or not vaccinate and the population optimal (equilibrium) vaccination rate. We are going to assume that the disease is endemic (${\mathcal{R}}_0>1$) and that the disease dynamics have reached an equilibrium state. In this case, the force of infection $\lambda$ can be computed as

$$\lambda =\beta {\displaystyle \frac{C^{*}+\epsilon I^{*}}{N^{*}}},$$

(12)

and the corresponding EE values are given by (5); they depend on the population vaccination rate $\phi$. The graph of the force of infection at equilibrium as a function of the population vaccination rate is shown in Figure 2b.

A focal susceptible individual should vaccinate when $E_{\mathrm{v}}>E_{\mathrm{nv}}$, that is, if

$$C<{\displaystyle \frac{\mu }{\omega +\mu }}{\displaystyle \frac{\lambda }{\lambda +\mu }}{\displaystyle \frac{\gamma }{\gamma +\rho +\mu }}.$$

(13)

In this case, the population vaccination rate is too low, and the risk of infection is greater than the relative cost of vaccination. Since susceptible individuals should prefer to vaccinate, the population vaccination rate would increase.

A focal susceptible individual should not vaccinate when $E_{\mathrm{v}}<E_{\mathrm{nv}}$, that is, if

$$C>{\displaystyle \frac{\mu }{\omega +\mu }}{\displaystyle \frac{\lambda }{\lambda +\mu }}{\displaystyle \frac{\gamma }{\gamma +\rho +\mu }}.$$

(14)

In this case, the population vaccination rate is too high, and the risk of infection is less than the relative cost of vaccination. Since susceptible individuals should prefer to not vaccinate, the population vaccination rate would decrease.

It follows that the optimal (equilibrium) population vaccination rate ${\phi }_{\mathrm{NE}}$ is the solution to the equation

$$C={\displaystyle \frac{\mu }{\omega +\mu }}{\displaystyle \frac{\lambda }{\lambda +\mu }}{\displaystyle \frac{\gamma }{\gamma +\rho +\mu }};$$

(15)

this is given by

$${\phi }_{\mathrm{NE}}={\displaystyle \frac{x\left[uv+u\mu \left((\alpha +\mu +d\right)\left(\rho +\mu +\theta \right)+\alpha \gamma )-\gamma \mu v\right]}{yz\left(\alpha +\mu +d\right)\left(u-\gamma \mu \right)}}-x,$$

(16)

where

$$\begin{array}{cc}\hfill x& =\omega +\mu ,\hfill \\ \hfill y& =\gamma +\rho +\mu ,\hfill \\ \hfill z& =\mu +\theta ,\hfill \\ \hfill u& =Cxy,\hfill \\ \hfill v& =z\beta \left(\alpha +\epsilon \gamma +\mu +d\right).\hfill \end{array}$$

(17)

The graph of the optimal population vaccination rate as a function of the relative cost of vaccination is shown in Figure 4a. There is a threshold value of the relative cost of vaccination $C_{\max }$, above which vaccinating is not a viable strategy: the cost of vaccination is too high to justify this preventive measure. The parameter region below the graph corresponds to the scenario described by Equation (13)—susceptible individuals should prefer to vaccinate, thus driving the population vaccination rate up. The parameter region above the graph corresponds to the scenario described by Equation (14)—susceptible individuals should prefer not to vaccinate, thus driving the population vaccination rate down.

Assuming the population adopts the optimal vaccination rate ${\phi }_{\mathrm{NE}}$, the basic reproduction number ${\mathcal{R}}_0$ is equal to 1 if $C=0$ (in this case, ${\phi }_{\mathrm{NE}}={\phi }_{\mathrm{HI}}$), and it is greater than 1 (the disease remains endemic in the population because ${\phi }_{\mathrm{NE}}<{\phi }_{\mathrm{HI}}$) otherwise. A graph of the basic reproduction number given the vaccination rate ${\phi }_{\mathrm{NE}}$ as a function of C is shown in Figure 4b.

The graphs of proportions of asymptomatic carriers and infected individuals in the population at equilibrium (with the vaccination rate ${\phi }_{\mathrm{NE}}$) as functions of the relative cost of vaccination are shown in Figure 5a and Figure 5b, respectively.

3.2. Uncertainty and Sensitivity Analysis

We performed uncertainty and sensitivity analysis Marino et al. (2008) of the outcomes of both epidemiological and game-theoretic models. We analyzed three response functions: (1) the basic reproduction number ${\mathcal{R}}_0$; (2) the optimal vaccination rate ${\phi }_{\mathrm{NE}}$; and (3) the relative difference between the eradication threshold vaccination rate and the optimal vaccination rate $({\phi }_{\mathrm{HI}}-{\phi }_{\mathrm{NE}})/{\phi }_{\mathrm{HI}}$. We sampled 1000 values of each model parameter from the intervals given in Table 2, assuming uniform distribution. We then used the Latin hypercube sampling (LHS) technique to construct 1000 samples of the entire parameter space. The results of the uncertainty (box plots on the left) and sensitivity (bar graphs on the right) analyses are shown in Figure 6. The box plots show the spread of values of the corresponding response functions due to uncertainty in the model parameter values. The bar graphs show the partial rank correlation coefficients (PRCC), which demonstrate how sensitive each response function is to changes in the parameter values.

The transmission rate $\beta$ and the vaccine wear-off rate $\omega$ have the biggest positive correlation effect on the value of the basic reproduction number (see Figure 6b). This is an expected outcome. The basic reproduction number is a linear function of $\beta$ according to (4), and hence, any change in the value of $\beta$ has a significant effect on the value of ${\mathcal{R}}_0$. The bigger values of $\omega$ correspond to shorter periods of immunity granted by the vaccine, and thus, vaccinated individuals are more likely to become susceptible to the infection; the disease spreads faster as a result. The recovery rate of carries $\rho$ and the population vaccination rate $\phi$ have the biggest negative correlation effect on the value of the basic reproduction number. The faster the carriers recover, the lower the prevalence of the disease is. When the vaccination rate increases, more susceptible individuals gain (temporary) immunity from meningitis, and the disease spreads more slowly.

Similar observations apply to the sensitivity of the optimal vaccination rate as a response function (see Figure 6d). The bigger the value of the basic reproduction number ${\mathcal{R}}_0$, the higher the vaccination rate required at equilibrium. The vaccine wear-off rate $\omega$ has a greater influence on the optimal vaccination rate than on the basic reproduction number because singularly vaccinating individuals face a greater risk of infection with shorter periods of vaccine-induced immunity. The probability of getting infected for a singularly vaccinating individual is therefore higher, and consequently, the vaccinating strategy enjoys a lower expected payoff. As a result, the incentive to vaccinate is lower, and the optimal population vaccination rate drops. In contrast, increasing the values of the disease transmission rate $\beta$ affects the probabilities of infection for both vaccinating and non-vaccinating individuals.

Finally, variations in the epidemiological model parameter values have little effect on the relative difference between the herd immunity vaccination rate and the optimal vaccination rate $({\phi }_{\mathrm{HI}}-{\phi }_{\mathrm{NE}})/{\phi }_{\mathrm{HI}}$ (see Figure 6f). This quantity is primarily determined by the cost of vaccination relative to the cost of infection.

4. Discussion

We adopted a version of an epidemiological model of meningococcal meningitis with immunity from disease and carriage Djatcha Yaleu et al. (2017); Irving et al. (2012) and constructed a game-theoretic model of voluntary individual vaccinations in the meningitis belt. If individuals participate in a preventative measure against an infectious disease (e.g., vaccination) voluntarily, then individual self-interest may prevent eradication of the disease Geoffard and Philipson (1997). The population vaccination coverage falls short of the eradication threshold because of the herd immunity effect: the more individuals vaccinate, the less likely a non-vaccinated individual is to become infected. Consequently, if sufficiently many individuals have vaccinated, then the (perceived) risk of infection becomes smaller than the (perceived) cost of vaccination, and rational individuals stop vaccinating before the eradication threshold is reached.

Our game-theoretic analysis of the voluntary adoption of the monovalent serogroup A meningococcal conjugate vaccine MenAfriVac in the meningitis belt arrived at the same conclusion: the population vaccination coverage falls short of the eradication threshold if the cost of vaccination is not negligible relative to the cost of the infection. Moreover, if the relative cost of vaccination is too high, then no one will vaccinate. When the relative cost of vaccination is sufficiently low, the disease remains in the population at low endemic values. It is this outcome that we should expect to see with voluntary vaccination protocols because the MenAfriVAc vaccine is cheap and effective.

Our conclusion that voluntary vaccination reduces meningitis to low endemic levels without achieving eradication is consistent with the broader findings of game-theoretic models applied to other infectious diseases. This body of research (referenced in the introduction) reveals a spectrum of outcomes largely determined by the perceived severity of a disease relative to the cost of intervention. At one extreme, for diseases with exceptionally high fatality rates such as Ebola, the perceived cost of infection is so immense that rational self-interest aligns closely with the public good, and voluntary vaccination is predicted to be nearly sufficient for eradication Brettin et al. (2018). At the other extreme, for diseases like typhoid fever, high perceived intervention costs—encompassing not just monetary costs but also factors like time, travel, and distrust—can lead to a significant vaccination shortfall and the persistence of high endemic levels, even with an inexpensive vaccine Acosta-Alonzo et al. (2020). Our model positions meningitis in the middle ground on this spectrum. The remarkably low cost of the MenAfriVac vaccine ensures a high optimal vaccination rate (${\phi }_{\mathrm{NE}}$) and a significant reduction in disease burden. However, the threat of meningitis, while serious, is not perceived as being as catastrophic as Ebola, meaning a gap between the individual optimum and the herd immunity threshold (${\phi }_{\mathrm{HI}}$) persists, thus preventing eradication. This contextualizes our results within a predictable theoretical framework where the strategic equilibrium of a vaccination game is determined by the population’s estimation of relative costs and risks.

When the population vaccination coverage gets close to the herd immunity threshold, individuals have little incentive to vaccinate. Yet non-vaccinating individuals may face greater danger in this case Fefferman and Naumova (2015) (this effect is particularly prominent for childhood diseases). It is thus critical to maintain strong vaccination campaigns at near-herd immunity vaccination levels.

One of our model parameters—the cost of vaccination relative to the cost of infection—is partially based on individual perception. These costs include both direct cost (e.g., cost of vaccine or medical treatment in case of infection) and indirect perceived costs (e.g., morbidity risk of the vaccine or the infection). The latter may be influenced by public education and social factors, resulting in a more favorable outcome of a voluntary immunization program. The campaign efforts should be directed to lowering the perceived costs of vaccination, or raising the perceived costs of the infection, or both.

We performed uncertainty and sensitivity analysis on our model. The epidemiological model parameters that had the greatest influence on the value of the basic reproduction number ${\mathcal{R}}_0$ were the disease transmission rate $\beta$ and the vaccine wear-off rate $\omega$ (positive correlation), as well as the recovery rate of carries $\rho$ and the population vaccination rate $\phi$ (negative correlation). The optimal population vaccination rate ${\phi }_{\mathrm{NE}}$ was sensitive to the variation in the values of the vaccine wear-off rate $\omega$ (positive correlation), and the recovery rate of carries $\rho$ and the population vaccination rate $\phi$ (negative correlation). The value of the relative difference between the optimal and herd immunity vaccination rates showed little sensitivity to the uncertainty in the epidemiological model parameter values. Therefore, our main conclusion that the voluntary vaccination coverage stays close to the herd immunity threshold if the relative cost of vaccination is sufficiently low is robust.

Our analysis assumes 100% vaccine efficacy. In reality, all vaccines are imperfect to some degree. However, this simplification was a deliberate choice to maintain the tractability of the model and the clarity of its outcomes. Recent studies have shown that incorporating imperfect vaccines introduces significant analytical complexity. Specifically, it can lead to the emergence of multiple Nash equilibria in static vaccination games Augsburger et al. (2023) and hysteresis loops in dynamic vaccination games Chen and Fu (2019). These behaviors can make it difficult to recover vaccination rates after a decline and complicate the prediction of an equilibrium outcome. However, these complex dynamics are most relevant for diseases with high basic reproduction numbers. For pathogens with a relatively low reproduction number (below approximately $2.62$), Augsburger et al. (2023) indicates that the strategic outcomes are insensitive to vaccine perfection, and simpler models assuming 100% efficacy serve as robust and adequate approximations. Our model of meningitis uses a baseline value ${\mathcal{R}}_0\approx 2$, placing it within the regime where the perfect vaccine assumption is justified.

Another key simplification in our model is the assumption that the cost of vaccination relative to the cost of infection C is homogeneous across the population, which is grounded in the foundational “vaccination games” modeling framework Bauch and Earn (2004). In reality, this cost is subjective and incorporates a wide range of factors—from financial means and access to healthcare to personal risk perception and trust in authorities—which may lead to significant heterogeneity. However, because our model assumes a large, well-mixed population, the use of a single, uniform cost can be interpreted as a reasonable approximation of the average perceived cost. Rigorously modeling cost heterogeneity would require a more complex approach, such as stratifying the population into numerous subclasses based on perceived cost or employing an agent-based model. Such an extension would provide a more nuanced view of population behavior but would sacrifice the analytical clarity that is central to our paper’s goal of illustrating the fundamental tension at the heart of voluntary vaccination programs. Assuming heterogeneous vaccination costs could constitute an important avenue of future research on eradication of meningitis.

Our model can be improved and generalized in several ways. We assumed that individuals possess perfect information on the disease prevalence to estimate probabilities of infection, which, in turn, informs their vaccination decisions. In reality, individuals base their decisions on partial knowledge only; this uncertainty could be incorporated into the next model iteration. We also conducted a so-called static analysis: we assumed that the disease dynamics reached an equilibrium state before individuals make their strategic choices in the vaccination game. But the timescale to reach an equilibrium state is typically longer than the timescale for individual vaccination decisions. Moreover, the incentive to vaccinate may change dynamically with the disease prevalence: individuals are more likely to take preventive action at the onset of an epidemic. Taking these considerations into account requires developing dynamic game-theoretic models of vaccination, which is generally difficult to do. Finally, we considered meningitis epidemics caused only by serogroup A bacteria because, historically, it accounted for 90% of the meningococcal meningitis cases in the meningitis belt. However, serogroup C and W bacteria were responsible for many recent epidemics. A future iteration of the model may incorporate meningitis transmission caused by serogroup C and W bacteria with the corresponding intervention measures.

In parallel with “pure” vaccination games, game-theoretic models can be applied to the strategic interactions among policymakers, international donors, pharmaceutical firms, and individuals. A four-period game between policymakers, the international community, and the population was introduced in Hausken and Ncube (2017) to show how free-riding undermines optimal prevention versus treatment funding. This model was extended to a five-period framework that derives commitment mechanisms to curb underinvestment in prevention Hausken and Ncube (2018) and characterizes when drugs are developed and purchased under various subsidy schemes Hausken and Ncube (2020, 2021). Further, a linked set of games has been used to analyze competing vaccine and drug companies, showing how donor subsidies and nature’s recovery probabilities jointly determine both market outcomes and individual risk-taking behavior Hausken and Ncube (2022). Integrating elements of these multi-stage models—such as pharmaceutical supply decisions, donor commitment schemes, and policy-level funding incentives—into our meningitis vaccination game could yield a more comprehensive picture of how all stakeholders (from WHO campaigns down to individual carriers) influence—and are influenced by—the strategic landscape of disease control in the African meningitis belt.