Abstract
This paper extends the Cournot duopoly model by allowing the government to impose firm-dependent specific taxes or subsidies while keeping the budget balanced. It considers two possible government goals: maximizing the social surplus and maximizing the consumer surplus. It shows that, with identical firms, the best government policy is not to intervene. In the case of cost asymmetry, social surplus and consumer surplus maximization goals require opposite strategies: to maximize the social surplus, the government should tax the high-cost firm driving the economy toward monopoly and increasing productive efficiency at the expense of lower production. In the case of consumer surplus maximization, the tax should be imposed on the low-cost firm reducing the gap between the firms’ outputs. Such a strategy, however, increases productive inefficiency and reduces the social surplus.
1. Introduction
There are two types of inefficiencies in Cournot oligopolistic markets: allocative inefficiency due to the equilibrium price being above the firms’ marginal costs, leading to a low production level, and productive inefficiency, where, in equilibrium, the marginal costs of production differ across firms. Production inefficiency may lead to a counterintuitive result, where a specific tax imposed on a firm with higher unit costs may improve social surplus. Indeed, such a tax will lead to production reallocation from the high- to the low-cost firm, with the resulting improvement in productive efficiency outweighing the decrease in consumer surplus due to an overall decrease in production (Daughety [1]). In fact, under certain conditions, a universal per-unit tax on all firms may lead to a higher social surplus (Dierickx et al. [2]). Since, from firms’ perspectives, a per-unit tax is similar to an upward shift in marginal costs, an increase in marginal costs will have the same effect on the outcome of the Cournot model. Bergstrom and Varian [3] showed that, in the case of constant marginal costs, the total production depends only on the simple average marginal cost among all firms in the industry, and not on how these costs are distributed across firms. Since firms with lower unit costs produce more, an increase in the cost difference across firms while keeping the simple average constant does not affect the consumer surplus, but increases the productive efficiency, thus leading to higher social surplus.
In this paper, we consider a Cournot model with two firms, where the firms have constant marginal costs, and analyze how the government can improve the equilibrium using balanced-budget discriminative per-unit taxes or subsidies, i.e., by taxing one firm and using the tax revenue to provide a subsidy to the other. The main reason for such a policy in a duopolistic market with homogenous goods is to reduce productive inefficiency due to the difference in the firms’ marginal costs. However, such intervention may increase the market power of the more efficient firm, which, in turn, may harm both the social and consumer surpluses. Based on this tradeoff, this paper investigates the optimal tax policy.
We consider two possible objective functions of the government: one is to maximize the social surplus, and the other is to maximize the consumer surplus. While social surplus maximization is generally considered to be the government’s main objective, in some instances, concern about consumer surplus may play an important role in governmental policies. For example, consumer surplus maximization may be useful in antitrust regulations, especially when lobbying is a concern (Pitman [4], Neven and Roller [5], Orbach [6]). In addition, given the existing income and wealth inequalities, the median resident benefits more from an increased consumer surplus (which is usually associated with lower prices, and, as an additional possible benefit, lower unemployment driven by a higher output level) and receives only a small share of the producer surplus. As a result, if the government is concerned about the median instead of the average person’s wellbeing, it may pay more attention to consumer surplus, even at the expense of an increase in productive inefficiencies that can be detrimental to the social surplus.
We show that, in the case of symmetric firms, the best government policy is not to intervene, regardless of whether it wants to maximize the social or the consumer surplus. When the costs are different and the maximum possible tax is sufficiently small, we show that imposing a tax on the high-cost firm (and, thus, giving a subsidy to the low-cost firm) increases the social surplus, while the opposite strategy of taxing the low-cost firm increases the consumer surplus. The former result is based on the tradeoff between allocative and productive inefficiency, since this policy shifts production from the high- to the low-cost firm, thus improving productive efficiency. This result, however, is not identical to Bergstrom and Varian [3]: given the balanced budget constraint, the equilibrium per-unit subsidy ends up being lower than the per-unit tax, leading to higher simple average marginal costs and, consequently, lower production. As a result, a non-trivial tradeoff between allocative and productive efficiencies exists. When the government’s objective is consumer surplus maximization, production costs are not important, as long as the total output increases. We show that, given the balanced budget constraint, imposing a small tax on the low-cost high-production firm and using the tax revenue to subsidize the high-cost low-production firm makes the simple average marginal costs lower, thus leading to a higher total output and consumer surplus.
When the government can set a greater tax level, the optimal solution to the government’s problem is no longer a corner solution. Using a numerical example, we show that, when the original cost difference is not too large, a social-surplus-maximizing government still wants to tax the high-cost firm, thus driving the economy closer to a monopoly. However, it does not tax the high-cost firm out of the market completely, retaining the oligopolistic competition. When the cost difference is high, production inefficiency becomes more important, and the government optimally sets a prohibitive tax level for the high-cost firm, driving it out of the economy. When the government wants to maximize consumer surplus and can set high tax rates, we show that it taxes the low-cost firm, but never sets the tax rate high enough to equalize the firms’ output levels.
There is a significant body of research that has investigated the effect of specific and ad valorem taxes in the Cournot model on social welfare (see, e.g., Delipalla and Keen [7], Levin [8], Reinhorn [9], and Ushio [10]). More recently, Collier [11] studied taxation in an oligopoly in the general equilibrium context and showed the opposite effects of lump-sum and profit taxation on social surplus. Häckner and Herzing [12] investigated how the magnitude of the effects of unit and ad valorem taxes depends on the market concentration both in price- and quantity-competing oligopolies. Zhang et al. [13] looked at the choice between specific and ad valorem tax policies in a duopolistic market with one private profit-maximizing firm and one partially state-owned social-surplus-maximizing firm. Wang et al. [14] pointed to the difference in the specific and ad valorem tax effects in the Cournot and Stackelberg models.
Most of the existing studies, however, assume a uniform tax on all firms within the industry. To the best of our knowledge, Dung [15] is the only study that provides a comprehensive analysis of the effect of firm-discriminating taxation in a single oligopolistic industry with asymmetric firms on industry concentration, tax revenue, and welfare. Their analysis, however, does not assume a balanced budget: instead, any tax revenue (positive or negative) collected from the firms were given as lump-sum subsidies (or collected as lump-sum taxes in the case of negative tax revenue) from the consumers, which is equivalent to simply adding the tax revenue to the consumer and producer surpluses. While in the case of large cost differences, specific taxes may increase social surplus, a subsidy that decreases unit costs is always a superior policy. Indeed, if a sufficient subsidy is offered, the equilibrium production can be made as high as the government wants it to be. As a result, it is likely that the total tax revenue from the optimal specific taxes in Dung [15] is negative, which, assuming the fixed level of personal taxes, results in a budget deficit. However, since the government cannot run a budget deficit forever, providing subsidies to firms in a specific industry requires either a cut in government spending that can negatively affect social programs or higher taxes levied on other firms and individuals, which may adversely affect efficiencies in different economic sectors. Thus, it is important to investigate how a balanced budget tax policy restricted to a single oligopolistic industry with asymmetric firms can improve efficiency. The main contribution of our paper is in conducting such an investigation.
2. The Model
Consider a simple Cournot model with two firms and a linear demand function , where is the market price and is the total production level. Assume each firm has unit production costs . Thus, the best response function of firm is given by . We will assume that the costs are sufficiently small, so that in the equilibrium , the maximum is achieved at . For example, requiring is sufficient to satisfy this condition. Thus, the equilibrium production level is given by:
Let and be the firms’ costs before any taxes or subsidies are provided, while and are the costs after taxes and subsidies. Let be the simple average cost and let . Without a loss of generality, assume ε ≥ 0. In the following, we will refer to firm 1 as a high-cost low-production firm and firm 2 as a low-cost high-production firm.
A government can impose a per-unit tax on firm 1 and give a per-unit subsidy to firm 2, where . Thus, the unit costs, as perceived by the firms, can be written as:
Here, can be any number, as long as the costs given by (2) are sufficiently small, so the equilibrium can be written as (1). In particular, a negative can be interpreted as a subsidy given to firm 1 and a tax on firm 2, while as no government intervention.
Assume also that the government wants to have a balanced budget, i.e., . While for any will satisfy the balanced budget condition, we will assume that the relationship between and is continuous, so the balanced budget condition can be written as:
The total utility of consumption can be written as , while the total production costs are . Since the total tax collected is equal to the total subsidy given, , the total production costs can also be written as . Thus, the social surplus is given by:
If the government wants to maximize the social surplus, its optimization problem can be written as:
where Ω is a compact set, such that , for some , and for any the costs given by (2) are small enough that the equilibrium in the Cournot model is given by (1). The requirement for for some is met to analyze the optimal solution when the government can impose only a small tax, and the condition that Ω is a compact set is met to guarantee the existence of the solution.
The consumer surplus can be written as:
Since consumer surplus positively depends on the total production, the problem of a government that wants to maximize consumer surplus can be written as:
To aid with future analysis, we can substitute (2) into (1) to rewrite the equilibrium production as:
We can also write the average equilibrium production as:
Equations (8) and (9) allow for writing:
Substituting (2) and (10) into (4) allows us to rewrite social surplus as:
Note that, consistent with Bergstrom and Varian [3], in the case of no government intervention social surplus positively depends on cost asymmetry . Substituting (8) into the balance budget constraint (3) allows for writing as a function of :
When , Equation (12) is a quadratic equation on and may have 0, 1, or 2 solutions, so is not a well-defined function. However, when Equation (12) has a unique solution:
Thus, can be defined in a small neighborhood of a point .
3. Symmetric Firms
When firms are identical, i.e., , substituting (12) into (9) leads to:
Thus, . The latter implies that social surplus is maximized when the total output and, thus, consumer surplus is maximized. From (14), is maximized at and, thus, from (12), at . Therefore, the following result can be stated:
Result 1.
When both firms have the same constant marginal costs, the best strategy for the government is not to intervene, regardless of whether the government’s objective is to maximize the social or the consumer surplus.
4. Asymmetric Firms—Small Tax
Next, consider a case when firms have different costs but assume that the government can only impose a small tax, i.e., limit the allowed set to a small neighborhood around point . Fully differentiating social surplus (11) at point while using (9) and (13) leads to:
Since social surplus increases with at point , if the government can choose only in a small neighborhood of , it must choose , i.e., taxing the high-cost firm. Thus, the following result can be stated:
Result 2.
If the government wants to maximize the social surplus but can only impose a small tax, it must tax the high-cost firm as much as possible and use the tax proceeds to subsidize the low-cost firm.
This optimal government policy leads to an even higher difference in firms’ costs and production levels. A production shift from a high-cost to low-cost firm will improve productive efficiency. This improvement comes at the cost of a lower consumer surplus: indeed, since the taxed firm produces less than the subsidized firm, the simple average of the firms’ marginal costs increases, leading to a lower total output. Nevertheless, as Result 2 shows, the former effect dominates the latter when the tax is small.
From (9), the total production (and, thus, the consumer surplus) is maximized when is maximized. Fully differentiating at while using (13) leads to:
Since consumer surplus decreases with at point , if the government can choose only in a small neighborhood of , it must choose , i.e., taxing the low-cost firm. Thus, the following result can be stated:
Result 3.
If the government wants to maximize the consumer surplus but can only impose a small tax, it must tax the low-cost firm as much as possible and use the tax proceeds to subsidize the high-cost firm.
From Equations (15) and (16), the goals of maximizing social surplus and consumer surplus are incompatible with each other. Consumer surplus is maximized when the tax policy is used to reduce the cost difference, thus leading to more competition and higher production. However, it also increases the production of the high-cost firm and decreases the output of the lower-cost firm, making production less efficient. As Result 2 shows, the latter dominates the former, and making the industry less competitive increases social surplus. However, when the government’s objective is to maximize consumer surpluses, it does not care about productive efficiency, as long as it does not become too inefficient to lead to a higher equilibrium price and, thus, chooses to make the industry more competitive, ignoring the increase in production inefficiency.
5. Asymmetric Firms—General Case
When the maximum tax that the government can impose is of a larger magnitude, analytically solving Optimization Problems (5) and (7) is not possible. To investigate how the optimal tax level depends on the firms’ cost asymmetry , a numerical solution for and was computed. The value was chosen to allow for the largest possible range of while keeping . For each between 0 and 0.25 with step 0.01, the optimal , as well as the maximum and minimum possible that guaranteed that the costs were small enough so that the equilibrium in the Cournot model was given by (1), were computed. Figure 1 presents the results of these calculations. Figure 2 and Figure 3 present the production levels when the government maximizes the social surplus and the consumer surplus, respectively.
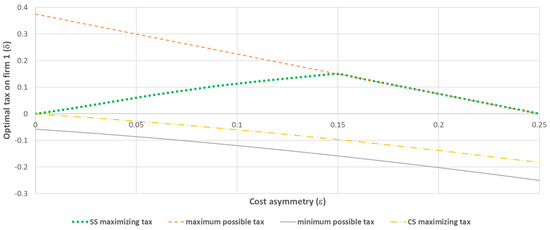
Figure 1.
Optimal tax level.
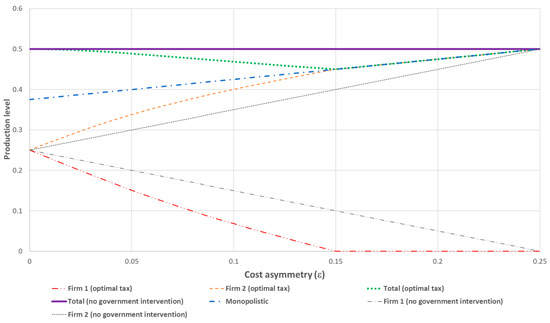
Figure 2.
Production level for social-surplus-maximizing government.
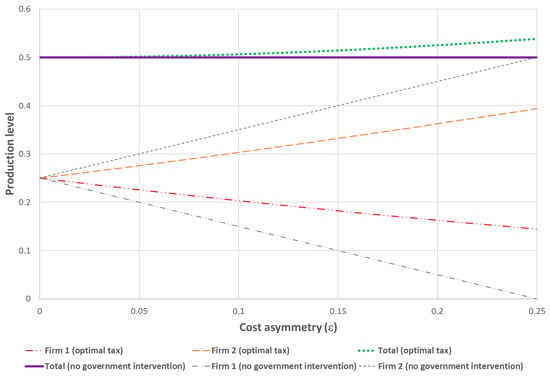
Figure 3.
Production level for consumer-surplus-maximizing government.
Figure 1 shows that, even when there is no limit on the tax size, taxing the high-cost firm maximizes the social surplus, while taxing the low-cost firm maximizes the consumer surplus. The optimal tax that maximizes the social surplus increases the production of the low-cost firm and decreases the production of the high-cost firm (Figure 2), making the difference in output levels even larger. When the cost asymmetry is not too high , the push toward the monopolistic market is not complete and the government Optimization Problem (5) has an interior solution. In this region, the optimal tax level also positively depends on the cost asymmetry: a higher initial cost difference makes improving productive efficiency (shifting production from high- to low-cost firm) more important, thus requiring higher optimal tax. When the cost asymmetry becomes too high , it becomes optimal for the government to set a prohibitive tax for the high-cost firm, driving it out of the market and making the market a de facto monopolistic market with a single low-cost firm. In this case, the solution to (5) becomes a corner solution. While Figure 1 shows that, in this region, negatively depends on , such a dependence exists only because the maximum allowed for keeping (1) as a solution to the Cournot model decreases with . Any tax above this level will deliver the same outcome, because, with , the collected tax will be zero and, from the balanced budget constraint , the per-unit subsidy will be zero as well.
When the government wants to maximize the consumer surplus, the solution to (7) is an interior solution for all . The optimal tax policy increases the output of the high-cost firm and decreases the output of the low-cost firm, bringing them closer together, while the total output becomes higher than the Cournot output without government intervention. However, the government does not push the firms’ production all the way to make them equal. Indeed, according to Bergstrom and Varian [3], the total output negatively depends on the simple average unit costs . When is added to and < 0 is subtracted from , the simple average marginal cost changes by . The balanced budget requires . With asymmetric costs at , we have , thus, for a small negative , the average cost will change by . However, if the chosen tax is too high so that , then and there is no reduction in the average cost relative to the no intervention scenario. The maximum cost reduction is achieved in between these values.
Figure 4 illustrates the effect of the government policies on the social surplus. When the government wants to maximize the social surplus, the highest effect is at intermediate values of . Indeed, as shown in Part 3, with symmetric firms, there is no productive inefficiency, and government intervention only adds to allocative inefficiency, so the optimal policy is not to intervene. At , even without the government intervention, the cost difference is high enough to drive the high-cost firm out of the market: the market is monopolistic on its own and productive efficiency is achieved, so there is nothing that the government can do to improve efficiency. For intermediate values of the optimal tax policy increases the social surplus by improving productive efficiency by a higher degree than decreasing the consumer surplus.
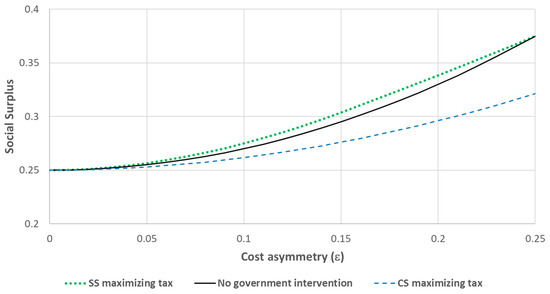
Figure 4.
Social surplus.
When the government wants to maximize the consumer surplus, production inefficiency and, as a result, social surplus decrease. The higher the cost asymmetry, the more aggressive the government policy is, and, thus, the higher the decrease in the social surplus. Even at , when the production cost difference is the highest and the high-cost firm is not able to operate on its own, the consumer surplus maximization tax policy brings the high-cost firm back to the market, leading to the highest decrease in the social surplus.
6. Conclusions
This paper extends the classic Cournot oligopoly model with asymmetric unit costs by incorporating a government that wants to maximize either social surplus or consumer surplus by strategically setting per-unit taxes or subsidies while keeping the budget balanced. It shows that, in the case of symmetric firms, the best government strategy is not to intervene, regardless of whether it wants to maximize the social surplus or the consumer surplus. In the case of cost asymmetry, a balanced-budget intervention leads to a tradeoff: a tax on the high-cost firm with a subsidy provided to the low-cost firm increases productive efficiency, but leads to a lower total output and, thus, a lower allocative efficiency and consumer surplus. For low tax levels, the former effect dominates the latter, so, to maximize the social surplus, the government should set the specific tax for the high-cost firm as high as possible (within the ex ante limit on the tax rate) and use the proceeds to give a per-unit subsidy to the low-cost firm. For greater tax levels with low and moderate cost asymmetry, an interior solution exists, where taxing the high-cost low-output firm increases the market share of the low-cost high-output firm. When the cost asymmetry is large, the productive inefficiency becomes even more important, and the optimal policy is a prohibitive tax on the high-cost firm that will drive that firm out of the market, making the market monopolistic. When the government wants to maximize the consumer surplus, it should ignore production inefficiency and subsidize the high-cost firm while taxing the low-cost firm, thus making the cost asymmetry smaller. This policy increases the consumer surplus, but harms both the productive efficiency and the social surplus. The optimal consumer surplus maximization tax, however, only reduces the cost asymmetry, but does not eliminate it completely.
There are several reasons for why firms producing identical products may have different costs. Inefficient management or technological differences (including suboptimal choices of labor and capital) are some of these reasons. Another reason may be differences in local laws. For example, for U.S. firms, labor costs may be affected by the minimum wage, which is different in different states. Total costs can be affected by the property tax rate set by local municipalities. Differences in the sale taxes across states benefit firms located closer to states with lower sale taxes, as this provides cheaper access (through lower transportation costs) to markets with a higher effective demand. In the past, when online retailers did not collect sale taxes in many states and without any enforcement of laws that require customers to declare out-of-state purchases and pay sale taxes directly to the government, such non-collected taxes were equivalent to ad valorem subsidies for online retailers. According to the model developed in this paper and assuming that online retailers incur lower costs, such non-collection of sale taxes led to a higher social surplus. It is important to note, however, that the result of the paper is limited to a single industry and does not consider the effect of the optimal industry policy on general equilibrium. For example, in the case of online retailers and retailers with physical stores, it does not consider the effect of increased unemployment among retail industry employees, as well as the effect on local economy. One possible extension of the model could be considering the external effect of production reallocation on the local economy.
Another possible extension could include incorporating negative production externalities, such as pollution. While firms may have similar production technologies, they may have different environmental technologies in place, which could lead to different total production costs. Furthermore, while the production process must meet some environmental threshold, different environmental technologies may make some firms more environmentally friendly than others. A possible extension of the model could explicitly incorporate the cost of pollution and, thus, have the optimal tax and subsidy level depending not only on the firms’ marginal costs, but also on their environmental impacts.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Daughety, A. Cournot competition. In The New Palgrave Dictionary of Economics; Palgrave Macmillan: London, UK, 2008; pp. 1–10. [Google Scholar] [CrossRef]
- Dierickx, I.; Matutes, C.; Neven, D. Indirect taxation and Cournot equilibrium. Int. J. Ind. Organ. 1988, 6, 385–399. [Google Scholar] [CrossRef]
- Bergstrom, T.C.; Varian, H.R. Two remarks on Cournot Equilibria. Econ. Lett. 1985, 19, 5–8. [Google Scholar] [CrossRef]
- Pittman, R. Consumer Surplus as the Appropriate Standard for Antitrust Enforcement. In EAG Discussions Papers; Department of Justice, Antitrust Division: Washington, DC, USA, 2007; p. 200709. Available online: https://www.justice.gov/atr/consumer-surplus-appropriate-standard-antitrust-enforcement (accessed on 12 July 2024).
- Neven, D.J.; Röller, L.H. Consumer Surplus vs. Welfare Standard in a political economy model of merger control. Int. J. Ind. Organ. 2005, 23, 829–848. [Google Scholar] [CrossRef]
- Orbach, B.Y. The antitrust consumer welfare paradox. J. Compet. Law Econ. 2010, 7, 133–164. [Google Scholar] [CrossRef]
- Delipalla, S.; Keen, M. The comparison between ad valorem and specific taxation under imperfect competition. J. Public Econ. 1992, 49, 351–367. [Google Scholar] [CrossRef]
- Levin, D. Taxation within Cournot Oligopoly. J. Public Econ. 1985, 27, 281–290. [Google Scholar] [CrossRef]
- Reinhorn, L.J. Optimal taxation with Cournot oligopoly. B.E. J. Econ. Anal. Policy 2005, 5, 0000101515153806371165. [Google Scholar] [CrossRef]
- Ushio, Y. Welfare effects of commodity taxation in Cournot Oligopoly. Jpn. Econ. Rev. 2000, 51, 268–273. [Google Scholar] [CrossRef]
- Collie, D.R. Taxation under oligopoly in a general equilibrium setting. J. Public Econ. Theory 2019, 21, 738–753. [Google Scholar] [CrossRef]
- Häckner, J.; Herzing, M. Tax incidence in oligopolistic markets. Econ. Lett. 2022, 213, 110352. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, L.F.S.; Yang, Y. Indirect taxation with Shadow Cost of public funds in mixed oligopoly. Manag. Decis. Econ. 2020, 41, 415–425. [Google Scholar] [CrossRef]
- Wang, L.F.S.; Zeng, C.; Zhang, Q. Indirect taxation and consumer welfare in an asymmetric Stackelberg oligopoly. N. Am. J. Econ. Financ. 2019, 50, 101034. [Google Scholar] [CrossRef]
- Dung, T.H. Optimal taxation and heterogeneous oligopoly. Can. J. Econ. 1993, 26, 933. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).