On a Special Two-Person Dynamic Game

Abstract

The asymptotical properties of a special dynamic two-person game are examined under best-response dynamics in both discrete and continuos time scales. The direction of strategy changes by the players depend on the best responses to the strategies of the competitors and on their own strategies. Conditions are given first for the local asymptotical stability of the equilibrium if instantaneous data are available to the players concerning all current strategies. Next, it is assumed that only delayed information is available about one or more strategies. In the discrete case, the presence of delays has an effect on only the order of the governing difference equations. Under continuous scales, several possibilities are considered: each player has a delay in the strategy of its competitor; player 1 has identical delays in both strategies; the players have identical delays in their own strategies; player 1 has different delays in both strategies; and the players have different delays in their own strategies. In all cases, it is assumed that the equilibrium is asymptotically stable without delays, and we examine how delays can make the equilibrium unstable. For small delays, the stability is preserved. In the cases of one-delay models, the critical value of the delay is determined when stability changes to instability. In the cases of two and three delays, the stability-switching curves are determined in the two-dimensional space of the delays, where stability becomes lost if the delay pair crosses this curve. The methodology is different for the one-, two-, and three-delay cases outlined in this paper.

1. Introduction

Game theory is one of the most frequently studied fields in mathematical economics. Its foundation and main concepts are discussed in many textbooks and monographs, for example, Dresher (1961), Szép and Forgó (1985), Vorob’ev (1994), and Matsumoto and Szidarovszky (2016) [1,2,3,4]. These include both two-person and general n-person games. In the earliest decades, the existence and uniqueness of the Nash equilibrium were the central research issues (von Neumann and Morgenstern, 1944; Nash, 1951; Fudenberg and Tirole, 1991; Rosen, 1965) [5,6,7,8], and then the dynamic extensions of these static games received increasing attention (Okuguchi, 1976; Hahn, 1962) [9,10]. Models have been developed and examined in both discrete and continuous time scales. In most studies, the dynamic processes are driven by either gradient adjustments or best-response dynamics. In the first case, only interior equilibria are the steady states of the resulting dynamic systems. In the second case, this difficulty is avoided; however, the construction of the dynamic processes requires knowledge of the best responses of the players (Bischi et al., 2010) [11]. In both cases, the asymptotical stability of the equilibrium in examined by applying the Lyapunov theory (Cheban, 2013, Saeed, 2017) [12,13] or local linearization (Bischi et al., 2010) [11]. In the discrete case, the theory of noninvertable maps and critical sets is a commonly used approach for nonlinear discrete systems (Gumowski and Mira, 1980; Mira et al., 1996) [14,15], while for continuous systems Bellman (1969), LaSalle (1968), and Sánchez (1968) [16,17,18] can be suggested as the main references. After developments in the stability theory of differential equations, time delays were added to dynamic models, in which it is usually assumed that the players make decisions based on delayed information about their own and others’ actions. This additional assumption makes the models more realistic, since data collection, determining the best decision alternatives, and their implementation need time (Bellman and Cooke, 1963) [19]. Delay systems have many applications in population dynamics (Kuang, 1993; Cushing, 1977) [20,21]; economics (Gori et al., 2014; Ösbay et al., 2017) [22,23]; and engineering (Berezowski, 2001; Wang et al., 1999) [24,25], among other disciplines.

A two-person continuous game is considered, in which the strategy sets $S_1$ and $S_2$ are compact intervals and the payoff functions ${\phi }_k(x_1,x_2)$ ($k=1,2$) are continuous and strictly concave in $x_k$, which is the strategy of player k. Under these conditions, ${\phi }_k(x_1,x_2)$ has a unique maximizer $R_k(x_{\ell })$ for all $x_{\ell }\in S_{\ell }(\ell \ne k)$. This function is called the best response of player k. At each time period, the players select strategies to move closer to their best responses. In the discrete case, this concept is realized by the difference equation system

$$x_1(t+1)=x_1(t)+{\alpha }_1\left[R_1(x_2(t))-x_1(t)\right],$$

(1)

$$x_2(t+1)=x_2(t)+{\alpha }_2\left[R_2(x_1(t))-x_2(t)\right],$$

(2)

where ${\alpha }_1$ and ${\alpha }_2$ are positive adjustment coefficients. In order to avoid overshooting, it is assumed that both are less than unity. In the continuous case, the following differential equation system describes the dynamic evolution of the strategies:

$${\dot{x}}_1(t)={\alpha }_1\left[R_1(x_2(t))-x_1(t)\right],$$

(3)

$${\dot{x}}_2(t)={\alpha }_2\left[R_2(x_1(t))-x_2(t)\right],$$

(4)

where ${\alpha }_1,{\alpha }_2>0$.

We provide one example here. Consider a duopoly, when two firms produce the same product and sell their outputs in the same market. Let $x_1$ and $x_2$ denote the production levels of the firms. The production costs are

$$C_1(x_1)=a_1{x}_1+b_1\mathrm{and}{C}_2(x_2)=a_2{x}_2+b_2,$$

and the selling unit price is

$$p(x_1+x_2)=A-B(x_1+x_2).$$

The profit of firm i ($i=1,2$) is given as the difference between its revenue and cost:

$${\phi }_i(x_1,x_2)=x_i\left(A-B{x}_i-B{x}_j\right)-\left(a_i{x}_i+b_i\right)\left(i\ne j\right).$$

It is a natural assumption that firm i does not have instantaneous information on the output level of the competitor, so at time t, it believes that the output of the competitor is $x_j(t-{\tau }_j)$. The marginal profit of the firm is clearly

$$\frac{\partial {\phi }_i(x_1,x_2)}{\partial x_1}=A-2B{x}_i-B{x}_j-a_i.$$

Hence, at time t, the best believed response of firm i is

$$R_i(x_j(t-{\tau }_j))=\left\{\begin{array}{c}{\displaystyle \frac{A-a_i-B{x}_j(t-{\tau }_j)}{2B}}\mathrm{if}\mathrm{numerator}\mathrm{is}\mathrm{positive},\hfill \\ 0\mathrm{otherwise}.\hfill \end{array}\right.$$

The best response dynamics have the following forms:

$$x_i(t+1)=x_i(t)+{\alpha }_i\left[R_i(x_j(t-{\tau }_j))-x_i(t)\right]\mathrm{for}i=1,2$$

in the discrete-time case, and

$${\dot{x}}_i(t)={\alpha }_i\left[R_i(x_j(t-{\tau }_j))-x_i(t)\right]\mathrm{for}i=1,2$$

in the continuous-time case, leading to a delay difference and differential equations.

In this paper, a special two-person game is examined with best-response dynamics in discrete and continuous time scales. The main question we try to answer is the following: How does the presence of time delays affect the asymptotical properties of a dynamics extension of a special stable two-person game? In the case of one delay, the stability interval or intervals are determined when the stability of the equilibrium is still preserved. In the case of multiple delays, the stability regions in the delay space are determined, where the equilibrium is still stable. This paper introduces a mathematical methodology to find the stability intervals and regions.

The paper is developed as follows. Section 2 considers discrete time scales and is divided into two parts: models with and without time delays. The structure of Section 3 is similar, with two subsections. Section 4 introduces and examines alternative models, and Section 5 offers concluding remarks and further research areas.

2. Discrete Systems

2.1. Stability without Time Delays

Assuming the differentiability of the best-response functions, we can linearize Equations (1) and (2) about an equilibrium that is also a steady state of the system. Let $x_1^{\ast }$ and $x_2^{\ast }$ denote the equilibrium strategies and let

$${\overline{x}}_1(t)=x_1(t)-x_1^{\ast }\mathrm{and}{\overline{x}}_2(t)=x_2(t)-x_2^{\ast }$$

be the discrepancies of the strategies from their equilibrium levels. Linearizing Equations (1) and (2) around $(x_1^{\ast },x_2^{\ast })$ gives the following:

$${\overline{x}}_1(t+1)=(1-{\alpha }_1){\overline{x}}_1(t)+{\alpha }_1{R}_1^{\prime }(x_2^{\ast }){\overline{x}}_2(t)$$

(5)

and

$${\overline{x}}_2(t+1)=(1-{\alpha }_2){\overline{x}}_2(t)+{\alpha }_2{R}_2^{\prime }(x_1^{\ast }){\overline{x}}_1(t).$$

(6)

This is a linear system. The asymptotic behavior of the state trajectories depends on the locations of the eigenvalues of the system. For finding the eigenvalues, we consider exponential solutions ${\overline{x}}_1(t)={\lambda }^{t}u$ and ${\overline{x}}_2(t)={\lambda }^{t}v$. Substituting them into Equations $(5)$ and $(6)$, we see that

$$\begin{array}{c}{\lambda }^{t+1}u=(1-{\alpha }_1){\lambda }^{t}u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast }){\lambda }^{t}v,\hfill \\ {\lambda }^{t+1}v=(1-{\alpha }_2){\lambda }^{t}v+{\alpha }_2{R}_2^{\prime }(x_1^{\ast }){\lambda }^{t}u.\hfill \end{array}$$

After simplifying both equations by ${\lambda }^t$, a linear algebraic system is obtained for u and v, and nonzero solutions exist if and only if the determinant of the system is zero:

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}1-{\alpha }_1-\lambda & {\alpha }_1{R}_1^{\prime }(x_2^{\ast })\\ {\alpha }_2{R}_2^{\prime }(x_1^{\ast })& 1-{\alpha }_2-\lambda \end{array}\right)\hfill \\ \hfill & ={\lambda }^2-\lambda \left(2-{\alpha }_1-{\alpha }_2\right)+(1-{\alpha }_1)(1-{\alpha }_2)-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }).\hfill \end{array}$$

(7)

This is a quadratic polynomial ${\lambda }^2+a_1\lambda +a_2$ with

$$a_1=-(2-{\alpha }_1-{\alpha }_2)\mathrm{and}{a}_2=(1-{\alpha }_1)(1-{\alpha }_2)-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }).$$

It is well known (see, for example, Appendix F of Bischi et al., 2010) [11] that its roots are inside the unit circle if and only if

$$\begin{array}{cc}1+a_1+a_2& >0,\\ 1-a_1+a_2& <0,\\ a_2& <1.\end{array}$$

In our case, these conditions can be written as

$$\begin{array}{cc}{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\hfill & <1,\hfill \\ R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\hfill & <1+{\displaystyle \frac{4-2{\alpha }_1-2{\alpha }_2}{{\alpha }_1{\alpha }_2}},\hfill \\ R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\hfill & >1-{\displaystyle \frac{{\alpha }_1+{\alpha }_2}{{\alpha }_1{\alpha }_2}}.\hfill \end{array}$$

Since ${\alpha }_1$ and ${\alpha }_2$ are below unity, the first inequality is stronger than the second one, so we have the following:

Proposition 1.

The equilibrium is locally asymptotically stable if and only if

$$1-{\displaystyle \frac{{\alpha }_1+{\alpha }_2}{{\alpha }_1{\alpha }_2}}<R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<1.$$

(8)

Notice that

$${\displaystyle \frac{{\alpha }_1+{\alpha }_2}{{\alpha }_1{\alpha }_2}}=\frac{1}{{\alpha }_2}+\frac{1}{{\alpha }_1}>2,$$

so the left-hand side of condition (8) is negative and below $-1.$

2.2. Stability with Delays

It is now assumed that the players have access only to delayed information about the strategies of the others. We can select the time unit as the length of the common delay. Thus, in Equation (1), $x_2(t)$ is replaced by $x_2(t-1)$, and in (2), $x_1(t)$ is replaced by $x_1(t-1)$. Assuming again exponential solutions ${\overline{x}}_1(t)={\lambda }^{t}u$ and ${\overline{x}}_2(t)={\lambda }^{t}v$, we have

$$\begin{array}{c}{\lambda }^{t+1}u=(1-{\alpha }_1){\lambda }^{t}u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast }){\lambda }^{t-1}v,\hfill \\ {\lambda }^{t+1}v=(1-{\alpha }_2){\lambda }^{t}v+{\alpha }_2{R}_2^{\prime }(x_1^{\ast }){\lambda }^{t-1}u.\hfill \end{array}$$

After simplifying by ${\lambda }^{t-1}$, the resulting algebraic system has the form

$$\begin{array}{c}{\lambda }^{2}u=(1-{\alpha }_1)\lambda u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })v,\hfill \\ {\lambda }^{2}v=(1-{\alpha }_2)\lambda v+{\alpha }_2{R}_2^{\prime }(x_1^{\ast })u.\hfill \end{array}$$

A nonzero solution of u and v exists if and only if

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}\left(1-{\alpha }_1\right)\lambda -{\lambda }^2& {\alpha }_1{R}_1^{\prime }(x_2^{\ast })\\ {\alpha }_2{R}_2^{\prime }(x_1^{\ast })& \left(1-{\alpha }_2\right)\lambda -{\lambda }^2\end{array}\right)\hfill \\ \hfill & ={\lambda }^4-{\lambda }^3\left(2-{\alpha }_1-{\alpha }_2\right)+(1-{\alpha }_1)(1-{\alpha }_2){\lambda }^2-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }).\hfill \end{array}$$

This is a quartic equation ${\lambda }^4+a_1{\lambda }^3+a_2{\lambda }^2+a_3\lambda +a_4$ with

$$a_1=-\left(2-{\alpha }_1-{\alpha }_2\right),a_2=(1-{\alpha }_1)(1-{\alpha }_2),a_3=0\mathrm{and}{a}_4=-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }).$$

Farebrother (1973) [26] showed that the sufficient and necessary conditions to only have roots inside the unit circle are as follows:

$$\begin{array}{c}{a}_4<1,\\ 3+3a_4>a_2,\\ 1+a_1+a_2+a_3+a_4>0,\\ 1-a_1+a_2-a_3+a_4>0,\\ (1-a_4)(1-a_4^2)-a_2{(1-a_4)}^2+(a_1-a_3)(a_3-a_1{a}_4)>0.\end{array}$$

Notice that the first four inequalities are linear in $a_4$ as well as in $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })$; however, the last inequality is cubic in $a_4$, so it is difficult to find simple stability conditions. Nevertheless, the first four inequalities give necessary stability conditions. They can be written as

$$R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\left\{\begin{array}{c}>-{\displaystyle \frac{1}{{\alpha }_1{\alpha }_2}},\hfill \\ <{\displaystyle \frac{{\alpha }_1+{\alpha }_2-{\alpha }_1{\alpha }_2+2}{3{\alpha }_1{\alpha }_2}},\hfill \\ <1,\hfill \\ <1+{\displaystyle \frac{4-2{\alpha }_1-2{\alpha }_2}{{\alpha }_1{\alpha }_2}}.\hfill \end{array}\right.$$

Notice that

$$-{\displaystyle \frac{1}{{\alpha }_1{\alpha }_2}}<-1$$

$${\displaystyle \frac{{\alpha }_1+{\alpha }_2-{\alpha }_1{\alpha }_2+2}{3{\alpha }_1{\alpha }_2}}=\frac{1}{3}\left({\displaystyle \frac{1}{{\alpha }_2}}+{\displaystyle \frac{1}{{\alpha }_1}}\right)-\frac{1}{3}+\frac{2}{3}{\displaystyle \frac{1}{{\alpha }_1{\alpha }_2}}>1$$

and

$$1+{\displaystyle \frac{4-2{\alpha }_1-2{\alpha }_2}{{\alpha }_1{\alpha }_2}}>1.$$

Hence, the necessary conditions are

$$-{\displaystyle \frac{1}{{\alpha }_1{\alpha }_2}}<R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<1.$$

(9)

In this case,

$$-{\alpha }_1{\alpha }_2<a_4<1.$$

Let $F(a_4)$ denote the left-hand side of last stability condition. Notice that

$$F(1)=-a_1^2<0\mathrm{and}F(0)=1-a_2>0,$$

so its sign is indeterminate in general.

We will now examine the addition condition $F(a_4)>0$ in interval $(-{\alpha }_1{\alpha }_2,1)$. Clearly,

$$\begin{array}{ccc}\hfill F(a_4)& =& (1-a_4)(1-a_4^2)-a_2{(1-a_4)}^2-a_1^2{a}_4\hfill \\ & =& a_4^3+a_4^2(-1-a_2)+a_4(-1+2a_2-a_1^2)+1-a_2.\hfill \end{array}$$

Notice first that

$$-1-a_2\le -1,1-a_2\ge 0$$

and

$$-1+2a_2-a_1^2=-{({\alpha }_1-1)}^2-{({\alpha }_2-1)}^2-1\le -1.$$

Since

$$F^{\prime }(a_4)=3a_4^2+2a_4(-1-a_2)+(-1+2a_2-a_1^2),$$

the stationary points of $F(a_4)$ are

$$a_4^{\pm }=\frac{1}{6}\left[2(1+a_2)\pm \sqrt{D}\right],$$

where

$$D=4{(1+a_2)}^2+12(1-2a_2+a_1^2)\ge 4{(1+a_2)}^2+12\ge 16,$$

implying that $a_4^{+}>0$ and $a_4^{-}<0.$ Clearly,

$$a_4^{+}>\frac{1}{6}\left[2+4\right]=1,$$

being outside the range of the necessary condition. Additionally,

$$F^{\prime }(a_4)>0\mathrm{for}{a}_4<a_4^{-}\mathrm{and}{a}_4>a_4^{+},$$

and

$$F^{\prime }(a_4)<0\mathrm{for}{a}_4^{-}<a_4<a_4^{+}.$$

Notice that

$$F(0)=1-a_2\ge 0\mathrm{and}F(1)=-a_1^2\le 0,$$

and so $F(a_4)$ has three real roots: one before $a_4^{-},$ one between 0 and $1,$ and one after 1. Consequently, if $a_4^{\ast }$ denotes the negative root and $a_4^{\ast \ast }$ the positive root between 0 and 1, then $F(a_4)>0$ if

$$a_4^{\ast }<a_4<a_4^{\ast \ast }$$

or

$$-\frac{a_4^{\ast \ast }}{{\alpha }_1{\alpha }_2}<R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<min\left\{1,-\frac{a_4^{\ast }}{{\alpha }_1{\alpha }_2}\right\}.$$

(10)

Proposition 2.

A necessary condition for the local asymptotical stability of the equilibrium in the delayed model is condition (9). A sufficient and necessary condition is the simultaneous satisfaction of (9) and (10).

3. Continuous Systems

3.1. Stability without Time Delays

We will now examine the stability of systems (3) and (4). Similarly to the discrete case, we linearize the system around the equilibrium $(x_1^{\ast },x_2^{\ast })$ to have the following:

$${\dot{x}}_1(t)=-{\alpha }_1{x}_1(t)+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })x_2(t),$$

(11)

$${\dot{x}}_2(t)={\alpha }_1{R}_2^{\prime }(x_1^{\ast })x_1(t)-{\alpha }_2{x}_2(t),$$

(12)

where overbar is avoided for simple notation. In order to find the eigenvalues, we look for the solutions in exponential forms as before:

$$x_1(t)=e^{\lambda t}u\mathrm{and}{x}_2(t)=e^{\lambda t}v.$$

The substitution of these solutions into Equations (11) and (12) gives

$$\lambda e^{\lambda t}u=-{\alpha }_1{e}^{\lambda t}u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{\lambda t}v,$$

$$\lambda e^{\lambda t}v={\alpha }_2{R}_2^{\prime }(x_1^{\ast })e^{\lambda t}u-{\alpha }_2{e}^{\lambda t}v.$$

After simplifying both equations by $e^{\lambda t}$, the resulting algebraic system for u and v has nonzero solutions if and only if

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}-{\alpha }_1-\lambda & {\alpha }_1{R}_1^{\prime }(x_2^{\ast })\\ {\alpha }_2{R}_2^{\prime }(x_1^{\ast })& -{\alpha }_2-\lambda \end{array}\right)\hfill \\ \hfill & ={\lambda }^2+\lambda \left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }).\hfill \end{array}$$

This is a quadratic polynomial, ${\lambda }^2+a_1\lambda +a_2$, with

$$a_1={\alpha }_1+{\alpha }_2\mathrm{and}{a}_2={\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right).$$

It is well known (Bischi et al., 2010) [11] that the real parts of the roots of this quadratic equation are negative if and only if both $a_1$ and $a_2$ are positive, which implies the following:

Proposition 3.

The equilibrium with dynamics (3) and (4) is locally asymptotically stable if

$$R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<1$$

(13)

and unstable if $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })>1$.

In comparing conditions (8), (9), (10), and (13), it is clear that the stability of the equilibrium with the continuous model is implied by its stability for the discrete cases with and without delays. In comparing the two discrete cases, notice that the sufficient and necessary stability condition of the no-delay case implies the necessary conditions for the delay case since

$$-\frac{1}{{\alpha }_1{\alpha }_2}<1-\frac{{\alpha }_1+{\alpha }_2}{{\alpha }_1{\alpha }_2}$$

or

$$\left(1-{\alpha }_2\right)\left({\alpha }_1-1\right)<0.$$

3.2. Stability with Delays

Assume again that both players face delays, ${\tau }_1$ and ${\tau }_2,$ in the information about the strategies of the others. Therefore, in Equation (3), $x_2(t)$ is replaced by $x_2(t-{\tau }_1)$, and in (4), $x_1(t)$ is replaced by $x_1(t-{\tau }_2)$. The linearized equations can therefore be written as follows:

$${\dot{x}}_1(t)=-{\alpha }_1{x}_1(t)+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })x_2(t-{\tau }_2),$$

(14)

$${\dot{x}}_2(t)={\alpha }_1{R}_2^{\prime }(x_1^{\ast })x_1(t-{\tau }_1)-{\alpha }_2{x}_2(t).$$

(15)

The eigenvalues clearly depend on the lengths of the delays. Searching for exponential solutions

$$x_1(t)=e^{\lambda t}u\mathrm{and}{x}_2(t)=e^{\lambda t}v$$

and substituting them into these equations, we obtain

$$\lambda e^{\lambda t}u=-{\alpha }_1{e}^{\lambda t}u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{\lambda (t-{\tau }_2)}v,$$

$$\lambda e^{\lambda t}v={\alpha }_2{R}_2^{\prime }(x_1^{\ast })e^{\lambda \left(t-{\tau }_1\right)}u-{\alpha }_2{e}^{\lambda t}v.$$

After simplifying by $e^{\lambda t}$, the resulting algebraic equations for u and v have nonzero solutions if and only if

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}-{\alpha }_1-\lambda & {\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{-\lambda {\tau }_2}\\ {\alpha }_2{R}_2^{\prime }(x_1^{\ast })e^{-\lambda {\tau }_1}& -{\alpha }_2-\lambda \end{array}\right)\hfill \\ \hfill & ={\lambda }^2+\lambda \left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })e^{-\lambda \left({\tau }_1+{\tau }_2\right)}\right).\hfill \end{array}$$

(16)

Notice first that the characteristic equation does not depend on the individual values of ${\tau }_1$ and ${\tau }_2$—it depends on only $\tau ={\tau }_1+{\tau }_2$. We know that at ${\tau }_1={\tau }_2=0$ (no-delay case), the equilibrium is locally asymptotically stable if (13) holds. By increasing the value of $\tau$ from zero, the stability might be lost. In this case, an eigenvalue has a zero real part, $\lambda =i\omega$. Since the complex conjugate of an eigenvalue is also an eigenvalue, we can assume that $\omega >0$. Substituting this eigenvalue into the characteristic Equation (16), we have the following:

$$-{\omega }^2+i\omega \left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\left(\cos \omega \tau -isin\omega \tau \right)\right)=0.$$

The separation of the real and imaginary parts shows that

$${\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })cos\omega \tau =-{\omega }^2+{\alpha }_1{\alpha }_2,$$

(17)

$${\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })sin\omega \tau =-\omega \left({\alpha }_1+{\alpha }_2\right).$$

(18)

By adding the squares of these equations, we have

$${\omega }^4+{\omega }^2\left({{\alpha }_1}^2+{\alpha }_2^2\right)+{\alpha }_1^2{\alpha }_2^2\left[1-{\left(R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)}^2\right]=0.$$

(19)

If $\left|R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right|\le 1$, then no stability switch occurs. If $-1\le R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<1$, then the equilibrium remains locally asymptotically stable for all $\tau >0$. If $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })=1$, then the characteristic equation of the no-delay case has a negative and a zero eigenvalue. Thus, no conclusion can be drawn about stability, and the same is the case for all $\tau >0$.

Assume next that $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })>1.$ In this case, Equation (19) has two real roots for ${\omega }^2,$

$${\omega }_{\pm }^2=\frac{-({\alpha }_1^2+{\alpha }_2^2)\pm \sqrt{D}}{2},$$

where

$$D={({\alpha }_1^2+{\alpha }_2^2)}^2-4{\alpha }_1^2{\alpha }_2^2\left[1-{\left(R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)}^2\right]>{({\alpha }_1^2+{\alpha }_2^2)}^2,$$

implying that ${\omega }_{+}^2>0$ and ${\omega }_{-}^2<0$. Thus, we have a unique solution ${\omega }_{+}$. From (17) and (18), we see that $sin\omega \tau <0$ and

$$cos\omega \tau \left\{\begin{array}{c}>0\mathrm{if}{\omega }_{+}^2<{\alpha }_1{\alpha }_2,\hfill \\ =0\mathrm{if}{\omega }_{+}^2={\alpha }_1{\alpha }_2,\hfill \\ <0\mathrm{if}{\omega }_{+}^2>{\alpha }_1{\alpha }_2.\hfill \end{array}\right.$$

Therefore, we have the critical values of the delay:

$${\tau }_n=\frac{1}{{\omega }_{+}}\left[2n\pi -{cos}^{-1}\left(\frac{-{\omega }_{+}^2+{\alpha }_1{\alpha }_2}{{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })}\right)\right]\mathrm{for}n=1,2,\dots$$

(20)

The direction of the stability switches can be determined by Hopf bifurcation. For this purpose, we select $\tau$ as the bifurcation parameter and consider the eigenvalues as functions of $\tau$: $\lambda =\lambda (\tau )$. Implicitly differentiating the characteristic Equation (16) with respect to $\tau$, we have

$$2\lambda {\lambda }^{\prime }+{\lambda }^{\prime }({\alpha }_1+{\alpha }_2)-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })e^{-\lambda \tau }(-\lambda -{\lambda }^{\prime }\tau )=0,$$

implying that

$${\lambda }^{\prime }\left[2\lambda +{\alpha }_1+{\alpha }_2+{\alpha }_1{\alpha }_2\tau R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })e^{-\lambda \tau }\right]+{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\lambda e^{-\lambda \tau }=0.$$

From Equation (16), we know that

$${\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })e^{-\lambda \tau }={\lambda }^2+\lambda ({\alpha }_1+{\alpha }_2)+{\alpha }_1{\alpha }_2,$$

implying that

$$\frac{1}{{\lambda }^{\prime }}=-\frac{2\lambda +{\alpha }_1+{\alpha }_2}{\lambda \left[{\lambda }^2+\lambda ({\alpha }_1+{\alpha }_2)+{\alpha }_1{\alpha }_2\right]}-\frac{\tau }{\lambda }.$$

Notice that the real parts of ${\lambda }^{\prime }$ and $1/{\lambda }^{\prime }$ have the same sign and at $\tau =i\omega$, the last term is a pure imaginary number with a zero real part. At $\lambda =i\omega$, the first term equals

$$-\frac{2i\omega +{\alpha }_1+{\alpha }_2}{i\omega \left[-{\omega }^2+i\omega ({\alpha }_1+{\alpha }_2)+{\alpha }_1{\alpha }_2\right]}=-\frac{2i\omega +{\alpha }_1+{\alpha }_2}{-{\omega }^2({\alpha }_1+{\alpha }_2)+i\omega (-{\omega }^2+{\alpha }_1{\alpha }_2)}.$$

The real part of this expression has the same sign as

$${\omega }^2{({\alpha }_1+{\alpha }_2)}^2-2{\omega }^2(-{\omega }^2+{\alpha }_1{\alpha }_2)={\omega }^2\left({{\alpha }_1}^2+{\alpha }_2^2+2{\omega }^2\right)>0,$$

implying that at any critical value, at least one eigenvalue changes the sign of its real part from negative to positive. Consequently, stability cannot be regained with delayed information.

Assume next that $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<-1$. The equilibrium is locally asymptotically stable without delays. From Equations (17) and (18), we see that $sin\omega \tau >0$ and

$$cos\omega \tau \left\{\begin{array}{c}>0\mathrm{if}{\omega }_{+}^2>{\alpha }_1{\alpha }_2,\hfill \\ =0\mathrm{if}{\omega }_{+}^2={\alpha }_1{\alpha }_2,\hfill \\ <0\mathrm{if}{\omega }_{+}^2<{\alpha }_1{\alpha }_2.\hfill \end{array}\right.$$

Hence, the critical values are

$${\overline{\tau }}_n=\frac{1}{{\omega }_{+}}\left[{cos}^{-1}\left(\frac{-{\omega }_{+}^2+{\alpha }_1{\alpha }_2}{{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })}\right)+2n\pi \right]\mathrm{for}n=0,1,2,\dots ,$$

(21)

and at the smallest critical value ${\overline{\tau }}_0,$ stability is lost.

In summary, we have the following results:

Proposition 4.

(a) If $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<-1$, then the equilibrium is locally asymptotically stable for $\tau <{\overline{\tau }}_0$. At $\tau ={\overline{\tau }}_0$, the stability is lost via Hopf bifurcation. (b) If $-1\le R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<1$, then the equilibrium is locally asymptotically stable for all $\tau \ge 0$. (c) If $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })>1$, then the equilibrium is unstable for all $\tau \ge 0$. (d) If $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })=1$, then no stability result can be determined for $\tau \ge 0$.

4. Alternative Models

4.1. One-Delay Models

Consider first the case where the first player faces delays in its own and the other player’s strategy. In this case, Equations (3) and (4) are modified as follows:

$${\dot{x}}_1(t)={\alpha }_1\left[R_1(x_2(t-\tau ))-x_1(t-\tau )\right],$$

(22)

$${\dot{x}}_2(t)={\alpha }_2\left[R_2(x_1(t))-x_2(t)\right].$$

(23)

Linearization around the equilibrium gives

$${\dot{x}}_1(t)=-{\alpha }_1{x}_1(t-\tau )+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })x_2(t-\tau ),$$

(24)

$${\dot{x}}_2(t)={\alpha }_2{R}_2^{\prime }(x_1^{\ast })x_1(t)-{\alpha }_2{x}_2(t).$$

(25)

Assuming again exponential solutions,

$$x_1(t)=e^{-\lambda t}u\mathrm{and}{x}_2(t)=e^{-\lambda t}v,$$

and substituting them into the linearized equations, we have

$$\lambda e^{\lambda t}u=-{\alpha }_1{e}^{\lambda \left(t-\tau \right)}u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{\lambda (t-\tau )}v,$$

$$\lambda e^{\lambda t}v={\alpha }_2{R}_2^{\prime }(x_1^{\ast })e^{\lambda t}u-{\alpha }_2{e}^{\lambda t}v.$$

After simplifying with $e^{\lambda t}$, the resulting algebraic equations have nonzero solutions if and only if

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}-{\alpha }_1{e}^{-\lambda \tau }-\lambda & {\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{-\lambda \tau }\\ {\alpha }_2{R}_2^{\prime }(x_1^{\ast })& -{\alpha }_2-\lambda \end{array}\right)\hfill \\ \hfill & ={\lambda }^2+\lambda {\alpha }_2+e^{-\lambda \tau }\left[{\alpha }_1{\alpha }_2+{\alpha }_1\lambda -{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right].\hfill \end{array}$$

(26)

We showed earlier that the equilibrium is locally asymptotically stable if $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<1$ and unstable if $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })>1$. By increasing the value of $\tau$ from zero, stability might be lost or regained when $\lambda =i\omega$. Substituting this eigenvalue into Equation (26), we have

$$-{\omega }^2+i\omega {\alpha }_2+\left(\cos \omega \tau -isin\omega \tau \right)\left(i\omega {\alpha }_1+{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)\right)=0.$$

The separation of the real and imaginary parts shows that

$${\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)cos\omega \tau +\omega {\alpha }_{1}sin\omega \tau ={\omega }^2,$$

$$-{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)sin\omega \tau +\omega {\alpha }_{1}cos\omega \tau =-\omega {\alpha }_2.$$

Adding up the squares of these equations, we have

$${\left[{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)\right]}^2+{\omega }^2{\alpha }_1^2={\omega }^4+{\omega }^2{\alpha }_2^2.$$

(27)

There is a positive solution for ${\omega }^2,$

$${\omega }_{+}^2=\frac{{\alpha }_1^2-{\alpha }_2^2+\sqrt{D}}{2},$$

with

$$D={\left({{\alpha }_1}^2-{\alpha }_2^2\right)}^2+4{\left[{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)\right]}^2\ge {\left({{\alpha }_1}^2-{\alpha }_2^2\right)}^2.$$

For the sake of notational convenience, let

$$A={\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)\mathrm{and}B=\omega {\alpha }_2$$

in order to give

$$Acos\omega \tau +Bsin\omega \tau ={\omega }^2,$$

(28)

$$-Asin\omega \tau +Bcos\omega \tau =-\omega {\alpha }_2,$$

(29)

implying that

$$cos\omega \tau =\frac{{\omega }^2-Bsin\omega \tau }{A}.$$

Thus,

$$-Asin\omega \tau +\frac{B{\omega }^2-B^{2}sin\omega \tau }{A}=-\omega {\alpha }_2$$

or

$$sin\omega \tau =\frac{\omega \left(B\omega +A{\alpha }_2\right)}{A^2+B^2},$$

(30)

and

$$cos\omega \tau =\frac{\omega \left(A\omega -B{\alpha }_2\right)}{A^2+B^2}.$$

(31)

If $A>0,$ then sin $\omega \tau >0$ and

$$cos\omega \tau \left\{\begin{array}{c}>0\mathrm{if}\omega >{\displaystyle \frac{B{\alpha }_2}{A}},\hfill \\ =0\mathrm{if}\omega ={\displaystyle \frac{B{\alpha }_2}{A}},\hfill \\ <0\mathrm{if}\omega <{\displaystyle \frac{B{\alpha }_2}{A}},\hfill \end{array}\right.$$

and the critical values are

$$n_n^{\prime }=\frac{1}{{\omega }_{+}}\left({cos}^{-1}\frac{{\omega }_{+}\left(A{\omega }_{+}-B{\alpha }_2\right)}{A^2+B^2}+2n\pi \right)\mathrm{for}n=0,1,2,\dots$$

(32)

If $A=0,$ then nothing can be concluded about stability in the no-delay case. From (27), the nonzero solution is

$${\omega }^2={\alpha }_1^2-{\alpha }_2^2.$$

Thus, if ${\alpha }_1\le {\alpha }_2,$ then no stability switch occurs, and if ${\alpha }_1>{\alpha }_2,$ then

$${\omega }_{+}=\sqrt{{\alpha }_1^2-{\alpha }_2^2}.$$

From (30) and (31), we know that $sin\omega \tau >0$ and $cos\omega \tau <0,$ implying that the critical values are also given by (32).

If $A<0$, then the equilibrium is unstable without delays. In this case, $cos\omega \tau <0$ and

$$sin\omega \tau \left\{\begin{array}{c}>0\mathrm{if}\omega >-{\displaystyle \frac{A{\alpha }_2}{B}},\hfill \\ =0\mathrm{if}\omega =-{\displaystyle \frac{A{\alpha }_2}{B}},\hfill \\ <0\mathrm{if}\omega <-{\displaystyle \frac{A{\alpha }_2}{B}}.\hfill \end{array}\right.$$

The critical values are as follows:

$${\tau }_n^{\ast }=\left\{\begin{array}{c}{\displaystyle \frac{1}{{\omega }_{+}}}\left({cos}^{-1}{\displaystyle \frac{{\omega }_{+}\left(A{\omega }_{+}-B{\alpha }_2\right)}{A^2+B^2}}+2n\pi \right)\mathrm{if}sin\omega \tau >0\mathrm{for}n=0,1,2,\dots \hfill \\ \\ {\displaystyle \frac{1}{{\omega }_{+}}}\left(-{cos}^{-1}{\displaystyle \frac{{\omega }_{+}\left(A{\omega }_{+}-B{\alpha }_2\right)}{A^2+B^2}}+2n\pi \right)\mathrm{if}sin\omega \tau >0\mathrm{for}n=1,2,\dots \hfill \end{array}\right.$$

(33)

The directions of the stability switches are determined by Hopf bifurcation. Assuming that $\lambda =\lambda (\tau )$, we differentiate implicitly Equation (26) with respect to $\tau$ to obtain

$$2{\lambda }^{\prime }\lambda +{\lambda }^{\prime }{\alpha }_2+e^{-\lambda \tau }{\alpha }_1+\left({\alpha }_1\lambda +A\right)e^{-\lambda \tau }(-{\lambda }^{\prime }\tau -\lambda )=0,$$

implying that

$${\lambda }^{\prime }\left[2\lambda +{\alpha }_2-\left({\alpha }_1\lambda +A\right)e^{-\lambda \tau }\tau \right]+e^{-\lambda \tau }\left({\alpha }_1-{\alpha }_1{\lambda }^2-A\lambda \right)=0.$$

From $(26),$ we know that

$$e^{-\lambda \tau }=-\frac{{\lambda }^2+\lambda {\alpha }_2}{\lambda {\alpha }_1+A},$$

implying that

$${\lambda }^{\prime }\left[2\lambda +{\alpha }_2+\left({\lambda }^2+\lambda {\alpha }_2\right)\tau \right]=\frac{{\lambda }^2+\lambda {\alpha }_2}{\lambda {\alpha }_1+A}\left[{\alpha }_1-\lambda ({\alpha }_1\lambda +A)\right],$$

from which we have

$$\frac{1}{{\lambda }^{\prime }}=\frac{\left(\lambda {\alpha }_1+A\right)\left[2\lambda +{\alpha }_2+\left({\lambda }^2+\lambda {\alpha }_2\right)\tau \right]}{\lambda \left(\lambda +{\alpha }_2\right)\left[{\alpha }_1-\lambda ({\alpha }_1\lambda +A)\right]}.$$

At $\lambda =i\omega$, this expression becomes

$$\frac{\left(i\omega {\alpha }_1+A\right)\left[2i\omega +{\alpha }_2+\left(-{\omega }^2+i\omega {\alpha }_2\right)\tau \right]}{i\omega \left(i\omega +{\alpha }_2\right)\left[{\alpha }_1-i\omega (i\omega {\alpha }_1+A)\right]}.$$

We first simplify the numerator,

$$\begin{array}{ccc}\hfill N& =& \left[A{\alpha }_2-A{\omega }^2\tau -{\alpha }_1\omega \left(2\omega +\omega {\alpha }_2\tau \right)\right]\hfill \\ & & +i\left[{\alpha }_1{\alpha }_2\omega -{\alpha }_1{\omega }^3\tau +2A\omega +\omega {\alpha }_2\tau A\right].\hfill \end{array}$$

The denominator is the following:

$$\begin{array}{ccc}\hfill D& =& \left(-{\alpha }_1{\omega }^2-{\alpha }_1{\omega }^4+{\alpha }_{2}A{\omega }^2\right)\hfill \\ & & +i\left(A{\omega }^3+{\alpha }_1{\alpha }_2\omega +{\alpha }_1{\alpha }_2{\omega }^3\right).\hfill \end{array}$$

After multiplying both N and D by the complex conjugate of D, the denominator becomes positive, and the real part of the numerator becomes

$$\begin{array}{ccc}& & \left(A{\alpha }_2-A{\omega }^2\tau -2{\alpha }_1{\omega }^2-{\alpha }_1{\alpha }_2{\omega }^2\tau \right)\left(-{\alpha }_1{\omega }^2-{\alpha }_1{\omega }^4+a_{2}A{\omega }^2\right)\hfill \\ & & +\left({\alpha }_1{\alpha }_2\omega -{\alpha }_1{\omega }^3\tau +2A\omega +\omega {\alpha }_2\tau A\right)\left(A{\omega }^3+{\alpha }_1{\alpha }_2\omega +{\alpha }_1{\alpha }_2{\omega }^3\right).\hfill \end{array}$$

(34)

It can be shown that (34) can be simplified as

$${\omega }^6\left(2{\alpha }_1^2\right)+{\omega }^4\left(A{\alpha }_1\tau +2{\alpha }_1^2+{\alpha }_1^2{\alpha }_2^2+2A^2\right)+{\omega }^2\left(A{\alpha }_1{\alpha }_2+A^2{\alpha }_2^2+{\alpha }_1^2{\alpha }_2^2+A{\alpha }_1{\alpha }_2^2\tau \right),$$

which is positve if $A>0$. Thus, if the equilibrium is stable with $A>0$ in the no-delay case, then stability is lost at ${\tau }_0^{\ast }$, and stability cannot be regained with larger values of delay.

Another model is obtained if we assume that both players have delays in their own strategies. Then, Equations (3) and (4) become

$${\dot{x}}_1(t)={\alpha }_1\left[R_1(x_2(t))-x_1(t-\tau )\right],$$

$${\dot{x}}_2(t)={\alpha }_2\left[R_2(x_1(t))-x_2(t-\tau )\right].$$

The linearized equations are

$${\dot{x}}_1(t)=-{\alpha }_1{x}_1(t-\tau )+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })x_2(t),$$

(35)

$${\dot{x}}_2(t)={\alpha }_2{R}_2^{\prime }(x_1^{\ast })x_1(t)-{\alpha }_2{x}_2(t-\tau ).$$

(36)

Substituting exponential solutions as before, we have

$$\lambda e^{\lambda t}u=-{\alpha }_1{e}^{\lambda \left(t-\tau \right)}u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{\lambda t}v,$$

$$\lambda e^{\lambda t}v={\alpha }_2{R}_2^{\prime }(x_1^{\ast })e^{\lambda t}u-{\alpha }_2{e}^{\lambda (t-\tau )}v.$$

After simplifying with $e^{\lambda t}$, the resulting algebraic system for u and v has nonzero solutions if and only if

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}-{\alpha }_1{e}^{-\lambda \tau }-\lambda & {\alpha }_1{R}_1^{\prime }(x_2^{\ast })\\ {\alpha }_2{R}_2^{\prime }(x_1^{\ast })& -{\alpha }_2{e}^{-\lambda \tau }-\lambda \end{array}\right)\hfill \\ \hfill & ={\lambda }^2+\lambda e^{-\lambda \tau }\left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2\left[e^{-2\lambda \tau }-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right].\hfill \end{array}$$

Multiplying these equations by $e^{\lambda t}$, we obtain

$${\lambda }^2{e}^{\lambda \tau }+\lambda \left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2{e}^{-\lambda \tau }-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })e^{\lambda \tau }=0.$$

(37)

Assuming again that the eigenvalue has a zero real part, $\lambda =i\omega$, we substitute it into this equation to obtain

$$\begin{array}{ccc}\hfill 0& =& -{\omega }^2\left(\cos \omega \tau +isin\omega \tau \right)+i\omega \left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2\left(\cos \omega \tau -isin\omega \tau \right)\hfill \\ & & -{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\left(\cos \omega \tau +isin\omega \tau \right).\hfill \end{array}$$

Separating the real and imaginary parts, we have

$$\left[-{\omega }^2+{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })\right)R_2^{\prime }(x_1^{\ast })\right]cos\omega \tau =0,$$

(38)

$$\left[-{\omega }^2-{\alpha }_1{\alpha }_2\left(1+R_1^{\prime }(x_2^{\ast })\right)R_2^{\prime }(x_1^{\ast })\right]sin\omega \tau =-\omega \left({\alpha }_1+{\alpha }_2\right).$$

(39)

Now, we have two cases:

(a)

$cos\omega \tau =0$.

Then, sin $\omega \tau =\pm 1$. If sin $\omega \tau =1$, from (39),

$${\omega }^2-\omega \left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2\left(1+R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)=0,$$

with roots

$${\omega }_{\pm }=\frac{{\alpha }_1+{\alpha }_2\pm \sqrt{D}}{2},$$

where

$$D={\left({\alpha }_1+{\alpha }_2\right)}^2-4{\alpha }_1{\alpha }_2\left(1+R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right).$$

If $D<0$, no stability switch occurs. If $D=0$, then the unique solution is

$${\omega }_{+}=\frac{{\alpha }_1+{\alpha }_2}{2},$$

and if $D>0$ and $1+R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\le 0$, then we have again one positive solution, ${\omega }_{+}$. Otherwise, both ${\omega }_{+}$ and ${\omega }_{-}$ are solutions. In the case of one solution, the critical values are

$${\tau }_n=\frac{1}{{\omega }_{+}}\left(\frac{\pi }{2}+2n\pi \right)\mathrm{for}n=0,1,2,\dots ,$$

(40)

and in the case of two solutions,

$${\tau }_{n+}=\frac{1}{{\omega }_{+}}\left(\frac{\pi }{2}+2n\pi \right)\mathrm{for}n=0,1,2,\dots$$

(41)

and

$${\tau }_{n-}=\frac{1}{{\omega }_{-}}\left(\frac{\pi }{2}+2n\pi \right)\mathrm{for}n=0,1,2,\dots$$

(42)

Assume next that $sin\omega \tau =-1$; then, Equation (39) implies that

$${\omega }^2+\omega \left({\alpha }_1+{\alpha }_2\right)+{\alpha }_1{\alpha }_2\left[1+R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right]=0,$$

with roots

$${\omega }_{\pm }=\frac{-({\alpha }_1+{\alpha }_2)\pm \sqrt{D}}{2}.$$

If $D\le 0$, then no stability switch occurs. If $1+R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\ge 0$, then $D\le {({\alpha }_1+{\alpha }_2)}^2$, implying that there is no stability switch. Otherwise, there is a unique positive root,

$${\omega }_{+}=\frac{\sqrt{D}-({\alpha }_1+{\alpha }_2)}{2}.$$

Then, the critical values are

$${\tau }_n=\frac{1}{{\omega }_{+}}\left(\frac{3\pi }{2}+2n\pi \right)\mathrm{for}n=0,1,2,\dots$$

(b)

$cos\omega \tau \ne 0$

$$-{\omega }^2+{\alpha }_1{\alpha }_2-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })=0.$$

(43)

The multiplier of $sin\omega \tau$ in (43) can be rewritten as

$$-{\omega }^2+{\alpha }_1{\alpha }_2-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })-2{\alpha }_1{\alpha }_2=-2{\alpha }_1{\alpha }_2.$$

From (43),

$${\omega }_{+}^2={\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right).$$

If $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })<1$, then the equilibrium is locally asymptotically stable without delay, and we have a positive $\omega$ value,

$${\omega }_{+}=\sqrt{{\alpha }_1{\alpha }_2\left(1-R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)}$$

Furthermore, the critical values are

$${\tau }_{n+}^{\ast }=\frac{1}{{\omega }_{+}}\left[{sin}^{-1}\left(\frac{{\omega }_{+}({\alpha }_1+{\alpha }_2)}{2{\alpha }_1{\alpha }_2}\right)+2n\pi \right]\mathrm{for}n=0,1,2,\dots$$

and

$${\tau }_{n-}^{\ast }=\frac{1}{{\omega }_{+}}\left[\pi -{sin}^{-1}\left(\frac{{\omega }_{+}({\alpha }_1+{\alpha }_2)}{2{\alpha }_1{\alpha }_2}\right)+2n\pi \right]\mathrm{for}n=0,1,2,\dots$$

In the special case, when $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })=1,$ Equation (43) shows that $\omega =0$ is the only solution implying that no stability switch occurs.

4.2. Two-Delay Model

Assume next that player 1 faces different delays in the data of its own strategy and that of the other player. The associated dynamic equations have the forms

$${\dot{x}}_1(t)={\alpha }_1\left[R_1^{\prime }(x_2(t-{\tau }_2))-x_1(t-{\tau }_1)\right],$$

(44)

$${\dot{x}}_2(t)={\alpha }_2\left[R_2^{\prime }(x_1(t))-x_2(t)\right],$$

(45)

and the corresponding linearized system is as follows:

$${\dot{x}}_1(t)={\alpha }_1\left[R_1^{\prime }(x_2^{\ast })x_2(t-{\tau }_2)-x_1(t-{\tau }_1)\right],$$

$${\dot{x}}_2(t)={\alpha }_2\left[R_2^{\prime }(x_1^{\ast })x_1(t)-x_2(t)\right].$$

Substituting exponential solutions again into these equations, after simplifying by $e^{\lambda t}$, we have

$$\lambda u={\alpha }_1\left[R_1^{\prime }(x_2^{\ast })e^{-\lambda {\tau }_2}v-e^{-\lambda {\tau }_1}u\right],$$

$$\lambda v={\alpha }_2\left[R_2^{\prime }(x_1^{\ast })u-v\right],$$

with determinant equation

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}\lambda +{\alpha }_1{e}^{-\lambda {\tau }_1}& -{\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{-\lambda {\tau }_2}\\ -{\alpha }_2{R}_2^{\prime }(x_1^{\ast })& \lambda +{\alpha }_2\end{array}\right)\hfill \\ \hfill & ={\lambda }^2+e^{-\lambda {\tau }_1}\left({\alpha }_1\lambda +{\alpha }_1{\alpha }_2\right)+{\alpha }_2\lambda -{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })e^{-\lambda {\tau }_2},\hfill \\ \hfill & =P_0(\lambda )+P_1(\lambda )e^{-\lambda {\tau }_1}+P_2(\lambda )e^{-\lambda {\tau }_2},\hfill \end{array}$$

(46)

where

$$P_0(\lambda )={\lambda }^2+{\alpha }_2\lambda ,$$

$$P_1(\lambda )={\alpha }_1\lambda +{\alpha }_1{\alpha }_2,$$

$$P_2(\lambda )=-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }).$$

In order to guarantee that Equation (46) is the characteristic equation of a delay system, we assume the following:

(a)

$deg\left(P_0(\lambda )\right)\ge max\left\{deg\left(P_1(\lambda )\right),deg\left(P_2(\lambda )\right)\right\},$ so there are finitely many eigenvalues on $C_{+}$. This clearly holds.

(b)

$P_0(0)+P_1(0)+P_2(0)\ne 0,$ which holds if $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\ne 1$, as is assumed in the following.

(c)

Polynomials $P_0(\lambda ),P_1(\lambda ),$ and $P_2(\lambda )$ have no common roots. This is obvious if $R_1^{\prime }(x_2^{\ast })$$R_2^{\prime }(x_1^{\ast })\ne 0$. If $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })=0,$ then $\lambda =-{\alpha }_2$ is a common root, which does not remove stability.

(d)

$$\underset{\lambda \to \infty }{lim}\left[\left|\frac{P_1(\lambda )}{P_0(\lambda )}\right|+\left|\frac{P_2(\lambda )}{P_0(\lambda )}\right|\right]<1,$$

which is again obvious, since $P_0(\lambda )$ is quadratic, $P_1(\lambda )$ is linear, and $P_2(\lambda )$ is constant.

We will now follow the suggestions given by Gu et al. (2005) [27]. Dividing both sides of (46) by $P_0(\lambda )$, we obtain

$$1+a_1(\lambda )e^{-\lambda {\tau }_1}+a_2(\lambda )e^{-\lambda {\tau }_2}=0,$$

(47)

where

$$a_1(\lambda )=\frac{P_1(\lambda )}{P_0(\lambda )}=\frac{{\alpha }_1}{\lambda }$$

and

$$a_2(\lambda )=\frac{P_2(\lambda )}{P_0(\lambda )}=\frac{-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })}{{\lambda }^2+{\alpha }_2\lambda }.$$

We are looking for pure complex solutions, $\lambda =i\omega$. If $P_0(i\omega )=0$, then from (46), we have

$$P_1(i\omega )+P_2(i\omega )e^{-i\omega \left({\tau }_2-{\tau }_1\right)}=0,$$

implying that

$${\tau }_2-{\tau }_1=\frac{1}{\omega }\left[arg\left(-\frac{P_2(i\omega )}{P_1(i\omega )}\right)+2n\pi \right].$$

However, if $P_1(i\omega )=0$ as well, then $P_2(i\omega )\ne 0$ implies no solution, and $P_2(i\omega )=0$ implies that arbitrary positive ${\tau }_1$ and ${\tau }_2$ values are solutions. Notice that this case cannot occur, since $P_0(i\omega )$ has only two real roots, $\lambda =0$ and $\lambda =-{\alpha }_2$.

Consider next the case of $P_0(i\omega )\ne 0$. Then, notice that the complex vectors $1,$$a_1(i\omega )e^{-i\omega {\tau }_1}$, and $a_2(i\omega )e^{-i\omega {\tau }_2}$ form a triangle in the complex plane, as shown in Figure 1.

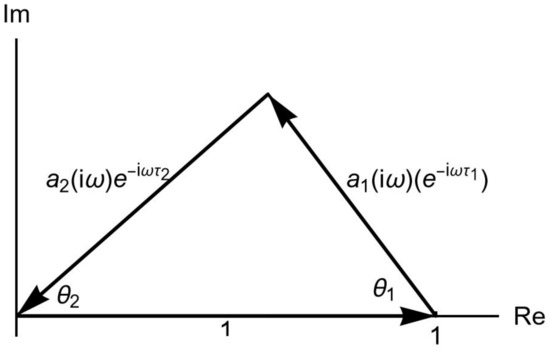
Figure 1. Triangle constructed by these vectors.

In the special case of $a_1(i\omega )=0,$(47) implies that

$$1+a_2(i\omega )e^{-i\omega {\tau }_2}=0,$$

so ${\tau }_1$ is arbitrary and

$${\tau }_2^n=\frac{1}{\omega }\left[arg\left(-a_2(i\omega )\right)+2n\pi \right].$$

If $a_2(i\omega )=0$, then, similarly,

$$1+a_1(i\omega )e^{-i\omega {\tau }_1}=0,$$

implying that ${\tau }_2$ is arbitrary and

$${\tau }_1^m=\frac{1}{\omega }\left[arg\left(-a_1(i\omega )\right)+2m\pi \right].$$

If $a_1(i\omega )$ and $a_2(i\omega )$ are nonzero, then the three vectors form a triangle if and only if

$$\left|a_1(i\omega )\right|+\left|a_2(i\omega )\right|\ge 1,$$

(48)

$$-1\le \left|a_1(i\omega )\right|-\left|a_2(i\omega )\right|\le 1.$$

(49)

In our case,

$$a_1(i\omega )=-i\frac{{\alpha }_1}{\omega }\mathrm{so}\left|a_1(i\omega )\right|=\frac{{\alpha }_1}{\omega },$$

$$a_2(i\omega )=\frac{-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })}{-{\omega }^2+i\omega {\alpha }_2}\mathrm{so}\left|a_2(i\omega )\right|=\frac{{\alpha }_1{\alpha }_2\left|R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right|}{\omega \sqrt{{\omega }^2+{\alpha }_2^2}}.$$

Relations (48) and (49) are quartic inequalities. In general, they cannot be solved, but if the numerical values are known, then the roots of the quartic equations can be determined, and certain segments between the roots provide solutions. The law of cosine can be used to find angles ${\theta }_1$ and ${\theta }_2$:

$${\theta }_1={cos}^{-1}\left(\frac{1+{\left|a_1(i\omega )\right|}^2-{\left|a_2(i\omega )\right|}^2}{2\left|a_1(i\omega )\right|}\right),$$

and

$${\theta }_2={cos}^{-1}\left(\frac{1+{\left|a_2(i\omega )\right|}^2-{\left|a_1(i\omega )\right|}^2}{2\left|a_2(i\omega )\right|}\right).$$

The triangle can be placed above and under the horizontal axis, so from Figure 1, we have

$$arg\left[a_1(i\omega )\right]-\omega {\tau }_1\pm {\theta }_1=\pi$$

and

$$arg\left[a_2(i\omega )\right]-\omega {\tau }_2\mp {\theta }_2=\pi ,$$

implying that the critical values are as follows:

$${\tau }_1^{n\pm }(\omega )=\frac{1}{\omega }\left[arg\left[a_1(i\omega )\right]+(2n-1)\pi \pm {\theta }_1\right]$$

(50)

and

$${\tau }_2^{m\pm }(\omega )=\frac{1}{\omega }\left[arg\left[a_2(i\omega )\right]+(2m-1)\pi \mp {\theta }_2\right].$$

(51)

Let $\mathsf{\Omega }$ denote the set of all solutions of conditions (48) and (49), which consists finitely of many intervals:

$${\mathsf{\Omega }}_k(k=1,2,\dots N).$$

For $k=1,2,\dots N,$ we define

$$T_{n,m}^{k\pm }=\left\{\left.\left({\tau }_1^{n\pm }(\omega ),{\tau }_2^{m\pm }(\omega )\right)\right|\omega \in {\mathsf{\Omega }}_k\right\}$$

and

$$T^k={\cup }_n{\cup }_m(T_{n,m}^{k+}\cup T_{n,m}^{k-})\cap R_{+}^2.$$

The set T of all stability-switching curves is the union of all sets $T^k$. By not restricting $arg\left[a_1(i\omega )\right]$ and $arg\left[a_2(i\omega )\right]$ to interval $[0,2\pi ]$, we make them continuous functions of $\omega$ in ${\mathsf{\Omega }}_k$, so with fixed n and m, $T_{n,m}^{k+}$ and $T_{n,m}^{k-}$ also become continuous curves.

Notice that any left endpoint ${\omega }_k^{\ell }$ and right endpoint ${\omega }_k^r$ of $\mathsf{\Omega }$ satisfy at least one of the conditions (48) and (49) by equality, so one of the following equalities must hold:

$$\left|a_1(i\omega )\right|+\left|a_2(i\omega )\right|=1,$$

(52)

$$\left|a_2(i\omega )\right|-\left|a_1(i\omega )\right|=1,$$

(53)

$$\left|a_1(i\omega )\right|-\left|a_2(i\omega )\right|=1,$$

(54)

and the case of ${\omega }_k^{\ell }=0$ and ${\omega }_k^r=\infty$ are also possible. If (52) holds, then ${\theta }_1={\theta }_2=0$ and $T_{n,m}^{k+}$ is connected with $T_{n,m}^{k-}$ at this endpoint. If (53) holds, then similarly, ${\theta }_1=\pi$ and ${\theta }_2=0$, so $T_{n,m}^{k+}$ is connected with $T_{n+1,m}^{k-}$ at this endpoint, and if (54) is satisfied, then ${\theta }_1=0$ and ${\theta }_2=\pi$, showing that at this endpoint $T_{n,m}^{k+}$ is connected with $T_{n,m-1}^{k-}$. If ${\omega }_k^{\ell }=0$, then as $\omega \to 0$, both $T_{n,m}^{k+}$ and $T_{n,m}^{k-}$ converge to infinity. This discussion shows that the stability-switching curve T is the intersection of $R_{+}^2$ and conforms to one of the following types:

(i)

A series of closed curves;

(ii)

A series of spiral-like curves with either horizontal, vertical, or diagonal axes;

(iii)

A series of open-ended curves with endpoints converging to infinity.

If a point (${\tau }_1,{\tau }_2$) crosses the stability-switching curve, then stability switching might occur. Before discussing the direction of stability switching (stability loss or gain), some comments are in order.

The direction of a curve is positive if it corresponds to an increasing value of $\omega$. The direction is reversed if a curve is passing through an endpoint. Moving along a curve in the positive direction, the region on the left-hand side is called the region on the left, and the region on the right right is similar. We define for any point on T the following:

$$R_{\ell }=\mathrm{Re}\left[a_{\ell }(i\omega )e^{-i\omega {\tau }_{\ell }}\right]\mathrm{and}{I}_{\ell }=\mathrm{Im}\left[a_{\ell }(i\omega )e^{-i\omega {\tau }_{\ell }}\right]\mathrm{for}\ell =1,2\mathrm{and}\omega \in \mathsf{\Omega }.$$

The following result is given by Gu et al. (2005) [27].

Theorem 1.

Let $\omega \in {\mathsf{\Omega }}_k$ and $({\tau }_1,{\tau }_2)\in T^k$ such that $\lambda =i\omega$ is a simple pure complex eigenvalue. As a point $({\tau }_1,{\tau }_2)$ moves from the right to the left of the corresponding curve of $T^k$, a pair of eigenvalues cross the imaginary axes to the right (stability loss) if $R_2{I}_1-R_1{I}_2>0$. If the inequality is reversed, then the crossing is from right to left (stability gain).

4.3. Three-Delay Model

Consider next the case in which the players have different delays in the data about their own strategies. In this case, the delay equations become

$${\dot{x}}_1(t)={\alpha }_1\left[R_1(x_2(t))-x_1(t-{\tau }_1)\right],$$

$${\dot{x}}_2(t)={\alpha }_2\left[R_2(x_1(t))-x_2(t-{\tau }_2)\right].$$

By linearizing these equations around the equilibrium, we obtain

$${\dot{x}}_1(t)=-{\alpha }_1{x}_1(t-{\tau }_1)+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })x_2(t),$$

(55)

$${\dot{x}}_2(t)={\alpha }_2{R}_2^{\prime }(x_1^{\ast })x_1(t)-{\alpha }_2{x}_2(t-{\tau }_2).$$

(56)

Substituting the exponential solutions

$$x_1(t)=e^{\lambda t}u\mathrm{and}{x}_2(t)=e^{\lambda t}v$$

into these equations, we have

$$\lambda e^{\lambda t}u=-{\alpha }_1{e}^{\lambda \left(t-{\tau }_1\right)}u+{\alpha }_1{R}_1^{\prime }(x_2^{\ast })e^{\lambda t}v,$$

$$\lambda e^{\lambda t}v={\alpha }_2{R}_2^{\prime }(x_1^{\ast })e^{\lambda t}u-{\alpha }_2{e}^{\lambda (t-{\tau }_2)}v.$$

After simplifying these equations by $e^{\lambda t}$, an algebraic equation system is obtained for u and $v,$ and nonzero solutions exist if and only if

$$\begin{array}{cc}0\hfill & =det\left(\begin{array}{cc}\lambda +{\alpha }_1{e}^{-\lambda {\tau }_1}& -{\alpha }_1{R}_1^{\prime }(x_2^{\ast })\\ -{\alpha }_2{R}_2^{\prime }(x_1^{\ast })& \lambda +{\alpha }_2{e}^{-\lambda {\tau }_2}\end{array}\right)\hfill \\ \hfill & ={\lambda }^2+{\alpha }_1\lambda e^{-\lambda {\tau }_1}+{\alpha }_2\lambda e^{-\lambda {\tau }_2}-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })+{\alpha }_1{\alpha }_2{e}^{-\lambda ({\tau }_1+{\tau }_2)},\hfill \end{array}$$

which can be written as

$$P_0(\lambda )+P_1(\lambda )e^{-\lambda {\tau }_1}+P_2(\lambda )e^{-\lambda {\tau }_2}+P_3(\lambda )e^{-\lambda ({\tau }_1+{\tau }_2)}=0,$$

(57)

where

$$P_0(\lambda )={\lambda }^2-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }),$$

$$P_1(\lambda )={\alpha }_1\lambda ,P_2(\lambda )={\alpha }_2\lambda \mathrm{and}{P}_3(\lambda )={\alpha }_1{\alpha }_2.$$

The following assumptions are made to guarantee that (57) can be the characteristic equation of a delay system and to exclude some trivial cases:

(a)

There are a finite number of eigenvalues on $C_{+}$ when

$$deg\left(P_0(\lambda )\right)\ge max\left\{deg\left(P_1(\lambda )\right),deg\left(P_2(\lambda )\right),deg\left(P_3(\lambda )\right)\right\}.$$

This holds, since $P_0(\lambda )$ is quadratic, while $P_1(\lambda )$ and $P_2(\lambda )$ are linear and $P_3(\lambda )$ is constant.

(b)

The zero frequency $\lambda =0$ is not an eigenvalue with any ${\tau }_1$ and ${\tau }_2,$

$$P_0(0)+P_1(0)+P_2(0)+P_3(0)\ne 0.$$

This condition holds if $R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\ne 1$, so we have to assume this relation in the following discussion.

(c)

Polynomials $P_0(\lambda ),P_1(\lambda ),P_2(\lambda )$, and $P_3(\lambda )$ have no common roots, which is trivial in our case.

(d)

$$lim\left[\left|\frac{P_1(\lambda )}{P_0(\lambda )}\right|+\left|\frac{P_2(\lambda )}{P_0(\lambda )}\right|+\left|\frac{P_3(\lambda )}{P_0(\lambda )}\right|\right]<1,$$

which also holds, since $P_0(\lambda )$ is quadratic and the others have lower degrees.

In examining the stability switches with Equation (57), we will follow the ideas of Lin and Wang (2012) [28]. We can rewrite Equation (57) at $\lambda =i\omega$ as follows:

$$P_0(i\omega )+P_1(i\omega )e^{-i\omega {\tau }_1}+\left(P_2(i\omega )+P_3(i\omega )e^{-i\omega {\tau }_1}\right)e^{-i\omega {\tau }_2}=0.$$

(58)

Since $\left|e^{-i\omega {\tau }_2}\right|=1$,

$$\left|P_0(i\omega )+P_1(i\omega )e^{-i\omega {\tau }_1}\right|=\left|P_2(i\omega )+P_3(i\omega )e^{-i\omega {\tau }_1}\right|$$

or

$$\left(P_0+P_1{e}^{-i\omega {\tau }_1}\right)\left({\overline{P}}_0+{\overline{P}}_1{e}^{i\omega {\tau }_1}\right)=\left(P_2+P_3{e}^{-i\omega {\tau }_1}\right)\left({\overline{P}}_2+{\overline{P}}_3{e}^{i\omega {\tau }_1}\right),$$

(59)

where an overbar indicates a complex conjugate and the arguments of $P_0,P_1,P_2$, and $P_3$ are omitted for simple notation. A simple calculation shows that (59) has the equivalent form,

$${\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2=2A_1(\omega )cos\omega {\tau }_1-2B_1(\omega )sin\omega {\tau }_1,$$

(60)

where

$$A_1(\omega )=\mathrm{Re}\left(P_2{\overline{P}}_3-P_0{\overline{P}}_1\right)\mathrm{and}{B}_1(\omega )=\mathrm{Im}\left(P_2{\overline{P}}_3-P_0{\overline{P}}_1\right).$$

With any value of $\omega$, this is a trigonometric equation for ${\tau }_1$. In our case,

$$P_0(i\omega )=-{\omega }^2-{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }),$$

$$P_1(i\omega )=i\omega {\alpha }_1,$$

$$P_2(i\omega )=i\omega {\alpha }_2,$$

$$P_3(i\omega )={\alpha }_1{\alpha }_2.$$

Thus,

$$A_1(\omega )=\mathrm{Re}\left[i\omega {\alpha }_1{{\alpha }_2}^2+\left({\omega }^2+{\alpha }_1{\alpha }_2{R_1}^{\prime }({x_2}^{\ast }){R_2}^{\prime }({x_1}^{\ast })\right)\left(-i\omega {\alpha }_1\right)\right]=0$$

and

$$B_1(\omega )=\omega {\alpha }_1{\alpha }_2^2-{\alpha }_1{\omega }^3-{\alpha }_1^2{\alpha }_2\omega R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast }).$$

Similarly,

$$\begin{array}{ccc}& & {\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2\hfill \\ & =& {\left({\omega }^2+{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)}^2+{({\alpha }_1\omega )}^2-{({\alpha }_2\omega )}^2-{({\alpha }_1{\alpha }_2)}^2\hfill \\ & =& {\omega }^4+{\omega }^2\left[2{\alpha }_1{\alpha }_2{R}_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })+{\alpha }_1^2-{\alpha }_2^2\right]-{({\alpha }_1{\alpha }_2)}^2\left[1-{\left(R_1^{\prime }(x_2^{\ast })R_2^{\prime }(x_1^{\ast })\right)}^2\right].\hfill \end{array}$$

(A) We assume first that $\omega$ is a solution of equation $P_2{\overline{P}}_3-P_0{\overline{P}}_1=0$. Then, $A_1(\omega )=B_1(\omega )=0$, and an arbitrary value of ${\tau }_1>0$ is a solution. The corresponding values of ${\tau }_2$ can be obtained from Equation (58) as

$${\tau }_2^n=\frac{1}{\omega }\left[arg\left(-\frac{P_2+P_3{e}^{-i\omega {\tau }_1}}{P_0+P_1{e}^{-i\omega {\tau }_1}}\right)+2n\pi \right].$$

(61)

If the denominator is zero, then (58) implies that the numerator is also zero, so an arbitrary ${\tau }_2>0$ is a solution.

(B) We assume next that $P_2{\overline{P}}_3-P_0{\overline{P}}_1\ne 0$, so $A_1{(\omega )}^2+B_1{(\omega )}^2>0$. Clearly, there is a ${\varphi }_1(\omega )$ such that

$$cos\left({\varphi }_1(\omega )\right)=\frac{A_1(\omega )}{\sqrt{{\left|A_1(\omega )\right|}^2+{\left|B_1(\omega )\right|}^2}}=0,sin\left({\varphi }_1(\omega )\right)=sign\left(B_1(\omega )\right).$$

Then, (60) can be rewritten as

$${\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2=2\sqrt{{\left|A_1(\omega )\right|}^2+{\left|B_1(\omega )\right|}^2}cos\left({\varphi }_1(\omega )+\omega {\tau }_1\right),$$

(62)

and by defining

$${\psi }_1(\omega )={cos}^{-1}\left[\frac{{\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2}{2\sqrt{{\left|A_1(\omega )\right|}^2+{\left|B_1(\omega )\right|}^2}}\right]\in [0,\pi ]$$

it becomes clear that

$${\tau }_{1n}^{\pm }=\frac{1}{\omega }\left(\pm {\psi }_1(\omega )-{\varphi }_1(\omega )+2n\pi \right).$$

(63)

From (62), we see that a solution for ${\tau }_1$ exists if and only if

$$\left|{\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2\right|\le 2\sqrt{{\left|A_1(\omega )\right|}^2+{\left|B_1(\omega )\right|}^2},$$

(64)

or in our case

$$\left({\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2-2B_1\right)\left({\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2+2B_1\right)\le 0.$$

The two factors must have different signs, or one of them has to be zero. This inequality and (64) cannot be solved in general, but if numerical values of the model parameters are available, then computer solutions can present finitely many segments ${\mathsf{\Omega }}_k$ as the set of all solutions for $\omega$, which is denoted by $\mathsf{\Omega }$. For each $\omega \in \mathsf{\Omega }$, the corresponding critical values are given by (63), and then from (58), we have

$${\tau }_n^m=\frac{1}{\omega }\left[arg\left(-\frac{P_2(i\omega )+P_3(i\omega )e^{-i\omega {\tau }_1}}{P_0(i\omega )+P_1(i\omega )e^{-i\omega {\tau }_1}}\right)+2m\pi \right]$$

if the denominator is nonzero. If it is zero, then (58) implies that the numerator is also zero, so an arbitrary ${\tau }_2$ is the solution.

A more simple method can be suggested by interchanging ${\tau }_1$ and ${\tau }_2$ and repeating the above procedure for ${\tau }_2$. It can be shown that for each segment ${\mathsf{\Omega }}_k,$ the critical values form the curves as follows:

$$T_{n,m}^{k\pm }=\left\{\left.\left(\frac{\pm {\psi }_1(\omega )-{\varphi }_1(\omega )+2n\pi }{\omega },\frac{\mp {\psi }_2(\omega )-{\varphi }_2(\omega )+2m\pi }{\omega }\right)\right|\omega \in {\mathsf{\Omega }}_k\right\},$$

which is continuous in ${\mathbb{R}}^2$.

With any left and right endpoints ${\tau }_k^{\ell }$ and ${\tau }_k^r$,

$$F({\omega }_k^{\ell })=F({\omega }_k^r)=0,$$

where

$$F(\omega )={\left({\left|P_0\right|}^2+{\left|P_1\right|}^2-{\left|P_2\right|}^2-{\left|P_3\right|}^2\right)}^2-4\left(A_1{(\omega )}^2+B_1{(\omega )}^2\right);$$

therefore,

$$cos\left[{\psi }_i({\omega }_k^{\ell })\right]={\delta }_i^{\ell }\pi \mathrm{and}cos\left[{\psi }_i({\omega }_k^r)\right]={\delta }_i^r\pi ,$$

where ${\delta }_k^{\ell },{\delta }_k^r\in \{0,1\}$. The connection of the segments of the stability-switching curves can be given as follows: $T_{n,m}^{k+}$ connects $T_{n+{\delta }_1^{\ell },m-{\delta }_2^{\ell }}^{k-}$ and $T_{n+{\delta }_1^{\ell },m-{\delta }_2^r}^{k-}$ at its two ends:

(i)

If $\left({\delta }_1^{\ell },{\delta }_2^{\ell }\right)=\left({\delta }_1^r,{\delta }_2^r\right)$, then $T_{n,m}^{k+}$ and $T_{n-{\delta }_1^{\ell },m-{\delta }_2^{\ell }}^{k+}$ form a loop, so the set of stability-switching curves is a collection of closed continuous curves.

(ii)

Otherwise, it is a collection of continuous curves with endpoints on the axes or extending to infinity in ${\mathbb{R}}^2$.

The direction of stability switching now depends on

$$R_{\ell }=\mathrm{Re}\left[P_{\ell }(i\omega )e^{-i\omega {\tau }_{\ell }}+P_3(i\omega )e^{-i\omega ({\tau }_1+{\tau }_2})\right]$$

and

$$I_{\ell }=\mathrm{Im}\left[P_{\ell }(i\omega )e^{-i\omega {\tau }_{\ell }}+P_3(i\omega )e^{-i\omega ({\tau }_1+{\tau }_2})\right],$$

and Theorem 1 remains valid with these quantities.

5. Conclusions

In engineering, population dynamics, and realistic economies, there are many examples where only delayed responses can be observed and instantaneous data are not available. In such cases, the design and decisions are based on delayed data and information. In this paper, we presented some important methods to deal with this situation. Under discrete time scales, it is usually assumed that the lengths of the delays are positive integers that only increase the order of the governing difference equations (Matsumoto and Szidarovszky, 2018) [29]. In the continuous case, different methods can be used based on the number of delays. It is always assumed that the equilibrium is locally asymptotically stable without delays, and stability is preserved if the delays are sufficiently small based on the fact that the matrix eigenvalues continuously depend on the matrix elements. However, by increasing the lengths of the delays, this stability might be lost. In the one-delay case, the critical value of the delay was determined when stability turns into instability (Section 3.2 and Section 4.1). In the two-delay case, the two-dimensional space of the delays was considered, and the stability-switching curves were determined (Section 4.2 and Section 4.3). If a pair of delays crosses this curve from the region containing the origin, then stability is lost. The same is the situation in the three-delay case, when two delays and their sum affect the dynamic properties of the equilibrium. The mathematical methodology is different in these cases, which was illustrated in the case of a special two-person game wherein the dynamic evolution of the strategies was governed by best-response dynamics. Several cases were used for the presentation of the methodology, which could be very useful in solving practical problems including one, two, or even three delays. The material of this paper can be extended in several directions. One could include more players, different dynamic rules, and more variants of the delayed quantities. In addition, the Bayesian methodology is used in population dynamics to assess the survival probabilities of competing species (Dragicevic, 2015) [30] or, in general, to find the probability of the occurence of certain properties among the players. For the same issues, artificial neural networks could be an alternative approach (Poulton, 2001; Swingler, 1996) [31,32].