Abstract
We consider the design of a contest in which the prize may motivate not only productive efforts, but also some damaging aggressive behavior by contestants. The organizer must choose prizes and an enforcement regime defined as a limit on how much aggressiveness will be tolerated and the probability of inspection. When the value of contestants’ output is low, it may be optimal to motivate much less effort than first best because the prize spread necessary to induce higher effort necessitates a high level of enforcement, which is not worth the cost. On the other hand, when the output value is sufficiently high, it becomes optimal to offer a high prize spread to motivate substantial but still below first-best effort, with costly enforcement then being employed to constrain damaging aggressive behavior. Additionally, a less accurate inspection technology is associated with a tighter limit on aggressive behavior, and “zero tolerance” can be optimal if the aggressive behavior has no value.
JEL Classification:
J33; K42
1. Introduction
Many organizations design contests to increase participants’ motivation, effort, and performance. In contests, participants invest effort toward winning a prize; those efforts are costly and irreversible. Without proper monitoring, contest participants may also engage in undesirable aggressive behavior which can improve their chance of winning but is damaging to contest organizers [1].
Tolerating some damaging actions creates greater deterrence power at the margin and therefore, can effectively reduce such actions [2]. However, the analysis of the optimal contest design when damaging actions can occur is limited and has not incorporated modeling of the level of damaging actions that is optimally prohibited, i.e., where to “draw the line.” We term this dimension of potentially damaging behavior “aggressiveness.”
This paper explores the optimal design of a contest when contestants’ aggressiveness can improve contestants’ performance while harming the organizer. Examples of aggressiveness that can be damaging include division managers competing for a promotion and treating workers in an abusive manner that extracts greater short-run output at a long-term cost. Sales staff in an organization may raise sales with aggressive tactics that damage their employer’s brand. Scientists manipulate research results to obtain more research funding and a better position. In sports, aggressive behavior may include doping, which damages the perception of the sport and possibly harms the athlete’s health. We assume that aggression in management, sales, research, or sport is difficult to observe and thus subject to a measurement error. Therefore, an enforcement regime to deter damaging aggressiveness creates a dynamic where a contestant’s choice does not fully determine the finding of a violation and the resulting disqualification. Similar to aggressive driving, as contestants engage in more aggressive behavior, they become more likely to be cited for a breach and, in our context, disqualified from winning.
The organizer chooses a contest design that maximizes the profit of holding the contest. The contest design consists of three instruments. First, the organizer sets a prize for the best-performing contestant and a common payoff to each of the rest. The prizes motivate contestants and guarantee their participation. Second, the organizer decides an inspection probability. An inspection yields an unbiased but noisy estimated level of aggressiveness for each contestant. Third, the organizer places a limit on aggressiveness, which results in disqualification if found to have been exceeded by a contestant.
The game proceeds as follows. The organizer moves first and commits to prizes, an inspection rate, and the limit on aggressiveness. Then contestants observe those parameters and simultaneously choose their effort and aggressiveness. The contestants’ final output determines relative rankings, which are impacted by random shocks in addition to chosen effort and aggressiveness. Note that we model the output generated by aggressiveness as valuable to the organizer (but also consider the particular case when this is not true). If no inspection occurs or at least one contestant is qualified after an inspection, the qualified contestant with the highest ranking wins. If all contestants are disqualified, no one receives the winning prize. Violations result in no sanction beyond disqualification.
Our framework enables us to characterize optimal contest design in the presence of damaging actions beyond previous studies. We identify a unique symmetric pure strategy equilibrium characterizing behavior by contestants and then show how the three contest design instruments jointly influence behavior.
The major findings are the following. First, increasing prize spread motivates both effort and aggressive actions. Although expanding the prize spread can discourage contestants’ effort when the incentive1 for more aggressive actions is high, the optimal contest design rules out such a condition. In contrast, raising the inspection rate always reduces aggressive actions but discourages contestants’ efforts when the incentive for aggressive actions is low.
Regarding the limit on aggressiveness, increasing the limit always motivates contestants’ effort and can effectively reduce aggressive actions until reaching a certain level. The results demonstrate that although the organizer can choose a limit on aggressiveness to minimize the aggressive behavior, it is optimal to tolerate more aggressiveness than that level. The reason is that tolerating aggressiveness reduces the probability of disqualification, thereby improving the marginal benefit of effort. Thus, the organizer will keep raising the limit until the cost of increased aggressiveness equals the benefit from the increased output. A zero-tolerance policy is not optimal when aggressive behavior contributes to the valuable output. However, when those behaviors are valueless, the zero-tolerance policy becomes a corner solution because the first-best outcome is to have no aggressive behavior; the limit on aggressiveness must be minimized to make the optimal aggressiveness close to the first best.
Second, when the measurement of aggressiveness becomes noisier (the inspection measure is less precise), it becomes optimal to inspect contestants only at a higher output value and, to do so, with a higher inspection probability.2 At each output value, the organizer also tolerates less aggressive behavior under a less accurate inspection measure.
Third, as to the optimal contest design, we find that the optimal prize spread, inspection rate, and limit on aggressiveness do not increase smoothly with the output value. When the output value is low relative to the inspection cost, it is not optimal to engage in enforcement. This situation can be characterized as an “amateur” contest, where the prize is set low to obviate the need for enforcement, but the effort is thus highly suboptimal. We observe that in simulations, as the value of output increases, it reaches a threshold at which the optimal inspection rate and prize spread increase rapidly.
Intuitively, the costly and imperfect enforcement prevents reaching the first-best outcome: the contestants’ behavior under optimal contest design yields sub-optimal effort and a supra-optimal level of damaging aggressive behavior. Interestingly, simulations show that when enforcement is employed, the welfare loss comes almost entirely from the enforcement cost; the enforcement mechanism brings the equilibrium effort and aggressiveness very close to the first-best level.
The paper proceeds as follows. In Section 2, we offer a short review of the literature. Section 3 builds the contestants’ model and analyzes contestants’ behavior. Section 4 describes the organizer’s contest design problem and identifies the optimal contest design. In this section, simulations are used to help depict the model. Section 5 considers the case when aggressive behavior does not generate valuable output and simply damages the organizer. Section 6 concludes.
2. Literature Review
At least since Lazear’s [1] work on sabotage, contest theory has considered how competition may motivate undesirable actions. Cheating and sabotage are typical undesirable behaviors. The significant difference is that cheating improves a contestant’s own performance, while sabotage, on the contrary, deteriorates the competitors’. We model aggressive actions as improving a contestant’s own performance, as is typical in the cheating literature.
Several papers have analyzed the deterrence of cheating in contests in various frameworks. A group of papers model cheating as a dichotomous choice. For example, contestants in Berentsen [3] decide whether to use performance-enhancing drugs before competition. Cheating leads to a chance of being caught and disqualified. He finds the favorite player is more likely to take drugs than the underdog but does not always have a higher chance of winning. Haugen [4] assumes homogeneous players and finds the Nash equilibria forcing players to use drugs is comparable to the prisoner’s dilemma. Konrad [5] adopts a tournament model and allows homogeneous players to choose both doping and effort. He finds that at the optimal prize, doping is always welfare-enhancing. Curry and Mongrain [6] alter the prize structure in tournaments to deter cheating and reduce monitoring costs.
In many circumstances, cheating is not just a dichotomous choice; contestants also decide the extent of cheating. Kräkel [7] identifies three effects of doping decisions and supports the idea that mutual doping enhances welfare. Gilpatric [8] treats cheating as a continuous variable and finds that greater enforcement—a higher probability or randomness of detection and a penalty for cheating behavior—reduces cheating but may also reduce effort. Similarly, Mohan and Hazari [9] find that when doping and effort are substitutes, a higher detection probability incentivizes players to dope because the marginal benefit of doping rises as legal effort drops. Music [10] also finds that in a Tullock contest, stricter doping regulations can increase the payoff for a doped player making doping sustainable in the long run.
Tolerating damaging actions such as cheating can make that enforcement and regulations more effective. Ours is not the first paper to incorporate the tolerance level in a contest. Gilpatric and Reiser [2] extend studies of cheating in contests by embracing the idea of marginal deterrence. In their study, “misconduct” is a continuous choice variable with higher levels of damaging actions constituting different/more severe behavior. In that model, if low-level damaging actions are tolerated, contestants can engage in them while not facing any risk of disqualification. Our framework in this paper differs in a key respect. We assume that increased aggressiveness is not qualitatively different but rather “more of the same.” As such, the probability of disqualification does not change discretely from zero when a contestant “crosses the line.” Instead, the probability of being caught exceeding a tolerated level increases continuously with aggressiveness. We find that this has quite different implications for the optimal design of deterrence mechanisms. One of our findings shows that the organizer tolerates some aggressive actions when they have value to the organizer; otherwise, the organizer optimally does not tolerate any aggressive actions.
Since Becker [11], Ehrlich [12], and Polinsky and Shavell [13], two instruments are widely considered for deterrence: a sanction and a monitoring technology that generates a probability of detection. Ours is the first to consider the joint influences of prize spreads, inspection rate, and tolerance level on contestants’ aggressive actions and efforts.
3. A Contest with Limited Aggressiveness
This section models contestants’ behavior in a two-player tournament. Here the contest design parameters are exogenous: the prize spread S, an inspection rate , and a limit on aggressiveness L. Contestants choose effort, , and aggressiveness, . Section 3.1 provides a basic setting for modeling the contestants’ game. Section 3.2 identifies the impact of a contest’s design instruments on contestants’ strategies.
3.1. Environment
In this tournament, two risk-neutral contestants (indexed as ) compete to generate the highest outputs . The organizer observes output but cannot perfectly ascertain how the output is generated. A contestant produces output according to
where represents effort. represents the extent of aggressiveness that improves output, and is an error term drawn from a known distribution with zero mean and variance . As is standard in tournament models, can be viewed as luck (i.e., unobserved and uncontrollable production forces). We denote e as the difference between two players’ output error terms, . e follows a joint distribution , and is the density function.
With probability , the organizer inspects both contestants. If an inspection occurs, the organizer observes an estimate of aggressiveness , where represents a measurement error. The measurement error is drawn from a known distribution with zero mean and variance . For example, the use of a performance-enhancing drug may be monitored by a marker of its impact, such as red-blood-cell count. A test of this marker may be used for enforcement but is an imprecise measure of the level of drug use. To simplify the model, we assume that the amount of effort and the extent of aggressiveness do not influence the distributions.
Before the contest starts, contestants observe the prize for the winner and the loser, denoted as and , respectively. S, the prize spread, represents the difference between and . Contestants are also informed about the possibility of being inspected for aggressiveness and the organizer’s limit on those actions, denoted as and L. These contestants simultaneously choose effort and aggressiveness . Aggressiveness may hurt the reputation of contestants and ethically/morally burden them. Therefore, we assume that effort and aggressiveness are costly to contestants and are produced at cost and , which are common to both, with , , and with , , . Contestant j’s expected payoff for participating in the contest is given by
The payoff function, reflecting the expected benefit from winning the contest, contains the expected benefit from winning without and with an inspection occurring. If the organizer does not inspect the contestants, contestant j wins by outperforming contestant k; the output of the contestants determines their rank. If the organizer inspects the contestants, contestant j is disqualified and receives 3 if the test result shows j participates in more aggressiveness than the organizer has agreed to tolerate, . The probability of disqualification is . If contestant j is still qualified after the inspection, j automatically wins if contestant k is disqualified; otherwise, contestant j must outperform contestant k to win. FOCs for maximization of the objective function yield contestant j’s best response functions as follows
FOC with regard to
On the left side of the equation, the marginal benefit of aggressiveness comes from winning under the chance of not being inspected and the possibility of being inspected but still qualified. The aggressiveness strictly increases the player’s marginal benefit without inspection. However, the contestant faces a trade-off when an inspection is executed. Although aggressiveness improves the contestant’s performance, it also increases the probability of being disqualified. Therefore, the marginal benefit of aggressiveness to the contestant largely depends on the winning prize, inspection rate, limit on aggressiveness, and the accuracy of the inspection measure. All four factors simultaneously influence the contestants’ decision on aggressiveness. Holding the effort level constant, the winning prize, and the limit on aggressiveness can increase the marginal benefit of aggressiveness. The impact of the inspection rate on the marginal benefit is more nuanced and discussed below
FOC with regard to
From the FOC above, the probability of qualification is independent of effort, and the effort only affects the likelihood of winning. Holding the aggressiveness constant, the marginal benefit of effort increases with the winning prize, inspection rate, and limit on aggressiveness.
Utilizing the symmetry of the game,4 we impose symmetry on the first-order conditions to identify the contestant’s unique symmetric equilibrium with regard to the choice of aggression; this is implicitly characterized by the following:
Note that equilibrium aggression is independent of equilibrium effort. For the contest design problem we study, expression (2) must hold at a strictly positive and for local maximum to exist.5 We assume throughout the paper that this condition is satisfied. The equilibrium level of effort is implicitly characterized as follows:
Expression (3) shows that all three contest design parameters and the equilibrium level of aggressiveness jointly affect the optimal effort .
3.2. Contestants’ Behavior in Equilibrium
To model contest design, we must identify how contestants’ equilibrium behavior changes with the contest’s design parameters: S, , and L. Comparative static analysis of expressions (2) and (3) allow us to identify the impact of contest design parameters on contestants’ effort and aggressiveness.
Proposition 1.
A larger prize spread induces more aggressiveness while the inspection rate reduces it, and . Denote . When , increasing the limit on aggressiveness reduces the equilibrium level of aggressive behavior . Otherwise, .
Proposition 1 shows clearly how the contest design parameters S, , and L affect the optimal level of aggressiveness separately. The prize spread induces aggressive behavior while the inspection rate reduces it. comes from the second order condition for . The value of the condition reflects the impact of L on the marginal benefit of aggressiveness and determines the sign of . When lifting the limit on aggressiveness from zero up to a point, the marginal net benefit of aggressiveness decreases because of the marginal deterrence effect.6 In a contest, the limit on aggressiveness establishes a line for the punishment of aggressive behavior: crossing the line results in disqualification, while not crossing the line yields no punishment. Therefore, contestants reduce aggressive behavior as the net benefit of “crossing the line” decreases.
Naturally, when the measurement error follows a different distribution, the contestants’ decision on aggressiveness in response to the limit L will change. We use the figure below to visualize the condition determining the sign and the magnitude of the comparative statics and show how the inspection measures change this condition.
Figure 1 depicts the condition for . For both figures, when the curve is above the x-axis, , meaning the limit on aggressiveness can reduce the aggressive behavior. When the curve is below the x-axis, , meaning the limit on aggressiveness can induce more aggressive behavior. We find that the accuracy of the inspection measure changes the value of the condition and the shape of the curve. Figure 1a assumes that the measurement error follows the standard normal distribution, and Figure 1b doubles the standard deviation making the inspection measure less accurate.
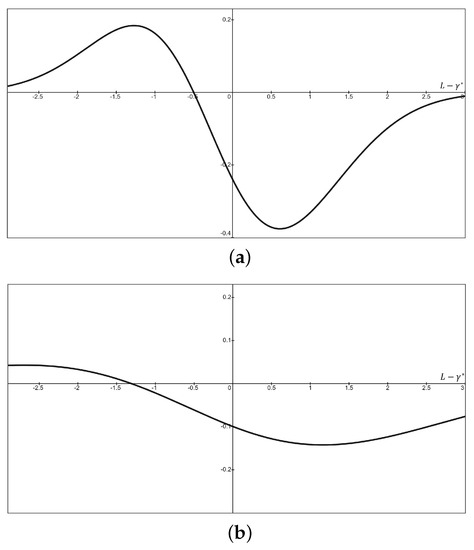
Figure 1.
The change in the value of where with different measurement errors. (a) , , the curve crosses the x-axis when ; (b) and , the curve crosses the x-axis when .
The curve in each figure crosses the x-axis (the point where the sign of changes) at a different point. The crossing point is closer to zero as the inspection measure becomes more accurate. The crossing point is when the measurement error follows the standard normal distribution and with the standard deviation equals 2. If ( for Figure 1b), the condition and . Moving from the left side of each figure, tolerating more aggressive behavior reduces such behavior until the crossing point. Given the same aggressiveness level, the limit on aggressiveness must be lower when the inspection measure is less precise (larger ). We verify this finding with simulations in Section 4.2.
The optimal effort is jointly determined by as expression (3) shows. The effort decreases as the probability of qualification, H, decreases. By applying Cramer’s Rule, we identify the sign of the comparative statics for .
Proposition 2.
Recall . Suppose
- (a)
- , contestants exert more effort when the organizer sets a higher prize spread or tolerates more aggressiveness, and . However, a higher inspection rate reduces effort, .
- (b)
- , all contest instruments motivate contestants’ effort, , , and .
- (c)
- , a higher inspection rate or limit on aggressiveness increases contestants’ effort, and . However, a higher prize spread reduces effort,
Proposition 2 identifies three cases for comparative statics of contestants’ effort . Similar to the condition for , those conditions reflect the change of the marginal benefit of aggressiveness. Unlike the effect on aggressiveness, in all three conditions, a higher limit on aggressiveness increases contestants’ effort, . Raising the limit on aggressiveness always encourages contestants’ effort because tolerating more aggressive behavior reduces the probability of disqualification, increasing the marginal benefit of effort at any given .
The impacts of the prize spread and the inspection rate on the effort are not monotonic. For example, the condition in case (c) indicates that when the marginal cost of aggressiveness increases slower than the marginal benefit of it, raising the prize spread reduces contestants’ effort because contestants find substituting costly effort with aggressive behavior more attractive; raising the inspection rate reduces the marginal benefit of aggressiveness, and therefore, motivates effort. However, this result from case (c) sounds counterintuitive because one indeed expects that the prize spread always inspires contestants’ effort.
In contrast, when the change in the marginal cost of aggressiveness is relatively high, as cases (a) and (b) show, raising the prize spread does motivate contestants’ effort because replacing effort with aggressive behavior increases too much of the marginal cost. Thus, contestants will only substitute effort with aggressive behavior. For the same reason, raising the inspection rate does not offer contestants strong incentives to replace aggressive actions with effort. Instead, it reduces contestants’ effort because the increased probability of disqualification raises the cost of effort.
Combining Propositions 1 with 2, we find that tolerating some aggressiveness always motivates the desired effort and can effectively restrain more aggressiveness when . Moreover, the inspection rate always reduces aggressiveness. On the other hand, it induces effort when the marginal cost of aggressiveness increases slower than the marginal benefit, , the substitution rate between effort and aggressive actions is high. On the other hand, the prize spread S always motivates aggressiveness and effort except for under case (c).
4. Optimal Contest Design
In this section, we identify the optimal contest design that maximizes the organizer’s expected payoff given an output value and inspection cost r. Then, we endogenize the organizer’s choice of three contest design instruments: the prize spread, the inspection rate, and the limit on aggressiveness. The organizer’s choices will determine contestants’ effort and aggressiveness according to the symmetric equilibrium identified in expressions (2) and (3). We begin the analysis by modeling the organizer’s contest design problem and then solve for the optimal choice of the contest design instruments, given the outside condition the organization faces ().
4.1. Organizer’s Problem
From the organizer’s perspective, aggressiveness benefits the organization through increased output. However, those actions are also detrimental to the organizer: damage may result in the organizer’s reputation declining; the organizer may face penalties and government sanctions or regulations afterward. The damages to the organizer caused by aggressiveness are denoted by , which is strictly increasing, strictly convex, and twice differentiable. To deter contestants from committing excessive aggressiveness, the organizer announces a limit on aggressiveness, L, and an inspection rate at the beginning of the contest. The cost of inspection per contestant is represented by a constant rate . If the contestant with the highest output is disqualified, the second-ranked qualified contestant wins by default.
The organizer holding the competition maximizes the expected payoff by modifying the contest design through the following instruments: the prizes for the winner and the loser, the inspection rate, and the limit on aggressiveness.
The organizer’s expected benefit comes from the total output value. The expected loss comes from the enforcement (inspection), contest awards, and contestants’ aggressiveness. With a probability , the organizer conducts an inspection costing r for each player. The organizer also expects to award the loser a prize of and to the winner. When both contestants are disqualified, the organizer reserves the winner’s prize and awards to both players. Contestants’ aggressiveness causes the expected damage, , to the organizer.
The payoff function is subject to the following constraints:
Expression (5) is the incentive compatibility constraint. In equilibrium, the identical contestants choose the effort and aggressiveness according to the equilibrium identified in Section 3.1.
The expected prize spread excludes the probability in which both contestants are disqualified. If at least one of the contestants is qualified, the organizer must provide to the contestant who produces the highest output and to the other contestant. Otherwise, both contestants are disqualified, and each receives . Therefore, the expected total prize awarded in the contest sums to , where we have
Inequality (7) is the participation constraint.
A contestant’s expected payoff must be higher than the reservation utility to ensure that joining the competition is better than any outside options. The inequality is binding at the optimum. The organizer bears the cost of the contestants’ effort and aggressiveness because contestants anticipate the equilibrium of the game and participate only if these are compensated in expectation.
Substituting constraints (5) and (8) into expression (4), the organizer’s objective function can be restated as
The first-order conditions of the organizer’s expected payoff function are
with regard to S
with regard to
with regard to L
First best. Since it is optimal to elicit effort to the point where the marginal cost equals the effort’s marginal benefit, the first-best effort can be derived from expression (9):
The same idea applies to the first-best aggressiveness,
Second best. Expression (11) shows that the first best outcome is not achievable because inspection to limit aggressiveness is costly. We denote the optimal prize spread, inspection rate, and tolerance level as , , and and obtain the following propositions from expressions (10)–(12).
Recall that Proposition 2 in Section 3.2 defines three cases for the comparative statics of , which are
- (a)
- ,
- (b)
- , and
- (c)
- .
where .
Under case (c), and must have the opposite sign, and according to expression (12), must be negative for an interior solution of L. However, the conditions and cannot occur. Suppose some S, , and L were chosen, resulting in case (c). In this case, both and are greater than their first-best outcome. By reducing S, the organizer would be strictly better off due to higher effort , less aggressiveness , and lower prize payouts. Therefore such a design cannot be optimal. Likewise, if the enforcement is presented, the case that and can neither occur. Because when both and are less than the first-best outcome, the organizer could effortlessly tolerate more aggressiveness to increase closer to the first-best outcome.
Next, we continue our analysis with cases (a) and (b) in Table 1. and must have the same sign under both conditions to guarantee interior solutions.7

Table 1.
(Organizer’s payoff) first-order conditions under three cases.
Proposition 3.
and at , , and . The contestants’ behavior under optimal design yields sub-optimal effort and a supra-optimal level of damaging behavior.
Proposition 3 is intuitive. Imperfect and costly inspection measurement prevents the contest from reaching the first-best outcome. Aggressive behavior displaces effort due to the trade-offs faced in contest design. As a result, the equilibrium effort is lower than the first-best outcome, and the equilibrium aggressiveness is greater than the first-best outcome.
Lemma 1.
Under cases (a) and (b), it is optimal to raise the prize spread as the output value α increases. A higher α can induce a higher inspection rate under case (b) but may reduce the inspection rate under case (a).
When the output is valued more, the organizer aims to induce more of it from contestants. Lemma 1 identifies conditions where the organizer can motivate the output by raising the prize spread. Increasing the inspection rate with the output value is also profitable under case (b) because a higher inspection rate can induce more effort while reducing aggressive behavior. However, in case (a), a higher inspection rate reduces effort and aggressive behavior. Therefore, the organizer may eventually reduce the inspection rate.
Figure 2 visualizes three cases specified in Proposition 2. As Figure 2a shows, case (b) covers the area between the top and the middle curves, and case (c) covers the space between the middle and the bottom curves. The middle curve drops to the bottom in Figure 2b as the inspection rate rises, expanding the case space (b). As a result, case (b) is more likely, and case (c) is less likely to occur when increases. This is because the higher inspection rate reduces the marginal benefit of aggressiveness, which diminishes the substituting effects between effort and aggressive actions. Contestants receive that signal and decide to put more effort rather than conduct more aggressive behavior.
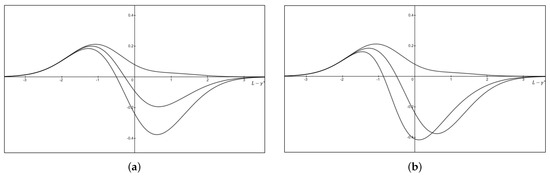
Figure 2.
Three conditions for comparative statics of effort, , . Curves from top to bottom on both figures are , , . We denote . In Figure 2b, the right side of the middle curve drops below the bottom curve as the inspection rate rises. (a) ; (b) .
Lemma 2.
The optimal limit on aggressiveness must be such that . is higher than the limit on the aggressiveness that minimizes it.
Although the organizer can impose a limit on aggressiveness to minimize it, the goal of the optimal contest design is not to minimize the aggressive behavior but to maximize the organizer’s expected profit. Tolerating aggressive behavior can induce more contestants’ effort and the final output. Thus, the organizer will raise the limit on aggressiveness until the cost from increased aggressive behavior equals the benefit from increased effort and output.
The crossing effects among the three optimal contest design variables are complicated and cannot be proved explicitly. Therefore, we use simulations to examine the optimal contest design.
4.2. Simulation
Simulations can further illustrate how the organizer’s decisions regarding the prize spread S, inspection rate , and limit on aggressiveness L optimally respond to changes in output value or inspection cost r. These simulations are conducted assuming the cost of aggressiveness to the organizer is , the cost of an inspection is or , and the output value increases from 1 to 10.
Observation 1.
When the cost of an inspection is sufficiently large, there exists an output value such that for , , for , . Both and increase with , and both increase rapidly in the neighborhood of .
Table 2 shows that when the output value is below the threshold, , the organizer optimally sets the prize spread low so that contestants have little incentive to engage in damaging activity, but also little effort incentive. In this parameter range, inspecting with any positive probability is not worth doing. As the output value rises, the output becomes more profitable, and the organizer is willing to provide a high S to motivate more effort. At the equilibrium, the effort is less than the first-best outcome, and the level of aggressiveness is higher than the first-best outcome. The optimal prize spread increasing from to 18 is observed to be discontinuous at . The optimal inspection rate in this simulation discretely increases from 0 to . For , welfare loss comes almost entirely from the inspection cost. The second-best effort and aggressiveness become very close to the first-best outcome. For , welfare loss is due to sub-optimal effort resulting from lack of incentive. When enforcement is in use, the optimal limit on aggressiveness is always set below the level of aggressiveness in equilibrium.

Table 2.
The optimal prize spread, inspection rate, limit on aggressiveness, and organizer’s payoff as the output value rises (, ).
In Table 3, the cost of inspection r is increased from 5 to 10. Comparing the simulation results with Table 2, the threshold for the organizer to inspect contestants lies at a higher output value, . Because the cost of an inspection is higher, the organizer chooses not to inspect contestants until the prizes motivate a high level of aggressiveness. Surprisingly, the optimal inspection rate in this simulation still increases suddenly from 0 to around when rises from 5 to 6, passing its critical value. In contrast, the optimal limit on aggressiveness is higher at this time due to the marginal benefit of an inspection.

Table 3.
The optimal prize spread, inspection rate, limit on aggressiveness, and organizer’s payoff as the output value rises (, ).
From the organizer’s perspective, aggressiveness can increase the output but potentially damage the organization. When the output value is not sufficiently high, the organizer weighs the negative impact more and wants to eliminate the most aggressiveness with the least cost. Therefore, the marginal deterrence power of an inspection must be high. Otherwise, the marginal benefit of an inspection cannot surpass its marginal cost.
The marginal deterrence power of an inspection is affected by the measurement error distribution. When the measurement error follows a normal distribution and the cheating level is high, the organizer has the incentive to raise the inspection rate because as the gap between and L shrinks, the unconditional probability of qualification, H, increases at an increasing speeduntil it reaches . On the other side, the deterrence power of an inspection can be significantly reinforced by limiting aggressiveness at a high or . Under a normal distribution, the unconditional qualification probability must be less than and more significant than the that yields the highest .
Observation 2.
When the distribution of inspection has a larger variability, the optimal inspection rate rises, and the optimal limit on aggressiveness decreases.
To examine how the inspection rate and limit on aggressiveness depend on the measurement error distribution, we double the standard normal distribution’s standard deviation. Hence, the measured extent of aggressiveness becomes noisier. Table 4 shows that the optimal inspection rate jumps to when the organizer inspects contestants. The organizer also tolerates less aggressiveness at each output value. Mathematically, when the measurement for aggressiveness is noisy, the inspection rate must be able to keep the unconditional probability of qualification H at the point where the marginal deterrence power for aggressiveness is sufficiently large; must be more negative in this case.

Table 4.
The optimal prize spread, inspection rate, limit on aggressiveness, and organizer’s payoff as the output value rises (, ).
Table 5 shows that increases with the cost of inspection; however, the optimal inspection rate remains at when the organizer engages in enforcement.

Table 5.
The optimal prize spread, inspection rate, limit on aggressiveness, and organizer’s payoff as the output value rises (, ).
5. Valueless Aggressiveness
Now we assume that aggressiveness has no market value, although such actions can improve contestants’ apparent relative performance. For example, in a promotion contest, firm managers have incentives to exaggerate their performance by manipulating their balance sheet, to make a division appear more profitable. However, such improved performance has no value to their firms in the long run and causes damages. We can rewrite the expression (9) as,
The first-best effort yields , and the first-best aggressiveness is 0 because such actions create no value to the organizer. The first-order conditions of the organizer’s expected payoff function become
with regard to S
with regard to
with regard to L
We obtain the following propositions under cases (a) and (b) in Proposition 2.
Proposition 4.
At , , and , the contestants’ behavior under optimal design yields sub-optimal effort and a supra-optimal level of damaging behavior.
Using the same simulation setting as in the previous section, we find that the optimal inspection rate is higher in the valueless case than in the original case when aggressiveness contributes to the output. In Table 6, the critical value of output is still 4, but the optimal inspection rate under increases from around in the original case to above . is significantly lower in this case.

Table 6.
The optimal prize spread, inspection rate, limit on aggressiveness, and organizer’s payoff as the output value rises (, ).
Proposition 5.
is a corner solution for the valueless aggressiveness case.
In the valueless case, the organizer does not tolerate any aggressiveness. Positive aggression will occur in the equilibrium, but a zero-tolerance policy is optimal. When enforcement is presented, the marginal benefit of increased effort is small because is close to . The marginal cost from increased aggressiveness outweighs the marginal benefit from the increased effort at any L. L fails to reduce close enough to because it requires to be more negative, but is bounded by zero. Thus, we obtain a corner solution for —the organizer does not tolerate any aggressiveness under the optimal contest design.
This result explains why we observe that under some circumstances, the organizer set the limit on aggressiveness to 0. In the valueless case, the optimal limit must be set lower than the first-best outcome, 0. Since the limit is bounded by 0, it is optimal for the organizer not to tolerate aggressive behavior. This may explain some tendency toward zero tolerance in athletic competition. If the entertainment value of the competition is not tied to absolute performance, doping or other aggressive behavior generates no value.
6. Conclusions
When aggressive behavior by competitors in a contest causes harm to the contest organizer, an essential aspect of contest design is the mechanism to constrain this behavior to mitigate the damages. We model this by assuming the contest organizer sets a limit on measured aggressiveness, which is subject to measurement error. A player will be disqualified, combined with a probability of inspection. In addition, of course, the prize at stake in a contest motivates aggressiveness along with effort, and contest design then entails choosing these three design parameters.
One exciting aspect of contestant behavior in this environment is that, under some circumstances, aggressiveness may decrease as the qualification limit increases. It is never optimal to set the limit such that this holds. In general, we find it optimal to limit aggressiveness (weakly) below the first-best level of such behavior. This is positive when aggressiveness does generate output, but zero tolerance is optimal when aggressive behavior is purely damaging. The equilibrium behavior involves contestants engaging in supra-optimal aggressiveness while exerting suboptimal effort. This is because of the tradeoff between motivating effort with a higher prize spread against the cost of inspections needed to constrain aggressive behavior. Broadly, we find that optimal design entails either very under-powered incentives—a minimal prize—and far-below-optimal effort, which is optimal when the value of output is low relative to the cost of inspections and damage from aggressiveness, or strong incentives and a very costly inspection regime. Interestingly, optimal contest design entails a higher inspection rate and a lower qualification limit on the level of aggressiveness, as the inspection process is subject to more significant errors.
Our model formalizes how enforcement must respond to constrain aggressive behavior as competitive incentives are strengthened to elicit greater effort. For example, we identify the optimal contest design under three scenarios: the output value is low, the output value is high, and the aggressive behavior has no output value. Consider a setting such as a school, where it is becoming more common to financially reward top-performing teachers based on results from high-stakes tests of students. Possibly damaging aggressive behavior in such a context may range from spending excessive time drilling students on test-specific topics (to the detriment of learning and student or family satisfaction with school) to unwarranted disciplinary measures to remove students from a class when the teacher expects a student will perform poorly. In the absence of high-powered incentives, such as when strong class performance is rewarded with verbal recognition but not monetary compensation, it may not be optimal to engage in enforcement against such aggressiveness because the teachers’ disutility of aggressive behavior adequately constrains it. However, systematic enforcement resulting in a significant probability of disqualification becomes optimal if the value of the effort motivated by competition (which would not be present in the absence of high prizes) is sufficient to warrant the shift. As the value of the output generated by teachers’ performance increases, it becomes optimal to raise the qualification limit and increase the enforcement. If the improved test grades through damaging aggressive behavior have no value to the school, then the school does best to adopt the “zero-tolerance” policy for such behavior.
Consider commercial banks such as Wells Fargo. The more products a customer has with the bank, the more information it has on that customer, allowing for better credit, products, and pricing decisions. Convincing consumers to use more bank products is a priority of sales teams. After the 2008 financial crisis, the U.S. market was reviving for several years, which means the employees’ output value is higher. Wells Fargo highly incentivizes its sales team to meet cross-sell and customer-service targets. Unfortunately, the bank’s managers tolerated some damaging aggressive behavior—illegal sales practices, such as creating a fake address using the customer’s cell phone number and carrier. However, when a high prize is set to motivate sales, a high inspection rate must be adopted. Otherwise, the extent of aggressiveness will grow. For example, Wells Fargo did not inspect sales more intensively and 200 million accounts were opened without customers’ consent.
We must acknowledge that this paper has its limitations. First, contests have different purposes. Our optimal design is not for player selection but for inducing the optimal output for the organizer, so we do not assume heterogeneous players. Secondly, this model can be extended to an N-player game. We use a simulation to show how optimal aggressiveness and effort respond to the change of limit on aggressiveness (See Figure A1 in Appendix C: The N-Player Game). Future research can further identify the comparative statics for contestants’ game and the optimal contest design. A researcher may adopt a different modeling method for this extension.
Author Contributions
Conceptualization, S.M.G.; methodology, S.M.G. and Y.H.; software, Y.H.; validation, S.M.G. and Y.H.; formal analysis, Y.H.; investigation, Y.H.; resources, Y.H.; writing—original draft preparation, Y.H.; writing—review and editing, Y.H. and S.M.G.; visualization, Y.H.; supervision, S.M.G.; project administration, S.M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicatable.
Conflicts of Interest
The author, Ye Hong, declares that she has no relevant or material financial interests that relate to the research described in this paper, “Optimal Contest Design when Policing Damaging Behavior.” The author, Scott M. Gilpatric, declares that he has no relevant or material financial interests that relate to the research described in this paper, “Optimal Contest Design when Policing Damaging Behavior.”.
Appendix A. Proofs
Proof.
We first consider the impact on aggressiveness. Note that as Equation (2) shows, in equilibrium, aggressiveness is independent of the effort . To find the impact of exogenous variables () on we apply the implicit theorem.
The denominator must be negative to guarantee an interior solution. The numerator represents the marginal benefit of participating in the contest normalizing the prize spread to 1, which must be positive to guarantee an interior solution of . Otherwise, contestants do not cheat—the optimal damaging action is 0.
is the probability of qualification given the contestant is inspected. The whole numerator is negative, and thus, the sign of is negative. Contestants commit less aggressiveness as the inspection rate rises, which is intuitive because a higher inspection rate elevates the marginal cost of aggressiveness (or the marginal benefit of qualification).
The sign of depends on A, in particular, the slope of the measurement error’s probability density function, . The measurement error follows a symmetric unimodal distribution with density monotonically decreasing as distance from the mean increases, thus, will be positive and then negative as L rises. At low L, can be negative, because the probability of qualification, H, will be small and will be large. As the organizer extends the limit on aggressiveness further, the probability of qualification increases, but the impact of aggressiveness on the probability of qualification diminishes ( becomes smaller and even negative). Eventually, becomes positive. Since the sign of changes from negative to positive as the organizer raises L, a yielding the minimum must exist. □
Proof.
Hessian Matrix
To guarantee a maximum of , it must have and . Because , we find .
The direct impact of exogenous variables on aggressiveness are given by
The direct impact of exogenous variables on effort are given by
Compare the equations above, we find
Mathematically solving the comparative statics for .
when ; otherwise, .
when . Otherwise, . □
Proof.
Suppose the organizer sets the S such that when . Contestants’ symmetric equilibrium (expressions (2) and (3)) becomes
The is obtained if . Since , must be greater than , and .
Note that we have proved when the S that induces is such that . Further, when enforcement is presented, is lower than under condition (a), holding other things constant. Therefore, in order for , i.e., effort above the first best, would require S be set above the level that would induce in the absence of enforcement or L be raised to a certain level. So it cannot be the case that and (i.e., supra-optimal and sub-optimal ), because the organizer could increase toward the optimal at a negative cost by reducing enforcement.
Both and are positive under condition (a). Thus, according to Equation (10), and must have the same sign. Therefore, it must be the case that and . The optimal , , and induce and .
In condition (b), both and must be positive due to expression (11). □
Proof.
From expression (11) we can see that if r is sufficiently large such that . Holding everything constant but increasing to , increases while decreases. becomes more negative under condition (a). The organizer does not have direct incentives to inspect contestants and does not need to consider setting L.
Meanwhile, as expression (10) shows, a larger output value makes . It is optimal for the organizer to raise , which creates an indirect incentive for inspection because the increased motivates more and . When , increasing motivates more aggressiveness than effort because the marginal cost of effort is higher. Thus, the marginal benefit of inspection increases with , and once the marginal benefit reaches r, we obtain an interior solution of . To reduce the expected cost of inspection, L must be set at the value that yields the largest .
Unlike in condition (a), a higher output value has both direct and indirect incentives for the organizer to raise the inspection rate under condition (b). Holding everything constant but increasing , becomes more positive under condition (a) since . The organizer has direct incentives to inspect contestants. Since increases with , the marginal benefit of inspection increases with . The organizer also has indirect incentives to inspect contestants. □
Proof.
This follows directly from the fact that and are positive.
Based on expression (12), the sign of must be the same as at the optimum. means the extent of aggressiveness exceeds the minimum. Since decreases and then increases with the limit on aggressiveness, the optimal limit is higher than the limit that yields .
If , expression (12) is greater than zero. The organizer will raise until . Again, is greater than that produces the minimal . □
Proof.
By expression (14), and must have the same sign. Therefore, it must be the case that and . The optimal , and induce and . □
Appendix B. Comparative Statics When δ Follows a Uniform Dist
Suppose follows a uniform distribution that is symmetrical at 0. The contest design instruments have the following impact on player j’s optimal effort and misconduct level.
Hessian Matrix
, because and so that .
The direct impact of exogenous variables on aggressiveness are given by
The direct impact of exogenous variables on effort is given by
Compare the equations above, we find
, and .
Mathematically solving the comparative statics for .
If , L has no impact on .
.
Replace with B. We find when
We obtain . As increases from 0 to infinity, decreases from 1 to 0. Since , H reaches the minimum when (). yields . Thus, guarantees .
.
and verifies that tolerating more aggressiveness and increasing the prize spread can motivate more effort. The sign of depends on H and .
Appendix C. The N-Player Game
In this section, we extend the two-player contest to N players, where . We denote as a binomial function which represents the probability of n out of players are qualified for the contest. The distribution of the output shock for each player is , and we use to show the difference between two players’ effort and aggressive actions, .
The contestant j maximizes his expected payoff over effort and hazardous actions. If no inspection is conducted, contestant j must outperform the rest contestants. If the organizer conducts an inspection and contestant j is still qualified, he will compete with the other qualified contestants on the final output.
Assuming all contestants are identical, applying symmetry in the first-order conditions for expression (A12).
We use one example below to illustrate that the limit on aggressiveness still reduces aggressiveness and motivates effort when the number of contestants is more than two.
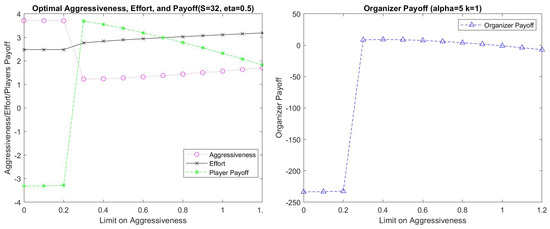
Figure A1.
The Optimal Aggressiveness, Effort, Each Contestant’s and Organizer’s Payoff Changes with the Limit on Aggressiveness (the Number of Contestants is Five).
Figure A1 shows that the organizer’s payoff is maximized if the prize is set at 32 and the limit on aggressiveness is at 0.4 given the inspection rate is 0.5, the output value is 5, and the cost of an inspection is 1. As Lemma 2 suggests, the optimal limit on aggressiveness is higher than the limit that minimizes it.
Notes
| 1 | In Proposition 2, the comparisons between how fast the marginal cost of aggressive actions changes with such actions, , and how quickly the marginal benefit changes with it, , reflect the incentive for aggressive actions. |
| 2 | This is contrary to the notion that one should utilize a tool less often when it is less precise. |
| 3 | is sufficiently large so that contestants always participate in the contest. However, the organizer will decide whether to hold the contest. |
| 4 | A common assumption in the tournament. |
| 5 | guarantees the local maximum because the second order condition for is less than 0 and the Hessian determinant for is greater than 0 (See the proof for Proposition 2 in Appendix: proofs). This condition indicates that the marginal cost of aggressiveness increases faster than the marginal benefit of such actions to contestants. We later denote as A. |
| 6 | Gilpatric and Reiser [2] find that if the enforcement prohibiting misconduct cannot effectively deter such conduct, that enforcement is not optimal. Their finding is analogous to findings about “marginal deterrence” in the enforcement literature. The notion has been articulated by Marchese di Beccaria [14], Shackleton [15], and Bentham [16] as “to induce a man to choose always the least mischievous of two offenses; therefore, where two offenses come in competition, the punishment for the greater offense must be sufficient to induce a man to prefer the less”. Stigler [17] originated the term marginal deterrence, which was later developed by Wilde [18], Mookherjee and Png [19], Shavell [20], and Friedman and Sjostrom [21]. They studied conditions under which marginal deterrence requires gradual penalties. Mookherjee and Png [22] extend the model to a general setting in which the activity level is a continuous variable, and individuals derive heterogeneous benefits. These researchers show that it is optimal to establish marginal expected penalties everywhere less than the marginal harm. |
| 7 | The corner solutions such as and non-interior solutions such as S tends to infinity do not contribute much to our contest design, thus, we focus on the conditions that can produce interior solutions. |
| 8 | If we add more digits to , , or , can be improved and falls under . For example, when , , and , and . The same issue occurs when . |
References
- Lazear, E.P. Pay equality and industrial politics. J. Political Econ. 1989, 97, 561–580. [Google Scholar] [CrossRef]
- Gilpatric, S.M.; Reiser, C.M. Why Zero Tolerance of Misconduct Is Undesirable in Contests. Econ. Inq. 2017, 55, 1145–1160. [Google Scholar] [CrossRef]
- Berentsen, A. The economics of doping. Eur. J. Political Econ. 2002, 18, 109–127. [Google Scholar] [CrossRef]
- Haugen, K.K. The performance-enhancing drug game. J. Sports Econ. 2004, 5, 67–86. [Google Scholar] [CrossRef]
- Konrad, K.A. Tournaments and Multiple Productive Inputs: The Case of Performance Enhancing Drugs; Technical report; IZA Discussion Papers: Bonn, Germany, 2005. [Google Scholar]
- Curry, P.A.; Mongrain, S. Deterrence in rank-order tournaments. Rev. Law Econ. 2009, 5, 723–740. [Google Scholar] [CrossRef]
- Kräkel, M. Doping and cheating in contest-like situations. Eur. J. Political Econ. 2007, 23, 988–1006. [Google Scholar] [CrossRef]
- Gilpatric, S.M. Cheating in contests. Econ. Inq. 2011, 49, 1042–1053. [Google Scholar] [CrossRef]
- Mohan, V.; Hazari, B. Cheating in contests: Anti-doping regulatory problems in sport. J. Sports Econ. 2016, 17, 736–747. [Google Scholar] [CrossRef]
- Music, K. The undesirable consequences of doping regulations: Why stricter efforts might strengthen doping incentives. J. Sports Econ. 2020, 21, 281–303. [Google Scholar] [CrossRef]
- Becker, G.S. Crime and punishment: An economic approach. J. Political Econ. 1968, 76, 169–217. [Google Scholar] [CrossRef]
- Ehrlich, I. The deterrent effect of criminal law enforcement. J. Leg. Stud. 1972, 1, 259–276. [Google Scholar] [CrossRef]
- Polinsky, A.M.; Shavell, S. The economic theory of public enforcement of law. J. Econ. Lit. 2000, 38, 45–76. [Google Scholar] [CrossRef]
- Marchese di Beccaria, C. An Essay on Crimes and Punishments; Newbery, E., Ed.; Available online: https://archive.org/details/essayoncrimespun00becc/page/86/mode/2up (accessed on 2 May 2023).
- Shackleton, R. The Spirit of Laws; Dodesley, P., Ed.; Printed for J. Almon, opposite Burlington-House, Piccadilly: London, UK, 1767; Available online: https://catalog.hathitrust.org/Record/008603896 (accessed on 2 May 2023).
- Bentham, J. The Collected Works of Jeremy Bentham: An Introduction to the Principles of Morals and Legislation; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Stigler, G.J. The optimum enforcement of laws. J. Political Econ. 1970, 78, 526–536. [Google Scholar] [CrossRef]
- Wilde, L.L. Criminal choice, nonmonetary sanctions, and marginal deterrence: A normative analysis. Int. Rev. Law Econ. 1992, 12, 333–344. [Google Scholar] [CrossRef]
- Mookherjee, D.; Png, I.P. Monitoring vis-a-vis Investigation in Enforcement of Law. Am. Econ. Rev. 1992, 3, 556–565. [Google Scholar]
- Shavell, S. A note on marginal deterrence. Int. Rev. Law Econ. 1992, 12, 345–355. [Google Scholar] [CrossRef]
- Friedman, D.; Sjostrom, W. Hanged for a sheep: The economics of marginal deterrence. J. Leg. Stud. 1993, 22, 345–366. [Google Scholar] [CrossRef]
- Mookherjee, D.; Png, I.P. Marginal deterrence in enforcement of law. J. Political Econ. 1994, 102, 1039–1066. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).