Abstract
Ignoring strategic interactions among final goods producers, the extant theoretical literature shows that lower costs of imported inputs increase the exports of the final goods using those inputs. Hence, it does not explain the empirically relevant positive relationship between the costs of imported inputs and the export of the final goods. We use a simple Cournot duopoly (i.e., duopoly quantity competition) with homogeneous products to show that if the exporters differ in input coefficients, lower costs of imported inputs may increase or decrease the exports of the final goods. Thus, we argue that strategic interdependence among the exporters can be an important factor for the positive relationship between lower costs of imported inputs and the export of the final goods. We further show that a lower cost of imported inputs may reduce the consumer surplus, total profits of the exporters, and world welfare. We also show the implications of a Bertrand duopoly (i.e., duopoly price competition) with horizontal product differentiation for our analysis.
JEL Classification:
D43; F23; L13; L23
1. Introduction
The empirical literature, which we review in the next section, shows that lower costs of imported inputs may increase or decrease the exports of the final goods using those inputs ([1,2,3,4,5]) 1. However, ignoring strategic interactions among final goods producers, the extant theoretical literature explains only the negative relationship between the costs of imported inputs and the export of the final goods using those inputs. The lower costs of imported inputs increase the exports of the final goods either by improving the productivities of the final goods producers or by diffusing knowledge about modern technologies ([1,2]) 2.
There is no theoretical paper explaining the positive relationship between the costs of imported inputs and the export of the final goods. We fill this gap with a simple explanation based on strategic interdependence among the exporters with different input coefficients 3.
We consider a simple Cournot duopoly (i.e., a duopoly quantity competition) with homogeneous products in which firms decide simultaneously whether to export. We normalise the profits under no export to zero. If a firm exports, it needs to incur a fixed cost of exporting 4. The firms differ in terms of input coefficients, and they import inputs from a competitive world market. In this framework, we discuss how a lower cost of imported inputs affects the firms’ equilibrium outputs (i.e., export volumes) and the incentive for export.
We show that a lower cost of imported inputs reduces the low-productive exporter’s incentive for exporting the final goods and the amount it exports. However, a lower cost of imported inputs may increase or decrease the high-productive exporter’s incentive for exporting the final goods and the amount it exports.
The lower costs of imported inputs increase cost efficiency for both firms. However, higher cost efficiency for an exporter tends to increase its output, profit, and incentive for export but tends to reduce the competitor’s output, profit, and incentive for export. Since the low-productive exporter uses more inputs than the high-productive exporter, a lower cost of imported inputs benefits the low-productive exporter more than the high-productive exporter.
If the gain of the low-productive exporter following a lower cost of imported inputs is significantly higher than that of the high-productive exporter, which happens if the productivity difference between the exporters is large, the lower cost of imported inputs may decrease the high-productive exporter’s output, profit, and incentive for export. Hence, if the productivity difference between the exporters is large, there may be a positive relationship between the costs of imported inputs and the export of the final goods for the high-productive exporter.
If the productivity gap between the exporters is not large, the lower cost of imported inputs increases the high-productive exporter’s output, profit, and incentive for export, thus showing a negative relationship between the costs of imported inputs and the export of the final goods.
However, following a lower cost of imported inputs, the higher benefit for the low-productive exporter compared to the high-productive exporter always increases the low-productive exporter’s output, profit, and incentive for export. Hence, there is always a negative relationship between the costs of imported inputs and the export of the final goods for the low-productive exporter.
We also show that a lower cost of imported inputs may reduce the consumer surplus, total profits of the exporters, and world welfare.
The extant theoretical literature ([1,2]), which explains only the negative relationship between the costs of imported inputs and the export of the final goods, ignores strategic interactions among the exporters. As a result, unlike our paper, where the relative cost reduction of the exporters is the important factor, in those papers, the own-cost reduction becomes the important factor. Hence, in those papers, a lower cost of imported inputs increases the exports of all exporters.
It is evident from our analysis that if there is a monopolist exporter in equilibrium, thus avoiding strategic interdependence among the exporters in equilibrium, the relationship between the costs of imported inputs and the export of the final goods is always negative in our analysis, as in [1,2].
We show that the relationship between the costs of imported inputs and the outputs (i.e., export volumes) shown under a Cournot duopoly holds under a Bertrand duopoly (i.e., duopoly price competition) with horizontal product differentiation. However, unlike with Cournot competition, the relationship between the costs of imported inputs and the incentive for exporting the final goods is negative for both firms under Bertrand competition. This happens because “only the low-productive firm exports” cannot be an equilibrium under Bertrand competition due to the following reason.
Under Cournot competition, if the low-productive firm exports, it may not leave enough residual demand to make exporting by the high-productive firm also profitable. Hence, exporting by the low-productive firm only can be an equilibrium under Cournot competition. However, under Bertrand competition, the high-productive firm’s ability to undercut price is always higher than that of the low-productive firm. Hence, we do not get an equilibrium under Bertrand competition where only the low-productive firm exports. Therefore, along with strategic interdependence, the type of product market competition is also important for the relationship between the costs of imported inputs and the export of the final goods.
We show that the implications for consumers and world welfare may also be different under Bertrand competition compared to Cournot competition. Unlike Cournot competition, a lower cost of imported inputs does not reduce the consumer surplus and world welfare under Bertrand competition.
As explained above, the positive relationship in our analysis is due to the relative benefits of the exporters following a lower cost of imported inputs. This is different from [5], where financial constraints or exposure to uncertainty in the international market following importing or the time lag in learning from importing reduces exports.
There is a vast amount of the literature following [6] that shows the relationship between firm productivity and exports. In contrast to that literature, we show how firm productivity affects the relationship between the costs of imported inputs and the export of the final goods.
The remainder of the paper is organised as follows. We provide a review of the relevant literature in Section 2. We introduce our model in Section 3 under Cournot competition between the exporters with homogeneous products. Section 4 derives the relationship between the costs of imported inputs and the export of the final goods. Section 5 shows the implications for consumers, the total profits of the exporters, and world welfare. Section 6 concludes. We show the implications of Bertrand competition with horizontal product differentiation in the Appendix A, Appendix B and Appendix C.
2. Literature Review
Kasahara and Lapman [1] consider heterogeneous final goods producers who simultaneously decide whether to export their products and whether to use imported inputs. They develop a theoretical model with monopolistic competition in the final goods market. Using the theoretical model, they develop a structural empirical model, which they estimate with Chilean plant-level data for a set of manufacturing industries. They show that policies that prevent the importation of inputs can affect the exportation of the final goods adversely.
Bas and Strauss-Kahn [2] develop a theoretical model with monopolistic competition in the final goods market and predict that importing more varieties of imported inputs increases the export scope, i.e., imported inputs may help to overcome and reduce the fixed costs of exporting, and low-priced imported inputs may increase expected export revenue. They show the empirical validity of these predictions with firm-level French Customs data.
Using Chinese data, Feng and Swenson [3] show that firms that increased the use of imported inputs increased their exports. They find this evidence by measuring the import activity through the transition to import, higher expenditure on imported inputs, and an increase in the range of imported inputs.
Aristei et al. [4] find that past importing activities increase productivities and product innovations, which help to increase exporting activities. However, the positive effect of past importing status on the current probability of exporting disappears when controlled for firms’ productivity and product innovations.
Using a panel of Chinese manufacturing firms, Elliott et al. [5] show a negative relationship between export and import—previous import experience reduces the propensity to export, and previous export experience reduces the likelihood of import.
Fan et al. [7] develop a theoretical model to see an exporter’s price and quality choice when importing inputs. They test the theory with disaggregated Chinese data to show that a lower tariff on imported inputs increases the quality of the export. They also show that if the scope for quality differentiation is large, a lower tariff on the imported inputs increases the price of the export by increasing the quality of the exports significantly. However, if quality differentiation is small or the products are homogeneous, a lower tariff on the imported inputs reduces the price of the export due to a higher amount of export.
Although the above-mentioned empirical papers show a mixed relationship between import and export, the theoretical models in [1,2,7] explain a negative relationship between the costs of imported inputs and export when there is not much scope for product differentiation. In contrast, we show under Cournot competition with homogeneous goods that there can be a negative or positive relationship between the costs of imported inputs and the export of the final goods.
3. The Model
Assume that two domestic firms, firm 1 and firm 2, export a homogeneous good to the world market and compete like Cournot duopolists. We assume for simplicity that the firms export their entire outputs. Our conclusion will not be affected if the firms export and sell their products in the domestic country as long as the markets are segmented and the firms can charge different prices in different markets. Assume that if a firm wants to export, it needs to incur a fixed-cost G (see, e.g., [8,9]).
Both firms use an imported input to produce their outputs. Assume that firm 1 requires one unit of the input to produce one unit of its output, while firm 2 requires λ units of the input to produce one unit of its output, where . Since the input-productivities are 1 and for firm 1 and firm 2, respectively, firm 2 is more productive than firm 1. We call firm 1 the “low-productive” firm and firm 2 the “high-productive” firm. The constant per-unit cost of importing the input is c > 0. For simplicity, we assume that no other inputs are required to produce the final goods.
Assume that the inverse market demand function is
where a > 0 is the demand intercept, P is the price, and q is the total output.
P = a − q,
We consider the following game. At stage 1, firms decide whether to export or not. At stage 2, firms choose their outputs conditional on the decision in stage 1, and the profits are realised. If both firms decide to export in stage 1, they compete like Cournot duopolists in the world market. If only one of them decides to export, the exporting firm is a monopolist. If neither firm decides to export, there will be no export. We solve the game through backward induction.
We assume for simplicity that , which will ensure that both firms will always export for G = 0. So, a firm may become a monopolist only for G > 0.
Table 1 summarises the profits of the firms under export and no export. and show the equilibrium profits of firms 1 and 2, respectively, when both firms export. and show the respective equilibrium profits of firms 1 and 2 when only firm 1 exports and only firm 2 exports, respectively.

Table 1.
Payoffs of the firms.
If both firms decide to export, firms 1 and 2 maximise the following profit functions respectively to determine their outputs:
We get the respective equilibrium outputs of firms 1 and 2 as:
The respective equilibrium profits of firms 1 and 2 are
If only the ith firm, i = 1, 2, decides to export, the ith firm maximises the following profit function to determine its output:
where if i = 1 and if i = 2. We get the equilibrium output of the ith firm as
The corresponding equilibrium profit of the ith firm is
If a firm does not export, its profit is zero.
Lemma 1.
Consider either or and . Since , we get the following equilibria:
(a) Both firms export for .
(b) Only firm 2 (the high-productive firm) exports for and .
(c) Either firm 1 (the low-productive firm) or firm 2 (the high-productive firm) exports for 5.
(d) No firm exports for .
Proof.
See Appendix A. □
As shown in Appendix A, all the possibilities shown in Lemma 1 occur if either or and . We assume in the following analysis that these conditions hold. If we consider and , we will not get the case (c) of Lemma 1. Since the implication of and follows easily from our analysis, we will briefly mention its implications.
Figure 1 shows the situations mentioned in Lemma 1.
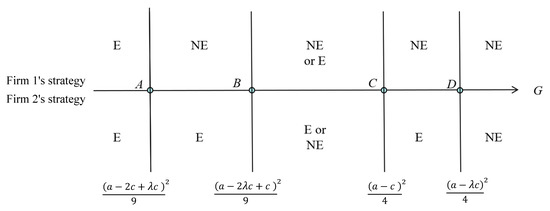
Figure 1.
Export decisions when either or and .
4. The Effects of a Lower Cost of Imported inputs
Now we want to see the effects of a lower cost of imported inputs, i.e., the effects of a lower c, on the firms’ incentive to export and export volumes.
We get
Given these conditions, Figure 2, which is drawn for , 6 shows how the ranges of G over which different equilibria occur change. The solid lines in Figure 2 show the situations under initial c, and the dashed lines show the situations after a reduction in c. Figure 2 helps to prove the following result.
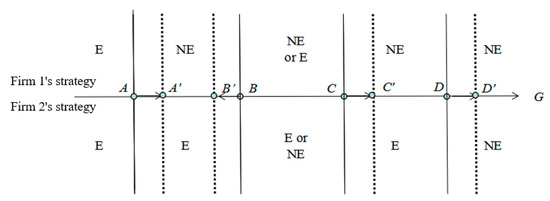
Figure 2.
Changes in the export decisions due to a lower c when either or and , and .
Proposition 1.
- (a)
- A lower cost of imported inputs, i.e., a lower c
- (i)
- Increases the possibility of export by firm 1, but
- (ii)
- May increase or decrease the possibility of export by firm 2.
- (b)
- A lower cost of imported inputs
- (i)
- Increases the volume of exports for firm 1, but
- (ii)
- May either increase or decrease the volume of exports for firm 2.
Proof.
See Appendix B. □
The reason for the above result is explained in the introduction. A lower cost of imported inputs increases the cost efficiency for both firm 1 (the low-productive exporter) and firm 2 (the high-productive exporter). On the one hand, higher cost efficiency for a firm helps to increase its output, profit, and incentive for export. On the other hand, it helps to reduce the competitor’s output, profit, and incentive for export. However, the benefit to firm 1 following a lower cost of imported inputs is more since it uses more inputs per unit of output. Hence, if firm 1’s input coefficient is significantly higher compared to firm 2 (i.e., ), a lower cost of imported inputs may decrease the output, profit, and the possibility of export for firm 2. However, the higher gain for firm 1 following a lower cost of imported inputs increases its output, profit, and the possibility of export.
As mentioned above, if we consider and , we will not get Lemma 1(c). In this situation, point C in Figure 1 and Figure 2 will be to the left of point B. Hence, unlike the case of or and , which we considered in Figure 1 and Figure 2, we will not get the positive relationship between the costs of imported inputs and the high-productive firm’s incentive to export. However, the results for the relationship between the costs of imported inputs and the export volumes will remain.
It is worth mentioning that if—unlike our structure in which the marginal cost difference is due to the difference in input coefficients—the firms have the same input coefficients and face the same input costs but differ in terms of other marginal costs, the positive relationship shown above does not occur. This is because the lower costs of imported inputs in this situation reduce the marginal costs of both firms by the same amount, and the own-cost effect dominates the competitor’s cost effect.
5. The Implications for Consumer Surplus, Total Profits, and World Welfare
We show in this section that an implication of Proposition 1 is that a lower cost of imported inputs may reduce the consumer surplus, total profits of the exporters, and world welfare. Of course, there will be situations where a lower cost of imported inputs increases the consumer surplus, total profits of the exporters, and world welfare. For example, it happens trivially if a lower c changes the equilibrium from (NE, NE) to (NE, E). However, we focus here on the more interesting case where a lower c decreases the consumer surplus, total profits of the exporters, and world welfare.
For our discussion, consider the case where G is between B’ and B or between C and C’ in Figure 2. In this situation, the equilibrium is (NE, E) with a higher c, but it could be (E, NE) with a lower c. The total output under (NE, E) is , while the total output under (E, NE) is , where . Hence, we get for . Since the consumer surplus for the above analysis is , it implies that a lower c in this situation may make the consumers worse off by changing the equilibrium strategies.
If a lower c changes the equilibrium strategies, it may also reduce the total profits of firms 1 and 2. For example, as considered in the above paragraph, if a lower c changes the equilibrium from (NE, E) to (E, NE), the total profits of firms 1 and 2 will change from to , and for .
Since a lower c may reduce the consumer surplus and the total profits of firms 1 and 2 when it changes the equilibrium from (NE, E) to (E, NE), it may reduce world welfare, which is the sum of consumer surplus and the total profits of firms 1 and 2 (as the input market is assumed to be competitive) 7. This happens because if a lower cost of imported inputs changes the equilibrium from (NE, E) to (E, NE), it creates production inefficiency in the industry by shifting the exporting decision from the high-productive firm to the low-productive firm.
If we have considered the situation where a lower cost of imported inputs changes the equilibrium from (NE, E) to (E, E), it will increase consumer surplus (due to higher competition), but it may create an ambiguous effect on the total profits of the firms (due to the opposite effects of competition and the lower cost of imported inputs). The effects of a lower cost of imported inputs on world welfare can also be ambiguous.
If a lower c does not change the equilibrium strategies, it will make the consumers better off, even if a lower c may reduce the equilibrium output of firm 2, which may happen under (E, E) 8. For equilibrium (E, E), we have seen a negative (ambiguous) relationship between the cost of imported inputs and export volume for firm 1 (firm 2). If we look at the effect of a lower c on the total outputs of firms 1 and 2, we get < 0. Hence, a lower cost of imported inputs will reduce the price in the export market by increasing the total outputs of the exporters and, therefore, will make the consumers better off, although it may reduce the equilibrium output of firm 2.
If a lower c does not change the equilibrium strategies, it may, however, reduce the total profits of the firms. Consider the equilibrium (E, E). In this situation, the total profits of firms 1 and 2 are . We get for and , implying that a lower c reduces the total profits of firms 1 and 2 in this situation 9. However, if either or and .
If the equilibrium is (E, E), we get that a lower c increases the consumer surplus but may reduce the total profits of firms 1 and 2. The world welfare for equilibrium (E, E) is . We get for and , implying that a lower c reduces world welfare in this situation. We get if either or and .
If a lower cost of imported inputs does not change the equilibrium, it can still reduce world welfare, and this happens because a lower cost of imported inputs creates production inefficiency. A lower cost of imported inputs reduces the marginal cost of the low-productive firm more than the high-productive firm, which helps the low-productive firm to steal business from the high-productive firm. This effect is similar to [10], where a marginal cost reduction in the high-cost firm may reduce welfare.
The following proposition follows from the above discussion.
Proposition 2.
(a) A lower cost of imported inputs may reduce the consumer surplus, total profits of the exporters and world welfare by changing the equilibrium strategies.
(b) If a lower cost of imported inputs does not change the equilibrium, it increases the consumer surplus but may reduce the total profits of the exporters and world welfare.
6. Conclusions
While the empirical evidence on the relationship between the costs of imported inputs and the export of the final goods is mixed, the extant theoretical literature explains only the negative relationship. This is because the extant theoretical literature ignored strategic interdependence between the exporters.
A simple Cournot duopoly (i.e., duopoly quantity competition) with homogeneous products of the exporters helps to explain both the negative and positive relationships between the costs of imported inputs and the export of the final goods in the presence of a fixed-cost of exporting and different input-productivities of the exporters. The lower costs of imported inputs increase (may increase or decrease) the incentive for export and the export volume for the low (high) productive exporters. Thus, we contribute to the literature by providing a simple theoretical explanation for the positive relationship between the costs of imported inputs and the export of the final goods, which is theoretically unexplained so far.
We also show under Cournot competition that a lower cost of imported inputs may reduce the consumer surplus, total profits of the exporters and world welfare.
We show the implications of Bertrand duopoly (i.e., duopoly price competition) with horizontal product differentiation in Appendix C. We find that a lower cost of imported inputs does not decrease the possibility of export but may reduce the export volume. Further, unlike Cournot competition, we find that a lower cost of imported inputs does not reduce the consumer surplus and world welfare. Hence, the positive relationship between the costs of imported inputs and the incentive to export the final goods, and lower consumer surplus and world welfare following a lower cost of imported inputs depend on the types of product market competition.
We have considered a duopoly model with a linear demand function for our analysis, which has helped to show our results in the easiest way. However, it must be clear from the intuitions that our results will hold even under general demand functions and in an oligopoly model. In our analysis under Cournot competition, the driving force for the positive relationship between the costs of imported inputs and the export of the final goods is the relative cost reduction in the high-productive firm and in the low-productive firm. If the relative cost reduction is significantly more in the low-productive firm compared to the high-productive firm, a lower cost of the imported inputs may increase or decrease the incentive for export and the export volume for the high-productive firm by reducing the residual demand for the high-productive firm significantly. This is for the strategic interactions between the firms and not for the demand function or for the number of firms. Hence, our qualitative results are expected to go through under non-linear demand functions and in an oligopolistic market.
Lower world welfare and lower consumer surplus following a reduction in the costs of imported inputs shown in our analysis are also expected to hold in an oligopoly model with non-linear demand functions. Whenever a lower cost of imported inputs reduces the high-productive firm’s incentive for export and changes the equilibrium export decision from a high-productive firm to a low-productive firm, it may reduce the consumer surplus and world welfare. If the lower cost of imported inputs does not change the equilibrium, the business stealing by the low-productive firm from the high-productive firm, which is responsible for reducing world welfare in our analysis, remains under a general demand function and in an oligopolistic market.
A simple duopoly model helps to explain both the negative and positive relationships between the costs of imported inputs and the export of the final goods. We show it under exogenously given productivity differences between the firms. A natural extension of this paper will be to determine the relationship between the costs of imported inputs and the export of the final goods in the presence of endogenous productivity differences. In this respect, one may consider the symmetric and asymmetric R&D capabilities of the exporters. We leave this issue for future research.
Author Contributions
Conceptualization, A.M. and Y.L.; Methodology, A.M. and Y.L.; Formal analysis, A.M. and Y.L.; Writing – original draft, A.M. and Y.L.; Writing – review & editing, A.M.and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We would like to thank four referees and the associate editor of this journal for helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proof of Lemma 1
For (NE, NE) to be a Nash Equilibrium, we need . Since (NE, NE) is the Nash equilibrium if .
(E, E) will be a Nash Equilibrium if . Since (E, E) will be a Nash Equilibrium if .
For (NE, E) to be a Nash Equilibrium, we need or .
Finally, for (E, NE) to be a Nash Equilibrium, we need or , which happens if for . Given the condition that and , we can get if or and . Therefore, (E, NE) may occur if or and . □
Appendix B. Proof of Proposition 1
(a) Export possibility: We get , if , and . Hence, a lower c moves A to A’, B to B’, C to C’ and D to D’.
(i) For firm 1: Consider that firm 1 does not export if G is higher than point A in Figure 2. Since a lower c moves A to A’, a lower c increases the possibility of export by firm 1.
Now consider equilibrium (E, NE), i.e., firm 1 exports, if G is between points B and C in Figure 2. Since a lower c moves B to B’ and C to C’, a lower c increases the possibility of export by firm 1.
The above discussion shows a negative relationship between the costs of imported inputs and the possibility of export by firm 1.
(ii) For firm 2: Consider that firm 2 exports for G less than point D in Figure 2. Since a lower c moves D to D’, a lower c increases the possibility of export by firm 2.
Now consider equilibrium (E, NE), i.e., firm 2 does not export if G is between points B and C in Figure 2. Since a lower c moves B to B’ and C to C’, a lower c decreases the possibility of export by firm 2 when the equilibrium is (E, NE) for G between points B and C and between points B’ and C’.
The above discussion shows the possibility of positive and negative relationships between the costs of imported inputs and the possibility of export by firm 2.
(b) For the equilibria (E, NE) and (NE, E), differentiating the equilibrium outputs of firms 1 and 2 with respect to c, we get , , which show a negative relationship between the costs of imported inputs and export volumes when a firm behaves like a monopolist in the export market.
For the equilibrium (E, E), differentiating the equilibrium outputs of firms 1 and 2 with respect to c, we get , for . Hence, there is a negative relationship between the costs of imported inputs and export volume for firm 1, but the relationship between the costs of imported inputs and export volume is positive for firm 2 if .
The above discussion shows that the relationship between the costs of imported inputs and export volumes is negative for firm 1 while it can be negative or positive for firm 2. □
Appendix C. Bertrand Competition
Consider Bertrand competition with horizontal product differentiation between firms 1 and 2. To ensure that both firms receive positive profits, we consider differentiated products under Bertrand competition. Assume that the market demand functions faced by firms 1 and 2 are, respectively
where , are the price and output of the ith firm, i = 1, 2, and shows the degree of product differentiation with .
If both firms decide to export, firms 1 and 2 maximise respectively to determine their prices. We get the respective equilibrium prices as:
The respective equilibrium outputs and profits of firms 1 and 2 are
If only the ith firm, i = 1, 2, decides to export, the ith firm maximises to determine its price, where if i = 1 and if i = 2. We get the equilibrium price of the ith firm as
The corresponding equilibrium output and profit of the ith firm are, respectively,
Lemma A1.
We get the following equilibria:
(a) Both firms export for .
(b) Only firm 2 (the high-productive firm) exports for and .
(c) No firm exports for .
Proof:
For (NE, NE) to be a Nash Equilibrium, we need . Since (NE, NE) is the Nash equilibrium if .
(E, E) will be a Nash Equilibrium if . Since (E, E) will a Nash Equilibrium if .
For (NE, E) to be a Nash Equilibrium, we need or .
Finally, for (E, NE) to be a Nash Equilibrium, we need or , which happens if . Since and , we get , implying . Therefore, (E, NE) cannot be a Nash equilibrium. □
Lemma A1 is different from Lemma 1. Lemma 1 shows that “only the low-productive firm (i.e., firm 1) exports” can be an equilibrium under Cournot competition. In contrast, Lemma A1 shows that “only the low-productive firm exports” cannot be an equilibrium under Bertrand competition. The reason for this difference is explained in the introduction.
Figure A1 shows the situations shown in Lemma A1.

Figure A1.
Export decisions under Bertrand competition.
Now we want to see how a lower cost of imported inputs affects the firms’ decisions to export. We get , . Given these conditions, Figure A2 shows how the ranges of G over which different equilibria occur change. The solid lines in Figure A2 show the situations under initial c and the dashed lines show the situations after a reduction in c.
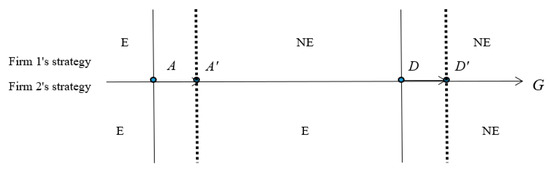
Figure A2.
Changes in the export decisions due to a lower c.
Proposition A1.
Consider Bertrand Competition.
(a) A lower cost of imported inputs increases the possibility of exports by firm 1 and firm 2.
(b) A lower cost of imported inputs
(i) Increases the volume of export for firm 1, but
(ii) May either increase or decrease the volume of export for firm 2.
Proof.
(a) Following the procedure used to prove Proposition 1, we can prove this result by consideringFigure A2.
(b) For equilibrium (NE, E), differentiating the equilibrium output of firm 2 with respect to c, we get , which shows a negative relationship between the costs of imported inputs and export volume for firm 2 when it behaves as a monopolist.
For equilibrium (E, E), differentiating the equilibrium outputs of firms 1 and 2 with respect to c, we get , for . Hence, the relationship between the costs of imported inputs and export volume is negative for firm 1, but it may be positive or negative for firm 2. □
The intuition for Proposition A1 is similar to that of Proposition 1.
Now we discuss the implications on the consumer surplus, total profits of the exporters and world welfare.
Unlike Proposition 1, Proposition A1 shows that a lower c increases the incentive for export. It is immediate that if a lower c moves the equilibrium from (NE, NE) to (NE, E), it increases the consumer surplus, total profits of firms 1 and 2 and world welfare.
If a lower c moves the equilibrium from (NE, E) to (E, E), it can be shown that it increases the consumer surplus (due to higher competition) and total profits of the firms (since more firms bring more varieties) although more firms increase the fixed costs of export. Hence, a lower c increases world welfare also10.
Now we consider the situation where a lower c does not change the equilibrium. It is immediate that if the equilibrium is (NE, E), a lower c increases the consumer surplus, the profit of the exporter and world welfare.
Now consider the equilibrium (E, E). In this situation, it can be shown that a lower c increases the consumer surplus and world welfare but has an ambiguous effect on the total profits of firms 1 and 2.
The next proposition follows from the above discussion.
Proposition A2.
(a) If a lower c changes the equilibrium from (NE, NE) to (NE, E) or from (NE, E) to (E, E), it increases the consumer surplus, total profits of the exporters and world welfare.
(b) If a lower c does not change the equilibrium, it increases the consumer surplus and world welfare but creates an ambiguous effect on the total profits of the exporters.
Although a lower cost of imported inputs reduces the marginal cost of the low-productive firm more than the high-productive firm and induces business stealing by the low-productive firm from the high-productive firm, the intensified price competition helps to increase consumer surplus and world welfare.
Notes
| 1 | Using firm-level Indian data, Goldberg et al. [11] discuss a related issue. Rather than considering the effects on exports, they look at the effects on new product development. They show that a lower tariff on imported inputs increases new product development by Indian firms. |
| 2 | Rather than considering the effect on the amount of export, Fan et al. [7] show the effects of a lower tariff on the imported inputs on export quality and export price. A thorough discussion of the related literature is contained in Section 2 below. |
| 3 | There is a vast literature on international trade using oligopoly models. However, that literature did not address the question discussed here. We are not going to review that literature here but refereeing to [12], which shows the role of oligopoly models in international trade and the references therein. |
| 4 | As mentioned, e.g., in [8,9], exporting activities require a significant amount of sunk costs. |
| 5 | We focus on the pure strategy equilibria. However, there is a mixed strategy equilibrium for . Since the consideration of the mixed strategy equilibrium will not add much to our purpose, we concentrate on the pure strategy equilibria only. |
| 6 | This condition holds for . |
| 7 | For simplicity, this discussion did not consider the tariff rate in the cost of imported inputs. Otherwise, world welfare will also have a component of tariff revenue. |
| 8 | If the equilibrium is either (E, NE) or (NE, E), only one firm exports, and it follows from Proposition 1 that a lower c increases the output of that firm. |
| 9 | If the equilibrium is either (E, NE) or (NE, E), only one firm exports, and it is immediate that a lower c increases the profit of the exporter. |
| 10 | The demand functions mentioned here can be found from a representative consumer’s utility function . Hence, the consumer surplus is , and world welfare is . |
References
- Kasahara, H.; Lapham, B. Productivity and the decision to import and export: Theory and evidence. J. Int. Econ. 2013, 89, 297–316. [Google Scholar] [CrossRef]
- Bas, M.; Strauss-Kahn, V. Does importing more inputs raise exports? Firm-level evidence from France. Rev. World Econ. 2014, 150, 241–275. [Google Scholar] [CrossRef]
- Feng, L.; Li, Z.; Swenson, D.L. The connection between imported intermediate inputs and exports: Evidence from Chinese firms. J. Int. Econ. 2016, 101, 86–101. [Google Scholar] [CrossRef]
- Aristei, D.; Castellani, D.; Franco, C. Firms’ exporting and importing activities: Is there a two-way relationship? Rev. World Econ. 2013, 149, 55–84. [Google Scholar] [CrossRef]
- Elliott, R.J.R.; Horsewood, N.J.; Zhang, L. Importing exporters and exporting importers: A study of the decision of Chinese firms to engage in international trade. Rev. Int. Econ. 2018, 27, 240–266. [Google Scholar] [CrossRef]
- Melitz, M.J. The impact of trade on intra-industry reallocations and aggregate industry productivity. Econometrica 2003, 71, 1695–1725. [Google Scholar] [CrossRef]
- Fan, H.; Li, Y.A.; Yeaple, S.R. Trade liberalization, quality, and export prices. Rev. Econ. Stat. 2015, 97, 1033–1051. [Google Scholar] [CrossRef]
- Bernard, A.B.; Jensen, J.B. Why some firms export. Rev. Econ. Stat. 2004, 86, 561–569. [Google Scholar] [CrossRef]
- Das, S.; Roberts, J.; Tybout, J.R. Market entry costs, producer heterogeneity and export dynamics. Econometrica 2007, 75, 837–873. [Google Scholar] [CrossRef]
- Lahiri, S.; Ono, Y. Helping minor firms reduces welfare. Econ. J. 1988, 98, 1199–1202. [Google Scholar] [CrossRef]
- Goldberg, P.K.; Khandelwal, A.K.; Pavcnik, N.; Topalova, P. Imported intermediate inputs and domestic product growth: Evidence from India. Q. J. Econ. 2010, 125, 1727–1767. [Google Scholar] [CrossRef]
- Neary, P. Two and a half theories of trade. World Econ. 2010, 33, 1–19. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).