Abstract
This paper examines a homogeneous-good Bertrand–Edgeworth oligopoly model to explore the role of firm size and number in pricing. We consider the price impact of merger, break up, investment, divestment, entry and exit. A merger leads to higher prices only when it increases the size of the largest seller and industry capacity is neither too big nor too small post-merger. Similarly, breaking up a firm only leads to lower prices when it concerns the biggest producer and aggregate capacity is within an intermediate range. Investment and entry (weakly) reduce prices, whereas divestment and exit yield (weakly) higher prices. Taken together, these findings suggest that size matters more than number in the determination of oligopoly prices.
Keywords:
Bertrand–Edgeworth competition; Edgeworth price cycle; firm size distribution; oligopoly pricing; price dispersion JEL Classification:
D43; L11; L13
1. Introduction
There are many reasons why market competition may not result in a competitive outcome, i.e., a situation where firms price at marginal cost. One of these reasons was provided by the Irish scholar Francis Y. Edgeworth (1925) [1], namely the presence of capacity constraints.1 Indeed, when demand is sufficiently large in comparison to production capacity, firms may well be capable of selling all of their supplies at supracompetitive prices, that is, at prices above marginal cost.
For a given level of demand, however, there are at least two distinct factors that affect available capacity, the number of firms and their size. For instance, capacity constraints tighten both when an incumbent divests part of its business and when it redeploys its assets to leave the industry all together. In case of exit, there is a reduction in the number of competitors, whereas this need not be true in case of divestment. Though one would expect both events to induce an upward pressure on prices, after all there is less production capacity available; the precise impact on prices is a priori unclear. In particular, one may wonder whether firm size and number have a comparable effect on oligopoly pricing and, if not, what drives the difference.
The purpose of this paper is to shed light on the role of firm size and number in capacity-constrained oligopoly pricing. Toward that end, we analyze an n-firm homogeneous-good Bertrand–Edgeworth oligopoly. 2 As is well known, this model captures three different types of market situation, each of which can be characterized by the ratio of industry capacity to market demand.
When production capacity is ‘small’ relative to market demand, there is a symmetric pure-strategy Nash equilibrium which equates aggregate capacity and demand. When capacity is ‘large’ relative to market demand, there also is a pure-strategy solution, which has firms pricing at marginal cost. In what follows, we refer to the first as the monopolistic zone and the second as the competitive zone. Finally, if industry capacity is ‘intermediate’, then there is no pure-strategy equilibrium. As pointed out by Edgeworth (1925) [1], prices are indeterminate in this case and oscillate indefinitely between some lower and upper bound. We refer to this as the Edgeworth zone.
To examine the role of firm size and number in pricing in a capacity-constrained oligopoly model, we consider the impact of changes in (the allocation of) production capacity. Specifically, we explore the price effects of six different capacity-altering events: merger, break up, investment, divestment, entry and exit. In case of merger or break up, there is a change in the number of sellers, but aggregate capacity is not affected. With investment and divestment, the number of firms remains constant, but capacity changes. Finally, with entry and exit, both capacity and the number of firms change.
These events can have two distinct types of effect, both of which may affect pricing. On the one hand, they can have an impact on the span of each of the three zones. This implies that the events can cause the industry to switch zones. For instance, when capacities are large and the market is in the competitive zone, divestment or exit might reduce production capacity to such an extent that the industry moves into the Edgeworth zone. On the other hand, given that the industry is in the Edgeworth zone, the events may also affect the degree of price dispersion. We refer to this as the price fluctuation range, i.e., the range of prices that are set with positive probability.
We find that a merger either has no effect on price or elevates price. There are two necessary conditions for prices to rise as a result of merger: (i) the merger increases the size of the largest seller (including the possibility of a merger between smaller producers that becomes the new leading firm post-merger) and () the industry is in the Edgeworth zone or the merger brings the industry into the Edgeworth zone. Mergers that have no effect on the market position or size of the biggest industry player do not affect price. Moreover, if the industry is in the monopolistic or the competitive zone, then a merger only affects prices when it causes the industry to move into the Edgeworth zone. As with mergers, breaking up a firm in smaller, separate entities has an impact on price only when it concerns the biggest seller. Moreover, it is only effective, in the sense of leading to lower prices, when the industry is in the Edgeworth zone. In all other cases, splitting up suppliers in smaller, independent units does not affect price.
Investment and entry increase production capacity and overall have a comparable price reducing effect. If the industry is in the monopolistic zone, then both these events may bring the industry into the Edgeworth zone and, ultimately, into the competitive zone. Roughly speaking, the opposite occurs with divestment and exit, both of which reduce available production capacity. Starting in the competitive zone, these events may lead the industry into the Edgeworth zone and, eventually, into the monopolistic zone. The fact that entry and investment as well as divestment and exit work in the same direction, indicates that production capacity is a more important price determinant than the number of competitors in these types of industry.
As to price dispersion, we find that a merger (break up) may yield a wider (narrower) price fluctuation range, but only when it affects the size of the industry leader. Investment by the largest industry player also leads to more price dispersion. Taken together, our findings thus suggest that size matters more than number in the determination of oligopoly prices.
The next section introduces the model and provides a detailed specification of the price fluctuation range. Section 3 explores the price effects of merger, break up, investment, divestment, entry and exit. Section 4 offers a brief discussion of our findings and Section 5 presents the conclusion. All proofs are relegated to the Appendix A.
2. Methods
2.1. Oligopoly Model
We examine a Bertrand–Edgeworth oligopoly comprising a given set of profit-maximizing firms: . Each firm has a production capacity and produces a homogeneous good on demand at a common marginal cost . Without loss of generality, it is assumed that . Total industry capacity is denoted by and is the combined production capacity of all firms other than i.
The market demand function is . It is assumed that and that is twice continuously differentiable, with and at any market price . Sellers select prices simultaneously from so that is the set of all possible price profiles. As products are perfect substitutes, consumers prefer to purchase from a lowest-priced seller. Since these suppliers may be capacity-constrained, however, it is possible that only part of them is served in which case higher-priced sellers might still face demand.
To specify individual (residual) demand, let and denote the set of firms that price at and below , respectively.3 Furthermore, let indicate the prices of all firms other than i. Demand for firm i’s product is then given by when all its competitors charge a strictly higher price. If there is at least one other seller setting the same price, then its demand is:
Finally, if firm i sets the strictly highest price in the industry, then its demand is:
Thus, (i) customers first visit the cheapest seller(s) at the set prices, (ii) at equal prices, demand is allocated in proportion to production capacity and (iii) rationing is efficient.4
A firm’s profit is then given by:
Hence, if firm i sets the strictly highest price in the industry, then its profits are given by . To facilitate our analysis, we write:
to indicate the corresponding residual profit-maximizing price. Note that, by concavity of the residual profit-function, there is a unique provided that there is a for which .
The next two results establish some properties that will prove useful in the ensuing analysis. The first states that the residual profit-maximizing price increases with firm size. This is so because a firm’s residual demand, ceteris paribus, depends positively on its production capacity. The second sheds light on the relation between a firm’s production capacity and market demand at the residual profit-maximizing price.
Lemma 1.
Fix K and suppose that . For all and , if , then .
Lemma 2.
Finally, let be the price for which total industry capacity equals market demand, i.e., . We refer to as the market-clearing price.For all and , does not depend on . Moreover,
As is well known, the existence of a pure-strategy Nash equilibrium in the above game critically depends on the relation between demand and available production capacity.5 Specifically, there is a pure-strategy solution when total industry capacity is sufficiently small (i.e., ) and when it is sufficiently large (i.e., ). In the following, we refer to the first case as the monopolistic zone and to the second as the competitive zone. In the monopolistic zone, there is a symmetric pure-strategy equilibrium in which all firms set the market-clearing price . In the competitive zone, there too is a symmetric pure-strategy solution which has all firms price at marginal cost.6
If joint industry capacity is intermediate (i.e., ), then there is no pure-strategy equilibrium. As envisaged by Edgeworth (1925) [1], price stability is unlikely in this case and prices are expected to oscillate indefinitely between some lower and upper bound. We refer to this as the Edgeworth zone.
2.2. Price Fluctuation Range
Before examining the price effect of changes in firm size and number, it is useful to distinguish two types of impact. First, a change in capacity allocation may affect the size of the Edgeworth zone (and therefore the size of the monopolistic and competitive zones). Second, given that joint capacity K is such that the industry is in the Edgeworth zone, it may impact what we refer to as the price fluctuation range, i.e., the difference between the maximum and minimum prices that are set with positive probability.
In order to characterize the price fluctuation range, define:
as firm i’s iso-profit price. That is, is the price below at which firm i sells at capacity and obtains the same profit as when it is the single highest-priced firm pricing at . Figure 1 graphically illustrates the concept for the industry leader (i.e., firm 1) with marginal cost normalized to zero.
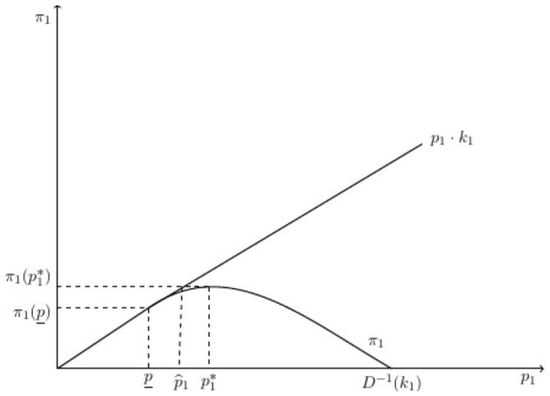
Figure 1.
Firm 1’s residual profit maximizing and iso-profit price for c = 0.
The next result relates the iso-profit price to production capacity. It shows that the iso-profit price positively depends on firm size when industry capacity is given. Roughly speaking, larger firms have a higher residual profit per unit of capacity. Since unit costs are the same, this implies that a firm’s iso-profit price is increasing in its capacity, all else unchanged.
Proposition 1.
This finding implicitly defines the lower bound of the price fluctuation range to be given by . To see this, first note that none of the firms has an incentive to put mass on prices in excess of their residual profit-maximizing price. Moreover, one can easily construct cases where charging the residual profit-maximizing price is a best response. Taken together and following Lemma 1 above, this implies that constitutes the upper bound of the price fluctuation range.Suppose that and fix K. For all and , if , then .
Suppose then that firm 1 sets . Since this is optimal only when firm 1 has residual demand at that price, it holds that . That is, all its rivals set a lower price and are capacity-constrained. Yet, in that case, each of its rivals can raise their price arbitrarily close to and still sell at capacity. If that happens, then it is a best response of the largest seller to undercut the price of its competitors by the smallest possible amount. This holds true, since it goes from producing below capacity to producing at capacity while selling at (approximately) the same price. In turn, this induces its rivals to cut their prices slightly. This hypothetical downward spiral stops when a firm prefers hiking its price to cutting it further. By Proposition 1, this is the largest seller.
Yet, if the largest seller does not put mass on prices below , then neither will any of its rivals. Because firm 1 has no incentive to cut price further, there is nothing to gain by pricing below . In fact, following the above logic, they have an incentive to follow the price hike by firm 1, which then induces a new Edgeworth price cycle. Combining the above then leads to the following conclusion.
Corollary 1.
Suppose that . The price fluctuation range is given by:
3. Results
We now proceed by studying three scenarios that may alter the size distribution of firms: (i) merger and break up, (ii) investment and divestment and (iii) entry and exit. For all these cases, we examine the impact on the Edgeworth zone and price fluctuation range, respectively.
3.1. Merger and Break Up
The first possibility that we consider is a change in the size distribution of firms that results from merger or break up. In the first case, the number of firms is reduced, whereas it increases in the second case. Importantly, in both cases it is assumed that total industry capacity K remains constant.
3.1.1. Edgeworth Zone
As pointed out above, the Edgeworth zone is characterized by the following condition: . This condition captures the range of industry capacity for which prices may be expected to be unstable. Notice that both the lower bound and the upper bound critically depend on the size of the largest seller. In fact, these boundaries are affected only when there is a change in the production capacity of the industry leader. This implies that the Edgeworth zone remains unaltered as long as is largest and unaffected by merger or break up.
Suppose then that there is a merger that becomes the new industry leader in terms of production capacity. Since has increased post-merger, the upper bound increases. Moreover, since K is constant, the (new) largest firm faces more residual demand. Following Lemma 1, this implies that increases, so that the lower bound decreases. Taken together, this implies an expansion of the Edgeworth zone when a merger leads to an increase in the largest supplier’s size. It is worth highlighting that a merger will never induce a shift from the Edgeworth zone to the monopolistic or competitive zone, whereas the opposite can occur.7 That is, if the industry is in the monopolistic or competitive zone, then a merger may bring the industry into the Edgeworth zone, thereby leading to more price dispersion.
This conclusion is reversed in case of a break up of firms in smaller, separate, entities. As with merger, both the lower bound and the upper bound remain unaffected when the split up does not involve the largest seller. If the break up concerns the biggest industry player, however, then the upper bound decreases. The decline in capacity moreover means that the residual profit-maximizing price of the biggest firm decreases, which implies an increase in the lower bound . Therefore, the Edgeworth zone contracts if and only if, the leading firm is split up in separate units. Notice that, in that case, there may be a shift from the Edgeworth zone into the monopolistic or competitive zones. In other words, if the industry is in the Edgeworth zone, then break up of the biggest industry player might lead to lower prices and potentially to more price stability.
3.1.2. Price Fluctuation Range
Let us now examine the effect of a merger or break up on the price fluctuation range. Starting with a merger, the next result shows that when the merger is the industry leader in terms of production capacity, the price fluctuation range shifts upward. In stating this result, let the merger be indicated with the subscript ‘s’.
Proposition 2.
The intuition behind this result is as follows. Since industry capacity remains unaltered, the (new) largest firm faces more residual demand, which means it has a higher residual profit-maximizing price (Lemma 1). Since the industry leader’s residual profits are higher post-merger, this implies an increase in the highest iso-profit price (Proposition 1). Such a merger, therefore, leads to an upward shift in the price fluctuation range.Suppose that and that there is a subset of firms that merge. If this merger is the biggest firm post-merger, then and . That is, the price fluctuation range shifts upward.
Since both the upper bound and the lower bound increase when the merger is the biggest seller, it is a priori unclear whether the fluctuation range expands or contracts. Assuming linear demand, the next example shows that it may expand:
Example 1.
Assume that market demand is given by and that . Assume further that . Now suppose that firm i is the highest priced seller facing residual demand:
with and . Its residual profit-maximizing price is then given by:
with corresponding residual demand and profits:
Firm i’s iso-profit price is given by:
Now consider the fluctuation range:
Taking the derivative with respect to gives:
We conclude that the fluctuation range is expanding with firm 1’s capacity.
If the merger is not the biggest firm post-merger, then the residual profit-maximizing price remains unaffected (since does not change). As firm 1’s residual profits are unaffected by the merger, the iso-profit should also stay the same. Since does not change in this case, this implies that does not change either. Hence, the price fluctuation range is not affected by a merger when the merger is not the biggest firm in the industry.
Finally, as to the impact of a break up, suppose that firm 1 is split up into smaller, separate entities. This implies that there is a new industry leader that is smaller than before the break up. That firm faces less residual demand when setting the highest price so that the upper bound of the price fluctuation range decreases. By Proposition 1, the same holds for the iso-profit price. Hence, a break up of the largest seller leads to a downward shift in the price fluctuation range. Moreover, the price fluctuation range remains unaffected when the break up concerns a smaller supplier.
3.2. Investment and Divestment
In the preceding subsection, we studied changes in the size distribution of suppliers under the assumption that aggregate capacity K is fixed. However, the size allocation may also change when there are modifications in industry capacity. In this subsection, we consider production capacity investments and divestments by incumbents. That is, we examine the impact of changes in K assuming that the number of producers remains constant. The question of what happens when the number of firms changes too is taken up in the next subsection.
3.2.1. Edgeworth Zone
Recall that the Edgeworth zone is defined by . Starting with the upper bound (i.e., ), it is clear that it increases when the biggest industry player invests in additional production capacity and decreases when this firm divests. The upper bound may also increase when there is a smaller supplier that invests to such a degree that it becomes the new industry leader in terms of capacity.
Since investments and divestments directly affect total industry capacity K, there may be a shift from the Edgeworth zone to the competitive zone. This can occur when a smaller seller invests, for example. The reverse cannot happen, because divestment by the biggest seller (or any other firm) reduces total industry capacity by the same amount. That is to say, the inequality is immune to divestments.
As to the lower bound (i.e., ), it is affected only when the residual profit-maximizing price of the largest producer changes. This price is effectively determined by the combined capacity of this firm’s rivals (i.e., ). Notice that is unaffected by firm 1’s investments or divestments as long as it maintains its leading position. The lower bound does change in response to investment or divestment by a smaller supplier, however, since this directly affects . For instance, divestment by a smaller producer yields a reduction in . This implies an increase in and, therefore, a decrease in the lower bound . Similarly, investment by a smaller supplier leads to an increase in . This induces a lower and, consequently, an increase in the lower bound .
Since total industry capacity is affected, it is then possible that the industry shifts from the monopolistic zone to the Edgeworth zone (e.g., when the leading industry player invests) and vice versa (e.g., when the leading industry player divests).
3.2.2. Price Fluctuation Range
Let us now direct our attention to the potential impact of investment or divestment on the price fluctuation range. The following result considers the case where the largest seller invests in extra capacity.
Proposition 3.
As an increase in does not affect , the residual profit-maximizing price remains unaffected. Since residual demand also stays the same, residual profits do not change either. By the very definition of the iso-profit price, this implies that should also stay the same. However, since increases, this requires a reduction in the iso-profit price . Taken together, this means that the price fluctuation range expands downward when the industry leader invests in additional production capacity, all else equal.Suppose that . The price fluctuation range increase in the size of the largest industry player .
The reverse holds when the largest supplier divests as long as it remains the industry leader. As with investment, the residual profit-maximizing price does not change. Yet, to keep constant, the iso-profit price rises to compensate for the decline in . In cases in which divestment is so severe that firm 1 loses its leading position, the new leader (firm 2) faces more residual demand than firm 1 when setting the highest price. This induces an increase in the price fluctuation range upper bound. Since firm 2’s capacity remains unaltered, this implies that its iso-profit price increases too. Hence, in this case, the fluctuation range shifts upward.
Let us now consider the impact of growth by a firm that is not the industry leader. When a smaller firm invests without taking over the leading role, it reduces firm 1’s residual demand and residual profit-maximizing price . This implies a reduction in firm 1’s residual profits. Since does not change, it follows that the iso-profit price decreases too. Notice that the effect is similar when a smaller firm invests to such a degree that it becomes the new industry leader. We conclude that the price fluctuation range shifts downward whenever a smaller supplier invests.
As to divestment by a smaller producer, this has a direct negative effect on . Since this increases firm 1’s residual demand, the residual profit-maximizing price rises. The resulting rise in residual profits implies that the iso-profit should increase as well. Since has not changed in this case, the iso-profit price increases too. Hence, divestment by a smaller supplier leads to an upward shift in the price fluctuation range.
3.3. Entry and Exit
Finally, let us consider the possibility of a simultaneous change in aggregate capacity and the number of firms. This may happen in cases of entry or exit. As before, we first discuss the impact on the Edgeworth zone and then examine how the price fluctuation range is affected.
3.3.1. Edgeworth Zone
Suppose that industry capacity expands as a result of entry. If the newcomer is the largest firm in the industry, then the upper bound of the Edgeworth zone (i.e., ) increases. This is so since there is a new ‘number one’ post-entry, which implies an increase in . At the same time, however, the lower bound (i.e., ) increases too. Indeed, the new industry leader faces less residual demand than its predecessor so that is lower and is higher post-entry.
If the newcomer is smaller than the largest firm in the industry, then this has no effect on the upper bound of the Edgeworth zone since does not change. Yet, also in this case, entry leads to a reduction in residual demand for the biggest firm and, consequently, to a reduction in . Hence, entry always leads to an increase in the lower bound of the Edgeworth zone .
Exit by the industry leader reduces the upper bound . It also implies that the new industry leader (i.e., firm 2 pre-exit) faces more residual demand when setting its residual profit-maximizing price, which therefore increases. As a result, decreases so that the Edgeworth zone shifts leftward. That is, the monopolistic zone becomes smaller, whereas the competitive zone expands. If the exiting firm is not the industry leader, then the upper bound remains unaltered. Yet, the leading firm faces more residual demand post-exit so that increases and, therefore, decreases. Consequently, the Edgeworth zone expands in this case.
3.3.2. Price Fluctuation Range
Entry and exit also affect the price fluctuation range. The next two results show that entry leads to a downward shift in the price fluctuation range, whereas exit induces an upward shift. In stating these results, let the prime indicate the situation post-entry.
Proposition 4.
Suppose that . If a new firm enters the industry, then and . That is, the price fluctuation range shifts downward.
Proposition 5.
Suppose that . If an incumbent exits the industry, then and . That is, the price fluctuation range shifts upward.
The logic behind these results is as follows. If a newcomer enters the industry that is smaller than the market leader, then this causes a drop in residual demand for the largest firm. Consequently, the residual profit-maximizing price is lower post-entry. Since the largest seller’s production capacity remains unaltered, this implies a drop in the iso-profit price . The same holds when the entrant is the new industry leader. First, its residual demand is lower than the residual demand of the preceding leader. This has the implication that the upper bound of the price fluctuation range () decreases. Since residual profits are lower and the industry leader’s capacity is larger, the corresponding iso-profit price () is lower post-entry. As a result, entry induces a downward shift in the price fluctuation range.
Exit mirrors the situation with entry. If a firm leaves the industry, then there is more residual demand for the (new) industry leader, i.e., increases. Since residual profits are higher and the largest firm is weakly smaller post-exit, the iso-profit price () increases too. Consequently, exit creates an upward shift in the price fluctuation range.
3.4. Recapitulation
The preceding analysis presents many different situations in which there may or may not be a price effect. In the following, we present three tables (one for each zone) Table 1, Table 2 and Table 3 that provide an overview of the impact of the six events on pricing. In these tables, the ‘↑’ and ‘↓’ mean that prices go up or go down, respectively. The ‘-’ sign means that there is no impact on price and the ‘x’ indicates that the situation cannot occur. Each of the three tables distinguishes between ‘same zone’ and ‘switch zone’. ‘Same zone’ means that the industry remains in the respective zone after the event, whereas ‘switch zone’ means that the event causes a shift to an adjacent zone. Lastly, ‘regular’ means that the industry leader (in terms of production capacity) is not involved, whereas ‘leader’ means that the largest firm takes part in the event.

Table 1.
Price Effects in the Monopolistic Zone.

Table 2.
Price Effects in the Competitive Zone.

Table 3.
Price Effects in the Edgeworth Zone.
Starting in the monopolistic zone (Table 1), a merger has a price effect only when it induces a switch to the Edgeworth zone. In that case, there is a ‘jump’ from a single market clearing price to a higher range of prices. This requires an increase in the production capacity of the largest player. If the biggest firm increases in size, then a merger may result in higher prices and create price dispersion. Break up has no effect and cannot lead to a shift in zones. The same holds for divestment and exit, i.e., these events cannot move the industry from the monopolistic zone to the Edgeworth zone. Yet, since they lead to a reduction in total industry capacity, they positively affect price levels. The opposite holds for investment and entry, which increase industry capacity and lead to a reduction in prices. This holds true independent of whether these events trigger a switch to the Edgeworth zone.8
Turning to the competitive zone (Table 2), the effect of a merger is comparable to when the industry is in the monopolistic zone. It affects price only when it results in a switch in zones, which requires an increase in size of the industry leader. When this happens, prices rise. Break up cannot induce a shift in zones and neither can capacity expanding events like investment or entry. Divestment and exit may bring the industry into the Edgeworth zone and, therefore, induce a price increase. Taken together, there may be a price increasing effect, but only when (1) there is a reduction in the number of firms or production capacity and (2) the industry leaves the competitive zone.
Finally, let us summarize the potential price effects when the industry is in the Edgeworth zone. Starting with the events that affect available industry capacity, divestment and exit always drive prices upward independent of whether there is a switch in zones. The reverse holds for investment and entry. Breaking up firms that are not the industry leader has no effect on price, whereas breaking up the largest firm leads to lower prices. A merger does not induce a shift to the competitive or monopolistic zone, but can have a price increasing effect when the largest industry player has grown post-merger.
4. Discussion
Recent years have seen a renewed interest in oligopoly pricing under capacity constraints (see, e.g., Bos and Vermeulen (2021) [17], Montez and Schutz (2021) [18] and Edwards and Routledge (2022) [14]) and, in particular, in providing rationales for Edgeworth price cycles in markets with perfect and less than perfect substitutes (see, e.g., Myatt and Ronayne (2019) [19] and Gabszewicz, Marini and Zanaj (2022) [20]).
Such a revamped interest comes from several sources, perhaps the most important one being the existing empirical evidence. Price dispersion is shown to be persistent in both physical and online shops (see, e.g., Aas, Wulfsberg and Moen (2018) [21] and Gorodnichenko, Sheremirov and Talavera (2018) [22]). Edgeworth price cycles are also well documented. For example, Eckert (2003) [23] and Noel (2007a, 2007b) [24,25] provide evidence of sawtooth pricing paths in the Canadian retail gasoline market. Wang (2008) [26] explores empirically the existence of collusive price cycles in the Australian retail gasoline market. Similarly, Foros and Steen (2013) [27] and Linder (2018) [28] describe Edgeworth-like price cycles in European retail gasoline markets. Furthermore, such pricing dynamics has also been documented for pharmaceutical markets and search-engine advertising (see, e.g., Hauschultz and Munk-Nielsen (2020) [29] and Zhang and Feng (2011) [30]). Finally, it is noteworthy that similar pricing patterns have been observed in controlled laboratory experiments (see, e.g., Kruse, Rassenti, Reynolds and Smith (1994) [31] and Fonseca and Normann (2013) [32]).
With few exceptions, these and similar studies take the size distribution of firms as given. Our analysis highlights the price impact of changes in firm size and number. In particular, we have shown how changes in market structure may affect the degree of price dispersion by making an industry more or less competitive. With an eye on the potential welfare implications, this warrants more (empirical) research into oligopoly pricing under capacity constraints.
5. Conclusions
We analyzed an n-firm homogeneous-good Bertrand–Edgeworth model to examine the impact of firm size and number on oligopoly pricing. We considered six different events that have an effect on the number of firms (merger and break up), available production capacity (investment and divestment) or both (entry and exit). We showed that a merger leads to higher prices only when it increases the size of the largest seller and industry capacity is neither too big nor too small post-merger. Similarly, breaking up a firm only leads to lower prices when it concerns the biggest producer and aggregate capacity is within an intermediate range. Investment and entry (weakly) reduce prices, whereas divestment and exit yield (weakly) higher prices. The overall takeaway from our explorations is, therefore, that size matters more than number in the determination of oligopoly prices.
We see several avenues for future research. One is to conduct a similar study assuming that products are less than perfect substitutes. Another is to consider cost (in)efficiencies that may result from merger. This may well create an (additional) downward or upward pressure on prices. As to the latter, we exclusively considered unilateral effects and ignored potential coordinated effects. Clearly, the upward price effect of a merger may well be stronger in case it facilitates a ‘mutual meeting of the minds’.
Author Contributions
Validation, I.B. and M.A.M.; Formal analysis, I.B. and M.A.M.; Investigation, I.B. and M.A.M.; Writing—original draft, I.B. and M.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
The second author gratefully acknowledges the financial support of Sapienza University of Rome, Italy and of Edgard Milhaud Foundation, Liège, Belgium.
Data Availability Statement
Not applicable.
Acknowledgments
We appreciate the comments of Luis Corchón, Emmanuel Petrakis, Attila Tasnádi, participants at the 2022 Oligo Workshop and three anonymous referees. All opinions and errors are ours alone.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Proofs
Proof of Lemma 1.
Consider some firm . Its residual profit-maximizing price, , is the price that solves:
Notice that, for a given industry capacity K, the LHS is decreasing in and the RHS is decreasing in . Hence, and , if , then . □
Proof of Lemma 2.
Following the proof of Lemma 1, the residual profit-maximizing price of firm i is implicitly defined by:
Rearranging gives:
Observe that the RHS does not depend on .
Next, note that:
where:
since , and . This implies . Moreover, , because and . □
Proof of Proposition 1.
Consider some firm . Its iso-profit price is given by:
Holding total industry capacity K fixed, we now show that increases with . Taking the first-derivative with respect to :
Rearranging gives:
Notice that, by the definition of the residual profit-maximizing price , it holds that:
Hence, the derivative (A1) reduces to:
which is positive since and . We conclude that if , then , for all and . □
Proof of Proposition 2.
Consider a merger that involves firm 1. The claims that and follow directly from Lemma 1 and Proposition 3.
This leaves the case where a subset of smaller suppliers merge and becomes the biggest firm in the industry. In that case, this new industry leader faces more residual demand when setting the highest price so that the upper bound of the fluctuation range increases (i.e., ). Moreover, by Proposition 3, the iso-profit price is increasing with capacity when total industry capacity is constant. Since , this implies that also in this case it holds that post-merger. □
Proof of Proposition 3.
Consider the price fluctuation range for a given industry capacity K:
Now suppose there is an increase in . To assess the impact on the fluctuation range, notice that:
In this case, it holds that since remains unaltered with an expansion of . Hence, the preceding equality simplifies to:
which is positive. We conclude that the price fluctuation range is increasing in the size of the largest industry player. □
Proof of Proposition 4.
Suppose there is an entrant with capacity , then this newcomer faces less residual demand than its predecessor (firm 1) when it is the highest-priced firm in the industry: . It follows that . This implies that residual profits of the industry leader are smaller post-entry. By definition of the iso-profit price, this means that must decrease too. Yet, , which implies that to ensure that .
Now suppose there is an entrant with capacity , then firm 1 faces less residual demand when it is the highest-priced firm in the industry: . It follows that . This implies that residual profits of the industry leader are smaller post-entry. By definition of the iso-profit price, this means that must decrease too. Yet, , which implies that to ensure that . □
Proof of Proposition 5.
Suppose that the largest seller (firm 1) leaves the industry. This means that firm 2 is the new industry leader that now has a higher residual profit-maximizing price, because . Hence, its residual demand is higher. Consequently, firm 2’s residual profit exceeds firm 1’s residual profit post-exit. This implies that firm 2’s residual profit post-exit exceeds and, therefore, also , because . By the definition of the iso-profit price this means that to ensure that the iso-profit post-exit equals the new leader’s residual profit.
Now suppose that a smaller supplier leaves the industry. This directly reduces , which increases the residual demand for firm 1. Consequently, . Since firm 1’s residual demand and price go up, its residual profits will also increase. In turn, this implies that its iso-profit must increase too. Yet, does not change so that its iso-profit price increases. We conclude that . □
[custom]
Notes
| 1 | For a general discussion, see Tirole (1988) [2] and Vives (1999) [3]. |
| 2 | Price competition under capacity constraints has been studied by Beckmann (1965) [4] Levitan and Shubik (1972) [5], Kreps and Scheinkman (1983) [6], Osborne and Pitchik (1986) [7], Vives (1986) [8], Allen and Hellwig (1986) [9], Maskin and Tirole (1988) [10], Deneckere and Kovenock (1992) [11], Tasnádi (1999) [12], amongst many others. |
| 3 | Formally, it is and , where is the vector of prices of all firms other than i. We use this shorthand notation to emphasize on which value of these sets are based. In the ensuing analysis, the effect of the complete price vector on demand will be clear from the context. |
| 4 | Such a surplus maximizing scheme is also used by Levitan and Shubik (1972) [5], Kreps and Scheinkman (1983) [6], Osborne and Pitchik (1986) [7], Bos, Marini and Saulle (2022) [13], Edwards and Routledge (2022) [14], amongst many others. |
| 5 | For a general discussion, see, e.g., Tasnádi (2004) [15]. |
| 6 | There are also many asymmetric equilibria with a subset of sellers pricing above costs. |
| 7 | A comparable finding in a three-firm Bertrand–Edgeworth model can be found in Chen and Li (2018) [16]. |
| 8 | It is worth noting that there is a boundary case where prior to investment or entry. In this situation, an increase in the leader’s production capacity induces a shift from the monopolistic to the Edgeworth zone, but its residual profit-maximizing price does not change. Notice, however, that there is still a price decrease in the sense that the price fluctuation range expands downward (i.e., decreases when moving into the Edgeworth zone). |
References
- Edgeworth, F.Y. The Pure Theory of Monopoly. Pap. Relat. Political Econ. 1925, 1, 111–142. [Google Scholar]
- Tirole, J. The Theory of Industrial Organization; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Vives, X. Oligopoly Pricing: Old Ideas and New Tools; The MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Beckmann, M. Edgeworth-Bertrand Duopoly Revisited. In Operations Research-Verfahren; Rudolf, H., Ed.; Sonderdruck, Verlag Anton Hain: Meisenheim, Germany, 1965; Volume III, pp. 55–68. [Google Scholar]
- Levitan, R.; Shubik, M. Price Duopoly and Capacity Constraints. Int. Econ. 1972, 13, 111–122. [Google Scholar] [CrossRef]
- Kreps, D.; Scheinkman, J. Quantity Precommitment and Bertrand competition yields Cournot outcomes. Bell J. Econ. 1983, 14, 326–337. [Google Scholar] [CrossRef]
- Osborne, M.J.; Pitchik, C. Price Competition in a Capacity-Constrained Duopoly. J. Econ. Theory 1986, 38, 238–260. [Google Scholar] [CrossRef]
- Vives, X. Rationing rules and Bertrand–Edgeworth Equilibria in Large Markets. Econ. Lett. 1986, 21, 113–116. [Google Scholar] [CrossRef]
- Allen, B.; Hellwig, M. Bertrand–Edgeworth Oligopoly in Large Markets. Rev. Econ. Stud. 1986, 53, 175–204. [Google Scholar] [CrossRef]
- Maskin, E.; Tirole, J. A Theory of Dynamic Oligopoly, II: Price Competition, Kinked Demand Curves and Edgeworth Cycles. Econometrica 1988, 56, 571599. [Google Scholar] [CrossRef]
- Deneckere, R.J.; Kovenock, D. Price Leadership. Rev. Econ. Stud. 1992, 59, 143–162. [Google Scholar] [CrossRef]
- Tasnádi, A. Existence of pure strategy Nash equilibrium in Bertrand–Edgeworth oligopolies. Econ. Lett. 1999, 63, 201–206. [Google Scholar] [CrossRef]
- Bos, I.; Marini, M.A.; Saulle, R.D. Myopic Oligopoly Pricing; Working Paper; Nota di Lavoro 32.2021; Fondazione Eni Enrico Mattei: Milano, Italy, 2021. [Google Scholar]
- Edwards, R.A.; Routledge, R.R. Information, Bertrand–Edgeworth Competition and the Law of One Price. J. Math. Econ. 2022, 101, 1–7. [Google Scholar] [CrossRef]
- Tasnádi, A. Production in Advance versus Production to Order. J. Econ. Organ. 2004, 54, 191–204. [Google Scholar] [CrossRef][Green Version]
- Chen, Z.; Li, G. Horizontal Mergers in the Presence of Capacity Constraints. Econ. Inq. 2018, 56, 1346–1356. [Google Scholar] [CrossRef]
- Bos, I.; Vermeulen, D. On Pure-Strategy Nash Equilibria in Price-Quantity Games. J. Math. Econ. 2021, 96, 1–13. [Google Scholar] [CrossRef]
- Montez, J.; Schutz, N. All-Pay Oligopolies: Price Competition with Unobservable Inventory Choices. Rev. Econ. Stud. 2021, 88, 2407–2438. [Google Scholar] [CrossRef]
- Myatt, D.P.; Ronayne, D. A Theory of Stable Price Dispersion; Working Paper, Economics Series Working Papers 873; University of Oxford, Department of Economics: Oxford, UK, 2019. [Google Scholar]
- Gabszewicz, J.; Marini, M.A.; Zanaj, S. Random Encounters and Information Diffusion about Product Quality. J. Econ. Manag. 2022, forthcoming. [Google Scholar] [CrossRef]
- Aas, Ø.N.; Wulfsberg, F.; Moen, E.R. Price Dispersion and the Role of Stores; Working Paper; BI Norwegian Business School, Oslo Business School and Université Libre de Bruxelles: Bruxelles, Belgium, 2018. [Google Scholar]
- Gorodnichenko, Y.; Sheremirov, V.; Talavera, O. Price Setting in Online Markets: Does IT click? J. Eur. Econ. 2018, 16, 1764–1811. [Google Scholar] [CrossRef]
- Eckert, A. Retail Price Cycles and the Presence of Small Firms. Int. J. Industrial Organ. 2003, 21, 151–170. [Google Scholar] [CrossRef]
- Noel, M.D. Edgeworth Price Cycles: Evidence from the Toronto Retail Gasoline Market. J. Ind. Econ. 2007, 55, 69–92. [Google Scholar] [CrossRef]
- Noel, M.D. Edgeworth Price Cycles, Cost-based Pricing and Sticky Pricing in Retail Gasoline Markets. Rev. Econ. Stat. 2007, 89, 324–334. [Google Scholar] [CrossRef]
- Wang, Z. Collusive Communication and Pricing Coordination in a Retail Gasoline Market. Rev. Ind. Organ. 2008, 32, 35–52. [Google Scholar] [CrossRef]
- Foros, Ø.; Steen, F. Vertical Control and Price Cycles in Gasoline Retailing. Scand. J. Econ. 2013, 115, 640–661. [Google Scholar] [CrossRef]
- Linder, M. Price Cycles in the German Retail Gasoline Market Competition or Collusion? Econ. Bull. 2018, 38, 593–602. [Google Scholar]
- Hauschultz, F.P.; Munk-Nielsen, A. The Role of Demand in Price Cycles: Evidence from Danish Pharmaceutical Markets; Working Paper; University of Copenhagen: Copenhagen, Denmark, 2020. [Google Scholar]
- Zhang, X.; Feng, J. Cyclical Bid Adjustments in Search-Engine Advertising. Manag. Sci. 2011, 57, 1703–1719. [Google Scholar] [CrossRef]
- Kruse, J.B.; Rassenti, S.; Reynolds, S.S.; Smith, V.L. Bertrand–Edgeworth Competition in Experimental Markets. Econometrica 1994, 62, 343–372. [Google Scholar] [CrossRef]
- Fonseca, M.A.; Normann, H.-T. Excess Capacity and Pricing in Bertrand–Edgeworth Markets: Experimental Evidence. J. Inst. Theor. Econ. 2013, 169, 199–228. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).