Exchange Networks with Stochastic Matching

Abstract

This paper tries to prove that the outcomes stemming from interactions on assignment markets bring about coordination in case of a stochastic matching subject to various forms of expectations. We consider an exchange network with stochastic matching between the pairs of players and analyze the dynamics of bargaining in such a market. The cases of convergent expectations, divergent expectations and of social preferences are studied. The extension of earlier works lies in the consideration of a stochastic matching on a graph dependent on the weights of edges. The results show that, in all three cases, the dynamics converges rapidly to the generalized Nash bargaining solution, which is an equilibrium that combines notions of stability and fairness. In the first two scenarios, the numerical simulations reveal that the convergence toward a fixed point is speedily achieved at the value of the outside option. In the third scenario, the fixed point promptly converges to the value of the outside option supplemented by the surplus share.

1. Introduction

Matching markets have been the subject of research in economics ([1]) and in operations research ([2,3]) for their capacity to take account of agents’ different preferences for different kinds of items. Just as much, they managed to consider the allocations of goods to agents in a decentralized manner ([4]). The early papers extended the initial model by [5] in which the authors analyzed the problem of achieving better partnerships. Despite the originality of their analysis of the assignment problems, its main limitation was to be found in the absence of consideration of uncertainty. Likewise, the competitive equilibrium that characterized the matching outcomes appeared extreme in a certain number of cases. Hence, it became a necessity to consider that trading prices—that matched agents agreed upon—divide the surplus from their matches through bargaining ([6]).

Parallel to the exchange networks, bargaining has received great attention from the economists ([7,8,9,10]). Nash bargaining solution, normatively satisfying axioms of rationality of players in a non-cooperative game, has been previously studied with regard to vertical markets ([11]), international relations ([12]), innovation partnerships ([13]), labor relations ([14]) and to power division among economic stakeholders ([15]). The Nash bargaining solution to a bilateral negotiation problem involves the determination of payoffs for each party with a specification of the disagreement point if the negotiation breaks down ([11]). Whereas the case of bargaining between two players—even in stochastic processes ([16,17])—is now well understood, the possible outcomes of bargaining on a large scale such as networked systems has been less explored. Those represent patterns of trading opportunities ([18,19]), which are not necessarily stable in time. The examples of networked structures can be found in markets for labor, agricultural and forestry activities, knowledge and information, housing, energy and in joint-venture partnering. Furthermore, the need for forecast—based on matching probabilities—arose in decision-making. This is how matching, bargaining on networks and randomness led to exchange networks ([20]).

Following the literature on assignment markets ([21,22,23]), which reveal games on graphs, we consider players to occupy the nodes of a network. The edges represent the trading partnerships between the nodes. The previous works notably studied the convergence properties of matched players’ allocations that happen to stand within the generalized Nash bargaining solutions ([23,24]). Those can be equal to or different from the standard Nash solutions. The generalized solution for such a game is an equilibrium concept that combines the notions of stability, by consolidating the trading partnership, and of balance or fair-trade, by equally splitting the trading surplus.1 If we now consider the process in which the partnership is concluded at random, this involves a process of stochastic matching and the construction of an edge-random graph. The random-graph-theoretic framework, where a potential edge occurs independently of the other edges with some non-null probability, has been mostly studied from the inaugural frame of reference proposed by [26].

Apropos of the literature on decentralized matching markets, we do not stipulate the absence of information about other agents’ payoffs nor do we take heed of coalitions of players ([27,28,29]). Our interest is based on the convergence properties instead. Otherwise, coalitions would lead to an oligopoly, with many-to-few trading opportunities, which is not addressed by the present research. In addition to the remark mentioned above, the matching probability functions that we shall take into consideration are, to some extent, comparable to that in [28]. We albeit focus on the economic valuations of model-players over an item, intended for trade, weighted by the network value of exchange.

More importantly, the number of research papers specifically exploring the strategic issues that appear in bargaining on networks with random matching are relatively infrequent to date. Among others, the topic has been previously discussed by [18,19,30,31]. In their models, the matching mechanism activates a number of linked pairs of agents. In each activated pair, one of the players is randomly selected to propose a division of the surplus created upon agreement. One of the recurrent technologies used in these models is termed linear search ([32]). The latter assumes that every player finds a bargaining partner with a fixed probability ([33]). In addition, the conditional probability of meeting a certain type of partner—as long as the conditioning event remains fixed—is given by the proportion of players in the market belonging to that type ([19]). In the following work, we approach random matching in a different way, for the assignment technology is built from the weights of edges ([34]), which are at the very heart of the exchange networks.

The purpose of such a choice is related to some of the emerging properties of complex systems. As a matter of fact, such systems are regarded as efficient if they manage to produce high coordinatedness among their constituent parts ([35]). For instance, catallactics or spontaneous order is a theory proposed by [36] to describe the order, brought about by the mutual adjustment of many individual economies, in a free-market system composed of various actors. The process can be understood as a network of firms and households taking part in a coordination game, where coordinatedness is a spontaneous outcome of individual trading activities that aims at reaching exchange rates and prices ([37]). In fact, individuals are making decisions based on their own market valuations without a centralized coordinator ([4]). Accordingly, the consideration of a time-evolving random matching is appropriate to study the mutually beneficial relationships on which are based free-market economies. Stochastic matching markets then have the capacity to study the likelihood of maladjustment and of lack of coordination in overall trading activities.2

Moreover, in the presence of such an assignment technology, can various forms of players’ expectations lead to a generalized outcome? It has long been well known that divergent expectations lead to a disagreement in bargaining ([39]). Agents that have the same information but interpret it differently are said to have divergent expectations ([40]). Our wish is to see if this divergence can purely and simply disappear in the presence of an assignment market, the very essence of which is to permit reaching an agreement. In addition, we want to verify whether converging expectations or social preferences, even if rare in nature, yield results that outperform the matching that can be reached with divergent expectations.

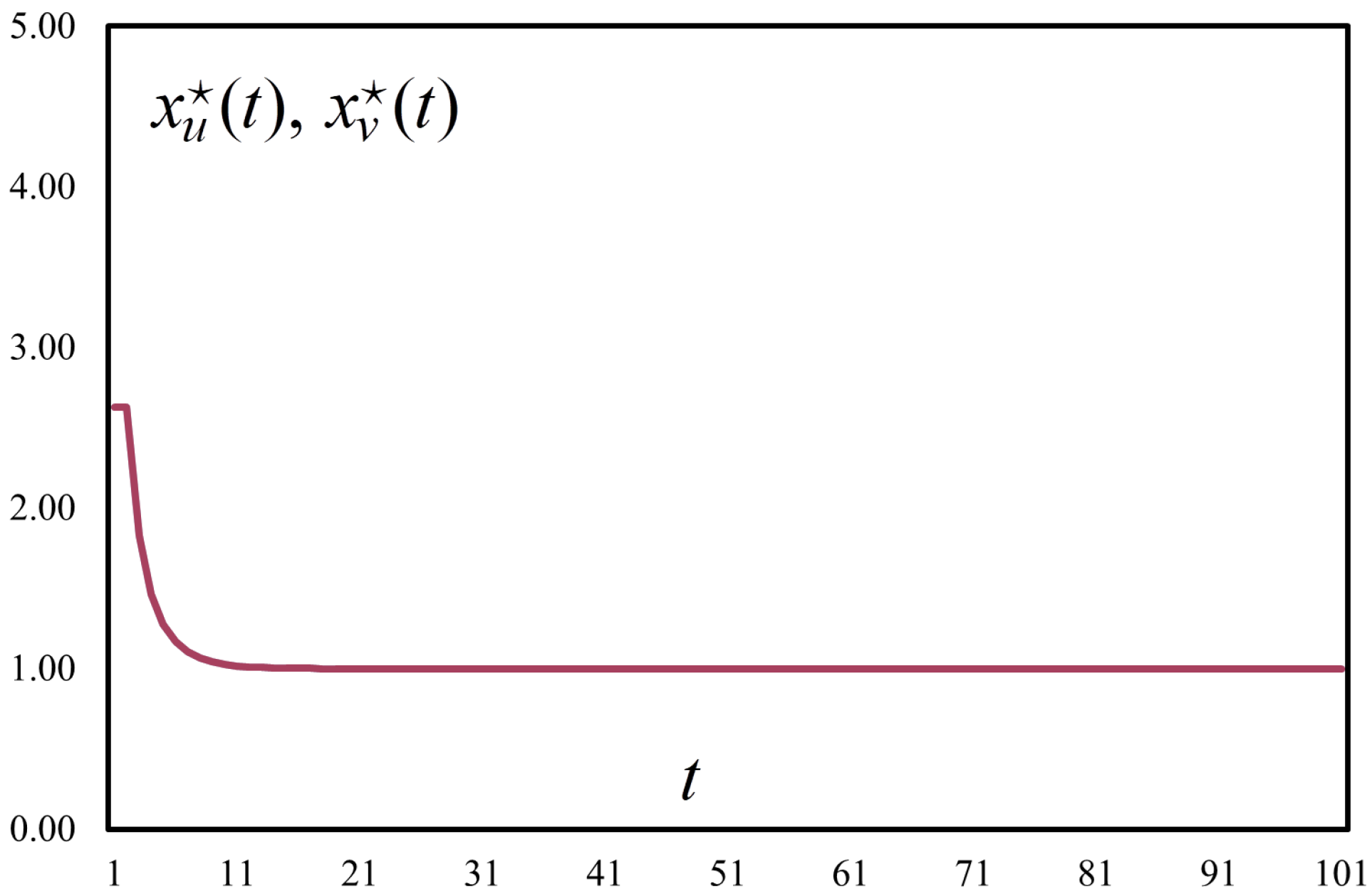
We consider an exchange network with stochastic matching between the pairs of players and analyze the dynamics of bargaining in such a market. The cases of convergent expectations, divergent expectations and of social preferences are studied. The results show that, in all three cases, the dynamics converge rapidly to the concept of generalized Nash bargaining solution. In the first two scenarios, the numerical simulations reveal that the convergence toward a fixed point is achieved at the value of the outside option. In the third scenario, the fixed point converges to the value of the outside option supplemented by the surplus share.

Section 2 provides a detailed description of the network model in the respective scenarios. Section 3 is devoted to illustrating simulation examples. Concluding remarks are given in Section 4.

2. Model

Let us first introduce the deterministic framework that has been used in the literature so far. Consider a network of players spread across a graph $G=(V,E)$, where $V=\left\{v_1,...,v_n\right\}$ denotes the set of nodes representing the players and $E=\left\{(u,v)\in V\times V\right\}$ is the set of edges or connections between those players. The graph is considered to be complete, in that any two network players can be seen as neighbors and can thus engage in a negotiation. No other graph property is reckoned with.

Players u and v, for $u,v=1,...,n$ and $u\ne v$, connected through an edge $(u,v)$, are allowed to play the bargaining game at time t, $\forall t\ge 0$. The game aims at splitting the value generated by their exchange. Before the negotiation between matched players takes place, let $\mathbf{w}\left(t\right):E\to {\mathbb{R}}_{+}^{V\times V}$ be the vector of edge weights at time t measuring the aggregated value of an item destined to negotiation. Put differently, it corresponds to the weight of a matching. Despite the simultaneous negotiation across the edges of G, each player can engage in at most one transaction ([21]). When one exists, the game outcome is related to a matching $M\left(t\right)\subseteq E$ of G, which defines the pairs of players involved in exchanges at time t.

When the game leads to a trade outcome, let a vector $\mathbf{x}\left(t\right)\in {\mathbb{R}}_{+}^V$ describe the allocations on V. The latter corresponds to the weights on edges incident on V. For example, if $x_u\left(t\right)$ is the allocation of node u, the outcome $x_u\left(t\right)+x_v\left(t\right)=w_{u,v}\left(t\right)\le \infty$, issued from an edge $(u,v)\in M\left(t\right)$, is the solution of the game at time t. Otherwise, $x_u\left(t\right)=0$ for every unmatched node $u\notin M\left(t\right)$. Let us specify that u would seek to match with v if and only if $x_u\left(t\right)-x_v\left(t\right)\ge 0$ in the first place. When $x_u\left(t\right)=x_v\left(t\right)$, the bargaining outcome is considered to be generalized. When the equality is verified on the entire time length, the generalized Nash bargaining solution is assumed to be stable.

We now extend the original model by injecting stochasticity in the networked system. In order to compute the expected trade outcomes, choice probabilities to all the pairs of players are assigned. That is, we consider a probability function that assigns to each node the likelihood that a neighbor chooses it as a trading partner among the set of nodes. Consider $\mathbb{P}\left[\right(u,v)\in M(t\left)\right]\in [0,1]$ to be the probability that two players decide to get involved in a negotiation, which implicitly puts a probability that an edge between u and v is chosen ([41]). Likewise, $\mathbb{P}\left[\right(u,k)\in M(t),k\ne v]$, or simply $\mathbb{P}\left[\right(u,v)\notin M(t\left)\right]$, represents the probability that player u, as a potential counterpart of player v in the bargaining game, chooses a neighbor k different from v. Denote by $n_G\left(u\right)$ the set of neighbors of player u, where $k\in n_G\left(u\right)\backslash v$. Therefore, we are faced with a random graph $G=(V,E,P)$, defined over the probability measure function $P\left(G\right):\mathcal{F}\to [0,1]$, with $\mathcal{F}$ the $\sigma$-field. Hence, all subsets of the probability space are measurable. A random graph then becomes a graph-valued random variable or a measurable mapping from a probability space to G ([42]). According to the methodology introduced by [43,44], the probability functions are defined to be3

$$\begin{array}{c}\hfill \mathbb{P}\left[\right(u,v)\in M(t\left)\right]\\ \hfill =\frac{{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(1)

$$\begin{array}{c}\hfill \mathbb{P}\left[\right(u,v)\notin M(t\left)\right]\\ \hfill =\frac{w_{u,v}{\left(t\right)}^{\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(2)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$. As for $\alpha \in [0,1]$, it represents the decay factor in the probabilistic method. Assuming a decay factor of 1 leads to certainty that u will engage in the comparison of weights with v, videlicet u has assured beliefs of being a match with v. Formally, the probability function is defined in terms of the difference in the weights of edges between players u and v, and of the difference in the weights of edges between player u and an alternative neighbor k, should the negotiation with the matching partner fail, reflecting the outside option.4 In parallel, the probability that players u and v do not match depends on the weight of a match, before the realization of the exchange, as well as on the gap in the weights of edges between player u and an alternative player k. It is ascertainable that both denominators contain the weight of a match $w_{u,v}\left(t\right)$, the presence of which is meant to adjust the likelihood of matching between nodes u and v and to ensure consistency to the probability functions. Indeed, the denominators reflect the network value of exchange.

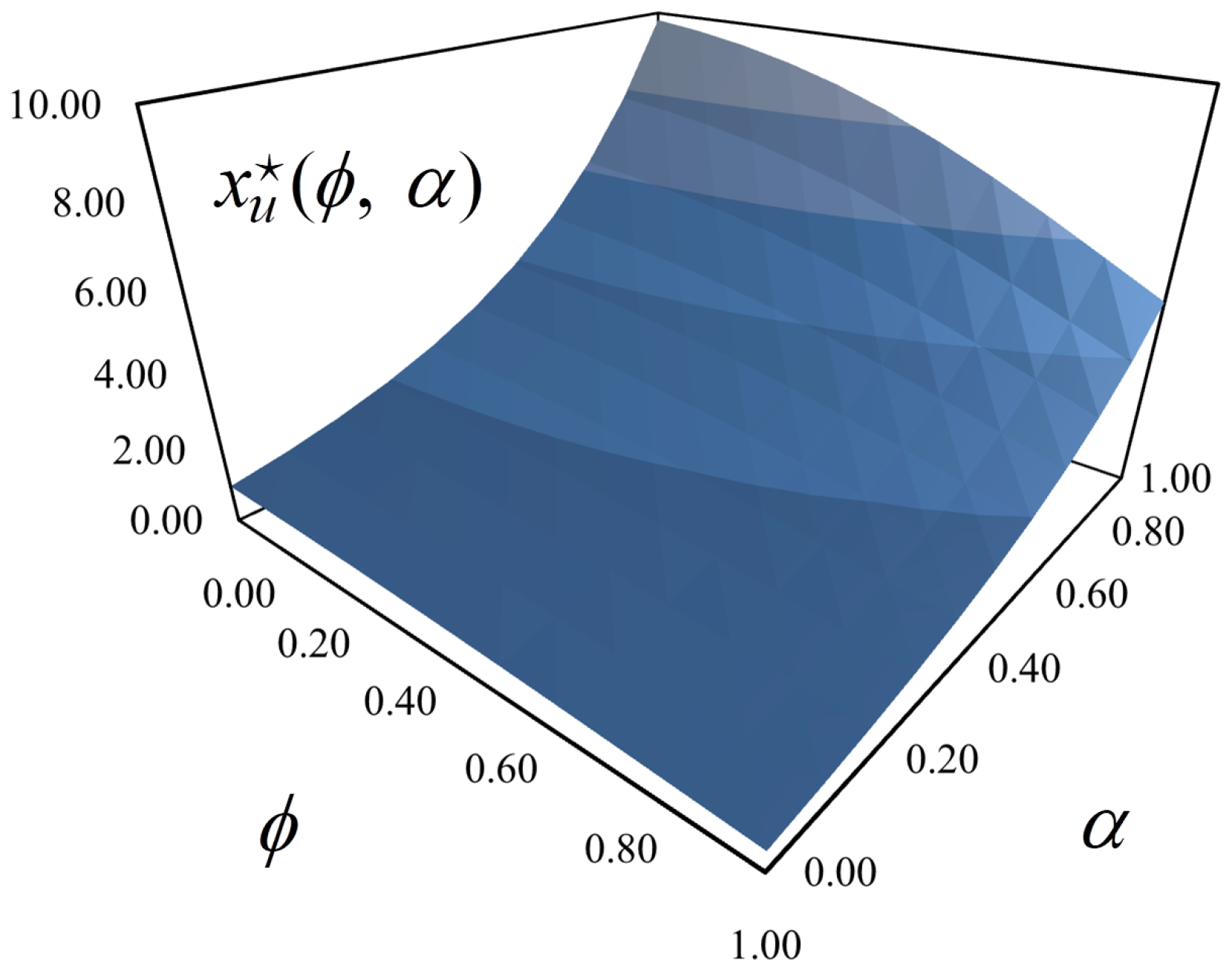
Following the methodology by [45], we have then conducted a simple investigation of the robustness when it comes to decay factor $\alpha$. For example, the relative risk aversion coefficient is defined as being in the vicinity of one ([46]), but there is not yet a commonly accepted estimate. By bounding $\alpha$ between 0 and 1, we ensure that the overweighting cannot take place, which would fall under a completely different paradigm, for we would need to deal with irrational agents.

2.1. Convergent Expectations

By means of identical decay factors ${\alpha }_u,{\alpha }_v\in [0,1]$, such that ${\alpha }_u={\alpha }_v=\alpha$, let players u and v exhibit convergent expectations on the possibility to initiate a trading exchange through the comparison of edge weights. In this case, the condition yields5

$$\begin{array}{c}\hfill \mathbb{E}[x_u\left(t\right)+x_v\left(t\right)]=\mathbb{E}\left[w_{u,v}\left(t\right)\right]\\ \hfill \iff [x_u\left(t\right)+x_v\left(t\right)]\mathbb{P}[(u,v)\in M\left(t\right)]\\ \hfill =w_{u,v}\left(t\right)\mathbb{P}[(u,v)\notin M\left(t\right)],\end{array}$$

(3)

$\forall t\ge 0$, for $u,v=1,...,n$, from which we obtain the following weight in expectation

$$\begin{array}{c}\hfill w_{u,v}\left(t\right)={\left[[x_u\left(t\right)+x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }\right]}^{\frac{1}{1+\alpha }},\end{array}$$

(4)

$\forall t\ge 0$, for $u,v=1,...,n$, $(u,v)\in E\backslash M\left(t\right)$. The notion of Nash solution that captures the rational play in the bargaining game resumes to a stable outcome. The latter comes from pairwise stability, which accounts for the mutual approval of both players. Such a requirement, where the sum of values is maximal, which implies a maximum weight matching ([33]), states that an unrealized exchange between two players cannot be better than the realized one. Put differently, the player cannot earn more by changing its trading partner. Formally,

$$\begin{array}{c}\hfill w_{u,v}\left(t\right)\le {\left[[x_u\left(t\right)+x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }\right]}^{\frac{1}{1+\alpha }}.\end{array}$$

(5)

Each player also has an alternative option, which represents its expected value in case they disagree on how to split the value. Let ${\beta }_u\left(t\right)=w_{u,v}\left(t\right)-x_v\left(t\right)$ and ${\beta }_v\left(t\right)=w_{u,v}\left(t\right)-x_u\left(t\right)$ denote the best alternatives that nodes u and v might obtain had they terminated their current agreements and formed new ones. The former could be interpreted as the threats of players in a match. Then, consider $\mathbb{E}\left[{\beta }_u\left(t\right)\right]$ and $\mathbb{E}\left[{\beta }_v\left(t\right)\right]$ to be the respective expected option values of players u and v such that6

$$\begin{array}{c}\hfill \mathbb{E}\left[{\beta }_u\left(t\right)\right]={\beta }_u\left(t\right)\mathbb{P}[(u,v)\in M\left(t\right)]\\ \hfill =\frac{[w_{u,v}\left(t\right)-x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(6)

$$\begin{array}{c}\hfill \mathbb{E}\left[{\beta }_v\left(t\right)\right]={\beta }_v\left(t\right)\mathbb{P}[(u,v)\in M\left(t\right)]\\ \hfill =\frac{[w_{u,v}\left(t\right)-x_u\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(7)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$. The exchange yields an expected surplus of

$$\begin{array}{c}\hfill \mathbb{E}\left[s_{u,v}\left(t\right)\right]=\mathbb{E}\left[w_{u,v}\left(t\right)\right]-\left[\mathbb{E}\left[{\beta }_u\left(t\right)\right]+\mathbb{E}\left[{\beta }_v\left(t\right)\right]\right]\\ \hfill =\frac{w_{u,v}{\left(t\right)}^{1+\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }}\\ \hfill -\frac{{\left[x_u\left(t\right)-x_v\left(t\right)\right]}^{\alpha }\left[2w_{u,v}\left(t\right)-x_u\left(t\right)-x_v\left(t\right)\right]}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(8)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$. While the stable outcome ensures that the outcome from a matched exchange is always preferred, a stable generalized Nash bargaining solution is an outcome in which the edge endpoints satisfy the Nash bargaining solution at any point of time ([22]). The latter posits that players split the surplus evenly between them, that is, the surplus of u over its alternative equals that of v over its own alternative. In expectation, the Nash bargaining solutions amount to

$$\begin{array}{c}\hfill x_u^{★}\left(t\right)=\mathbb{E}\left[{\beta }_u\left(t\right)\right]+\mathbb{E}\left[s_{u,v}\left(t\right)\right]/2\\ \hfill =\frac{1}{2}\frac{{[x_u\left(t\right)-x_v\left(t\right)]}^{1+\alpha }+w_{u,v}{\left(t\right)}^{1+\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(9)

$$\begin{array}{c}\hfill x_v^{★}\left(t\right)=\mathbb{E}\left[{\beta }_v\left(t\right)\right]+\mathbb{E}\left[s_{u,v}\left(t\right)\right]/2\\ \hfill =\frac{1}{2}\frac{w_{u,v}{\left(t\right)}^{1+\alpha }-{[x_u\left(t\right)-x_v\left(t\right)]}^{1+\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(10)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in M\left(t\right)$.

Proposition 1.

In exchange networks with stochastic matching and convergent expectations of players, the bargaining outcome is stable and thus a generalized Nash bargaining solution.

Proof. 

Following [23], the condition for an outcome to be stable corresponds to the efficiency property of $x_u^{★}\left(t\right)+x_v^{★}\left(t\right)\ge w_{u,v}\left(t\right)$. The sum of individual weights of an edge incident on V is an upper bound on the weight of a matching and thus of an edge at issue. The latter is obtained by assigning values to the nodes—equivalent to their weighting of the matching—such that their sum is greater than or equal to the weight of the edge. Ergo, the individual values of the edges in the matching have a maximal value on G. Provided the values of $x_u^{★}\left(t\right)$ and $x_v^{★}\left(t\right)$, coming from the expressions (9) and (10), and of $w_{u,v}\left(t\right)$, we obtain

$$\begin{array}{c}\hfill x_u^{★}\left(t\right)+x_v^{★}\left(t\right)\ge w_{u,v}\left(t\right)\\ \hfill \iff x_u\left(t\right)+x_v\left(t\right)\\ \hfill \le \frac{w_{u,v}{\left(t\right)}^{{(1+\alpha )}^2}{[x_u\left(t\right)-x_v\left(t\right)]}^{-\alpha }}{{\left({\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }\right)}^{1+\alpha }},\end{array}$$

(11)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$. When the surplus is meant to be split equally, the disparity between the allocations goes to zero or ${[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }\to 0$. This implies that $x_u\left(t\right)+x_v\left(t\right)\le \infty$, which is valid by assumption. Thereby, the Nash bargaining solutions with convergent expectations prove to be stable. □

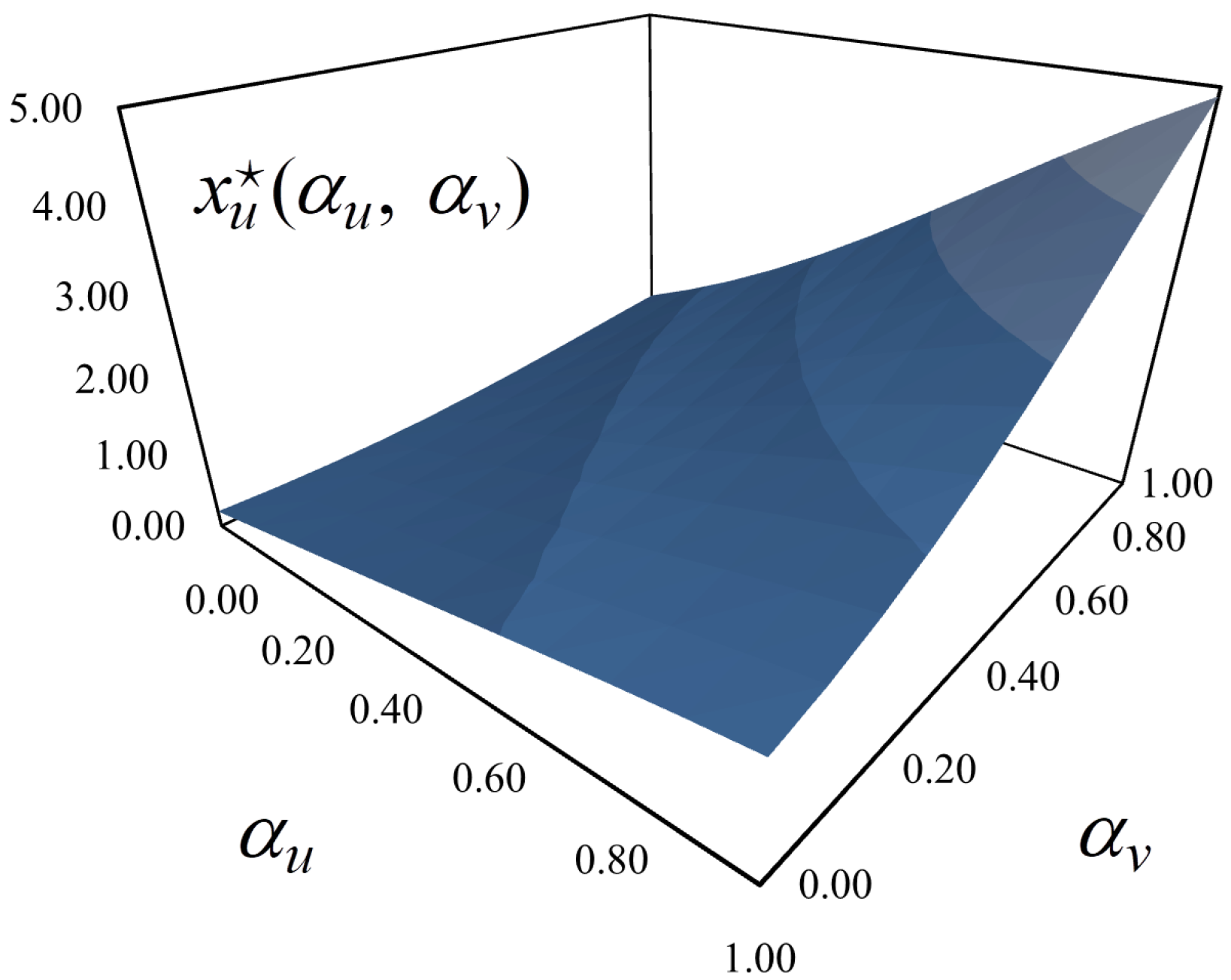
Proposition 2.

In exchange networks with stochastic matching and convergent expectations of players, the generalized Nash bargaining outcome converges to a fixed point.

Proof. 

Following [47], we need to differentiate either $x_u^{★}\left(t\right)$ or $x_v^{★}\left(t\right)$ with respect to time. In point of fact, their similar expressions ought to lead us to an equivalent interpretation of results. Although the bargaining process can be considered to take place in discrete time, the connection between discrete and continuous times enables us to obtain the same conclusion as with the difference operator ([48]). Namely, due to the iterative re-matching process, $\delta x_u\left(t\right)=(x_u(t+1)-x_u\left(t\right))\Delta t^{-1}\simeq \frac{d{x}_u\left(t\right)}{dt}$ at $x_u\left(t\right)=x_u(\Delta t)$. By virtue of fairness in the generalized Nash bargaining solution, such that $x_u^{★}\left(t\right)-x_v^{★}\left(t\right)=0$, we consider an equal split. This is due to the fact that the initial bargaining outcome is not meant to be unfair or unbalanced. Provided the existence of a match and of Nash allocations of u and v, we then deliberately ignore the time evolution of the weighting of alternative player $k\in n_G\left(u\right)\backslash v$. The latter is nonetheless accounted for, by means of the denominator of $x_u^{★}\left(t\right)$ or $x_v^{★}\left(t\right)$, in the network value of exchange. One obtains a final differential equation in the form of

$$\begin{array}{c}\hfill \frac{\left[C(1+\alpha )w_{u,v}{\left(t\right)}^{\alpha }-\alpha w_{u,v}{\left(t\right)}^{2\alpha }\right]w_{u,v}^{\prime }\left(t\right)}{C^2}=0,\end{array}$$

(12)

where $C={\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }$, the solution of which is a constant related to edge value $w_{u,v}\left(t\right)$ to be split between u and alternative player k. As one runs the bargaining dynamics, the Nash bargaining solution converges. A convergence value dependent on the edge weight and on an alternative player reflects the realignment toward the outside option of player u engaging into a new negotiation. The same rationale applies to player v. □

2.2. Divergent Expectations

Now, consider divergent expectations of players u and v through the use of differentiated decay factors ${\alpha }_u,{\alpha }_v\in [0,1]$, where ${\alpha }_u\ne {\alpha }_v$, such that the probability functions rely on different expectations apropos of the comparison of edge weights. Let us in turn differentiate ${\mathbb{P}}_u[(u,v)\in M\left(t\right)]$ from ${\mathbb{P}}_v[(u,v)\in M\left(t\right)]$, such that ${\mathbb{P}}_u[(u,v)\in M\left(t\right)]\ne {\mathbb{P}}_v[(u,v)\in M\left(t\right)]$. They represent the respective probability functions of matching of u and v. The differentiation is based on the earlier distinction between the decay factors. The condition for the expected Nash bargaining outcomes to exist is represented in the form of a Diophatine equation ([49]), which yields

$$\begin{array}{c}\hfill {\mathbb{E}}_u\left[x_u\left(t\right)\right]+{\mathbb{E}}_v\left[x_v\left(t\right)\right]={\mathbb{E}}_{u\times v}\left[w_{u,v}\left(t\right)\right]\\ \hfill \iff x_u\left(t\right){\mathbb{P}}_u[(u,v)\in M\left(t\right)]\\ \hfill +x_v\left(t\right){\mathbb{P}}_v[(u,v)\in M\left(t\right)]\\ \hfill =w_{u,v}\left(t\right){\mathbb{P}}_u[(u,v)\notin M\left(t\right)]{\mathbb{P}}_v[(u,v)\notin M\left(t\right)],\end{array}$$

(13)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$. The use of the equation enables us to assign an expected weight of

$$\begin{array}{c}\hfill w_{u,v}\left(t\right)\\ \hfill =\frac{x_u\left(t\right)\mathbb{P}[(u,v)\in M\left(t\right)]+x_v\left(t\right)\mathbb{P}[(u,v)\in M\left(t\right)]}{{\mathbb{P}}_u[(u,v)\notin M\left(t\right)]{\mathbb{P}}_v[(u,v)\notin M\left(t\right)]}\\ \hfill ={\left[x_u\left(t\right){[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}A+x_v\left(t\right){[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}B\right]}^{\frac{1}{1+{\alpha }_u+{\alpha }_v}},\end{array}$$

(14)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$, $(u,v)\in E\backslash M\left(t\right)$ and ${\alpha }_u\ne {\alpha }_v$, where $A={\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{{\alpha }_v}+w_{u,v}{\left(t\right)}^{{\alpha }_v}$ and $B={\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{{\alpha }_u}+w_{u,v}{\left(t\right)}^{{\alpha }_u}$. Accordingly, the stable outcome corresponds to

$$\begin{array}{c}\hfill w_{u,v}\left(t\right)\\ \hfill \le {\left[x_u{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}A+x_v{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}B\right]}^{\frac{1}{1+{\alpha }_u+{\alpha }_v}}.\end{array}$$

(15)

As for the option values, they now amount to

$$\begin{array}{c}\hfill {\mathbb{E}}_u\left[{\beta }_u\left(t\right)\right]={\beta }_u\left(t\right){\mathbb{P}}_u[(u,v)\in M\left(t\right)]\\ \hfill =\frac{[w_{u,v}\left(t\right)-x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{{\alpha }_u}+w_{u,v}{\left(t\right)}^{{\alpha }_u}},\end{array}$$

(16)

$$\begin{array}{c}\hfill {\mathbb{E}}_v\left[{\beta }_v\left(t\right)\right]={\beta }_v\left(t\right){\mathbb{P}}_v[(u,v)\in M\left(t\right)]\\ \hfill =\frac{[w_{u,v}\left(t\right)-x_u\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{{\alpha }_v}+w_{u,v}{\left(t\right)}^{{\alpha }_v}},\end{array}$$

(17)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$, $(u,v)\in E\backslash M\left(t\right)$ and ${\alpha }_u\ne {\alpha }_v$. The latter serve to compute the updated expression of the expected surplus

$$\begin{array}{c}\hfill {\mathbb{E}}_{u\times v}\left[s_{u,v}\left(t\right)\right]\\ \hfill ={\mathbb{E}}_{u\times v}\left[w_{u,v}\left(t\right)\right]-\left[{\mathbb{E}}_u\left[{\beta }_u\left(t\right)\right]+{\mathbb{E}}_v\left[{\beta }_v\left(t\right)\right]\right]\\ \hfill =\frac{w_{u,v}{\left(t\right)}^{1+{\alpha }_u+{\alpha }_v}}{AB}\\ \hfill -\frac{\left[w_{u,v}\left(t\right)-x_v\left(t\right)\right]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}A}{AB}\\ \hfill -\frac{\left[w_{u,v}\left(t\right)-x_u\left(t\right)\right]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}B}{AB},\end{array}$$

(18)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$, $(u,v)\in E\backslash M\left(t\right)$ and ${\alpha }_u\ne {\alpha }_v$. Finally, the Nash bargaining solutions are equal to

$$\begin{array}{c}\hfill x_u^{★}\left(t\right)={\mathbb{E}}_u\left[{\beta }_u\left(t\right)\right]+{\mathbb{E}}_{u\times v}\left[s_{u,v}\left(t\right)\right]/2\\ \hfill =\frac{w_{u,v}{\left(t\right)}^{1+{\alpha }_u+{\alpha }_v}}{2AB}\\ \hfill +\frac{[w_{u,v}\left(t\right)-x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}A}{2AB}\\ \hfill -\frac{[w_{u,v}\left(t\right)-x_u\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}B}{2AB},\end{array}$$

(19)

$$\begin{array}{c}\hfill x_v^{★}\left(t\right)={\mathbb{E}}_v\left[{\beta }_v\left(t\right)\right]+{\mathbb{E}}_{u\times v}\left[s_{u,v}\left(t\right)\right]/2\\ \hfill =\frac{w_{u,v}{\left(t\right)}^{1+{\alpha }_u+{\alpha }_v}}{2AB}\\ \hfill -\frac{[w_{u,v}\left(t\right)-x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}A}{2AB}\\ \hfill +\frac{[w_{u,v}\left(t\right)-x_u\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}B}{2AB},\end{array}$$

(20)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$, $(u,v)\in M\left(t\right)$ and ${\alpha }_u\ne {\alpha }_v$.

Proposition 3.

In exchange networks with stochastic matching and divergent expectations of players, the bargaining outcome is stable and thus a generalized Nash bargaining solution.

Proof. 

Equivalent to that of Proposition 1. We have

$$\begin{array}{c}\hfill x_u^{★}\left(t\right)+x_v^{★}\left(t\right)\ge w_{u,v}\left(t\right)\iff \frac{w_{u,v}{\left(t\right)}^{{(1+{\alpha }_u+{\alpha }_v)}^2}}{{\left(AB\right)}^{1+{\alpha }_u+{\alpha }_v}}\\ \hfill \ge x_u{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}A+x_v{[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}B.\end{array}$$

(21)

Despite divergent expectations, when the surplus is intended to be split equally, both ${[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_u}$ and ${[x_u\left(t\right)-x_v\left(t\right)]}^{{\alpha }_v}$ will tend to zero. In this way, the left-sided expression has to be greater than or equal to zero, which is verified by $x_u\left(t\right)-x_k\left(t\right)\le w_{u,v}\left(t\right)$, for $x_k\left(t\right)\ge 0$ and $w_{u,v}\left(t\right)\ge x_u\left(t\right)$. As a result, the generalized Nash bargaining solutions with divergent expectations prove to be stable. □

Proposition 4.

In exchange networks with stochastic matching and divergent expectations of players, the generalized Nash bargaining outcome converges to a fixed point.

Proof. 

Equivalent to that of Proposition 2. The rationale yields the following differential equation

$$\begin{array}{c}\hfill \frac{(1+{\alpha }_u+{\alpha }_v)w_{u,v}{\left(t\right)}^{{\alpha }_u+{\alpha }_v}{w}_{u,v}^{\prime }\left(t\right)}{AB}=0,\end{array}$$

(22)

where $A={\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{{\alpha }_v}+w_{u,v}{\left(t\right)}^{{\alpha }_v}$ and $B={\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{{\alpha }_u}+w_{u,v}{\left(t\right)}^{{\alpha }_u}$, the solution of which is a constant related to edge value $w_{u,v}\left(t\right)$ to be split between u and alternative player k, the former being obtained by multiplying both sides of the fraction by $AB$. As one runs the balancing dynamics, the Nash bargaining solution converges. A convergence value dependent on the edge weight and on an alternative player reflects the realignment toward the outside option of player u engaging into a new negotiation. The same rationale applies to player v. □

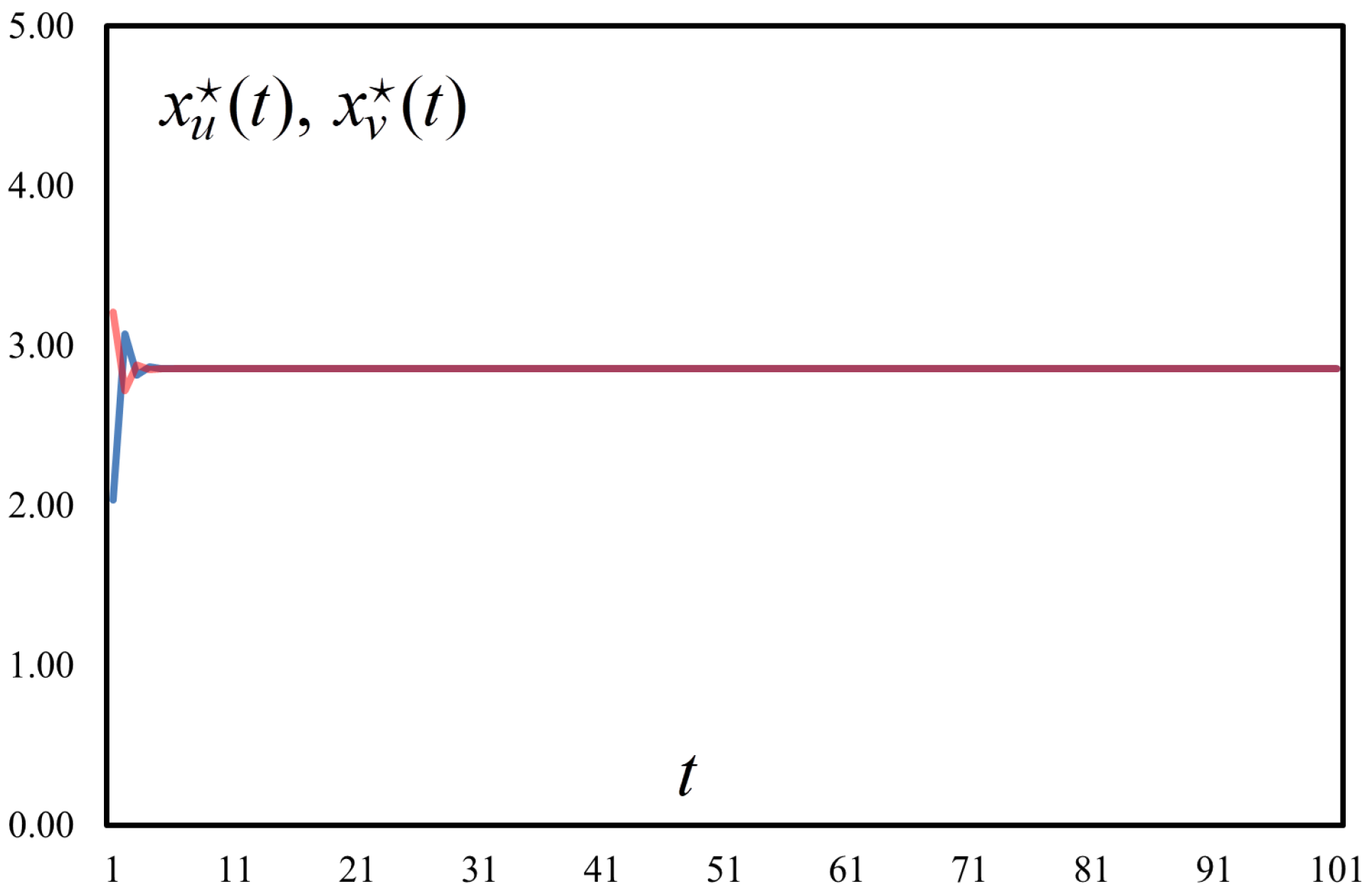
2.3. Social Preferences

It is reasonable to expect that some nodes are likely to have more bargaining power than others ([4,50]). One might also think about the contribution of social preferences or ex-ante preferences for equity ([51]). Social preferences are based upon the postulate that a player sacrifices a positive amount of its share to accommodate the other player’s well-being. In such a context, a player decides to allocate a portion of its value to the other player. Despite the general presumption that social preferences are ignored in settings such as competitive markets, it fails to hold when uncertainty is important ([52]). While maintaining the previous assumption of convergent beliefs, let $\varphi \in [0,1]$ be the outcome share that player u keeps on the edge $(u,v)$, so $1-\varphi$ would be the share value that player v receives ([10,53]). In that case,

$$\begin{array}{c}\hfill \mathbb{E}[[\varphi x_u\left(t\right)+(1-\varphi )x_v\left(t\right)]+x_v\left(t\right)]=\mathbb{E}\left[w_{u,v}\left(t\right)\right]\\ \hfill \iff [[\varphi x_u\left(t\right)+(1-\varphi )x_v\left(t\right)]+x_v\left(t\right)]\mathbb{P}[(u,v)\in M\left(t\right)]\\ \hfill =w_{u,v}\left(t\right)\mathbb{P}[(u,v)\notin M\left(t\right)],\end{array}$$

(23)

$\forall t\ge 0$, for $u,v=1,...,n$ and $k\in n_G\left(u\right)\backslash v$. When $\varphi =1$, player u is only concerned by its own outcome. Otherwise, when $\varphi =[0,1)$, it is also concerned by the allocation that player v obtains. The stable outcome is in the form of

$$\begin{array}{c}\hfill w_{u,v}\left(t\right)\\ \hfill \le {\left[[\varphi x_u\left(t\right)+(1-\varphi )x_v\left(t\right)]+x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }\right]}^{\frac{1}{1+\alpha }}.\end{array}$$

(24)

The corresponding option values are equal to

$$\begin{array}{c}\hfill \mathbb{E}\left[{\beta }_u\left(t\right)\right]={\beta }_u\left(t\right)\mathbb{P}[(u,v)\in M\left(t\right)]\\ \hfill =\frac{[w_{u,v}\left(t\right)-x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(25)

$$\begin{array}{c}\hfill \mathbb{E}\left[{\beta }_v\left(t\right)\right]={\beta }_v\left(t\right)\mathbb{P}[(u,v)\in M\left(t\right)]\\ \hfill =\frac{[w_{u,v}\left(t\right)-[\varphi x_u\left(t\right)+(1-\varphi )x_v\left(t\right)]]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(26)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$. The expected surplus from exchange is now

$$\begin{array}{c}\hfill \mathbb{E}\left[s_{u,v}\left(t\right)\right]=\mathbb{E}\left[w_{u,v}\left(t\right)\right]-\left[\mathbb{E}\left[{\beta }_u\left(t\right)\right]+\mathbb{E}\left[{\beta }_v\left(t\right)\right]\right]\\ \hfill =\frac{w_{u,v}{\left(t\right)}^{1+\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }}\\ \hfill -\frac{{\left[x_u\left(t\right)-x_v\left(t\right)\right]}^{\alpha }\left[2w_{u,v}\left(t\right)-\varphi x_u\left(t\right)-(2-\varphi )x_v\left(t\right)\right]}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(27)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$. Finally, the Nash bargaining solutions endowed with social preferences amount to

$$\begin{array}{c}\hfill x_u^{★}\left(t\right)=\mathbb{E}\left[{\beta }_u\left(t\right)\right]+\mathbb{E}\left[s_{u,v}\left(t\right)\right]/2\\ \hfill =\frac{1}{2}\frac{\varphi {[x_u\left(t\right)-x_v\left(t\right)]}^{1+\alpha }+w_{u,v}{\left(t\right)}^{1+\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(28)

$$\begin{array}{c}\hfill x_v^{★}\left(t\right)=\mathbb{E}\left[{\beta }_v\left(t\right)\right]+\mathbb{E}\left[s_{u,v}\left(t\right)\right]/2\\ \hfill =\frac{1}{2}\frac{w_{u,v}{\left(t\right)}^{1+\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }}\\ \hfill -\frac{1}{2}\frac{[(2\varphi -1)x_u\left(t\right)-\varphi x_v\left(t\right)]{[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }},\end{array}$$

(29)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in M\left(t\right)$.

Proposition 5.

In exchange networks with stochastic matching and social preferences of players, the bargaining outcome is stable and thus a generalized Nash bargaining solution.

Proof. 

Equivalent to that of Proposition 1. The condition for an outcome to be stable yields

$$\begin{array}{c}\hfill x_u^{★}\left(t\right)+x_v^{★}\left(t\right)\ge w_{u,v}\left(t\right)\\ \hfill \iff \frac{w_{u,v}{\left(t\right)}^{{(1+\alpha )}^2}}{{\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }}& \ge & 0,\hfill \end{array}$$

(30)

$\forall t\ge 0$, for $u,v=1,...,n$, $k\in n_G\left(u\right)\backslash v$ and $(u,v)\in E\backslash M\left(t\right)$, with ${[x_u\left(t\right)-x_v\left(t\right)]}^{\alpha }\to 0$. The expression has to be non-negative, which is verified by $x_u\left(t\right)-x_k\left(t\right)\le w_{u,v}\left(t\right)$ given that $x_k\left(t\right)\ge 0$ and $w_{u,v}\left(t\right)\ge x_u\left(t\right)$. □

Proposition 6.

In exchange networks with stochastic matching and social preferences of players, the generalized Nash bargaining outcome converges to a fixed point.

Proof. 

Equivalent to that of Proposition 2. One obtains a time-derivative in the following form:

$$\begin{array}{c}\hfill \frac{\varphi \alpha w_{u,v}{\left(t\right)}^{2\alpha }{w}_{u,v}^{\prime }\left(t\right)}{C^2}=0,\end{array}$$

(31)

where $C={\sum }_{(u,k)\in M\left(t\right)}{[x_u\left(t\right)-x_k\left(t\right)]}^{\alpha }+w_{u,v}{\left(t\right)}^{\alpha }$, the solution of which is a constant, proportional to the surplus share $\varphi$ decided by player u, related to edge value $w_{u,v}\left(t\right)$ to be split between u and alternative player k, the latter being obtained by multiplying both sides of the fraction by C. As one runs the balancing dynamics, the Nash bargaining solution converges. With social preferences, a convergence value dependent on the edge weight and on an alternative player reflects the realignment toward the outside option, supplemented by the surplus share, of player u engaging into a new socially-oriented negotiation. The same rationale applies to player v. □

3. Simulations

Based on the properties and conditions previously obtained, the aim of this section is to illustrate, through numerical simulations, the results previously obtained. Three examples are presented, each of which respectively covers the generalized Nash bargaining outcomes obtained with convergent expectations, divergent expectations and with social preferences. For the purpose of triggering the bargaining process, consider the values of model parameters to be fixed at $w_{u,v}\left(0\right)=10.00$, $x_u\left(0\right)=5.10$, $x_v\left(0\right)=4.90$, such that the initial allocations are slightly unbalanced at $t=0$. That way, the calibration score will be off by at most $0.10$, i.e., $5.10-5.00=0.10$ or $5.00-4.90=0.10$. We can thus choose the edge weight to be convergent to the generalized Nash bargaining solution, which completes the proof ([54]).

3.1. Convergent Expectations

Figure 1 depicts the levels of allocations with convergent expectations. Despite the initial disparity between the allocations, we observe that the Nash bargaining solutions, which are $x_u^{★}$ and $x_v^{★}$, lead to an equal split of surplus, or a stable outcome, for all levels of $\alpha$. As expected, the identical values of $\left\{5,5\right\}$ are obtained at $\alpha =1$. In addition to the validity of Proposition 1, we also see that the continuum of Nash bargaining values takes the form of a concave distribution function, with a bargaining outcome of half the allocation values at $\alpha =0$.

For illustrative purposes, Figure 2 represents the levels of option values. We denote that, given the initial unbalance, the convergence of values alternative to Nash allocations takes place as $\alpha \to 1$. Even if outside options tend to 0 when the expectations head toward 1, they always remain strictly positive. Nevertheless, the continuum of values is subject to an s-shaped distribution, with an inflection point at $\alpha =0.37$, which coincides with the concave rise in the Nash bargaining solutions previously described. In addition, however, the fall in option values is neither proportional nor symmetric to the increase in Nash allocations. This can be justified through the equal split of the exchange value in the Nash bargaining outcomes, the latter exceeding the outcomes obtainable with alternative players.

The convergence dynamics of Nash bargaining solutions is outlined in Figure 3, which has been simulated from the mean coordinates previously presented. The results show a drop in Nash allocations at early time steps, which then stabilize, from $t=13$, at the levels of values alternative to Nash allocations observed at the inflection point located at $\alpha =0.37$. Those are below the Nash bargaining solutions with null expectation of being matched. Thereby, not only do we confirm Proposition 2, but we also find that long-term Nash bargaining solutions are positioned at the coordinates of the outside options subject to iterative re-matching. This implies that, in the long-run, the convergence of Nash bargaining solutions occurs at the levels of expected values in case the players fail to agree: a property that has been found through the convergence toward the outside option.

Result 1.

In exchange networks with stochastic matching and convergent expectations, the bargaining outcome is stable and converges to the fixed value of the outside option.

3.2. Divergent Expectations

Figure 4 and Figure 5 illustrate the levels of allocations with divergent expectations. As can be noticed, the Nash bargaining solutions, which are $x_u^{★}$ and $x_v^{★}$, rise up to the levels of $\left\{5,5\right\}$ when both decay parameters equal 1. The respective values of solutions are found to be similar at low values of ${\alpha }_u$ and ${\alpha }_v$; they are identical at levels close to 1. For this reason, we validate Proposition 3.

The convergence dynamics in case of divergent expectations, where ${\alpha }_u=0.60$ and ${\alpha }_v=0.70$, is pictured in Figure 6. Like in the previous case, we observe a decrease in expected values at the early time interval, which then freeze, from $t=9$, at the level observable with the outside options with $\alpha =0.37$. We validate Proposition 4, and corroborate the convergence of Nash bargaining solutions toward a constant relative to the outside option.

Result 2.

In exchange networks with stochastic matching and divergent expectations, the bargaining outcome is stable and converges to the fixed value of the outside option.

3.3. Social Preferences

With respect to the scenario dedicated to social preferences, Figure 7 and Figure 8, which have been differentiated—due to the inversely proportional share of allocations—by reversing the values of the abscissa, show equivalent patterns of Nash allocations of both. Thus, the simulation results confirm Proposition 5. Another interesting outcome provided by the numerical simulations is that, in expectation, both Nash allocations tend to $\left\{10,10\right\}$ when the share that u keeps to itself heads toward 0. This implies that, with stochastic matching and social preferences, both obtain levels equal to the expected surplus from the trading exchange.

This last result validates the soundness of the model based on reciprocity preferences developed by [55] and extended by [56]. According to those, two players increase each other’s payoffs when they expect to be treated by their partner fairly. In other words, given that v benefits from the social concern of u, it behaves toward its counterpart in a similar manner. Therefore, as $\alpha \to 1$, they both end up having expected allocations that attain the amount of the total surplus.

In case of social preferences, based on an expectation of match of $0.5$, with a level of share fixed to $\varphi =0.80$, the convergence dynamics observed in Figure 9 validates the statement of Proposition 6. After an early swinging in respective allocations, both obtain, from $t=4$, identical Nash allocations throughout the time span. By that, because of reciprocal preferences, the Nash bargaining solutions head toward a constant which—due to the median expectation—is less than proportional to the equal split of the total surplus, but greater than the outside option, for it amounts to a level almost two times higher.7

Result 3.

In exchange networks with stochastic matching and social preferences, the bargaining outcome is stable and converges to the fixed value of the outside option supplemented by the surplus share.

4. Conclusions

This work tried to prove that generalized Nash outcomes, as a result of interacting on exchange networks or assignment markets, can be achieved in the case of a stochastic matching subject to various forms of expectations, which, to the best of our knowledge, has not been considered in the study of matching markets. The model outputs explain the perenniality of market-driven economies grounded in a countless number of unconstrained and randomly established trade connections ([57]). Distinct types of expectations of market players do not prejudice such long-term outcomes. The convergent fixed point is also shown to be identical, both in allocations and in time quantiles, in the cases of convergent and divergent expectations. Conversely, the social preferences’ scenario comes with larger velocity toward convergence. Furthermore, the preferences for reciprocity generate the highest expected outcomes between the three cases in point. Subsequently, the concern for inequity aversion ([58,59]), promoted as a constitutive element of pathways toward sustainable development, does find an economic justification in market-based coordination mechanisms.

Unlike the assumption encountered in the literature, where agents are either fully aware of the best alternatives of their neighborhood ([60]) or they lack knowledge about the availability of a matching partner ([61]), we can consider our players to be pseudo-strategic, for the probability of matching depends on the measurable difference between the weights of edges. Put another way, players are provided with information on the best alternative of their neighborhood: they can deduce the expectations of their neighborhood. This attribute can give a reason for the stability of outcomes along the timeline. It also provides consistency between our results—obtained inside networked architectures—and those of [62,63], who justify, through the comparison of alternatives, the partitions between two players. In consequence, our results do have a game-theoretic meaning. However, we do not provide the informational assumption of common knowledge, which categorizes them among the models of incomplete information and of bounded rationality.8 Even if these characteristics prevent an immediate stable allocation ([65]), a stochastic process with repeated re-matching leads to stochastically stable core allocations ([66]).

Despite the fact that our work can be considered as an extension of or as a complement to the existing literature, complementary works on stochastic shocks and on risk-transfer allocations ought to be conducted. Likewise, we do not take account the possibility of having multiple simultaneous possibilities of matching. This topic could also be studied in an additional work, by dint of implementation of an ordering rule, in the sense of [67] that would sort out the subset of compatible partners. Taking into account a form of aversion to fairness, which could be representative of the rational and selfish nature of economic agents ([68,69]), could just as much be the subject of appended investigation. Finally, our findings may, to some degree, be relevant for control engineering when it comes to decision-making in uncertainty. For example, the blockchain technology proposed for smart grid applications in the electricity sector could undergo specific negotiation protocols ([70]). The consideration of cognitive radio networks with externalities may be a further interesting study field ([29]).

In summary, let us state that the model is a simplified representation of stochastic bargaining in real-world complex trading systems. We stress that our findings should be read as those of an exploratory work. Therefrom, their interpretation must be undertaken with a reasonable level of caution.