1. Introduction
Katherine Coman, in the first paper that appeared in the American Economic Review over 100 years ago [
1], discusses the need for large collective investments that could transform the lands in the American Midwest from prairies into the nation’s breadbasket. She focuses on the collective action problems associated with bringing farmers together to invest into and maintain groundwater irrigation systems.
1 Most of the steps she recommended in the article were subsequently taken.
From a game-theoretic perspective, farmers overcame the collective action problem, because, given a number of initial infrastructural investments (e.g., street and railroad networks, storage and collection facilities, etc.), further investment decisions were strategic complements. That is, individual costs decreased with investments overall (e.g., existing canalization, pumping and irrigation systems made extensions thereof cheaper), and it became increasingly profitable for farmers individually to participate, which eventually caused a rush to farm in the Midwest.
Today, irrigation technologies are efficient and relatively cheap. The problem has not been for a long time that farmers fail to access groundwater. Instead, collective over-usage with resulting depletion and pollution of groundwater reservoirs has been a major concern globally, in particular in the Midwest of the United States of America. The Global Groundwater Crisis is underway:
“Groundwater is being pumped at far greater rates than it can be naturally replenished, so that many of the largest aquifers on most continents are being mined, their precious contents never to be returned. These include the North China Plain, Australia’s Canning Basin, the Northwest Sahara Aquifer System, the Guarani Aquifer in South America, the High Plains and Central Valley aquifers of the United States, and the aquifers beneath northwestern India and the Middle East. Nearly all of these underlie the word’s great agricultural regions and are primarily responsible for their high productivity.” ([
2], page 946).
An important aspect to understanding groundwater usage is whether farmers’ decisions to pump (more or less) groundwater are strategic complements or strategic substitutes, that is, if others’ increased groundwater usage decreases a farmer’s marginal cost of pumping (as would be the case with complements) or increases a farmer’s marginal cost pumping (as would be the case with substitutes). Understanding the strategic dependencies of farmers’ decisions is relevant, because the nature of the strategic incentives determines the dynamic risk of tragedy of the commons [
3], in particular whether the same rush to over-exploitation as well-known from over-fishing scenarios [
4], for the first discussions of the ’race to fish’) ought to be expected also in the groundwater context.
In Part I [
5] of our study of observational data of groundwater usage from the American Midwest, we come to the conclusion that farmers’ decisions were strategic complements. The approach we take in that paper is a network regression framework with instrumental variables. We reject strategic substitutes in favor of strategic complements. The underlying data from that study are from one of two farming districts that we consider here in this paper. Here, we consider data from a second district and take a different analytical (revealed preference) approach, ultimately reaching the same conclusion regarding the nature of the strategic interaction in favor of strategic complements, not substitutes. We refer the reader to our companion paper for a broader motivation of the Global Groundwater Crisis.
In the present paper, we build on theory by [
6] to formulate a general class of games for our groundwater interactions. We propose new non-parametric revealed preference tests of strategic substitutes versus strategic complements in groundwater usage for this class of games that we conduct on a dataset from two farming districts in Nebraska. There are three closely related papers. First and foremost, our own companion paper is related, which we discussed in the paragraph above. Second, Ref. [
7] propose the type of revealed preference test procedure that we shall adapt. Their model is Cournot, and their application is testing for collusion amongst Organization of Petroleum Exporting Countries (OPEC). Our setting is a dynamic CPR game, and considers groundwater decisions by individual farmers. Third, Ref. [
8], adapting [
7], test and reject canonical (static) tragedy-of-the-commons models as proposed by Gordon in a fishery setting. Their use of revealed preference tests inspired our formulation of a more permissive and–in our views crucially–dynamic model that allows to test strategic complements versus strategic substitutes, hence we have a different use case (groundwater) and a different angle (dynamic). For a recent paper on dynamic game theory of CPR dynamics, see [
9]. For some recent papers focussing on dynamic game theory and policy, see [
10,
11].
2. The Application
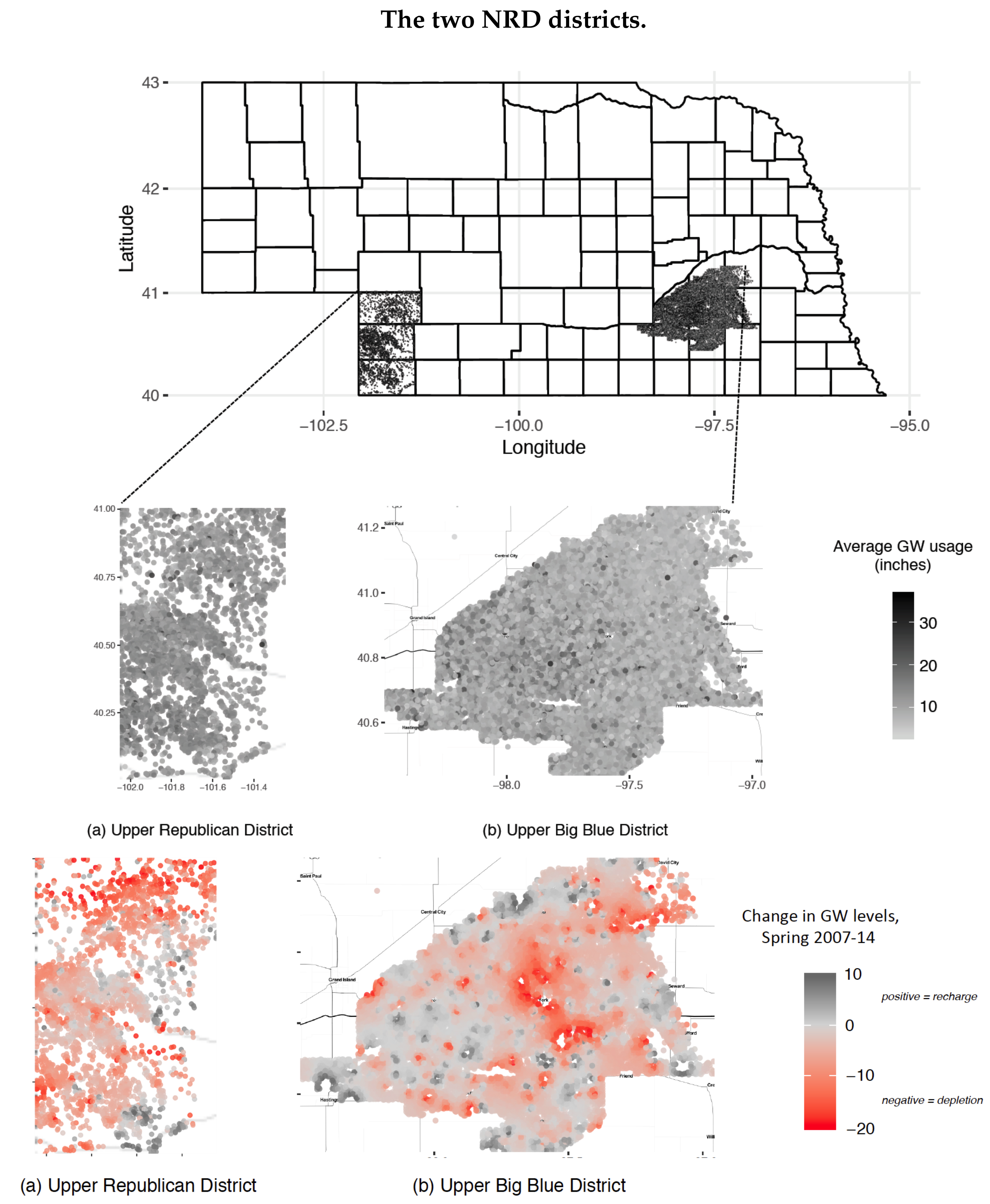
The datasets considered in this paper concern two of the 23 Natural Resources Districts (NRDs) that govern groundwater pumping in Nebraska, namely the “Upper Big Blue” NRD (UBB) and “Upper Republican” NRD (URD). The two are particularly interesting districts in the context, because the UBB is the largest district that has not implemented
any restriction on groundwater usage, and the URD is the first district that introduced restrictions via quotas. Data from the UBB was considered in [
5], which pursued a parametric analysis that was not suited for the URD dataset.
We refer the reader to an extended working paper version of our work on the subject in [
12] for a detailed discussion of the context of our data, particularly of the local farming context. However, here are some interesting facts: The UBB has 15% (2%) of Nebraska’s (America’s) irrigated acres, making it one of the most important agricultural districts in the United States. It is and has been entirely policy-free, placing no restrictions on pumping. The only formal rule is that usage has to be monitored by meters. This rule was put in place in 2006, which is why our UBB data start in 2007.
2 The URD is roughly half the size of the UBB in terms of groundwater irrigated land. Unlike the UBB, the URD was the first district in Nebraska to introduce a
quota policy to govern individual-level groundwater usage. The policy requires farmers to pump less groundwater than a certain set quota over the course of five years (with usage being monitored via meters comparable to those used in the UBB since 2001); farmers who fail to do so are subject to a fine. The first quota was implemented from 1982–87, allowing farmers to pump 80 inches. Since, this quota was decreased to 75 for 1988–92, 72.5 for 1993–2007, 67.5 for 2008–12, and 65 for 2013–17. Our data cover 2001–2014.
3For each of the circa 10,000/3000+ farmers in UBB/URD, we have data on total groundwater usage for each season, which amounts to nearly 150,000 observations, with latitude-longitude coordinates and acres serviced. See
Figure 1 for the spatial location of farmers, and for changes in groundwater levels. Based on location data, we define what hydrologists call the “
radius of influence”, within which local drawdown of the groundwater table is measurable by the end of a farming season. This radius ranges from 200ft to a mile [
13]. In addition, we have relevant water table data for UBB and URD for our years of interest that measures within- and between-season depletion at over 500 locations, pre- and post-season, which allows us to obtain estimates for our whole dataset by interpolation.
4 Other controls concern depths of wells, ground transmissivity, soil types, seasonal rain and temperature, and average prices of corn (70% of production is corn), electricity and farmland rental. Our core dataset considers the years 2008–2012, which spans one full quota period for the URD, and for which we have the full set of data for both districts. See
Table 1.
5 3. Dynamic Game Setup
Building on [
6], we model the groundwater interaction by a class of games that subsumes both policy-free and quota-policy environments relevant for UBB and URD. Each game consists of four ingredients:
(
Section 3.1.2) Intra-seasonal groundwater depletion due to pumping.
Definitions are in bold. For notation, we let and .
3.1. Groundwater Games
Consider a set of farmers
producing (possibly different) crops during each season
. The farmers are the active players in our game.
6 Each farmer
is characterized by a land-size
. For every
, farmers plant crops in spring and harvest in the late summer, and in between pump groundwater in order to increase crop yield (or total supply that can be sold after harvest). We denote farmer
i’s action space in season
as
. An element
represents groundwater usage-per-acre (this is the unit in
Figure 1), and
represents the total volume of groundwater pumped.
3.1.1. Revenue
Farmers make revenue by selling crops at the spot market (at possibly different prices in October, November or December) or on the futures market. Alternatively, farmers can store crops in long-term storage facilities (e.g., for raising cattle or selling later on). To capture these diverse revenue streams, we define a revenue function , which may be both farmer- and season-dependent, thus controlling for different yield and sale strategies across farmers and price changes across seasons. We assume that is absolutely continuous and concave in .
3.1.2. Intra-Season Groundwater Depletion
Groundwater usage and recharge determine the evolution of the resource. Here, we first focus on how groundwater levels change during the season as a result of farmers pumping. For farmer in season , we denote as the distance between the water table level and wellhead in the spring. We denote as this distance when farmers stop pumping (i.e., at the beginning of harvest). Two dynamics determine .
The first is due to aquifer-wide groundwater withdrawals,
, where depletion is offset by recharge from rain,
. We define
as a global depletion function, which we assume is (i) absolutely continuous and nondecreasing in
and (ii) slowly changing in individual groundwater-usage (i.e.,
for any
).
7 We then let
represent the decline/recharge of
i’s groundwater level that is caused by aquifer-wide groundwater withdrawals.
The second type of change is a local, heterogeneous depletion called
local drawdown, which is a widely used measure of how much the groundwater table reduces locally before it equilibrates with the surrounding aquifer as water travels through rock slowly.
8 Let
denote the set of farmers inducing local drawdown on farmer
i. The groundwater-usage of these farmers is
. We define
as a local drawdown function, which is assumed to be absolutely continuous and nondecreasing in
. We then let
represent the local decline in
i’s groundwater level due to local drawdown.
A farmer’s groundwater level at the start of harvest is the result of local and global depletion:
3.1.3. Cost of Pumping Groundwater
The cost of pumping groundwater is proportional to the distance between water table and the pump wellhead, which is increasing as farmers pump. We capture the costs that accrue from a changing pumping distance through
where
is the farmer-specific energy cost of pumping, which takes into account whether the farmer has a diesel or electricity pump, the age of the pump, etc. The interpretation of (
2) is that, taking other farmers’ groundwater usage as given, a farmer accounts for self-imposed costs associated with his/her own contribution to the depletion he/she experiences.
3.1.4. Future Profits
We suppose that every farmer is forward-looking and anticipates that present groundwater usage impacts future payoffs. For many farmers, future profits can be extrapolated from the amount of groundwater available next season. Farmers may also use neighbors’ groundwater-usage a means of extrapolating local groundwater depletion, which may be more important than global depletion concerns (see [
5,
12]).
We capture the possibly diverse ways of viewing future profits via , where represents farmer i’s perceived future profits in seasons if others’ groundwater is and i’s groundwater-usage is . We make two assumptions about . The first is that is absolutely continuous in all variables. The second is that is concave in for each , which means that the marginal self-imposed cost of depletion is increasing. As we show below, the latter assumption is permissible enough to explain real-world data.
There are several ways to derive
from first principles, which opens the possibility of taking into account discount factors, future groundwater-usage decisions, and information. While doing so is beyond the scope of the present paper, we refer the interested reader to [
14] for one possible derivation of
.
3.1.5. Profits
A farmer
i’s profit function is given as
A farmer’s goal in season
t is to maximize
.
3.1.6. Definition of Groundwater Games
Having described the model ingredients and assumptions, we can now define a groundwater game formally.
Definition 1. A groundwater (GW) game consists of revenue functions , a global depletion function , local drawdown functions , energy costs , and future profit functions , which, together, form a non-cooperative game at each time period: 3.2. Integrating a Quota Policy
Because one of our datasets is from a district (the URD) where a specific quota policy exists, it is worth considering how such an environment could fit into the class of GW games. The type of quota policies considered here work as follows. Going into a quota period, the URD first estimates the total amount of groundwater usage that can be withdrawn sustainably, which determines the overall quota. Each farmer can then pump up to his/her share of that quota over the span of T-years, where for the URD. If any farmer uses more (less) than his/her quota by X amount, then his/her quota is reduced (increased) by X during the next quota period.
To see how such a quota policy fits into a GW game, consider
. First note that, because the quota has no
immediate impact on profits, we can relegate the strategic consequences of the quota to the future profit function. That is, the profit function of a farmer pumping groundwater under a quota policy is given as
where
added to
reflects the future consequences of using more/less than the quota. The second line of (
3) follows by treating
past decisions,
, as
exogenous variables. This means that such terms can be incorporated into
via the superscript
t.
The main takeaway is that a quota policy is already included in the class of GW games. This feature plays an important role in our analysis below.
3.3. GW Games Can Rationalize Any Dataset
We aimed to define our model as generally as possible so as not to depend on arbitrary parameterizations. Compared with the revealed preference test procedure that also concerns a CPR setting by [
8], we introduce a future profit dimension to the problem. Now we ask the question:
can GW games account for real-world groundwater-usage behavior? Given the size and permisiveness of the class of GW games defined above, it is perhaps unsurprising to find that the answer is ’yes’ in general, before we introduce further restrictions through strategic substitutes versus complements assumptions.
3.3.1. Dataset
Our goal is to show that GW games can rationalize
datasets. A dataset concerns farmers
in seasons
. For each season, each farmer’s groundwater usage
is observed. Several control variables are also observed, including farmers’ land-size
, groundwater levels at the beginning of the season
, and rainfall
. A
dataset is the collection of such observations:
3.3.2. Rationalizability
We say that a GW game can rationalize a dataset if the Nash equilibrium of the GW game coincides with observed behavior. We formalize this notion in the following definition.
Definition 2. A dataset is rationalizableif there exists a GW game such that, for each and , In other words, rationalizability says that, at each observation t, each farmer i’s observed groundwater usage maximizes profit given the groundwater usage of other farmers.
3.3.3. A Characterization of Rationalizability
It turns out that rationalizability of a dataset is characterized by a linear program, which we call the GW program.
Definition 3. For a dataset , there exists a solution to the GW programif and only if there are positive numbers that satisfy the following three conditions:
(CGD) Common global depletion, (MGD) Monotone global depletion, (MLD) Monotone local depletion,
The logic of the GW program works as follows. First, a dataset is substituted into the system of linear equations above to create the GW program. Second, the GW program works by identifying positive numbers that solve the system of linear equations—if such coefficients exist. It turns out that the existence of a solution to this system provides the key to determining whether or not GW games can rationalize UBB and/or URD data.
The following theorem is the first theoretical contribution of this paper, which shows that the GW program is necessary and sufficient for rationalizing a dataset with a GW game.
Theorem 1. The following sentences about are equivalent:
- (A)
There exists a solution to the GW program defined by .
- (B)
is rationalizable by a GW game.
In other words, Theorem 1 provides a non-parametric test that works as follows: (sufficiency) if there is a solution to the GW program, then there is at least one GW game, policy-free or with a quota policy, that can rationalize a dataset; (necessity) if there does not exist a solution to the GW program, then no GW game can rationalize the dataset of interest. This means that, by virtue of being necessary and sufficient, studying the GW program is equivalent to studying whether we can account for behavior in the UBB and/or URD using a GW game.
The proof of Theorem 1 clarifies what each part of the GW program represents. (CGD) represents the assumption that farmers are optimizing profits whilst drawing from a common resource (hence the = sign). (MGD) is derived from the assumption that global depletion is nondecreasing in aquifer-wide groundwater withdrawals. Finally, (MLD) represents the assumption that local drawdown is nondecreasing in local groundwater-usage.
There are two somewhat surprising features of Theorem 1. First, we find that the non-parametric class of GW games is characterized by a parametric, simple, and easy-to-implement linear system of equations. Second, we find that the same test can be used to study policy-free datasets and quota policy datasets. This means that we have a somewhat unique opportunity to compare strategic behavior in policy-free vs. policy regions in an unbiased manner.
3.3.4. Rationalizing Behavior in the UBB and URD
By means of Theorem 1 and the GW program, it is relatively straightforward to show that
any dataset can be rationalized with a GW game. Consider some arbitrary
. For all
and
, let
—this means that (MLD) is always satisfied. For all
and
, let
. Consequently,
for every
and
, which means that (CGD) and (MGD) are always satisfied. Taken together, a solution to the GW program always exists for any dataset. It thus follows from Theorem 1 that both the UBB and URD datasets are rationalizable via a GW game. This observation is perhaps unsurprising as it reflects the many folk theorems that exist for these types of games [
15,
16,
17].
We summarize this observation in the following corrollary.
Corollary 1. Any dataset is rationalizable by a GW game.
Although GW games as stated above do not have any testable predictions, there are two advantages of using this framework as a starting point. First, we assure ourselves of studying a sufficiently general class of models that can describe UBB and URD behavior. Second, this generality helps clarify the role of any additional assumptions we impose on GW games below for our purpose of testing strategic substitutes versus complements.
4. Revealed Preference Results
In this section, we test whether those games exhibiting strategic substitutability or strategic complementarity within the class of games we proposed in the previous section are able to rationalize our groundwater data. In sum, our hypotheses are as follows:
Substitutes null hypothesis,: Farmers’ groundwater-usage decisions are strategic substitutes.
Substitutes alternative hypothesis, : Farmers’ groundwater-usage decisions are strategic complements, or neither strategic substitutes nor complements.
Complements null hypothesis, : Farmers’ groundwater-usage decisions are strategic complements.
Complements alternative hypothesis, : Farmers’ groundwater-usage decisions are strategic substitutes, or neither strategic substitutes nor complements.
In this section, we pose our null hypotheses as revealed preference tests. We do so in two steps. First, we incorporate strategic substitutes and complements into the class of GW games defined above. Second, we identify linear programs that are necessary and sufficient for checking whether there exists any GW game with strategic substitutes/complements that can rationalize our data. We conclude by presenting empirical results. In the end, our main finding is a resounding rejection of strategic substitutes in favor of complements.
4.1. Strategic Substitutes vs. Complements
Following [
18], strategic substitutes and complements are defined according to marginal cost. We say
i’s and
’s pumping decisions are strategic substitutes (complements) if a decrease in
increases (decreases)i’s marginal cost of pumping. The comparative statics consequence is that, if
decreases groundwater-usage, then
i has the incentive to free-ride (reciprocate) by increasing (decreasing) groundwater-usage (we formalize this comparative statics observation in
Appendix A.3.2).
Equivalently, strategic substitutes (complements) can be defined in terms of submodularity (
supermodularity). We say that
is submodular (supermodular) in
if
ceteris paribus implies that, for each
,
Submodularity (supermodularity) means that decreasing
increases (decreases)
i’s marginal cost of pumping.
9We incorporate strategic substitutes and complements in GW games in the following way.
Definition 4. A tuple is a GW game with strategic substitutes (complements) if, for every and :
- (i)
and ;
- (ii)
is submodular (supermodular) in .
As discussed above, the second assumption distinguishes between strategic substitutes and complements. The first assumption is needed to derive meaningful revealed preference tests. The first part of this assumption asserts that revenue and future profits functions are the same across seasons. This is obviously a strong condition, and its consequences are clear in the final results—however, we can somewhat attenuate this condition with our test procedure described below. The second part of this assumption, , asserts that neighbors’ behavior is sufficient to formulate future profits. This can be viewed as a condition that emphasizes the importance of locality for groundwater-usage decisions (and, it turns out, this condition is particularly important for deriving the revealed preference tests below).
4.2. A Test Based on Revealed Preferences
Our test of the null hypotheses is based on Definition 4. We are interested in whether strategic substitutes—
—and/or strategic complements—
—can characterize real-world behavior. The test procedure is similar to
Section 3.3. We find evidence in favor of (against)
if, for a given dataset
, we can (cannot) find a GW game with strategic
substitutes that can
rationalize (see Definition 2 for the definition of ’rationalize’). We find evidence in favor of (against)
if, for a given dataset
, we can (cannot) find a GW game with strategic
complements that can
rationalize .
Similar to Theorem 1, we operationalize our test procedure by means of a linear program, which builds directly on the GW program (see Definition 3).
Definition 5. For a dataset , consider the following equations:
There exists a solution to the GW program with strategic substitutes if and only if there are nonnegative numbers that satisfy (CGD, MGD, MLD) and (SUBS).
There exists a solution to the GW program with strategic complements if and only if there are nonnegative numbers that satisfy (CGD, MGD, MLD) and (SUBS).
The following theorem is the second main theoretical contribution of this paper, which shows that the GW program with strategic substitutes (complements) is a necessary and sufficient for rationalizing a dataset with a GW game with strategic substitutes (complements).
Theorem 2. The following sentences about are equivalent:
- (C)
There exists a solution to the GW program with strategic substitutes (complements) defined by .
- (D)
is rationalizable by a GW game with strategic substitutes (complements).
Similar to above, Theorem 2 provides a straightforward way of testing whether farmers’ behavior exhibit strategic substitutes vs. complements. This test is nonparametric, simple, and easy to implement as a system of linear equations. In addition, we can employ this test on both UBB and URD data, which provides us with an unbiased way of comparing behavior in a policy-free vs. policy region.
4.3. Test Setup
In implementing the GW program, testing all UBB and URD data at the same time with a somewhat unforgiving revealed preference test is perhaps not the most informative test. We are trying to account for nearly 15,000 farmers and 100,000 decisions. If a single farmer is acting ’irrationally’ or a single decision is ’irrational’, then the test will fail and we loose information about how the remaining farmers are behaving. This is one of several issues we can overcome by taking a more nuanced testing approach.
Following [
7], we run the GW program on subsets of UBB and URD data, with each subset consisting of
farmers over two consecutive seasons. All our tests take a two-period view exclusively. It follows from Theorem 2 that the GW program with strategic substitutes (complements) is necessary and sufficient for any subset of the data to be rationalized by a GW game with strategic substitutes (complements). We also restrict attention to
farmers who are mutual neighbors.
10 This is because our goal is to test farmers who are likely to view each others’ actions as strategically interdependent—this argument is more compelling for farmers in a one mile proximity rather than, e.g., a thirty mile proximity.
As noted above, there are several advantages to testing subsets of our data, rather than the entire dataset. First, we exclude the possibility that the GW program is rejected because a few farmers are not responding optimally to others. Second, running the test on subsets of the data mitigates errors that might result from unobserved variable bias. It is very likely that idiosyncratic shocks impact farmers’ behavior during the season, such as the mechanical failure of a center pivot irrigator, which may render behavior as seemingly irrational. Third, we rule out the possibility of spurious rejection rates due to farmers learning and innovating to improve their farming practices between seasons. Such learning can change a farmer’s revenue function and/or cost function over time, which is a process that is not captured by the class of GW games presented above. Looking at smaller samples addresses this issue. Finally, as is made clear below, we demonstrate the ability of the test to reject behavior on a small number of observations notwithstanding the permissiveness of our non-parametric framework.
Unlike [
7] (and also [
8]), the size of our dataset renders it computationally impossible to sample over the 4.7 trillion farmer pairs, 3.7
farmer quadruplets, let alone each consecutive time sequence. We thus randomly sample subsets of our data, run the GW program on each such subset, and record the percentage of cases with a solution to the corresponding GW program—we call this the
acceptance rate. In doing so, we can leverage the law of large numbers and randomly sample until we reach a convergence in the rejection rate (in practice, running the GW program on 1000 random sub-samples is sufficient).
4.4. Results
Results for the UBB can be found in
Table 2. Each reported number is an
acceptance rate, and it is interpreted as the probability of sampling a subset of farmers whose behavior is rationalizable by a GW game with (Panel A) strategic substitutes or (Panel B) strategic complements. Acceptance rates are clearly decreasing in the number of farmers, because, if a dataset consisting of (e.g.,) five farmers passes the GW program test, then any subset of this dataset involving four or less farmers will also pass the GW program test. This is unsurprising because of the season-independence assumption made in the definition of GW games with strategic substitutes/complements. For the UBB, we find that the GW programs with strategic substitutes exhibit low acceptance rates compared with high acceptance rates for strategic complements.
Following [
22], we evaluate the explanatory power of our revealed preference results discussed above based on [
23]’s
index for predictive success, which accounts for prediction accuracy
and precision. With
A for accuracy and
P for precision, Selten’s index is given by
In our case,
A represents the acceptance rate reported in
Table 2. We estimate the precision associated with GW games by assuming that
(40 in is the most common groundwater-usage observed in our datasets). We randomly sample
and farmers, and then run the GW program with strategic substitutes/complements;
P is then the acceptance rate using this randomly sampled data. See
Table 3 for the results. The evidence shows that strategic complements are more successful at predicting behavior than substitutes in the UBB: with strategic substitutes, we find that
for each
case; this means that the theory is systematically predicting the wrong region of
; by contrast, with strategic complements, we find that
for each
case.
The URD results are reported in
Table 2 and
Table 3. A similar pattern emerges as for the UBB. Strategic complements describe better than strategic substitutes. However, the difference is not as stark as for the UBB. While strategic complements rationalizes 25% more UBB data than strategic substitutes, we find that only 7% more URD data are rationalized by strategic complements than strategic substitutes. This qualitative confirmation of the UBB with a smaller differential is also confirmed by the predictive success comparison.
4.5. Robustness Check: Larger N
Our main results were reported for neighborhoods of eight farmers or less. We now repeat the analysis for
(we stopped at 300 because of computational limitations) for both the UBB and URD. The question here amounts to asking whether the long-term trend of acceptance rates go up or down for the strategic substitutes/complements models—if both acceptance rates go down, then our results might not map to UBB- and URD-wide behavior more generally. We report our findings in
Figure 2. They reinforce the findings in
Table 2 and
Table 3: especially for large
N, strategic complements is a better predictor of behavior than strategic substitutes. In both the UBB and URD, acceptance rates for the GW program with strategic complements
increases with increasing
N. The opposite is true for the strategic substitutes, where acceptance rates
decrease with increasing
N. The difference in explanatory power is most obvious in the UBB for
: in this case, GW games with strategic complements rationalizes nearly 80% more data than GW games with strategic substitutes.