A Qualitative Game of Interest Rate Adjustments with a Nuisance Agent
Abstract
1. Introduction
2. What Are Viability Problems and Their Solutions?
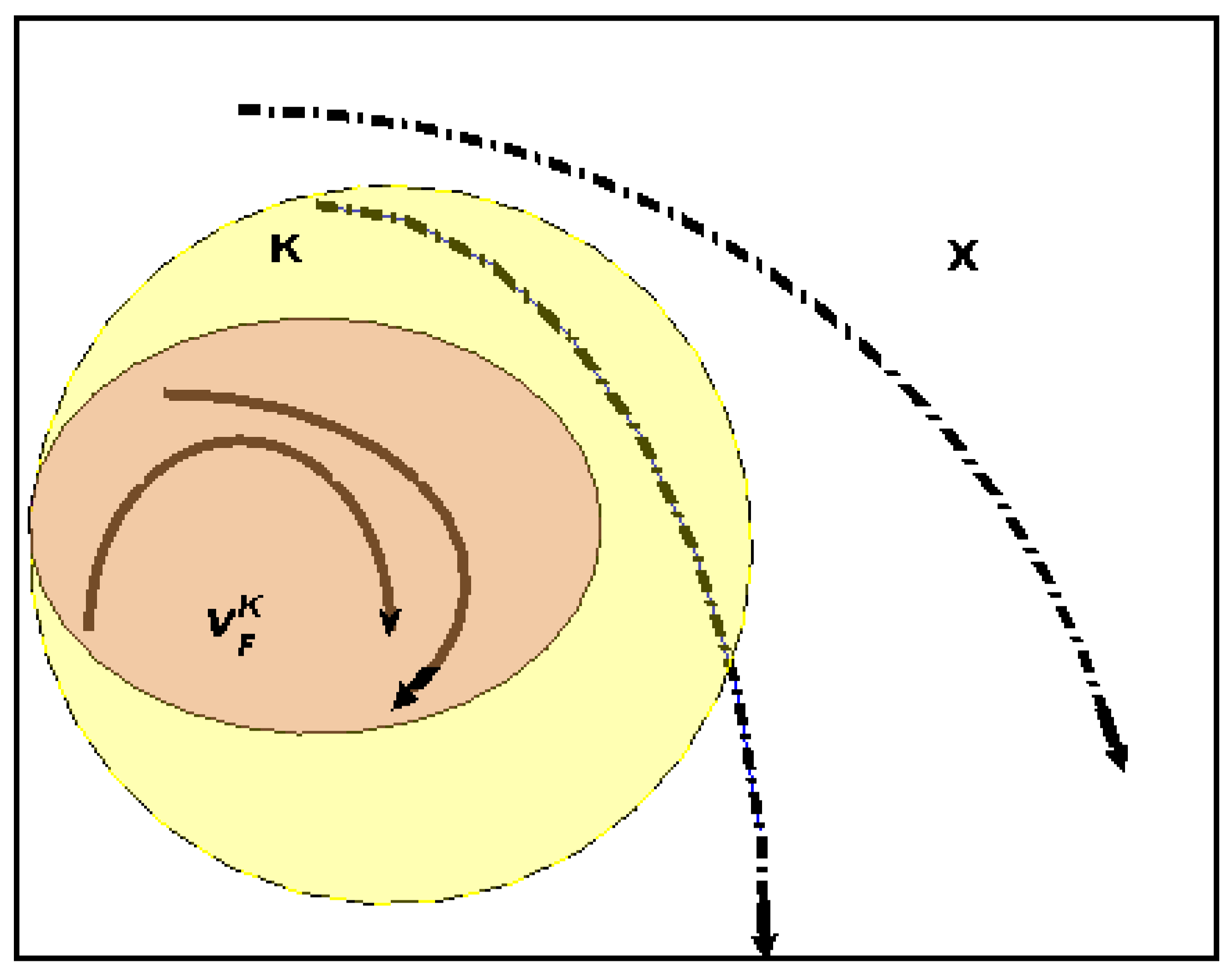
2.1. The Meaning of Viability
2.2. Mathematical Formulation
2.3. A Qualitative Game
3. A Macroeconomic Model
3.1. A Viability Theory Problem
3.2. The Central Bank’s Problem
- I.
- Output gap is the log deviation of actual output from “natural” output. Since this is a log deviation, it is interpreted as a fraction of natural output.
- II.
- Inflation is defined as the CPI inflation rate. The symbol denotes the deviation of CPI inflation from a reference value of inflation.
- III.
- Interest rate is the short-term nominal interest rate that is used by the central bank as the policy instrument. We denote the deviation of the nominal interest rate from its reference value by .Both rates are expressed as fractions rather than percentages. We also follow the convention in this literature by considering annualised rates. The reference values can be steady-state values (if available) or some typical long-term averages. In this paper, we assume that the reference values of inflation and nominal interest rate are 0.02 and 0.04, respectively. Hence, the level inflation and interest rates will be and , respectively. We will use I to denote the level interest rate.
- IV.
- Exchange rate is the log ratio ofIt can be viewed as an aggregate measure of the strength of a country’s currency. If the local currency weakens, then increases. That is, a larger value of implies real depreciation: the domestic goods become relatively cheaper when is large. Conversely, if decreases, the local currency strengthens, hence the domestic goods become relatively more expensive.
3.3. How Can the Viability Kernel Be Used by the Domestic Central Bank?
4. Calibrated Qualitative Monetary Policy NA-Game
5. Viability Analysis: Parameter-Specific Solutions
5.1. A Method for the Determination of Viability Kernels
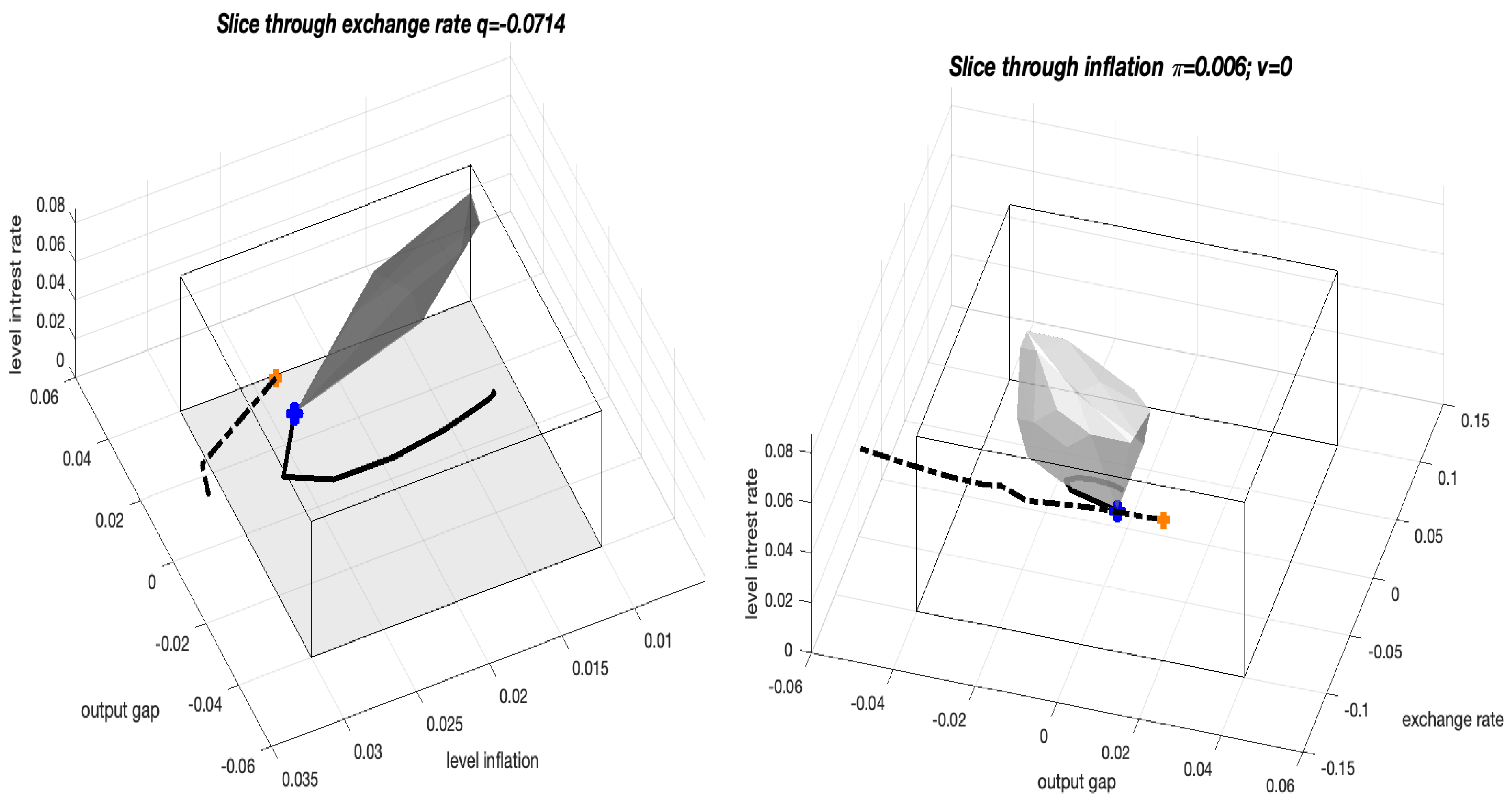
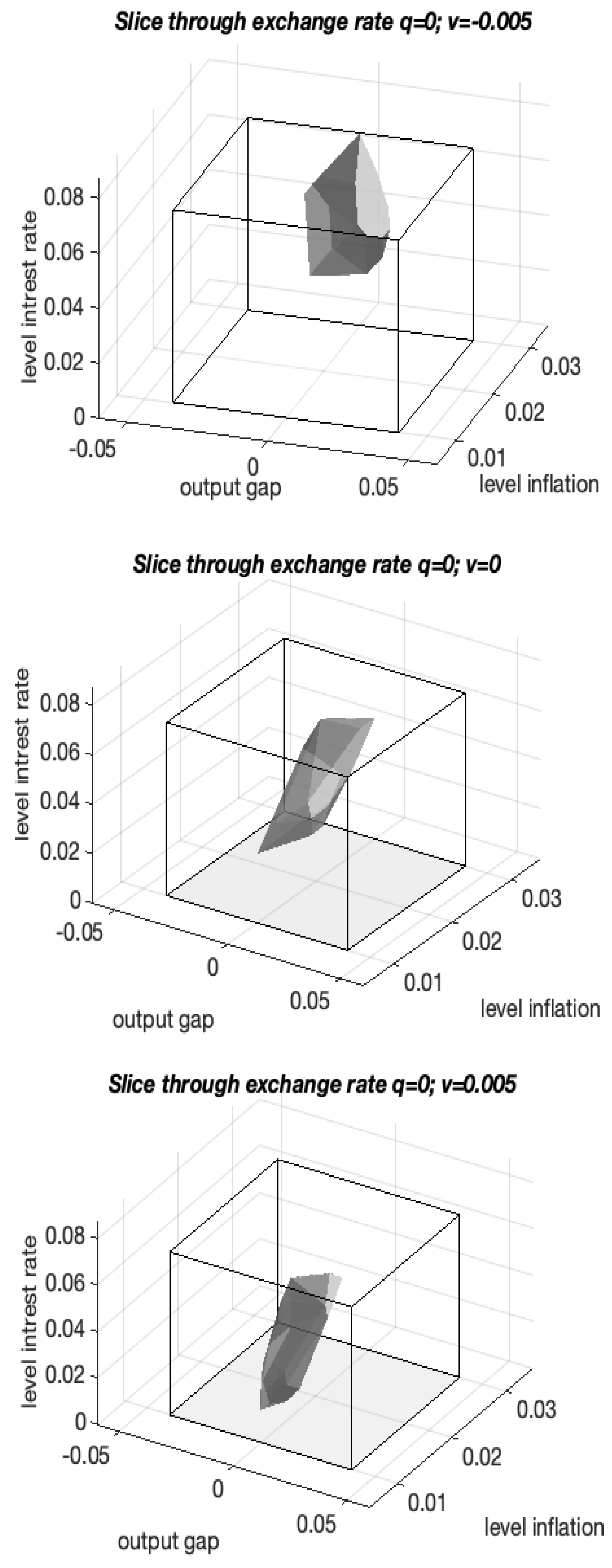
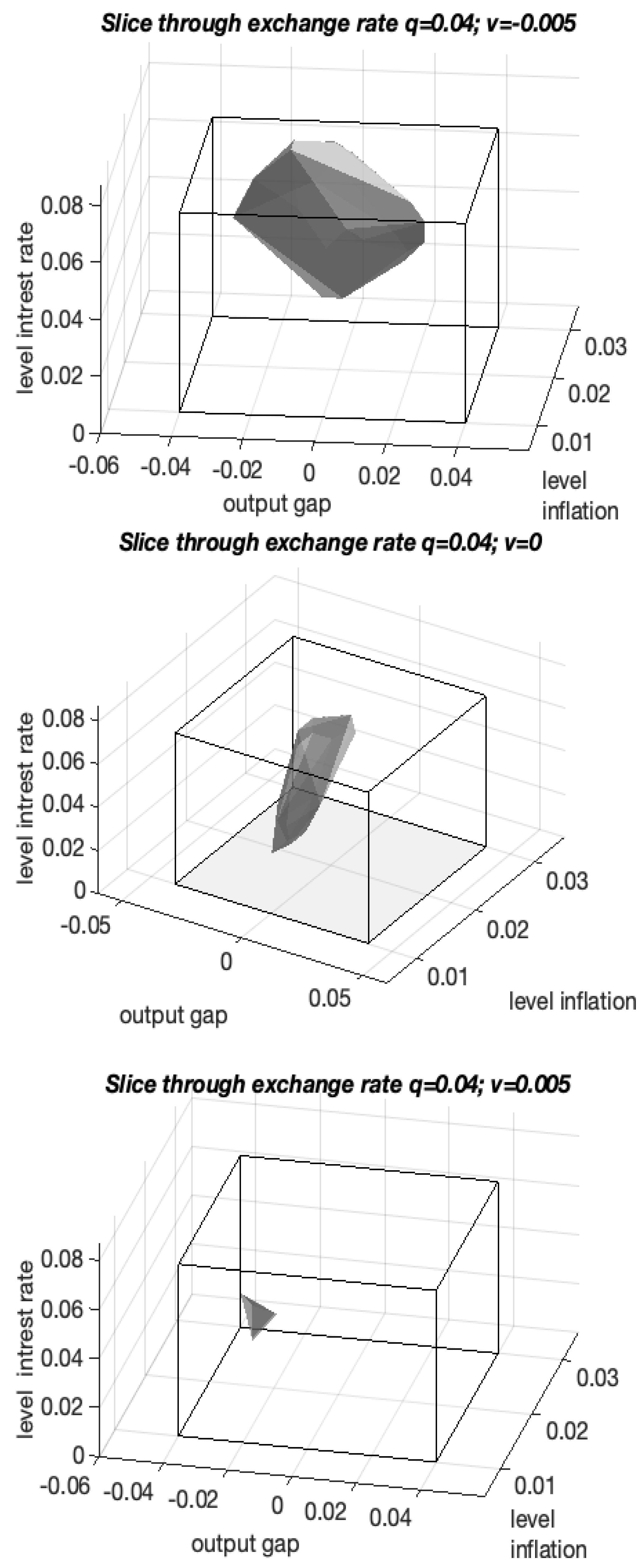
5.2. Analysing Monetary Policy in Four Dimensions
5.3. How to Interpret a 3D Projection of a 4D Kernel
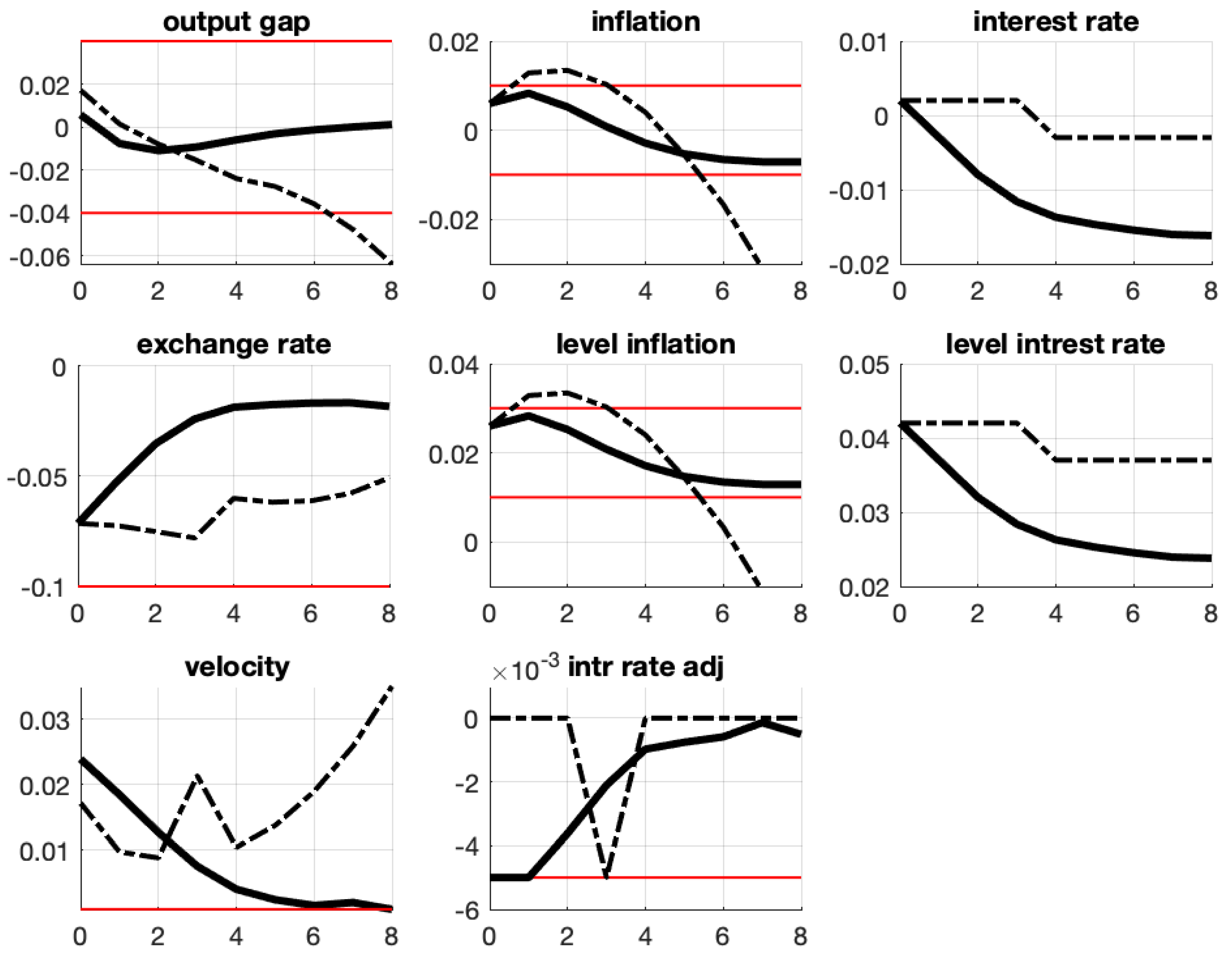
6. Impact of Foreign Real Interest Rate on the Domestic Economy
6.1. Neutral Exchange Rate
- the bank should keep the domestic interest rate close to the upper limit when the foreign real interest rate is negative;
- the bank should keep the domestic interest rate close to the lower limit when the foreign real interest rate is positive.
6.2. Undervalued and Overvalued Currency
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Viable Areas
Appendix B. Exchange Rate Responsiveness to Interest Rate Adjustments
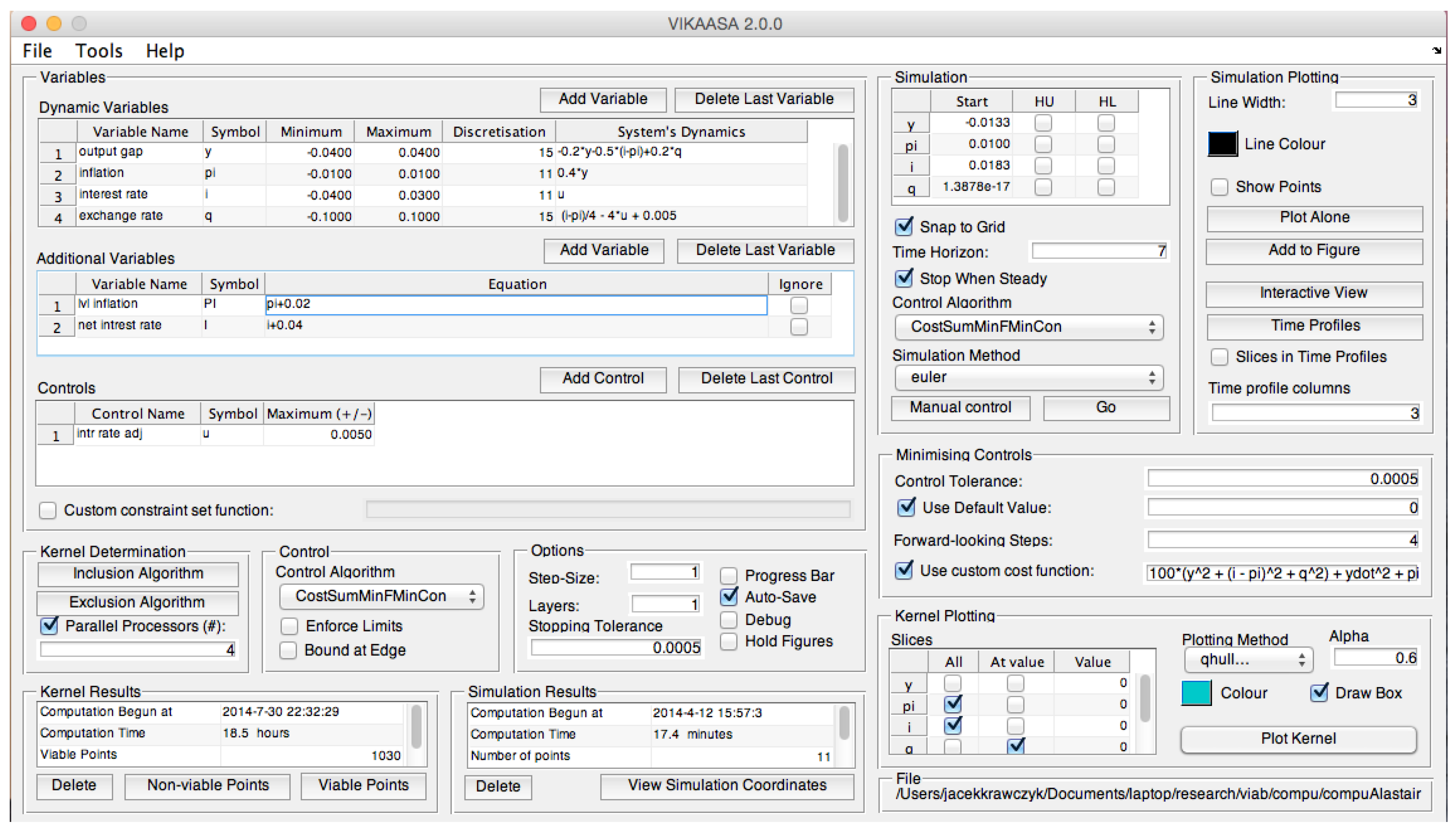
Appendix C. VIKAASA
| 1 | This paper draws from [1]. |
| 2 | In the two-person game context, we cannot use the gender-neutral pronoun their to describe a singular player action. Instead, we will use he and his to refer to a single genderless agent. |
| 3 | |
| 4 | Viability is normally defined for an infinite time horizon, but it is also possible to define , and consider viability in finite-time. |
| 5 | The parameter notation is chosen to reflect some compatibility of our model with Batini-Haldane’s discrete-time model in [39]. |
| 6 | This is the reason we refer to our game as a nuisance agent game. |
| 7 | This algorithm (called the inclusion algorithm, see [9]) employed by VIKAASA will miss any viable points that cannot reach a steady state; e.g., because they form (large) orbits. However, experimenting with our monetary policy models, which consisted of using different discretisation grids and trying various controls did not lead to the discovery of points like that. |
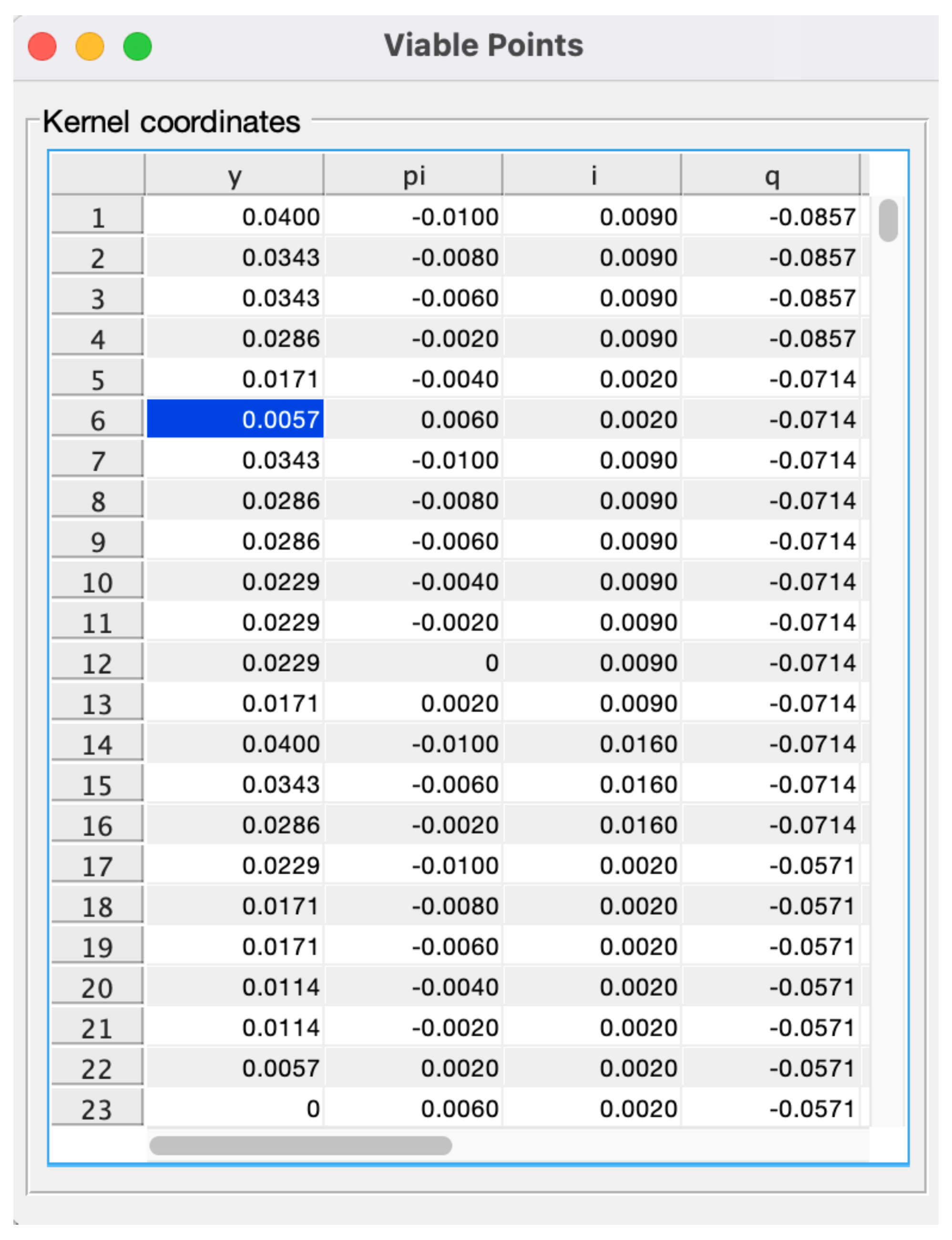
| 8 | The total number of rows of the array for the selected discretisation (see Appendix C) is 683. |
| 9 | The penultimate subplot is the economy’s velocity norm, i.e., the sum of absolute values of the right-hand sides of (20)–(23). We consider this number a measure of an aggregate system’s velocity and call it velocity in the figure. If this velocity is close to zero, the economy has approached a steady state. If the steady-state is inside and no state variable has ever breached the bounds of K then the evolution starting point is viable; refer to Appendix C. |
| 10 | See [37] for a discussion on building systemic resilience in the context of viability theory. |
| 11 | Let denotes the set of proximal normals to D at x i.e., the set of such that the distance of to D is equal to |
| 12 | If D were a disc, then a contingent cone at any point of the circumference would be a half-space. When is an interior point of D, then the contingent cone for this point is the whole space. |
| 13 | VIKAASA stands for Viability Kernel Approximation, Analysis and Simulation Application = VIKAASA, which happens to be a Sanskrit word that means “progress” or “development”. |
| 14 | VIKAASA is also compatible with GNU Octave, but without the GUI. See the manual for more information. |
References
- Krawczyk, J.B.; Kim, K. An analysis of monetary policy of a small open economy with a ‘nuisance’ agent. In Proceedings of the Conference Maker, 20th International Conference on Computing in Economics & Finance, Oslo, Norway, 22–24 June 2014. [Google Scholar]
- Cardaliaguet, P.; Quincampoix, M.; Saint-Pierre, P. Set valued numerical analysis for optimal control and differential games. In Stochastic and Differential Games. Annals of the International Society of Dynamic Games; Birkhäuser: Boston, MA, USA, 1999; Volume 4, pp. 177–274. [Google Scholar]
- Hertwig, R.; Hoffrage, U. Simple Heuristics in a Social World; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Beckenkamp, M. Playing Strategically against Nature?—Decisions Viewed from a Game-Theoretic Frame; MPI Collective Goods: Bonn, Germany, September 2008. [Google Scholar]
- Hansen, L.P.; Sargent, T.J.; Turmuhambetova, G.; Williams, N. Robust control and model misspecification. J. Econ. Theory 2006, 128, 45–90. [Google Scholar] [CrossRef]
- Dennis, R.; Leitemo, K.; Söderström, U. Methods for robust control. J. Econ. Dyn. Control 2009, 33, 1604–1616. [Google Scholar] [CrossRef]
- Dennis, R.; Leitemo, K.; Söderström, U. Monetary Policy in a Small Open Economy with a Preference for Robustness; Working Paper 2007-04; Federal Reserve Bank of San Francisco: San Francisco, CA, USA, 2009. [Google Scholar]
- Žaković, S.; Rustem, B.; Wieland, V. A Continuous Minimax Problem and its Application to Inflation Targeting. In Decision and Control in Management Science; Zaccour, G., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Krawczyk, J.B.; Pharo, A.; Serea, O.S.; Sinclair, S. Computation of viability kernels: A case study of by-catch fisheries. Comput. Manag. Sci. 2013, 10, 365–396. [Google Scholar] [CrossRef]
- Krawczyk, J.B.; Kim, K. Viable stabilising non-Taylor monetary policies for an open economy. Comput. Econ. 2014, 43, 233–268. [Google Scholar] [CrossRef]
- Aubin, J.P.; Bayen, A.M.; Saint-Pierre, P. Viability Theory: New Directions, 2nd ed.; Springer: Berlin, Germany, 2011. [Google Scholar] [CrossRef]
- Aubin, J.P.; Da Prato, G.; Frankowska, H. Set-Valued Analysis; Springer: Berlin, Germany, 2000. [Google Scholar]
- Krawczyk, J.B.; Kim, K. “Satisficing” Solutions to a Monetary Policy Problem: A Viability Theory Approach. Macroecon. Dyn. 2009, 13, 46–80. [Google Scholar] [CrossRef]
- The Economist. Why the Federal Reserve Has Made a Historic Mistake on Inflation. The Economist, 23 April 2022. [Google Scholar]
- Krawczyk, J.B.; Sethi, R. Satisficing Solutions for New Zealand Monetary Policy; Technical report, Reserve Bank of New Zealand, No DP2007/03; Reserve Bank of New Zealand: Wellington, New Zealand, 2007.
- Béné, C.; Doyen, L.; Gabay, D. A viability analysis for a bio-economic model. Ecol. Econ. 2001, 36, 385–396. [Google Scholar] [CrossRef]
- De Lara, M.; Doyen, L.; Guilbaud, T.; Rochet, M.J. Is a management framework based on spawning stock biomass indicators sustainable? A viability approach. ICES J. Mar. Sci. 2007, 64, 761–767. [Google Scholar] [CrossRef][Green Version]
- Martinet, V.; Doyen, L. Sustainability of an economy with an exhaustible resource: A viable control approach. Resour. Energy Econ. 2007, 29, 17–39. [Google Scholar] [CrossRef]
- Martinet, V.; Thébaud, O.; Doyen, L. Defining viable recovery paths toward sustainable fisheries. Ecol. Econ. 2007, 64, 411–422. [Google Scholar] [CrossRef]
- Pujal, D.; Saint-Pierre, P. Capture Basin Algorithm for Evaluating and Managing Complex Financial Instruments. In Proceedings of the 12th International Conference on Computing in Economics and Finance, Limassol, Cyprus, 22–24 June 2006. [Google Scholar]
- Krawczyk, J.B.; Sissons, C.; Vincent, D. Optimal versus satisfactory decision making: A case study of sales with a target. Comput. Manag. Sci. 2012, 9, 233–254. [Google Scholar] [CrossRef]
- Clément-Pitiot, H.; Doyen, L. Exchange Rate Dynamics, Target Zone and Viability; Université Paris X Nanterre: Nanterre, France, 1999. [Google Scholar]
- Krawczyk, J.B.; Kim, K. A Viability Theory Analysis of a Macroeconomic Dynamic Game. In Proceedings of the Eleventh International Symposium on Dynamic Games and Applications, Tucson, AZ, USA, 4 December 2004. [Google Scholar]
- Clément-Pitiot, H.; Saint-Pierre, P. Goodwin’s models through viability analysis: Some lights for contemporary political economics regulations. In Proceedings of the 12th International Conference on Computing in Economics and Finance, Limassol, Cyprus, 22–24 June 2006. [Google Scholar]
- Bonneuil, N.; Saint-Pierre, P. Beyond Optimality: Managing Children, Assets, and Consumption over the Life Cycle. J. Math. Econ. 2008, 44, 227–241. [Google Scholar] [CrossRef]
- Bonneuil, N.; Boucekkine, R. Viable Ramsey economies. Can. J. Econ./Revue Can. D’économique 2014, 47, 422–441. [Google Scholar] [CrossRef]
- Krawczyk, J.B.; Judd, K.L. A note on determining viable economic states in a dynamic model of taxation. Macroecon. Dyn. 2016, 20, 1395–1412. [Google Scholar] [CrossRef]
- Kim, K.; Krawczyk, J.B. Sustainable Emission Control Policies: Viability Theory Approach. Seoul J. Econ. 2017, 30, 291–317. [Google Scholar]
- Krawczyk, J.B.; Serea, O.S. When can it be not optimal to adopt a new technology? A viability theory solution to a two-stage optimal control problem of new technology adoption. Optim. Control Appl. Methods 2013, 34, 127–144. [Google Scholar] [CrossRef]
- Krawczyk, J.B.; Pharo, A. Viability theory: An applied mathematics tool for achieving dynamic systems’ sustainability. Math. Appl. 2013, 41, 97–126. [Google Scholar]
- Aubin, J.P. Viability Theory; Systems & Control: Foundations & Applications; Birkhäuser: Boston, MA, USA, 1991. [Google Scholar] [CrossRef]
- Quincampoix, M.; Veliov, V.M. Viability with a target: Theory and Applications. In Applications of Mathematics in Engineering; Heron Press: Rubery, UK, 1998; pp. 47–58. [Google Scholar]
- Veliov, V.M. Sufficient conditions for viability under imperfect measurement. Set-Valued Anal. 1993, 1, 305–317. [Google Scholar] [CrossRef]
- Simon, H.A. A Behavioral Model of Rational Choice. Q. J. Econ. 1955, 69, 99–118. [Google Scholar] [CrossRef]
- Martinet, V.; Thébaud, O.; Rapaport, A. Hare or Tortoise? Trade-offs in Recovering Sustainable Bioeconomic Systems. Environ. Model. Assess. 2010, 15, 503–517. [Google Scholar] [CrossRef]
- Doyen, L.; Saint-Pierre, P. Scale of viability and minimal time of crisis. Set-Valued Anal. 1997, 5, 227–246. [Google Scholar] [CrossRef]
- Karacaoglu, G.; Krawczyk, J.B. Public policy, systemic resilience and viability theory. Metroeconomica 2021, 72, 826–848. [Google Scholar] [CrossRef]
- Isaacs, R. Differential Games; Wiley: New York, NY, USA, 1965. [Google Scholar]
- Batini, N.; Haldane, A. Monetary policy rules and inflation forecasts. In Bank of England Quarterly Bulletin; Bank of England: London, UK, 1999. [Google Scholar]
- Walsh, C. Monetary Theory and Policy; MIT Press: Boston, MA, USA, 2003. [Google Scholar]
- Svensson, L. Open-economy inflation targeting. J. Int. Econ. 2000, 50, 155–183. [Google Scholar] [CrossRef]
- Eaton, J.; Turnovsky, S.J. Covered Interest Parity, Uncovered Interest Parity and Exchange Rate Dynamics. Econ. J. 1983, 93, 555–575. [Google Scholar] [CrossRef][Green Version]
- Batini, N.; Haldane, A. Forward-looking rules for monetary policy. In Monetary Policy Rules; Taylor, J.B., Ed.; National Bureau of Economic Research: Cambridge, MA, USA, 1999; pp. 157–202. [Google Scholar] [CrossRef]
- Gaitsgory, V.; Quincampoix, M. Linear Programming Approach to Deterministic Infinite Horizon Optimal Control Problems with Discounting. SIAM J. Control Optim. 2009, 48, 2480–2512. [Google Scholar] [CrossRef]
- Krawczyk, J.B.; Pharo, A. Manual of VIKAASA 2.0: An Application for Computing and Graphing Viability Kernels for Simple Viability Problems; SEF Working Paper 08/2014; Victoria University of Wellington: Wellington, New Zealand, 2014. [Google Scholar]
- Krawczyk, J.B.; Pharo, A.S. Viability Kernel Approximation, Analysis and Simulation Application—VIKAASA Code. 2014. Available online: https://github.com/socsol/vikaasa (accessed on 17 August 2022).
- Cardaliaguet, P.; Quincampoix, M.; Saint-Pierre, P. Set-Valued Numerical Analysis for Optimal Control and Differential Games. Ann. Int. Soc. Dyn. Games 1999, 4, 177–247. [Google Scholar] [CrossRef]

| 0.01 | 0.02 | 0.023 | 0.04 | 0.056 | 0.07 | |
| 0.01 | 0.03 | −0.034 | 0.028 | 0.035 | 0.07 |
| 0.01 | 0.03 | −0.016 | 0.032 | 0.035 | 0.056 | |
| 0.01 | 0.03 | −0.032 | 0.008 | 0.021 | 0.042 |
| 0.01 | 0.03 | −0.029 | 0.029 | 0.007 | 0.042 | |
| 0.022 | 0.03 | −0.04 | −0.023 | 0.014 | 0.021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krawczyk, J.B.; Petkov, V.P. A Qualitative Game of Interest Rate Adjustments with a Nuisance Agent. Games 2022, 13, 58. https://doi.org/10.3390/g13050058
Krawczyk JB, Petkov VP. A Qualitative Game of Interest Rate Adjustments with a Nuisance Agent. Games. 2022; 13(5):58. https://doi.org/10.3390/g13050058
Chicago/Turabian StyleKrawczyk, Jacek B., and Vladimir P. Petkov. 2022. "A Qualitative Game of Interest Rate Adjustments with a Nuisance Agent" Games 13, no. 5: 58. https://doi.org/10.3390/g13050058
APA StyleKrawczyk, J. B., & Petkov, V. P. (2022). A Qualitative Game of Interest Rate Adjustments with a Nuisance Agent. Games, 13(5), 58. https://doi.org/10.3390/g13050058





