1. Introduction
Recently, online rating systems have become a significant part of potential customers’ decisions. According to a survey [
1], 90% of consumers used the Internet to find a local business in 2019, businesses without 5-star ratings risk losing 12% of their customers, and only 53% of people would consider using a business with less than 4-star ratings. Due to the importance of such ratings, fraudulent users attempt to impact the rating of a service (arating system can be applied to different entities such as a service, product, community, or a business. For the rest of the paper, we refer to such an entity as a service) by submitting fake scores. For example, a fraudulent service owner would submit fake 5-star ratings to increase their service’s aggregated rating, as depicted in
Figure 1. On the other hand, a fraudulent competitor would submit fake low ratings to subvert rivals’ reputation. Moreover, rating systems are vulnerable to sybilattacks in which a fraudulent entity can forge fake users and utilize them for fake ratings. Such a vulnerability caused the advent of companies offering on-demand fake reviews and ratings [
2].
To support consumers and services, the US Federal Trade Commission (FTC) takes legal actions against fake reviewers [
3]. Furthermore, rating platform providers such as Amazon, Google, and Yelp have restricted policies for fake reviews and banned incentivized reviews in which a service owner provides incentives in return for positive reviews [
4,
5,
6].
Different safeguards can be implemented to reduce the number of fake reviews. For instance, a review platform can verify the identity of a reviewer before allowing the review submission, and a reviewer should have a valid email address and phone number. Furthermore, review platforms can use machine-learning tools to detect and remove fake reviews [
7]. Although filters for checking the authenticity of reviews are necessary, studies show that still many reviews and ratings are fake, and filters cannot prevent them [
8,
9]. On the other hand, despite the fact that sybil attacks have been widely studied in various networks [
10,
11,
12], such studies especially targeted towards preventing sybil attacks on rating systems are few and far between.
The detection of fake reviews using machine-learning techniques has been studied widely in the literature [
13,
14,
15,
16]. These methods use the linguistic features of a review, metadata associated with a review, and the service history to check the validity of reviews. However, the task of detecting fake ratings is more challenging, mainly due to the fact that users might have different preferences or expectations for a service. For instance, two authentic and independent users might receive the same service and truthfully rate it quite differently (1 star vs. 5 stars). It is difficult to detect if one of these ratings is fake or that they are just simply referring to different aspects of a service (e.g., quality of food vs. air conditioning in a restaurant). On the other hand, Monaro et al. [
17] studied the detection of fake 5-star ratings using mouse movements. This study discovered users spend more time and wider mouse trajectories to submit false ratings.
Considering the lack of an appropriate safeguard to prevent fake ratings, in this paper, we take a novel mechanism-design approach to increase the fraudulent users’ cost for submitting fake ratings while providing incentives for honest raters. Our proposed mechanism, RewardRating, is inspired by the stock market in which reviewers can invest in their ratings for services and receive a reward on the basis of their investments. RewardRating is equipped with a profit-sharing scheme to satisfy incentive compatibility and budget-balanced properties. In contrast with previous works, in this study, we propose a novel mechanism design approach to improve the quality of the aggregated ratings for the services by increasing the cost for fake ratings while incentivizing honest ratings. Our proposed mechanism’s goal is not to detect fake ratings but to incentivize honest ratings. The main contributions of this paper are the two parts:
We propose a new mechanism to increase the cost of fake ratings for fraudulent users while providing incentives for honest users.
We investigate an incentive-compatible self-sustained profit-sharing model for a rating system.
2. System Model
Let be the strictly totally ordered set that represents rating scores that reviewers can assign to a service. We indicate a rating is higher than () if and only if . For example, in the Google review system, n is 5, and indicates a 5-star rating, which is a higher rating compared to , which represents a 2-star rating. For the sake of simplicity and without loss of generality, we consider for the examples that we present in the rest of the paper. Let represent the set of reviewers who submit ratings for a service. There is no limitation on the number of reviewers. Moreover, a reviewer can submit multiple ratings under different identifiers for the same service. In other words, the system is vulnerable to a sybil attack. For example, a service owner can submit unlimited 5-star ratings for themselves or a competitor can submit unlimited 1-star ratings for a rival service. This can be achieved by recruiting fake reviewers.
Reviewers submit ratings to obtain their desired outcomes. We assumed that there were three types of reviewers based on their intents:
Attacker—submits false ratings to change the aggregated rating score to their preference. For example, a restaurant owner wants to increase their restaurant’s rating score by submitting fake 5-star ratings or a competitor submits fake 1-star ratings to adversely impact the aggregated rating score.
Honest—submits the rating truthfully on the basis of the evaluation of a service’s quality.
Strategic—submits the rating to increase their payoff from the system.
The main objective of the mechanism is to decrease the number of fake ratings by increasing the cost for attackers. On the other hand, we want to provide incentives for honest reviewers and motivate strategic players to invest in an honest rating. We aim to achieve these goals by producing a market where reviewers invest in their ratings, and the rating system rewards the reviewers on the basis of future investments.
3. Marketizing Ratings
The main idea of RewardRating is to create a market for ratings where reviewers invest in their ratings. This idea is inspired by the stock market. In the stock market, investors invest in a business on the basis of their prediction of a business’s performance in the future when they want to sell their stocks.
Mapping this to the rating system, in RewardRating, reviewers invest in a service’s performance. To clarify this, let us continue with an example:
Assume Alice goes to a restaurant and she is happy about the restaurant’s service. Alice thinks this restaurant deserves a 5-star rating. However, the current aggregated rating for this restaurant is 3 stars. Using the RewardRating mechanism, Alice can invest in a 5-star score for the restaurant’s service. If future reviewers agree with Alice and rate the restaurant higher than 3 stars, then Alice has made a successful investment, and as a result, she receives a reward from the system.
3.1. Requirements
RewardRating should satisfy the following requirements:
Budget-Balanced: The system should be self-sustained, as there are no external financial subsidies. In other words, the total asset in the system should be supported by the reviewers.
Incentive-Compatibility: The system should provide incentives for honest reviewers (i.e., truthful ratings). On the other hand, the system should increase the cost for attackers (i.e., fraudulent ratings).
3.2. Mechanism Narrative
Specifying requirements, now let us study the design of a mechanism that satisfies these properties. The design objective is to place a set of rules for the rating system’s game to meet the aforementioned requirements. A mechanism can be specified by a game where is the set of possible input messages, and is the set of possible outputs of the mechanism. In the rating system model, players are reviewers. A player chooses their strategy to increase their utility. A player’s strategy (i.e., the mechanism’s input), is the rating, corresponding investment, and the time of investment. Lastly, the mechanism’s output is the aggregated rating of the service and the reviewers’ profit.
In RewardRating, each rating is accompanied by a corresponding stock value. Reviewers can invest in a rating for a service by buying the stock associated with it. Let us use the term cointo represent the smallest unit that a user can invest in for such a rating stock. A new coin is minted for a rating’s stock when a reviewer requests to buy such a coin from the rating system (here, coins are virtual assets, and minting a new coin means that the system adds to the total value of a rating’s stock). The price of buying a coin from the system is fixed. Users can sell their coins to the rating system. The selling price of a coin is also fixed; however, the price of buying a coin from the system is higher than the price of selling a coin to the system. The difference in the buying price and selling price is a fund that is shared among stakeholders as profit.
We discuss the details and the reasoning behind the design decisions in the next sections.
Figure 2 and
Figure 3 demonstrate the overall picture of buying or selling coins from or to the rating system.
3.3. Mechanism Components
In this section, we formally define the components of the RewardRating mechanism. Let represent the set of n types of coins for ratings available in the rating system, such that represents coins for score . Let represent the price of buying a coin from the system. Let represent the number of coins that user owns in the rating system at time t. Let represent the stakeholders in the rating system at time t. Once a user pays to the rating system to buy a new coin , the system mints a new coin and updates the stakeholder list accordingly.
On the other hand, users can sell their coins to the rating system. Let represent the price that the rating system pays to a user in return for a coin. Then, we have in RewardRating. Here, is a profit that the system earns from selling a new coin. Such a profit is distributed among stakeholders as a reward. Once a user sells a coin to the system, the system removes that coin from the corresponding rating stock and updates the stakeholder list.
For example, assume buys a new coin of a 4-star rating with the price of (i.e., ). Assume decides to sell their coin to the rating system later on, and the price of selling a coin is (i.e., ). Then, receives from the rating system. In this example, the system earns profit (i.e., ), which is shared among stakeholders. Only the profit of the first minted coin of a service is earned by the rating system’s owner. This is due to the fact that, for the first coin, there is no previous stakeholder to earn the profit.
Let
represent the number of
coins minted in the rating system at time
t. Let
be the aggregated score of a service at time
t. The system calculates
on the basis of the total investments in the rating stocks for a given service as follows:
In other words, the aggregated score of a service is calculated on the basis of the total investments on ratings’ stocks.
Profit Sharing
RewardRating collects a profit from minting every new coin. This profit is the difference in the price of buying a new coin by a user from the rating system and the price of selling that coin to the rating system, which can be calculated as . The mechanism strategically distributes such a profit among stakeholders to satisfy the mechanism requirements. The main challenge here is to minimize the profit that attackers can earn from the system. If attackers earn profit from the system, then RewardRating encourages attackers instead of honest reviewers. This is a big challenge, as it is hard to distinguish between honest users and attackers in the system.
To solve this problem, we consider the fact that, if a service’s rating is affected by a fake rating, then the aggregated rating is biased toward the direction of the fake rating.
For example, if attackers submitted fake 5-star ratings, then the aggregated rating is biased toward 5 stars, and if attackers submitted fake 1-star ratings, then the aggregated score is biased toward 1-star ratings. Considering this fact, our proposed system shares the profit of a new minted coin as follows:
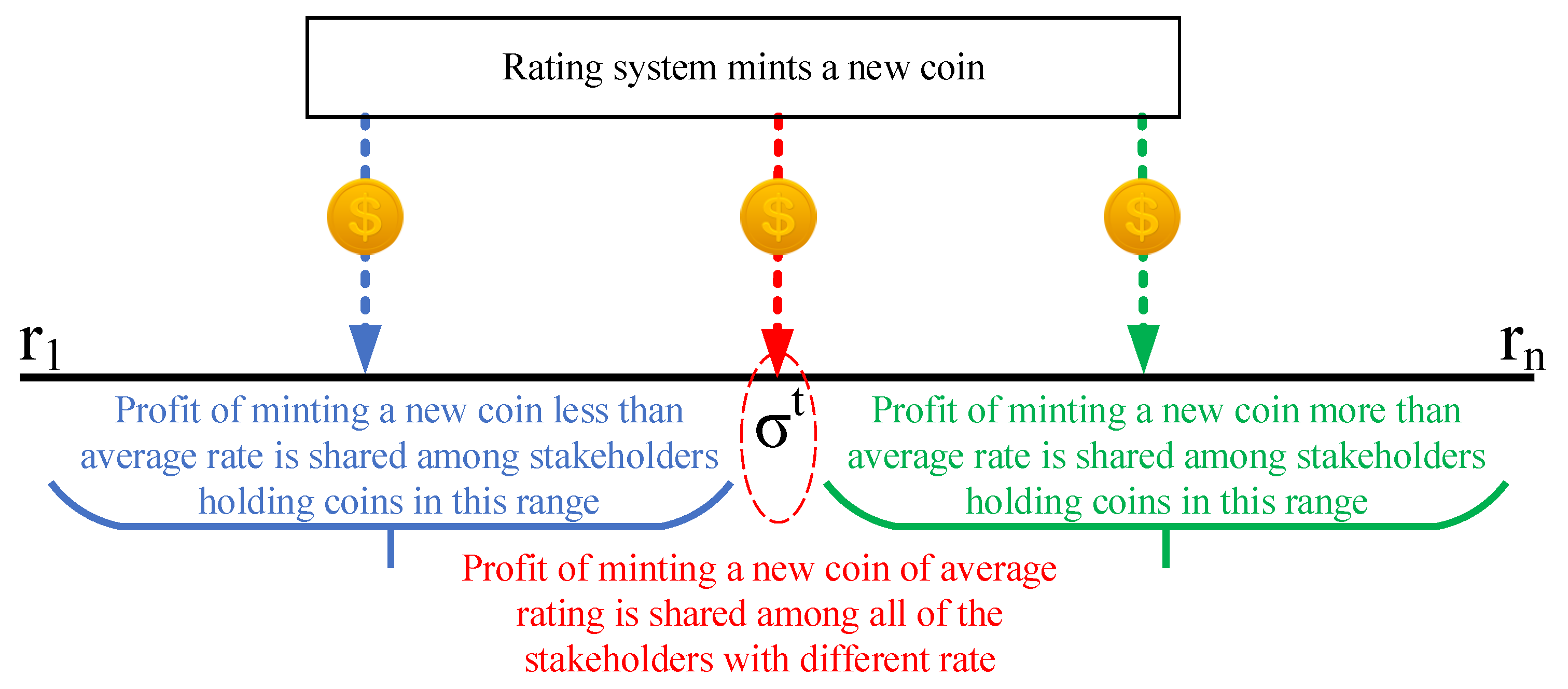
If the new minted coin is higher for rates than the aggregated score, this in turn increases the aggregated score. In this case, the profit of the new minted coin is shared among those stakeholders holding coins of higher rates than the current aggregated rating.
If the new coin is for lower rates than the aggregated score, this in turn decreases the aggregated score. In this case, the profit of the new minted coin is shared among those stakeholders holding coins of lower rates than the current aggregated rating.
If the new coin matches the aggregated rating, then the aggregated score does not change, and the profit is shared among all of the rating system’s stakeholders. This case is rare, as the coin types (i.e., the options for ratings) do not necessarily match the number of possible values for the aggregated score. For example, in the Google review system, we assumed that users have 5 options for selecting rates (1 star, …, 5 stars); however, the aggregated rating has 1 decimal point, which produces 50 possible options for the aggregated score.
Such a profit sharing model is depicted in
Figure 4. To model this profit sharing, first, we need to define a set of stakeholders who earn profit from the system once there is a new investment. Let
represent the type of a new minted coin at time
t. Let
represents the set of indices of ratings’ stocks which their stakeholders are rewarded for the new minted coin
. In other words, a user does not receive a reward if they do not own a rating coin in the set of
when a new coin
is minted at time
t. Then, we model
as:
RewardRating distributes the profit in a way such that stakeholders are earning more profit if they have the rating coins closer to the rating of the new minted coin. In other words, with the growth of distance between
j (i.e., new minted coin’s rating index) and
(i.e., the index of a stakeholder’s coin which is eligible for reward), the profit for a stakeholder of a coin
is decreasing. To model this, let
represent a function, such that
, which indicates that, with the increase in the distance between
w and
j, the value of
decreases. Functions
and
are two candidates for
:
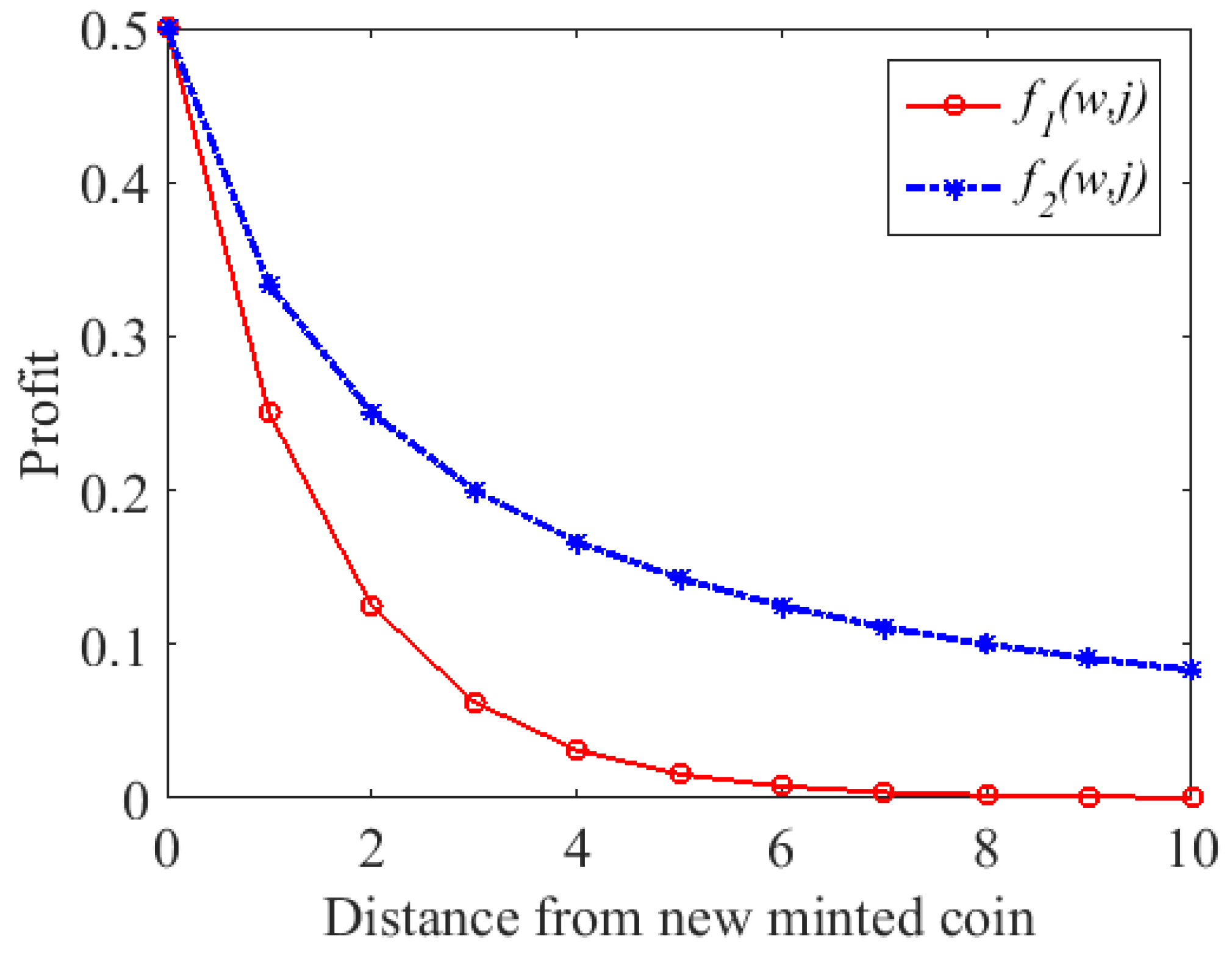
Figure 5 shows the profit sharing of a new coin using
and
candidate functions. As can be seen, with the increase in the distance of a new coin’s rating and the rating of a stakeholder’s coin, the share of profit decreases.
Let
represent the profit a user earns from staking a coin
at time
t. Then,
RewardRating calculates
as follows:
To keep the system budget-balanced and simple, we assumed that there is a defined decimal point for the receiving profit, and the remainder of profit is received by the rating system’s owner. For example, we can set 2 decimal points for the reward; in this case, if we need to divide to three stakeholders with the equal share, each of stakeholders receives , and the rating system’s owner receives as a profit.
This design provides incentives for the reviewers who correctly predict the future investments in ratings same as stock market. We analyze the benefits of such a profit-sharing model in the next section. The following example is given to clarify the profit-sharing scheme.
3.4. Example
Assume that
RewardRating’s parameters were set for a restaurant as
, and
. The profit of selling the first coins is given to the rating system. Assume that, at time
t, we have
, and
. In this case, the aggregated score is:
Assuming that we set 2 decimal points for the aggregated score, then we have
. The restaurant owner is fraudulent and wants to improve the restaurant’s rating; therefore, they buy a
coin. For the purchase of a
coin, 1 profit is shared among the stakeholders of coins
, and
following Equation (
2). Therefore, the owner of the
coin receives
, and the owner of a
coin receives
as a reward following Equation (
5). Then, the aggregated score updates to
. Later on, an honest user predicts that the aggregated score of the service will be decreased and they buy a
coin. At this point, the reward is shared among stakeholders of coins
, and
following Equation (
2). In this case, the owner of a
coin receives
and the owner of a
coin receives
and the rating system receives the
profit. Then, the aggregated score updates to
.
4. Mechanism Analysis
In this section, we analyze RewardRating. We check budget-balanced and incentive-compatibility features. Afterward, we investigate the increase in attackers’ cost. Lastly, we discuss the limitations.
Proposition 1. RewardRating satisfies the budget-balanced property.
Proof. We need to show that the total input assets into the system is equal to the total output. Input assets to the system are total coins the system sells to users, and total output is the money that the system pays to the users to buy their coins in addition to the profit, which is shared among users and the reward system. For every coin, we have
; if we show that the total profit shared among all of the stakeholders for all of their coins is equal to
, then we can conclude that the system is budget-balanced. The profit of selling the first coin is received by the reward system. For every new minted coin
, the total profit that is shared among stakeholders is as follows:
□
Proposition 2. RewardRating satisfies the incentive-compatibility property as long as honest users participate in the rating process irrespective of attackers and strategic user investment.
Proof. For incentive-compatibility, we need to show that RewardRating provides incentives for honest reviewers and increases the cost for attackers. The goal of the RewardRating system is not to satisfy the strategic users. More specifically, the RewardRating game can be classified as follows:
Sequential: when players choose their actions consecutively.
Perfect: when players are aware of the previous players’ actions.
Noncooperative: when players compete to earn more profit.
Incomplete information: when players do not have complete knowledge about the number of players and future ratings.
As the number of players, their types (i.e., honest, attackers, and strategic), and their rating strategies are unknown, this game is classified as an Incomplete-information game. Therefore, we analyze the strategic player’s best response strategy considering different estimations for future investments. As there are three type of players, namely, honest, attackers, and strategic, in our system model, we sketched the proof by analyzing the payoff for each type of players. For honest users, RewardRating produces profit as long as other honest users participate in the rating process. This is due to the fact that honest users are rewarded by the new honest ratings. However, honest raters who rate closer to the majority’s rate of future raters earn more. RewardRating increases the cost of attack as attackers should buy coins from the system. This is because, when attackers invest in fake scores, the aggregated score is changed toward a lower or a higher score. As a result, the majority of honest reviewers invest in the opposite direction, and attackers do not profit from such investments based on the profit-sharing model. For strategic users, the best response strategy is to invest in a coin in which there is more profit. Therefore, as long as the profit earned from choosing the honest rating is higher than that from other ratings, the best response strategy is to not rate on attacker’s side. On the other hand, if the strategic user estimates that the profit of investing on attacker’s side is higher, then a strategic user would invest in the attacker’s side to achieve more profit. However, the profit that the system earns from selling coins to attackers is shared among strategic users as well, following the profit-sharing model. In this case, the system increases the cost for attackers, and attackers endure more cost. This does not negatively affect honest users as they receive their profit from future honest users. Such a profit is not shared among attackers and strategic users who chose the attacker’s side. Therefore, although the valid estimation of the aggregated rating is not fulfilled, the system still satisfies the incentive-compatibility feature while causing extra cost for the attacker. Therefore, the proposed mechanism satisfies the incentive-compatibility feature as long as honest users participate in the rating process irrespective of attackers and strategic user investment. □
4.1. Attacker’s Cost
In this section, we analyze the cost for an attacker to increase the aggregated rating. In this experiment, the initial honest aggregated score was set to 1, with the three different settings of having 100, 200, and 500 honest rating coins. We assumed that an attacker invests in the highest possible rating, which is 5 in our example.
Figure 6 depicts the cost of an attacker for increasing the aggregated rating. As can be seen, when an attacker wants to increase the aggregated rating by investing in the highest possible rating, the cost for an attacker grows exponentially. Therefore,
RewardRating is more efficient for services with a higher number of reviewers. This is due to the fact that, in this case, an attacker should invest in more to compensate the impact of honest ratings.
Although RewardRating can increase the cost for attackers, it cannot prevent fake ratings. Therefore, other countermeasures such as a strong authentication mechanism should be applied to reduce the fake ratings. In the case that the rating system’s policy limits one rating for each user, a reviewer should not be able to purchase more than one coin from the system.
4.2. Discussion
Although RewardRating can potentially increase the cost for fraudulent rates while stimulating honest rates, such a system cannot guarantee the actual aggregated rating for a service as well. One of the main reasons is that RewardRating requires reviewers to invest in ratings, and the aggregated rating is calculated on the basis of the amount of investments in ratings. In this case, reviewers who do not want to invest in ratings cannot participate in the rating review process. On the other hand, despite the increase in cost for attackers, they can still effectively affect the aggregated rating score. However, the main goal of the design of RewardRating is not to guarantee the actual aggregated rating, but to provide a mechanism to incentivize honest users while increasing the cost for attackers. Considering this fact, RewardRating satisfies the mechanism design requirements, and it can be accompanied by available rating systems to provide a better image for the quality of a service.
Another concern is the rate of profit that reviewers can earn from future investments. As the number of stakeholders increases, the profit earned from each new investment decreases. Thus, strategic users do not participate in the rating process when the profit they can earn is less than what they can earn in other markets. On the other hand, new honest users are reluctant to invest in ratings as the amount of profit that they can make is not competitive. To overcome the aforementioned problem, the system should set a fixed value for the total profit that can be earned from staking a coin. Once this profit is achieved, the system automatically buys the coin from the corresponding stakeholder. In this case, the aggregated score should be calculated on the basis of the number of minted coins in a specified time-window as the number of coins is limited, and all of the ratings can reach a maximum number. By adding this feature, the total number of coins is fixed, and as a result, the profit that a stakeholder can earn from a new investment is stabilized. Moreover, the ratings become more dynamic as stocks are updated more quickly. On the other hand, the system should have a resource for supporting the raters’ profit from the system. This is due to the fact that, if there is no resource for supporting the raters’ profit, then the number of users owning the coins is outgrowing faster than the number of users selling their coins, which can potentially lead to a Ponzi scheme. Therefore, the system should charge the service provider and use this asset to share with raters for their profits. If the system uses another resource for raters’ profit, then the service provider is incentivized more to submit malicious rates to earn more profit while submitting fake rates. The profit sharing follows the proposed model in the previous section; however, once all the fixed numbers of coins have been purchased by raters, upon a new coin request, the system automatically purchases a coin from a stakeholder from the same stock on the basis of the first-in first-out model and using the funding resource available from the service provider as a resource for the rater’s profit. An authentication scheme needs to be applied to restrict users from purchasing more than one coin.
5. Conclusions
In this paper, we studied the challenge of designing a mechanism to increase the cost of fake ratings while incentivizing honest ratings. First, we formally modeled the requirements for having a market for the rating system. Then, we proposed RewardRating with a profit-sharing model to increase the cost for attackers while providing incentives for honest users. Our analysis shows that RewardRating satisfies budget-balanced and incentive-compatibility requirements. Our proposed mechanism can potentially increase the cost for malicious raters while stimulating honest rates. For future work, the implementation of RewardRating using the smart contract can be investigated. The policy implication of our study is that designing a secure incentive mechanism to prevent fake rates on the rating system is an extremely challenging task. To this end, the mechanism designer should carefully consider the profit-sharing model to prevent malicious raters to earn benefits from the system while providing incentives for honest raters.